Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Industrial Engineering
On-line version ISSN 2224-7890
Print version ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.23 n.3 Pretoria Jan. 2012
GENERAL ARTICLES
Forecasting modeling and simulation analysis of a power system in China, based on a class of semi-parametric regression approach
Xiaojia WangI, 1, *; Zhiqiang ChenII, 1; Shanlin YangIII, 1
IChina Key Laboratory of Process Optimization and Intelligent Decision-Making, School of Management, HeFei University of Technology, Hefei, Anhui, China. tonysun800@sina.com
IIChina Key Laboratory of Process Optimization and Intelligent Decision-Making, School of Management, HeFei University of Technology, Hefei, Anhui, China. hfut211@163.com
IIIChina Key Laboratory of Process Optimization and Intelligent Decision-Making, School of Management, HeFei University of Technology, Hefei, Anhui, China. hgdysl@gmail.com
ABSTRACT
Forecasting electricity consumption is one of the most important challenges in electricity system planning. This paper presents an improved semi-parametric regression model using the Student distribution function of residual to replace the nonparametric component of the traditional semi-parametric model, thus eliminating the effects of the residual disturbance term. Compared with general linear models, the models make statistical inferences and can automatically regulate the boundary effect, which gives the forecast result a higher accuracy. A case study using data from China is presented to demonstrate the effectiveness of the approach.
OPSOMMING
Die vooruitskatting van elektrisiteitverbruik is een van die belangrikste uitdagings in elektrisiteitstelselbeplanning. Dié artikel bevat 'n verbeterde, semi-parametriese regressie-model, wat gebruik maak van die Studentverdelingsfunksie van residuee om die nie-para-metriese komponent van die tradisionele semi-parametriese model te vervang, en sodoende die effekte van die residuversteuringsterm uit te skakel. In vergelyking met algemene lineêre modelle, kan die model statistiese afleidings maak en outomaties die grenseffek reguleer, wat lei tot groter akuraatheid van die vooruitskatting. 'n Gevallestudie wat gebruik maak van data van China demonstreer die effektiwiteit van die benadering.
Nomenclature
The notations used throughout the paper are stated below:
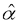 estimator of the parameter α
estimator of the parameter α
AT transpose of A
x(t) value of influence factors at time t
y electricity consumption function
N (µ,σ2) normal distribution function
EC electricity consumption
GDP gross domestic product
TEIV total import and export volume
IFA investment in fixed assets
IAV industrial added value
DI disposable income
1. INTRODUCTION
In recent decades, the total consumption of electricity in China has undergone a sustained and significant increase. According to official figures [1], during the period from 1980 to 2009, the annual rates of variation ranged from 2.97% (1980/81) to 6.79% (2008/09), while the electricity consumption in 2009, at 3.6595 χ 1012 kwh, was 1117% higher than in 1980. After the United States, China has the second largest electricity consumption rate in the world. Despite the relationship between the growth of electricity demand and certain social, economic, and policy factors, the pace of change between them is sometimes not consistent. There have been widespread electricity shortages throughout the last 60 years of Chinese history. During the 1997 Asian financial crisis, China experienced an electricity surplus for the first time. However, electricity shortages again appeared in 2002 and worsened in 2004. In 2004, 24 provinces had power shortages, and the total gap in China was 31 GW. With the rapid growth of China's economy since 2005, there has been an electricity shortage in China almost every year.
The disharmony between electricity demand and these factors in China suggests an important task. According to the factors already obtained, the demand drivers and the fundamental pillars in building a forecasting model [2-4] both need to be determined. Furthermore, methods of predicting electricity consumption precisely, effectively, and practically also need to be created. A proper solution of these problems will help to accelerate the future development of China, and also help one to understand the power operating environment, since inaccurate consumption forecasting will increase the operating costs of utility companies.
Since there is no consensus about the best approach to forecasting electricity consumption, various methods have been developed in recent years. Generally speaking, from the classification analysis of the predictive behaviour itself, the methodology for electricity consumption forecasting can be divided into three categories: numerical approximation class processing methods, statistical regression class processing methods, and intelligent optimisation class processing methods.
First, numerical approximation class processing methods (NACPM) rely solely on the variation of the data itself to find the information supporting predictive behaviour; they do not consider the effects of the other factors. Based on this view, many scholars have drawn a number of useful results. Wang et al. [5] investigated a dynamic GM (1,1) model based on the cubic spline function interpolation principle to forecast the electricity consumption of China. The authors used piecewise polynomial interpolation thought processing electricity consumption data to analyse the electricity consumption trends to make predictions. In references [6]-[7], Wang et al. use Gauss orthogonalisation theory to improve the grey prediction model, and, in constructing the grey combinative interpolation model to forecast the electricity consumption of China, they achieved good prediction results. In addition,- Wang also introduced Markov Chain theory to the grey combinative interpolation model, and constructed the Markov grey orthogonalisation model for electricity consumption prediction [8]-[9], which also obtained good prediction accuracy.
Second, statistical regression class processing methods (SRCPM) often consider the synergy of multiple factors that affect predictor variables to measure predictive behaviour. Statistical regression class methods are widely used for the electricity consumption forecasting problem. For example, Ching Lai [10] investigated the impact of weather variables on monthly electricity demand in England and Wales. A multiple regression model was developed to forecast monthly electricity demand based on weather variables, gross domestic product, and population growth. Egelioglu et al. [11] studied the influence of economic variables on the annual electricity consumption in northern Cyprus between 1988 and 1997. Through multiple regression analysis, it was found that the number of customers, the price of electricity, and the number of tourists correlated with the annual electricity consumption. Wei et al. [12] have estimated the long-term electricity load by applying system dynamics, which construct the model according to an analysis of historical electricity consumption. This method discovered the significant influence of uncertain factors such as economy and policy. Narayan and Prasad [13] studied any causal effects between electricity consumption and real GDP for 30 OECD countries, using the bootstrapped causality testing approach to show electricity consumption affecting the real GDP in Australia, Iceland, Italy, the Slovak Republic, the Czech Republic, Korea, Portugal, and the UK. They found that electricity conservation policies will negatively impact real GDP in the eight countries mentioned above and, for the remaining 22 countries of the OECD, the electricity conversation policies will not affect real GDP. Nikolopoulos et al. [14] compared multiple linear regression (MLR) with the artificial neural network, nearest neighbour analysis, and human judgment; the application results showed that the MLR was less accurate than other methods as a result of its inability to handle complex non-linearities in the relationship between the dependent variable and the cues, as well as its tendency to misaddress the in-sample data. Abdel-Aal et al. [15] applied an abductory induction mechanism (AIM) model to the domestic consumption in the eastern province of Saudi Arabia in terms of key weather parameters, demographics, and economic indicators. It was found that an AIM model, which uses only the mean relative humidity and air temperature, gave an average forecasting error of about 5-6% over the year. Yan [16] also presented residential consumption models using climatic variables for Hong Kong.
Third, intelligent optimisation class processing methods (IOCPM) simulate or reveal some natural phenomena to obtain optimisation methods that adapt to the environment, and thus solve the combination forecasting problems that are difficult for traditional forecasting techniques to address, by presenting a series of practical programmes. Research on this method (IOCPM) provides new and useful ideas for predicting behaviour itself. Nasr et al. [17] presented an Artificial Neural Networks (ANN) approach to electrical energy consumption forecasting in Lebanon. Four ANN models are presented and implemented in the research: a univariate model based on past consumption values; a multivariate model based on energy consumption forecasting time series and degree days; a multivariate model based on energy consumption forecasting total imports; and a model combining energy consumption forecasting, degree days, and total imports. Niu et al. [18] used a particle swarm optimisation (PSO) algorithm to predict the electricity load in China. The PSO algorithm was adopted to solve the disturbance vector α , as it has the virtue of optimum-seeking. Metaxiotis [19] provides an overview of the studies examining Artificial Intelligence (AI) technologies, as well as their current use in the field of short-term electrical load forecasting. Santos [20] has also used the ANN algorithm to make load forecasts, and with this method, the possibility of including weather-related variables in the input vector has also been analysed.
Based on the analysis of the literature above, one may refer to the researchers' experience of how they chose the factors for electricity consumption forecasting in the correlation field. Considering the actual situation of China's national conditions, after comprehensive data analysis and filter processing of electricity consumption data, we chose the following five factors that best reflect the truth of China's electricity consumption data during the period 1980 to 2009:
(1) Gross domestic product (GDP)
(2) Total import and export volume (TEIV)
(3) Investment in fixed assets (IFA)
(4) Industrial added value (IAV)
(5) Disposable income (DI)
The factors chosen above are the main reasons for complexity and periodic shape. They reflect the status of China's current development in accordance with its national conditions.
The remainder of the paper is organised as follows: Section 2 introduces an overview of electricity consumption in China. Section 3 discusses the methodology and the data of the study, and provides an accurate model for electricity consumption forecasting. Case analysis and results comparisons are used in Section 4, leading to the conclusion in Section 5.
2. OVERVIEW OF ELETRICITY CONSUMPTION IN CHINA
With the rapid development of China's economy, total electricity energy consumption increases sharply. The changes in electricity supply and demand in China since 1980 can be described in three stages. During the first stage, from 1978 to 1996, electricity consumption grew steadily by 7% per annum. Stage two stretched from 1997 to 2000 and, with the influence of the Asian financial crisis, electricity consumption grew slowly. However, from 2001 electricity consumption increased rapidly by 15% per annum, keeping pace with China's economic development.
Electricity consumption, economic growth, and environmental constraints interact in a dynamic way. Continued growth in electricity consumption and the enhancement of environmental factors have led the transformation of economic development in China by promoting industrial structure reforms and improving electricity availability. At present, China's power structure is mainly dominated by thermal power. Coal consumption for energy accounts for 50% of the total national coal consumption. The rapid growth of electricity consumption led to the rapid growth of coal consumption, which increased environmental pollution. It is therefore necessary to improve the accuracy with which electricity consumption is predicted to obtain a more accurate understanding of future environmental pollution. This predictive ability can provide policymakers with more accurate information for the development of relevant policies, and eventually achieve the goal of having reduced the 2020 carbon dioxide emissions per unit of GDP by about 40-45% when compared with 2005.
3. METHODOLOGY AND DATA
3.1 Data sets
China is at a critical stage of its economic development, which is China's first priority. Therefore we select the mainly economic factors that affect electricity consumption because, in this context, indicators of economic performance can better reflect the trends and levels of electricity consumption.
So, how can one discover suitable economic indicators? One knows that the volatility of GDP continuously influences the trend of electricity consumption; therefore, the GDP value can be seen as one indicator. At the same time, the 'troika' of total import and export volume (TEIV), investment in fixed assets (IFA), and disposable income (DI) can also accurately describe the trends of China's economic growth. Thus these three indicators can be included in the indicator system, since they are representative and rational.
Furthermore, industrial production is an important component of economic production in China's current industrial structure. Industrial electricity consumption accounts for a large proportion of total electricity consumption - generally 70% or more. On the one hand, industrial production creates huge economic benefits; but on the other, it consumes a large amount of electricity resources. Therefore the industrial added value (IAV) indicator, which reflects the growth trend of industrial production, can also be included in the indicator system.
In summary, we use the indicators GDP, TEIV, IFA, IAV, and DI to construct the index system. Not only do these indicators reflect the true background of China's power consumption, but their inclusion also enhances the integrity of the index selection.
For the period 1980-2009, the annual figures for electricity consumption were obtained by the National Bureau of Statistics of China in its survey called 60 Years of New China Statistical Data Compilation.
The annual data for the GDP, TEIV, IFA, IAV, and DI for the same period were also taken by the 60 Years of New China Statistical Data Compilation.
The historical data of electricity consumption are reported in Figure 1, and the independent variables (i.e., GDP, TEIV, IFA, IAV, and DI) are presented in Figure 2.
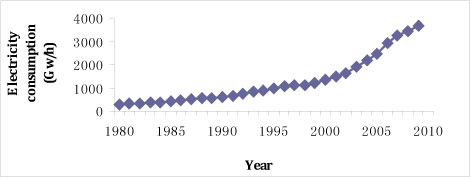
Figure 1: Historical data for electricity consumption in China
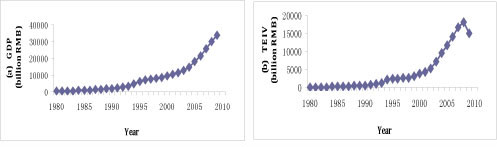
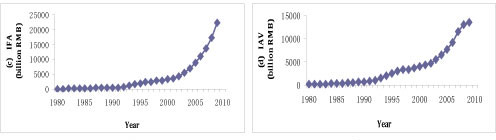
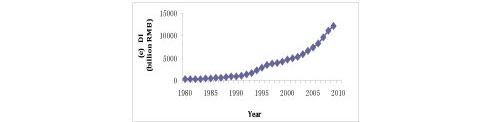
Figure 2: Historical data for the variables: (a) GDP; (b) TEIV; (c) IFA; (d) IAV; (e) DI
In Figure 1, electricity consumption shows a trend of substantial linear growth. In 1997 a marked decrease in the electricity consumption was detected. The growth rate of electricity consumption at 2.79% (1997/98) was much lower than the average growth rate of 9.06%, probably due to the Asian financial crisis of that period.
Generally, the trends of the other five factors are consistent with electricity consumption, but each of the factors also presents differing characteristics. From Figure 2 (a), the GDP trend of China maintains a sustained, significant increase; an inflection point only appears in 1997, and the period of inflection terminated in 2004, explained by the Asian financial crisis. Interestingly, the level of GDP growth has been slightly greater than the growth rate for electricity consumption, while the other four factors (TEIV, IFA, IAV, DI) are more closely associated with electricity consumption than with GDP. In Figure 2, the trend of TEIV, IFA, IAV, and DI only keeps pace with electricity consumption from 1993, after which their rates start a modest rise, slightly higher than consumption. It is worth noting that the TEIV value had a clear downward trend in 2008 (dropping by 16.27% on link relative ratio), owing to the global financial crisis; but it did not appear to impact electricity in China significantly. From Figure 2, one can garner information on two aspects. First, these characteristics show that since 1993, the growth rate of China's economy has increased quickly, and the economic structure is increasingly diversified. Second, there was a strong relationship between the aforementioned factors and electricity consumption. The trend comparison chart of electricity consumption and the factors are presented in Figure 3.
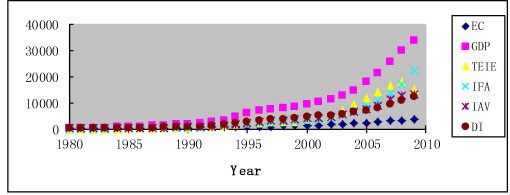
Figure 3: Trend comparison of electricity consumption and the five factors
3.2 Data standardisation
Many researchers have noted the importance of standardising variables for multivariate analysis. Otherwise variables measured at different scales do not contribute equally to the analysis. For example, in boundary detection, a variable that ranges between 0 and 100 will outweigh a variable that ranges between 0 and 1. In effect, using these variables without standardisation gives the variable with the larger range a weight of 100 in the analysis. Transforming the data to comparable scales can prevent this problem. Typical data standardisation procedures equalise the range and/or data variability.
The methodology for data standardisation can be divided into three categories: extreme value methods, standardised methods, and mean value methods. In this paper, standardised methods for data standardisation are used for two reasons. Initially they eliminate the variation of the difference of each variable when making dimensionless processing. Second, they consider the distribution of original data, which is what is required to establish the semi-parametric forecasting model. The calculation method is as follows:
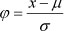
where X is raw data to be standardised, µ = E[x] is the mean value, and 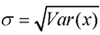 is the standard deviation of the raw data.
is the standard deviation of the raw data.
After standardisation, all variables will have the same weight during analysis. In addition, one may decide to weight the data based on knowledge of the relative importance of the variables.
3.3 Build the semi-parametric prediction model
In the course of electricity consumption data processing, one sees from the literature that many researchers use the parametric model, since its construction is simple and its processing convenient. Furthermore, for a majority of situations (for instance, kinds of static problems of conventional historical consumption data), the use of this model accords with objective facts, and it can satisfy practical needs because a majority of system errors are compensated, rectified, and can be expressed in the parameter model before data processing. However, under certain situations (for instance, some dynamic forecast issues of consumption), as observed values include system errors that cannot be rectified and parametric, there are non-ignored differences between the parametric model and objective practicality.
In fact, the system errors contain considerable information that influences the observed values. Therefore, if they can be identified and withdrawn correctly, not only can the accuracy of the parameter estimate be increased, but data can be provided for the study of the other subjects.
In addition, the factor of impacting observed values can be divided into two parts. The first is a linear relation; the second is a certain interference factor in which the relation to observation values is completely unknown, causing it to fall under the error item without any reason. In this case, too much information will be lost if the non-parametric model is used (though it has greater flexibility); thus, the imitated result is unacceptable if the linear model is adopted.
Given the above problems, other data forecast processing models need to be considered, such as the semi-parametric model:

where Y¡ = (yn,"-,yid) are observations, or historical electricity consumption, and X ¡ = (χil···, xip )T are explanatory variables, or indicators. The errors ε = (ε1, "'->Sid ) are assumed to be independent and identically distributed (denoted as iid). Ω = (β,···,βά) is the pχ d matrix of unknown parameters, and g(ξ) = (g1(ξ),",gd(ξ)) is the 1χ d vector of unknown functions. In this paper, the distribution function of Student residuals replaces the unknown function g(ξ). For simplicity, let
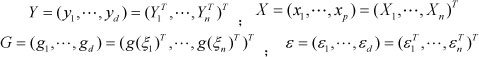
The matrix form of the model (1) is

This is an important type of statistical model developed in the 1980s (Engle [21]). Because it not only contains the parameter weight (which describes the known composition of function relation in observation values) but also contains the non-parameter weight (which exclusively shows the model deviation that is unknown in function relation), the model can generalise and describe numerous actual problems, bringing it closer to reality.
In this sub-section, the prediction principle diagram based on the semi-parametric multiple regression model is provided to analyse the forecasting process, which has multiple impact factors. Subsequently the specific steps on how to build the improved semi-parametric prediction model are given.
3.3(a) Prediction principle diagram
In Figure 4, the tagging below the horizontal axis are the factors for each time period. Assuming that one has collected M kinds of factors associated with the predictive objecty , one denotes X = [x1,x2,···,xm] . Supposing X, = [x1t,x2t,···,xmt] at the historical time period t (1 < t <Δ) that the amount of value to be predicted is y,, we need to predict the future at the time period t&[Δ + α,Δ + b] under the law of historical development. In Figure 4, if the time axis is the horizontal axis, and if one considers the vertical line with the current time point as the vertical axis, then Figure 4 can be regarded as a two-dimensional coordinate system with the time point 'present' as the coordinate origin. Thus Figure 4 can be divided into four quadrants, I to IV. Therefore, from Figure 4 one finds that the implication of semi-parametric regression forecasting is as follows. First, use the data of quadrants II and III to precede a historical fitting operation and derive the forecasting model. Next, use the data of quadrant IV as the input of the forecasting model, thus obtaining the forecasting result of quadrant I.
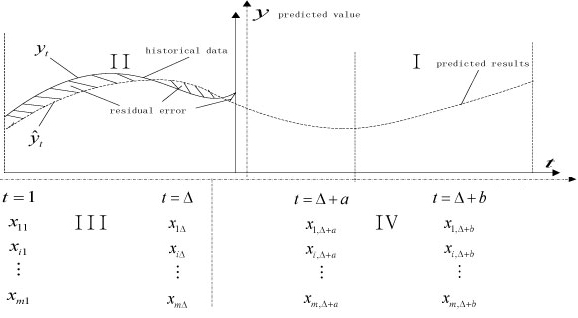
Figure 4: Prediction principle diagram of semi-parametric model with multiple impact factors
3.3(b) Modelling steps
Step 1: By establishing the multiple linear regression method and solving the parameter part Y = XΩ , obtain 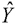 , the estimated value of Y ;
, the estimated value of Y ;
Step 2: List the fitting residuals, calculate the standardised residuals and Student residual, make a distribution test on the Student residual, and draw the Q-Q plot, observing whether it satisfies the normal distribution. The specific process is as follows:
(1) Calculate the Student residual r1
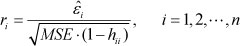
Where 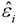 is the residual vector and
is the residual vector and 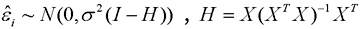 , lever quantity hii is the i-th element on the leading diagonal of H , MSE is the mean-square error.
, lever quantity hii is the i-th element on the leading diagonal of H , MSE is the mean-square error.
(2) Normal Q-Q plot test for Student residual
2.1 obtain the Student residual r in ascending order r(1), r(2), - ,r(n);
2.2 calculate
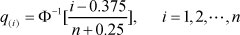
Here, Φ-1(χ) is the inverse function of the standard normal distribution function, constant 0.375 and 0.25 are corrections; 2.3 use points (q(Í),r(i)) (i = 1,2, ···,n) in the Cartesian coordinate system to draw a scatter diagram, observe the points (q{i),r(i)) (i = 1,2, - ,n); if they are roughly in a straight line, then the Student residual satisfies the normal distribution. If not, the means dissatisfy.
Similarly, if the random variable ri satisfies the following probability distribution law, one can also conclude that the Student residual satisfies the normal distribution.
Step 3: If the Student residual satisfies the normal distribution, select the appropriate residual fitting function, replace the unknown function G , and eliminate the local disturbance caused by the residual. Generally, if the Student residual satisfies the normal distribution, we select the Gaussian function - that is where ri is the Student residual, µ and σ are, respectively, defined as sample mean and sample standard deviation operated by ri ;

Step 4: Let g(ξ,) into system (1), make transposition processing, obtain improved semi-parametric model
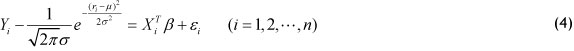
Solving system (4), estimate the parameter β ;
Step 5: Build the semi-parametric forecasting model
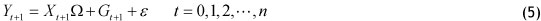
4. CASE STUDY
The main goal of this study is to predict electricity consumption in China using the semi-parametric regression model. We first present an empirical illustration of China's annual electricity consumption forecasting to examine the performance of the semi-parametric regression approach. Because the reforms of 1978 significantly altered the economic development mode of China, one usually takes 1980 as the time division point. Thus we use the annual electricity consumption data after 1980 in this paper, using the 1980-2005 data for model building and the 2006-2010 data as testing data.
Improving the accuracy of prediction is one of the main tasks in establishing a prediction model. However, any type of forecasting method is essential to produce the prediction error; therefore, an important task is to work out how to control the prediction error and thus provide feedback to the forecasting technique. In this paper, we give three statistical measures to evaluate the prediction accuracy of the approach: mean absolute error (MAE), mean absolute deviation (MAD), and mean squared error (MSE). MAE was used to measure the forecasting accuracy of the method; it usually expresses accuracy as a percentage, and can also be written as mean absolute percentage error (MAPE). MAD and MSE are two measures of the average errors. The three measures are defined as follows:

where y and y¡ represent the forecast and observed values, respectively.
When the semi-parametric regression forecasting approach is used to model and predict China's annual electricity consumption, we first standardise the electricity consumption data and the impact factors data from 1980 to 2009. Using the method mentioned in section 2, we give the following standardised data in Table 2.
Table 1: The frequency inspection of Student residual normality

Table 2: Standardised data, 1980-2009
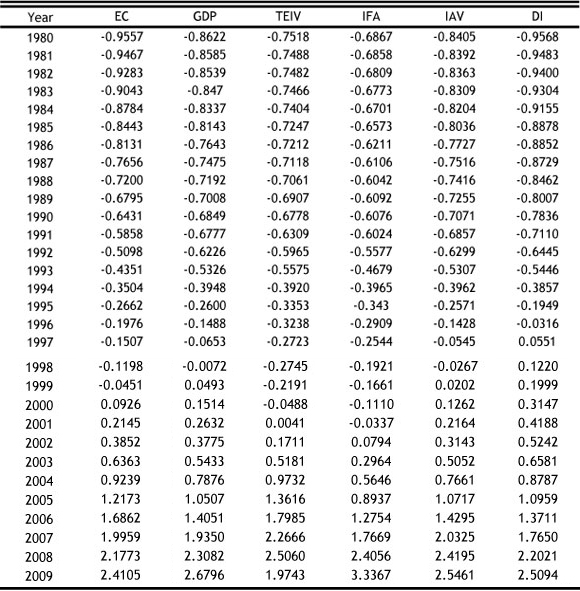
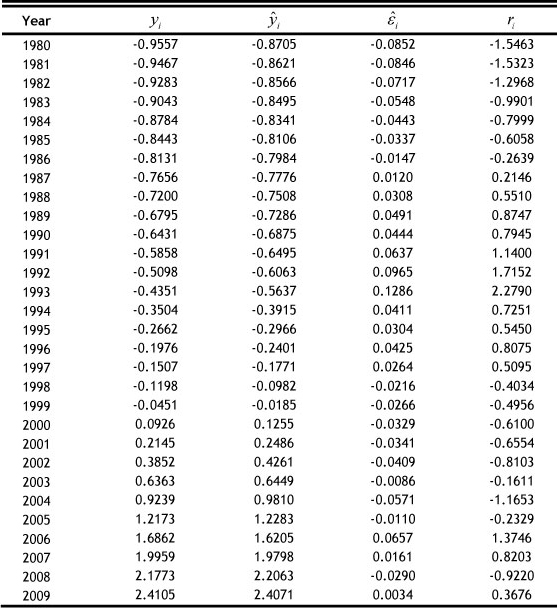
Next, we establish the multiple linear regression model, which uses the standardised data from Table 2 to calculate the fitted values 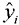 , residual
, residual 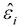 and Student residual
and Student residual 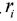 .
.
Next, we test the distribution of the Student residuals by means of the normal Q-Q plot test. If the Student residuals satisfy the normal distribution, we select an appropriate function to replace the unknown function G and eliminate the local disturbance of the forecast process.
Using the method given in section 2.3 (b) for data normality inspection, one can draw a Q-Q scatter diagram for Figure 5. One can see from Figure 5 that the scatter points are approximately in a straight line, which means that the Student residuals satisfy the normal distribution.
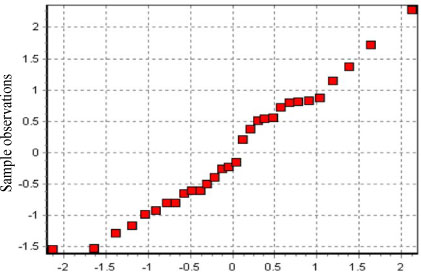
Figure 5: Q-Q scatter diagram
Similarly, we can also verify the above result by using the frequency inspection in Table 1. By frequency analysis of the Student residuals in Table 3, we can see that 73.3% ( 22/30 = 0.733 * 0.68 ) of the η (i = 1,2,-,30) falls within the interval (-1, 1), 86.6% ( 26/30 = 0.867 * 0.87 ) falls within the interval (-1.5, 1.5), and 96.6% (29/30 = 0.967 * 0.95 ) falls within the interval (-2, 2).
Table 3: Residual value, 1980-2009
After verifying the distribution of the Student residuals, the non-parametric part G of the forecasting model is calculated. From system (3), it follows that
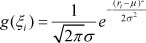
and G = ···,gd) = (g(ξι)τ,···,g(ξ)T)T , so we have
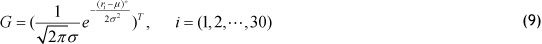
Here, with a sample mean of µ = 0.007583 and σ = 0.986877 .
Let µ and σ into system (9). Next, one obtains the value
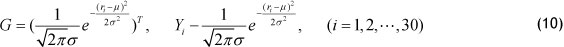
And, taking the results of system (10) into system (4), we can estimate the parameters 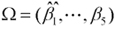 of the linear part of the semi-parametric prediction model (4).
of the linear part of the semi-parametric prediction model (4).
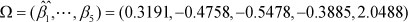
and β0 = 0.0518 .
Therefore, the semi-parametric prediction model is
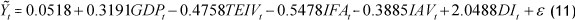
Here
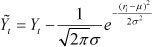
Thus, we can use system (11) to make an electricity consumption forecasting study. We also apply the GM (1, 1) and ANN models for comparison purposes. In the case of the GM (1, 1) model, the resulting model is x(t +1) = 18882.9496e"0099067t +15876.6496, t = 1,2,3, - . Table 4 shows the forecast values as well as the relative errors (RE) for the three methods.
Table 4: Observed and forecast electricity consumption in China, 1980-2010, for three different approaches
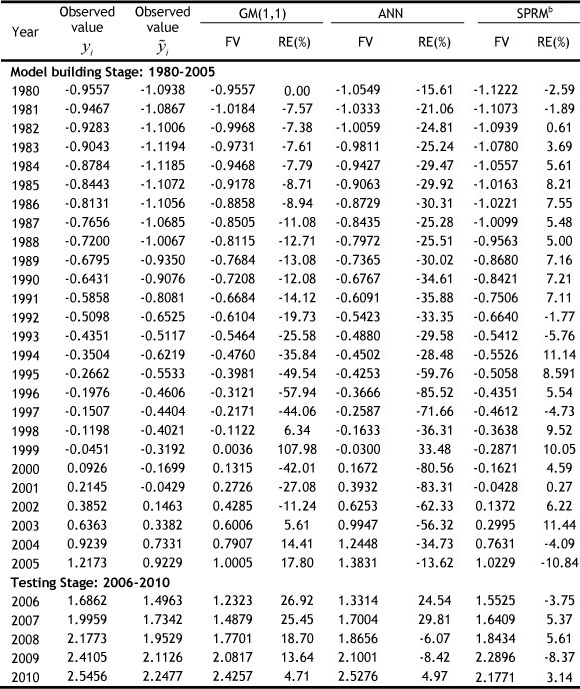
Remarks: ªThe electricity consumption values are standardised data;
bThe proposed semi-parametric regression model in this paper.
FV: forecasted value.
Measures of the corresponding forecasting errors are shown in Table 5. Both in the model building stage and in the testing stage for this particular case, the SPRM prediction approach outperforms the GM (1,1) and ANN models. Figure 6 shows the model percentage error distributions for the SPRM prediction approach. In this figure, calibrations 1 to 26 correspond to the model building stage, and calibrations 27 to 31 correspond to the testing stage.
Table 5: Comparative analysis of forecasting errors
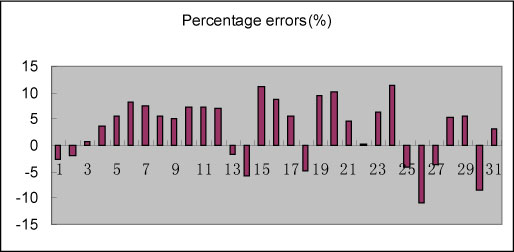
Figure 6: Percentage errors for the SPRM approach
5. CONCLUSION
The major contribution of this paper is to propose a new statistical methodology to forecast electricity consumption. The proposed semi-parametric regression models, which are an integration of parametric and nonparametric regression models, capture the complex cooperative relationship between electricity consumption and its drivers. By analysing the distribution characteristics of the Student residuals, we introduce a corresponding distribution function, and use it as the non-parametric part of this semi-parametric regression model, thereby eliminating the local disturbance of the forecast process and effectively reducing the prediction error or other system errors. The forecast results demonstrate that the model performs remarkably well, and also demonstrate the effectiveness and reliability of the approach.
ACKNOWLEDGEMENTS
The authors thank the China Key Laboratory of Process Optimization and Intelligent Decision-Making for their valuable comments and feedback regarding this research study. This paper was supported by the National Natural Science Foundation of China Grant No.71101041 and No.71071045.
REFERENCES
[1] The National Bureau of Statistics. 2009. National Bureau of Statistics of China. 60 Years of New China. China Statistics Press. [ Links ]
[2] Harris, J.L. & Lon-Mu, L. 1993. Dynamic structural analysis and forecasting of residential electricity consumption. International Journal of Forecasting, 9, pp. 437-455. [ Links ]
[3] Jannuzzi, G. & Schipper, L. 1991. The structure of electricity demand in the Brazilian household sector. Energy Policy, 19(9), pp. 879-891. [ Links ]
[4] Ranjan, M. & Jain, V.K. 1999. Modeling of electricity energy consumption in Delhi. Energy, 24(4), pp. 351-361. [ Links ]
[5] Wang, X.J., Yang, S.L. et al. 2010. Dynamic GM (1,1) model based on cubic spline for electricity consumption prediction in smart grid. China Communications, 7(4), pp. 83-88. [ Links ]
[6] Wang, X.J. & Yang, S.L. 2010. Electricity demand forecasting based on threepoint Gaussian quadrature and its application in smart grid. The 6th International Conference on Wireless Communications Networking and Mobile Computing. [ Links ]
[7] Wang, X.J., Shen, J.X. & Yang, S.L. 2010. Application research on Gaussian orthogonal interpolation method for electricity consumption forecasting of smart grid. Power System Protection and Control, 38(21), pp. 141-145,151. [ Links ]
[8] Wang, X.J., Yang, S.L. & Ding, J. 2010. Simulation of orthogonalization prediction based on grey Markov chain for electricity consumption. Journal of System Simulation, 22(10), pp. 2253-2256. [ Links ]
[9] Wang, X.J., Yang, S.L. & Wang, H.J. 2010. Application research on grey orthogonal prediction model based on Markov chain for electricity consumption forecasting of smart grid. The 12th Chinese Annual Conference on Management Science. [ Links ]
[10] Ching-Lai, H., Marnont, A., Simon, W. & Shanti, M. 2005. Analyzing the impact of weather variables on monthly electricity demand. IEEE Trans, 20, pp. 2078-2085. [ Links ]
[11] Egelioglu, F., Mohamad, A.A. & Guven, H. 2001. Economic variables and electricity consumption in Northern Cyprus. Energy, 26, pp. 355-362. [ Links ]
[12] Wei, L., Wu, J. & Liu, Y. 2000. Long-term electricity load forecasting based on system dynamics. Automation of Electric Power Systems, 20, pp. 24:47. [ Links ]
[13] Narayan, P. K. & Prasad, A. 2008. Electricity consumption - real GDP causality nexus: Evidence from a bootstrapped causality test for 30 OECD countries. Energy Policy, 36, pp. 910-918. [ Links ]
[14] Nikolopoulos, K., Goodwin, P., Patelis, A. & Assimakopoulos, V. 2007. Forecasting with cue information: A comparison of multiple regression with alternative forecasting approaches. European Journal of Operational Research, 180, pp. 354-368. [ Links ]
[15] Abdel-Aal, R.E., Al-Garni, A.Z. & Al-Nassar, Y.N. 1997. Modeling and forecasting monthly electric energy consumption in eastern Saudi Arabia using abductive networks. Energy, 22(9), pp. 911-921. [ Links ]
[16] Yan, Y.Y. 1998. Climate and residential electricity consumption in Hong Kong. Energy, 23(1), pp. 17-20. [ Links ]
[17] Nasr, G.E., Badr, E.A. & Younes, M.R. 2002. Neural networks in forecasting electricity energy consumption: Univariate and multivariate approaches. International Journal of Energy Research, 26, pp. 67-78. [ Links ]
[18] Niu, D.X., Zhao, L., Zhang, B. & Wang, H.F. 2007. The application of particle swarm optimization based grey model to power load forecasting. Chinese Journal of Management Science,15(1), pp. 69-73. [ Links ]
[19] Metaxiotis, K., Kagiannas, A., Askounis, D. & Psarras, J. 2003. Artificial intelligence in short term electricity load forecasting: A state of the art survey for the researcher. Energy Conversion and Management, 44, pp. 1525-1534. [ Links ]
[20] Santos, P.J., Martins, A.G., Pires, A.J., Martins, J.F. & Mendes, R.V. 2006. Short term load forecast using trend information and process reconstruction. International Journal of Energy Research, 30, pp. 811-822. [ Links ]
[21] Engle, R.F., Granger, C.W.J., Rice, J. & Weiss, A. 1986. Semi-parametric estimates of the relation between weather and electricity sales. Journal of the American Statistical Association, 81, pp. 310-320. [ Links ]
[22] Taylor, J.W. 2006. Density forecasting for the efficient balancing of the generation and consumption of electricity. International Journal of Forecasting, 22, pp. 707-724. [ Links ]
[23] Taylor, J.W., de Menezes, L.M.M. & McSharry, P.E. 2006. A comparison of univariate methods for forecasting electricity demand up to a day ahead. International Journal of Forecasting, 22, pp. 1-16. [ Links ]
[24] Akay, D. & Atak, M. 2007. Grey prediction with rolling mechanism for electricity demand forecasting of Turkey. Energy, 32, pp. 1670-1675. [ Links ]
[25] Zhou, P., Ang, B.W. & Poh, K.L. 2006. A trigonometric grey prediction approach to forecasting electricity demand. Energy, 31, pp. 2839-2847. [ Links ]
* Corresponding author
1 The author was enrolled for a PhD (Engineering Management) degree in the School of Management, Hefei University of Technology.














