Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Industrial Engineering
On-line version ISSN 2224-7890
Print version ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.23 n.3 Pretoria Jan. 2012
GENERAL ARTICLES
A differential evolution algorithm developed for a nurse scheduling problem
P. Shahnazari-ShahrezaeiI, *, 1; R. Tavakkoli-MoghaddamI; M. AzarkishIII; A. Sadeghnejad-BarkousaraieIV
IDepartment of Industrial Engineering Science and Research Branch, Islamic Azad University, Tehran, Iran. parisa_shahnazari@iaufb.ac.ir
IIDepartment of Industrial Engineering University of Tehran, Tehran, Iran. tavakoli@ut.ac.ir
IIIDepartment of Industrial Engineering and Center of Excellence for Intelligence-Based Experimental Mechanics University of Tehran, Tehran, Iran. shadi_azarkish@yahoo.com
IVDepartment of Industrial Engineering and Center of Excellence for Intelligence-Based Experimental Mechanics University of Tehran, Tehran, Iran. azar_sadeghnezhad@yahoo.com
ABSTRACT
Nurse scheduling is a type of manpower allocation problem that tries to satisfy hospital managers' objectives and nurses' preferences as much as possible by generating fair shift schedules. This paper presents a nurse scheduling problem based on a real case study, and proposes two meta-heuristics - a differential evolution algorithm (DE) and a greedy randomised adaptive search procedure (GRASP) - to solve it. To investigate the efficiency of the proposed algorithms, two problems are solved. Furthermore, some comparison metrics are applied to examine the reliability of the proposed algorithms. The computational results in this paper show that the proposed DE outperforms the GRASP.
OPSOMMING
Verpleegsterskedulering is 'n mannekragtoedelingsprobleem wat deur regverdige skof-skedules beide hospitaalbestuurders se teikens en verpleegpersoneel se voorkeure bevredig. Dié artikel handel oor 'n verpleegsterskeduleringprobleem wat gebaseer is op 'n werklike gevallestudie en stel twee metaheuristieke voor om die probleem op te los - 'n differensiaal evolusionêre metode en 'n gulsige, ewekansige, aanpasbare soekprosedure. Om die doel-treffendheid van die voorgestelde algoritmes te ondersoek word twee probleme opgelos. Verder word vergelykende maatstawwe gebruik om die betroubaarheid van die voorgestelde algoritmes te ondersoek. Die berekende resultate in die artikel toon dat die differensiaal evolusionêre algoritme beter vaar as die gulsige, ewekansige, aanpasbare soekprosedure.
1. INTRODUCTION
Manpower scheduling is a challenging problem in which an extensive field of research has been done since the 1970s, dealing with different aspects in management sciences and operational research. It is a managerial process in which the required manpower level for each craft or skill is selected to complete the work in the most effective manner. Proper scheduling, therefore, leads to increased efficiency, maximum use of the capacity of the resources, less time to finish the work, and increased profitability in the organisation.
Manpower scheduling is classified into three groups: individual scheduling (nurse, physician, surgery, and the like); personnel scheduling; and group scheduling (crew, etc). Providing a schedule that almost satisfies all constraints and objectives is often troublesome, and needs specialised knowledge. Different classifications of manpower are observed in industrial and service environments, including homogeneous and heterogeneous, part-time and full-time, skilled and unskilled workforces, and so on [21,36,49,52]. Manpower scheduling and simultaneous allocation have been much considered by researchers. For instance, Cerulli et al. [17] introduced a mathematical model for scheduling and allocating workforces. Emmons & Fuh [25] scheduled full-time and part-time workforces, taking vacations and weekends into account. Blochliger [13] also presented a tutorial for staff scheduling problems.
Selecting a suitable solution method is another important matter in scheduling. Alfares [6] suggested a two-phase algorithm based on mathematical models to schedule manpower, taking cyclic days-off into consideration. Lagodimos et al. [32] used greedy heuristic algorithms. Akjiratikarl et al. [5] introduced a particle swarm optimisation-based algorithm to schedule home care workers in the UK to minimise the total distance travelled by all workers. Musliu et al. [37] also stated that network flow, a combination of management science and artificial intelligence techniques, and mixed approaches joining constraint satisfaction and local improvement algorithms, are just some of the approaches that have been applied so far to solve manpower scheduling problems. Ernst et al. [26] examined literature reviews, applications, models, and algorithms of manpower scheduling, and finally proposed some points for future research.
As mentioned before, a nurse scheduling problem (NSP) is a kind of manpower allocation problem that deals with demand oscillations on different days and shifts. This problem requires hospitals to use their nurses efficiently. On the other hand, shift scheduling must be done so that it provides the opportunity for all nurses to have a safe social life in order to maintain their morale.
An NSP tries to distribute the workload fairly among nurses, reduce the costs, and satisfy both the nurses' preferences and those of the hospital managers. Sometimes these objectives conflict with each other. Nurses' preferences may not be completely satisfied and hospital managers may be forced to pay some penalties. Since hospital managers are often under pressure to control costs, satisfy the nurses, and deliver high-quality services, developing an appropriate nurse scheduling can balance these pressures and use the nurses more effectively.
Over the years, a wide range of models and solution approaches have been developed to deal with NSP. An extensive overview of NSP can be found in Cheang et al. [18] and Burke et al. [15].
As a general rule, nurse scheduling can be categorised into centralised, self, and cyclical scheduling. Two major advantages of centralised scheduling [24,44,46,54] are: (1) fairness to employees through consistent, objective, and impartial application of policies, and (2) opportunities for cost containment through better use of existing resources. When head nurses or unit managers are responsible for generating the schedules locally, it is called 'unit scheduling' [2,14,23,33,34,45]. In this case, nurses usually get more personalised- attention. Self-scheduling is a manual process [35,43] that takes more time than automatic scheduling. Nurses cooperate and are asked for advice. It is usually performed by the personnel members themselves and coordinated by the head nurse of a ward. In cyclical scheduling, each nurse works a cycle of a number of weeks [11,30]. Nurses know their schedule in advance, and the same shift schedule patterns are used over an extended time. Unfortunately, this type of scheduling cannot incorporate many flexible features or personal preferences unless major modifications take place.
Over the last few decades, various approaches have been applied to solve NSP. The more common methods that are applied are mathematical programming, meta-heuristic, and artificial intelligence approaches.
Mathematical programming models are employed to solve NSP using traditional methods that guarantee to find an optimal solution. Azaiez & Al Sharif [9] developed a 0-1 linear goal programming model for nurse scheduling in Riyadh Al-Kharj hospital (in Saudi-Arabia) that considered hospital objectives and nurses' preferences. Bard & Purnomo [10] used a column generation approach, including a combination of integer programming and heuristics, to solve a multi-objective nurses' preference scheduling model. Glass & Knight [28] solved four nurse rostering benchmark problems using mixed integer linear programming. They reduced the solution space of the problems and obtained optimal solutions for all instances within a practical execution time. Topaloglu & Selim [50] presented a novel multi-objective integer programming model for NSP. They converted the presented model to three fuzzy goal programming models using different fuzzy solution approaches.
In real-size problems, mathematical programming approaches are faced with computational difficulties due to increasing complexity. To overcome this, meta-heuristic methods have been developed by some researchers. Meta-heuristics strive to obtain good solutions within a reasonable time, although they cannot be guaranteed to find optimal solutions. Meta-heuristics have been employed in solving NSP since the 1990s. Bellanti et al. [12] suggested a tabu search procedure completed by a greedy procedure to avoid generating infeasible solutions to the NSP. Aickelin & Dowsland [3] presented a genetic algorithm coupled with a decoding routine for solving an NSP at a major UK hospital. Gutjahr & Rauner [29] used an ant colony optimisation approach for a dynamic regional NSP at the Vienna hospital compound. Chiaramonte & Chiaramonte [19] recommended a new heuristic using a competitive agent-based negotiation that focuses on nurse preferences. Tsai & Li [51] extended a two-stage mathematical modeling for an NSP using genetic algorithms. Burke et al. [16] combined integer programming and variable neighborhood search to solve a highly-constrained NSP.
Artificial intelligence is another approach to solving NSP. Meyer auf'm Hofe [34] applied hierarchical constraint programming for nurse scheduling where legal regulations and the preferences of nurses were hard and soft constraints respectively. Abdennadher & Schlenker [1] presented an interactive constrained based scheduler that assigned a working shift to each nurse on each day of a planning horizon.
NSP is a complex combinatorial optimisation problem. Factors that make this problem complex are the organisational structure and characteristics, work agreements, nurses' recruitment, different skill levels of nurses, substitution of skill levels, working preferences, patient necessities, circumstances in particular nursing units, and so forth. Since most NSPs in the real world are NP-hard [19,31,39,55], traditional methods (e.g. mathematical programming) are generally used to solve small problem instances. The high level of computational complexity of NSP has been widely recognised in the nurse scheduling literature, and has led some authors to develop meta-heuristic solution methods.
An almost new meta-heuristic algorithm, called differential evolution (DE), is used to solve the given problem in this paper. DE was first introduced by Storn & Price [47,48]. DE is a- mathematical global optimisation method, based on population generation, which tries to minimise the non-linear and non-differentiable continuous space functions as much as possible. In order to examine the performance of the proposed DE algorithm, the problem is also solved by another meta-heuristic - the greedy randomised adaptive search procedure (GRASP) - that was introduced by Feo & Resende [27] and Resende [42]. The results are subsequently compared.
The rest of this paper is organised as follows. Section 2 deals with the formulation of the proposed nurse scheduling model. An effective DE algorithm to solve the problem, and a GRASP algorithm to compare the related results, are presented in Section 3. The computational results and validation of the proposed solution methods are found in Section 4. Finally, Section 5 provides some concluding remarks.
2. FORMULATION OF PROPOSED NURSE SCHEDULING MODEL
The proposed nurse scheduling model is based on the rules used in the maternity ward of Sina Hospital in Isfahan City, Iran, to schedule nurses in that ward. Nurses are assigned to work in three shifts: a six-hour morning shift, a six-hour afternoon shift, and a 12-hour night shift. The planning horizon is 35 days (five weeks). Nurses are classified into three skill levels: nurse, auxiliary nurse, and co-auxiliary nurse. The highest and lowest skill levels are 'nurse' and 'co-auxiliary nurse' respectively. Each nurse at a higher skill level can be assigned to work at his/her real skill level, or at any lower skill level, but not more than one skill level in a shift. If a nurse is assigned to work at a lower skill level than his/her real skill, hospital managers are forced to pay a penalty. There are limitations on the daily, Friday, weekly, and monthly work hours for nurses. Deviation from the determined weekly work hours is permitted if needed. The total number of required nurses at any skill level in each shift per day is pre-determined. Each nurse cannot be assigned to work for more than 12 hours consecutively. Therefore, nurses cannot be assigned to work the afternoon and night shifts of the same day, or a night shift of a considered day and the morning shift of the next day successively. Nurses are limited to a maximum number of night shifts during the planning period. Also, each nurse who works three night shifts in a row should be off for at least two days to rest. From an efficiency point of view, nurses should not be assigned to work between the two days off, but deviation from this rule is permitted if needed. Nurses prefer to rest for some days or for some shifts determined by them at the beginning of planning. But sometimes, due to the lack of qualified nurses for a shift, they may be assigned to work the days or shifts when they would have preferred to rest.
2.1 Notations
The following notations are used in the presented model.
2.1.1 Indices
i Index for the nurses, (i=1,...., i)
k Index for the days, (k=1,...., K)
Ik Index for the last day of each week during the scheduling period, (lk=7, ...,LK); in this case: (lk=7, 14, 21, 28, 35) and |LK| is equal to cardinality (size) of set LK (e.g., |LK|=5).
j Index for the shifts, (j=1, J); in this case: (j = 1: Morning, 2: Afternoon, 3: Night)
s Index for the skill levels, (s=1, S); in this case: (s =1: Nurse, 2: Auxiliary nurse, 3: Co-auxiliary nurse)
2.1.2 Sets
l Set of nurses
K Set of days during the scheduling period
LK Set of the last days of all weeks during the scheduling period
J Set of shifts
S Set of skill levels
2.1.3 Parameters
hkj Length of shift j on day k
dhmin Lower bound on the total number of hours worked by each nurse in a day
dhmax Upper bound on the total number of hours worked by each nurse in a day
whmin Lower bound on the total number of hours worked by each nurse during a week
whmax Upper bound on the total number of hours worked by each nurse during a week
fhmin Lower bound on the total number of hours worked by each nurse on Fridays during the planning period
fhmax Upper bound on the total number of hours worked by each nurse on Fridays during the planning period
mhmin Lower bound on the total number of hours worked by each nurse during the planning period
mhmax Upper bound on the total number of hours worked by each nurse during the planning period
RNkJS Total number of required nurses at skill level s in shift j on day k
RSLi Real skill level of nurse i
Max - Night Maximum number of night shifts that each nurse can be assigned to work during the planning period
Penl A penalty coefficient for assignment at lower skill level
ki Set of days that nurse i is interested in taking a rest in some/all shifts
jki Set of shifts of day k¿ that nurse i is interested in taking a rest
ASLlkjs 1, if nurse i can be assigned to work at his/her real skill level or at any lower skill level s in shift j on day k ; otherwise 0
d1ik2 Deviation from lower bound on the total number of hours worked by nurse i during a week
d2ik2 Deviation from upper bound on the total number of hours worked by nurse i during a week
d3ik Deviation from off-on-off for nurse i
d4ikj Deviation from days/shifts that nurse i is interested in taking a rest
2.1.4 Decision variable
xikjs 1, if nurse i is assigned to work at skill level s in shift j on day k; otherwise 0
qik 1, if nurse i is assigned to work three successive night shifts on days k-2, k-1, and k; otherwise 0
2.2 Objective functions
- The first objective is to minimise the sum of deviations from lower and upper bounds on the total number of hours worked by nurses during a week:

- The second objective is to minimise the sum of deviations from off-on-offs for nurses:

- The third objective is to minimise the sum of deviations from days/shifts that nurses are interested in taking a rest:

- The fourth objective is to minimise the nurses' assignment at lower skill levels than their real skill:
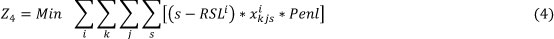
2.3 Constraints
In the presented model, constraints are divided into hard constraints that must be satisfied in all cases, and soft constraints that may be violated so that a feasible schedule can be obtained.
2.3.1 Hard constraints
- Lower and upper bound on the total number of hours worked by each nurse on a day:

- Lower and upper bound on the total number of hours worked by each nurse during the planning period:

- Lower and upper bound on the total number of hours worked by each nurse on Fridays during the planning period:

- Each nurse can be assigned to work at his/her real skill level or any lower skill level in each shift per day:

- Total number of required nurses at any skill level in each shift per day:

- Each nurse cannot be assigned to work for more than 12 hours consecutively:
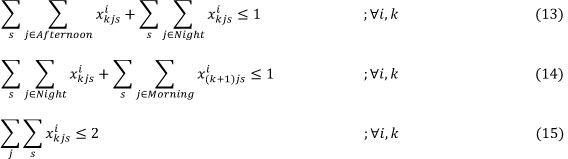
- Each nurse cannot be assigned to work at more than one skill level in each shift per day:

- Maximum number of night shifts that each nurse can be assigned to work during the planning period:
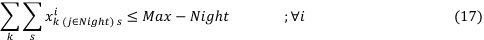
- Each nurse cannot be assigned to work more than three successive night shifts:

- Each nurse should be off for at least two days after working three successive night shifts:
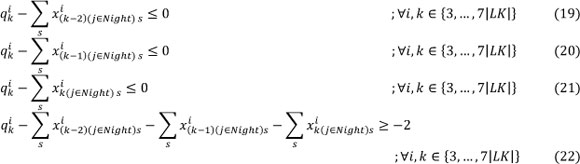
The constraints (19) to (22) ensure that:
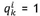 , if nurse i is assigned to work three successive night shifts on days k-2, k-1, and k; otherwise 0.
, if nurse i is assigned to work three successive night shifts on days k-2, k-1, and k; otherwise 0.
Then, the rule is verified by adding the following constraints:
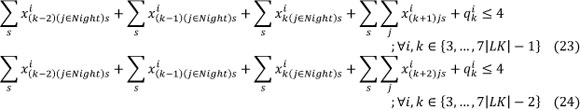
2.3.2 Soft constraints
- Lower and upper bound on the total number of hours worked by each nurse during a week:

- Each nurse should not be assigned to work between two days off (off-on-off is not allowed):
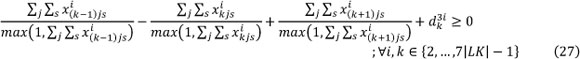
- Each nurse is interested in taking a rest in pre-determined days/shifts:
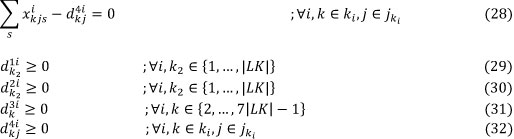
2.4 Simplification of the presented nurse scheduling model
Objective functions and soft constraints of the presented model can be rewritten as follows:
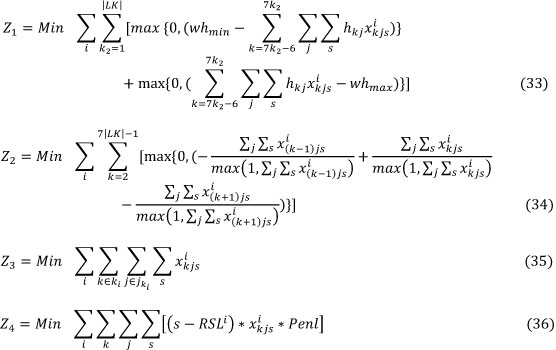
which are subject to the constraints (5) to (24).
3. META-HEURISTIC SOLUTION METHODS
The DE technique, which belongs to the class of evolutionary algorithms, is established on the principles of mutation, crossover, and selection [47,48]. It is based on a special way of creating new individuals. Mutation and crossover operators are used to generate new individuals, and the selection operator chooses the best generated individual for the next generation. This algorithm, which has recently become increasingly popular, is very efficient. For instance, Pan et al. [40] presented a discrete DE algorithm to solve the permutation flow-shop scheduling problem with total flow-time criterion. Damak et al. [22] recommended a DE algorithm to solve the resource-constrained project scheduling problem with multiple execution modes for each activity and minimisation of the makespan. Wang et al. [53] presented a new hybrid discrete DE algorithm to solve the blocking flow-shop scheduling problems in order to minimise the maximum completion time. Pan et al. [41] also developed an effective hybrid discrete DE algorithm to minimise the maximum- completion time for a flow-shop scheduling problem, with intermediate buffers located between two consecutive machines.
In order to investigate the quality of generated solutions by the proposed DE in this paper, a GRASP algorithm is also applied to solve the given problem. GRASP is a meta-heuristic that is characterised by multiple initialisations [27,42]. In this algorithm, a feasible solution is initially obtained, and then is improved by a local search technique. This process is repeated in an iterative manner to reach the best solution. Some applications of the GRASP algorithm are observed in [4,7,8,38]. The proposed structures of both algorithms are thoroughly explained.
3.1 The proposed structure of the DE algorithm
The proposed structure of DE in pseudo-code format is as follows:

The initialisation method, mutant operator, crossover operator, repair procedure, solution feasibility check procedure, solution improvement procedure, and Pareto Archive updating procedure propounded in the above pseudo-code are described in subsections 3.1.1 to 3.1.7 below.
3.1.1 Initialisation method
The initial solutions generation method that can produce high quality and feasible initial population has been designed as follows:

3.1.2 Mutant operator
In a similar way to the genetic algorithm (GA), the parent and offspring theory is used to search in the solution space. In this paper, a mutant matrix is produced for each solution as follows [53]:

where A, which is used to control the population's evolution rate, is greater than 1 (e.g., 2) and rand is a random number in the interval [0,1]. Note that each generated mutant matrix Mi corresponds to a solution si.
3.1.3 Crossover operator
Once the mutant matrix is produced in the DE algorithm, the crossover operator must be specified for each solution structure too. In this paper, the crossover operator is defined by Equation (38):

where cr is a random number in the interval [0,1], and ri is a matrix whose elements are generated randomly in the interval [0,1] for each s¡ and Mi. Obviously r¡ has the same size as s¡. It should be noted that Equation (38) is applied to each solution s¡ and to its corresponding mutant matrix Mi in order to obtain a matrix Ti.
3.1.4 Repair procedure
There is a matrix Ti for each solution s¡ and its corresponding M¡ that is used to convert solution s¡ to a feasible one by using a repair procedure. Each element of Tt includes a number that has been generated by applying mutant and crossover operators. These elements are used to prioritise the nurses who will be assigned to shifts. The repair procedure is applied to all solutions to produce new feasible ones where possible.

3.1.5 Solution feasibility check procedure
Since new solutions are generated while running the proposed DE algorithm, a procedure has been designed to check the satisfaction of all constraints for the generated solution, which tries to convert an infeasible solution to a feasible one if possible. This procedure is expressed as the following:
For the rest constraints, nurses are assigned in this manner, and the schedules change as much as possible until all constraints are satisfied. If assigning a nurse while taking all conditions into consideration is not possible, this solution cannot be converted into a feasible one, and the procedure will end.
3.1.6 Solution improvement procedure
This procedure improves all generated feasible solutions, as far as possible. Three neighborhood search operators (NSO1, NSO2, and NSO3) are used in parallel to improve the feasible solutions as below:

The applied NSOs are defined as follows:
- NSO1: A nurse is selected randomly. If he/she has been assigned to work some shifts/days that he/she prefers to rest, his/her assignment will be cancelled for that shift/day and another nurse who is able to work this shift/day will replace him/her.
- NSO2: A nurse is selected randomly and his/her assignments are checked for all shifts. If this nurse has been assigned to work at a lower skill level than his/her real skill in a shift, his/her assignment will be cancelled for this shift and a qualified nurse in the same shift will replace him/her if possible; or his/her assignment will be displaced with a nurse who has been assigned to work in the same shift at a skill level closer to the considered skill level.
- NSO3: The assignment of nurses who have been assigned to work between two off-days is cancelled, and is replaced by some qualified nurses, if possible.
It should be mentioned that the improvement procedure is even applied to the infeasible solutions obtained by the NSOs in order to convert them to feasible ones. If this conversion is impossible, the solution st will be considered as the output of the improvement procedure. The population acquired by the improvement procedure is regarded as the population of the next iteration, after checking the feasibility.
3.1.7 Pareto Archive updating procedure
In any iteration, non-dominated solutions are stored in a set called the Pareto Archive. The best solution obtained in each iteration is compared with the solutions existing in the Pareto Archive set by using non-dominated relations. The selected non-dominated solutions are then considered as a new Pareto Archive.
3.2 The proposed structure of the GRASP algorithm
The general structure of the GRASP algorithm is as follows:

In the proposed GRASP algorithm, non-dominated solutions in any iteration are stored in a set, and eventually a set of solutions is considered as the output of the GRASP algorithm. The proposed structure of GRASP in pseudo-code format is as follows:

3.2.1 Greedy randomised construction procedure
In this phase, one solution is initially constructed. Solution construction starts from the first shift of the first day and continues to the last shift of the last day of the planning horizon.

3.2.2 Repair procedure
The solution feasibility check procedure proposed in Section 3.1.5 is used to repair the solutions.
3.2.3 Local search procedure
The three neighborhood search operators (NSO1, NSO2, and NSO3) proposed in Section 3.1.6 are used in parallel as a local search procedure.
3.2.4 Solution updating procedure
In this procedure, the best solution is selected from among the current solution and the three solutions obtained by the NSOs in the local search procedure using non-dominated relations. If more than one solution is found to be the best, one will be randomly selected.
3.2.5 Pareto Archive updating procedure
The updating procedure proposed in Section 3.1.7 is used to update the Pareto Archive.
4. COMPUTATIONAL RESULTS
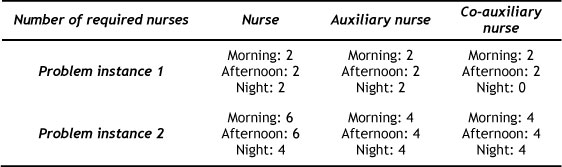
To examine the efficiency of the model presented in Section 2 (formulated according to a real case study carried out in the maternity ward of Sina Hospital in Isfahan), two numerical examples are solved by the proposed DE and GRASP algorithms on an Intel(R) Core(TM) i3 with 4 GB of memory and 2.27 GHZ of Dual Core CPU, and MATLAB R2009a software. The parameters of the given model are presented in Table 1. The planning horizon is considered to be 35 days (5 weeks).
Table 1: Common features of problem instances

Table 2 lists the real skill level of all nurses for both problem instances. For example, the real skill level of nurses with I D=1 to 8 in Problem instance 1 is 'nurse', and they are able to work at 'auxiliary nurse' and 'co-auxiliary nurse' skill levels as well as their real skill; and the real skill level of nurses with ID=21 to 35 in Problem instance 2 is 'auxiliary nurse', and they are able to work at 'co-auxiliary nurse' skill level as well as their real skill. As mentioned before, all nurses with a higher real skill level are capable of working at lower skill levels. Nurses with 'co-auxiliary nurse' real skill level can only work at their real skill level.
Table 2: Real skill level of nurses

Table 3 represents the number of nurses required in each shift of the planning period. For example, two nurses at 'auxiliary nurse' skill level are needed in 'Morning', 'Afternoon', and 'Night' shifts of all days in Problem instance 1 (remembering that all nurses with 'Nurse' and 'Auxiliary nurse' real skill levels can work at this skill level).
Table 3: Number of nurses required in each shift of the planning period
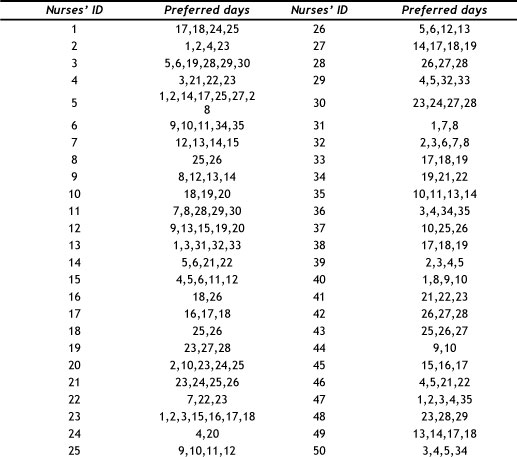
Tables 4 and 5 summarise the rest days that nurses prefer in both problem instances. These days are determined by nurses at the beginning of planning.
Table 4: Preferred rest days (Problem instance 1)
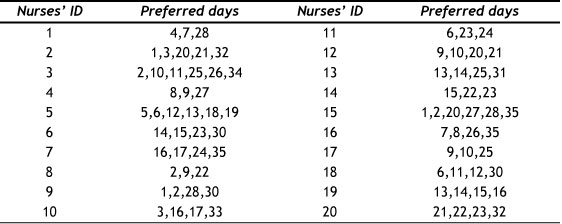
Table 5: Preferred rest days (Problem instance 2)
Tables 6 and 7 illustrate the objective values of non-dominated solutions existing in Pareto Archives of the proposed DE and GRASP algorithms for Problem instances 1 and 2 respectively. Note that non-repetitive non-dominated solutions (non-identical non-dominated solutions) existing in a Pareto Archive set may have equal objective values. For example, non-repetitive non-dominated solutions 2 and 14 obtained by the proposed DE for Problem instance 1 have equal objective values, as shown in Table 6.
Table 6: Objective values of Pareto Archived set by the proposed DE and GRASP (Problem instance 1)
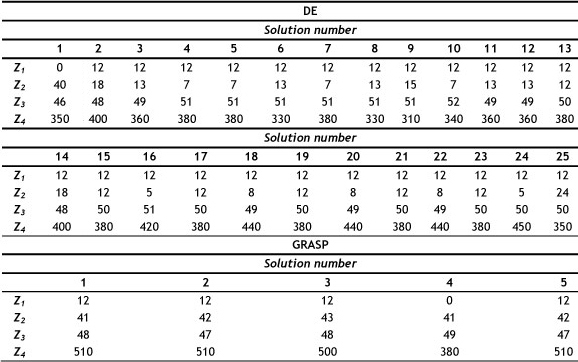
Table 7: Objective values of Pareto Archived set by the proposed DE and GRASP (Problem instance 2)
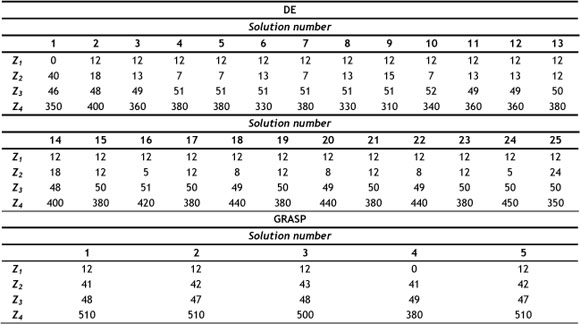
Table 8 lists all possible assignments that may be used in the shift schedule tables. Due to insufficient space in this paper, all assignments are displayed as an abbreviation.
Table 8: Abbreviations of all possible assignments used in the shift schedule tables

The validation of the presented model is proved by solving a small-sized problem (Problem instance 1) and comparing the results with a shift schedule provided manually by the maternity ward supervisor. Tables 9 to 11 represent a comparison between a manual shift schedule and two sample shift schedules obtained by the proposed algorithms (e.g., Solution 1 obtained by the DE, and Solution 4 obtained by the GRASP in Problem instance 1). This comparison confirms the performance of the constraints considered in the model.
Table 9: Shift schedule provided manually and two sample shift schedules obtained by the proposed DE and GRASP (Problem instance 1: Solution no. 1 of DE and Solution no. 4 of GRASP) for Nurses (ID=1 to 8)

Table 10: Shift schedule provided manually and two sample shift schedules obtained by the proposed DE and GRASP (Problem instance 1: Solution no. 1 of DE and Solution no. 4 of GRASP) for Auxiliary nurses (ID=9 to 14)

Table 11: Shift schedule provided manually and two sample shift schedules obtained by the proposed DE and GRASP (Problem instance 1: Solution no. 1 of DE and Solution no. 4 of GRASP) for Co-auxiliary nurses (ID=15 to 20)

It takes more than four days for the ward supervisor to provide a shift schedule manually in the small-sized problem (Problem instance 1). When the number of nurses is greater than 25, and the nurses' preferences increase, the ward supervisor is not capable of providing a shift schedule manually. Since Sina hospital intends to develop the maternity ward and employ more nurses, the hospital managers have decided to automate the nurses' shift scheduling.
To validate the reliability of the proposed algorithms, the following comparison metrics are taken into account:
- Quality metrics: This metric puts together the non-dominated solutions found by both algorithms, and measures the ratios between them. In fact, this metric considers the non-dominated solutions found by both algorithms as a set of solutions. It then acquires non-dominated solutions from this set by using non-dominated relations, and measures what percentage of these non-dominated solutions belongs to each algorithm.
- Spacing metric (SM) [20]: This metric is defined by the following formula:

where d¡ is the Euclidean distance between successive solutions in the obtained non-dominated set of solutions, and dmean is the average of these distances. Spacing metric allows measuring the uniformity of the spread of the solution set points.
- Diversification metric (DM) [20]: This metric measures the spread of the solution set by the following formula:

where
is the Euclidean distance between the non-dominated solutions
and
.
- Hyper area ratio metric (HR) [20]: This metric is defined by the following formula:

where Hes and Hsc are the areas occupied by the solution set of practical PF and the solution set of theoretical PF respectively. (The set of all globally optimal solutions is called the Pareto optimal set, and the set of all non-dominated objective vectors is called the Pareto front (PF). Obtaining an approximation to either the Pareto optimal set or the PF is referred to as Pareto optimisation). Since obtaining theoretical PF is practically impossible, it is produced by all non-dominated solutions provided from both algorithms in this paper. If the value of HR is smaller than 1, the points of practical tradeoff surface are not spread over the whole tradeoff surface, and if the value of HR is greater than 1, the practical tradeoff surface is distant from the tradeoff surface.
- The relative metric (C(F',F")) [20]: The following function transforms two given sets F' and F'' to a real value in the interval [0,1]:
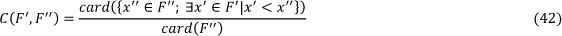
- where card(F") corresponds to the number of elements inside the set F", and x' < x"means that the vector x' dominates the vector x". Therefore, this metric allows for computing the portion of the surface '' that is dominated by the tradeoff surface '. If points in ' dominate to all points in '', then by definition C(F', F") = 1. C(F', F") = 0 implies the opposite.
Table 12 lists the computational time of both algorithms and the values of these comparison metrics.
Table 12: Computational results
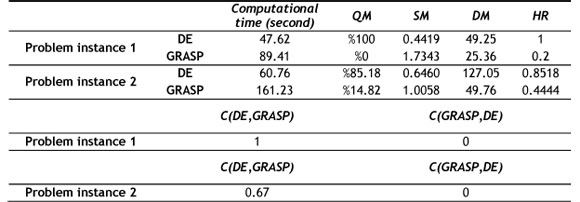
The proposed DE takes less time than the proposed GRASP. Meanwhile, the values of the comparison metrics show that the proposed DE is superior to the proposed GRASP in both problem instances. As a result:
- The proposed DE consumes less time than the proposed GRASP.
- The proposed DE can obtain a greater number of Pareto-optimal solutions with higher qualities than the proposed GRASP.
- The proposed DE acquires non-dominated solutions that have lower less values of spacing metric. This shows that the non-dominated solutions obtained by the proposed DE are distributed more uniformly in comparison with the proposed GRASP.
- The values of the diversification metric in the proposed DE are suffiiciently greater than the proposed GRASP.
- The values of hyper area ratio metric show that the proposed DE has a higher convergence towards the tradeoff surface, i.e. the closer the value of this metric is to 1, the better is the tradeoff surface.
- Based on the relative metric, it is obvious that the proposed DE provides a better performance than the proposed GRASP.
5. CONCLUDING REMARKS
This paper has presented a nurse scheduling problem (NSP) based on a real case study in the maternity ward of Sina Hospital in Isfahan that takes both hospital managers' objectives and nurses' preferences into consideration. Because of the NP-hard class of an NSP, two meta-heuristic algorithms - differential evolution (DE) and greedy randomised adaptive search procedure (GRASP) - have been proposed to solve the given problem. Two problem instances have been designed to evaluate the performance of the constraints considered in the model and the proposed algorithms. The results obtained from the small-sized problem (Problem instance 1) have been compared with a shift schedule that has been drawn up manually by the maternity ward supervisor. The related results have confirmed the performance of the model. Furthermore, some useful comparison metrics - quality metric, spacing metric, diversification metric, hyper area ratio metric, and the relative metric -have been applied to validate the efficiency of the proposed algorithms. The results in this paper show that the proposed DE outperforms the proposed GRASP, and also show that it is capable of improving the quality of acquired solutions. The model presented is applicable to other wards and hospitals with some modifications. Future research will be developed around the fuzzy nature of hospital managers' objectives and nurses' preferences, and new solution methods.
REFERENCES
[1] Abdennadher, S. & Schlenker, H. 1999. Nurse scheduling using constraint logic programming, in Proceedings of the 16th National Conference on Artificial Intelligence, pp 838-843. [ Links ]
[2] Aickelin, U. & Dowsland, K.A. 2000. Exploiting problem structure in a genetic algorithm approach to a nurse rostering problem, Journal of Scheduling, 3(3) pp 139-153. [ Links ]
[3] Aickelin, U. & Dowsland, K.A. 2004. An indirect Genetic Algorithm for a nurse-scheduling problem, Computers & Operations Research, 31(5), pp 761-778. [ Links ]
[4] Aiex, R.M., Binato, S. & Resende, M.G.C. 2003. Parallel GRASP with path-relinking for job shop scheduling, Parallel Computing, 29(4), pp 393-430. [ Links ]
[5] Akjiratikarl, C., Yenradee, P. & Drake, P.R. 2007. PSO-based algorithm for home care worker scheduling in the UK, Computers & Industrial Engineering, 53(4), pp 559-583. [ Links ]
[6] Alfares, H.K. 1998. An efficient two phase algorithm for cyclic days-off scheduling, Computers & Operations Research, 25(11), pp 913-923. [ Links ]
[7] Alvarez-Valdes, R., Crespo, E., Tamarit, J.M. & Villa, F. 2008. GRASP and path relinking for project scheduling under partially renewable resources, European Journal of Operational Research, 189(3), pp 1153-1170. [ Links ]
[8] Armentano, V.A. & de Franca Filho, M.F. 2007. Minimizing total tardiness in parallel machine scheduling with setup times: An adaptive memory-based GRASP approach, European Journal of Operational Research, 183(1), pp 100-114. [ Links ]
[9] Azaiez, M.N. & Al Sharif, S.S. 2005. A 0-1 goal programming model for nurse scheduling, Computers & Operations Research, 32(3), pp 491-507. [ Links ]
[10] Bard, J. & Purnomo, H.W. 2005. Preference scheduling for nurses using column generation, European Journal of Operational Research, 164(2), pp 510-534. [ Links ]
[11] Bechtold, S.E. & Jacobs, L.W. 1990. Implicit modeling of flexible break assignments in optimal shift scheduling, Management Science, 36(11), pp 1339-1351. [ Links ]
[12] Bellanti, F., Carello, G., Della Croce, F. & Tadei, R. 2004. A greedy-based neighborhood search approach to a nurse rostering problem, European Journal of Operational Research, 153(1), pp 2840. [ Links ]
[13] Blochliger, I. 2004. Modeling staff scheduling problems: A tutorial, European Journal of Operational Research, 158 (3), pp 533-543. [ Links ]
[14] Bradley, D. & Martin, J. 1990. Continuous personnel scheduling algorithms: A literature review, Journal of the Society of Health Systems, 2(2), pp 8-23. [ Links ]
[15] Burke, E.K., De Causmaecker, P., Van den Berghe, G. & Van Landeghem, H. 2004. The state of the art of nurse rostering, Journal of Scheduling, 7(6), pp 441-499. [ Links ]
[16] Burke, E.K., Li, J. & Qu, R. 2010. A hybrid model of integer programming and variable neighbourhood search for highly-constrained nurse rostering problems, European Journal of Operational Research, 203(2), pp 484-493. [ Links ]
[17] Cerulli, R., Gaudioso, M. & Mautone, R. 1992. A class of manpower scheduling problems, Methods and Models of Operations Research, 36(1), pp 93-105. [ Links ]
[18] Cheang, B., Li, H., Lim, A. & Rodrigues, B. 2003. Nurse rostering problems - a bibliographic survey, European Journal of Operational Research, 151(3), pp 447-460. [ Links ]
[19] Chiaramonte, M.V. & Chiaramonte, L.M. 2008. An agent-based nurse rostering system under minimal staffing conditions, International Journal of Production Economics, 114(2), pp 697- 713. [ Links ]
[20] Coello Coello, C.A., Lamont, G.B. & Van Veldhuizen, D.A. 2007. Evolutionary algorithms for solving multi-objective problems, Springer Science+Business Media, LLC, New York, USA. [ Links ]
[21] Costa, M.C., Jarray, F. & Picouleau, C. 2006. An acyclic days-off scheduling problem, 4OR: A Quarterly Journal of Operations Research, 4(1), pp 73-85. [ Links ]
[22] Damak, N., Jarboui, B., Siarry, P. & Loukil, T. 2009. Differential evolution for solving multimode resource-constrained project scheduling problems, Computers & Operations Research, 36(9), pp 2653-2659. [ Links ]
[23] Dowsland, K.A. 1998. Nurse scheduling with tabu search and strategic oscillation, European Journal of Operational Research, 106(2-3), pp 393-407. [ Links ]
[24] Easton, F., Rossin, D. & Borders, W. 1992. Analysis of alternative scheduling policies for hospital nurses, Production and Operations Management, 1(2), pp 159-174. [ Links ]
[25] Emmons, H. & Fuh, D.S. 1997. Sizing and scheduling a full-time and part-time workforce with off-day and off-weekend constraints, Annals of Operations Research, 70(1), pp 473-492. [ Links ]
[26] Ernst, A.T., Jiang, E., Krishnamoorthy, M. & Sier, D. 2004. Staff scheduling and rostering: A review of applications, methods and models, European Journal of Operational Research, 153(1), pp 3-27. [ Links ]
[27] Feo, T. & Resende, M.G.C. 1995. Greedy randomized adaptive search procedures, Journal of Global Optimization, 6(2), pp 109-133. [ Links ]
[28] Glass, C.A. & Knight, R.A. 2010. The nurse rostering problem: A critical appraisal of the problem structure, European Journal of Operational Research, 202(2), pp 379-389. [ Links ]
[29] Gutjahr, W.J. & Rauner, M.S. 2007. An ACO algorithm for a dynamic regional nurse-scheduling problem in Austria, Computers & Operations Research, 34(3), pp 642-666. [ Links ]
[30] Hung, R. 1991. A cyclical schedule of 10-Hour, four-day workweeks, Nursing Management, 22(5), pp 30-33. [ Links ]
[31] Karp, R.M. 1972. Reducibility among combinatorial problems, in R.E. Miller, J.W. Thatcher (eds), Complexity of Computer Computations, Plenum Press, New York, pp 85-103. [ Links ]
[32] Lagodimos, A.G. & Leopoulos, V. 2000. Greedy heuristic algorithms for manpower shift planning, International Journal of Production Economics, 68(1), pp 95-106. [ Links ]
[33] Meisels, A., Gudes, E. & Solotorevski, G. 1995. Employee timetabling, constraint networks and knowledge-based rules: A mixed approach, in E.K. Burke, P. Ross (eds), Practice and Theory of Automated Timetabling; First International Conference Edinburgh, Springer, pp 93-105. [ Links ]
[34] Meyer auf'm Hofe, H. 1997. ConPlan/SIEDAplan: Personnel assignment as a problem of hierarchical constraint satisfaction, in Proceedings of the 3rd International Conference on Practical Application of Constraint Technology, pp 257-272. [ Links ]
[35] Miller, H.E. 1984. Implementing self scheduling, The Journal of Nursing Administration, 14(3), pp 33-36. [ Links ]
[36] Mohan, S. 2008. Scheduling part-time personnel with availability restrictions and preferences to maximize employee satisfaction, Mathematical and Computer Modeling, 48(11-12), pp 18061813. [ Links ]
[37] Musliu, N., Gartner, J. & Slany, W. 2002. Efficient generation of rotating workforce schedules, Discrete Applied Mathematics, 118(1-2), pp 85-98. [ Links ]
[38] Nascimento, M.C.V., Resende, M.G.C. & Toledo, F.M.B. 2010. GRASP heuristic with path- relinking for the multi-plant capacitated lot sizing problem, European Journal of Operational Research, 200(3), pp 747-754. [ Links ]
[39] Osogami, T. & Imai, H. 2000. Classification of various neighborhood operations for the nurse scheduling problem, Lecture Notes in Computer Science, 1969, pp 72-83. [ Links ]
[40] Pan, Q.K., Tasgetiren, M.F. & Liang, Y.C. 2008. A discrete differential evolution algorithm for the permutation flow shop scheduling problem, Computers & Industrial Engineering, 55(4), pp 795-816. [ Links ]
[41] Pan, Q.K., Wang, L., Gao, L. & Li, W.D. 2011. An effective hybrid discrete differential evolution algorithm for the flow shop scheduling with intermediate buffers, Information Sciences, 181(3), pp 668-685. [ Links ]
[42] Resende, M.G.C. 2000. Greedy randomized adaptive search procedures (GRASP), Technical Report TR 98.41.1, AT & T Labs-Research. [ Links ]
[43] Ringl, K.K. & Dotson, L. 1989. Self-scheduling for professional nurses, Nursing Management, 20(2), pp 42-44. [ Links ]
[44] Siferd, S.P. & Benton, W.C. 1992. Workforce staffing and scheduling: Hospital nursing specific models, European Journal of Operational Research, 60(3), pp 233-246. [ Links ]
[45] Sitompul, D. & Randhawa, S. 1990. Nurse scheduling models: A state-of-the-art review, Journal of the Society of Health Systems, 2(1), pp 62-72. [ Links ]
[46] Smith-Daniels, V., Schweikhart, S. & Smith-Daniels, D. 1988. Capacity management in health care services: Review and future research directions, Decision Sciences, 19(4), pp 889-919. [ Links ]
[47] Storn, R. & Price, K. 1995. Differential evolution: A simple and efficient adaptive scheme for global optimization over continuous spaces, Technical Report TR-95-012, International Computer Science Institute, Berkeley, California. [ Links ]
[48] Storn, R. & Price, K. 1997. Differential evolution: A simple and efficient heuristic for global optimization over continuous spaces, Journal of Global Optimization, 11(4), pp 341-359. [ Links ]
[49] Techawiboonwong, A., Yenradee, P. & Das, S.K. 2006. A master scheduling model with skilled and unskilled temporary workers, International Journal of Production Economics, 103(2), pp 798809. [ Links ]
[50] Topaloglu, S. & Selim, H. 2010. Nurse scheduling using fuzzy modeling approach, Fuzzy Sets and Systems, 161(11), pp 1543-1563. [ Links ]
[51] Tsai, C.C. & Li, S.H.A. 2009. A two-stage modeling with genetic algorithms for the nurse scheduling problem, Expert Systems with Applications, 36(5), pp 9506-9512. [ Links ]
[52] Valls, V., Perez, A. & Quintanilla, S. 2009. Skilled workforce scheduling in service centers, European Journal of Operational Research, 193(3), pp 791-804. [ Links ]
[53] Wang, L., Pan, Q.K., Suganthan, P.N., Wang, W.H. & Wang, Y.M. 2010. A novel hybrid discrete differential evolution algorithm for blocking flow shop scheduling problems, Computers & Operations Research, 37(3), pp 509-520. [ Links ]
[54] Warner, M. 1976. Nurse staffing, scheduling, and reallocation in the hospital, Hospital & Health Services Administration, 21(3), pp 77-90. [ Links ]
[55] Winstanley, G. 2004. Distributed and devolved work allocation planning, Applied Artificial Intelligence, 18(2), pp 97-115. [ Links ]
* Corresponding author.
1 The author was enrolled for a PhD degree (Industrial Engineering) in the Department of Industrial Engineering, Islamic Azad University - Science and Research Branch.















