Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Industrial Engineering
versão On-line ISSN 2224-7890
versão impressa ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.23 no.2 Pretoria Jan. 2012
GENERAL ARTICLES
Can complexity analysis support business performance insight?*
A.C.J. van Rensburg
Department of Industrial and Systems Engineering University of Pretoria, South Africa Antoniej@up.ac.za
ABSTRACT
Most people intuitively understand complexity, but being able to analyse it scientifically is not a common practice. For business executives, 'complexity' must be one of the most important concepts to understand, as it directly impacts business performance. From a business improvement perspective it is critical to quantify complexity, as engineering optimisation models require some level of clarity and understanding for decision making. Excess complexity prevents a proper understanding of the business system, which makes accurate forecasting impossible, and so increases the risk of failure. This paper uses Shannon's entropy to measure and gain insight into complexity, and shows how it can be used to gain better insight into the performance of a business system - especially when dealing with non-linear relationships between business components.
OPSOMMING
Alhoewel die meeste mense kompleksiteit verstaan, is die ontleding daarvan op 'n wetenskaplike manier nie algemene praktyk nie. Vir die uitvoerende direkteure van maatskappye is 'kompleksiteit' een van die belangrikste faktore omrede dit die prestasie van die onderneming direk beïnvloed. Gesien vanuit die perspektief van besigheidsoptimisering, raak dit krities dat kompleksiteit kwantitatief uitgedruk moet word sodat die nodige ingenieursmodelle ingespan kan word vir besluitnemingsdoeleindes. Indien die besigheidstelsel te veel kompleksiteit ervaar, maak dit die verstaan van die stelsel onnodig moeilik, wat op sy beurt weer veroorsaak dat voorspellingsmodelle onbruikbaar raak. Dit verhoog die kans op mislukking van die onderneming. In hierdie artikel word 'Shannon's entropy' gebruik om kompleksiteit te meet om sodoende beter insig in besigheidsprestasie te verkry - veral wanneer daar nie-lineêre verwantskappe bestaan tussen die verskillende komponente.
1. INTRODUCTION
In its simplest definition, we can describe a business as the interaction of 'man', 'machine', and 'money' working together towards a common goal. The harmony of this is important for executives: they are accountable for ensuring that the business operates at an optimal level in order to generate maximum shareholder value. Unfortunately, in the ordinary course of business executives are faced with the negative consequences of events due to uncertainty. Traditionally a number of risk strategies are followed to mitigate the effect of these events, depending on their origin. For example, where one wants to deal with uncertainty in supply or demand, one will follow a 'buffering' strategy; industrial strikes will invoke another strategy; and 'acts of God' yet another [7]. When a crisis occurs, it disrupts how these organisational components work together, and puts the survival of the business at risk.
According to Professor Steven Schwarcz of Duke University, a financial crisis can be divided conceptually into a number of categories [12]. He calls them the 3Cs and the TOC: 'conflict', 'complacency', and 'complexity', and a type of 'tragedy of the commons'. This doesn't only apply to a financial crisis, but also to crisis in business, as businesses are microcosms of larger business and financial networks. In this study, we focus on the category of 'complexity', and on how complexity can hide relationships in a business' key performance numbers. This study shows that traditional statistical analysis measures can miss these relationships, especially if they are non-linear. This is done with the proposition that a crisis within a business system is closely linked to the business' level of complexity and to its surrounding environment. The implication of this is that complexity plays an important role in the lifecycle of a crisis - that is, how it originates, the propagation routes it follows in the business, and how one could deal with it.
Most people intuitively understand complexity, but being able to analyse and manage it scientifically is not common practice in boardrooms. In the discipline of business improvement it is imperative that complexity be quantified, as engineering and scientific models require some level of quantitative clarity in order to provide predictability in business performance models. Excess complexity in a business system effects forecasting and understanding of the impact of change on the business, thus increasing the risk of a crisis if it is not understood and managed well. The purpose of this paper is to show how certain basic components of complexity can be measured through Shannon's entropy in order to gain a deeper understanding of the business system performance - especially if there are non-linear relationships between business components. To do this, the well-known Anscombe data [1] set is used to demonstrate how non-linear relationships can skew business performance indicators.
2. UNDERSTANDING COMPLEXITY
Very few people agree about the meaning of the word 'complexity'. To describe the discipline of complexity management as complex is an understatement. The New England Complexity Institute [19] defines the following terminology as important in the complexity discipline: emergence, system, information, patterns, chaos, observer, network, ecosystem, fractals, feedback, entropy, thermodynamics, fuzzy, correlation, hierarchy, vagueness, evolution, dynamics, pattern formation, non-linear, relationships, interdependence, environment, organisation, superposition, and universality. All of these concepts sound interesting; but ultimately to measure is to have the ability to manage what is important to manage. This means that if we want to manage complexity - and especially if we use words like 'fuzzy', 'entropy', or 'robustness' - we need to be able to quantify complexity in some measurable way.
In the quest for a definition of complexity, Rissanen's explanation of complexity provides a simple but elegant approach: that 'complexity' is a function of information and noise [11]. This means that if we want to focus on complexity within a business system, we need to express it in terms of the information (structure) of the system and the noise (variation)- within the system. The structure of a business system can be explained according to a number of system thinking principles [18]. In essence, the structure of a business system consists of system objects, which can be one of two classes: 'objects' or 'relationships'. Objects can be classified into 'entities', 'activities', or 'resources', where entities are transformed through activities while using resources. This happens according to the various relationships between the objects [17]. For a particular business system being studied, this occurs with a common purpose, within definable boundaries, control, and relevant system attributes.
According to the second law of thermodynamics, these relationships will not be stable over time, but will change due to the energy in the system [4]. To relate this to the definition of complexity: one should identify the system components and measure the variation in relationships between them in order to get an understanding of the level of complexity of the system.
3. IMPORTANT COMPLEXITY CONCEPTS
Before complexity in a business system can be understood, one needs to understand a number of core concepts when dealing with it. The first concept, 'complicated versus complex', addresses the issue of stochastic versus deterministic systems [6]. For example, a Breitling watch has more than a thousand handcrafted mechanical parts assembled in a small casing to deliver its purpose - telling the time. No one wants this watch if it has elements of randomness in telling the time; it is thus a complicated deterministic system. However, experiencing a crowd at Euro Disney during the European summer holidays is the opposite of a complicated deterministic system. Here individuals form a complex system, moving according to their own individual needs and wants, creating random crowd movement which is largely unpredictable. A complex system does not necessarily have to have thousands of moving parts; if it has stochastic behaviour in its structure, it is complex.
The second important concept is that of 'incompatibility'. Zadeh [23] defined the law of incompatibility: the more complex a system becomes, the less precise it can be. Figure 1 and Figure 2 demonstrate this. Figure 1 depicts a system that is apparently more random than that in Figure 2. This means that it is difficult to describe it more precisely. Figure 2 can easily be modelled by the equation y=a+bx; while it is not so evident which equation will adequately describe Figure 1.
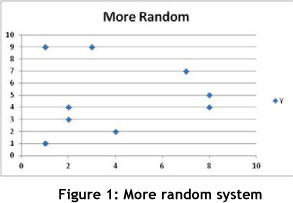
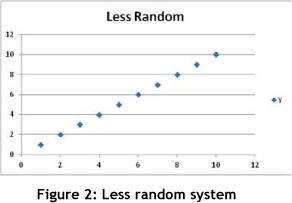
The third important concept deals with 'fragility'. Fragility becomes important when one starts to manage complex business systems, and especially if one needs to create a certain level of robustness in the system. In the case of the Euro Disney example, park operations cannot manage every single individual, but they can make sure that there is sufficient capacity in the park to allow for the random behaviour of people. If this were not done, the system could collapse due to its fragility. This means that fragility is that point in the system where a state change occurs - i.e. the system collapses due to the impact of external factors on the system. The fragility of a system is then a function of the uncertainty of its environment and the level of complexity within the system itself [10]. A- business system with high complexity will be fragile if its own environment is highly uncertain.
The effect of this is that in a system - whether it be business, economic, governmental, or personal - it is more important to survive than to strive to be optimal. One cannot predict the future; nature constantly changes. Neither can one understand or calculate the probability of events happening. But all is not lost: one can manage the structure of the system so that the point at which relationships can collapse is kept at a good distance. This means that an organisation should focus on ensuring that the system is robust and operates at a good distance from its fragility - the point where changes in state will occur if the external environment changes.
The purpose of understanding and measuring complexity is to obtain good insight into the complexity of the system, and then be able to formulate strategies for making the business system survive. According to Dr Ian Dover of the Simpler Business Institute [22], management can focus on creating a less complex business environment by:
a) Focusing on the most from the least by applying the 80/20 Pareto principle in all that happens in the business.
b) Ensuring simple, consistent problem-solving so that people 'bring solutions rather than problems'.
c) Making all understand that the focus should be on delivering customer value, which is simply 'the things we do that make our customers more successful'.
d) Searching for and removing bottlenecks across all business processes to make it easier for them to do good work.
e) Always simplifying things before automating them.
These concepts underpin the fact that, although one cannot predict uncertainties, one should gain insight into the business system to understand how complex the system is, and what strategies should be followed to ensure a level of robustness for survival when a crisis happens.
4. THE IMPACT OF COMPLEXITY ON A BUSINESS SYSTEM
The number of common and critical problems described earlier in this paper directly impacts on the ability of the business to execute operations effectively and efficiently [12]. To test this hypothesis, a recent empirical study was completed by the Department of Industrial and Systems Engineering at the University of Pretoria. In this study, ten publically-listed South African companies in the information technology sector were studied to test the relationship between profitability and complexity. The results showed that there is a high correlation of 98% between profitability and an organisation's robustness to deal with complexity [3].
One of the most common results of complexity is that it keeps stakeholders from gaining an adequate understanding of the business and thus from managing it efficiently and effectively. Technology can be blamed for this, as this situation results from the increased amount of information to be processed in order to create organisational understanding. Within this amount of information, complexity hides seemingly unrelated events in such a way that lower level sub-activities are not visible. From a risk perspective, actual risks such as fraud can be embedded in the layers of the business activities, becoming even more critical if there is limited time to assess all possible outcomes of these events.
Inter-related relationships in the business are created through information technology, communication systems, and social networks. Information can be transmitted rapidly through these systems, causing an exponential ripple effect of events. As complexity creates critical hubs in this system, it can produce a much more rapid propagation of contamination through the system. The 2007 financial crisis taught the world a lesson about these types of problems: it is vital to manage complexity in financial and business systems.
It is common knowledge that, in order to manage and improve, we need to be able to measure in order to understand. In the next section we create a way to measure and understand complexity in a simple way.
5. MEASURING COMPLEXITY
As stated earlier, one can adopt a 'meta view' of the world and see all systems as consisting of interacting objects. These relationships change over time; and while some of the objects 'die', new ones will emerge from unions. This forms the basis for volatility and risk in the system, because as the system grows, it can explode, implode, or start behaving irrationally. The most important and insightful exercise in complexity management is to think about the interdependencies in the system.
This thinking provides the basis for understanding unpredictable behaviours as objects create hidden interdependencies through non-linear relationships. This behaviour is simply a result of the strength of interdepencies as they increase or decrease over time. If we state that complexity is a dynamic attribute of any system, represented by the combination of 'structure' and 'variation', then we need to be able to measure this to begin to understand the complexity within the system [6,16].
During the 1940s, Edward Tolman [14] developed the concept of fuzzy cognitive maps (FCM), with the sole purpose of helping individuals to process information in metaphorical spatial environments (see Figure 3). This happens as information is acquired, coded, stored, recalled, and decoded in the context of the relative locations and attributes of phenomena. A fuzzy cognitive map calculates the relationships between the objects within this mental landscape (fitness landscape), based on the strength of the relationship. Applying this to a system, we can define its FCM if we can measure the correlations of the relationships in the system, and use them to create the FCM.
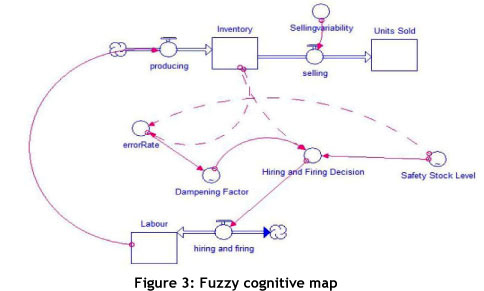
Traditionally, an analyst develops an FCM from structured interviews with functional experts, based on how they perceive the system under study [14]. We cannot use this approach to model structure and variation, as a more quantitative, unbiased measurement of relationships between the system objects is required.
Using the standard Pearson correlation coefficient, one can calculate whether there is a strong linear relationship (R) between two variables. This means that if R is close to 1, then a strong relationship exists; or if R is close to 0, then a weak relationship exists. Where one has to measure non-linear relationships between variables (system components), this poses a problem, as the correlation coefficient is not suitable to deal with non-linear relationships [8].
One way of overcoming this problem is to use Shannon's entropy and mutual information calculations. In 1948, Shannon surprised the communication theory community by showing how one could calculate communication channel capacity from the channel noise characteristics [13]. This he named 'entropy', in reference to the second law of thermodynamics, arguing that if the entropy of the source is less than the capacity of the channel, asymptotically error-free communication can be achieved [13]. The entropy of a discrete random variable X with a probability mass function p(x) is defined by:
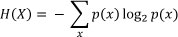
If entropy is the uncertainty of a single random variable, one can define conditional entropy H(X|Y) where the entropy of a random variable (X) is conditionally explained by another variable (Y). The reduction of uncertainty due to another variable is called 'mutual information'. The measure of dependence between the two variables is then calculated as follows:
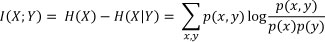
Mutual information is always non-negative and equal to zero only if X and Y are independent [4].
Instead of using the correlation calculation (R), we calculate the mutual information between two variables to determine the relationship between them. If we calculate this for every variable in relation to all other variables, an M X N matrix is obtained that represents a valued undirected graph. This MXN matrix provides insight into the non-linear relationships in the business system, and hence into the level of complexity that exists due to structure and the variation between the variables. An example is given in the next part of the paper.
6. EXAMPLE
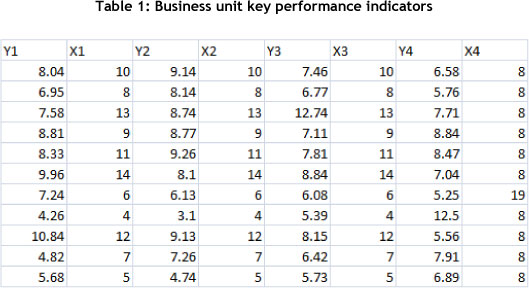
The following dataset represents the key performance indicators for a hypothetical company XYZ, consisting of four main business units: BU1, BU2, BU3, and BU4 (Table 1). The Yn variables represent the business unit performance output (dependent variables), while Xn represents the input (independent variables) (where n = business unit number).
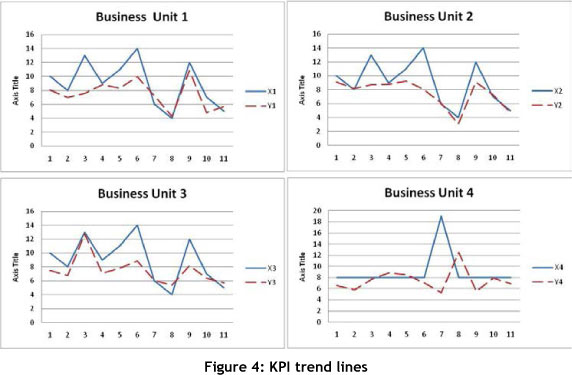
The following figures show the trend lines for the business unit variables over time. To understand future behaviour, traditional time series analysis techniques can be used to forecast the future performance of these variables [9].
Very often, management do not want to manage their business key performance indicators (KPIs) with a black box approach, and are more interested in the explanatory relationships between them. This enables significantly deeper control and judgment insight into their behaviour for increased efficiency and effectiveness [9].
6.1 Standard statistical measurements
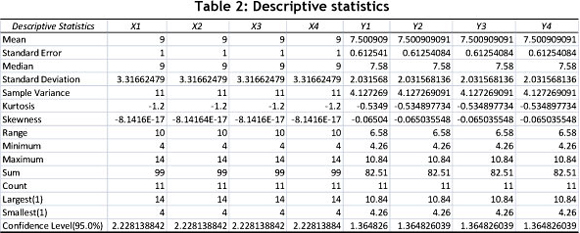
The first step is to analyse the descriptive statistics, correlations, and regression results of the data. Table 2 shows typical descriptive statistics, as calculated in Microsoft Excel.
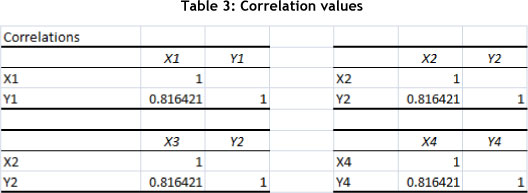
Correlation analysis between the independent and dependent variable pairs shows that a similar correlation value is calculated for each pair: 0.816421. This indicates a strong correlation between the input and the output, suggesting that the right KPIs were selected for measurement.
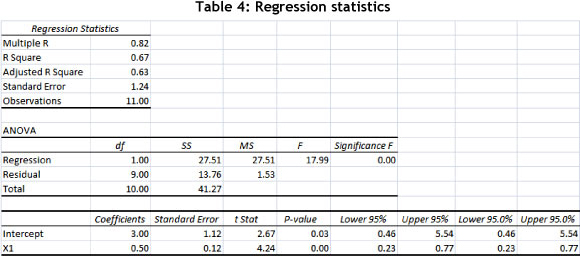
Regression analysis per business unit calculates the same output, as can be seen in Table 4. The single regression equation y = 0.5Xn + 3 provides a forecasting tool for each of the business units to understand the behaviour of Yn against anticipated changes in Xn (Figure 4).
6.2 Entropy measurement
From a business analysis and forecasting perspective, all four business units appear to share identical statistical properties - a fact that enables good insight into the business unit performance. But what happens if we analyse the complexity (structure and variation) of the datasets using Shannon's entropy, mutual information, and standard graph measurements? For entropy and mutual information calculations, the statistical package R is used with the natural logarithm and bin size based on the square root of the number of samples (n=11 )[4,21]. The following table (Table 5) shows the results for entropy calculations.

Table 6 shows the mutual information values as calculated between the variables. Note that the diagonal values are the entropy values of the individual variables.
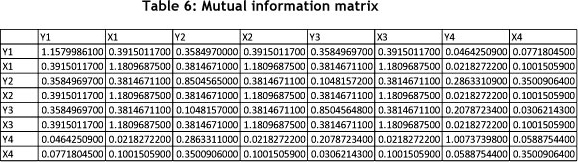
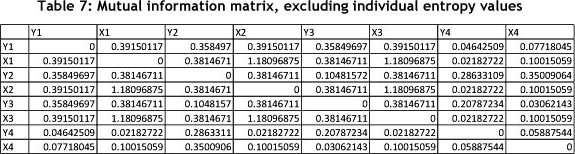
Table 7 excludes the diagonal values, and shows the matrix sum of the symmetrical mutual information values as 18.25 [4]. Note that this value is relative, and only carries value if one compares different time periods or similar systems with each other.
6.3 Network measurements
In order to create a visual FCM map, the mutual information matrix in Table 7 is imported into the social network analysis (SNA) software package Netminer [20]. To prepare the 1-mode matrix for analysis, the mutual information values are used as relationship weights to create the valued undirected matrix. The matrix is further dichotomised with any mutual information values below 0.2 as 0, and above 0.2 as actual values in order to filter meaningful relationships.
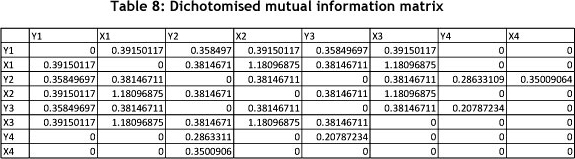
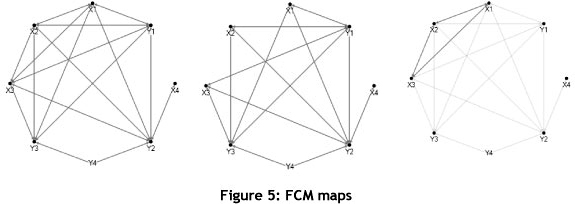
Figure 5 shows the circular graph models for all mutual information values; the far left graph shows all values, the middle graph shows values between zero and 0.40, and the far right graph shows all values above 0.4.
The density of the network can be calculated with the following formula:
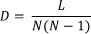
where D = density of network, L = number of relationships, and N = number of active objects [20]. For this problem, L= 34 and N = 8, which gives a network density of 0.61.
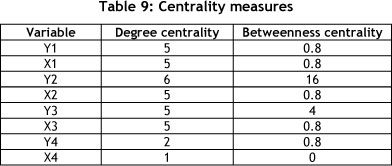
By applying standard SNA centrality measures [20] to the FCM, one gains insight into the importance of these relationships. Two popular measures - 'degree centrality' and 'betweenness centrality' - are shown in Table 9. 'Degree centrality' measures the number of relationships with each system object, indicating the hubs in the system, while 'betweenness centrality' measures the importance of the object relationships in the network.
6.4 Interpretation of results
From the entropy and network measurements, the following comments can be made for the business system within the context of the Shannon's entropy complexity understanding:
a) From Table 5, Shannon's entropy informs us that the eight variables have different levels of variation. Variable Y1 contains the most variation, with X1, X2, X3, Y4, Y2, and Y3 in descending order. X4 contains the least entropy (variation).
b) Shannon's entropy states that the entropy of the variables (as measured in bits) determines the required capacity to transfer the signal from the receiver to the sender. Similarly, we can deduce that because of the variation in the different variables, capacity in the business units needs to cater for the levels of variation experienced with the variables. That is, capacity to deal with the output variable Y1 needs to be greater than that of the input variable X4, due to the variation. According to Hopp [7], we can assume that variation exists in the arrival times of X1 as input variable, and Y1 due to the variation in processing to produce Y1.
c) As opposed to the traditional statistical results obtained in paragraph 6.1, mutual information measurements show the top three correlations and the weakest three relationships in Table 10 and Table 11 respectively.


This shows that the independent input variables are highly correlated, while the output variables show little correlation. Of concern within the context of results obtained in paragraph 6.1, dependent (Yn) and independent variables (Xn) are not correlated. Assuming that the business units have control over how input is converted into output, the lack of correlation between them should cause concern.
d) The density of the network is 0.61. Networks with a density of above 0.5 are difficult to change, mostly due to the number of relationships between the variables [10].
e) From a hub perspective, Y2 has six relationships, while Y1, X1, X2, Y3, and X3 have five each [Table 9]. This means that this particular system has redundancy in terms of hubs, with the most connected hub being Y2.
f) The 'betweenness centrality' measurement indicates that Y2 (value=16) is the most important hub in the system, with Y3 (value=4) the second most important one with regard to propagation properties. This means that any change impact on Y2 and Y3 will spread the quickest through the system.
This seemingly contradictory behaviour in the data sets from the point of view of static behaviour (traditional statistical analysis) and dynamic behaviour (complexity analysis) should not surprise those who are familiar with Anscombe's quartet [1]. Anscombe developed the quartet during the 1970s to demonstrate how dangerous it is to analyse data without any visual inspection.
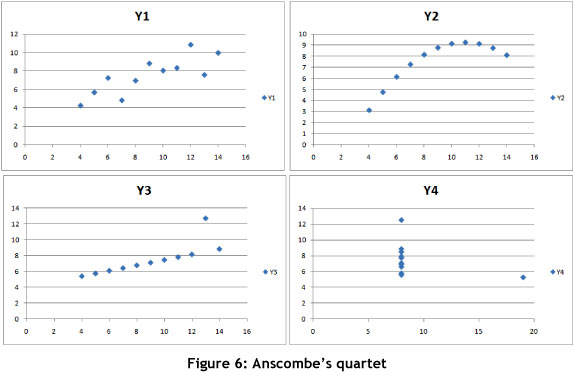
This clearly demonstrates that complexity analysis provides deeper insights into the dynamic behaviour of an organisation's key performance indicators. Using traditional statistical analysis on the static indicators is only half the story. One needs to understand how indicators behave both collectively and individually within the operating domain. Analysis of these dynamic insights offers a business insight into how the system behaves, and with quantitative support it can create strategies to reduce complexity in the business to acceptable levels of risk. This means that complexity analysis provides a much deeper- insight into the behaviour of the KPIs, enabling better planning, control, and forecasting of the business systems than do traditional approaches.
7. CONCLUSION
Complexity is a dynamic property of any system, including our business systems. It exists because of the structural relationships between the system components, together with variation in these relationships. Technology can be blamed for driving the evolution of modern organisations into complex interdependent systems with many non-linear cause-and-effect relationships; but trying to manage this through traditional methods alone can produce unforeseen failures and events. Organisations therefore need to identify complexity and its origins, measure it, and quantify strategies to deal with it. Complexity management thus becomes an important risk mitigation strategy to deal with crisis events in the organisation, including an understanding of where they might occur, and how they can propagate through the business.
Various arguments about the 2007/2010 financial crisis call for the establishment of central banking entities to monitor and intervene in the financial markets to pre-empt future crashes. Similarly, organisations need to define their own roles and responsibilities to deal with internal complexity. One could argue that these roles should be given to strategy or finance units; but a strong case can be made for risk management being the ideal vehicle to deal with mitigation strategies and actions on complexity. Whether its task should be to measure and report on complexity is not relevant; executives should agree to keep complexity management on the agenda as a standard point of discussion.
In 1998, in The collapse of complex societies, Joseph Tainter argued that the value of complexity is positive early in the system cycle - that is, it creates more than is required [15]. He found that societies collapse because, as stress increases in the system, they become too inflexible to respond. It is not that the system does not want to respond: it cannot. It becomes a huge interlocking system that is unlikely to respond to any change.
Collapse is nature's last remaining method of simplification. And that is exactly where the risk lies for an organisation's stakeholders. Complexity analysis - and the subsequent management of it - provides insight into the behaviour of the business system, and whether a crisis is imminent. Rather than ignoring it, organisations need to focus on complexity, measure it, analyse it, and act upon it. In this paper we have used Shannon's entropy to measure the correlation of typical non-linear relationships in a hypothetical system to show that it can be used to identify important characteristics of complexity through a fuzzy cognitive map.
REFERENCES
[1] Anscombe, F.J. 1973. Graphs in statistical analysis, The American Statistician, February, 17-21. [ Links ]
[2] Checkland, P. & Scholes, J. 1992. Soft systems methodology in action, John Wiley. [ Links ]
[3] Clarens, J. 2011. Determining the relationship between complexity and company profitability, Final year report, Department of Industrial Engineering, University of Pretoria. [ Links ]
[4] Cover, T.M. & Thomas, J.A. 2006. Elements of information theory, Wiley & Sons, New York. [ Links ]
[5] Gottfredson, M. & Aspinall, K. 2005. Innovation versus complexity, Harvard Business Review, November, 62-71. [ Links ]
[6] Grassberger, P. 1986. Toward a quantitative theory of self-generated complexity, International Journal of Theoretical Physics, 25(9), 907-938. [ Links ]
[7] Hopp, W.J. 2008. Supply chain science, McGraw-Hill. [ Links ]
[8] Li, W. 1990. Mutual information functions versus correlation functions, Journal of Statistical Physics, 60, 823-837. [ Links ]
[9] Makridakis, S.G., Wheelwright, S.C. & Hyndman, R.J. 1993. Forecasting: Methods and applications, 3rd edition, Wiley & Sons, New York. [ Links ]
[10] Marczyk, J. 2010. A new theory of risk and rating, Editrice, Italy. [ Links ]
[11] Rissanen, J. 1989. Stochastic complexity in statistical inquiry, World Scientific Publishing Company, New Jersey. [ Links ]
[12] Schwarcz, S.L. 2010. The global financial crisis and systemic risk, Leverhulme Lectures 2010, University of Oxford. [ Links ]
[13] Shannon, C.E. 1948. A mathematical theory of communication, The Bell System Technical Journal, July, 379-423. [ Links ]
[14] Tolman, E.C. 1948. Cognitive maps in rats and men, Psychological Reviews, 55(4), 189-208. [ Links ]
[15] Tainter, J. 1988. The collapse of complex societies, Cambridge University Press, New York. [ Links ]
[16] Van Emden, M.H. 1975. An analysis of complexity, Mathematical Centre Tracts, Amsterdam. [ Links ]
[17] Van Rensburg, A. 1996. An open solution methodology to problem solving, PhD thesis, University of Pretoria, South Africa. [ Links ]
[18] Van Rensburg, A. 2011. Principles for modelling business processes. The IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, ISBN 978-1-145770738-4, 1710-1714. [ Links ]
[19] www.necsi.edu. Last accessed 20 December 2011. [ Links ]
[20] www.netminer.com. Last accessed 20 December 2011. [ Links ]
[21] www.r-project.org. Last accessed 20 December 2011. [ Links ]
[22] www.simplerbusiness.com. Last accessed 2 June 2011. [ Links ]
[23] Zadeh, L. 1969. Biological application of the theory of fuzzy sets and systems. The Proceedings of an International Symposium on Biocybernetics of the Central Nervous System, Boston: Little Brown, 199-206. [ Links ]
* This article is an extended version of a paper presented at the 2011 ISEM conference.














