Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.12 n.1 Johannesburg 2022
http://dx.doi.org/10.4102/sajce.v12i1.1191
ORIGINAL RESEARCH
Associations between early numeracy and mathematics-specific vocabulary
Hanrie S. Bezuidenhout
Department of Education, Faculty of Education, University of Johannesburg, Johannesburg, South Africa
ABSTRACT
BACKGROUND: Early numeracy development is supported by linguistic features such as mathematics-specific vocabulary. Researchers have established a link between the amount and quality of children's exposure to mathematics-specific vocabulary and their numeracy learning. Studies have also shown that children from low socio-economic status are less exposed to mathematics-specific vocabulary and also tend to underperform on mathematics assessments. South African children consistently perform poorly on local and international mathematics assessments.
AIM: To describe associations between numeracy and mathematics-specific vocabulary of the sample who participated in the study.
SETTING: Participants in this study are from Quintile 1 schools and receive social grants from the South African government.
METHOD: 133 Grade 1 and 2 children completed assessments for (1) early numeracy (MARKO-D SA), (2) mathematics-specific vocabulary (MMLT) and (3) early reading (EGRA). Correlation analyses were conducted to investigate associations between variables and developmental continuity of number concept development and reading skills were described.
RESULTS: An association between numeracy and mathematics-specific vocabulary was found. The data confirm that number concepts and reading skills develop hierarchically. Although English-speaking children performed better on the numeracy assessment, isiZulu and Sesotho speakers performed better on the reading test.
CONCLUSION: Mathematics-specific vocabulary is a key tool for early number concept development, also in isiZulu and Sesotho. Teachers' pedagogical content knowledge (PCK) should include how number concept development intersects with mathematics-specific vocabulary. Explicit teaching of mathematics-specific vocabulary should be included in the Foundation Phase curriculum.
Keywords: early numeracy; mathematics-specific vocabulary; early reading; foundation phase; pedagogical content knowledge; social grants; hierarchical number concept development.
Introduction
Achievement in early grade numeracy has been shown to have predictive power for learning mathematics throughout the school years (Bezuidenhout 2018; Desoete 2015; Fyfe, Rittle-Johnson & Farran 2019) and to lay the foundation for later development of mathematical skills (Dowker 2005; Sarama & Clements 2009). A growing body of research indicates that early numeracy development is supported by the understanding of linguistic features, including mathematics-specific vocabulary (e.g. more, in between, after, just as many and so forth) (Bezuidenhout 2018; Gunderson & Levine 2011; He et al. 2022; Hornburg, Schmitt & Purpura 2018; Purpura et al. 2017). Although there is significant evidence of associations between mathematics-specific vocabulary and early numeracy skills of children who learn in English, there is limited evidence of connections between mathematics-specific vocabulary and mathematical knowledge of children who learn in other local South African languages such as isiZulu and Sesotho.
In a previous study (Bezuidenhout 2018), isiZulu and Sesotho first-graders who learn mathematics in their second language (i.e. English) were assessed to investigate, amongst others, associations between their performance on numeracy and mathematics-specific vocabulary assessments. Significant associations were found between their numeracy and mathematics-specific vocabulary, but that study did not include a measure of foundational reading skills and was also conducted in a community with better socio-economic circumstances than this study. This study continued to investigate associations between children's early mathematics knowledge and their mathematics-specific vocabulary, whilst foundational reading skill was also measured. In this study, numeracy, mathematics-specific vocabulary and foundational reading skills of 133 children were assessed in their first languages (i.e. isiZulu, Sesotho or English) and second-graders were also included in the sample. A connection was found between their early numeracy attainment and their mathematics-specific vocabulary, confirming that young children require specific words to learn mathematical concepts. However, this sample did not yield a significant correlation between foundational reading and the other two skills.
The children who participated in this study are from five 'Quintile 1' schools, where the schools receive more resources because their feeder communities are poor. In the research sample, the families of the participants receive social development grants1 from the South African government. In investigating the influence of socio-economic status (SES) on mathematics-specific vocabulary and early numeracy, several researchers found that SES is a key factor in predicting variance in caregivers' and children's mathematics-specific vocabulary (Verdine et al. 2014) and children's numeracy skills (Jordan & Levine 2009). Caregivers and teachers from low-SES households tend to use less mathematics-specific vocabulary than their higher SES peers (Levine et al. 2010). This can result in limited development of early math skills, which is evident in the outcomes of assessments in local and international mathematics testing (e.g. Department of Basic Education 2014, 2019; The Southern and Eastern African Consortium for Monitoring Educational Quality [SACMEQ] 2017; Trends in International Mathematics and Science Study 2015). The purpose of this study was to describe associations between numeracy, mathematics-specific vocabulary and foundational reading skills of the learners who participated in the study.
Early numeracy
Essential early numeracy skills, such as counting (Wynn 1990), ordinality and number lines (McCrink, Dehaene & Dehaene-Lambertz 2007), cardinality (Sarnecka & Wright 2013) and relationality (Fritz, Ehlert & Balzer 2013) are built on the foundations of two innate number systems, namely the object tracking system (OTS) and the approximate number system (ANS) (Carey 2009; Elliott et al. 2019; Feigenson, Dehaene & Spelke 2004; Gallistel 2021; Spelke 2000). The OTS is a working memory system that tracks up to three individual objects. This system allows children to pick out 'this', 'this' and 'this' but does not enable children to provide a summary symbol for a set of objects (Levine & Baillargeon 2016). The second system, the ANS, allows children to estimate sizes with increased close approximation with larger sets. By using the ANS, children can compare magnitudes of two groups of objects without counting. According to Weber's law, the larger the distance between two groups, the easier it is to compare. This phenomenon is known as the 'distance effect' (Dehaene 2011:61). Although the OTS system does not become more refined in older children or adults, the ANS gradually refines as children grow older. For instance, a 6-month-old can discriminate between 8 and 16 objects but not between 8 and 12, whilst at the age of 9 months, a child can discriminate between 8 and 12 (Levine & Baillargeon 2016).
Neither of these two systems capture exact representations of natural numbers but form the foundation for the development of knowledge of counting, cardinality and other aspects of foundational numeracy, which are learned through formal instruction via the medium of language and through demonstration. This type of instruction may happen informally at home and in the community and in more formal settings such as schools, where children learn to calculate and to reason about numerosity by using symbols. Several researchers agree that the development of these more sophisticated concepts and mental skills depends on the quality and quantity of children's exposure to mathematics-specific vocabulary (Pruden, Levine & Huttenlocher 2011; Purpura & Reid 2016; Ramani et al. 2015). The more children encounter conversation about magnitude, the more they will use the terms they encounter to advance from their basic, 'intuitive' ANS knowledge to understanding concepts such as cardinality.
To capture the development of such concepts, Fritz et al. (2013) developed a theoretical model in which they describe how children develop the more formal number skills hierarchically. The key assumption for such a hierarchical model is that a certain learning domain, such as arithmetic, can be divided into observable knowledge 'levels' which are formed successively, with increasing conceptual sophistication. Although Fritz et al. (2013) described five distinctive levels of successive competencies of children between 4 and 8 years of age, Rittle-Johnson, Siegler and Alibali (2001) explained that such 'levels' should be thought of as 'overlapping waves'. The Fritz et al. model was used to develop the assessment instrument which was used in this study to assess early numeracy skills (Henning, Ehlert & Balzer 2019). The model consists of five levels of number concept development.
Drawing on the OTS and ANS, coupled with their language development, 2-year-olds learn how to count (Level I: Counting). At first, their counting words are a 'list of meaningless lexical items' (Carey 2009: 308) and are not always recited in the correct order. Gradually, they begin to assign objects to number words by way of one-to-one correspondence. Next, children discover the order of successive quantities, and they learn how numbers are represented on what has become known as the 'mental number line' (Level II: Ordinality). The principles of ordinality allow them to identify preceding and succeeding numbers and to establish which number comes between two numbers that enables them to compute by means of counting. Unless they acquire the concept of cardinality (Level III: Cardinality), the counting strategy will remain a dominant strategy2.
Cardinality of a number implies that the last word uttered in the counting of items in a group indicates how many items are in that group. Understanding cardinality means that children can decompose numbers adequately by drawing on knowledge of each individual number's 'manyness' (e.g. 7 + 8 is also 7 + 3 + 5 = 15) and no longer only use counting strategies for addition or subtraction tasks. Sarnecka and Wright (2013) explained that:
[I]t is the cardinality principle that gives number words their meanings, by making the cardinal meaning of any number word knowable from that word's ordinal position in the counting list. (p. 2)
As they learn how to decompose numbers, children realise that each number can be divided into various combinations of smaller parts of numbers and that each number also forms part of larger numbers or quantities (Level IV: Part-Part-Whole). For example, 8 can be decomposed into 3 and 5 or 6 and 2 but it also forms part of 9 and 10 and so forth. Systematic decomposition of a number doesn't change the meaning of a number because numbers can also be recomposed through addition (Langhorst, Ehlert & Fritz 2012). If two quantities in an equation are known, the third one can be determined, no matter which part is missing.
Lastly, Fritz et al. (2013) described a fifth level (Level V: Relationality) of early number concept development. Children discover that each number is generated by adding a constant of one (+1) to the previous number and that all numbers are related: the distance between two consecutive numbers is always an equal distance. This idea is a prerequisite for understanding multiplicative relationships and the place value system.
Mathematics-specific language
In thinking of how language influences the forming of concepts, Carey (2009) proposed that language learning allows children to represent concepts that they could not previously represent and that language makes concepts that they can already represent more accessible. This is why Levine and Baillargeon (2016) and He et al. (2022) highlighted the importance of the quality of the mathematics-specific language input children experience. The more linguistic tools available to represent new or already developed math concepts, the better their chances are to represent and develop these concepts.
Linguistic tools also create interlocking networks of concepts connected to numbers. Language - in particular words - act like scaffolding networks. They provide structures for conceptual development (Kozulin 1990; Sarnecka 2016:152). Dowker and Nuerk (2016) explained that the scaffolding purpose makes vocabulary critical for forming linguistically named concepts. This idea was initially proposed by Vygotsky (1978, 1986), who claimed that there is a constant pattern of interaction between the development of concepts (such as number concepts) and the development of language. He explained that cognitive modelling intersects with linguistic representation (Kozulin 1990; Vygotsky 1986). Similarly, Spelke (2017) proposed that children discover the meaning of mathematics-specific vocabulary when they learn a natural language. She claims that language itself is the source of number concepts, more than cognitive evolution or culture. For her, thus, the principle is that mathematics-specific vocabulary scaffolds a child's number concept development through an interplay between the development of language and conceptual representations. In this view, I argue that young children rely on mathematics-specific vocabulary to represent numeracy concepts.
I concur with Purpura et al. (2017), who defined mathematics-specific vocabulary as children's understanding of key words in mathematics. To that I add that mathematics-specific vocabulary can be divided into numerical language qualifiers (e.g. many), comparative language (e.g. less) and spatial language (e.g. first and behind) (He et al. 2022; Purpura et al. 2017). Understanding numerical qualifiers enables children to find the equinumerosity (exact quality) and cardinality of numbers (Sarnecka & Wright 2013); comparative language enables children to describe comparisons between sets of numbers, and spatial language allows children to talk about relations between objects and between numbers on a number line (Purpura et al. 2017).
Literacy skills
Piper (2022) found that the predictive value of early literacy for numeracy is strong. According to Piper (2022), the assessment of basic literacy skills is important, not only for its word recognition assessment but also for its vocabulary indications. If young children develop a fair number of words and build a lexical inventory that will assist them with learning mathematics, it is arguably also important that they learn to read well. Like the claim that vocabulary is necessary to build mathematical understanding, vocabulary is also required for reading comprehension. The expansion of a child's vocabulary repertoire thus adds to both reading comprehension skills and mathematic abilities. Several studies have found a relationship between achievement in mathematics and language during early academic development (Negen & Sarnecka 2012; Purpura et al. 2011). Difficulties in mathematics (often presented in dyscalculia) also often co-occur with difficulties in language (often presented in dyslexia) (Landerl 2015). Unfortunately, children who come from low-SES backgrounds tend to experience difficulties in both mathematics and language (Jordan, Huttenlocher & Levine 1994; Jordan & Levine 2009). Despite these associations, improvements in general language skills have not yet been proven to improve young children's mathematical knowledge (Jordan et al. 2012), although in the studies in Kenya (Piper 2022), it was evident that literacy achievement in the first grade predicts mathematical competence in the second grade. Nevertheless, there was no significant correlation between early reading and mathematics-specific vocabulary or numeracy in this study's sample.
Knowledge of the alphabetic principle, letter knowledge and phonemic awareness are foundational reading skills that develop in the early school years and form the bedrock of children's coding skills, which ultimately enable them to recognise written words (Tunmer & Hoover 2019). Together with language comprehension skills, coding skills enable children to read. When these skills are amalgamated with children's background knowledge - which includes vocabulary knowledge - interpretation of written text becomes possible. Several applications of these skills were assessed in the present study, including letter identification, familiar word reading, invented word reading, oral reading fluency and reading comprehension.
Connections between language, mathematics-specific vocabulary and numeracy
Several researchers have offered explanations for the relations between mathematics and language. In the introductory chapter of Language in Mind, Gentner and Goldin-Meadow (eds. 2003) argued that language is like a lens; it enables children to 'look at' number concepts and represent these concepts in new ways. They argue that language is a tool that children can use to expand existing representations of their world. This type of explanation resonates with the explanation that Vygotsky suggested many decades ago about the constant interaction between language and concept formation: '[l]earning to direct one's own mental processes with the aid of words or signs is an integral part of the process of concept formation' (Vygotsky 1962:59). It is because of such a constant interaction that variations in parents' (Gunderson & Levine 2011; Levine et al. 2010) and teachers' (Klibanoff et al. 2006) number talk can influence children's mathematical knowledge: increased exposure to mathematics-specific vocabulary increases children's chances to develop an understanding of the conceptual properties of these words (Dowker & Nuerk 2016). Gopnik and Meltzoff (1997:208-209) agreed that 'children who hear language relevant to a particular conceptual problem are more likely to solve that problem than children who do not'.
In a seminal article, Dowker and Nuerk (2016) distinguished between several linguistic levels that influence number concept development. The syntactic structure, semantic meaning, lexical structure and unique phonemes of different languages, amalgamated with children's conceptual knowledge of constructs, contribute to their understanding of mathematics. For example, the structure of number names in agglutinative languages like isiZulu and Sesotho (which are two of the languages in which the children in this study were assessed), allows for conceptual transparency. By using a transparency rule, Sesotho and isiZulu children can understand all number names after they have learnt the number words up to 10. For instance, yishumi nanye (11) in isiZulu means 'ten and one' and yishumi nambili (12) means 'ten and two'. Leshome le motso o mong (11) in Sesotho, means 'ten and one' and leshome le metso e mmedi (12) means 'eleven and one'. The disadvantage of this structure is that some Sesotho and isiZulu number names are very long and overload children's working memory. For instance, the isiZulu word for eight, isishiyagolombili consists of eight syllables and is more difficult to process quickly in working memory and to ultimately remember, compared with the one syllable word 'eight' in English.
Semantic structures of languages also differ and influence conceptual development. Some languages, such as Afrikaans, invert the order of tens and units. In Afrikaans 15 is vyftien, which is a direct translation of 'five and ten', 17 is sewentien, which means 'seven and ten', 23 is drie en twinting, which is directly translated as 'three and twenty' and 34 is vier en dertig, which is directly translated as 'four and thirty'. English follows the same pattern up to 20 (e.g. 16 = six te[e]n, 17 = seven te[e]n). Thereafter, the tens are presented before the units (22 = twenty-two, 34 = thirty-four). The counting nouns are therefore already a cause for confusion in children's development of conceptual understanding.
In Bezuidenhout (2018), the author summarised the interpretation of the connection between language and mathematics:
Mathematics is not only about number names in isolation, but children learn to understand number names when these words appear in sentences which adhere to a specific language's grammatical structure and syntax. If they do not understand the linguistic properties of a language and cannot make sense of the conceptual properties that is embroidered in a mathematic specific word (conceptual properties of language), children cannot learn mathematics. They cannot learn or develop if they do not understand. Some children are exposed to rich linguistic environments and others are less exposed. Their exposure to language and in particular, mathematics-specific vocabulary - influences how and when they learn number concepts. (p. 52)
Research methods and design
Participants
The sample of 133 Grade 1 and 2 children were selected from a population of five Quintile 1 schools in the area of greater Johannesburg. The schools were purposefully selected from a list of 'no-fee-paying' schools. Because data were gathered during the COVID-19 pandemic, children were not attending school full-time, and most schools had implemented a rotational learning schedule, meaning that classes had half the usual occupancy. In light of this, it was not possible to make a random selection of the children as planned. Instead, convenience sampling was used based on original selection criteria: children were either in Grade 1 or Grade 2, received a social grant and parents had given parental consent. Fifty-one per cent of participants were male. Forty-one per cent received instruction in isiZulu, 38% in Sesotho and 21% in English. Eighteen children from School 1 participated; 24 from School 2; 37 from School 3; 26 from School 4; and 26 from School 5. Three tools were used to assess each child individually: the MARKO-D SA for numeracy, the Meerkat Maths Language Test (MMLT) for mathematics-specific vocabulary and the Early Grades Reading Assessment (EGRA) for foundational reading. In the sample of 133, two participants did not complete the EGRA or MMLT and four did not complete the MARKO-D SA. Correlations were calculated with a sample of 127 participants.
Tools
Two standardised instruments and one custom-designed vocabulary assessment tool were used to assess children's competence in three components, namely early numeracy, mathematics-specific vocabulary and foundational reading. The assessment instrument for early number concept development, published in South Africa as the MARKO-D SA test (Henning et al. 2019, 2021), was selected because it provides succinct results per individual. The EGRA (RTI International 2016) assesses children's first steps into literacy. The MMLT assesses vocabulary knowledge required for early mathematics learning. Children were assessed in their language of instruction: isiZulu, Sesotho or English.
MARKO-D SA
The Mathematics and arithmetic competence diagnostic (MARKO-D) was originally developed in Germany by the same authors who created the theoretical model of number concept development (Fritz et al. 2013). The aim of this test is to indicate on which level a child performs - according to levels described by the model. The German MARKO-D was translated and adapted for use in South Africa. The test was culturally adapted for children in this country. For instance, in the German test, squirrels are used as characters. This was not suitable for South African children and the characters were changed to meerkats. The illustrations were kept noninvasive and minimalistic in terms of colour and background so as not to overload working memory.
During a pilot study (Henning et al. 2019), which was conducted in schools in Gauteng (n = 224), the aim was to ensure that the test continued to assess the same constructs that it was designed to assess and to make sure that the conceptual content of the test was not changed during the translation process. Firstly, the German test was translated into English, and thereafter the English test was used to translate the test into isiZulu, Afrikaans and Sesotho. In total the translations went through five iterations during pilot studies before proving validity of the model in all four translated tests. The MARKO-D SA consists of 48 items. The items assess concepts described in the theoretical model. However, the test does not progress in difficulty, but the questions of the five levels are mixed throughout the test.
Meerkat Maths language test
The MMLT was custom-designed for a previous study (Bezuidenhout 2018) to measure children's early mathematics-specific vocabulary. This measure consists of 24 items, assessing numerical language qualifiers (more, many, just as many, fewer, few), comparative language (same size, bigger, tallest, biggest, big/large, tall, shortest, small, smaller, short) and spatial language (in between, first, last, on top of, behind, above, under, after, in front of). Each question required participants to point to the picture representing the concept. None of the items required exact quantitative knowledge, but only an understanding of the word that represents a certain concept. The MMLT was designed to test the vocabulary presented in the MARKO-D SA, and therefore the vocabulary of the MMLT concepts cohere with the MARKO-D SA. The idea is that children must know the vocabulary for them to understand the questions and instructions given in the MARKO-D SA. Table 1 provides examples of how the MMLT coheres with the concepts in the MARKO-D SA.

Early grades reading assessment
The EGRA (RTI International 2016) is used in different parts of the world and is also recommended by the Department of Basic Education in South Africa as a diagnostic tool to assess foundational reading skills. Unlike the often-cited Progress in International Reading Literacy Study (PIRLS) test (Spaull & Kotze 2015), which is administered to older children, the EGRA test captures the foundational reading competence of children in the early grades (Brink, Motolo & Henning 2021).
Procedure
During data collection, te fieldwork team adhered to strict COVID-19 health and safety protocols as stipulated by the government. All participants and testers wore masks, children were provided with additional masks, furniture was sanitised, hand sanitisers were used when participants entered the interview rooms and social distancing was practised. In addition, all participants were screened by health officers when entering school premises, their temperatures were checked, hands sanitised and the wearing of masks was enforced.
Descriptive statistics were determined for each assessment instrument. Shapiro-Wilk (n < 50) and Kolmogorov-Smirnov tests were used to test for normality of the MARKO-D SA, MMLT and EGRA data. The tests were also used to describe the distributions of gender, language and schools for each assessment. If data were normally distributed, parametric tests (e.g. t-tests) were used to compare mean scores of between groups and when data were not normally distributed, nonparametric tests, the Kruskal-Wallis (used to compare more than two groups) test or Mann-Whitney test (used to compare two groups) were used to test for differences against normality. Although the data for the MARKO-D SA and MMLT were not normally distributed, t-tests were used to test for differences because the t-test is robust enough for deviations against normality if group sizes are large enough and similar in size. To assess associations between the variables, correlations were determined. Although the data were skewed, parametric correlations were conducted because of a large enough sample size.
Results
Descriptive statistics
Table 2 depicts the descriptive statistics for the instruments used.

The results of the MARKO-D SA were similar to a previous study conducted in Gauteng (Bezuidenhout 2018) with a mean score of 23.86 and to another study conducted by Kellelo (JET Educational Services 2018) where the mean score in one district of the Western Cape was 16.5 at baseline and 25.9 at endline and means = 18.8 at baseline and 25.4 at endline in another district of the Western Cape. The MMLT mean score in Bezuidenhout (2018) was 19.41, which is similar to the results of this sample, who were tested in the same languages as Bezuidenhout (2018), that is, isiZulu, Sesotho and English. Data from a recent randomly selected study of Grade 1-3 learners (n = 287) in an isiZulu school (Simelane in press) showed a mean score of 37.72% for Grade 1 and 74.24% for grade 2, which was significantly higher than the mean score of this sample. Yet she found that competent reading of the majority of children was achieved only after 2 years.
Differences between groups
In terms of differences between gender, language and schools, no significant differences were found between male and female learners for either of the three tests. For differences between schools, no significant differences were found between schools for MMLT. School 2 performed slightly better than the other four schools for the MARKO-D SA (mean1 = 45.83; mean2 = 53.56; mean3 = 47.80; mean4 = 44.67; mean5 = 40.22). School 1 performed significantly lower than the other schools in the EGRA and Schools 3 and 5 performed the best on the EGRA (mean1 = 5.62; mean2 = 12.08; mean3 = 37.46; mean4 =27.83 mean5 =38.70, p ˂ 0.05). It is interesting that the majority of children who performed poorly on the EGRA were English-speaking. English-speaking children performed significantly lower than the other languages groups in the EGRA (meanZ = 27.28; meanS = 32.66; meanE = 14.15, p ˂ 0.05). Although this topic was not a focus of this study, future research should focus on elaborating on this finding, because authors such as Dehaene (2011) mentioned that English is one of the most difficult languages to learn to read. In terms of language in the MMLT and MARKO-D SA, no significant differences were found between the language groups for the MMLT. English-speaking children performed better than the isiZulu- and Sesotho-speaking children on the MARKO-D SA (meanZ = 42.96; meanS = 46.71; meanE = 53.13, p ˂ 0.05).
Associations between variables
To assess associations between the variables, correlations were determined. Although the data were skewed, parametric correlations were conducted because of a large enough sample size. Table 3 depicts the correlations between the three variables, indicating a significant correlation between number concept development and mathematics-specific vocabulary (0.60, p ˂ 0.01).
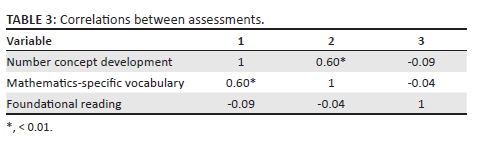
A previous study (e.g. Bezuidenhout 2018) also indicated significant correlations between number concept development and mathematics-specific vocabulary when Grade R and Grade 1 children were tested in isiZulu, Sesotho and English. The coherence between the MARKO-D SA and MMLT, as depicted in Table 4, explains the correlation between early numeracy and mathematics-specific vocabulary. For instance, only 37.2% of children answered Item 2 correctly on the MARKO-D SA and 34.9% answered item 4 correctly. Both items assess the concept 'in between'. Only 19.8% of children understood the word 'in between' which was assessed by item 3 on the MMLT. Another example is item 21 (3.9% correct) and item 23 (1.6% correct) on the MARKO-D SA, assessing the concept 'fewer', which is associated with the low score of 40% on the MMLT's item 21, which also assess the word 'fewer'.

Developmental continuity in numeracy and reading
Several authors (e.g. Fritz et al. 2013; Resnick 1989) have argued that number concepts develop hierarchically. The results of the MARKO-D SA in this sample also indicate such a development pattern. Table 4 shows that participants achieved higher percentages on the Level 1 questions (87.44%) and increasingly lower on the more advanced questions of Level 2 (51.74%), Level 3 (36.50%), Level 4 (9.46%) and Level 5 (6.20%).
This type of increased difficulty in items for each level was also indicated in the pilot study of the MARKO-D SA (Henning et al. 2019, 2021) and in De Villiers (2015).
Increasing difficulty is also indicated in the data of this sample's EGRA results (Table 5). Participants achieved an average of 49.98% on the letter sound items, 13.03% on word reading, 11.06% on passage reading and a concerning 2.14% on comprehension.
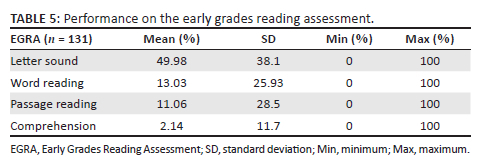
These findings are in line with a previous study conducted by Simelane (in press).
Discussion and conclusion
The most important finding of this study is that mathematics-specific vocabulary is a key tool for early number concept development, also in isiZulu and Sesotho. The significant correlation between mathematics-specific vocabulary and numeracy can be explained by theories reviewed in this article. Vygotsky's theory of constant interaction between concept and language formation (Kozulin 1990) described this relationship accurately, and also the argument posed by several authors that the quality and amount of mathematics-specific vocabulary contributes to the formation of number concepts in the early years (Gunderson & Levine 2011; Klibanoff et al. 2006; Levine et al. 2010). Dowker and Nuerk (2016) and Carey (2009) also explained that the conceptual properties of mathematics-related words are formed through a scaffolding structure of language. If children have a restricted input of number talk, poor numerical competence is likely to be observed in Grades 1 and 2, which was evident in the low performance on the numeracy assessment (mean = 46.77%).
As in previous studies (e.g. Bezuidenhout 2018; Henning et al. 2021) the data of this study also confirm the hierarchical development of number concepts. Children performed the best on the questions that assess counting skills (mean = 87.44%), the scores of questions assessing ordinality were lower (mean = 51.74%), the mean for questions associated with cardinality was lower (mean = 36.50%), part-part-whole even lower (mean = 9.46) and questions assessing relationality were the most difficult (mean = 6.20%). Increasing difficulty is also shown in the data of this sample's EGRA results (Table 5).
These findings emphasise the suggestion that teachers' pedagogical content knowledge (PCK) should include the development of number concepts and how it intersects with mathematics-specific vocabulary and other linguistic features such as reading (Bezuidenhout 2018). Adding to that, the author highly recommends that explicit teaching of mathematics-specific vocabulary should be included in the Foundation Phase curriculum. Although some researchers (e.g. Purpura et al. 2017; Purpura, Litkowski & Knopik 2019) have turned their focus to finding best teaching practices to expand and develop children's number concept understanding through language development, there is still a scarcity in the development of tools (e.g. reading books) to develop mathematics-specific vocabulary. This is a focus area for further research, especially in samples of children who come from low SES.
The data of this study confirm that number concepts develop hierarchically as previous research has indicated (e.g. Fritz et al. 2013). It also shows developmental continuity in the development of reading skills, confirming that the ability to read with comprehension relies on the foundation of sound knowledge and the ability to decode words whilst, in tandem, recognising their meaning, as proposed by Tunmer and Hoover (2019).
An interesting finding in this study was that, although English-speaking children performed better on the MARKO-D SA, their results were the weakest on the EGRA. Researchers such as Dehaene (2009) have explained why English is one of the most difficult languages to decode because of its complex linguistic structures and its 'opaque' orthography. In comparison, isiZulu and Sesotho, which are known as languages with a 'transparent' orthography, are more easily decoded because of the direct connections between graphemes and phonemes (Henning & Simelane in press).
To conclude, assessing children's early development of number concepts and foundational reading skills, together with their mathematics-specific vocabulary knowledge, serves important diagnostic purposes in the Foundation Phase of schooling. The assessment also provides glimpses of the enactment of the curriculum in a particular school or in a sample of a specific learner population. To continue to support children to learn mathematics, significant efforts should be made to develop their mathematics-specific vocabulary. Future research should focus on finding optimal teaching practices to support linguistic development.
Acknowledgements
The author would like to acknowledge financial assistance of the National Research Foundation (no. 125648), South Africa, towards this research.
Competing interests
The author declares that he has no financial or personal relationships that may have inappropriately influenced him in writing this article.
Author's contributions
H.B. is the sole author of this article.
Ethical considerations
Ethical clearance to conduct this study was obtained from the University of Johannesburg Faculty of Humanities Research Ethics Committee (ref. no. REC-01-050-2020).
Funding information
The financial assistance of the National Research Foundation (no. 125648), South Africa, towards this research is hereby acknowledged.
Data availability
The data sets generated and analysed during this study are available from the corresponding author on reasonable request.
Disclaimer
The views and opinions expressed in this article are those of the author and do not necessarily reflect the official policy or position of any affiliated agency of the author.
References
Bezuidenhout, H.S., 2018, 'Input for young children's number concept development', Doctoral dissertation, University of Johannesburg, Johannesburg. [ Links ]
Brink, S., Motolo, N. & Henning, E., 2021, Teaching reading in Grade 3: English first additional language classrooms in six Mpumalanga schools, Research Report for the Department of Basic Education and the WITS Health Consortium of part of the Second Early Grade Reading Study (EGRS II), Department of Basic Education. Pretoria, DBE.
Carey, S., 2009, The origin of concepts, Oxford University Press, Oxford.
Dehaene, S., 2009, Reading in the brain. The new science of how we read, Penguin, London.
Dehaene, S., 2011, The number sense (How the mind creates mathematics), Oxford University Press, Oxford.
Department of Basic Education, 2014, Report on the Annual National Assessment of 2014: Grades 1 to 6 & 9, viewed 28 December 2014, from http://www.education.gov.za/Curriculum/AnnualNationalAssessment/tabid/424/Default.aspx.
Department of Basic Education, 2019, Introducing the trends in International Mathematics and Science Study 2019 results, viewed 13 February 2022, from https://www.education.gov.za/TIMSS2019ReportRelease.aspx.
Desoete, A., 2015, 'Predictive indicators for mathematical learning disabilities/dyscalculia in kindergarten children', in S. Chinn (ed.), The Routlegde international handbook of dyscalculia and mathematical learning difficulties, pp. 90-100, Routledge, NY.
De Villiers, H.S., 2015, Die werkbaarheid van die Afrikaanse vertaling van 'n Wiskunde diagnostiese toets vir die Grondslagfase, University Press, Johannesburg.
Dowker, A., 2005, 'Early identification and intervention for students with mathematics difficulties', Journal of Learning Disabilities 38(4), pp. 324-332. https://doi.org/10.1177/00222194050380040801 [ Links ]
Dowker, A.D. & Nuerk, H., 2016, 'Linguistic influences on mathematics', Frontiers in Psychology 7, 1035. https://doi.org/10.3389/fpsyg.2016.01035 [ Links ]
Elliott, L., Feigenson, L., Halberda, J. & Libertus, M.E., 2019, 'Bidirectional, longitudinal associations between math ability and approximate number system precision in childhood', Journal of Cognition and Development 20(1), 56-74. https://doi.org/10.1080/15248372.2018.1551218 [ Links ]
Feigenson, L., Dehaene, S. & Spelke, E., 2004, 'Core systems of number', Trends in Cognitive Science 8, 307-314. https://doi.org/10.1016/j.tics.2004.05.002 [ Links ]
Fritz, A., Ehlert, A. & Balzer, L., 2013, 'Development of mathematical concepts as basis for an elaborated mathematical understanding', South African Journal of Childhood Education 3(1), 21-37. https://doi.org/10.4102/sajce.v3i1.31 [ Links ]
Fyfe, E.R., Rittle-Johnson, B. & Farran, D.C., 2019, 'Predicting success on high-stakes math tests from preschool math measures among children from low-income homes', Journal of Educational Psychology 111(3), 402. https://doi.org/10.1037/edu0000298 [ Links ]
Gallistel, C.R., 2021, 'The approximate number system represents magnitude and precision', Behavioral and Brain Sciences 44, E187. https://doi.org/10.1017/S0140525X21000959 [ Links ]
Gentner, D. & Goldin-Meadow, S. (eds.), 2003, Language in mind: Advances in the study of language and thought, MIT Press, Cambridge, MA.
Gopnik, A. & Meltzoff, A.N., 1997, Words, thoughts and theories, MIT Press, Cambridge, MA.
Gunderson, E.A. & Levine, S.C., 2011, 'Some types of parent number talk count more than others: Relations between parents' input and children's cardinal-number knowledge', Developmental Science 14(5), 1021-1032. https://doi.org/10.1111/j.1467-7687.2011.01050.x [ Links ]
Henning, E., Balzer, L., Ehlert, A. & Fritz, A., 2021, 'Development of an instrument to assess early number concept development in four South African languages', South African Journal of Education 41(4), a1979. https://doi.org/10.15700/saje.v41n4a1979 [ Links ]
Henning, E., Ehlert, A. & Balzer, L., 2019, Marko-D SA: Assessment of number concept development, University of Johannesburg, Johannesburg.
Henning, E. & Simelane, F. (in press), 'The science of reading in a foundation phase teacher's toolkit', in N. Petersen & S. Gravett (eds.), Future-proofing teacher education. Voices from South Africa and beyond, pp. 78-93, Routledge, London.
He, S., Graf, E., Webber, R.J., Leffel, K.R., Suskind, E., Levine, S. & Suskind, D., 2022, 'Assessing efficacy and benefit of a behavioral mathematics-specific vocabulary intervention for caregivers of young children', in Child & youth care forum, pp. 1-19, Springer, Berlin.
Hornburg, C.B., Schmitt, S.A. & Purpura, D.J., 2018, 'Relations between preschoolers' mathematical language understanding and specific numeracy skills', Journal of Experimental Child Psychology 176, 84-100. https://doi.org/10.1016/j.jecp.2018.07.005 [ Links ]
JET Education Services, 2018, Evaluation of the Grade R Mathematics project implemented in the Western Cape: Endline report, Zenex, Pretoria.
Jordan, N.C., Glutting, J., Dyson, N., Hassinger-Das, B. & Irwin, C., 2012, 'Building kindergartners' number sense: A randomized controlled study', Journal of Educational Psychology 104(3), 647. https://doi.org/10.1037/a0029018 [ Links ]
Jordan, N.C., Huttenlocher, J. & Levine, S.C., 1994, 'Assessing early arithmetic abilities: Effects of verbal and nonverbal response types on the calculation performance of middle-and low-income children', Learning and Individual Differences 6(4), 413-432. https://doi.org/10.1016/1041-6080(94)90003-5 [ Links ]
Jordan, N.C. & Levine, S.C., 2009, 'Socioeconomic variation, number competence, and mathematics learning difficulties in young children', Developmental Disabilities Research Reviews 15(1), 60-68. https://doi.org/10.1002/ddrr.46 [ Links ]
Klibanoff, R.S., Levine, S.C., Huttenlocher, J., Vasilyeva, M. & Hedges, L.V., 2006, 'Preschool children's mathematical knowledge: The effect of teacher "math talk"', Developmental Psychology 42(1), 59. https://doi.org/10.1037/0012-1649.42.1.59 [ Links ]
Kozulin, A., 1990, Vygotsky's psychology: A biography of ideas, Harvard, Cambridge, MA.
Landerl, K., 2015, 'How specific is the specific disorder of arithmetic skills?', in S. Chinn (ed.), The Routledge international handbook of dyscalculia and mathematical learning difficulties, pp. 115-124, Routledge.
Langhorst, P., Ehlert, A. & Fritz, A., 2012, 'Non-numerical and numerical understanding of the part-whole concept of children aged 4 to 8 in word problems', Journal fur Mathematik-Didaktik 33(2), 233-262. https://doi.org/10.1007/s13138-012-0039-5 [ Links ]
Levine, S. & Baillargeon, R., 2016, 'Different factors of language in numerical development: Exact number and individuation', in D. Barner & S. Baron (eds.), Core knowledge and conceptual change, pp. 127-150, Oxford University Press, Oxford.
Levine, S.C., Suriyakham, L.W., Rowe, M.L., Huttenlocher, J. & Gunderson, E.A., 2010, 'What counts in the development of young children's number knowledge?', Developmental Psychology 46(5), 1309. https://doi.org/10.1037/a0019671 [ Links ]
McCrink, K., Dehaene, S. & Dehaene-Lambertz, G., 2007, 'Moving along the number line: Operational momentum in nonsymbolic arithmetic', Perception & Psychophysics 69(8), 1324-1333. https://doi.org/10.3758/BF03192949 [ Links ]
Negen, J. & Sarnecka, B.W., 2012, 'Number-concept acquisition and general vocabulary development', Child Development 83(6), 2019-2027. https://doi.org/10.1111/j.1467-8624.2012.01815.x [ Links ]
Piper, B., 2022, 'Early numeracy interventions in Kenya', in conference presentation, Department of Basic Education Early Grade Mathematics Research Indaba, February 10, 2022, pp. 1-18.
Pruden, S.M., Levine, S.C. & Huttenlocher, J., 2011, 'Children's spatial thinking: Does talk about the spatial world matter?', Developmental Science 14(6), 1417-1430. https://doi.org/10.1111/j.1467-7687.2011.01088.x [ Links ]
Purpura, D.J., Hume, L.E., Sims, D.M. & Lonigan, C.J., 2011, 'Early literacy and early numeracy: The value of including early literacy skills in the prediction of numeracy development', Journal of Experimental Child Psychology 110(4), 647-658. https://doi.org/10.1016/j.jecp.2011.07.004 [ Links ]
Purpura, D.J., Litkowski, E.C. & Knopik, V., 2019, 'Mathematics and reading develop together in young children: Practical and policy considerations', Policy Insights from the Behavioral and Brain Sciences 6(1), 12-20. https://doi.org/10.1177/2372732218815923 [ Links ]
Purpura, D.J., Napoli, A.R., Wehrspann, E.A. & Gold, Z.S., 2017, 'Causal connections between mathematical language and mathematical knowledge: A dialogic reading intervention', Journal of Research on Educational Effectiveness 10(1), 116-137. https://doi.org/10.1080/19345747.2016.1204639 [ Links ]
Purpura, D.J. & Reid, E.E., 2016, 'Mathematics and language: Individual and group differences in mathematical language skills in young children', Early Childhood Research Quarterly 36, 259-268. https://doi.org/10.1016/j.ecresq.2015.12.020 [ Links ]
Ramani, G.B., Rowe, M.L., Eason, S.H. & Leech, K.A., 2015, 'Mathematics-specific vocabulary during informal learning activities in head start families', Cognitive Development 35, 15-33. https://doi.org/10.1016/j.cogdev.2014.11.002 [ Links ]
Resnick, L.B., 1989, 'Developing mathematical knowledge', American Psychologist 44(2), 162. https://doi.org/10.1037/0003-066X.44.2.162 [ Links ]
Rittle-Johnson, B., Siegler, R.S. & Alibali, M.W., 2001, 'Developing conceptual understanding and procedural skill in mathematics: An iterative process', Journal of Educational Psychology 93(2), 346. https://doi.org/10.1037/0022-0663.93.2.346 [ Links ]
RTI International, 2016, Early grade reading assessment (EGRA) toolkit: Second addition, viewed 13 February 2022, from https://shared.rti.org/content/early-grade-reading-assessment-egra-toolkit-second-edition.
SACMEQ, 2017, The SACMEQ IV project in South Africa: A study of the conditions of schooling and the quality of education, viewed 23 July 2020, from http://www.sacmeq.org/sites/default/files/sacmeq/publications/sacmeq_iv_project_in_south_africa_report.
Sarama, J. & Clements, D.H., 2009, Early childhood mathematics education research: Learning trajectories for young children, Routledge, London.
Sarnecka, B.W., 2016, 'How numbers are like the earth (and unlike faces, loitering, or knitting)', in Barner & Baron (eds.), Core knowledge and conceptual change, pp. 151, Oxford University Press, New York.
Sarnecka, B.W. & Wright, C.E., 2013, 'The idea of an exact number: Children's understanding of cardinality and equinumerosity', Cognitive Science 37(8), 1493-1506. https://doi.org/10.1111/cogs.12043 [ Links ]
Simelane, W.F. (in press), 'Learning to read in isiZulu', Doctoral thesis study in the Faculty of Education of the University of Johannesburg, Johannesburg. [ Links ]
Spaull, N. & Kotze, J., 2015, 'Starting behind and staying behind in South Africa. The case of insurmountable deficits in mathematics', International Journal of Educational Development 41(1), 13-24. https://doi.org/10.1016/j.ijedudev.2015.01.002 [ Links ]
Spelke, E., 2000, 'Core knowledge', American Psychologist 55, 1233-1243. https://doi.org/10.1037/0003-066X.55.11.1233 [ Links ]
Spelke, E.S., 2017, 'Core knowledge, language, and number', Language Learning and Development 13(2), 147-170. https://doi.org/10.1080/15475441.2016.1263572 [ Links ]
Trends in International Mathematics and Science Study (TIMSS), 2015, International mathematics achievement, viewed 23 July 2020, from http://timssandpirls.bc.edu/.
Tunmer, W.E. & Hoover, W.A., 2019, 'The cognitive foundations of learning to read: A framework for preventing and remediating reading difficulties', Australian Journal of Learning Difficulties 24(1), 75-93. https://doi.org/10.1080/19404158.2019.1614081 [ Links ]
Verdine, B.N., Golinkoff, R.M., Hirsh-Pasek, K., Newcombe, N.S., Filipowicz, A.T. & Chang, A., 2014, 'Deconstructing building blocks: Preschoolers' spatial assembly performance relates to early mathematical skills', Child Development 85(3), 1062-1076. https://doi.org/10.1111/cdev.12165 [ Links ]
Vygotsky, L.S., 1962, Thought and language, MIT Press, Cambridge, MA.
Vygotsky, L.S., 1978, Mind in society, Harvard University Press, Cambridge.
Vygotsky, L.S., 1986, Thought and language, ed. A. Kozulin, MIT Press, Cambridge.
Wynn, K., 1990, 'Children's understanding of counting', Cognition 36, 155-193. https://doi.org/10.1016/0010-0277(90)90003-3 [ Links ]
 Correspondence:
Correspondence:
Hanrie Bezuidenhout
hsbezuidenhout@uj.ac.za
Received: 14 Feb. 2022
Accepted: 25 May 2022
Published: 19 Sept. 2022
1 . This study was conducted as part of an interdisciplinary development project - in the form of a community of practice (CoP) - to describe the development and well-being of children whose families receive social grants from the South African government. The objectives of the CoP include creating an assessment tool to describe child well-being and establishing collaborating relationships between partners to improve child well-being - including academic achievement.
2 . This phenomenon of counting in units is typical in South African studies of mathematical performance in the early grades.














