Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.10 n.1 Johannesburg 2020
http://dx.doi.org/10.4102/sajce.v10i1.923
ORIGINAL RESEARCH
The interface between early numeracy, language and learning environments: Pedagogical implications
Hanrie S. Bezuidenhout
Department of Education, Faculty of Education, University of Johannesburg, Johannesburg, South Africa
ABSTRACT
BACKGROUND: In South Africa, many children learn mathematics in English, which is often not a home language. This type of linguistic situation intersects with their learning environments, their numeracy attainment and their executive functions. Ultimately, these aspects collectively contribute to children's numeracy attainment in Grade 1.
AIM: To describe how teachers draw on their views of the intersection of (1) pre-school numeracy competence, (2) language for mathematics and (3) the home and classroom environment, and (4) executive functions as cognitive filter for the teaching of mathematics, specifically of number concepts.
SETTING: A well-resourced school in a township area of urban Johannesburg, where Grade 1 children are taught in English, although their home language and Grade R language of instruction is isiZulu or Sesotho.
METHODS: Qualitative content analysis and discourse analysis were used to analyse interview data of four purposefully selected teachers.
RESULTS: Teachers' discourse showed that they were able to reflect on their teaching and to provide examples of how children's language, the environment and executive functions could feature in their early numeracy development. Yet, the teachers did not link theoretical ideas to their personal pedagogical theories.
CONCLUSION: Teachers need robust theoretical models to continuously develop personal pedagogical theories of cognitive development to integrate theoretical knowledge with their teaching practices
Keywords: early numeracy; language proficiency; language for mathematics; multilingual setting; executive functions; learning environment; foundation phase pedagogy.
Introduction: Everyday social interaction as bedrock for early numeracy
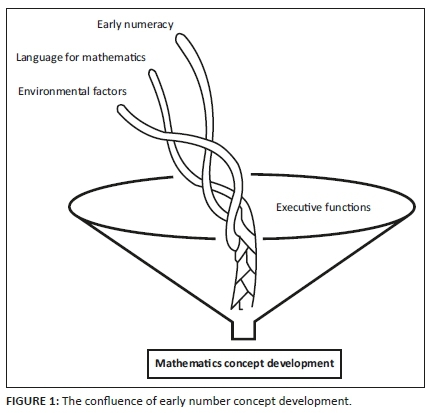
Upon entering Grade R, children already have substantial knowledge of the natural and the social world, which includes basic numeracy (Carey 2009; Clements & Sarama 2016; Dehaene 2011) and language competence (Dehaene 2009, 2020; Spelke 2017). During young children's daily engagement with their environment and with some formal instruction and free play, a dynamic interplay between conceptual and linguistic development is fostered (Condry & Spelke 2008; Schmitt, Purpura & Elicker 2019). In this article, I discuss theoretical perspectives, coupled with teachers' personal theories of this intersection between pre-schoolers' social environment, their unfolding numeracy and their language development. In addition, I argue that this intersection is cognitively filtered by children's executive functions (EF), and that, collectively, these factors contribute, ultimately, to children's Grade 1 numeracy achievement (Figure 1).
Early numeracy skills and language 'for' mathematics have been shown to be related to and predictive of mathematics learning (Aunio et al. 2019; Bezuidenhout, Henning, Fitzpatrick & Ragpot 2019; Clements & Sarama 2016; Schmitt et al. 2019). Dyrvold (2020:2), referring to Niss and Højgaard (2011), argues that mathematical proficiency requires 'communicative and reasoning competencies, ones that are language dependent'. She continues, '(a)ccordingly, students must be given opportunities to learn (the) mathematics subject language'.
Learning the discourse of mathematics, and in this instance, the discourse of number concepts, is part and parcel of almost all natural languages, with a few exceptions such as reported in a study of Australian indigenous children in which no language effects were found in 3-5-year-old children (Butterworth et al. 2008). According to Spelke (2017), early number concepts, beyond innate, core knowledge develops from natural language numerals.
Despite the proven power of languages to mediate conceptual understanding, linguistic resources by themselves are not enough. I argue that language resources have to be used and managed well to develop, amongst others, children's reasoning skills. Such management of cognitive resources has been studied extensively in recent years, examining their function in 'executing' cognitive 'orders'. These mental workings have become known as EFs, which comprises a set of higher order cognitive skills that regulates cognition (Miyake et al. 2000) and which serves as a central control 'centre' for cognitive processes (Diamond et al. 2007). And, importantly, in studies during the last decade, EFs have been shown to be related to - and predictive of mathematical achievement (Bull et al. 2011; Cragg et al. 2017). On the view of these authors, I argue that if teachers have an understanding of EF and of cognitive development of children, which includes early numeracy - and language development, they could establish and strengthen a firm pedagogical foundation in which their understanding can feature in their teaching.
To this end, this study was conducted not to assess learners, but to find out what their teachers' personal theories are about children's learning and how they view their own teaching in this regard. The inquiry was conducted at a well-resourced school in a township area of urban Johannesburg, where Grade 1 children are taught in English, although their home language and Grade R language of instruction is isiZulu or Sesotho. The specific linguistic setting of this school increased the depth of the inquiry about early numeracy, language for mathematics, EF and environmental factors as contributors to mathematics development in Grade 1: Because children in this school alternate between using more than one language, they rely heavily on EF and draw on their experiences of language and numeracy in the home and in their class environment. Regarding the teachers, I make the claim that teachers' mathematics pedagogy should be rooted in their personal theories of the architecture of interrelated, contributing constructs for mathematics learning (see Figure 1) - especially in a multilinguistic setting (Henning 2012) such as South Africa.
The research question for this study was: What are teachers' personal theories about children's mathematics (specifically numeracy) concept development? The aim was to describe how teachers draw on their views of the intersection of (1) pre-school numeracy competence, (2) language for mathematics and (3) the home and classroom environment, with (4) EF as cognitive filter for the teaching of mathematics, specifically of number concepts.
Background
Early numeracy skills (Fritz, Ehlert & Balzer 2013; Geary & Van Marle 2016), language for mathematics (Dowker & Nuerk 2016; Toll & Van Luit 2014), EF (Clark et al. 2013; Cragg et al. 2017), the home numeracy environment (Gunderson & Levine 2011; Napoli & Purpura 2018) and classroom numeracy environment (Klibanoff et al. 2006) have all received substantial attention in research about mathematics learning. Each of the four domains seems to correlate with, are predictive of, or are causally related to achievement in mathematics. Although a few studies have also described associations between more than one of these domains (e.g. Aunio et al. 2019; Bezuidenhout 2019; Schmitt et al. 2017), less is known about teachers' personal theories about the combinatorial contribution of pre-school (existing) numeracy competence, language for mathematics, together with EF and environmental factors to performance in Grade 1 mathematics. There is, as yet, no substantive finding on how these theoretical gains contribute to teachers' pedagogy.
In a previous study (Bezuidenhout, Ragpot, Fitzpatrick, Henning 2019), the investigation was about correlations between Grade 1 numeracy achievement and the predictive power of number concept development, mathematics-specific vocabulary, logical reasoning and EF in Grade R. The results indicated a significant correlation between the Grade R predictors and Grade 1 numeracy achievement as outcome variable. That study also examined concurrent associations between Grade R numeracy, mathematics-specific vocabulary, logical reasoning and EF; standardised regression coefficients showed concurrent associations between all four Grade R cognitive skills. However, teachers' personal theories about how such connections can influence their pedagogy were not described.
In this follow-up study, I set out to elaborate on the quantitative findings of Bezuidenhout, Henning, Fitzpatrick and Ragpot (2019) by discussing teachers' personal theories. In a school where Grade 1 children learn mathematics in English, with some code switching to their home language, four teachers were interviewed. The interview protocol focused on how the intersection between the environment and children's learning achievement in Grade R helped the teachers to theorise, or to reflect on how these contributors may collectively be processed or filtered by the children's EF. The environment of a multilingual class was emphasised.
The working hypothesis of the study was that teachers are not informed about how a transition from home language instruction to English as learning medium draws strongly on children's EF and that numeracy development will be influenced when children learn concepts in a somewhat unfamiliar language. This hypothesis is based on the idea that there is a complex interaction between children's language competence, their numeracy competence, their EF and the social environment.
Teachers' knowledge of language and numeracy dynamics in a multilingual classroom
'Instruction should follow research-based learning trajectories' (Clements & Sarama 2016:75). I would add to this assertion that teachers' pedagogy should be informed by their personal theories of the interplay between various cognitive contributors to children's learning trajectories.
Unfortunately, when such [research-based learning trajectories] education doesn't begin in pre-school and continue through the early years, this potential may be unrealized, leaving children trapped in a trajectory of failure. (Clements & Sarama 2016:77-78)
Many children in South Africa are indeed trapped in a 'starting behind and staying behind' (Spaull & Kotze 2015:13) trajectory of unrealised mathematical potential. It is evident in several studies such as the Trends in International Mathematics and Science Study (TIMSS 2015), and Southern and Eastern Africa Consortium for Monitoring Educational Quality (SACMEQ 2017) and in the now discontinued Annual National Assessments (Department of Basic Education 2014) in South Africa.
South African teachers feel obliged to situate their practice in the curriculum, policies, teaching methods and to complete the prescribed assessments, rather than to include cognitive development theories (Henning 2013), which describe the various factors that impact early learning. This is evident in teachers' discourse (Bezuidenhout 2019; Henning 2013).
In this study, similar to Henning's (2013) study, teachers' talk indicated that they have some idea about some aspects of pre-school learning, but:
[T]hey see themselves, with their methods and techniques, and leaning on the school curriculum, as somewhat mechanical conduits for child learning, gleaning skills and knowledge from whatever source comes their way. But they do not appear to know themselves as professionals. (p. 150).
The four teachers who were interviewed in this study found it difficult to talk about the interface of the four constructs that I have been discussing in the article so far. They were hesitant to talk about how they adapt their personal teaching theories according to what they know about EF, prior knowledge of children, linguistic issues and learners' social environment when asked to do so. They preferred to elaborate on curriculum issues and on policy directives, whereto they directed the discussion consistently. I acknowledge that teachers find this difficult because South Africa follows a very strict set curriculum (DBE 2011) with detailed daily tasks to be completed by teachers and children, leaving the minimum room for teacher authority to teach according to the individual children's developmental needs as suggested by the policy about inclusive education. By focusing on 'getting through the curriculum' and completing the prescribed assessment tasks, teachers are limited in their freedom to follow a conceptual development approach where their pedagogy is informed by a strong epistemic character based on concept development theories (e.g. Fritz et al. 2013) and on an understanding of general cognitive skills and features of language. Teacher autonomy is one of the factors that contribute to a successful education system (Morgan 2014).
'Interactionalism': Numeracy, language, environment and executive function
The neologism, 'interactionalism', comes from Clements and Sarama's review on several mathematics education studies (2015:250). According to them, the individual domains of pre-school learning each consists of its own components, and connections between individual components of each domain should be researched. In Figure 1, the conceptual model for the study is depicted as an image of intertwined strands of a rope that are combined and shaped by their pattern and coherence and their manifestation through an 'EF' filter to become the final 'rope' of early number concept development.
Already over 100 years ago, Lev Vygotsky studied how the development of concepts and the development of speech or language become intertwined, 'whereupon thought becomes verbal, and speech intellectual' (Kozulin 1990:153). He described how children relate concepts to the meaning of words and how concepts are verbally embodied. One of his greatest contributions to our understanding of cognitive development is his description of a dynamic pattern of engagement between verbal and intellectual functions (Kozulin 1990:157): 'The relationship between language and thought looks more like a nodical line with some threads from one string being interwoven into those of the other'. He, with many authors, such as Carey (2009), presented the idea that learning is, essentially, a socially and culturally derived outcome; children learn because they interact with their world and so the already rich neural networks of new-born babies extend through life, with optimal brain plasticity moments (Dehaene 2020) in childhood.
In the metaphor of the rope (Figure 1), if one strand unravels, or a child struggles with the development of a particular domain (whether it be language, numeracy or EF), the rope becomes too thick and unravels or loses its shape in a bottleneck in the executive 'filter'. This, in turn, makes conceptual processing and learning difficult. The result of stressors in the environment, such as unfamiliar words or sounds of a language, numeracy concepts which were not developed as foundation for further learning, etc. can result in an overloaded working memory (which forms part of the EF). As a result, children can struggle to process and develop new mathematical concepts, because strands in the 'rope's' pattern may be obstructive and may cause a delay in the development of early numeracy.
Early numeracy
Duncan et al.'s (2007) analysis of six longitudinal data sets highlight that one of the strongest predictors for success in mathematics is achievement on numeracy assessments at school entry. According to Clements and Sarama (2018), early numeracy competence provides a strong foundation for further mathematics learning, because it is based on the principle that mathematics learning is hierarchical and concepts build cumulatively on previously developed concepts. This is a constructivist principle on which various models of number development is based, with the one of Fritz et al. (2013) being an example. The theories of number concept development take into account what Dehaene (2009, 2011, 2020) and cognitive behavioural scientists and cognitive neuroscientist agree upon, namely that all children are born with the equipotential to develop their intuitive number knowledge into mathematical knowledge because of their modifiable and placate brain (Dehaene 2011).
Even young babies can use their visual cortex to estimate and accurately distinguish between small sets of objects (Spelke & Kinzler 2007). As they develop and engage with numerical constructs, parts of the brain learn to specialise in abstract mathematics through neuronal recycling (Dehaene 2009). By neuronal recycling, Dehaene (2009:147) means 'the partial or total invasion of a cortical territory initially devoted to a different function (such as object tracking), by a cultural invention' such as counting. According to him (Dehaene 2009), a useful metaphor would be to compare
[O]ur visual cortex to a Lego construction set, with which a child can build the standard model shown on the box, but also tinker with a variety of other inventions. (p. 146)
such as the development understanding of mathematics concepts.
When children learn natural language - especially nouns, number words and noun phrases (Spelke 2017) - these evolutionary inherited intuitions concurrently and progressively develop into more refined and sophisticated abstract networks of mathematical concepts. More or less at the age of two, knowledge of natural numbers and the ability to classify and count begin to develop (Sarnecka & Carey 2008). Then, children discover that there exists a stable, increasing order of natural numbers and they slowly start to grasp the cardinality of numbers (Sarnecka & Wright 2013). Later, they develop an understanding for the interrelatedness of numbers and master the idea that all numbers can be decomposed, form part of larger numbers and that there exist many relations between natural numbers (Langhorst, Ehlert & Fritz 2012). These foundational number concepts, together with concepts of space and time (eds. Dehaene & Brannon 2012), form a solid bedrock for mathematics achievement in Grade 1 (Aunio & Niemivirta 2010; Bezuidenhout 2019).
Inadequate early numeracy skills can result in continuous low performance in mathematics (Desoete 2015). Researchers also report that insufficient numerical skills often co-occur with other insufficiently developed cognitive skills, including language difficulties (Sharma 2015) and limited EF (Cragg et al. 2017).
Aunio and Räsänen (2015) argued that if pre-school teachers incorporate knowledge of numeracy foundations in their personal theories, it can improve the efficacy of their teaching and assessment practices and assist them to structure their planning for teaching and support more comprehensively. I suggest that teachers should include a comprehensive theoretical numeracy model (e.g. Fritz et al. 2013), together with cognitive development knowledge of language and EF, in their personal theories. Furthermore, teachers should continuously adapt such theories according to the needs of their everyday teaching.
Language for mathematics
In an editorial for Frontiers in Psychology, Dowker and Nuerk (2016) discuss linguistic influences on mathematics. They describe six linguistic levels which influence mathematics learning: (1) phonological (phonemic properties of language), (2) lexical composition of words, (3) semantic meaning, (4) syntactic (grammatical structures beyond word level influences), (5) conceptual properties of words (vocabulary) and (6) visuospatial (orthographic properties, including reading or writing direction). They also include working memory and other domain general EF in their theoretical model.
I maintain that a multilinguistic classroom context features in learning beyond mere vocabulary knowledge. Phonological properties, differences in the fine nuances of word meanings that cannot always be translated directly, and grammatical structures that give meaning to sentences, particularly impact children's mathematics learning and contribute to cognitive development. Dehaene (https://www.youtube.com/watch?v=0esnsHI4opA&feature=emb_rel_end) describes how babies develop a phonological awareness for vowels by the age of 6 months and consonants at 12 months whilst they also master syntax. By the age of three, their language system is well organised. If children don't use the neurons of particular sounds (such as a th-, sh- or -ch in English), the neurons for those sounds are pruned and it may be extremely difficult for children to 'hear' these sounds later in life to process such sounds. According to this view, if children learn a new language with new phonemes at Grade 1 level, it could be troublesome to 'hear' unfamiliar sounds of a language. Learning, for instance mathematics, in that particular new language, could become problematic.
For example, in terms of the translation of number names, isiZulu and Sesotho-speaking children are used to transparency in the meanings of number names. For instance, leshome le motso o mong (eleven) in Sesotho, means 'ten and one' and leshome le metso e mmedi (twelve) means 'eleven and one'. In English, however, the word 'eleven' has no obvious connection to the word 'ten', or 'twelve' to 'eleven'. Translating the meaning of number names from Sesotho to English may thus be difficult for young children who expect this type of conceptual transparency.
It may also be challenging for children to make sense of the grammatical structures of a new language - even if they know the vocabulary and sounds. Meaning is indeed lodged in the order of the words in a sentence just as much as it is rooted in vocabulary (Chomsky 1965). For instance, in a question, how many more is five than two?, two should be subtracted from five, whilst how many is five more than two? means that five should be added to two. The order of the words in the sentence generates the meaning and this could be troublesome for children who are not familiar with the grammatical structures of a language and the rules that govern its use.
The connection between numeracy, language for mathematics and EF (Diamond 2013; Schmitt et al. 2017) should also be considered in this context. For example, isiZulu or Sesotho children who are asked a mathematics question in English often mentally translate the question into their mother tongue; deploy their working memory (WM) to hold the information, which they have translated; reason by using their home language as mental function (Kozulin 1990:7); determine an answer; translate the answer back into English and then give an appropriate answer in English. This process can quickly overload the WM and requires competent cognitive shifting skills in the EF repertoire of skills.
Executive functions: A cognitive filter
When children enter Grade 1, they transition from a semi-informal pre-school setting to a more structured and formal education context, which demands a rapid rise in adaptive, goal-directed behaviour. Academic tasks increasingly require children to hold information in their mind (in the WM - see Cockroft 2015), whilst simultaneously processing other information, inhibiting environmental input and sustaining focus. The Grade 1 classroom setting calls for the ability to flexibly transition between tasks and to adapt to changing demands. In a formal learning environment such as Grade 1, children are expected to regulate their behaviour more than what they are used to in informal settings, such as a Grade R class or a pre-school centre. In Grade 1, ongoing mental processes are expected to be synchronised and well managed, whilst, simultaneously, as is the case of the school where this study was conducted, making sense of the linguistic environment with new terminology. Fortunately, structural changes in the prefrontal cortex during early childhood (Zelazo & Müller 2010) support an increase of executive control during early school years, which enable children to deal with the cognitive demands of Grade 1.
In the theoretical model, I presented in Figure 1, EF operates like a filter, or a control centre which manages all incoming, outgoing and ongoing processes. It regulates and organises the mixture of cognitive input; directs and filters output so that responses and behaviours are appropriate and goal-directed; and maintains, coordinates and harmonises all ongoing mental processes (Bull & Lee 2014; Diamond 2013; Miyake et al. 2000).
Researchers in the field of EF describe three distinct, yet related components of the executive control system (Bull & Lee 2014; Diamond 2013; Fitzpatrick 2014; Miyake et al. 2000), namely WM, inhibitory control and cognitive switching. Working memory allows an individual to monitor and hold information and to revise it by updating and replacing information with more appropriate information (Cockcroft 2015; Diamond 2013; Miyake et al. 2000). Inhibitory control enables deliberate inhibition of responses to stimuli and allows children to choose more appropriate reactions (Diamond 2013; Miyake et al. 2000). Switching, also referred to as cognitive flexibility, allows children to hold focus and to refocus or switch attention to more relevant tasks (Diamond 2014; Miyake et al. 2000).
Pre-schoolers' numerical, relational and counting skills have been reported to be impacted by inhibition and WM (Harvey & Miller 2017). Inhibition and cognitive flexibility also influence numeracy skills such as simple addition (Shaul & Schwartz 2014). Tasks like following multiple steps to perform operations, selecting appropriate strategies or algorithms and logical reasoning involve keeping, and repeatedly updating information in the mind, whilst processing new information.
In the editorial of a special issue in Frontiers in Psychology, Executive function and Education, Huizinga, Baeyens and Burack (2018) wrote:
[T]he study of development of executive function in relation to academic outcomes cannot be confined solely to the study of the child, but must be broadened to include the impact of the essential persons and contexts in the child's life, including teachers, parents, and family situation. (p. 6)
In the same vein, Devine, Bignardi and Hughes (2016) argued that children's learning environments at home and in school exist within relationships with parents, teachers and other significant people and impact the interface between EF and school performance. Also, Blankson and Blair's (2016) findings suggest that classroom practices affect children's mathematics achievement and EF. In other words, there is not just a link between mathematics achievement and numeracy or language but also between these constructs and the social environment itself.
Language input in a multilingual classroom makes an interesting case for the EF, filtering and coordinating the cognitive functions that I have discussed in this section of the article. Working memory fulfils a crucial function in EF, comprising two sub-systems. The sub-system known as the phonological loop, a phonological store and a rehearsal system holds and maintain information (Cockroft 2015). The phonological loop integrates 'auditory information into meaningful sounds, such as phonemes, words and sentences' (Cockroft 2015:3). The sub-system known as the visuospacial sketchpad stores and rehearses static visual/spatial information. 'These processes are critical for interpreting and integrating information from the visual (and auditory) world around us, which would otherwise constitute a series of disjointed snapshots' (Cockroft 2015:3). Both systems have limited capacity. Learning in a classroom environment where teachers switch between English and the children's home language, requires cognitive flexibility and WM. If teachers do not know how to mediate learning in a multilingual environment, meaning could get lost in translation.
The mediating role of the classroom and home learning environment
Clements and Sarama (2018:540) referred to Bronfenbrenner and Morris (2006): 'Complex interactions between the child and her environment in the early schooling years are likely to leave long-lasting influences on the child's developmental trajectory'. Pre-school children's interaction with family members, teachers or other adults and siblings who can calculate, count and read have a better chance to develop numeracy skills, whilst a lack of opportunities to engage with numerate and literate people on a regular basis may hamper pre-schoolers' numeracy abilities (Dillon et al. 2017). Early numeracy is dependent on home and school surroundings. (The home environment in this study is defined as the environment outside the formal school setting and may include shopping with parents, playing at a friend's home, going to the zoo and other learning environments in and around the home setting.) Interaction and feedback are important and this happens largely through language as communication medium. Clements and Sarama (2018) argued that children who perform well in early numeracy are likely to receive encouraging feedback from the people in their immediate environment.
Connections have been found between numeracy and non-numeracy aspects of the home mathematics environment and early mathematics development (Gunderson & Levine 2011; Napoli & Purpura 2018; Skwarchuk, Sowinski & LeFevre 2014). In their study, Skwarchuk et al. (2014) established that formal activities, such as practicing simple additions predicted symbolic number knowledge. They also found that home exposure to informal numeracy, together with parents' attitudes and enjoyment of mathematics activities, predicted non-symbolic arithmetic skills. In a subsequent study, Susperreguy et al. (2020) found that parents with high academic expectations and positive attitudes towards numeracy more frequently engaged in formal numeracy activities at home, which in turn predicted skills such as problem solving.
Particularly relevant to my study is research that shows a relationship between children's number knowledge and parents' number talk in the home environment (Gunderson & Levine 2011). Levine and Baillargeon (2016) argued that both the quality and quantity of parents' use of language for mathematics contribute to children's understanding of natural number. A child with a solid understanding of number concepts is more likely to have received better and more mathematics language input at home and at school than a child who struggles to understand number concepts (Levine & Baillargeon 2016:136).
In another study by Klibanoff et al. (2006), pre-school teachers' use of language for mathematics predicted how children's mathematics knowledge increases. The classroom environment is filled with language and other factors that mediate mathematics learning. Classroom environments not only influence children's interest in mathematics but a positive classroom environment also sets the tone for intrapersonal attributes (such as EF) development, which in turn mediate mathematics performance (Tosto et al. 2016).
Research methods and design
Two Grade R teachers and two Grade 1 teachers were purposefully selected to participate in individual semi-structured interviews. The isiZulu Grade 1 teacher was on maternity leave and a B.Ed. (Hons) student, who was the locum teacher, participated on behalf of the class teacher. Although she had no experience like the other three teachers, it was clear that her theoretical knowledge was up to date with current literature. This provided a valuable dimension to the interview data. The Sesotho Grade 1 teacher - with a Junior Primary Teaching Diploma (JPTD) - had 18 years of teaching experience and was able to provide rich examples during her interview. The Grade R teachers (isiZulu and Sesotho), each with an Early Childhood Development (ECD) Level 5 qualification, respectively, had 8 and 9 years' teaching experience.
Each teacher answered six questions which addressed (1) influences on early numeracy, (2) Grade R number concept attainment, (3) school's characteristics, (4) diagnostic instrument use1, (5) language for mathematics learning and (6) executive functions. The interviews were recorded, with the teachers' permission. Henning, Van Rensburg and Smit (2004) reminded us that the power of an interview is logged in how the participants read social life - and particularly in this study how teachers read children's development in a particular linguistic environment.
To protect the identity of the participants, teachers remain anonymous and are referred to as teacher 1, 2, 3 or student teacher (T1, T2, T3 or ST). They participated voluntarily and were allowed to exit the interview at any stage. Ethics clearance (Information redacted to maintain the integrity of the review process) was obtained from the University of Johannesburg's faculty of education and from the school's board.
For the interviews to be trustworthy tools, the questions were conceptualised on the foundation of theoretical models as described in this article and the recording, transcription and analyses were performed systematically as Henning, Van Rensburg and Smit (2013) suggest. To capture an understanding of the data in writing, I conducted content - and discourse analyses (Henning et al. 2013). I utilised the craft of an inductive process of open coding (Henning et al. 2013:104), categorisation and thematic organisation, which ultimately led to a comprehensive theme.
Ethical consideration
Ethical approval to conduct the study was obtained from the board of the school where interviewed teachers teach and the Ethics Committee of the University of Johannesburg. The author certified that the study was performed in accordance with the ethical standards. All participants remain anonymous. Ethical clearance number is 2017-053 of 22 June 2017.
Results
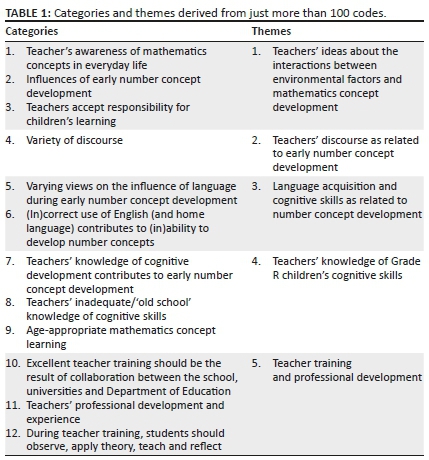
Each interview was transcribed verbatim and the data were coded to name units of meaning in the teachers' responses. More than 100 codes were grouped to form 12 categories, which are analogous to Strauss and Corbin's notion of 'axial coding' (Henning et al. 2013). Subsequently, five themes were derived from the categories, demonstrating how the categories coalesced. Figure 2 is an example of how categories were derived from codes.
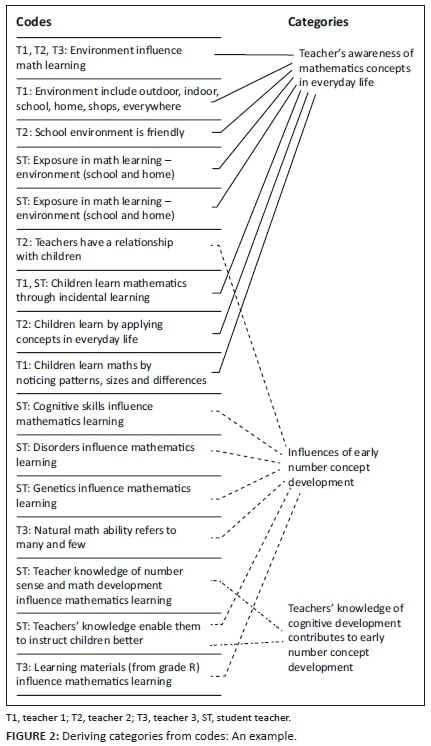
Table 1 depicts the categories and themes derived from just more than 100 codes.
By grouping the themes and contemplating their meaning as a coherent set of findings, the following pattern in the data was formulated: Teachers' personal theories about the interface between Grade R children's learning and Grade 1 mathematics concept development shows some emergent critical reflective capability. Teachers' discourse shows that they have some inclination to reflect on individual aspects of child learning. They also have the craft knowledge to reflect on their pedagogy in a multilingual environment. Nevertheless, they have not yet developed personal pedagogical theories for the integration between features of Grade R learning and the link to Grade 1 mathematics achievement.
Discussion and conclusion
Dehaene (2011) and Dillon et al. (2017) call for findings of studies in laboratories to be confirmed by studies in the field of everyday classroom life. Added to this plea, I argue that the perspectives of teachers should be incorporated into empirical findings to provide an indication of (1) focus areas for teacher education, (2) how policy impacts teaching and (3) to identify research topics for classroom research.
During the interviews of the current study, teachers were able to invoke their experience to talk about how pre-school numeracy prepares children for Grade 1 mathematics. Teacher 1 said, 'They need to learn colours, shapes, quantities, many, few, less, more. Just basic counting but not route learning - counting with meaning. One-to-one correspondence …' and Teacher 2,
'I think in Grade R what they need to learn is position in space; she learn like more of practical things like maybe measurements, the quantity. They also learn patterns. And counting as well.' (Participant 2, Grade R teacher, 22 June 2017)
These concepts are age appropriate and are also described in the literature (e.g. Fritz et al. 2013; Sarnecka & Carey 2008; Spelke & Kinzler 2007).
Some teachers were also able to identify individual links between numeracy and EF as described in the literature (Bull & Lee 2014; Diamond 2013; Fitzpatrick 2014; Miyake et al. 2000). From a more theoretical background, the student teacher said, 'Working memory in terms of developing number concepts because it's a build up from one thing to the other thing to the next thing in number concept development.'
One of the Grade 1 teachers, who has the most experience concluded:
'This was a sum that needed me to add, now the sum wants me to subtract. I can block the addition part, now I can switch over to subtraction. They will just see addition. You give them something in subtraction, now it's all addition,' (Participant 1, Grade 1 teacher, 22 June 2017)
which indicates that she can link cognitive flexibility to mathematics.
In the more formal discourse of the student teacher, it was evident that she formulated some kind of personal theoretical perspective on the association between language and numeracy:
'Language is pivotal to mathematics. I think we should include mother tongue language in our mathematics teaching. So that the child may have a proper grasp of this concept. And using the correct mathematical language at all times is very pivotal as well to learning'. (Participant 4, student teacher, 22 June 2017)
The other teachers leaned to practical examples. Teachers 1 and 3 indicated that they have the craft to reflect on language and their everyday teaching, but perhaps lack the ability to combine their experience with an integrated pedagogical theory: 'Sometimes they do not exactly … it's not a correct equivalent of English. So sometimes it causes a lot of clashes.' (Participant 1, Grade 1 teacher, 22 June 2017)
and
'Say we are teaching them a concept we start by teaching it in their home language because we are a home language school (Grade R uses home language). And as we realize that they have grasped the concept we promote it by interpreting it by saying this is how we say it in English - preparing them for Grade 1 of course.' (Participant 3, Grade R teacher, 22 June 2017)
Teacher 1's use of the words 'is not an exact equivalent of …' links with Dowker and Nuerk's model (2016), which posits that the phonemic properties of language, lexical composition of words and conceptual properties impact how children learn. Children who struggle to switch between languages, experience 'a lot of clashes' (Participant 1, Grade R teacher, 22 June 2017). She explained that phonemes and vocabulary could be the doorway to conceptual understanding, not only the constructs on their own. Teacher 3 also linked vocabulary to numeracy conceptual properties but was unable to explain it from a theoretical perspective such as Vygotsky's theory (Kozulin 1990). She highlighted that children should simultaneously be introduced to mathematical language and numeracy constructs as Dillon et al. (2017) suggest.
In terms of EF, teachers commented with general remarks which can be linked to attention, such as, 'Because you cannot learn if your brain is on the other side of town' (Participant 4, student teacher, 22 June 2017) and
'Remember, children's minds are everywhere and anywhere and sometimes you have to recollect it every time. So as a teacher you have to have the strategies to collect them for a period of time and you must be able to shift them and they must be able to shift with time.' (Participant 3, Grade R teacher, 22 June 2017)
Yet, remarks such as '… if I'm answering this correctly, …' (Participant 3, Grade R teacher, 22 June 2017), '… not really sure …' (Participant 4, student teacher, 22 June 2017) and '… I think this is something I must still think about …' (Participant 3, Grade R teacher, 22 June 2017) suggest that a sound understanding of EF and its relation to mathematics were not yet part of their personal pedagogical theories.
All four teachers referred to the home and class learning environment as important contributors for mathematics learning. Like some researchers (Gunderson & Levine 2011; Napoli & Purpura 2018), they also mentioned how mathematics language at home and in school (Klibanoff et al. 2006) impact mathematics learning. Teacher 2 gave the example of the home environment: 'Maybe the mother or father is pouring the drink in the cup and the child will say, no I want half, or please I don't want a full glass.' (Participant 2, Grade R teacher, 22 June 2017) Teacher 3 referred to the class environment and mentioned that the class and home environments should be connected: 'My relationship with them because I will be teaching them and after repetition they can take it home'. (Participant 3, Grade R teacher, 22 June 2017) The student teacher also reminded us, like Levine and Baillargeon (2016) that it's not only the amount of number talk at home or school but also the quality of mathematics-specific language to which the child is exposed that matters.
To conclude, in a review of recent research, Clements and Sarama (2015) acknowledged that many studies present findings of concurrent and predictive associations between cognitive contributors for numeracy development, but highlight that many researchers do not consider cultural contexts. They argue that it is vital to establish connections between contributors for mathematics and argue that 'interrelationships among cognitive components may be altered by different educational contexts' (Clements & Sarama 2015:14). The findings of this study are consistent with several studies that showed interactions between the domains described in this study. Yet, the main finding of this study is that teachers do not yet ground their pedagogy in personal theories about the interface between Grade R children's learning and Grade 1 mathematics achievement.
In the words of the teachers:
'If the teacher is really knowledgeable of number sense development, of mathematical development, the teacher will be able to instruct the learners better. It's good to have a teacher that is able to integrate all these concepts.' (Participant 4, student teacher, 22 June 2017)
'An experienced and qualified Grade R practitioner who knows what to teach them and how to teach them.' (Participant 3, Grade R teacher, 22 June 2017) is vital.
This finding calls on teacher education to design robust models to prepare prospective teachers, as well as in-service teachers, to formulate and continuously adapt their personal pedagogical theories of cognitive development and its interface with teaching. A shift towards a strong theoretical, conceptual teaching approach could alter the way in which mathematics is being taught (Clements & Sarama 2018). More research about how language for mathematics could be developed in Grade R should be conducted so that we can better understand how children draw on language and the environment whilst learning mathematics in Grade 1. Future research should also focus on the improvement of teaching development programmes to support teachers in the maturation of their pedagogical theories.
Acknowledgements
The author would like to acknowledge and thank Prof. Elizabeth Henning for critically reading and commenting on the manuscript, as well as the reviewers.
Competing interests
The author declares that no competing interests exists.
Author's contributions
H.S.B. is the sole author of this research article.
Funding information
The financial assistance of the National Research Foundation (NRF Grant Number 98573), South Africa, towards this research is hereby acknowledged.
Data availability statement
Data for the interviews are available on request.
Disclaimer
The views and opinions expressed in this article are those of the author and do not necessarily attributed to the NRF.
References
Aunio, P., Korhonen, J., Ragpot, L., Törmänen, M., Mononen, R. & Henning, E., 2019, 'Multi-factorial approach to early numeracy: The effects of cognitive skills, language factors and kindergarten attendance on early numeracy performance of South African first graders', International Journal of Educational Research 97, 65-76. https://doi.org/10.1016/j.ijer.2019.06.011 [ Links ]
Aunio, P. & Niemivirta, M., 2010, 'Predicting children's mathematical performance in grade one by early numeracy', Learning and Individual Differences 20(5), 427-435. https://doi.org/10.1016/j.lindif.2010.06.003 [ Links ]
Aunio, P. & Räsänen, P., 2015, 'Core numerical skills for learning mathematics in children aged five to eight years: A working model for educators', European Early Childhood Education Research Journal 24(5), 684-704. https://doi.org/10.1080/1350293X.2014.996424 [ Links ]
Bezuidenhout, H.S., 2019, 'Input for young children's number concept development', Doctoral dissertation, University of Johannesburg, Johannesburg. [ Links ]
Bezuidenhout, H., Henning, E., Fitzpatrick, C. & Ragpot, L., 2019, 'Early mathematics vocabulary and number concept development', in Southern African Association for Research in Mathematics, Science and Technology Education: Research for inclusive, relevant and equitable quality Mathematics, Science and Technology Education: Promoting research-based opportunity for all, University of Kwazulu Natal, Durban, South Africa, 15-17 January 2019, p. 2.
Bezuidenhout, H.S., Ragpot, L., Fitzpatrick, C. & Henning, E., 2019, 'A variety of early grade mathematics assessments and their uses in South Africa', in Mathematical cognition and learning society, Carleton University, Ottawa, Canada, 16-18 June 2019, p. 63, viewed 10 February 2020, from https://www.the-mcls.org/fileadmin/user_upload/MCLS_Full_program_.pdf.
Blankson, A.N. & Blair, C., 2016, 'Cognition and classroom quality as predictors of math achievement in the kindergarten year', Learning and Instruction 41, 32-40. https://doi.org/10.1016/j.learninstruc.2015.09.004 [ Links ]
Bronfenbrenner, U. & Morris, P., 2006, 'The bioecological model of human development', in W. Damon & R.M. Lerner (eds.), Handbook of child psychology, Vol. 1. Theoretical models of human development, 6th edn., pp. 793-828, Wiley, New York, NY.
Bull, L. & Lee, K., 2014, 'Executive functioning and mathematical achievement', Child Development Perspectives 8(1), 36-41. https://doi.org/10.1111/cdep.12059 [ Links ]
Bull, R., Espy, K.A., Wiebe, S.A., Sheffield, T.D. & Nelson, J.M., 2011, 'Using confirmatory factor analysis to understand executive control in preschool children: Sources of variation in emergent mathematic achievement', Developmental Science 14(4), 679-692. https://doi.org/10.1111/j.1467-7687.2010.01012.x [ Links ]
Butterworth, B., Reeve, R., Reynolds, F. & Lloyd, D., 2008, 'Numerical thought with and without words: Evidence from indigenous Australian children', Proceedings of the National Academy of Sciences 105(35), 13179-13184. https://doi.org/10.1073/pnas.0806045105 [ Links ]
Carey, S., 2009, The origin of concepts, Oxford University Press, Oxford.
Chomsky, N., 1965, Aspects of the theory of syntax, MIT Press, Cambridge, MA, pp. 16-75, ISBN 9780262260503.
Clark, C.A.C., Sheffield, T.D., Wiebe, S.A. & Espy, K.A., 2013, 'Longitudinal associations between executive control and developing mathematical competence in preschool boys and girls', Child Development 84(2), 662-677. https://doi.org/10.1111/j.1467-8624.2012.01854.x [ Links ]
Clements, D. & Sarama, J., 2015, 'Discussion from a mathematics education perspective', Mathematical Thinking and Learning 17(2-3), 244-252. https://doi.org/10.1080/10986065.2015.1016826 [ Links ]
Clements, D.H. & Sarama, J., 2016, 'Math, science, and technology in the early grades', The Future of Children 26(2), 75-94. https://doi.org/10.1353/foc.2016.0013 [ Links ]
Clements, D.H. & Sarama, J., 2018, 'Myths of early math', Education Sciences 8(2), 71. https://doi.org/10.3390/educsci8020071 [ Links ]
Cockcroft, K., 2015, 'The role of working memory in childhood education: Five questions and answers', South African Journal of Childhood Education 5(1), 1-18. https://doi.org/10.4102/sajce.v5i1.347 [ Links ]
Condry, K.F. & Spelke, E.S., 2008, 'The development of language and abstract concepts: The case of natural number', Journal of Experimental Psychology: General 137(1), 22. https://doi.org/10.1037/0096-3445.137.1.22 [ Links ]
Cragg, L., Keeble, S., Richardson, S., Roome, H.E. & Gilmore, C., 2017, 'Direct and indirect influences of executive functions on mathematics achievement', Cognition 162, 12-26. https://doi.org/10.1016/j.cognition.2017.01.014 [ Links ]
Dehaene, S., 2009, Reading in the brain: The new science of how we read, Penguin group publishers, USA.
Dehaene, S., 2011, The number sense. (How the mind creates mathematics), Oxford University Press, Oxford.
Dehaene, S., 2020, How we learn: Why brains learn better than any machine… for now, Penguin, Century City, Cape Town.
Dehaene, S. & Brannon, E. (eds.), 2012, Space, time and number in the brain. Searching for the foundations of mathematical thought, Elsevier, Amsterdam.
Department of Basic Education, 2011, Curriculum and assessment policy statement (CAPS), Foundation Phase. Mathematics, Grade R - 3, viewed 24 December 2014, from http://www.education.gov.za/Curriculum/CurriculumAssessmentPolicyStatements/tabid/419/Default.aspx.
Department of Basic Education, 2014, Report on the Annual National Assessment of 2014: Grades 1 to 6 & 9, viewed 28 December 2014, from http://www.education.gov.za/Curriculum/AnnualNationalAssessment/tabid/424/Default.aspx.
Desoete, A., 2015, 'Predictive indicators for mathematical learning disabilities/dyscalculia in kindergarten children', in S. Chinn (ed.), The Routledge international handbook of dyscalculia and mathematical learning difficulties, pp. 90-100 Routledge, New York, NY.
Devine, R.T., Bignardi, G. & Hughes, C., 2016, 'Executive function mediates the relations between parental behaviours and children's early academic ability', Frontiers in Psychology 7, 1902. https://doi.org/10.3389/fpsyg.2016.01902 [ Links ]
Diamond, A., 2013, 'Executive functions', Annual Review of Psychology 64, 135-168. https://doi.org/10.1146/annurev-psych-113011-143750 [ Links ]
Diamond, A., Barnett, W.S., Thomas, J. & Munro, S., 2007, 'Preschool program improves cognitive control', Science 318(5855), 1387. https://doi.org/10.1126/science.1151148 [ Links ]
Dillon, M.R., Kannan, H., Dean, J.T., Spelke, E.S. & Duflo, E., 2017, 'Cognitive science in the field: A preschool intervention durably enhances intuitive but not formal mathematics', Science 357(6346), 47-55. https://doi.org/10.1126/science.aal4724 [ Links ]
Dowker, A.D. & Nuerk, H., 2016, 'Linguistic influences on mathematics', Frontiers in Psychology 7, 1-4. https://doi.org/10.3389/fpsyg.2016.01035 [ Links ]
Duncan, G.J., Dowsett, C.J., Claessens, A., Magnuson, K., Huston, A.C., Klebanov, P. et al., 2007, 'School readiness and later achievement', Developmental Psychology 43(6), 1428-1446. https://doi.org/10.1037/0012-1649.43.6.1428 [ Links ]
Dyrvold, A., 2020, 'Relations between semiotic resources in mathematics tasks: A source of students' difficulties', Research in Mathematics Education, 1-19. https://doi.org/10.1080/14794802.2019.1689160 [ Links ]
Fritz, A., Ehlert, A. & Balzer, L., 2013, 'Development of mathematical concepts as basis for an elaborated mathematical understanding', South African Journal of Childhood Education 3(1), 21-37. https://doi.org/10.4102/sajce.v3i1.31 [ Links ]
Fitzpatrick, C., 2014, 'Bridging the gap between advantaged and disadvantaged children: Why should we be concerned with executive functions in the South African context?' South African Journal of Childhood Education 4(1), 156-166. https://doi.org/10.4102/sajce.v4i1.66 [ Links ]
Geary, D.C. & Van Marle, K., 2016, 'Young children's core symbolic and nonsymbolic quantitative knowledge in the prediction of later mathematics achievement', Developmental Psychology 52(12), 2130. https://doi.org/10.1037/dev0000214 [ Links ]
Gunderson, E.A. & Levine, S.C., 2011, 'Some types of parent number talk count more than others: Relations between parents' input and children's cardinal-number knowledge', Developmental Science 14(5), 1021-1032. https://doi.org/10.1111/j.1467-7687.2011.01050.x [ Links ]
Harvey, H.A. & Miller, G.E., 2017, 'Executive function skills, early mathematics, and vocabulary in head start preschool children', Early Education and Development 28(3), 290-307. https://doi.org/10.1080/10409289.2016.1218728 [ Links ]
Henning, E., 2012, 'Learning concepts, language, and literacy in hybrid linguistic codes: The multilingual maze of urban grade 1 classrooms in South Africa', Perspectives in Education 30(4), 70-79. [ Links ]
Henning, E., 2013, 'Teachers' understanding of mathematical cognition in childhood: Towards a shift in pedagogical content knowledge?' Perspectives in Education 31(3), 139-154. [ Links ]
Henning, E., Van Rensburg, W. & Smit, B., 2004, Finding your way in qualitative research, Van Schaik Publishers, Pretoria.
Huizinga, M., Baeyens, D. & Burack, J.A., 2018, 'Executive function and education', Frontiers in Psychology 9, 1357. https://doi.org/10.3389/fpsyg.2018.01357 [ Links ]
Klibanoff, R.S., Levine, S.C., Huttenlocher, J., Vasilyeva, M. & Hedges, L.V., 2006, 'Preschool children's mathematical knowledge: The effect of teacher "math talk"', Developmental Psychology 42(1), 59. https://doi.org/10.1037/0012-1649.42.1.59 [ Links ]
Kozulin, A., 1990, Vygotsky's psychology: A biography of ideas, Harvard, Cambridge, MA.
Langhorst, P., Ehlert, A. & Fritz, A., 2012, 'Non-numerical and numerical understanding of the part-whole concept of children aged 4 to 8 in word problems', Journal fur Mathematik-Didaktik 33(2), 233-262. https://doi.org/10.1007/s13138-012-0039-5 [ Links ]
Levine, S. & Baillargeon, R., 2016, 'Different factors of language in numerical development: Exact number and individuation', in D. Barner & S. Baron (eds.), Core knowledge and conceptual change, pp. 127-150, Oxford University Press, Oxford.
Miyake, A., Friedman, N.P., Emerson, M.J. Witzki, A.H. & Howerter, A., 2000, 'The unity and diversity of executive functions and their contributions to complex "Frontal Lobe" tasks: A latent variable analysis', Cognitive Psychology 41(1), 49-100. https://doi.org/10.1006/cogp.1999.0734 [ Links ]
Morgan, H., 2014, 'Review of research: The education system in Finland: A success story other countries can emulate', Childhood Education 90(6), 453-457. https://doi.org/10.1080/00094056.2014.983013 [ Links ]
Napoli, A.R. & Purpura, D.J., 2018, 'The home literacy and numeracy environment in preschool: Cross-domain relations of parent-child practices and child outcomes', Journal of Experimental Child Psychology 166, 581-603. https://doi.org/10.1016/j.jecp.2017.10.002 [ Links ]
Niss, M. & Højgaard, T., 2011, Competencies and mathematical learning: Ideas and inspiration for 485, Roskilde Universitet, Roskilde.
SACMEQ, 2017, The SACMEQ IV project in South Africa: A study of the conditions of schooling and the quality of education, viewed 23 July 2020 from, http://www.sacmeq.org/sites/default/files/sacmeq/publications/sacmeq_iv_project_in_south_africa_report.
Sarnecka, B.W. & Carey, S., 2008, 'How counting represents number: What children must learn and when they learn it', Cognition 108(3), 662-674. https://doi.org/10.1016/j.cognition.2008.05.007 [ Links ]
Sarnecka, B.W. & Wright, C.E., 2013, 'The idea of an exact number: Children's understanding of cardinality and equinumerosity', Cognitive Science 37(8), 1493-1506. https://doi.org/10.1111/cogs.12043 [ Links ]
Schmitt, S.A., Geldhof, G.J., Purpura, D.J., Duncan, R. & McClelland, M.M., 2017, 'Examining the relations between executive function, math, and literacy during the transition to kindergarten: A multi-analytic approach', Journal of Educational Psychology 109(8), 1120. https://doi.org/10.1037/edu0000193 [ Links ]
Schmitt, S.A., Purpura, D.J. & Elicker, J.G., 2019, 'Predictive links among vocabulary, mathematical language, and executive functioning in pre-schoolers', Journal of Experimental Child Psychology 180, 55-68. https://doi.org/10.1016/j.jecp.2018.12.005 [ Links ]
Sharma, M.C., 2015, 'A window into dyscalculia and other mathematics difficulties', in S. Chinn (ed.), The Routledge international handbook of dyscalculia and mathematical learning difficulties, p. 277, Routledge, New York, NY.
Shaul, S. & Schwartz, M., 2014, 'The role of the executive functions in school readiness among preschool-age children', Reading and Writing 27(4), 749-768. https://doi.org/10.1007/s11145-013-9470-3 [ Links ]
Skwarchuk, S.L., Sowinski, C. & LeFevre, J.A., 2014, 'Formal and informal home learning activities in relation to children's early numeracy and literacy skills: The development of a home numeracy model', Journal of Experimental Child Psychology 121, 63-84. https://doi.org/10.1016/j.jecp.2013.11.006 [ Links ]
Spaull, N. & Kotze, J., 2015, 'Starting behind and staying behind in South Africa. The case of insurmountable deficits in mathematics', International Journal of Educational Development 41(1), 13-24. https://doi.org/10.1016/j.ijedudev.2015.01.002 [ Links ]
Spelke, E. & Kinzler, K.D., 2007, 'Core knowledge', Developmental Science 10(1), 89-96. https://doi.org/10.1111/j.1467-7687.2007.00569.x [ Links ]
Spelke, E.S., 2017, 'Core knowledge, language, and number', Language Learning and Development 13(2), 147-170. https://doi.org/10.1080/15475441.2016.1263572 [ Links ]
Susperreguy, M.I., Douglas, H., Xu, C., Molina-Rojas, N. & LeFevre, J.A., 2020, 'Expanding the home numeracy model to Chilean children: Relations among parental expectations, attitudes, activities, and children's mathematical outcomes', Early Childhood Research Quarterly 50(3), 16-28. https://doi.org/10.1016/j.ecresq.2018.06.010 [ Links ]
Toll, S.W. & Van Luit, J.E., 2014, 'The developmental relationship between language and low early numeracy skills throughout kindergarten', Exceptional Children 81(1), 64-78. https://doi.org/10.1177/0014402914532233 [ Links ]
Tosto, M.G., Asbury, K., Mazzocco, M.M., Petrill, S.A. & Kovas, Y., 2016, 'From classroom environment to mathematics achievement: The mediating role of self-perceived ability and subject interest', Learning and Individual Differences 50, 260-269. https://doi.org/10.1016/j.lindif.2016.07.009 [ Links ]
Trends in International Mathematics and Science Study (TIMSS), 2015, International mathematics achievement, viewed 23 July 2020, from http://timssandpirls.bc.edu/.
Zelazo, P.D. & Müller, U., 2010, 'Executive functioning in typical and atypical children', in U. Goswami (ed.), The Wiley-Blackwell Handbook of childhood cognitive development, 2nd edn., pp. 574-603. https://doi.org/10.1002/9781444325485.ch22
 Correspondence:
Correspondence:
Hanrie Bezuidenhout
hsbezuidenhout@uj.ac.za
Received: 05 Aug. 2020
Accepted: 05 Oct. 2020
Published: 14 Dec. 2020
1 . The purpose of another study was to investigate the use of a diagnostic numeracy test. The results of this question do not form part of the current study and are therefore not discussed.














