Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.10 n.1 Johannesburg 2020
http://dx.doi.org/10.4102/sajce.v10i1.802
ORIGINAL RESEARCH
Proposing and modifying guided play on shapes in mathematics teaching and learning for Zambian preschool children
Nagisa Nakawa
Architecture and Environmental Design, Kanto Gakuin University, Yokohama, Japan
ABSTRACT
BACKGROUND: Early childhood education (ECE) has recently been introduced in Zambian government schools, leading to a need to examine the quality of mathematics lessons.
AIM: This study focussed on guided play lessons on shapes in pre-mathematics classes and examined how they could be implemented and what children could learn in the class.
SETTING: The lessons were conducted in two early childhood mathematics classes in two different schools in Zambia.
METHODS: A qualitative design-based research method was applied. For data collection, teachers implemented a trial lesson in one school and a main lesson in another school in Lusaka, the capital of Zambia.
RESULTS: In the first lesson, the activity differed from what was planned and discussed. In the second lesson, the content and objective of the guided play were changed from those of the trial lesson. In the main lesson, children engaged in a more basic activity involving shapes and created many kinds of shapes that they were familiar with in and out of school. This was particularly effective for children in terms of explicitly learning the basic features of the shapes and important mathematical ideas such as congruency, similarity and symmetry
CONCLUSION: The main lesson was successful because the level of mathematical content was more appropriate for the children and allowed them to enjoy the activity. Two points regarding developing more effective lessons for ECE, to identify pupils' readiness and sociocultural status, were also assessed and discussed.
Keywords: mathematics; early childhood mathematics; playing; guided play; shapes.
Introduction
Early childhood mathematics education is crucial for children, as mathematical competencies in preschool are relevant for learning performance and outcomes in their future education and as challenging and appropriate mathematical learning needs to be offered to children for their cognitive and affective development (Duncan et al. 2007; Vogt et al. 2018; Weisberg, Hirsh-Pasek & Golinkoff 2013). To assist children's cognitive and affective development, it is important to take into account pedagogy, of which playing is a key factor that should be investigated, as emphasised by previous studies (Brandt 2013; Thomas, Warren & De Vries 2011; Vogel 2013; Vogt et al. 2018; Worthington & Van Oers 2016). Because playing is crucial for young children's development, the national curriculum and syllabus in several countries worldwide (e.g. Japan, Korea, Germany and Australia), including some African countries (e.g. Kenya, Zimbabwe, Zambia and South Africa), emphasise the importance of playing in teaching and learning. However, little is known about early childhood mathematics education in sub-Saharan countries, apart from South Africa where academic staff is sufficiently employed, and there have only been a few studies on the topic in sub-Saharan countries (e.g. Mutemeri & Mugweni 2013). Moreover, it is crucial to consider the sociocultural aspects (Bishop 2010) of playing to implement related activities in sub-Saharan African countries.
An increasing number of studies have discussed the development of early childhood education (ECE) programmes in different countries (Müller & Wittmann 2004a, 2004b; South African Numeracy Chair Project 2016), the improvement of teachers' pedagogical content knowledge (Lee 2017; McCray & Chen 2008) and their professional development (Warren & Quine 2013). Recent studies have revealed that children can engage in many mathematical practices, such as reasoning, measuring and algebraic thinking, a previously unexpected finding (e.g. Hachey 2013; Sophian 2013). Learning through playing has been regarded as a vehicle for learning that is important for children in terms of both their mental and physical development (Hauser 2005; Singer 2013; Vogt et al. 2018); however, the meaning and interpretation of playing at the implementation level differ depending on social and cultural settings (Worthington & Van Oers 2016). Several studies on playing have stated the importance of a connection between playing and children's culture and environment (Worthington & Van Oers 2016).
In the Zambian context, as ECE has only recently been implemented in government schools (National Assembly of Zambia 2011; Ministry of Education, Science, Vocational Training and Early Education [MESVTEE] 2013), teachers and educators need to understand how Zambian children learn mathematics in a given situation to improve the quality of lessons and for better curriculum development. Therefore, using a design-based research (DBR) method (Bakker & Van Eerde 2015), this study aimed to develop an ECE mathematics lesson using guided play (Weisberg et al. 2013) with shapes. Compared to the domain of numbers, there are a relatively smaller number of studies on children's learning of shapes in spite of its importance and great influence on people's graphic production in human's history (Villarroel & Ortega 2017). For example, Piaget and Inhelder (1948) considered that children younger than 7 years old did not develop enough geometrical thinking. Clements and Sarama (2011) stated that in the United States, geometry has received minimal focus in ECE compared to numbers and calculation, which is also true for the rest of the world. Nowadays, studies regarding geometrical thinking have revealed that geometric form plays an important role in general ECE (Villarroel & Ortega 2017). Clements and Sarama (2011) went on to emphasise the importance of geometry learning in early childhood mathematics education, as it also supports children's understanding of number and arithmetic concepts (Arcavi 2003). Clements and Sarama (2014) also indicated a few important factors regarding children's knowledge of shapes. Firstly, children's preferences towards shapes are influenced by culture. In the case of children in the United States, they prefer closed, symmetric shapes. Secondly, children are capable of much more than simply knowing the names of various shapes, and they acquire knowledge and skills related to shapes through playing. In line with this, Cohrssen et al. (2017) emphasised that geometry and spatial reasoning were crucial in early childhood mathematics education; however, geometry has been generally overlooked and teachers have not created opportunities to develop children's thinking. The authors mainly dealt with children's spatial thinking, but not with two-dimensional shapes. Villarroel and Ortega (2017) concluded in their study that the use of geometric shapes in ECE accompanies the process of developing children's graphical expression skills. These studies demonstrated that before entering primary school, young children can relate to shapes in many ways. On the other hand, they did not focus on the development of lessons on shapes, neither did they discuss the children's cultural background and how it influenced their process of learning shapes in the class. Luneta (2014) also stated that teachers in South Africa have a lack of knowledge required to effectively teach space and shapes for ECE. In South Africa, one study was conducted related to shapes: Du Plessis (2018) mentioned the importance of young children recognising patterns. However, his focus was on algebra and geometric patterns. He also stated that the understanding of patterns and their structures will enhance learners' algebraic and generalised thinking in the future, proposing possible activities for geometric patterns; however, he neither implemented them nor discussed specifics.
Therefore, this article examined what and how children learned through the proposed and implemented activity and how their culture and surroundings influenced their mathematical abilities and skills regarding shapes. Thus, the following research questions were addressed: (1) 'how can a guided play lesson on shapes in pre-mathematics be developed and modified according to pupils' challenges in the class?' and (2) 'what is the outcome of children's learning in reception classes encounter during a guided play lesson on shapes?'. This study also aimed to show the effectiveness of guided play in cultural and social conditions that are different from the Western setting.
Zambian early childhood mathematics education
Zambia started ECE in 2004 and has been expanding the number of ECE programmes in primary schools throughout the country. The objective of ECE in Zambia is to help children acquire knowledge, skills, attitudes and positive values to attain their developmental milestones (MESVTEE 2014:xi). In ECE, there are two learning levels: the nursery level for 3-4-year-olds and the reception level for 5-6-year-olds. Their learning areas are equivalent to the subjects they will receive in primary school and include social studies, environmental science, language and literacy, pre-mathematics and expressive arts (MESVTEE 2014:36). The importance of a child-centred approach is also emphasised for children's effective learning, for example, group work, role play, exploring and discussion (Curriculum Development Centre [CDC] 2016; MESVTEE 2013).
The aim of pre-mathematics is to develop children's mathematical knowledge, skills and values, in addition to an interest in mathematics for everyday use (CDC 2016; MESVTEE 2013). Children should learn mathematics through manipulating objects; therefore, learning should be practical. Furthermore, informal mathematical activities should be conducted for a solid foundation of mathematical concepts and skills for later education. Pre-mathematics at the reception level includes algebra, numbers, geometry, measurements and commercial arithmetic. In particular, regarding shapes in the syllabus (MESVTEE 2013) and textbooks, children are given opportunities to say the names of different shapes, such as circles, rectangles, squares and triangles, in their local languages and to draw these shapes. However, they do not seem to be given a chance to manipulate shapes in their lessons.
Conceptual framework: Guided play
Weisberg et al. (2013) mentioned that the role of play in ECE has been controversial in terms of the dichotomy between learning and play (Anders & Rossbach 2015; Clements & Sarama 2009). The most subjective play is called free play, and the least subjective play is performed according to direct instruction (Weisberg et al. 2013). Weisberg et al. (2013) discussed the middle ground between the two contrasting forms of play: guided play. Its theoretical basis includes the aspects of respect for exploration, investigation and children's autonomy with teacher-guided instruction (Fisher et al. 2011; Weisberg et al. 2013). Guided play works effectively when certain learning goals are established and children learn new things through adult support. In mathematics learning, young children can become familiar with mathematical concepts in their environment during free play; on the other hand, they also need to learn new concepts that they have not seen before in the classroom setting, as some mathematical concepts cannot be understood without the assistance or intervention of adults. Guided play can thus work well. In guided play, teachers' or adults' guidance is also crucial (Weisberg et al. 2013). This is because adults' support determines if guided play can help children meet the educational objectives set in the class. Therefore, guided play is in line with Zambian ECE in mathematics and can be an effective method for learning - as the formal structure of lessons in Zambian ECE in mathematics is similar to that in primary education - in addition to another period for free play. This study thus focusses on a usual pre-mathematics class, examining how guided play can help children's learning in the mathematics classroom.
In addition, in the sub-Saharan African context, Jemutai and Webb (2019) emphasised the importance of guided play, particularly for the development of visuospatial abilities, introducing a guided block play intervention for young children and concluding that it was effective for the promotion of the development of numeracy skills for children. Nakawa (2018) reported that Zambian preschool teachers in government schools employed more guided play approaches compared to free play or direct teaching. The teachers included many guided play activities; however, no mathematics-focussed activities were included. Therefore, this study deals with the development and implementation of meaningful mathematics-related guided play.
Method
Data collection was performed by conducting experimental lessons on shapes in two schools, examining the effectiveness of guided play in the teaching and learning of shapes, and identifying what children learn as an outcome of guided play. A DBR method (Bakker & Van Eerde 2015) was utilised for this purpose because the number of ECE facilities in Zambia was still small at that time, and in the current Zambian context, teachers do not receive adequate educational input and struggle with daily teaching on their own. Educational consultants working in the CDC, as well as the district resource centre coordinator, selected several primary schools in which reception classes were attached with a fully employed teacher by the government. At that point, only eight schools started ECE programmes and teaching and learning materials were not sufficiently provided; therefore, the two schools with better management were chosen. In the class, the author communicated with the teachers in English, and the medium of instruction was Nyanja, one of Zambia's local languages. The author had a basic understanding of Nyanja, and local teachers assisted her in case she did not understand what children were saying in the class.
The first and second experimental lessons were video-recorded by the author. As the lessons were being conducted, the author observed the class and took memos on the teacher's and children's actions. A descriptive analysis was then run on the obtained data.
Participants
The two experimental lessons were conducted on 11 - 15 September 2017 in two different government schools and with two different teachers. The first demo lesson was conducted by Ms. Sakala (a pseudonym) in School A, and the second experimental lesson (the main lesson) was conducted by Ms. Mukonka (a pseudonym) in School B. In School A, there were 22 pupils (8 girls and 14 boys), while in School B there were 35 pupils (17 girls and 18 boys). Almost all of the students in both schools were within the age range of 5-6 years; however, there were a few children in School B who were 4 or 7 years old, either because they were repeating a year or because they were not provided with the earlier classes to start with. In School B, there were three pupils with learning difficulties. The two schools were located in urban areas of Lusaka, the capital of Zambia. The second experimental lesson was conducted in School B, which was the first school that introduced ECE amongst the government primary schools in Lusaka; it was near the first school, School A. In School B, more time was spent on creating a teaching plan than in School A, to ensure that the teacher clearly understood the important aspects of mathematics education, as well as guided play. In both schools, teachers encountered similar teaching experiences in between obtaining their diploma for ECE and in the process of obtaining their bachelor's degree at the university. Parents in these regions generally tend to send their children to private schools if they can afford it; thus, some children from these two schools are from low-income families.
Ethical considerations
Ethical clearance was obtained from the National Science Centre, Ministry of General Education of Zambia (MoGE) (NSC/10/7/4). The study conformed to ethical requirements, and permission was obtained from National Science Centre under the ministry. The author agreed to respect the rights of teachers and children and ensure the participants' privacy, confidentiality and anonymity. The author also followed the guidelines of the affiliated university's ethical rules for research.
Results
Lesson plan for the first lesson
The material that the author utilised was first developed by Matsuo (2010). She created an embedding and disembedding activity in shape, taking the idea of learning trajectory proposed by Clements and Sarama (2009), who demonstrated the learning trajectory for the disembedding of geometric shapes. Clements and Sarama (2014) explained that embedding refers to creating a complex diagram combining simple shapes, rather than only a piece of a shape such as a triangle, circle and rectangle. Furthermore, they explained that disembedding two-dimensional shapes is meant to separate structures within embedded figures and to find 'hidden shapes' within more complex diagrams. According to the learning trajectory concept, many 4-year-old children in the United States could not find embedded circles or squares in some structures of shapes, while, on the other hand, 5-6-year-old children could embed shapes into other shapes (Clements & Sarama 2014). Children's ability to embed and disembed shapes can be strengthened in early childhood mathematics education lessons before entering primary school, which will be useful for their later development of geometrical perspective. In Matsuo's (2010) geometrical programme, she proposed an activity called 'Making a fish' and created a teaching plan. As Matsuo (2010) did not implement the lesson planned, the current author developed the teaching plan described below and shared it with the local teacher:
-
Setting: Pupils work individually or in pairs.
-
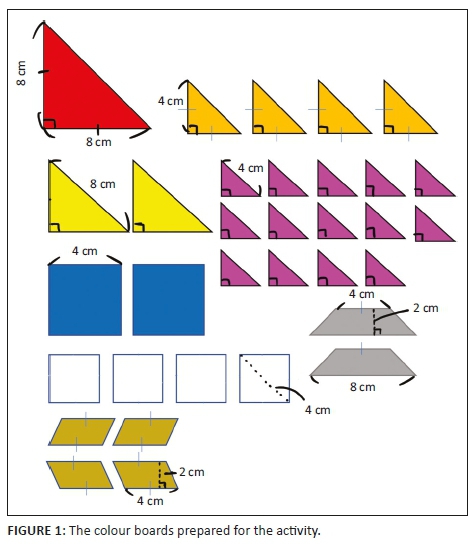
Materials: A sheet of paper showing an example fish and one set of shapes for each child as shown in Figure 1 (right-angled isosceles triangles [a red one with equal sides of 8 cm, four orange ones with equal sides of 4 cm, two yellow oblique ones with the hypotenuse of 8 cm and 14 pink oblique ones with the hypotenuse of 4 cm], squares [two blue ones with 4 cm sides and four white ones with a diagonal measurement of 4 cm], parallelograms [two kinds gold ones with the bottom being 4 cm and the height being 2 cm, but there were two pairs that were the opposite shapes of the others] and isosceles trapezoid [two with a 4-cm upper side, 8-cm bottom side and 2-cm height, coloured silver]).
-
Lesson objective: Pupils should make a fish that is identical to the example fish by embedding shapes, and then should create the same fish again using different patterns by replacing some shapes, as shown in Figure 2.
-
Method Pupils will first make the fish shown to them; they will then start making the same type of fish but using different combinations of shapes.
■ Firstly, the teacher asks, 'what is this shape?' and shows them the fish. 'Let's make the same fish on our own'. The teacher then distributes the sets of shapes.
■ When some pupils complete the fish, the teacher introduces the idea that the fish can be changed, for instance, an orange triangle can be replaced with two pink triangles. 'Can you make other patterns of fish?'
■ When they finish, the teacher can present some of the fish made by the children and discuss their differences.
After conducting the first trial lesson in School A, the present author intended to include guided play in the form of clear, short instructions given by the teacher for physical activities that the children could engage in before introducing the fish activity, because of the children's readiness, which will be discussed in more detail later. The physical activity should be similar to the fish activity; however, it should be easier for children to understand its rules (e.g. Müller & Wittmann 2004a, 2004b) and should respect their cultural background (Worthington & Van Oers 2016). For children to work more subjectively, it was decided that the teacher should not constantly talk and control the children. It was also decided that a set of small paper shapes would be distributed to each child to enhance the activity because some studies have noted that play should be implemented through interactions with the environment via a concrete object (Matsuo 2010; Mielonen & Paterson 2009; Jemutai & Webb 2019).
Implementation of the first lesson
In School A, Ms. Sakala and the author had a planning session the day before the implementation to ensure that the teacher could confidently carry out the activity. In the class, children were seated in a semicircle manner on the floor. Ms. Sakala first pointed to one pupil and asked him to come to the front of the classroom; he was shown the fish like the ones in Figure 2, and he then started embedding the shapes by looking at the fish. Alongside the child, she also started to make several fish for demonstration purposes, and everybody could see what he was doing. When they finished making two fish, she explained to the children what they were supposed to do. She also asked them the different shapes' names in Nyanja and English, and they repeated her all together. However, she did not understand the meaning of embedding the shapes, and instead showed varying sizes of fish. During the planning stage, for the children to think about embedding and disembedding, we had agreed to let them make the same size of fish with different patterns. It seemed that she did not understand the importance of using the same size of fish during our planning discussion; moreover, she did not understand the mathematical meaning of embedding.
After 5 minutes, the teacher pointed to two other pupils, and they came forward and began the activity next to the first pupil. The teacher showed a sample fish by putting some shapes on the floor, so the children also tried to create different-sized fish using the material mentioned, imitating the teacher's fish. The teacher pointed to two pupils every 5 minutes, and soon everybody had started the activity, which lasted for 30 minutes. While they made fish, the teacher sat next to each child, using one example to assist and encourage them to make different fish. Thus, they ended up making different types of fish with different patterns and sizes. All of the children successfully made different sizes of fish, as shown in Figure 3, and only four of them succeeded in making the same size of fish using embedding. Everyone was engaged in the activity and Ms. Sakala reflected on the lesson, saying that it was good for the students to touch and arrange the shapes on their own, experiencing the shapes. However, the aim of the lesson was not achieved because of the misleading lesson conducted by the teacher. This was caused because, during the planning, the author did not let the teacher play with the paper shapes but instead simply verbally explained the process. The children's readiness was also an issue that should be considered for an improved lesson. This was the first time they manipulated concrete two-dimensional shapes in the class, so the provided materials were very new to the children. Ms. Sakala also mentioned that the children had never engaged with such shapes on their own, so this embedding activity seemed too advanced for them as the majority of the children could not make congruent fish with different patterns with the given shapes. In the process of the children's work, although the objective of the activity was not achieved, the pupils were rotating different shapes, and manipulated triangles and quadrilaterals of the same length. This showed that the children, without being told by the teacher, were interested in manipulating shapes on their own. It could be assumed that there was a need to include extra time for them to get use to the materials before introducing the activity.
Lesson plan for the second lesson
After reflecting on the first lesson in School A and planning with Ms. Mukonka in School B, the lesson objective was changed to an activity based on creating instead of copying the fish. It was decided that children should engage in more subjective play that helped them acquire mathematical skills at the same time, such as seeing shapes from different viewpoints and manipulating the paper shapes, like the pupils' actions observed in the demo lesson in School A, which would help them develop a good foundation in shapes. Manipulating shapes allows children to build ideas based on shapes (Sarama & Clements 2014) as they gradually begin to recognise shapes and understand how each shape is formed through this manipulation.
The new goal was to examine what kind of figures children would create, what kind of mathematical properties they would discover during the activity and what they would learn from one another in the class.
For this second experimental lesson (the main lesson), the activity in the demo lesson in School A was modified, and it was called 'Making figures':
-
Settings: Pupils work individually.
-
Materials: The same set of shapes as in the first lesson for each pupil.
-
Lesson objective: Pupils should be able to recognise various shapes, using the set of shapes from the colour board, to combine different shapes and create various interesting figures.
-
Method:
■ The teacher explains the names of the shapes and distributes a set of shapes to each child.
■ The children start to create figures that they like and show them to their friends and the teacher.
It was decided that the set of paper shapes described in the first lesson would also be distributed to each child to enhance his or her subjectivity. Furthermore, it was agreed that Ms. Mukonka would provide children with short, clear instructions for the play at the beginning of the lesson, encourage them no matter what they created through the play and respect whatever they discovered through the play.
How did children play in the second lesson?
Children sat next to each other with enough space between them, which was demarcated with three big groups of desks. The teacher explained in Nyanja what the different shapes were, and the children understood what they were supposed to do after a few minutes, because suddenly, after the teacher's explanation, almost all of them (except for a few children with learning disabilities) opened the plastic bag and started to arrange the paper shapes on their own. They concentrated on making different figures for 40 minutes. When the children finished a certain shape, they called the teachers to come and assess the shape. Aside from those interactions, the teacher did not mention anything. Table 1 shows the figures made by the children (N = 35). Three of the children (nos. 9, 11 and 32 with daggers shown in Table 1) were mentally disabled. Except for the one of those three (no. 11), who bent every piece of the shape that was given to her, all of the 34 pupils made one or more than one figure during the activity. Another one (no. 22) showed a figure that was not understood by Ms. Mukonka, but he also made something. A few children (nos. 1, 2, 5, 12, 15, 17 and 21) made more figures than those mentioned in Table 1. There were not big differences based on the different ages of children; the majority of the children were 5-6 years old. Of course, a few 7-year-old children made several figures (e.g. no. 23); on the other hand, a 4-year-old child (no. 15) and a 6-year-old child (no. 21) created unique figures. The most popular shape the children made was that of a house, which was made by 19 out of 35 pupils during the activity. Children made houses with different patterns and sizes, as shown in Figure 4. All of them made congruent houses. The second most popular shapes were squares, as shown in Figure 5. Six children made squares, combining right-angled triangles with the same length of hypotenuses together. A few pupils produced some mathematically interesting shapes, as shown in Figure 6. Figure 6 shows a variety of figures as well as geometric patterns. Pupils first looked at each other's creations and tended to imitate others' work. Table 1 also shows that 16 pupils only made one kind of figure, such as a house, squares, a robot, circles, stairs, planes and so on, and they produced many examples of the one type of shape with different or congruent figures. Geometrical patterns (1) and (2), 'b' and 'e' in Figure 6 do not express a certain figure, but it can be inferred that children are very keen about the size of triangles, especially their colours, congruency and similarity. Robots, faces and handles have symmetrical features, as do the rockets and patterns in Figure 6. Twelve pupils successfully made more than one kind of figure, which was their intention and hope. One of these nine pupils (no. 12) made six kinds of figures - faces, birds, houses, humans, rockets and masks - and reported their work to the teacher, expressing their satisfaction and sense of accomplishment. In the second part of the lesson, the teacher showed the children the shape of a fish; because the pupils were already involved in the activity, they were allowed to make a fish, connected to the activity in the demo lesson in School A. Fourteen pupils, ranging from 4-year-old to 7-year-old children, succeeded in making one fish; however, they did not change the arrangement of the shapes from the first one they made because of time limitations.


The activity lasted for 40 minutes, 10 minutes longer than a normal lesson; a few pupils wanted to continue with the activity for longer. Thus, they concentrated well during the activity.
Finding and discussion
In this section, two issues related to the current study's findings will be discussed: differences and similarities of children's actions and outcomes in the two lessons, and sociocultural characteristics in children's learning about shapes and mathematical properties they implicitly had in their mind in the second main lesson in School B. Then, the author summarises the comparison of the process of development and modification of both lessons to answer the research questions.
Differences and similarities of children's actions and outcomes in the two lessons
The flow of the two lessons was written down on an Excel sheet. The teacher's actions and verbal explanations, as well as the children's actions and responses to the teacher's questions, were also written on the Excel sheet. Pupils' outcomes on the given task were also summarised based on the author's memo, in the form of, for instance, Table 1. In comparing the two lessons, differences and similarities were readily apparent. Regarding the difference, the importance of identifying the pupils' readiness towards learning something new is emphasised. In the demo lesson, the planned activity, which was focussed on embedding and disembedding, seemed mathematically important; however, as compared to the first lesson, the children in the second lesson better understood the meaning of the activity and enjoyed engaging in mathematical play more than the children in the first lesson. As the children from the second lesson were able to get used to manipulating the shapes, perhaps, in the future, they may be able to progress to the originally planned activity. Clements and Sarama's (2009) findings might hold true if children have a rich mathematical background that involves manipulating concrete shapes that have been given in an activity. By providing Zambian children such an experience beforehand, their educational gaps can be better addressed, and this guided play approach would be more effective for them. Therefore, the lesson applied in this study should be implemented again after children are first given the chance to become accustomed to manipulating concrete shapes in a guided play approach. Regarding the similarities, although the objectives of the two lessons were not the same, children were engaged in manipulating colour boards in the process of learning. The children's work from both groups also suggested that they were drawn to symmetry, which was also noted by Clements and Sarama (2014). Thus, Zambian children also liked manipulations that have been emphasised in other studies (Linder, Powers-Costello & Stegelin 2011).
Sociocultural characteristics in children's learning about shapes and implicit understanding of mathematical properties in the second main lesson in School B
The result of the demo lesson can be used to infer that the learning trajectory by Clements and Sarama (2009) may not always be appropriate considering Zambian children's sociocultural background, such as in the case that their experiences with shapes outside of school were not very well connected to learning at school. In Zambian children's sociocultural setting, some types of play, such as with plastic balls, making wire cars and so on, allow them to implicitly manipulate, rotate or flip over concrete shapes. However, there is a big gap between their life experiences and school mathematics. In fact, the textbook that has been approved and published by the Ministry of General Education of Zambia (MoGE) only shows two-dimensional shapes, such as rectangles and circles, and does not encourage children to manipulate shapes physically (MoGE 2016). Thus, children may be given opportunities to see geometrical shapes in their lives; however, there are not many chances in which this primitive sense about shapes can be explicitly elicited and discussed with a focus on shape properties. Thus, this type of lesson (the second lesson) can be a bond between experiences outside the school and fundamental mathematics.
In the second lesson, the pupils enjoyed handling different shapes and were engaged in the activity as shown in Table 1 and Figures 4-6. This could be because the purpose of the second lesson was not as challenging for the children as the first one, because they were asked to create what they liked. Everything the children produced fully depended exclusively on their creativity and motivation. This also meant that there was no correct or incorrect way of completing the task. The activity was crucial for children to implicitly learn what shapes are. Furthermore, without the teacher's verbal support, a good number of children learned from their friends and successfully created a subjective play atmosphere. This shows that activities focusing on playing will only function if the contents and aims are appropriate for children's sociocultural background.
In Zambia, as mentioned earlier, children in ECE learn to fold paper, trace the outline, create and colour shapes; however, they are not proposed any activities involving handling a variety of shapes by hand (MESVTEE 2013). In the Western context, as Williams-Pierce et al. (2018) mentioned, artificial playing is possible in and out of the classroom, with block puzzles or games aimed at increasing children's spatial reasoning and their ability to composition and decomposition of shapes, as well as Rubik's cubes to develop students' ability to understand algebraic group structure. In the Zambian context, the vast majority of children who commute to public primary schools do not have access to this kind of artificial toys. Both lessons, in this case, could offer an opportunity for children to acquire geometrical skills, such as the embedding of shapes (in the first demo lesson), and implicitly notice geometrical properties for congruency, similarity and symmetry. In the second lesson, the pupils were more engaged in the activity than in the first lesson, and their resulting work could be related to their daily lives. Fish are something familiar in a child's life, but some children in Lusaka have never seen living fish before because they have never been to the sea; some of them have seen cooked fish, but this also depends on their family. Many children created familiar objects from their daily lives, such as houses, people and faces. It can be inferred that this is the beginning of the moment when they were trying to connect the semi-abstract paper shapes with what they usually see; this connection can be more heavily emphasised in early childhood mathematics education to make the lessons more effective. This result could also be connected to various studies, for example, the enactive, iconic and symbolic (EIS) principle (Bruner 1966), the structure of observed learning outcome (SOLO) taxonomy (Biggs & Collis 1982) and the concrete-pictorial-abstract (C-P-A) sequence (Chang, Lee & Koay 2017). These are different models to explain how children's development occurs, but each one of them emphasises that children's development starts from the concrete to abstract. Thus, for pre-school-aged children, the opportunity to learn in the concrete environment where they can touch, feel and experience is crucial to allow them to move onto abstract mathematics in which symbols and mathematical terms are used.
Moreover, except for a few pupils with learning disabilities in the class, the children learned together without much support or advice from the teacher. This represents an ideal situation of guided play. At first, a few children started to make houses, and their classmates noticed and imitated their work. Later, some still continued copying their friends' work for the whole lesson, while others gradually started to develop their thinking in different ways. For example, some of them made bigger houses, some made many of the same type of houses in a line and others made random houses. Thus, there was a wide variety of houses in the class. Moreover, mathematically, their ideas were connected to the fundamental idea of congruency, similarity and symmetry without them explicitly knowing these concepts at this stage through exploring and investigating shapes with their autonomy (Fisher et al. 2011; Vogel 2013; Weisberg et al. 2013). Thus, imitation is a natural first response when children learn, and they subsequently become able to develop their ideas through play.
How can a guided play lesson on shapes in pre-mathematics be developed and modified according to pupils' challenges in the class?
Taking into consideration the pupils' challenges, in the first lesson, as well as previous research, the lesson plan was developed and implemented in the class. However, the lesson was unsuccessful. This was because of the lack of understanding of the children's characteristics in a sociocultural context, as well as the lack of the accumulation of practical knowledge regarding how children learn in the class in the context of Zambia, including their readiness for learning foundational mathematics. After the modification of the objective of the lesson based on the pupils' actions in the demo lesson, the second lesson's mathematical activity, which was keenly focussed on a manipulative activity, became easier, and the teacher (along with the author) focussed on the children's fundamental ability to relate to the crafting of shapes. Embedding and disembedding activity seemed very advanced to children; however, the analysis revealed that handling concrete shapes will be a good starting point for children to learn to be familiar with the mathematical shapes and their mathematical properties. Consequently, the modifications were based on the children's processes of actions and readiness; this led to the success of a guided play activity that met children's sociocultural conditions.
Conclusion
This study was exploratory in nature because this was the very first attempt to study shapes in ECE in Zambia. Based on the results of the first and second lessons, this study showed that guided play works effectively as long as the planned activity is adapted to children's sociocultural backgrounds as well as their readiness. From a curriculum development point of view, firstly, embedding and disembedding activities can be implemented when children become familiar with flexibly manipulating shapes in the class. Secondly, manipulating various shapes will implicitly enhance children's skills and abilities regarding congruency and similarity; thus, this activity is recommended for the Zambian classroom. As this study was conducted in only two schools in Zambia, the generalisability of the findings and the effectiveness of the guided play lessons should be carefully examined in other schools in the future. Also, guided play with different mathematical content, such as numbers or spatial figures, should be implemented in future investigations.
Additionally, the author recommends that adding manipulative activities for early childhood mathematics education in a play-based setting to Zambia's national curriculum and syllabus should be reconsidered in the future, as this study shows children's eagerness with the proposed activity that is based on fundamental mathematics. Going forward, further research will be necessary to conduct on children's activities related to shapes, especially focusing on children's languages, because other studies have suggested that geometric thinking appears through verbal languages (Diaz 2002).
Acknowledgements
Competing interests
The author has declared that no competing interests exist.
Authors' contributions
I declare that I am the sole author of this research article.
Funding information
This research received the research fund from Japan Society for the Promotion of Science (Grant no. 18K13175).
Data availability statement
Data sharing is not applicable to this article as no new data were created or analysed in this study.
Disclaimer
The views and opinions expressed in this article are those of the author and do not necessarily reflect the official policy or position of any affiliated agency of the author.
References
Anders, Y. & Rossbach, H.G., 2015, 'Preschool teachers' sensitivity to mathematics in children's play: The influence of math-related school experiences, emotional attitudes, and pedagogical beliefs', Journal of Research in Childhood Early Education 29(3), 305-322. https://doi.org/10.1080/02568543.2015.1040564 [ Links ]
Arcavi, A., 2003, 'The role of visual representations in the learning of mathematics', Educational Studies in Mathematics 52, 215-241. https://doi.org/10.1023/A:1024312321077 [ Links ]
Bakker, A. & Van Eerde, D., 2015, 'An introduction to design-based research with an example from statistics education', in A. Bikner-Ahsbahs, C. Knipping & N.C. Presmeg (eds.), Approaches to qualitative research in mathematics education, pp. 429-466, Springer, Dordrecht.
Biggs, J. & Collis, K., 1982, Evaluating the quality of learning: SOLO taxonomy, Academic Press, New York.
Bishop, A., 2010, 'General introduction', in A. Bishop (ed.), Mathematics education major themes in education, pp. 1-14, Routledge, London.
Brandt, B., 2013, 'Everyday pedagogical practices in mathematical play situations in German "Kindergarten"', Educational Studies in Mathematics 84(2), 227-248. https://doi.org/10.1007/s10649-013-9490-6 [ Links ]
Bruner, J.S., 1966, Toward a theory of instruction, Academic Press, Cambridge.
Chang, S.H., Lee, N.H. & Koay, P.L., 2017, 'Teaching and learning with concrete-pictorial-abstract sequence-A proposed Model', The Mathematics Educator 17(1&2), 1-28. [ Links ]
Clements, D.H. & Sarama, J., 2009, Learning and teaching early math: The learning trajectories approach, Routledge, New York.
Clements, D.H. & Sarama, J., 2011, 'Early childhood teacher education: The case of geometry', Journal of Mathematics Teacher Education 14(2), 133-148. https://doi.org/10.1007/s10857-011-9173-0 [ Links ]
Clements, D.H. & Sarama, J., 2014, Learning and teaching early math: The learning trajectories approach, 2nd edn., Routledge, New York, NY.
Cohrssen, C., De Quadros-Wander, B., Page, J. & Klarin, S., 2017, 'Between the big trees: A project-based approach to investigating shape and spatial thinking in a kindergarten program', Australasian Journal of Early Childhood 42(1), 94-104. https://doi.org/10.23965/AJEC.42.1.11 [ Links ]
Curriculum Development Centre, 2016, Pre-mathematics teachers' book 3-4 and 5-6 (English), Zambia Educational Publishing House, Lusaka.
Diaz, C., 2002, 'Literacy as social practice', in L. Makin, C. Diaz & C. McLachlan (eds.), Literacies in childhood: Changing views, challenging practice, pp. 31-42, MacLennan and Petty, Sydney.
Duncan, G.J., Dowsett, C.J., Claessens, A., Magnuson, K., Huston, A.C., Klebanov, P. et al., 2007, 'School readiness and later achievement', Developmental Psychology 43(6), 1428-1446. https://doi.org/10.1037/0012-1649.43.6.1428 [ Links ]
Du Plessis, J., 2018, 'Early algebra: Repeating pattern and structural thinking at foundation phase', South African Journal of Childhood Education, 8(2), a578. https://doi.org/10.4102/sajce.v8i2.578 [ Links ]
Fisher, K., Hirsh-Pasek, K., Golinkoff, R.M., Singer, D. & Berk, L.E., 2011, 'Playing around in school: Implications for learning and educational policy', in A. Pellegrini (ed.), The Oxford handbook of play, pp. 341-363, Oxford University Press, New York.
Hachey, C.A., 2013, 'The early childhood mathematics education revolution', Early Education and Development 24(4), 419-430. https://doi.org/10.1080/10409289.2012.756223 [ Links ]
Hauser, B., 2005, 'Das Spiel als Lernmodus: Unter Druck von Verschulung - im Lichte der neueren Forschung' [The game as a learning mode: Under pressure from schooling - In the light of recent research], in T. Guldimann & B. Hauser (eds.), Bildung 4- bis 8-jähriger Kinder [Education 4- to 8-year-old children], pp. 143-168, Waxmann, Münster.
Jemutai, S. & Webb, P., 2019, 'Effects of a 6 Brick Duplo Block guided play intervention on pre-literate learners' visual perception', South African Journal of Childhood Education 9(1), a634. https://doi.org/10.4102/sajce.v9i1.634 [ Links ]
Lee, E.J., 2017, 'Preschool teachers' pedagogical content knowledge in mathematics', International Journal of Early Childhood 49(2), 229-243. https://doi.org/10.1007/s13158-017-0189-1 [ Links ]
Linder, M.S., Powers-Costello, B., Dolores A. & Stegelin, A.D., 2011, 'Mathematics in early childhood: Research-based rationale and practical strategies', Early Childhood Education Journal 39(1), 29-37. https://doi.org/10.1007/s10643-010-0437-6 [ Links ]
Luneta, K., 2014, 'Understanding student teachers' needs in geometry at foundation phase', South African Journal of Childhood Education 4(3), 71-86. https://doi.org/10.4102/sajce.v4i3.228 [ Links ]
Matsuo, N., 2010, 'Geometrical education for preschool children and early graders in primary school: Focus on disembedding of shapes', in Y. Shimizu, Y. Sekiguchi & K. Hino (eds.), Proceedings of the 5th East Asia Regional Conference on Mathematics Education (EARCOME5), vol. 2, pp. 615-621, Tokyo, Japan, August 18-22, 2010.
McCray, J.S. & Chen, J.Q., 2008, 'Pedagogical content knowledge for preschool mathematics: Construct validity of a new teacher interview', Journal of Research in Childhood Education 26(3), 291-307. https://doi.org/10.1080/02568543.2012.685123 [ Links ]
Mielonen, A. & Paterson, W., 2009, 'Developing literacy through play', Journal of Inquiry and Action in Education 3(1), 2. [ Links ]
Ministry of Education, Science, Vocational Training and Early Education, 2013, Early childhood education syllabus, Curriculum Development Centre, Lusaka.
Ministry of Education, Science, Vocational Training and Early Education, 2014, Primary literacy programme resource book for early childhood care, development and education teachers, Curriculum Development Centre, Lusaka.
Müller, G.N. & Wittmann, C.E., 2004a, Das kleine Zahlenbuch Teil 1 Spielen und Zählen [The small number book no. 1, playing and counting], Schulbuch, Klett Ernst.
Müller, G.N. & Wittmann, C.E., 2004b, Das kleine Zahlenbuch Teil 2 Schauen und Zählen [The small number book no. 2, seeing and counting], Schulbuch, Klett Ernst.
Mutemeri, J. & Mugweni, R., 2013, 'The extent to which mathematics instructional practices in early childhood education in Zimbabwe relate to or make use of children's experiences', African Journal of Research in Mathematics, Science and Technology Education 9(1), 49-54. https://doi.org/10.1080/10288457.2005.10740576 [ Links ]
Nakawa, N., 2018, 'Using the co-construction approach to improve the quality of mathematics learning through play in Japanese preschools: A case study', in Feng-Jui Hsieh (ed.), Proceedings of the 8th ICMI-East Asia regional conference on mathematics education 2, Taipei, Taiwan, May 7-11, 2018, pp. 166-173.
National Assembly of Zambia, 2011, The Education Act, The Government Printer, Lusaka.
Piaget, P. & Inhelder, B., 1948, 'La représentation de l'espace chez l'enfant [The child's conception of space]', Presses Universitaires de France, Paris.
Sarama, J. & Clements, D.H., 2014, 'Preschoolers getting in shape', Teaching Young Children 7(5), 30-32. [ Links ]
Singer, E., 2013, 'Play and playfulness, basic features of early childhood education', European Early Childhood Education Research Journal 21(2), 172-184. https://doi.org/10.1080/1350293X.2013.789198 [ Links ]
Sophian, C., 2013, 'Vicissitudes of children's mathematical knowledge: Implications of developmental research for early childhood mathematics education', Early Education and Development 24(4), 436-442. https://doi.org/10.1080/10409289.2013.773255 [ Links ]
South African Numeracy Chair Project, 2016, Early number fun grade r teacher development programme: Session six teacher handbook, South African Numeracy Chair Project, Rhodes University, Grahamstown.
Thomas, L., Warren, E. & De Vries, E., 2011, 'Play-based learning and intentional teaching in early childhood contexts', Australasian Journal of Early Childhood 36(4), 69-75. https://doi.org/10.1177/183693911103600410 [ Links ]
Villarroel, J.D. & Ortega, S.O. 2017, 'A study regarding the spontaneous use of geometric shapes in young children's drawings', Educational Studies in Mathematics 94(1), 85-95. https://doi.org/10.1007/s10649-016-9718-3 [ Links ]
Vogel, R., 2013, 'Mathematical situations of play and exploration', Educational Studies in Mathematics 84, 209-225. https://doi.org/10.1007/s10649-013-9504-4 [ Links ]
Vogt, F., Hauser, B., Stebler, R., Rechsteiner, K. & Urech, C., 2018, 'Learning through play - Pedagogy and learning outcomes in early childhood mathematics', European Early Childhood Education Research Journal 26(4), 589-603. https://doi.org/10.1080/1350293X.2018.1487160 [ Links ]
Warren, E. & Quine, J., 2013, 'Enhancing teacher professional development for early years mathematics teachers working in disadvantaged contexts', in D.L. English & T.J. Mulligan (eds.), Reconceptualizing early mathematics learning, Springer, Dordrecht, pp. 309-325.
Weisberg, D.S., Hirsh-Pasek, K. & Golinkoff, M.R., 2013, 'Guided play: Where curricular goals meet a playful pedagogy', Mind, Brain, and Education 7(2), 104-112. https://doi.org/10.1111/mbe.12015 [ Links ]
Williams-Pierce, C., Plaxco, D., Reimer, N.P., Ellis, B.A. & Dogan, F.M., 2018, 'Mathematical play: Across ages, context, and content', in E.T. Hodges, J.G. Roy & M.A. Tyminski (eds.), Proceedings of the 40th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, University of South Carolina & Clemson University, Greenville, pp. 1507-1513.
Worthington, M. & Van Oers, B., 2016, 'Pretend play and the cultural foundations of mathematics', European Early Childhood Education Research Journal 24(1), 51-66. https://doi.org/10.1080/1350293X.2015.1120520 [ Links ]
 Correspondence:
Correspondence:
Nagisa Nakawa
nagisa@kanto-gakuin.ac.jp
Received: 05 Aug. 2019
Accepted: 07 Mar. 2020
Published: 04 June 2020














