Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.9 n.1 Johannesburg 2019
http://dx.doi.org/10.4102/sajce.v9i1.739
ORIGINAL RESEARCH
Formative assessment as 'formative pedagogy' in Grade 3 mathematics
Poomoney GovenderI, II
IDepartment of Early Childhood Education, University of Johannesburg, Johannesburg, South Africa
IIDepartment of Early Childhood Education, University of South Africa, Pretoria, South Africa
ABSTRACT
BACKGROUND: Formative assessment, as an integral component of teaching, has recently gained prominence in educational environments globally. Poor performances in mathematics by learners in early grades, and its negative effect on later learning, have been an ongoing concern in South African schools. Several former studies tend to generalise the pedagogical reasons for learners' underperformance in Foundation Phase teaching.
AIM: This case study of selected Grade 3 teachers examined how the teachers integrated formative assessment into their pedagogy, with the purpose of gaining insight into teachers' understanding of the developmental aspects of learning in mathematics
SETTING: This study was conducted at four schools in a selected district in the Gauteng Province.
METHODS: Data were mainly collected through focus group interviews and observations of at least three classroom sessions for each teacher of mathematics, thereby gaining an overview of their formative assessment practices.
RESULTS: This article reports on the two strongest themes to have emerged from the case study, which were teachers' tokenistic use of 'Assessment for Learning' strategies and teachers' awareness of learning processes and curriculum requirements.
CONCLUSION: The study's main conclusion was that teachers are likely to practise formative assessment more intuitively if they had a sound knowledge of children's mathematical cognition and conceptual development. This study pointed out that formative assessment is a co-constructed activity involving the teacher, the learner and peers rather than a teacher-directed activity. The study recommends how continuous professional learning initiatives can design initiatives that integrate research-based knowledge of children's learning of early grades mathematics.
Keywords: formative assessment; early grades mathematics; conceptual understanding; formative pedagogy; integrated.
Introduction: Towards a formative pedagogy
In this case study of Grade 3 teachers' enactment of formative assessment in mathematics teaching, it became evident that while the participating teachers seemed to know 'about' formative assessment, they still struggle to integrate it fully into their daily practice. Foundation Phase teachers from priority schools in Tshwane South District (where the study was conducted) underwent training in Assessment for Learning (AfL). At this training, teachers were introduced to the following five strategies as recommended by Black and Wiliam (2009): clarifying and sharing learning outcomes and success criteria, engineering effective classroom discussions and other learning tasks that elicit evidence of learner's learning, providing feedback, and promoting self and peer assessment. A key finding that partially explains teachers' technical approach to formative assessment techniques is lodged in the curriculum requirements - specifically, the need to comply with a curriculum's prescribed teaching tempo as specified in the Annual Teaching Plan (ATP). The curriculum coverage model (CCM) specifies the subject content as well as the teaching pace for public schools in Gauteng. Teachers feel pressurised to teach a curriculum with prescribed milestones, irrespective of various contextual factors such as school location, learner profile and teacher competency.
I argue that the continual monitoring of curriculum coverage - via the tracking of completed formal assessments and teachers' pacing - undermines the professional agency of teachers and leaves little room for continuous formative assessment. The pressures of accountability and curriculum coverage have compelled teachers to omit deep engagement with assessment for what I would like to refer to as a 'formative pedagogy'. The enactment of formative assessment requires teachers to continually halt and adapt their instruction in accordance with their learners' actual needs (Leahy & Wiliam 2012). Teachers are more concerned about covering segments of the curriculum at designated dates than sustaining the children's coherent understanding and application of their acquired knowledge.
Background to the study
Previous researchers have reported on the potential of formative assessment to improve mathematical learning outcomes (Black & Wiliam 2009; Heritage 2007; Popham 2009; Wiliam & Thompson 2017). This study investigated the problem of underutilisation of formative assessment in Grade 3 mathematics teaching, which may explain why many learners struggle to achieve the learning outcomes in mathematics as reported in studies by Spaull (2013). The studies conducted by Aunio and Räsänen (2016), Banerjee and Duflo (2011), Mononen and Aunio (2016), Pritchett and Beatty (2012), Spaull (2013) and Spaull and Kotze (2015) remind us that learning deficits in the early years are a root cause of underperformance in the later years of schooling.
The diagnostic report on Annual National Assessments (ANA) in Mathematics and Language (Department of Basic Education [DBE] 2014) revealed that a significant number of learners in early grades do not reach the expected levels of mathematical competencies. This finding was supported by Spaull and Kotze (2014) whose study illustrated that only the top 16% of Grade 3 learners in South African schools were achieving a level appropriate to Grade 3. My sense is that one of the reasons for this overall weak performance may be the absence of an integrated approach to formative assessment as a primary component of daily teaching.
I was motivated to conduct this study as a means of ascertaining how formative assessment practices feature in classrooms and whether such practices could arguably contribute to improved learning. I initiated a study of classroom practice because, as a teacher, I believe the study of everyday classroom practice is a basis for identifying, firstly, the formative assessment practices evident in classrooms; secondly, the specific pedagogical techniques in their pedagogic content knowledge (PCK) toolkit. I maintain that, in the absence of a formative assessment based on an understanding of children's learning progression (or conceptual development), the teaching practice may be merely mechanical and solely oriented to the policy of 'continuous assessment'. I have hence realised that a descriptive case study of four different Grade 3 classrooms may shed some light on what happens in reality when the curriculum is activated.
The primary analytical framework for this study was cultural-historical activity theory (CHAT) which is premised on the view that learning as a human activity is dependent on the social and cultural context which shapes the activity. The activities in the classroom are interrelated and interdependent comprising (1) the acting subjects (teachers), (2) the object (the learners, whose learning is the objective), (3) the rules (of conduct and in documents such as the curriculum), (4) the community (the classroom and the school), (5) tools (such as books and interaction modalities) and (6) division of labour (who does what in the classroom). The community component in the activity system is especially important for this article - it represents the 'collective nature of the activity' (Engeström 2009:139). In the case of this study, a community, directly and indirectly, includes district departmental officials, the school management team and external training service providers. Furthermore, the activity system postulated by Engeström (1999) recognises that there are many voices, traditions and views that influence the system. Hence, in an activity system of formative assessment in Grade 3 classrooms, these influences can change the expected outcomes for learners. Formative assessment is viewed as such an activity, situated in the community of a classroom. Formative assessment is not only a technical instrument but also a complex process that embraces activities ranging from pedagogical tool-use - as described in classical Vygotskian theory (Kozulin 2017; Vygotsky 1978, 1986).
This article, drawing on a part of a PhD study, shines a spotlight on the affordances provided by a formative assessment that can arguably enable learners to achieve learning outcomes in mathematics. The thesis study provides a brief overview of teachers' formative assessment practices, based on the data obtained from the study participants. This article, however, discusses only the two most prominent themes that were identified in the data analysis. The primary argument of the article is that although teachers may know 'about' formative assessment, they are unlikely to apply it effectively if they do not understand how children engage in mathematics learning. The demands of the curriculum, specifically the need to comply with the prescribed content and a fixed teaching schedule, preclude teachers from focusing on how learners think and what social science tells us about the development of mathematics concepts. There simply does not seem to be enough time for expanded mathematical conversation in the classroom.
Formative assessment as a pedagogical tool
A compelling body of evidence indicates that the integration of formative assessment in teaching will improve learning outcomes in mathematics (Black & Wiliam 2009; Heritage 2007; Popham 2009). Formative assessment has a significant influence on teaching content and methods, as well as children's learning prowess (Bell & Cowie 2001b; Black & Wiliam 1998; Hattie 2012; Shepard 2008; Torrance 2001; Wiliam 2011). While varied and inconsistent interpretations of formative assessment exist, I adopted the definition by Leahy and Wiliam (2012) who state that the term formative describes practitioners' use of assessment tools as an everyday practice. This definition implies that different types of assessment, as well as other evidence provided through classroom data, may be 'formative' if teachers use them appropriately to inform their instructional decisions - regardless of the intended use of the tools as determined by policy.
I present a case that formative assessment, when aimed at diagnosing learners' difficulties and developing appropriate improvement strategies (if integrated into the process of adaptive teaching), could support and enhance learning. As formative assessment is an integrated pedagogical tool, teachers need to have specific skills and knowledge to apply it properly. A mathematics teacher's knowledge base needs to include, inter alia, knowing how children learn and develop early numerical knowledge (Fritz, Ehlert & Balzer 2013; Sarnecka & Lee 2009); knowing about typical learning difficulties; knowing the concepts involved in children's learning, mathematical facts and task procedures; and also knowing how children learn through symbolical means (Henning & Ragpot 2015). I hence argue that teachers who have such an equipped PCK toolkit will be able to inflect, almost spontaneously and as part of daily discourse, the pedagogical principles of formative assessment by continually focusing on assessments of learners' skills and understanding, and by consistently addressing learners' needs. Because teachers' PCK doubtlessly forms the basis of effective mathematics teaching, formative assessment should be an inherent component of everyday teaching. Crucially, the enactment of formative assessment practices would enable teachers to identify knowledge gaps, diagnose learning difficulties, perform error analyses, provide feedback and, ultimately, plan for improvement. Formative assessment, according to my perception, is a vital component of a teacher's PCK toolkit.
The underutilisation of formative assessment in classrooms
Although formative assessment is legitimised in the South African curriculum policies (DBE 2011a, 2011b, 2011c), formative assessment is practised ineffectively in many classrooms (Kanjee & Sayed 2013; Olusola & Luneta 2015; Vandeyar & Killen 2007). Kanjee and Sayed (2013) cite the following reasons for teachers' limited use of formative assessment: the tension between formative assessment and summative assessments that hold schools accountable for learner achievements; teachers' weak understanding of formative assessment caused by inadequate training; and the curriculum policies that favour formal testing over informal assessments. Vandeyar and Killen (2007) add another reason: teachers' unpreparedness to teach learners with diverse abilities.
The pressure imposed on teachers to perform well in the (now-suspended) ANA prompted teachers to 'teach to the test', as they needed to meet the performance goals of excelling in tests, which occurred at the expense of learning outcomes (learning for conceptual understanding). The ANAs were utilised to hold schools accountable for failing to meet certain standards, which have had negative consequences for schools deemed to be 'underperforming'.
Another aspect that explains teachers' underutilisation of formative assessment is the fact that the curriculum policies lack detailed guidelines on the tools and techniques needed to effectively implement formative assessment. Contrarily, the summative assessment guidelines that stipulate the number of formal tasks, recording procedures and reporting protocols are well structured (Kanjee & Sayed 2013).
Research design and methodology
As part of the strategy to explore teachers' practices and their enactment of formative assessment, I observed the teachers in their everyday context. I designed a classroom case study inquiry to explore a 'bounded system' (Stake 2010; Yin 2009) - a cluster of four schools in the Tshwane South District. Through this design, I was able to capture the 'complexity and situatedness' of the behaviour of the teachers, thereby gaining rich and 'thick descriptions' (Cohen, Manion & Morrison 2013:85) of how Grade 3 teachers enact formative assessment (if at all). Case studies in general - and classroom case study research designs in particular - are best suited to research that asks 'how' and 'why' questions (Stake 2010; Yin 2009). In this study, such responses would contribute to data on teachers' activities, such as their explanations of what they do and why they invest in certain practices pertaining to formative assessment.
I selected a sample purposively (Cohen et al. 2013) to include a particular profile of teachers that are employed within only one school district. I then selected the Tshwane South District, which is one of the larger districts in Gauteng, as it offered me a large sampling frame. Aside from this advantage, schools in the Tshwane South District had participated in the Assessment for Learning (AfL) professional development programme (PDP). Assessment for Learning is a term used synonymously with formative assessment (Harlen & Winter 2004). The National Research Foundation and the Zane Foundation (in collaboration with the Tshwane University of Technology) funded the AfL PDP - their interest being to improve the quality of learning and teaching for all learners.
My study started with 12 teachers who were purposively selected through the recommendation of the district subject advisor, based on the following two criteria: firstly, the teachers had to equitably represent two types of school categories, which were 'priority' and 'non-priority' schools. Teachers from priority schools were engaged in ongoing training by AfL facilitators, while teachers from non-priority schools were trained by district officials. Secondly, a selected teacher had to possess a Foundation Phase qualification with a minimum of five years of experience in Foundation Phase teaching. I conducted two separate focus group interviews, with six teachers in each group. Each focus group comprised teachers from both school types (priority and non-priority) for optimal variation. Through further purposive sampling, I selected four members (from the 12 participants) who showed better knowledge of formative assessment through their responses, for further data collection through classroom observations.
To get an actual sense of the 'scene' of the teachers' formative assessment practices during mathematics teaching, I, as a 'silent observer', conducted the Grade 3 classroom observations according to a pre-designed observation schedule (Babbie & Mouton 2014:331; Merriam 2009). Being in the classroom afforded me an opportunity to collect primary data in an authentic way, being able to observe the teachers' formative assessment practices through 'my own eyes' (Yin 2011:143). I took field notes in the classrooms and recorded the events on video (Babbie & Mouton 2014). At least three sequential lessons were observed for each teacher to capture the teaching of 'place value' (topic) from beginning to end and to obtain a comprehensive picture of their formative assessment practices.
I used a thematic content system of analysis and, wherever I deemed it feasible, discourse analysis as described by Henning, Van Rensburg and Smit (2004). The 'raw' data were organised and prepared alongside each data source (Henning et al. 2004) by identifying the segments of data that were responsive to the research questions and sub-questions (Merriam 2009:176). I gathered the raw data from the focus group interview transcriptions, field notes from classroom observations and video recordings. The collected data were then segmented into meaningful units and coded in grounded theory mode (Corbin & Strauss 2015; Henning et al. 2004). Following the suggestion of Merriam (1998:180) to analyse data concurrently with data collection, I transcribed the data immediately as the data was collected. While transcribing the data, I coded the data pages at the top right-hand corner to make it easier to identify the source of the data (Maykut & Morehouse, 1994:127). For example, the FG1 in the code FG1/Elrie/3 refers to the source of the data, namely focus group, Elrie is the pseudonym given to the interviewee and 3 is the page number of the transcript. I followed a similar process for coding the observation field notes as follows: CO1 in the code CO1/Elrie/3 refers to Classroom Observation lesson 1, Elrie refers to the pseudonym and 3 refers to the page number of the field notes/transcribed data.
I then coded the data from one theme 'backwards' to the codes (Maykut & Morehouse 1994:76) as illustrated in Figure 1. I used this strategy to strengthen the reliability of my data analysis.
Using activity systems analysis (ASA), which is a preferred analytical tool for studies in a CHAT framework (Engeström 1999), I interpreted the findings according to the thematic clusters. These clusters were complex and interlocking. The themes together illustrated, in an integrated manner, how the activity of formative assessment - as the Grade 3 teachers defined and practised it - centred on learning that is situated and relational. In the discussion, I combined the empirical text and the relevant theoretical knowledge by 'recontextualising' the emerging data with the literature (Henning et al. 2004) to illustrate formative assessment's distinct contribution to effective teaching and learning of mathematics.
The following discussion of the analysed data reflects my own interpretation and includes the participants' voices. The various tensions and contradictions that emerged within the activity system of the classrooms are included in the discussion of each theme. Contradictions are 'springboards' that alter the subjects' practices and offer possible explanations for the dynamic nature of the practices (Engeström 1999:19). They are a characteristic feature of all activity systems and are viewed not as a problem, but as 'the motive force of change and development' of the formative assessment activity (Engeström 1999).
Discussion of findings
The study's overarching finding was that teachers are likely to practise formative assessment more intuitively (and less technically) if they know more about mathematical cognition and the development of children's concepts. They would also be able to pitch their feedback on a level suited to individual learners' (and groups') 'misunderstandings'. This article reports on the two strongest themes to have emanated from the case study, namely, teachers' tokenistic use of the AfL strategies and teachers' awareness of learning processes and the curriculum requirements.
Teachers' tokenistic use of Assessment for Learning strategies
The study showed that teachers' idiosyncratic understanding of formative assessment was a likely cause of their tokenistic use of formative assessment strategies. Teachers' conceptualisation of formative assessment was vague and fragmented. Most of the responses alluded to single components of the formative assessment process, such as data gathering, but none mentioned multiple processes involved in the formative assessment process as suggested in the following quotes:
'It's about gathering information about whether learners have learnt or not. ' (Sam, Teacher 2, female, 48 years)
'… helps to identify learning gaps. ' (Elrie, Teacher 4, female, 56 years)
'… helps me to identify learners at risk.' (Sandy, Teacher 6, female, 28 years)
Similar studies by Elwood and Klenowski (2002) reported that teachers' varied definitions and conceptual perceptions of formative assessment resulted in overall confusion about the practical implications of formative assessment. This finding is exemplified in studies by Bell and Cowie (2001a), Black and Wiliam (2009) and Stobart (2008) that illustrated why teachers' lack of understanding of the theoretical underpinnings of formative assessment strategies - and their integration with pedagogy and learning - was a major cause of the ineffective implementation thereof.
The ineffective use of strategies to elicit evidence of learning was observed in teachers' technical use of the traffic light strategy, white boards, popsicle stick strategy and questions to find out if learners have learnt something. The study showed that teachers find it difficult to operationalise these techniques effectively in their mathematics teaching. Most teachers perceived the traffic light strategy as being useful as it allowed learners to express their understanding without any fear as expressed in the following statement by Sue (Teacher 1, female, 51 years) 'Learners are willing to describe their knowledge as "red" rather than "I don't know"' and Sam (Teacher 2, female, 48 years) 'Learners will even raise their red block to tell you where they are struggling. Some learners use their red block to ask for help'. However, Sue's utterance was not practised in her classroom as Sue seldom used the data for the formative purpose (as I observed in her three learning episodes). In one of her learning episodes, a learner raised a yellow block, to indicate that he did not understand the place value of the digits in 134. Instead of supporting the learner's understanding, Sue asked other learners to give the correct answer. One learner (Learner 1, boy, Grade 3) answered 'In 134, the 1 is hundred, the 3 is tens and 4 is units'. Another learner (Learner 2, boy, Grade 3) gave a slightly different answer and gave the place value of each digit as follows: '1 is one hundred, 3 is 30 and 4 is 4'. The differences in response were not explained by the teacher, hence the learner was confused.
An analysis of teacher's use of whiteboards indicated that most of the teachers looked for correct or incorrect answers, and were less interested in correcting learners' misconceptions and errors. In one episode, the teacher identified four learners as they wrote incorrect answers on the white board and asked them to show their answers to the others. Interestingly, each learner had different answers that were incorrect and required different explanation aligned to their specific error or misconception. Rather than providing feedback to individual learners, the teacher (Sue) asked another learner to write the correct answer on the board. In another episode, Sue asked the learners to write on the whiteboard how many tens in 43. Most learners wrote 4, but one learner wrote 40 on the whiteboard. Sue (Teacher 1, female, 51 years) repeated the instruction to the learner 'Listen carefully. I said how many tens in 40' and walked away without providing feedback to help the learner. I would describe their teaching as being product-driven rather than process-oriented. This finding resonates with studies by Leatham et al. (2015), which identified teachers' difficulties in identifying and interpreting the evidence of thinking to build on learners' mathematical understanding. The inconsistent manner in which teachers enacted the 'popsicle stick' strategy - a strategy intended to engage all learners in the thinking exercise before selecting learners for individual responses - indicated teachers' lack of understanding of the purpose of the strategy. Instead of posing a question to the whole class first before identifying a learner for a response, both 'Sam' and 'Sue' (teachers - pseudonyms) opted to first pose the question to an individual learner in class. This practice directly conflicts with the intended purpose of the popsicle stick strategy. Inefficient pre-service teacher training programmes and inadequate support at district and school levels may explain why teachers are disconnected and are unable to implement innovative or effective formative assessment strategies. The subject advisors practically confirmed this explanation when they stated that their monitoring efforts have become 'tick box' exercises; they were not mathematics specialist themselves and, therefore, were not able to support the implementation of the AfL programme in mathematics.
Another finding related to this theme is teachers' questions provided limited opportunities for formative assessment. Teachers are aware that questions are useful and are asked at different stages of the lesson as stated in the following responses:
'In our morning recap, I ask questions and make a note. The most important is to see whether they remember the next day what you taught them the previous day.' (Bela, Teacher 3, female, 32 years)
'Questions asked during the lesson is to track understanding of teaching. Questioning is a daily routine exercise. Even if you forget, learners will remind you.' (Sam, Teacher 2, female, 48 years)
'At the end of the lesson, the teacher assess the learning by asking them for example questions on what they have learned, what they think about the lesson. ' (Sue, Teacher 1, female, 51 years)
However, the types of questions asked afforded little opportunities for teachers to understand learners' cognition. In my analysis, I drew upon the mathematics taxonomies proposed by Smith et al. (1996); Andrews et al. (2005) and Watson (2007) to categorise the questions used by the teachers in the study. The questions were categorised and analysed according to the following seven categories, namely, factual, procedural, structural, reasoning, reflective, derivational and yes or no response questions as illustrated in Table 1.

The grouping of the questions into the different categories is significant as it helped me understand how the types of questions used by teachers shaped their formative assessment practices.
Table 2 represents an analysis of the type of questions asked by the selected teachers during the 12 lessons observed. This is followed by Figure 2, which is the graphical representation of the question types used by all four teachers during the 12 lessons observed.
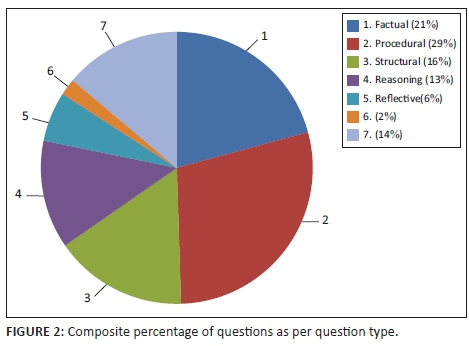
As shown in Table 2, the proportion of question type varies between teachers. Despite teachers attributing the topic to the level of complexity of questions, the data collected do not support this claim. Bela taught decomposition of numbers that lends itself to open questions; however, Bela asked mostly closed questions.
As illustrated in Figure 2, the factual and procedural questions (lower order) constituted 50% of the total questions used among the four teachers selected for classroom observation. Reasoning, reflective, and derivative (higher order) questions were least used in mathematics teaching, yet are the most cognitively stimulating types of questions. The use of procedural, factual and structural questions yielded limited information about learners' thinking as evident in the following episodes below:
'Do you remember what we learned yesterday? No response from the learner. So the teacher answered.'
'It was about greater and less than. Eh, do you remember?'
'Can you remember this sign?' [Teacher shows less than and greater than sign]
'Do the signs look the same?' (Bela, Teacher 3, female, 32 years)
In the above example, most of the questions posed by Bela were factual, closed-ended questions requiring learners to recall memorised information with yes or no responses. Low-order question 'limits learners' thinking and opportunities to process content and to achieve the learning outcome' (Ruiz-Primo & Brookhart 2017:7). It is my contention that Bela did not ponder on the outcomes of the lesson, nor did she reflect on the assessment questions used. In this context, I agree with Schön (2017) concerning the value of reflection on action and reflection in action. Reflection on action occurs during the stage of activity planning, requiring teachers to anticipate how learners may respond and to generate appropriate interventions and questions. Contrary to procedural, factual and yes or no response questions, reasoning and structural questions provided teachers with rich information to understand learners' thinking as evident in the following vignettes which was observed in Elrie's mathematics lesson:
Vignette 1: Elrie asked the learners to write their answers on the white board. Erie (Teacher 4, female, 56 years) asked 'How many tens in 136?' Some learners wrote 3 and some wrote 30. Elrie (Teacher 4, female, 56 years) then asked the class follow up questions such as:
'Which one is correct? Are there three tens or are there 30 tens in 136? How do you know? Are they the same? Why is 1 ten not the same as 10 tens? Show me with your counters?' (CO1/Elrie/5)
The learners were actively involved in the discussion. She then asked the learners to show three tens and 10 tens using their Dienes blocks.
The above vignette highlights the learner-teacher interaction that was initiated through questions. There was evidence of misconception of three tens and 30 tens. Elrie then used prompts to stimulate the learner's thinking. Guided by the prompts, learners were able to reason that three tens are not the same as 30 tens. Elrie also used Dienes blocks to reinforce learners' understanding that three tens are not the same as 30 tens. It can, therefore, be concluded that reasoning questions were open-ended and provided rich data on how learners think.
While the teachers attribute the variation in the type of questions asked to the ability of the class and the topic, the findings suggest that it is in fact the teacher's planning for questioning which influences the depth and type. The data suggest that it is more down to the teacher than the topic to determine depth of intended mathematical thought in the questions. Understanding learners' thinking is an important component of formative assessment; therefore, teachers need to keep learners' thinking skills in mind when they define the learning goals, select their strategies to elicit useful information from learners, interpret the related information and respond to learners' needs in effective ways (Ginsburg 2009).
While interpreting this theme, a variety of tensions and contradictions emerged; all of which hampered teachers' application of formative assessment. Viewed through the lens of CHAT, teachers have the tools (strategies) to establish what learners know or do not know. My observation is that although teachers acquired the AfL techniques (tools) during the PDPs, they did not internalise the logic of the process during the AfL training. Teachers viewed formative assessment as a technical execution of tools (AfL) strategies and did not reflect on the purpose of the strategies for formative use. One explanation could be aligned to Wertsch's (1993) study, which found that teachers tend to apply the strategies directly because their own history of learning at school was through rote learning. In support of the claims advanced by McCallum, Hargreaves and Gipps (2000:265) that 'teachers do not deliver, they develop, define and interpret', I argue that teachers need to adapt and translate their learning from the professional development workshops according to the needs of learners and their classroom context. To promote the effective enactment of the formative assessment strategies, I draw on the suggestions proposed by Heritage (2007:142) on the need to 'redress the balance of formative assessment as an instrument towards formative assessment as a process for enabling learning by channelling the investment into teachers rather than tools. This implies that teacher development should focus more on developing teachers' knowledge and skills to help teachers enact formative assessment (Heritage & Niemi 2006). The ineffective use of the tools precluded teachers from understanding their learners' thinking processes, thereby inhibiting the teachers' formative assessment practices.
Another possible explanation for teachers' difficulties in operationalising the strategies into their pedagogical practice is explained through the tensions between the subject-tool-object nodes of the activity theory. The tensions between the teachers (subjects), the role of the subject advisors (division of labour) and the departmental regulations (rules) may account for the subject advisors' description of teachers as being maliciously compliant. In my view, the subject advisors' views of learners need to be problematised. I therefore question whether subject advisors, in making such judgements, really know the teachers all that well in order to support them. My experience of the hierarchical structures in the schooling environment and the strict enforcement of practice that requires teachers to follow policies and prescriptions without interrogating whether the context is conducive to learning say otherwise.
During a post-observation discussion, some teachers mentioned that the formative assessment strategies were new to them and that they found it challenging to integrate them into their existing lesson plans. As Sue (Teacher 1, female, 51 years) remarked, 'We were never shown how to integrate it in our lesson plans. But we [are] told to do this now'. This sentiment suggests a perceived lack of support from the department and school management team. Furthermore, the teachers failed to grasp how the strategies should be implemented because they view the strategies as 'add-ons' to the lessons, instead of an integrated process. According to Sue (Teacher 8, female, 42 years), 'The strategies are good, but now we must teach our children the learning intentions. Where is the time to do this?' This comment suggests teachers' misunderstanding of AfL as something that has to be taught to learners.
Using the theoretical 'lens' of CHAT and the accompanying ASA tool enabled me to gain some insight into the teacher (as subject) and the teacher's dominant use of lower order questions in relation to higher order questions (Baird et al. 2017). I concluded that several factors could explain the situation. I could argue that the teachers in this study have become 'technicists' and tend to ask the type of questions that they were asked when they, themselves, were learners. When formative strategies are employed, the variety of question type ought to increase and the depth of questioning is improved. This requires teachers to plan these techniques as a tool to encourage and probe deeper mathematical thinking. I therefore argue that reflection related to formative assessment is a necessary component of teaching. Although teachers may be under the impression that they are assessing learners in a formative sense, they often fail to recognise these activities as components of formative assessment, and hence miss opportunities to maximise the formative impact of the activities. The tools used by teachers were ineffectively mediated, which prevented the learners (as object) from attaining the outcomes of improved mathematics learning.
In conclusion, if teachers do not possess the skills to apply formative assessment strategies - and resultantly, find themselves limited by the various tensions within the classroom activity system - then it may explain why learners struggle to become adept in learning mathematics. I have come to the conclusion that teachers know about formative assessment, but they do not regard it as a vital component of children's learning, nor as an instrumental element in their own teaching applications. Their enactment of formative assessment principles, therefore, tends to be ill-considered.
Teachers' awareness of learning processes and curriculum requirements
Another important finding was that teachers are aware of how children learn, but their teaching and assessment methods are constrained by a prescribed curriculum that does not consider learner diversity. This situation is exemplified in observations such as this remark made by 'Bela': 'That is where the problem lies, to follow the same pacing of the curriculum with all learners, yet they have such diverse abilities'.
'Elrie (Teacher 4, female, 56 years)' said:
'It seems like we have to go back to multi-level teaching. The stronger learners are always the ones that you can feed the curriculum as it is and they will be fine. In addition, the weaker learners are the ones you have to break it down and you need to find ways to teach them. As soon as you realise the child is not going to get this, you now have to think about how am I going to teach this to the child? It's really not easy.' (FG1/Elrie/8)
Here, Elrie acknowledges the value of multi-level teaching strategies in accommodating learners with diverse abilities, but simultaneously argues that it is a daunting task to integrate this concept with their established teaching methods.
In response to Elrie, Sandy (Teacher 6, female, 28 years) added:
'it's [multi-level teaching] easier said than done. We are working with Grade 3. Our work tempo is so, so, so busy, we are really putting it like this … pumping the children with knowledge to get through the whole CAPS [Curriculum and Assessment Policy Statement], just giving them what they need according to policy. In the end, all that you worry about is trying to get through it and not trying to teach to make them learn.' (FG1/Sandy/8)
Sandy alluded to the notion of 'ticking the right boxes' for the sake of compliance.
Teachers experience another challenge posed by the knowledge gaps that exist among Grade 3 learners. Those gaps arise from the previous years of less-than-ideal learning circumstances, which complicate the mediation of the Grade 3 curriculum. Dona (Teacher 7, female, 32 years) said: 'Our children in Grade 3 are struggling, because maybe in Grade 1 and 2 they were not taught these concepts. The problem lies somewhere in the previous grades'. Here, Dona alludes to the problems that teachers experience in navigating a way through the Grade 3 curriculum, caused by the knowledge gaps spilling over from the inadequate and uneven curriculum knowledge base as spread among the learners.
The data relating to this theme suggest that teachers are aware that learning is a process harbouring its own complexities while simultaneously having to be vigilantly mindful of the curriculum requirements. The participant-teachers in this study expressed their uniform frustrations with the variety of curriculum-related regulations imposed by the CCM, prescribed lesson plans and the ATP, all of which prevent them from providing individual support to learners. Sam, 'Nelly' and 'Anna' expressly stated that the prescribed lesson plans and ATPs are hindrances to their teaching efforts, as they exclude the diverse needs of their learners. They are quoted as follows:
'Our teaching has become ATP-paced, not learner-paced. If we are behind with the assessment, we must account for this. Then you are in the spotlight for not complying.' (Sam, Teacher 2, female, 48 years)
'It seems like we are teaching and assessing for the officials.' (Nelly, Teacher 9, female, 35 years)
'We know about the policies…that we need to accommodate every learner. But we don't consider the policies anymore.' (Anna, Teacher 10, female, 39 years)
In addition, the teachers alluded to the difficulties associated with the administering of common formal assessments with their learners. The formal assessment tasks, in most instances, seem to be beyond the abilities of the slower learners. Elrie (Teacher 3, female, 56 years) succinctly expressed her feelings on this topic:
'I try to assess when the majority of learners are ready, but it's not possible. To keep [up with] the curriculum requirement, we end up assessing learners even though learners are not ready. Why can't we just assess learners according to another level, a level they are currently working on? It would be so much more useful.' (FG1/Elrie/10)
The teachers' misguided understanding of ATP usage was evident in the following perspective offered by the district official, 'Sally': 'Teachers use the ATP as a lesson plan, instead of a tracking document'. The teachers' inaccurate perception of the ATP's purpose largely prompted teachers to strictly adhere to the pacing of the ATP content, as illustrated by Elrie's (Teacher 4, female, 56 years) response during the focus group interview:
'In addition, if you know there is trouble with addition, now in the first term, you just leave it and move on. There is no time to support the slow learners. So in the second term, when you are doing addition again, you go back to first term's work and explain that work again. You then follow on with the term 2 content.' (FG1/Elrie/14)
Upon further probing, Elrie stated that although she tries to provide needed support at opportune moments, the pressure of having to adhere to the ATP schedules limits her available time to provide additional assistance to individual learners. Three other participants, Elrie, 'Kayla' and Nelly, expressed their frustrations regarding the use of the ATPs as follows:
'There is just no time to go back and reteach. If you do this, then you are going to lag behind in your ATPs. So the poor learners just remain behind.' (Elrie, Teacher 3, female, 56 years; FG1/Elrie/12)
'And you end up doing it, even if it is not on your plan for that day, because really it bothers you. Then you need to check along the way where you can just squeeze it in your ATP.' (Kayla, Teacher 8, female, 42 years; FG1/Kayla/13)
'That is actually where you leave the ATPs aside. Then you leave everything aside and say "today I am just focusing on that." At the end you are getting behind, you do not know where to really start teaching again.' (Nelly, Teacher 9, female, 35 years; FG 2/Nelly/6)
Judging by those (and other) responses by the participant-teachers, it seems that the ATP requirements related to teaching tempo and curriculum coverage generally serve to hamper - rather than facilitate - the development of conceptual understanding and effective learning techniques. The teachers experienced the ATPs as aggressive pacing guides that add pressure to stay on a fast teaching track, denying opportunities to slow down and reteach when the need arises. The teachers also felt that the ATPs disregard respective differences within classroom groups. For instance, while some learners are able to learn at the required pace, others require repeated opportunities to grasp mathematical concepts. The teachers felt that the ATPs did not accommodate learners who need more time. In addition, from a teaching perspective, the effective implementation of AfL requires time and flexibility for the teachers to adapt their lessons, use different strategies and 'take risks in their practice' (Earl 2012).
With all this information based on empirical data in mind, I hence argue that teachers' formative assessment practices were constrained by the pressures enforced on them to rigidly adhere to the scripted lessons and ATPs, without their receiving any incentive to reflect on the effectivity of their practices. Teachers were led to believe that 'curriculum coverage', as a concept, meant that they had to teach everything included in the schedules, rather than getting to teach in such a way that learners were given a fair chance to understand the content before moving on to later learning. This misconception was evidenced by the way that teachers completed the CCM reporting tool. Teachers reported what they had managed to teach, without noting whether their learners actually grasped the learning content. To stay on track with the ATPs, teachers tended to focus on content coverage, which resulted in surface learning with little time allotted to formative assessment that could have helped to identify and address individual and group learning needs.
Spillane, Reiser and Reimer's research results (2002) correspond with this study's findings, which is that teachers (the implementing agent) deserve the freedom and flexibility to implement the prevailing policy while being mindful of their situation and context at the time. This means that curriculum policy - even though it is prescribed - must allow for flexibility when teachers implementing it in their classrooms. In this way, central-based curricula will not serve as barriers to effective teaching and learning. The participating teachers largely emphasised the roles of summative assessment, departmental pressures (to complete the curriculum) and accountability. I hence argue that the current issues related to formative assessment may be attributed to several factors. These factors include the diverse interpretations of what constitutes formative assessment, the pressures to complete the curriculum and the overemphasis on summative assessment. The variety of inflexible demands (CHAT) compromise teachers' abilities to effectively apply formative assessment in their classrooms. Furthermore, a formative assessment policy may initially be difficult to achieve because teachers will have to accommodate certain shifts in their practices and perhaps have to alter some of their personal teaching convictions.
Another finding related to this theme is the tension between the respective accountability measures of summative and formative assessments. Several teachers proposed that formative assessment is not prioritised because of the higher status bestowed on summative assessment because of its perceived purpose of accountability. Kayla's (Teacher 8, female, 42 years) (following response succinctly articulated the situation regarding accountability:
'Unfortunately, because the department has to answer to someone else, they have pressure to supply favourable figures and numbers on learners' performance. So further down the line, the production has pushed up, the quality of the product is of a low standard. If we as teachers had to take an oath like the medical professional, all of us would be guilty and our practice number would have been taken away. It because we are not doing what we said we would do as an oath. That is the nature of the beast: We need to produce. The question is: Do we produce enough; do we produce the right quality of the right quantity? The answer is: Quantity YES, Quality NO.' (FG2/Kayla/11)
A subject advisor supported this perspective by stating, 'Teachers have become results-driven due to departmental pressures to produce high scores in the assessment'.
The pressures to produce high scores in summative assessment resulted in teachers' asking the exact same questions that they will be assessed on in formal assessments. As Anna (Teacher 10, female, 39 years): stated:
'Before the assessment, we work through it in class and the children do them as homework. So two, three four days down the line, with a little bit of tweaking it becomes the formal assessment. By the time the children do the formal assessment, they know what to do.' (FG2/ Anna/15).
Sam (Teacher 2, female, 48 years) alluded to the consequences imposed on teachers for low scores: 'Schools that are underperforming become target schools for school support visits in the following term'. It is, therefore, no surprise that the teachers resorted to using procedural ways to get their learners to focus on and remember certain steps. Bela (Teacher 3, female, 32 years) said:
'We drill and drill until learners can remember what they need to know in their formal assessments. So much of time goes into drilling, leaving teachers with less time to teach new concepts.' (FG1/Bela/18).
Procedural ways of teaching, however, results in mere surface learning. Kayla (Teacher 8, female, 42 years) explained the problems that arise from concentrating on assessment content as such:
'We focus more on the assessment target at the end of the term to get the child on that level. Then we end up assessing only what the child was taught - not what the child knows.' (FG 2/ Kayla/23)
Bela (Teacher 3, female, 32 years) added:
'Even the questions that are asked in the ANAs, learners show that they do not understand. It is because we teach only a method that we know is going to be tested.' (FG1/Bela/16)
A subject advisor reiterated the teachers' view: 'Teachers have become so results driven that they teach only what's in the formal assessments so that they can get high scores'. Anna (Teacher 8, female, 42 years) also said:
'Before the assessment, we work through it in class and the children do [the questions] as homework. So two, three, four days down the line, with a little bit of tweaking it becomes the formal assessment. By the time the children do the formal assessment, they got some idea.' (FG2/Anna/13)
The matter of available time was also listed as a barrier to the implementation of formative assessment. Elrie felt that 'formative assessment should inform our formal assessment but [we cannot] because we just don't have the time to do that at the moment'. Sue and Elrie expressed similar frustrations at the pressure of having to rush through their teaching plans, just to keep pace with the scheduled formal assessments. As Sue admitted, 'Most of the time we are assessing them on work they have not done. We rush through our teaching to get to the assessments'. Elrie (Teacher 3, female, 56 years) said:
'When the number of assessment tasks [were] determined for every grade, it became a real problem. It meant rushing through my teaching to get through the required tasks so that I can have my recording up to date. So there is no time for formative assessment.' (FG1/Elrie/7)
Teachers clearly felt that the new approaches to pedagogy and assessment were in themselves too time-consuming to be practical. The reigning perception is that actions such as involving learners in self- and peer assessments, presenting more discursive and interactive lessons and improving the methods of asking questions in class would lead to a slower pace of curriculum 'delivery'. This creates concerns that the prescribed curriculum may not be covered. Other recorded comments further alluded to the lack of available time as an obstacle to formative assessment practices, such as:
'But tell me, where is there time to do all this? With the GPLMS [Gauteng Primary Literacy and Mathematics Strategy], every day it is a new concept. If there's no written work, you are in trouble.' (FG1/Sandy/13)
An analysis of the second theme reveals that teachers' formative assessment practices are clearly constrained by certain curriculum requirements, particularly 'curriculum bossiness', 'curriculum compliance' and curriculum tempo. As researcher, I can present a case based on the collected data that the integration of formative assessment principles into the curriculum would enable teachers to know which learners truly struggle in mathematics, and to identify the specific areas where their learners will need support. Too many South African learners do not perform well in mathematics - not because they are too slow in grasping the concepts, but because the curriculum pacing is too fast for those learners. If teachers are less driven by the dictates of curriculum compliance and, instead, are allowed to pause proceedings and to reteach the relevant elements to those children who have not yet fully understood everything, then they would be freed to properly assist their learners in achieving the learning outcomes in mathematics.
Ethical considerations
Ethical approval was obtained from the University of Johannesburg to undertake this study. Ethical Clearance number: 2016-093.
Conclusion
In this article, I have concluded that teachers in priority schools, who teach middle class children and who have completed AfL training, find it hard to integrate what they know 'about' formative assessment with their daily practice. This may well be because the discourse around formative assessment is clouded by blanket statements about it, in which it is not viewed as one of the building blocks of a solid pedagogy and not to be confounded with 'assessments', 'evaluations' or even 'tests', instead of it simply being an integral part of daily teaching practice. To that end, I propose the notion of formative pedagogy, which, I would argue, may have more currency with teachers. In my quest to ascertain how teachers actually do this work known as 'assessment for learning' in their classrooms, I found that they do 'implement' the techniques (to a degree), but that the implementation does not occur in an integrated fashion. My experience in this study presents me with a sense that the term 'formative assessment' emphasises the notion of 'assessment' more than the intended forming of a pedagogy in which learning is the key focus.
Acknowledgements
The author is grateful for the financial assistance from the National Research Foundation (NRF), South Africa, towards this research. The author is also grateful to the University of Johannesburg where she completed her PhD studies.
Competing interests
The author has declared that no competing interests exist.
Authors' contributions
P.G. is the primary researcher and author of this article.
Funding information
The researcher received the NRF-DST (National Research Foundation-Department of Science and Technology) SARChI (South African Research Chairs Initiative): Integrated Studies of Learning Language, Mathematics and Science in the Primary School towards her PhD studies.
Data availability statement
Data sharing is not applicable to this article as no new data were created or analysed in this study.
Disclaimer
The views and opinions expressed in this article are those of the author and do not necessarily reflect the official policy or position of any affiliated agency of the authors.
References
Andrews, P., Hatch, G. & Sayers, J., 2005, What do teachers of mathematics teach? An initial episodic analysis of four European traditions, in D. Hewitt & A. Noyes (eds.), Proceedings of the 6th British Congress of Mathematics Education, University of Warwick, pp. 9-16.
Aunio, P. & Räsänen, P., 2016, 'Core numerical skills for learning mathematics in children aged five to eight years - A working model for educators', European Early Childhood Education Research Journal 24(5), 684-704. https://doi.org/10.1080/1350293X.2014.996424 [ Links ]
Babbie, E. & Mouton, J., 2014, The practice of social research, Oxford University Press, Cape Town.
Baird, J.A., Andrich, D., Hopfenbeck, T.N. & Stobart, G., 2017, 'Assessment and learning: Fields apart?', Assessment in Education: Principles, Policy & Practice 24(3), 317-350. https://doi.org/10.1080/0969594X.2017.1319337 [ Links ]
Banerjee, A.V. & Duflo, E., 2011, 'Why aren't children learning', Development Outreach 13(1), 36-44. https://doi.org/10.1596/1020-797X_13_1_36 [ Links ]
Bell, B. & Cowie, B., 2001a, 'Teacher development for formative assessment', Waikato Journal of Education 7(1), 37-49. https://doi.org/10.15663/wje.v7i1.430 [ Links ]
Bell, B. & Cowie, B., 2001b, 'The characteristics of formative assessment in science education', Science Education 85(5), 536-553. https://doi.org/10.1002/sce.1022 [ Links ]
Black, P. & Wiliam, D., 1998, 'Inside the black box: Raising standards through classroom assessment', Phi Delta Kappan 80(2), 139-148. [ Links ]
Black, P. & Wiliam, D., 2009, 'Developing the theory of formative assessment', Educational Assessment, Evaluation and Accountability (formerly: Journal of Personnel Evaluation in Education) 21(1), 5-26. https://doi.org/10.1007/s11092-008-9068-5 [ Links ]
Cohen, L., Manion, L. & Morrison, K., 2013, Research Methods in Education, 7th edn., Routledge, New York.
Corbin, J. & Strauss, A., 2015, Basics of qualitative research, 4th edn., Sage, Thousand Oaks, CA.
Department of Basic Education, 2011a, Curriculum and Assessment Policy Statement (CAPS): Foundation Phase Mathematics, Grades R-3, National Department of Basic Education, Pretoria.
Department of Basic Education, 2011b, Curriculum and Assessment Policy Statement (CAPS): Intermediate Phase Mathematics, Grades 4-6, National Department of Basic Education, Pretoria.
Department of Basic Education, 2011c, Curriculum and Assessment Policy Statement (CAPS): Senior Phase Mathematics, Grades 7-9, National Department of Basic Education, Pretoria.
Department of Basic Education, 2014, Report on the Annual National Assessments of 2014, National Department of Basic Education, Pretoria.
Earl, L.M., 2012, Assessment as learning: Using classroom assessment to maximize student learning, Corwin Press, Thousand Oaks, CA.
Elwood, J. & Klenowski, V., 2002, 'Creating communities of shared practice: The challenges of assessment use in learning and teaching', Assessment & Evaluation in Higher Education 27(3), 243-256. [ Links ]
Engeström, Y., 1999, 'Activity theory and individual and social transformation', in Y. Engeström, R. Miettinen & R-L. Punamäki-Gitai (eds.), Perspectives on activity theory, pp. 19-38, Cambridge University Press, Cambridge.
Engeström, Y., 2009, 'The future of activity theory: Learning and expanding with activity theory', Journal of Education and Work 14(1), 133-156. [ Links ]
Fritz, A., Ehlert, A. & Balzer, L., 2013, 'Development of mathematical concepts as basis for an elaborated mathematical understanding', South African Journal of Childhood Education 3(1), 38-67. https://doi.org/10.4102/sajce.v3i1.31 [ Links ]
Ginsburg, H.P., 2009, 'The challenge of formative assessment in mathematics education: Children's minds, teachers' minds', Human Development 52(2), 109-128. https://doi.org/10.1159/000202729 [ Links ]
Harlen, W. & Winter, J., 2004, 'The development of assessment for learning: Learning from the case of science and mathematics', Language Testing 21(3), 390-408. [ Links ]
Hattie, J., 2012, Visible learning for teachers: Maximizing impact on learning, Routledge, New York.
Henning, E. & Ragpot, L., 2015, 'Pre-school children's bridge to symbolic knowledge: First literature framework for a learning and cognition lab at a South African university', South African Journal of Psychology 45(1), 71-80. https://doi.org/10.1177/0081246314545199 [ Links ]
Henning, E., Van Rensburg, W. & Smit, B., 2004, Finding your way in qualitative research, Van Schaik, Pretoria.
Heritage, M., 2007, 'Formative assessment: What do teachers need to know and do?', Phi Delta Kappan 89(2), 140-145. https://doi.org/10.1177/003172170708900210 [ Links ]
Heritage, M. & Niemi, D., 2006, 'Toward a framework for using student mathematical representations as formative assessments', Educational Assessment 11(3-4), 265-282. [ Links ]
Kanjee, A. & Sayed, Y., 2013, 'Assessment policy in post-apartheid South Africa: Challenges for improving education quality and learning', Assessment in Education: Principles, Policy & Practice 20(4), 442-469. https://doi.org/10.1080/0969594X.2013.838541 [ Links ]
Kozulin, A., 2017, 'Sociocultural paradigm', in J.W. Clegg (ed.), The observation of human systems, pp. 15-34, Routledge, New York.
Leahy, S. & Wiliam, D., 2012, 'From teachers to schools: Scaling up professional development for formative assessment', Assessment and Learning 2, 49-71. http://doi.org/10.4135/9781446250808.n4 [ Links ]
Leatham, K.R., Peterson, B.E., Stockero, S.L. & Van Zoest, L.R., 2015, 'Conceptualizing mathematically significant pedagogical opportunities to build on student thinking', Journal for Research in Mathematics Education 46(1), 88-124. https://doi.org/10.5951/jresematheduc.46.1.0088 [ Links ]
Maykut, P. & Morehouse, R., 1994, Beginning qualitative research: A philosophic and practical guide, Falmer Press, London.
McCallum, B., Hargreaves, E. & Gipps, C., 2000, 'Learning: The pupil's voice', Journal of Education 30(2), 275-289. [ Links ]
Merriam, S.B., 1998. Qualitative Research and Case Study Applications in Education. Jossey-Bass Publishers, San Francisco.
Merriam, S.B., 2009, Qualitative research: A guide to design and implementation, Jossey-Bass, San Francisco, CA.
Mononen, R. & Aunio, P., 2016, 'Counting skills intervention for low-performing first graders', South African Journal of Childhood Education 6(1), 1-9. https://doi.org/10.4102/sajce.v6i1.407 [ Links ]
Olusola, A. & Luneta, K., 2015, Assessing the primary school mathematics in South African: Literature and teachers perspective, viewed 30 June 2016, from https://core.ac.uk/download/pdf/83637377.pdf.
Popham, W.J., 2009, 'Assessment literacy for teachers: Faddish or fundamental?', Theory into Practice 48(1), 4-11. https://doi.org/10.1080/00405840802577536 [ Links ]
Pritchett, L. & Beatty, A., 2012, The negative consequences of overambitious curricula in developing countries, Center for Global Development, Working Paper 293, Harvard University Press, London, viewed 10 June 2018, from http://nrs.harvard.edu/urn-3:HUL.InstRepos:9403174.
Ruiz-Primo, M.A. & Brookhart, S.M., 2017, Using feedback to improve learning, Routledge, New York.
Sarnecka, B.W. & Lee, M.D., 2009, 'Levels of number knowledge during early childhood', Journal of Experimental Child Psychology 103(3), 325-337. https://doi.org/10.1016/j.jecp.2009.02.007 [ Links ]
Schön, D.A., 2017, The reflective practitioner: How professionals think in action, Routledge, New York.
Shepard, L., 2008, 'The role of assessment in a learning culture', Educational Researcher 29(7), 4-14. https://doi.org/10.3102/0013189X029007004 [ Links ]
Smith, G., Wood, L., Coupland, M., Stephenson, B., Crawford, K. & Ball, G., 1996, 'Constructing mathematical examinations to assess a range of knowledge and skills', International Journal of Mathematical Education in Science and Technology 27(1), 65-77. https://doi.org/10.1080/0020739960270109 [ Links ]
Spaull, N., 2013, South Africa's education crisis: The quality of education in South Africa, 1994-2011, Report Commissioned by Centre for Development and Enterprise (CDE), Johannesburg.
Spaull, N. & Kotze, J., 2014, Starting behind and staying behind in South Africa, A working paper of the Department of Economics and Bureau for Economic Research, University of Stellenbosch.
Spaull, N. & Kotze, J., 2015, 'Starting behind and staying behind in South Africa: The case of insurmountable learning deficits in mathematics', International Journal of Educational Development 41(March 2015), 13-24. https://doi.org/10.1016/j.ijedudev.2015.01.002 [ Links ]
Spillane, J.P., Reiser, B.J. & Reimer, T., 2002, 'Policy implementation and cognition: Reframing and refocusing implementation research', Review of Educational Research 72(3), 387-431. https://doi.org/10.3102/00346543072003387 [ Links ]
Stake, R.E., 2010, Qualitative research: Studying how things work, Guilford Press, New York.
Stobart, G., 2008, Testing times: The uses and abuses of assessment, Routledge, New York.
Torrance, H., 2001, Investigating formative assessment: Teaching, learning and assessment in the classroom, Open University Press, Buckingham.
Vandeyar, S. & Killen, R., 2007, 'Educators' conceptions and practice of classroom assessments in post-apartheid South Africa', South African Journal of Education 27(1), 101-115. [ Links ]
Vygotsky, L.S., 1978, Mind in society - The development of higher psychological processes, Harvard University, Cambridge, MA.
Vygotsky, L.S., 1986, Thought and language, MIT Press, Cambridge, MA.
Watson, A., 2007, 'The nature of participation afforded by tasks, questions and prompts in mathematics classrooms', Research in Mathematics Education 9(1), 111-126. [ Links ]
Wertsch, J., 1993, Voices of the mind: A sociocultural approach to mediated action, Harvard University Press, Cambridge, MA.
Wiliam, D., 2011, 'An integrative summary of the research literature and implications for a new theory of formative assessment', in H.L. Andrade & G.J. Cizek (eds.), Handbook of formative assessment, pp. 30-52, Routledge, New York.
Wiliam, D. & Thompson, M., 2017, 'Integrating assessment with learning: What will it take to make it work?', in C.A. Dwyer (ed.), The future of assessment, pp. 53-82, Routledge, New York.
Yin, R.K., 2009, Introducing the world of education. A case study reader, Sage, Thousand Oaks, CA.
Yin, R.K., 2011, Applications of case study research, Sage, Thousand Oaks, CA.
 Correspondence:
Correspondence:
Poomoney Govender
govenp2@unisa.ac.za
Received: 18 Feb. 2019
Accepted: 01 Aug. 2019
Published: 21 Oct. 2019














