Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
South African Journal of Childhood Education
versión On-line ISSN 2223-7682
versión impresa ISSN 2223-7674
SAJCE vol.9 no.1 Johannesburg 2019
http://dx.doi.org/10.4102/sajce.v9i1.716
ORIGINAL RESEARCH
Accelerating mathematics word problem-solving performance and efficacy with think-aloud strategies
Piia M. BjörnI; Aino ÄikäsII; Airi HakkarainenI; Minna KyttäläIII; Lynn S. FuchsIV
ISchool of Educational Sciences and Psychology, University of Eastern Finland, Joensuu, Finland
IIDepartment of Special Education, School of Educational Sciences and Psychology, University of Eastern Finland, Joensuu, Finland
IIIDepartment of Education, University of Turku, Turku, Finland
IVPeabody College, Vanderbilt University, Tennessee, Nashville, United States
ABSTRACT
BACKGROUND: The previous body of research literature has reported several separate cognitive processes relevant in solving mathematics wps. Therefore, it is of the essence to seek for effective intervention and instruction for students in need for support in learning
AIM: This article reports the outcome of an intervention targeted at mathematics word problem (wp) skills.
SETTING: This study included three data collection points: (1) Premeasurements, (2) post-measurements and (3) follow-up measurements. Pre-measurements were performed in August, post-measurements immediately after the intervention period in October and follow-up measurements in December.
METHODS: A programme, which included face-to-face support in mathematics wp strategies with the think-aloud protocol, was applied. The participants were 28 Finnish third-graders (14 training group students and 14 control students). Their mathematics wp skills were tested three times (pre-, post- and follow-up assessments). The groups were matched by gender, family type and the mathematics wp pre-measurement score level. The groups differed neither by literacy skills (i.e. technical reading, reading comprehension) nor by task orientation at baseline.
RESULTS: Some acceleration of mathematics wp skills among the training group students was found but the growth dramatically declined as soon as the face-to-face support stopped. The results further showed improvement in the efficacy of correct answers or attempted mathematics wp items among training group students.
CONCLUSION: The results suggested that training consisting of face-to-face support is crucial for accelerating mathematics wp strategies among students struggling with mathematics. Repeated, cyclic periods of support are suggested for sustained effect.
Keywords: third-graders; mathematics word problem-solving; efficacy; think-aloud protocol; intervention.
Introduction
Arithmetic word problems (wps) constitute an important part of mathematics in elementary school. They integrate formal school mathematics and the real world, and require the learners to apply previously learned skills (Verschaffel, De Corte & Lasure 1994; Verschaffel, Greer & De Corte 2000). School children at varying ages and skill levels often find these wps difficult (Verschaffel & De Corte 1993). These tasks are demanding particularly for the students struggling with learning mathematics (Fuchs & Fuchs 2002; Krawec 2014). Therefore, it is of the essence to seek for effective intervention and instruction, probably benefiting all students at least to some extent (see Xin & Jitendra 1999). In other words, exactly the same teaching provided the same way for all the students is probably not the key to the successful acceleration of mathematics wp-solving performance. Thus, in the present study, we investigated the extent to which an intensive, short-term intervention provided in face-to-face conditions for third-graders will accelerate mathematics wp-solving performance and efficacy among students receiving support in mathematics.
The previous body of research literature has reported several separate cognitive processes relevant in solving mathematics wps. Based on those studies, it may be argued that in addition to basic arithmetics skills (Schoppek & Tulis 2006), solving mathematics wps requires several other skills and abilities such as arithmetic skills, like technical reading skills (Lau 2006), and reading comprehension (Vilenius-Tuohimaa, Aunola & Nurmi 2008). Also, domain general abilities such as metacognition (Desoete, Roeyers & Buysse 2001) and self-regulation (Thorndsen 2011), spatial awareness skills (Boonen et al. 2013) and working memory (Passolunghi & Siegel 2001, 2004; Swanson, Orosco & Lussier 2014; Zheng, Flynn & Swanson 2012) are relevant.
In elementary school, most of the mathematics wps are presented in written form (e.g. Fuchs, Fuchs & Compton 2012; Verschaffel, De Corte & Vierstaete 1999), and thus, also the mathematics wps are usually solved in written form. Therefore, the high interrelationship with language and literacy skills is evident, although situations in which verbal communication while solving math wps are not common (Mercer & Sams 2006). Children often make mistakes in wps because they do not fully comprehend verbal or written instructions (Cummins et al. 1988). However, previous studies suggest that also reading fluency is related to mathematics wp-solving performance (Vilenius-Tuohimaa et al. 2008). To comprehend a mathematics wp task, to identify the task type and to activate relevant prior mathematical knowledge structures, a person has to be able to read the task correctly, as well as to comprehend the meaning of it literally (e.g. Kintsch & Greeno 1985). However, to solve a mathematical wp, the mathematical meaning of the task at hand should be comprehended as well (Pape 2004). Hence, procedural knowledge is also needed.
As stated before, the mathematics wp-solving process integrates many essential knowledge-processing phases, some of which are parallel and others are concurrent. Previous intervention research seeking amelioration of mathematics wp-solving skills has emphasised training separate cognitive strategies (Swanson, Lussier & Orosco 2013; Zhang & Xin 2012). However, also metacognition and self-regulation (Montague 1998; Thorndsen 2011) could be expected to be ameliorated via verbalised thought processes.
The present study considers the think-aloud method as one cognitive strategy, which is suitable to certain contexts (Ericsson & Simon 1993). There are some prior reports on think-aloud protocols used to accelerate mathematics skills (Rittle-Johnson 2006; Rosenzweig, Krawec & Montague 2011). For example, in the Rittle-Johnson's (2006) intervention study on learning principals of mathematical equivalence, children aged 8-11 (n = 85) were placed under one of four conditions varying in instruction on versus invention of a procedure and self-explanation (think-aloud protocol) versus no explanation. Both self-explanation and instruction ameliorated procedural skills, and self-explanation promoted transfer regardless of the instructional condition. Neither manipulation promoted greater improvements on an independent measure of conceptual knowledge, suggesting that the think-aloud protocol is not the only effective method for intervention. However, as a pedagogical tool among others, the think-aloud protocol seems to effectively guide a student to verbally tell the teacher how she is approaching the mathematics wp and how she will solve it.
Using think-aloud protocols as a tool for supporting learning is easier if the teaching context allows individual face-to-face contact. A comprehensive report by Gersten et al. (2009) clearly suggests small-group instruction for struggling students in mathematics over a within-classroom context. Fuchs et al. (2015) reported results of a randomised condition in which the students were randomly assigned for inclusive instruction or specialised small-group instruction for fractions. The results indicated that small-group instruction yielded better learning results than the inclusive instruction condition in which the students received support in the regular classroom. In the same Fuchs et al. (2015) study, the achievement gaps between students in need of support in mathematics versus typically achieving peers widened, even in the small-group condition. The present study utilises a form of co-teaching with the highest possible intensity and individual approach, even though the intervention takes place in the regular classroom.
Think-aloud skills are connected with good reading comprehension skills (Ghaith 2003; Laing & Kamhi 2002) as well as more developed reading comprehension strategies (Lau 2006). Therefore, literacy skills need to be taken into account when examining the effects of the think-aloud intervention on mathematics wp-solving skills (Boonen et al. 2013, 2014). Along with literacy skills, motivation plays a role in successful mathematics learning onwards from early years (Fitzpatrick & Pagani 2013). Previous research has shown that children's task orientation (for an in-depth presentation on the concept of task orientation, see Björn, Räikkönen, Aunola & Kyttälä 2017) is an important factor that explains mathematics performance (Aunola, Leskinen & Nurmi 2006). As one of the learning orientation domains, task orientation describes positive concentration ability and willingness, as well as engagement in a given task. As at the beginning, wps are often found difficult (Verschaffel & De Corte 1993), which leads to lower task orientation (Aunola et al. 2006). Hence, literacy skills and task orientation were examined as potential control variables in the present study.
The present study
As we now understand that the mathematics wps represent a cognitive 'hub' combining a large set of different cognitive processes such as reading fluency, reading comprehension, procedural skills and the ability to understand the context of each problem, the think-aloud protocol was chosen as one tool of the intervention, as language and verbalisation of thoughts are in the core of the approach. We utilised a think-aloud protocol by Ericsson and Simon (1993) in addition to strategy instruction as suggested by Kajamies, Vauras and Kinnunen (2010) (Appendix 1) in the present intervention study. In more details, think-aloud protocols are expected to guide and encourage the participants to gradually learn how to verbally explain what they are doing and how they are trying to solve the tasks at hand.
The early theoretical background of the think-aloud method could be related to Wundt's (1888) psychological concept 'introspection' which encourages one to focus on what types of individual thought processes are detectable and accelerated when solving a problem (see Güss 2018). In addition, socio-cultural learning theories via Vygotsky's original idea of internal speech and external speech fit well to the idea of think-aloud protocols: It is a different cognitive process to silently solve a mathematics wp than first reading it aloud and then orally starting to break the problem into parts and planning how to solve it (Frawley 1997; please also see the intervention lesson plan in Appendix 1). Furthermore, as the student is required to tell about her plans to solve the problem at hand, this method also allows the teacher or interventionist to immediately and more accurately find the problem-solving patterns which need to be re-taught or further explained to the participants. Previous educational intervention studies utilising the think-aloud method have yielded generally positive results, as they usually aim to enhance the metacognitive awareness related to one's understanding of current skills and need for more practice (see Montague, Warger & Morgan 2000; Rittle-Johnson 2006; Rosenzweig et al. 2011). However, Güss (2018) very recently suggested that there are also limitations worth noting concerning the concurrent verbalisation of thoughts while solving a problem (e.g. think-aloud strategy): for example, it might not be effortless for anyone to verbalise thought processes, if a person rather prefers to first process the problem at hand silently. Also, the questions posed before, during and after the problem-solving process might in one way or another serve to intervene the thinking process and therefore end up as a wrong problem-solving path or unexpected answer.
Along with teaching problem-solving strategies, another important feature of the think-aloud intervention is to teach efficacy in solving mathematics wps: it includes the ability to recognise items that are solvable items one finds too hard and items a student may try to solve, even though they seem hard. In the present study, the mathematics wp efficacy is determined to serve as the efficacy consisting of the input-output ratio between correctly solved items and attempted items. The larger the ratio is, the higher the efficacy in solving the mathematics wps. For example, if a student succeeds in solving three items correctly, but has attempted to solve 10 items, the input-output ratio is 0.30. If a student succeeds in solving 10 items and has attempted to solve 10 items, the ratio is 1.00. The number of attempted mathematics wps was considered important, because students with difficulties in mathematics (Passolunghi 2011; Wu et al. 2014) often experience anxiety in mathematics-related situations (Kyttälä & Björn 2013), which, furthermore, may lead to a situation where they do not even attempt to solve the problems in fear of failure.
The study questions and hypotheses were as follows:
-
To what extent do the effects of the intervention on mathematics wp skills differ between the training group students (receiving overall mathematics wp strategy instruction and face-to-face think-aloud strategy instruction) and control group students (only receiving an overall mathematics wp strategy instruction). The effects of intervention were calculated as the amount of correct answers to the wp tasks. We hypothesised that the intervention combining strategy instruction and the think-aloud protocol would accelerate math wp performance among the training group students (Rittle-Johnson 2006). However, a sustained effect was not expected (Fuchs et al. 2015).
-
To what extent does the intervention improve math wp-solving efficacy? Mathematics wp efficacy was defined as the input-output ratio of correct answers and attempts to solve wp tasks. In addition, the efficacy was inspected over the three measurement time points (pre-, post- and follow-up measurements). An attempt was calculated, if the student had marked down calculations and an answer to the item, regardless of whether the answer was correct or not. We hypothesised that the intervention would improve the mathematics wp efficacy, as it is a combined measure of skills, metacognition and self-regulation (Montague 1998; Thorndsen 2011).
Methods
Participants
A total of 148 Finnish third-graders were invited to participate in the study at the beginning of the school year, in August, including 76 boys and 72 girls (Mage = 8.72, SD [standard deviation] = 0.47). The Finnish school year starts in the middle of August and ends in late May or at the beginning of June. The summer vacation lasts from early June to around the 15th of August. Compulsory schooling in Finland lasts for 9 years. It starts from Grade 1 the year the child turns 7 years old. Finnish schools are becoming more multicultural. However, the present data consisted solely of students who speak Finnish as their primary home language.
Informed consent for participation in the study was obtained from 136 participants' parents. The educational level of parents is usually relatively good in Finland. In the present data, 15.5% of the fathers had a university degree or a degree from a polytechnic university, 69.0% had a vocational school or vocational institute degree and again 15.5% of the fathers had only a compulsory school diploma. Regarding the mothers, 33.8% had a university degree or degree from a polytechnic university and 58.0% had a vocational school or vocational institute degree, while 5.4% of the mothers had only a compulsory school diploma.
This study included three data collection points: (1) Pre-measurements, (2) post-measurements and (3) follow-up measurements. Pre-measurements were performed in August, post-measurements immediately after the intervention period in October and follow-up measurements in December.
The training group inclusion criteria were (1) teacher referral and (2) each participant who had regularly received Tier 2 support in mathematics during earlier years (n = 14; 10 girls, 4 boys; Mage = 8.75, SD = 0.60). Tier 2 support for learning in the Finnish Response-To-Intervention-like framework is called 'intensified support' (for further details, see Fuchs & Fuchs 2005). It may be provided as within-classroom support in the form of co-teaching provided together with classroom teacher and a special needs teacher, for example. It may also be provided as small-group support outside the regular classroom, which is then provided by a special needs teacher. The average amount of support for Tier 2 students for the subject the student needs support for is two to three sessions per week. No formal assessments (i.e. no formal diagnosis for learning difficulties in mathematics, e.g.) are required for referral to special educational services in Finland. The forms of support, as well as intensity and duration of support, vary depending on schools, as no formal instructions for support services exist (see Björn et al. 2016).
The control group students (n = 14; 10 girls, 4 boys; Mage = 8.77, SD = 0.46) were selected from the remaining 122 students. The gender, family type and baseline mathematics wp score were matched as closely as possible, by pairwise matching of each training group participant and a control group participant. The matched pairs were otherwise identical in terms of these criteria with one major exception: the control group students were not among those that the teachers had referred as in need of support in mathematics. Additionally, in one training group student-control group student pair, family type was 'unmarried spouse and children' for one and 'other' for the other student (other criteria practically identical; baseline mathematics wp score between-group difference p > 0.05). The groups were also very similar in terms of parental education level (particularly maternal education). Demographic information about participants is displayed in Table 1.

The students' mathematics wp skills were measured using MATTE (Matematiikan sanallisten tehtävien ja laskutaidon arviointi [Evaluation of the student's mathematical problem-solving and arithmetic skills]) (Kajamies et al. 2003) in pre-, post- and follow-up measurements. The students' literacy skills (technical reading skills and reading comprehension) were tested at the baseline using a standardised ALLU (Ala-asteen lukutesti [Elementary school's reading test]) reading test (Lindeman 2000). The students also filled in a questionnaire on their mathematics task orientation.
Measures
Mathematics word problem skills
Mathematical wp-solving was assessed by a parallel set (set A for pre-measurement, B for post-measurement and C for follow-up measurement) at each measurement time point. Each set consisted of 15 one- and multi-step wps (e.g. You bought 11 marshmallows and 12 chocolate candies from a store. Your friend bought 9 marshmallows and 8 chocolate candies. How many candies did you have altogether?). These assessment forms were from the MATTE test (Kajamies et al. 2003). Problems required realistic consideration and not only straightforward application of arithmetic operations. We used the total number of attempted wps, as well as the total number of correct answers in the analyses. The cronbach's alpha for the test is reported as 0.809.
Literacy skills: Technical reading
Technical reading was used as one of the control measures in the study. It was assessed using the word recognition subtest of the ALLU reading test (Lindeman 2000). The word recognition subtest measures participants' speed and accuracy in separating words written in sets by marking lines between each words (e.g., 'kilpakohtiparialla' should become 'kilpa/kohti/pari/alla'; or 'racetowardspairunder' should become 'race/towards/pair/under'). The technical reading subtest designed for fourth-graders consists of six items for practice and 78 test items. Each test item contains one word chain of two to four words. The time limit for the test is 3 minutes 30 seconds. One point is given for each correctly separated, meaningful word; thus, the maximum score for the test is 214.
Reading comprehension
Text comprehension was another control measure in the present study. It was measured using a subtest of the standardised primary school reading test (Lindeman 2000). The test consisted of two texts based on narrative context (1, 2) and two texts based on expository context (3, 4; see also Sáenz & Fuchs 2002). The texts included short stories with relevant vocabulary. The length of each story was one page. In the testing situation, the children were asked to read each text silently (two texts or testing session) and then to provide an answer to multiple-choice questions accompanying each text. Texts were presented in two sessions, each of which included one expository and one narrative text, with a total of 12 questions per text. The child was able to see the text for the entire duration of the task. The time limit for completing the questions related to the texts was 60 min per session. Text comprehension was measured by summing up the number of correct answers in all four texts. One point was given for each correct answer, resulting in a maximum score of 48 for all the reading comprehension texts combined. Cronbach's alpha for the test was 0.870.
Task orientation in mathematics
As the third control measure, the participants' motivation towards mathematics tasks (Salonen et al. 1994) was self-evaluated by filling in a five-point, Likert-scale questionnaire (for a more precise description, see Vauras et al. 1993) in which the ability to sustain attention while solving mathematics tasks and enthusiasm during mathematics tasks and lessons were rated. The students filled in the questionnaire. The introduction text for the test is meant to guide the student to think about behaviour towards mathematics or during mathematics lessons. So, this test is expected to be domain-specific. For example, in the students' questionnaire, the first item was: 'I think I can concentrate on a given task and do it from the beginning to the end without being distracted' (1) never, (2) seldom, (3) sometimes, (4) often and (5) very often. There were four questions concerning task orientation. Consequently, the raw maximum score was 20. We calculated an arithmetic mean from the maximum score. The Cronbach's alpha ranged from 0.636 to 0.728 over the measurement time points in the present study. The reliability according to the test manual is 0.832.
The intervention
Procedure
This study applied a design with (1) mathematics wp strategy instruction to all the students in participating classrooms (including training group students, control group students and other students within the classrooms) and in addition to that (2) face-to-face think-aloud strategy instruction for the training group students, provided by a trained teacher. The intensity of mathematics wp strategy instruction was three times per week and the duration was 15 min. This way, exposure to the intervention (strategy instruction) was 3 × 15 min per week. Exposure to the intervention (strategy instruction + face-to-face think-aloud instruction) was 3 × 45 min per week for the training group. The overall duration for the intervention was 6 weeks. We included a 2-week 'resting' gap in the middle, so the actual intervention was given in 2 × 2-week sets. During the 2 week gap, all the students participated in their regular school days. In summation, training group students received a total of 540 min of (intensive) support during the intervention, whereas the control group students (only participating in the overall strategy instruction) received a total of 180 min of support during the intervention period.
Mathematics word problem strategy instruction
Each intervention session started with an overall strategy instruction (duration 15 min) in solving mathematics wp tasks during mathematics lessons (see also Appendix 1). During this strategy instruction, all the students (including the training group students) were using the Vauras et al. (2003) model of efficient mathematics wp-solving (see Kajamies et al. 2010). It includes six different phases: (1) reading the problem, (2) describing the problem, (3) planning solving of the problem, (4) calculations, (5) interpreting the result and answering the problem and (6) evaluating the result. This instruction was given to all students and an example mathematics wp item was calculated together.
The working phase
After the overall mathematics wp strategy instruction, the training group students started the face-to-face work with the trained teacher (duration 20 min). Those students within the control group, as well as other students in the classrooms participating in this study, started to calculate the MATTE (Kajamies et al. 2003) tasks on their own, but received help from the regular classroom teacher, if needed.
Face-to-face think-aloud strategy instruction for the training group students
In the present study, we applied a set of pre-determined questions, 'a protocol' (see Ericsson & Simon 1993, 1998) designed to build and support think-aloud strategies within each intervention session in addition to more commonly used strategy instruction (see Kajamies et al. 2010). When using think-aloud questions as part of an intervention, the student's growing ability to speak about his or her strategy choices is the main point. These think-aloud questions act as a supporting means of strategy instruction for mathematics wp-solving aimed at students struggling with learning mathematics. The trained teachers were instructed to use the same pre-defined sets of questions aimed to help the students with solving the mathematics wps. The questions were aimed to help the student before the actual problem-solving process (e.g. Where else have you seen mathematics wps like this one?), during the problem-solving process (e.g. Do you remember how the problem was solved in the previous wp?) and after the problem-solving process (e.g. Can you come up with another way of solving this?). These sets of think-aloud questions had been piloted prior to this intervention.
Ending and interviews
After each session, the students were asked to rate the MATTE tasks using a form that comes with the material. Additionally, the training group students were interviewed to close the session and to get feedback on the tasks. The interviews were recorded and used to improve the instruction. For example, if a student suggested spending more time on example mathematics wps, this was individually taken into account immediately during the next session.
Teachers' perceptions about the usability of the think-aloud procedure along with the intervention material were ensured by giving the teachers delivering the intensive individual instruction condition as well as the small-group condition questionnaires including three five-point Likert-scale items: (i.e. How well did you succeed in guiding the student(s) to do the tasks; How well did you succeed in asking the think-aloud questions; How well did you manage to instruct the students' learning process?). They gave their usability judgement assessment to the researcher group after the last intervention session. The overall usability score over all sessions was moderate (M = 3.5; SD = 0.5).
Data analysis strategy
To answer the first research aim the effects of the intervention were inspected by the amount of correct answers to the wp tasks, repeated measures of analysis of variance (ANOVA) were calculated. There was no need for using literacy skills (i.e. technical reading and reading comprehension) or task orientation as control variables, as there were no statistically significant differences between groups in these measures (ps > 0.05) in the baseline. We also calculated paired-samples t-tests to inspect within-group differences between pre-measurements and post-measurements. The results were confirmed using related-samples of the Wilcoxon signed-rank test that is calculated by the median of differences between z-scores.
Next, to answer the second research aim on the mathematics wp-solving efficacy, the input-output ratio of attempts and correct answers to solve wp tasks was inspected over the three measurement time points (pre-, post- and follow-up measurements). Again, repeated measures of ANOVAs with paired-samples t-tests between pre-measurements and post-measurements were calculated, paired-samples t-tests were followed and the results were finally confirmed with related-samples Wilcoxon signed-rank tests. The analyses were conducted using the Statistical Package for Social Sciences (IBM SPSS) programme (version 25).
Ethical considerations
This article followed all ethical standards for research without direct contact with human or animal subjects.
Results
Mathematics word problem performance between the training and control groups
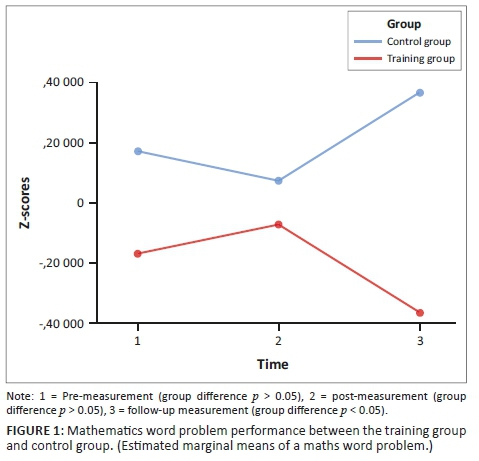
Firstly, differences between the groups were calculated with repeated measures ANOVAs. See Table 2 for mean scores, standard deviations and Wilcoxon's signed-rank test ps at measurement times within the training and control groups. The results showed that the group and measurement time in mathematics wp performance did not have a statistically significant interaction effect (F = 1.665). To inspect further on the impact of the intervention, paired-samples t-tests between pre-measurements and post-measurements showed that there was neither a significant difference when inspected within training group [t(13) = −1.66, p = 0.12] nor within the control group [t(13) = −1.88, p = 0.82]. These results suggested that this particular short-time intervention did not completely succeed in closing the gap between the training group and control group students' mathematics wp skills.
However, an important trend suggesting actually quite opposite changes in mathematics wp scores may be detected in Figure 1 describing the differences between groups at different measurement time points: there was a clear (although not significant) growth in training group students' mathematics wp skills between the pre-measurement and post-measurement time point, whereas there was a decline of the same-size among control group students. Further, there was a clear decline in mathematics wp scores among training students after the intensive intervention had stopped, whereas in contrast, among control group students, the growth is evident after the intervention period, resulting in a statistically significant difference between groups at the follow-up measurement time point. Overall, this finding suggested that the face-to-face think-aloud strategy support started to accelerate the mathematics wp-solving performance among the training group students, but after the support stopped, their performance also rapidly declined. We used parallel test versions from the MATTE to test the mathematics wp performance for pre-, post- and follow-up measurements. We think that it is partly because of the parallel test versions that the training group students performed slightly lower at the follow-up measurement time point than at the pre-measurement time point.
Mathematics word problem-solving efficacy between the training and control groups
Next, group differences in the efficacy, measured as the input-output ratio of the correctly calculated items and attempted items, were inspected. The results showed again that group and measurement time in mathematics wp performance did not have a statistically significant interaction effect (F = 0.70). To inspect further on the change in the input-output ratio, within-group paired-samples t-tests between pre-measurements and post-measurements showed that the difference was nearly statistically significant within the training group [t(13) = −2.03, p = 0.065]. This result was confirmed by the related-samples Wilcoxon signed-rank test which was statistically significant (p < 0.05). There was no such improvement within the control group [t(13) = −1.90, p = 0.80]. These results bring an important addition to the results of the study: the accuracy and effort put into solving mathematics wps was accelerated as a result of the face-to-face think-aloud intervention among students struggling with mathematics.
Discussion
Overall, the results of the present study suggested that even though the interaction between the measurement time and group did not prove this particular think-aloud intervention as statistically significant, it is safe to say that applying a systematic face-to-face think-aloud strategy instruction could be used as one tool to accelerate and improve the mathematics wp strategy skills among students struggling with mathematics. Additionally, the results showed that the efficacy to solve mathematics wps grew significantly higher among the training group students: the efficacy in mathematics wps as an input-output ratio measured as correct answers or attempted items was ameliorated during the intervention period. These findings may contribute to the field of special education and mathematics intervention taking into account how the support should be provided for different learners.
Firstly, the extent to which the number of correct solutions in mathematics wps increased over pre-, post- and follow-up measurements was examined. It has been suggested that think-aloud questions are very task-specific (Ostad & Sorensen 2007; Rosenzweig et al. 2011) which might mean that effects on specific target skills such as mathematics wps are expectable. Based on these results, it seems that face-to-face individual intensive support accelerates wp skills, but the effect was not sustained. As for the correct solutions in wps, individual intensive face-to-face support seemed to increase the number of correct solutions suggesting that as long as individual support may be provided, it can yield positive results even though the context would be within-classroom. At the same time, the results showed that as soon as the support stopped, the teacher-referred students struggling with mathematics stopped performing better in mathematics wps. Instead, the students in the control group showed a clear increase in mathematics wp performance later on. It has to be remembered that the students in the training group condition performed slightly weaker in general mathematics skills at the baseline, even though there was no statistically significant difference with the control group students. Therefore, they could have benefited more from the simple explicit instruction on basic calculations, as well as on mathematics wp-solving strategies without any think-aloud components at the beginning. However, the work by Güss (2018) might additionally help in finding an explanation for this result. Firstly, he found that it might not be effortless for anyone to verbalise thought processes, and secondly, during and after the problem-solving process, posing the questions that belong to the think-aloud protocol might in one way or another even intervene in the thinking process and therefore end up as a wrong problem-solving path or wrong answers. Nonetheless, the think-aloud method was novel for the training group students. Therefore, it would have been very interesting to repeat the intervention after a while and then find out if the students would be able to benefit even more from the instruction, as the think-aloud protocol would have been familiar to them.
However, it needs to be noted that mathematics wps are essential in the curriculums for third-graders and they are present in textbooks in almost all lessons. Therefore, the student would continue to be exposed to the mathematics wps even after the intervention was over. The differences between the training group and control group grew over time which suggested that the regular classroom instruction was not sufficient for the training group students. The dramatic decline of training group students' mathematics wp-solving skills could be explained firstly by the fact that we utilised parallel versions of the same test, but not exactly the same items. Secondly, Fuchs et al. (2015) also found that the gap between training group and control group students grew over time in mathematics skills after an intervention. Relatedly, as we trained the teachers to use the Kajamies et al. (2010) structure while teaching mathematics wps, it seems that those students without need for support in mathematics were able to benefit from the improved instruction, while the training group students struggling with mathematics would very likely have still needed very intensive face-to-face support. During the intervention, the teachers were able to offer exceptionally face-to-face support, but also small-group support has often been suggested to be a very beneficial context for children struggling in mathematics (see also Fuchs et al. 2012, 2015; Gersten et al. 2009; Montague 2008; Swanson et al. 2014).
Secondly, the extent to which the input-output ratio of correct answers or attempted mathematics wps is increased over pre-, post- and follow-up measurements was examined. This was an important aim to be looked at, as students struggling with mathematics tend to learn to avoid even attempting to solve the tasks they find difficult (Aunola et al. 2006; Passolunghi 2011; Wu et al. 2014). The results showed that overall, the added think-aloud strategy intervention seemed to enhance the efficacy (measured here as correct answers or attempts) in solving mathematics wps. This might, in future, mean that as the result of the intervention, the students in the training group felt less anxiety to try wp-solving. It is also possible that during the intervention period, they learned to identify the types of wps and this time knew the ones that would be too hard for them to solve. In this way, a more realistic understanding of their skills, as a sign of growth in metacognitive awareness, was likely accelerated among these students (Desoete 2009; Owen & Fuchs 2002; Montague 2008).
Limitations
There are at least three limitations to be considered when attempting to generalise the results presented here. Firstly, the sample was very small in the present study. However, intervention studies are hard work, and therefore, small samples are not unusual within the educational intervention research paradigm. Secondly, this study did not aim to identify students with mathematics difficulties in a diagnostic sense. This means that no strict criteria for selecting students to be randomised in one of the intervention conditions were used. Instead, we asked the teachers to indicate the students who would benefit from the intensive intervention and who also have been engaged in part-time special education. Thirdly, we aimed to simulate an authentic situation in classrooms in terms of diversity in mathematics skills by selecting a little over 10% of the students as participants for the intervention (by teacher referral), as opposed to 25% used many times in a similar research design.
Conclusion
The present study adds to the previous literature by providing a set of results for a small-scale intervention study, utilising a face-to-face think-aloud strategy instruction as an added feature to general mathematics wp strategy instruction. Our research outlined that the individual face-to-face support provided was very intensive, as a trained interventionist spent all the intervention sessions solely instructing the target students. This way, we simulated one type of an extreme condition of co-teaching. There is an ongoing discussion on the effects of inclusive co-teaching versus small-group instruction outside the classroom (see Fuchs et al. 2015), but to date, no published studies including Finnish students exist. The present study now also provides a small-scale baseline result for the effectiveness and the need for intensive support given individually in active face-to-face interaction. Further, based on our result, cyclic and repeated, intensive periods of support for students at risk for mathematical learning difficulties are suggested for further investigation (see also Björn et al. 2018).
Acknowledgements
Competing interests
The authors have declared that no competing interests exist.
Authors' contributions
All authors equally contributed to the writing of the manuscript.
Funding information
This research received no specific grant from any funding agency in the public, commercial or not-for-profit sectors.
Data availability statement
Data sharing is not applicable to this article as no new data were created or analysed in this study.
Disclaimer
The views and opinions expressed in this article are those of the authors and do not necessarily reflect the official policy or position of any affiliated agency of the authors.
References
Aunola, K., Leskinen, E. & Nurmi, J.E., 2006, 'Developmental dynamics between mathematical performance, task-motivation and teachers' goals during the transition to primary school', British Journal of Educational Psychology 76, 21-40. [ Links ]
Björn, P.M., Aro, M.P., Koponen, K.T., Fuchs, L.S. & Fuchs, D.H., 2016, 'The many faces of special education within RTI frameworks in the United States and Finland', Learning Disability Quarterly 39(1), 58-66. https://doi.org/10.1177/0731948715594787 [ Links ]
Björn, P.M., Aro, M., Koponen, T., Fuchs, L.S. & Fuchs, D., 2018, 'Response-to-intervention in Finland and the United States: Mathematics learning support as an example', Frontiers in Psychology 5, 1-10 https://doi.org/10.3389/fpsyg.2018.00800 [ Links ]
Björn, P.M., Räikkönen, E., Aunola, K. & Kyttälä, M., 2017, 'Dynamics between student vs. teacher perceptions of mathematics task-orientation and mathematics performance among adolescents', Learning and Individual Differences 55C, 21-28. https://doi.org/10.1016/j.lindif.2017.02.005 [ Links ]
Boonen, A.J.H., Van der Schoot, M., Wesel, F., Vries, M. & Jolles, J., 2013, 'What underlies successful word problem solving? A path analysis in sixth grade students', Contemporary Educational Psychology 38(3), 271-279. https://doi.org/10.1016/j.cedpsych.2013.05.001 [ Links ]
Boonen, A.J.H., Van Wesel, F., Jolles, J. & Van Der Schoot, M., 2014, 'The role of visual representation type, spatial ability, and reading comprehension in word problem solving: An item-level analysis in elementary school children', International Journal of Educational Research 68, 15-26. https://doi.org/10.1016/j.ijer.2014.08.001 [ Links ]
Cummins, D.D., Kintsch, W., Reusser, K. & Weimer, R., 1988, 'The role of understanding in solving word problems', Cognitive Psychology 20(4), 405-438. https://doi.org/10.1016/0010-0285(88)90011-4 [ Links ]
Desoete, A., 2009, 'Metacognitive prediction and evaluation skills and mathematical learning in third-grade students', Educational Research and Evaluation 15(5), 435-446. https://doi.org/10.1080/13803610903444485 [ Links ]
Desoete, A., Roeyers, H. & Buysse, A., 2001, 'Metacognition and mathematical problem solving in Grade 3', Journal of Learning Disabilities 34(5), 435-350. https://doi.org/10.1177/002221940103400505 [ Links ]
Ericsson, A.K. & Simon, H.A., 1993, Protocol analysis: verbal reports as data, MIT Press, Cambridge, MA.
Ericsson, A.K. & Simon, H.A., 1998, 'How to study thinking in everyday life: Contrasting think-aloud protocols with descriptions and explanations of thinking', Mind, Culture, and Activity 5(3), 178-186. https://doi.org/10.1207/s15327884mca0503_3 [ Links ]
Fitzpatrick, C. & Pagani, L., 2013, 'Task-orientation in kindergarten pays off in later childhood', Journal of Developmental & Behavioral Pediatrics 34(2), 94-101. https://doi.org/10.1097/DBP.0b013e31827a3779 [ Links ]
Fuchs, L.S. & Fuchs, D., 2002, 'Mathematical problem-solving profiles of students with mathematics disabilities with and without comorbid reading disabilities', Journal of Learning Disabilities 35, 563-574. https://doi.org/10.1177/00224669050390010501 [ Links ]
Fuchs, D. & Fuchs, L.S., 2005, 'Responsiveness-to-intervention: A blueprint for practitioners, policymakers and parents', Teaching Exceptional Children 38(1), 57-61. https://doi.org/10.1177/004005990503800112 [ Links ]
Fuchs, D., Fuchs, L.S. & Compton, D., 2012, 'Smart RTI: A next-generation approach to multilevel prevention', Exceptional Children 78, 263-279. https://doi.org/10.1177/001440291207800301 [ Links ]
Fuchs, L.S., Fuchs, D., Compton, D., Wehby, J., Schumacher, R.F., Gersten, R. et al., 2015, 'Inclusion versus specialized intervention for very low-performing students: What does access mean in an era of academic challenge?', Exceptional Children 8, 132-157. https://doi.org/10.1177/0014402914551743 [ Links ]
Frawley, W., 1997, Vygotsky and cognitive science: Language and the unification of the social and computational mind, Harvard University Press, Cambridge.
Gersten, R., Beckmann, S., Clarke, B., Foegen, A., Marsh, L., Star, J.R. et al., 2009, Assisting students struggling with mathematics: Response to Intervention (RtI) for elementary and middle schools, NCEE 2009-4060, Washington, DC, viewed 05 September 2019, from http://ies.ed.gov/ncee/wwc/publications/practiceguides/.
Ghaith, G., 2003, 'Effect of think alouds on literal and higher-order reading comprehension', Educational Research Quarterly 26, 13-22. [ Links ]
Güss, C.D., 2018, 'What is going through your mind? Thinking aloud as a method in cross-cultural psychology', Frontiers in Psychology 9, 1291. https://doi.org/10.3389/fpsyg.2018.01292/full [ Links ]
Kajamies, A., Vauras, M. & Kinnunen, R., 2010, 'Instructing low-achievers in mathematical word problem solving', Scandinavian Journal of Educational Research 54, 335-355. https://doi.org/10.1080/00313831.2010.493341 [ Links ]
Kajamies, A., Vauras, M., Kinnunen, R. & Iiskala, T., 2003, MATTE-Matematiikan sanallisten tehtävien ja laskutaidon arviointi [Evaluation of the student's mathematical problem solving and arithmetic skills], University of Turku, Centre for Learning Research, Turku.
Kintsch, W., & Greeno, J.G., 1985, 'Understanding and solving word arithmetic problems', Psychological Review 92(1), 109-129. https://doi.org/10.1037/0033-295X.92.1.109 [ Links ]
Krawec, J.L., 2014, 'Problem representation and mathematical problem solving of students of varying math ability', Journal of learning Disabilities 47, 103-115. https://doi.org/10.1177/0022219412436976 [ Links ]
Kyttälä, M. & Björn, P.M., 2013, 'The role of literacy skills in mathematics word problem skills: Controlling for visuo-spatial ability and mathematics anxiety', Learning and Individual Differences 29, 59-66. https://doi.org/10.1016/j.lindif.2013.10.010 [ Links ]
Laing, S.P. & Kamhi, A.G., 2002, 'The use of think-aloud protocols to compare inferencing abilities in average and below-average readers', Journal of Learning Disabilities 35(5), 436-448. https://doi.org/10.1177/00222194020350050401 [ Links ]
Lau, K-L., 2006, 'Reading strategy use between Chinese good and poor readers: a think-aloud study', Journal of Research in Reading 29(4), 383-399. https://doi.org/10.1111/j.1467-9817.2006.00302.x [ Links ]
Lindeman, J., 2000, Ala-asteen lukutesti: Käyttäjän käsikirja [Elementary school's reading test: User's manual], Gummerus, Jyväskylä.
Mercer, N. & Sams, C., 2006, 'Teaching children how to use language to solve maths problems', Language & Education: An International Journal 20(6), 507-528. https://doi.org/10.2167/le678.0 [ Links ]
Montague, M., 2008, 'Self-regulation strategies to improve mathematical problem solving for student with learning disabilities', Learning Disability Quarterly 31(1), 37-44. https://doi.org/10.2307/30035524 [ Links ]
Montague, M., Warger, C. & Morgan, T., 2000, 'Solve it! Strategy instruction to improve mathematical problem solving', Learning Disabilities Research & Practice 15(2), 110-116. https://doi.org/10.1207/SLDRP1502_7 [ Links ]
Ostad, A. & Sorensen, P.M., 2007, 'Private speech and strategy-use patterns: Bidirectional comparisons of students with and without mathematical disabilities in a developmental perspective', Journal of Learning Disabilities 40, 2-14. https://doi.org/10.1177/00222194070400010101 [ Links ]
Owen, R.L. & Fuchs, L.S., 2002, 'Mathematical problem-solving strategy instruction for third-grade students with learning disabilities', Remedial & Special Education 23(5), 268-279. https://doi.org/10.1177/07419325020230050201 [ Links ]
Pape, S.J., 2004, 'Middle school children's problem-solving behavior: A cognitive analysis from a reading comprehension perspective', Journal for Research in Mathematics Education 35, 187-219. [ Links ]
Passolunghi, M.C., 2011, 'Cognitive and emotional factors in children with mathematical learning disabilities', International Journal of Disability, Development & Education 58, 61-73. https://doi.org/10.1080/1034912X.2011.547351 [ Links ]
Passolunghi, M.C. & Siegel, L.S., 2001, 'Short-term memory, working memory, and inhibitory control in children with difficulties in arithmetic problem solving', Journal of Experimental Child Psychology 80, 44-57. https://doi.org/10.1006/jecp.2000.2626 [ Links ]
Passolunghi, M.C. & Siegel, L.S., 2004, 'Working memory and access to numerical information in children with disability in mathematics', Journal of Experimental Child Psychology 88, 348-367. https://doi.org/10.1016/j.jecp.2004.04.002 [ Links ]
Rittle-Johnson, B., 2006, 'Promoting transfer: Effects of self-explanation and direct instruction', Child Development 77(1), 1-15. https://doi.org/10.1111/j.1467-8624.2006.00852.x [ Links ]
Rosenzweig, C., Krawec, J. & Montague, M., 2011, 'Metacognitive strategy use of eighth-grade students with and without learning disabilities during mathematical problem solving: A think-aloud analysis', Journal of Learning Disabilities 44(6), 508-520. https://doi.org/10.1177/0022219410378445 [ Links ]
Sáenz, L.M. & Fuchs, L., 2002, 'Examining the reading difficulty of secondary students with learning disabilities: Expository versus narrative text', Remedial and Special Education 23, 31-41. https://doi.org/10.1177/074193250202300105 [ Links ]
Salonen, P., Lepola, J., Vauras, M., Rauhanummi, T., Lehtinen, E. & Kinnunen, R., 1994, Diagnostic tests 3: Motivation, Metacognition and Mathematics, Turun yliopisto, Oppimistutkimuksen keskus, University of Turku, Center for Research in Learning.
Schoppek, W. & Tulis, M., 2006, 'Enhancing arithmetic and word-problem solving skills efficiently by individualized computer-assisted practice', Journal of Educational Research 103(4), 239-252. https://doi.org/10.1080/00220670903382962 [ Links ]
Swanson, H.L., Lussier, C. & Orosco, M., 2013, 'Effects of cognitive strategy interventions and cognitive moderators on word problem solving in children at risk for problem solving difficulties', Learning Disabilities Research & Practice 28(4), 170-183. https://doi.org/10.1111/ldrp.12019 [ Links ]
Swanson, H.L., Orosco, M.J., Lussier, C.M., 2014, 'The effects of mathematics strategy instruction for children with serious problem-solving difficulties', Exceptional Children 80(2), 149-168. [ Links ]
Thorndsen, I., 2011, 'Self-regulated learning of basic arithmetic skills: A longitudinal study', British Journal of Educational Psychology 81, 558-578. https://doi.org/10.1348/2044-8279.002008 [ Links ]
Vauras, M., Lehtinen, E., Olkinuora, E. & Salonen, P., 1993, 'Devices and desires: Integrative strategy instruction from a motivational perspective', Journal of Learning Disabilities 26, 384-391. https://doi.org/10.1177/002221949302600603 [ Links ]
Vauras, M., Iiskala, T., Kajamies, A., Kinnunen, R. & Lehtinen, E., 2003, 'Shared regulation and motivation of collaborating peers: A case analysis', Psychologia 46(1), 19-37. [ Links ]
Verschaffel, L. & De Corte, E., 1993, 'Teaching realistic mathematical modeling in the elementary school: A teaching experiment with fifth graders', Journal for Research in Mathematics Education 28(5), 577-601. https://doi.org/10.2307/749692 [ Links ]
Verschaffel, L., De Corte, E. & Lasure, S., 1994, 'Realistic considerations in mathematical modeling of school arithmetic word problems', Learning and Instruction 4, 273-294. https://doi.org/10.1016/0959-4752(94)90002-7 [ Links ]
Verschaffel, L., De Corte, E. & Vierstaete, H., 1999, 'Upper elementary school pupils' difficulties in modeling and solving nonstandard additive word problems involving ordinal numbers', Journal for Research in Mathematics Education 30(3), 265-285. https://doi.org/10.2307/749836 [ Links ]
Verschaffel, L., Greer, B. & De Corte, E., 2000, Making sense of word problems, Swets & Zeitlinger, Heereweg, The Netherlands.
Vilenius-Tuohimaa, P.M., Aunola, K. & Nurmi, J.-E., 2008, 'The association between mathematical word problems and reading comprehension', Educational Psychology 28(4), 409-426. https://doi.org/10.1080/01443410701708228 [ Links ]
Wu, S.S., Willcutt, E.G., Escovar, E. & Menon, V., 2014, 'Mathematics achievement and anxiety and their relation to internalizing and externalizing behaviors', Journal of Learning Disabilities 47, 503-514. https://doi.org/10.1177/0022219412473154 [ Links ]
Wundt, W., 1888, 'Selbstbeobachtung und innere Wahrnehmung [Self-observation and inner perception]'. Philosophical Studies 1, 615-617. [ Links ]
Xin, Y.P. & Jitendra, A.K., 1999, 'The effects of instruction in solving mathematical word problems for students with learning problems: A meta-analysis', Journal of Special Education 32(4), 207-226. https://doi.org/10.1177/002246699903200402 [ Links ]
Zhang, D. & Xin, Y.P., 2012, 'A follow-up meta analysis for problem-solving interventions for students with mathematics difficulties', Journal of Educational Research 105(5), 303-318. https://doi.org/10.1080/00220671.2011.627397 [ Links ]
Zheng, X., Flynn, L.J. & Swanson, H.L., 2012, 'Experimental intervention studies on word problem solving and math disabilities: A selective analysis of the literature', Learning Disability Quarterly 36(2), 97-111. https://doi.org/10.1177/0731948712444277 [ Links ]
 Correspondence:
Correspondence:
Piia Björn
piia.bjorn@uef.fi
Received: 01 Nov. 2018
Accepted: 24 Aug. 2019
Published: 16 Oct. 2019















