ORIGINAL RESEARCH

 

Pre-service mathematics teachers' development process in using manipulatives in number operations

 

 

Zanele A. Ndlovu; Lytion Chiromo

Department of Mathematics Education, School of Education, University of KwaZulu-Natal, Durban, South Africa

Correspondence

 

 

---

ABSTRACT

BACKGROUND: Teaching using manipulatives is emphasised, especially in the early grades, to help learners conceptualise operations on whole numbers. Therefore, teachers' competencies in using manipulatives is the key in helping learners master these basic operation skills.
AIM: Drawing from the literature on using manipulatives to improve learners' performance in mathematics, this study recounts foundation phase pre-service teachers' conception of using manipulatives to enhance their competencies and reasoning skills to model the solution in number operations.
SETTING: Data presented here was collected from 31 participants. These pre-service teachers either passed mathematics or mathematical literacy with 40% at the grade 12 level.
METHODS: Data was collected from participants' written work (e.g. classroom tasks, homework, tests and examinations) and during class discussions. Interviews were conducted with some students. We analysed their conception guided by the APOS theory, namely, Action-Process- Object-Schema.
RESULTS: We observed improvement in the conception of using manipulatives among pre-service teachers. In the first semester, most students display action conception of using manipulatives to either represent or model a solution. However, in the second semester, most students either display process or object conception as explained in the genetic decomposition. We attributed the improvement to change of instruction in the second semester as we taught in accordance with the APOS theory.
CONCLUSION: It is evident that there are a number of contributing factors to pre-service teachers' conception of mathematical concepts, and teacher educators need to pay particular attention to these to help pre-service teachers master the concepts they would teach at school.

Keywords: ACE Teaching Style; Manipulatives; Number Operations; Pre-Service Mathematics Teachers; Competencies; Development Process.

---

 

 

Introduction

This article focusses on analysing foundation phase pre-service mathematics teachers' evolution of their conception of using manipulatives in number operations. The literature has long advocated for the use of manipulatives to improve learners' understanding of mathematical concepts (Ball 1992; Larbi & Okyere 2016; Furner & Worrell 2017; Saka & Roberts 2018; Shaw 2002); however, debates have been uneven when it comes to exploring teachers' use of the manipulatives. We argue that if manipulatives have been proven to be effective in improving learners' understanding of mathematics concepts, it is therefore imperative to understand teachers' conception of using manipulatives because it will impact their teaching. With this in mind, we aim to answer the following research questions: To what extent has pre-service teachers' conception of using manipulatives in number operations evolved? What are the contributing factors that enable or hinder their conception?

The lens of teaching for understanding

In his article entitled 'What it means to understand mathematics', Usiskin (2015:19) argues that for a person to have a full understanding of mathematical concepts, one needs to be well versed with skills and algorithms associated with the concept, uses and applications of the concept, representations and metaphors, and the history of the concept. Although these dimensions are important for concept development, they cannot be developed all at once because as much as they are interrelated they are independent of each other (Usiskin 2015). However, it is of utmost importance that they are developed for conceptual understanding of mathematical concepts. Along these lines of thoughts, this study explores pre-service teachers' conception of skills and algorithms associated with using manipulatives in number operations and its applications to model solutions in addition and subtraction of whole numbers. Understanding pre-service teachers' conception of using manipulatives in number operations would probably provide knowledge about pre-services teachers' competences to solve related problems and indirectly about the development of their subject matter knowledge, as defined by Ball, Phelps and Thames (2008).

Use of manipulatives in the teaching and learning of mathematics

'Mathematical manipulatives are physical objects that are designed to represent explicitly and concretely mathematical ideas that are abstract' (Moyer 2001:176). Teaching and learning using concrete models is currently recommended for the development of number concepts. In South Africa, the Curriculum Assessment Policy Statement (CAPS) (DBE 2012) for grades 1-3 emphasises the development of deep conceptual understanding of mathematical concepts and acquisition of specific skills and knowledge, for example, the development of number vocabulary, number concept and calculation, and application skills. In the current South African curriculum for Foundation Phase mathematics, more than 55% of the content to be taught is number operations, as shown in Table 1.

 

 

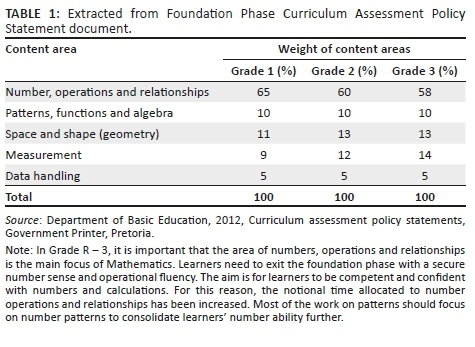
Although a certain percentage is specified, the truth is that number operations are embedded in all the topics. Therefore, it is imperative that teachers' conception of number operations are intact. The literature that pays particular attention to teaching and learning for understanding mathematics still emphasises the use of concrete materials and modelling mathematical concepts (Van de Walle 2007) and so is the CAPS document. The use of manipulatives to develop understanding of abstract mathematics is deemed necessary to build a solid foundation of the concept. This entails the competence to translate and integrate knowledge and to solve problems in a different format. For example, using physical concrete objects to model the problem or symbols; once the action is interiorised, it can be illustrated by means of a diagram.

Benefits of using manipulatives

Studies on the use of manipulatives had shown that manipulatives are important in enhancing the understanding of abstract mathematics (e.g. Ball 1992; Brijlall & Niranjan 2015; Furner & Worrell 2017; Saka & Roberts 2018). These authors argue that manipulatives helped to improve both procedural and conceptual understanding of mathematical concepts among learners. Larbi and Okyere (2016:53-61) investigated the use of algebra tiles with 56 junior high school learners. The findings showed that the use of algebra tiles enables learners to model mathematical ideas, which are essential to learning. Shaw (2002) argued that manipulatives assist with the development of mental mathematics and engaging students in the language and communication of mathematical ideas. Sandir (2016:2112) investigated pre-service mathematics teachers' design and use of manipulatives in different mathematical concepts. In that study, the findings showed that pre-service teachers encountered difficulties in using manipulatives to transform their mathematical ideas. While benefits of using manipulatives have been researched, evidence showed that teachers' conception of using manipulatives in their classroom instructions is limited (Furner & Worrell 2017; Marzola 2006). Although the reasons for the lack of effective use of manipulatives have not been extensively researched, the literature shows that the lack of teacher knowledge or expertise in a particular dimension is the main reason why certain resources or topics are not taught well. By way of illustration, Puchner et al. (2010:313) postulated that teachers had problems in using manipulatives when teaching mathematical concepts during lesson delivery. Therefore, because the use of manipulatives has been identified as one of the resources that help learners learn abstract mathematics, it is imperative that pre-service teachers have the expertise and knowledge to use it themselves to solve mathematical concepts - in turn they will effectively apply it in their teaching. As Laski et al. (2015:1-8) pointed out that using manipulatives in foundation phase mathematics classes does assist in promoting effective learning, plethora of research has paid particular attention to researching the benefit of using manipulatives with learners. However, there is a dearth in the literature when it comes to pre-service teachers' conception of using manipulatives to solve mathematical concepts.

Framework for this study

This study was conducted according to a specific framework for research and curriculum development in undergraduate mathematics, which guided the systematic enquiry of how students cognitively construct mathematical knowledge. The framework consists of three components, namely, theoretical analysis, design and implementation, and observation and assessments of student learning, as proposed by Asiala et al. (1997:4) (Figure 1).

 

 

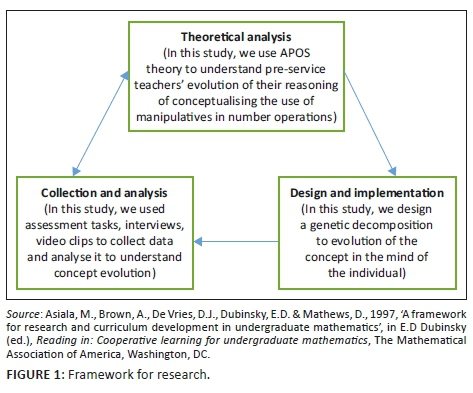
Under theoretical analysis, this study used Action-Process-Object-Schema (APOS) theory to describe and analyse pre-service teachers' evolution of their conception of using manipulatives in number operations. By using manipulatives in number operations, in this study we refer to pre-service mathematics teachers' ability to compute and model the solution by means of concrete objects and diagrammatic representation to show the conceptualisation of place value. The genetic decomposition explaining the cognitive constructs associated with using manipulatives in number operations is provided in the 'Key concepts in Action-Process-Object-Schema theory' section that serves as the analytic tool to analyse students' responses in relation to APOS theory. To ascertain the evolution of pre-service teachers' conception of using manipulatives, assessment tasks were designed and implemented and responses were analysed by means of the genetic decompositions that allow for the categorisation of responses, as shown in the 'Results' section.

Key concepts in Action-Process-Object-Schema theory

Action-Process-Object-Schema theory is deemed useful for explaining student conception of mathematical concepts. In APOS theory, conception refers to individual understanding and concept refers to collective understanding of that content by community of mathematicians (Arnon et al. 2014). Action-Process-Object-Schema theory is premised on the idea that conceptualisation of a concept is first conceived as an action, which suggests that transformation needs to be performed explicitly. This means that an individual relies on external cues to make sense of a concept. As the actions are repeated and reflected on, an individual moves away from relying on external cues and develops an ability to imagine the whole process (Arnon et al. 2014:19). In that way, action becomes interiorised into a process, which is a mental structure. The process can be encapsulated into an object. Encapsulation happens when an individual sees a process as a static structure to which action can be applied (Arnon et al. 2014:21). Furthermore, once a process has been encapsulated into a mental object, it can be de-encapsulated to its underlying processes when the need arises (Arnon et al. 2014:22). When an individual can encapsulate a process into an object or de-encapsulate the object to its underlying process, we consider that an individual has developed schema conception of the concept. The application of these mental constructs in the conception of using manipulatives in number operations is explained in the genetic decomposition. Its link to certain primary mathematics concepts can be found in Ubah and Bansilal (2018).

Genetic decomposition for operations on whole numbers using manipulatives

The design of genetic decomposition is premised on three factors, namely, researchers' mathematical understanding of the concept; researchers' experience of teaching a particular concept; and research on students' thinking about the concept and historical perspectives on the development of the concept. As there has been limited research focussing on pre-service teachers' thinking of the concepts and historical perspectives on the development of the concept among pre-service teachers, this genetic decomposition is premised on the researchers' understanding of the use of manipulatives and experiences in teaching this concept to pre-service teachers.

Understanding the concept of using manipulatives to represent whole numbers

Action

An action (Arnon et al. 2014):

[I]s an externally directed transformation of a previously conceived object(s). It is external in the sense that each step of the transformation needs to be performed explicitly and guided by instructions, each step cannot yet be imagined and none can be skipped. (p. 19)

In this study, when an individual represents numbers using concrete objects, his or her reasoning is considered to be at an action level. This includes the knowledge of constructing or deconstructing numbers. For example, given 123 an individual uses manipulatives to deconstruct the number to its components. An individual understands that 7 can be constructed in various ways such as 2 + 5 or 1 + 6 and can build these numbers using different manipulatives. However, the place value of each digit is not considered.

Process

As actions are repeated and reflected on, an individual moves from relying on external cues to having internal control over them. 'This is characterised by an ability to imagine carrying out the steps without necessarily having to perform each one explicitly' (Arnon et al. 2014:20). An individual begins to build mental images of the numbers. The action of gathering concrete objects is interiorised and can be represented by images, for example, drawings and illustrations are seen as representations of the physical objects. Furthermore, at this level, an individual uses appropriate mathematical language to explain the mental images.

Object

'This occurs when an individual applies an action to a process that sees a dynamic structure as a static one to which actions can be applied' (Arnon et al. 2014:21). At this level, the process of representing a number diagrammatically is encapsulated into an object, and an individual conceives the concept of place value of each digit. For example, a two-digit number is thought of as a bundle of ones. A two-digit or three-digit number is conceived as an object to which transformations can be performed. At this level, an individual can de-encapsulate a number so that it can be coordinated with other processes to form a new number.

Modelling the solution when adding or subtracting whole numbers

Action

To add whole numbers, an individual requires an understanding of the differences between unary and binary operations. An individual would first use standard algorithm to perform the computation process, and the action of representing the solution is done separately. Because the representation of numbers diagrammatically is not yet fully conceived, even the solution is not accurately represented diagrammatically.

Process

The action of performing binary operation is interiorised into a process when an individual performs the computation without relying on standard algorithms. An individual not only performs operations but also is able to make choices of appropriate mental illustrations to use and consider the efficiency of alternatives (Saka & Robert 2018). Furthermore, the action of adding or subtracting is interiorised and the solution is modelled either using physical manipulatives or diagrams.

Object

The process of modelling the solution using manipulatives is encapsulated into an object when an individual transforms the solution to its components and uses appropriate mathematical language to explain the process.

 

Methodological approach

This study is underpinned by an interpretive paradigm as it strives to inquire participant's conception of using manipulatives in number operations. With respect to approach, this study used qualitative approach as it allows for the voice of the participant to be heard and allows for more diversity in responses (Flick 2016).

A cohort of 98 pre-service teachers enrolled for the undergraduate full-time course to study towards becoming primary mathematics teachers. However, the data presented here are from 31 pre-service teachers who consented to participate in this study. The cohort of 98 students were divided into tutorial groups. The categorisation into tutorial groups was not academically based. Those who consented to take part in this study were put into one tutorial group, and fortunately, they were of diverse academic performance. Data were collected in two semesters by means of written work, video recordings and interviews. Interviews were audio recorded and later transcribed. Written work includes tutorial tasks, homework, tests and examination. During tutorial sessions, students engage in group discussions. These discussions were video recorded to capture students' thought process as they talk about their solutions. These discussions were transcribed and analysed together with the written work by means of the genetic decomposition, as presented in Figure 1.

The aim of the interviews was to probe and interrogate students' conceptions. Before the interviews, students were given time to reflect on their written work and where necessary video clips from tutorial discussions were played. Reflections were an hour long, followed by interviews that also lasted approximately an hour. Reflections were done with the whole group, but interviews were conducted with students purposefully selected.

In this study, we draw upon three students purposefully selected, and attention was on those students where we noticed evolution of their reasoning in using manipulatives in number operations.

The transcription of video and audio recordings to textual data allowed us to use the genetic decomposition to analyse students' conception. Using various methods of data collection allowed for triangulation of the data captured ensuring trustworthiness of our findings. Moreover, students were given time to reflect on their written work and class discussions before being interviewed to verify their responses and that the work they were commenting on is theirs.

Ethical considerations

Ethical clearance was obtained from the Humanities and Social Sciences Research Ethics Committee of the University of KwaZulu-Natal (reference number: HSS/0050/016).

 

Results and discussion

In this section, we used extracts to explain our observation of pre-service teachers' conception of using manipulatives in number operations. A variety of activities were administered, and a sample of questions and responses is presented below.

Understanding the concept of using manipulatives to represent whole numbers in semester 1

The data presented in Tables 2 and 3 were collected in the first mathematics foundation module. Students were in their second year. According to the BEd programme in the institution concerned, students start with major modules in the second year. Table 2 shows students' performance when they engage with the use of manipulatives in whole numbers.

 

 

 

 

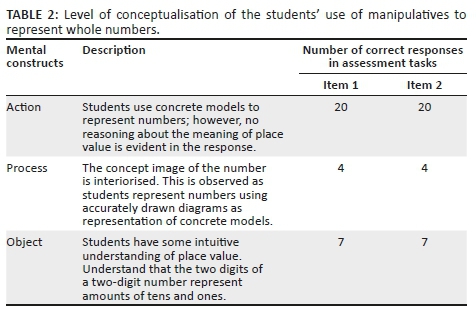
The sample of responses selected for discussion here were those that all students attempted to answer. In Table 2, we observed that the majority of pre-service teachers were able to use manipulatives to represent numbers or to construct or de-construct numbers. However, this action of representing or constructing numbers was performed routinely with no conceptualisation of place value. This was observed when students were asked, for example, to represent tens as ones or represent ones as a group of tens and then the number of correct responses decreased drastically to four. Moreover, when physical objects were removed, students could not represent the numbers diagrammatically. Even when attempts were made, the diagrammatic representation was not reflecting the place value of the number. When representing numbers using diagrams, students were not taking into cognisance the place of each number represented or proportionality when using Dienes blocks, as shown in Figure 2. Furthermore, the majority had difficulties in drawing number builder cards to represent 4023; most students wanted to show zero hundreds.

Modelling the solution when adding or subtracting whole numbers in module 1

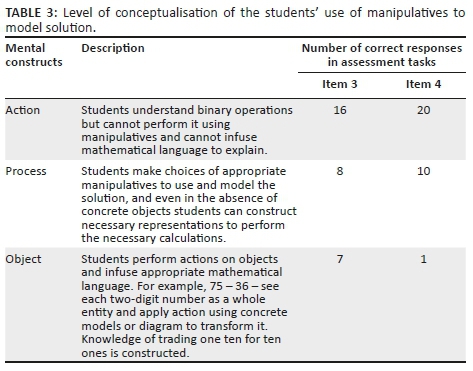
Table 3 shows pre-service teachers' level of conceptualisation of using manipulatives to model the solution.

When students were asked to model the solutions using manipulatives, as shown in the sample of responses below, we observed that the majority of them could use manipulatives to illustrate or represent inputs of binary operations, however, they could not model the solution. As observed in the extracts below, the majority determined the solution using standard algorithms, thus showing that their conception was restricted to the action level (Figure 3).

In the interview, Kadizo said:

I did not use the standard algorithm, but I used a calculator. The arrows were used to show how I subtracted, e.g. 70 - 30 = 40; 5 - 1 = 4; then add 40 + 4 = 44. (Kadizo, male, student)

Although Kadizo tried to argue that he did not use standard algorithm, he agreed that he did not use manipulatives. From his interview response, we assumed that he considered standard algorithm to be the vertical column method and because his solution was not structured vertically, he argued that he did not use the standard method. However, the arrows and his explanation, during the interview, focus on subtracting from left to right strategy, suggesting that he used the standard method. It was observed that in the absence of concrete objects, Kadizo had challenges in modelling the computation using diagrams as representation of concrete objects. It was captured in the video clip that Kadizo could not recall using number builder cards even as a learner or he was never exposed to using manipulatives to perform operations. His exposure to manipulatives was for counting purposes. The extract taken from video clips suggested that the lack of previous knowledge in the use of manipulatives to compute hindered Kadizo's concept development. In the learning of mathematics, previous knowledge plays a crucial role in the construction of new knowledge, it seems the lack of previous knowledge therefore hindered Kadizo's conception of using manipulatives (Figure 4).

Again, in this extract, Kadizo did not only struggle with modelling the solution but he also had difficulties with using mental images to represent digits, thus confirming that the action of using physical objects has not been interiorised into a process. This we observed as he represents tens and hundreds by the same diagrams, suggesting that he has not conceived the place value concept of each digit in two-digit or three-digit numbers.

Similarly, Azinga, as is evident in Figure 5 of item 4, failed to model the solution to 47 + 76.

However, she was able to use mental images to represent the inputs of the binary operation, but not the solution. During the interview, she was given different numbers to compute and was asked to model the solution. He first used standard method and then used Dienes block to represent the solution, as shown in Figure 5. Although the researcher explained to her that she needs to use the Dienes block to show the addition of 18 and 23 and show how she reached the answer by using Dienes block she could not conceptualise that. Even, the language used was not mathematical, but it is the language generally used at the primary level, that is, 'eight plus three is eleven carry one instead of saying trading ten ones for one ten'. As Sandir (2016) posits, it seemed that these pre-service teachers have not been able to conceptualise the use of manipulatives to an extent that allows them to transform their mathematical ideas about place value.

Urmilla's written response suggested that she was also still restricted to the action level. The response below was extracted from the video clip taken during tutorial discussion (Figure 6).

Urmilla like Azinga used the standard algorithm to determine the solution and only used the concrete objects to represent the solution. However, her explanation during the interview revealed the evolution of the process conception, although not yet fully constructed. This observation was based on her attempt to infuse appropriate mathematical language, explaining that nine plus eight gives 17 ones and traded ten ones for one ten to get six tens, as shown in Figure 7. Similarly, in a different sum, she also did not show how she used number builder cards but provided an explanation of how she used it. Furner et al. (2017) assert that the use of manipulatives provides teachers with great potential to use their creativity in mathematics concepts rather than relying on the rules. However, the above findings show that these pre-service teachers have not yet acquired that creativity.

Table 4 shows students' performances in certain tasks in semesters 1 and 2. Tasks assessing similar concepts across both semesters were selected. The aim was to explore pre-service teachers' conception of using manipulatives to model solution over two semesters. In Table 4, we opted to show students' competencies in the items done either during class time or during tutorial time or in tutorial tests because students answered those in the presence of the researcher and in no time did the researcher try to enhance their thinking like in interviews.

 

 

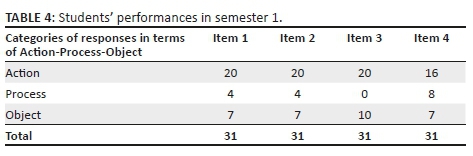
From Table 4, it is evident that most pre-service teachers' conception of using manipulatives was limited to action stage. Tasks of a similar nature were used across two semesters to enhance pre-service teachers' conception of using manipulatives. Table 5 shows the performance of students towards the end of semester 2 in the second module they enrolled in.

 

 

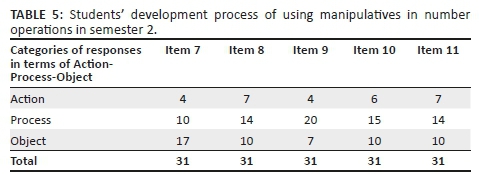
From Table 5, we observed an improvement in students' conceptions of using manipulatives either to represent numbers diagrammatically or in modelling the solution. As students get more exposure and opportunities to engage co-operatively with tasks that challenge their intellect, we saw evolution in their reasoning about the concept. In semester 2, co-operative learning was used in a different way than it was used in the first module. Instead of students working together or individually to solve the problem during tutorials, they had to first do the task individually and then collaboratively, to ensure that all students participated during group discussions as each student was required to explain his or her response rather than having one or two students explaining to the rest of the group. Although we could not conclude that it is the change of instructions that contributed immensely to students' improved performance, from the responses presented below we observed evolution of their conception of the concept.

Use of manipulatives to represent numbers and to model the solution in number operations

In Figure 7, we noticed that Urmilla attempted to model the solution, unlike in Figure 6 where she only represented the solution. In Figure 8, we saw her representing 125 + 137 and illustrating how she combined the hundreds, tens and ones and traded ten ones for one ten to get 262.

Similarly, during the group discussion, we observed evolution of students' thinking process in using manipulatives to model the solution. Kadizo's group could use diagrams to represent inputs of the binary operation 47 + 76 and use the physical objects to model the solution 123 and show the process of trading ten tens for one hundred.

Furthermore, when performing subtraction sums, as shown in Figure 9, Kadizo explained how he used the Dienes block to model the solution of 75 - 31, unlike in the above extracts where his explanation of finding the solution was embedded in standard algorithms and did not involve the use of appropriate mathematical language. During the second interview, we observed that actions of using concrete objects has been interiorised as he could translate the physical objects to mental images and use appropriate diagrams to represent binary inputs and model the solution. Furthermore, the process of using diagrams has been encapsulated into an object. This was observed as he exhibited an understanding of the relationship between a bundle of ones to make ten and infused correct mathematical terminology to explain his thought process (Figure 10):

I will make 7 tens from Dienes blocks and 5 ones which makes 75. Thirty one has 3 tens and one one. Since I am subtracting, I am not building 31 but I will take it away from 75. First take away one unit from five ones, I am left with 4 ones - then take away 3 tens from 7 tens, I am left with 4 tens. 4 tens is 40 + 4 ones = 44. (Kadizo, male, student)

The above findings support the suggestion by Ball (1992:47) that talk and interaction between teachers and students are necessary in creating meaning of how to use manipulatives. However, based on the findings, we extend this idea and argue that structured talk informed by structured activities is necessary for effective learning.

In item 10, students were asked to use diagrams to represent a different set of numbers. Students were not restricted to use any particular model. They could either use Dienes blocks, number builder cards or abacus. Most students used Dienes block; unlike in semester 1 students take cognisance of proportionality when representing different digits, as shown in Azinga's response (Figure 11).

Although still not accurately drawn, the proportionality is taken into account to differentiate tens from hundreds.

Item 11 was the same as item 4 in semester 1. This question was poorly answered in semester 1, therefore, we wanted to see if students could now use manipulatives to model the solution. In Table 5, we observed that more students can either accurately represent the inputs of the binary operations and solution using diagrams and other could model the solution. Even Azinga who could not represent the solution in item 4 was able to in item 11, thus showing evolution of her conception of using manipulatives. Although in the written response she did not illustrate how she arrived at the solution, during the interview she was able to express her thought processes (Figure 12):

4 tens plus 7 tens equals eleven tens but eleven tens is made up of ten tens which is same as hundred. 6 ones plus 7 ones equals 13 ones but 13 ones is made of ten ones and 3 ones so tens ones is the same as one ten. Putting it all together I will have one hundred, two tens and 3 ones and that is what I was trying to show here. (Azinga, female, student)

In item 11 in semester 2, we saw an evolution of pre-service teachers' conception of using manipulatives from action to process.

 

Conclusion

In the quest to answer our perennial question about pre-service teachers' conception of using manipulatives and exploring the contributing factors that enable or hinder their conception, we concluded that indeed student conception of using manipulatives to represent whole numbers and model solution in addition and subtraction of whole numbers gradually evolved. This we observed as we saw from the above data in semester 2 that many students showed the interiorisation of action into a process and further encapsulating process into objects, thus showing conceptualisation of the concept. While it can be argued that there could be many contributing factors associated with development in their cognitive growth, we observed that as students engage in structured co-operative learning and engage effectively in mathematics talk, students' reasoning improved. These findings, to a certain extent, concur with findings by Ubah and Bansilal (2018) that pre-service teachers are conversant in answering questions requiring action-level engagement, as we observed in semester 1, however, the prolonged time spent on engaging pre-service teachers with structured tasks in a co-operative manner allowed for the evolution of their thought processes. Saka and Roberts (2018) argue for the use of bow abacus to improve cognitive development among learners in the early grades. In this study, we argue for the use of any appropriate manipulative, not restricted to any form, for the cognitive development of foundation phase pre-service mathematics teachers.

In the three cases of students we analysed, we observed evolution of the thought processes when using manipulatives in number operations, mainly the concept of modelling the solution and the use of appropriate mathematical language, leading to the development of place value notion. There is much concern in the literature about pre-service mathematics teachers' subject matter knowledge of school mathematics (Ball et al. 2008; Ndlovu, Amin & Samuel 2017). This study has shown that there is a possibility for the development of subject matter knowledge of school mathematics when pre-service teachers do engage with school mathematics concepts that challenge their intellect.

 

Acknowledgements

The authors would like to thank PrimTed project for the support in this study.

Competing interests

The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.

Authors' contributions

Z.A.N., as a lecturer of the module, was responsible for coordinating the research project and writing up of the article. L.C. assisted with the data collection and structuring of the article. Z.A.N. has also assisted L.C. as a young researcher to present preliminary findings at the AMESA regional conference in 2016.

Funding information

This research received no specific grant from any funding agency in the public, commercial or not-for-profit sectors.

Data availability statement

Data sharing is not applicable for this article as no new data were created or analysed in this study.

Disclaimer

The views and opinions expressed in this article are those of the authors and do not necessarily reflect the official policy or position of any affiliated agency of the authors.

 

References

Arnon, I., Cottrili, J., Dubinsky, E.D., Oktac, A., Fuentes, S.R., Trigueros, M. et al. (eds.), 2014, APOS theory: A framework for research and curriculum development in Mathematics education, Springer, New York, NY.

Asiala, M., Brown, A., De Vries, D.J., Dubinsky, E.D. & Mathews, D., 1997, 'A framework for research and curriculum development in undergraduate mathematics', in E.D Dubinsky (ed.), Reading in: Cooperative learning for undergraduate mathematics, The Mathematical Association of America, Washington, DC.

Ball, D.L., 1992, 'Magical hopes: Manipulatives and reform of math education', American Educator 16(2), 14-18, 46-47.         [ Links ]

Ball, D.L., Thames, M.H. & Phelps, G., 2008, 'Content knowledge for teaching: What makes it special?', Journal of Teacher Education 59(5), 389-407.         [ Links ]

Brijlall, D. & Niranjan, C., 2015, 'Using manipulatives to support an embodied approach to learning trigonometry in a South African school: A case study', Africa Education Review 12(3), 361-380, https://doi.org/10.1080/18146627.2015.1110893        [ Links ]

Department of Basic Education, 2012, Curriculum assessment policy statements, Government Printer, Pretoria.

Flick, U. (ed.), 2016, Introduction to qualitative research, Sage, London.

Furner, J.M. & Worrell, N.L., 2017, 'The importance of using manipulatives in teaching math today', Transformations 3(1), 1-26.         [ Links ]

Larbi, E. & Okyere, M., 2016, 'The use of manipulatives in mathematics education', Journal of Education and Practice 7(36), 53-61.         [ Links ]

Laski, E.V., Jordan, J.R., Daoust, C. & Marry, K.A., 2015, 'What makes mathematics manipulatives effective? Lessons from cognitive science and Montessori education', Sage Journal 5(2), 1-8.         [ Links ]

Marzola, E., 2006, 'Using manipulatives in maths instruction', Journal of Reading, Writing and Learning Disabilities 3(1), 9-12.         [ Links ]

Moyer, P.S., 2001, 'Are we having fun yet? How teachers use manipulatives to teach mathematics', Educational Studies in Mathematics 47(2), 175-197.         [ Links ]

Ndlovu, Z., Amin, N. & Samuel, M., 2017, 'Examining pre-service teachers' subject matter knowledge of school mathematics concepts', Journal of Education 70, 46-72.         [ Links ]

Puchner, L., Taylor, A., O' Donnell, B. & Fick, K., 2010, 'Teacher learning and mathematics manipulatives: A collective case study about teacher use of manipulative in elementary and middle school mathematics', Science and Mathematics 108(7), 313-325.         [ Links ]

Saka, T. & Roberts, N., 2018, 'Manipulatives for early grade whole number and relationships: The potential of the Malawian bow-abacus', in R. Govender & K. Junquira (eds.), Proceedings of the 24th annual national congress of the association for mathematics education of South Africa, Bloemfontein, South Africa, n.d., 2018, n.p.

Sandir, H., 2016, 'Investigating pre-service mathematics teachers' manipulative material design processes', Eurasia Journal of Mathematics, Science and Technology Education 12(8), 2103-2114. https://doi.org/10.12973/eurasia.2016.1292a        [ Links ]

Shaw, J., 2002, Manipulatives enhance the learning of mathematics, Student Guide, Grade 2, edition, viewed 23 July 2018, from http://www.eduplace.com.

Ubah, I.J.A. & Bansilal, S., 2018, 'Pre-service primary mathematics teachers' understanding of fractions: An action-process-object-schema perspectives', South African Journal of Childhood Education 8(2), a 539. https://doi.org/10.4102/sajce.v8i2.539.         [ Links ]

Usiskin, Z., 2015, 'What does it mean to understand some Mathematics?', in S. Cho (ed.), Selected regular lectures from the 12th International congress on mathematical education, Springer, Cham.

Van De Walle, J.A. (ed.), 2007, Elementary and middle school mathematics: Teaching Developmentally, Pearson, Sydney.

Weyer, R.S., 2010, 'APOS theory as a conceptualisation for understanding mathematics learning', Summation 3, 9-15.         [ Links ]

 

 

Correspondence:
Zanele A. Ndlovu
ndlovuz3@ukzn.ac.za

Received: 30 Aug. 2018
Accepted: 23 Mar. 2019
Published: 05 Sept. 2019