Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.9 n.1 Johannesburg 2019
http://dx.doi.org/10.4102/sajce.v9i1.655
ORIGINAL RESEARCH
Distribution of additive relation word problems in South African early grade Mathematics workbooks
Ingrid Mostert
Centre for Education Practice Research, University of Johannesburg, Soweto, South Africa
ABSTRACT
BACKGROUND: Workbooks were introduced by the South African Department of Basic Education (DBE) in 2011. Although the workbooks were designed as supplementary materials, in some schools they are used as the sole teaching text. Therefore, an analysis of the content coverage of the workbooks is warranted. This article provides such an analysis in terms of additive relation word problems
AIM: This article aims firstly to expound on the existing literature to propose a comprehensive additive relation word problem typology and secondly to analyse the prevalence of particular word problem types in the foundation phase Mathematics workbooks
SETTING: This research was conducted in South Africa, focusing on additive relation word problems in foundation phase Mathematics workbooks
METHODS: A comprehensive typology of additive relation word problem types was developed based on typologies used in previous studies. All the additive relation word problems in the 2017 Grades 1-3 foundation phase Mathematics workbooks were categorised according to this typology
RESULTS: In total there were 61 single-step additive relation word problems with numerical answers across the three grades. This is a small number in comparison to other countries. There was also an uneven distribution of problem types, with more problems in the easier subcategories and fewer or no problems in the more difficult subcategories
CONCLUSION: This article provides evidence for the need to revise the word problems in the DBE workbooks. It also provides a theoretical framework to use in the revision of the workbooks and in any supplementary teaching material developed for teachers
Introduction
Since 2011 the South African Department of Basic Education (DBE) has provided all Grade 1-6 learners in public schools with Language, Mathematics and Life Skills workbooks. The intention of the workbooks, as explained on the DBE website (DBE 2018), is that they 'provide every learner with worksheets to practise the language and numeracy skills they have been taught in class'. This implies that the workbooks are not to be used as a teaching resource but as a supplementary resource. They are not meant to replace textbooks but rather to replace the need for teachers to create their own worksheets. Designing the workbooks in this way both acknowledges what the 2012 National Education Evaluation and Development Unit (NEEDU) report (Taylor 2013:44) describes as South Africa's 'ubiquitous worksheet culture' and addresses the concern raised by the report, namely that only a minority of teachers are capable of creating a well-developed set of worksheets.
Although the intention is that the workbooks do not replace textbooks, Hoadley and Galant (2016) refer to recent calls to trial the workbooks as the sole text given to teachers. Anecdotal evidence from the Eastern Cape suggests that there are many schools, particulary text-poor schools, where workbooks are already the sole teaching resource. This is because, while most schools do not have sufficient textbooks, they do have workbooks 'in the right quantities and correct language' (NEEDU 2016, slide 10). Not only do schools have workbooks, but teachers have generally taken up the workbooks positively (Taylor 2013).
Should it be true that teachers use workbooks as their sole teaching resource, it implies that learners will only see the examples and exercises that appear in the workbooks and will not be exposed to any other examples. It is therefore important that variety and frequency of problems is given considerable attention. Even if it is not the case that a large number of teachers rely solely on the workbooks, the workbooks still represent an exemplification, by the DBE, of the curriculum and therefore warrant careful and detailed examination in terms of coverage of the prescribed curriculum.
This study provides such an analysis in relation to one aspect of foundation phase Mathematics, namely word problems. As such, it sets out to contribute to the small amount of literature on foundation phase Mathematics workbooks. This literature includes the work of Mathews, Mdluli and Ramsingh (2014) on how teachers use the workbooks and of Davis (2012) and Galant (2013), who point out misconceptions in the workbooks about addition and multiplication, respectively.
Word problems are a key aspect of early grade Mathematics curricula, internationally and in South Africa (Department of Basic Education 2011). Word problems are linguistically expressed Mathematics problems and therefore have implications for vocabulary, syntax and even morphology (Halliday & Matthiessen 2013). Three diagnostic reports on the South African Annual National Assessments (ANA) have identified word problems as a recurring weakness (Department of Basic Education 2012, 2014, 2015) in the foundation phase, thus warranting further research. Although the ANA is no longer an annual part of the South African basic education landscape, these standardised assessments provide useful data around curriculum expectations at the level of classroom assessment practices.
In Grades 1-3, word problems focus on additive relations and multiplicative reasoning. Various Mathematics education researchers have invested time in classifying additive relation word problems and developing typologies against which a curriculum or text could be evaluated. In schools where workbooks are the sole teaching text, the only examples of word problems that learners see are those in the workbooks. It is therefore both important and practically relevant to reflect on the extent to which South Africa's Mathematics workbooks in Grades 1-3 cover the different word problem types and how frequently different types of problems are posed.
Although similar studies have been done in a number of different countries, such an analysis has not been done on South African foundation phase textbooks or the workbooks. Stigler et al. (1986) compared US textbooks to Soviet textbooks and found that both textbooks had between 300 and 400 word problems across the first three grades. However, while US textbooks over-represented some problem types and under-represented others, Soviet textbooks had a more even distribution of problem types. More recently, a number of studies have shown that the distribution of word problems in other countries such as Turkey (Olkun & Toluk 2006; Tarim 2017), Malaysia (Parmjit, Sahari & Moideen 2006), Brunei (Dhindsa, Veloo & Singh 2014) and Greece (Despina & Harikleia 2014) is similar to the uneven distribution in the US textbooks. This study will establish whether South Africa's foundation phase workbooks also have a similar uneven distribution of word problem types or whether they are more evenly distributed as in the Soviet Union in 1986.
This study will not only differ from other similar studies in terms of its focus on South Africa, it will also differ in terms of the level of attention paid to the typology used in the analysis. While other studies have adopted (or slightly adapted) an existing typology, this study describes alternative typologies and explains why they were not chosen. It also argues for the renaming of certain problem types (building on the work by Roberts [2016a]) and extends the chosen typology by including variations of certain problem types.
The renamed, extended and exemplified typology that is developed in this article provides not only an analysis tool for the current workbooks but also a practical reference tool for curriculum developers, workbook and textbook writers and teachers - both in South Africa and internationally - to make informed decisions about the types and spread of word problems offered to learners. In South Africa such a tool is valuable in the light of the problematic typologies uncovered by Roberts (2016a) in the South African Curriculum and Assessment Policy Standard (CAPS). It is also potentially valuable should the foundation phase Mathematics workbooks be reworked.
It is for these reasons that this article aims firstly to expound on the existing literature to propose a comprehensive additive relation word problem typology and secondly to analyse the prevalence or absence of particular word problem types in the DBE foundation phase Mathematics workbooks.
Theoretical framework
Early typologies
Researchers have focused on classifying additive relationship word problems since the early 1980s. In particular, two groups of researchers developed similar, but not identical, typologies. The first was developed by Riley, Greeno and Heller (1984). The second was developed by Carpenter, Hiebert and Moser, who were working on their Cognitively Guided Instruction framework. Both groups published a comprehensive version of their typologies (Carpenter & Moser 1983; Riley, Greeno & Heller 1984) but later only included a subset of these problems in their research. Although other research groups have produced typologies, they can all be traced back to these two original typologies.
This section first discusses the category that was 'dropped' by both research groups and explains why it is included in the proposed comprehensive typology used in this article. Secondly, the difference between the two original typologies is highlighted and an argument is made for reflecting this difference in the comprehensive topology. Thirdly, a more recent typology that differs from the original typologies in one important aspect is considered and discarded. These three sections provide the theoretical foundation for the comprehensive and exemplified typology used to analyse the workbooks in this article. The section ends by providing possible reasons for the problematic typologies used in the South African Foundation Phase CAPS. The problems with the typologies in CAPS were described by Roberts (2016a) and the possible reasons for these problematic formulations were uncovered when the early papers about word problem types were studied for this article.
What happened to the 'equalise' problem type?
Carpenter and Moser (1983) and Riley et al. (1984) published comprehensive typologies that included four main problem types. The four categories, the names used by the two research groups and an exemplification of the problem types are detailed in Figure 1.

In this article categories are named according to the labels used by Roberts (2016a). Roberts explains that the label 'change' is preferable to 'join/separate' because it emphasises the common action. 'Collection' is preferable to 'combine' (which implies an action although considered a static problem type) and to 'part-part-whole' (which emphasises a structure shared by all additive relation problem types).
While all work on word problems identifies the difference between dynamic and static problem types, only Carpenter et al. (1981) differentiate between problem types that refer to a single set and those that refer to two separate sets. Figure 2 sets out the relationship between the four problem types and includes the general number sentence for each problem type. While Carpenter et al. (1981) label these different problems as 'set inclusion' and 'no set inclusion' problem types, in this article the labels 'single set' and 'separate sets' are used, as these are considered to be more descriptive. Also note that the names of the categories correspond to the names used in this article.
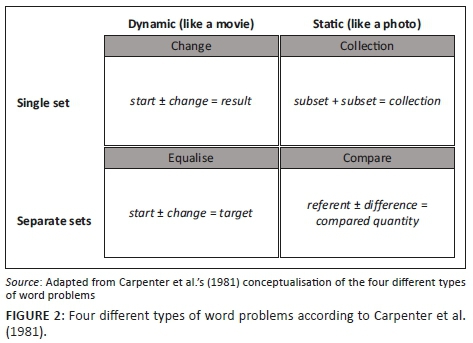
The category that is most often excluded and that does not appear at all in later work is the 'equalise' problem type. Carpenter and Moser (1983) describe equalise problems as being a combination of change-type problems and compare-type problems (as can also be seen from their position in the grid in Figure 2). Equalise problems are similar to change-type problems because they involve an action (albeit an implicit one) and are similar to compare-type problems because they involve the comparison of two separate sets. It is not clear why equalise problems are no longer referred to in the literature, but I argue that they are an important category when attempting to give a complete range of possible types of word problems.
Is there a difference between 'combine' and 'part-part-whole' problems?
This section discusses the differences between the two 'original' typologies. Even though the two research groups used different names for their problem types, as early as 1982 the categories were mapped onto each other (Nesher, Greeno & Riley 1982). Although the mapping implies that the problem types are the same, a closer look at the exemplification of the categories shows slight differences in one of the categories. To highlight the difference between the categories, the names and numbers from the Riley et al. (1984) typology have been used in both exemplifications (see Figure 3).

One way to understand the difference is in terms of ownership. In Riley et al.'s (1984) example, each of the subsets belongs to a different person. In Carpenter and Moser's (1983) example, the subsets belong to the same person but have different attributes (e.g. colour). This difference is reflected in the labels given to the categories by the two research groups. In Riley et al.'s work (1984), where the subsets are owned separately, the problems are known as 'combine' problems - items owned by two individuals need to be combined. In contrast, in Carpenter and Moser's work (1983), the problems are known as part-part-whole problems, thus emphasising the single ownership of the whole set, which has two distinct subsets, identified by different attributes.
Although it is not clear that the distinction between these two exemplifications is sufficient to be evident in learner performance, both types of problems occur in the DBE workbooks and therefore the comprehensive typology developed in this article differentiates between the 'different attributes' and 'different ownership' subcategories for collection-type problems (see Figure 9).
This article argues that the exemplification of the collection-type problems is the main difference between the two original typologies (not the difference in names) and that all other typologies can be traced back to these two classic typologies by considering both the names used for the categories and, more importantly, how the compare-type problems are exemplified. In particular, the extensive work on word problems by De Corte and Verschaffel (1987) uses Riley et al.'s (1984) typology, while the work of Van de Walle, Karp and Bay-Williams (2015) and Clements and Sarama (2009) is based on Carpenter and Moser's (1983) typology.
Is there a difference between the 'larger unknown' and 'referent unknown' compare-type subcategories?
Although the typologies used by Van de Walle et al. (2015) and Clements and Sarama (2009) are based on Carpenter and Moser's typology (1983), they differ in one important aspect. In order to discuss this difference, it is necessary to look at the subcategories used in the different typologies.
Subcategories are created in two ways. The first way is by reversing the 'direction' of change in the dynamic problems. This also equates to separating into two the general number sentences (see Figure 2) for the change, equalise and compare problem types.
For example, a change problem where a child is given marbles can be changed to a change problem where marbles are taken away. A compare problem where the compared quantity is more than the referent can be changed to one where the compared quantity is less than the referent (see Figure 4). Note that such a reversal is not possible for collection-type problems (as can be seen from the general number sentence in Figure 2, which does not include a ±). Instead, the collection-type problems are divided into 'different ownership' and 'different attributes' subcategories. This results in a total of eight subcategories.
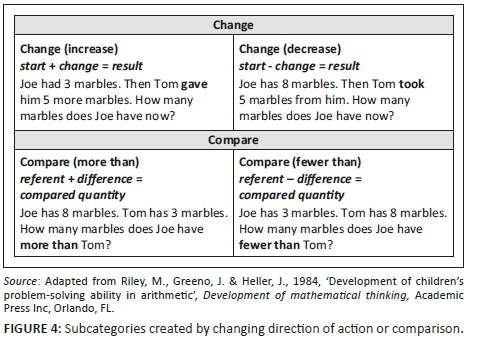
The difference between the two change subcategories is made very explicit in Carpenter et al.'s work (1981), which does not include a label for the overarching category but refers to the two subcategories as 'join' and 'separate'. In this article, once again, the labels proposed by Roberts (2016a) - namely 'change increase' and 'change decrease' - are used because this draws attention to 'the problem situation and not the assumed likely operation' (p. 110). By extension this article refers to 'equalise increase' and 'equalise decrease' subcategories.
What is less explicit in the literature is the difference between what is referred to in this article as the 'compare more than' and 'compare fewer than' subcategories. Although these subcategories are exemplified in the original typologies, they are not named. In some other typologies (such as the one used by Roberts [2016a]) only the 'compare more than' problems are exemplified. In the comprehensive typology developed in this article all the possible subcategories are included and named.
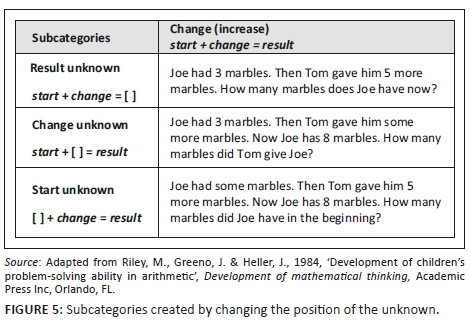
The second way in which subcategories are created is by changing the position of the unknown in the general number sentence for each of the categories. Figure 5 exemplifies how the change increase category can be used to generate three subcategories by keeping the general number sentence the same (3 + 5 = 8) and changing the position of the unknown.
Note that the collection-type word problems, unlike the other categories, which generate three subcategories, only generate two distinct subcategories. This is because there is no need to differentiate between the two subsets, so collection = subset + [ ] is the same as collection = [ ] + subset. This further subdivision results in a total of 22 subcategories as seen in Figure 6.
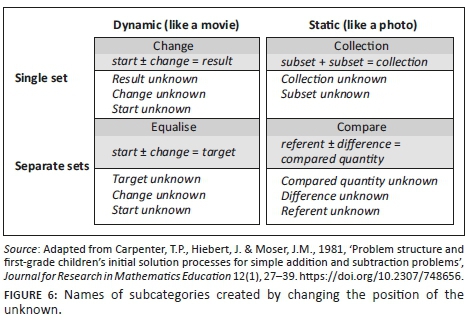
The labels used for these subcategories are largely based on Roberts (2016a), except for the compare-type problem. For compare problems the label 'compared quantity unknown' (Riley et al. 1984) is used instead of 'whole unknown' because compare-type problems do not have a whole in the sense that collection-type problems do.
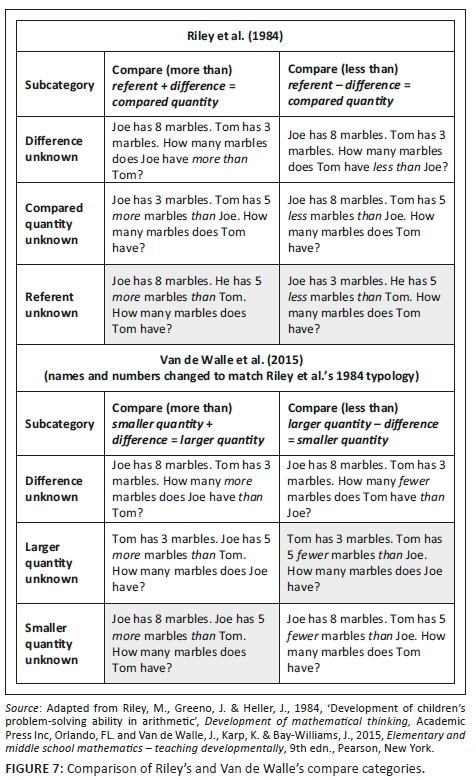
A closer look at the typologies used by Van de Walle et al. (2015) and Clements and Sarama (2009) shows an important difference in the way that the compare-type subcategories are generated. Van de Walle et al.'s (2015) typology is discussed here in detail because it is the typology used by most studies that analyse the prevalence of word problems in textbooks (see Despina & Harikleia 2014; Dhindsa et al. 2014; Olkun & Toluk 2006; Parmjit et al. 2006), the one exception being the study by Stigler et al. (1986), which uses the Carpenter and Moser (1983) typology.
The original typologies (Carpenter and Moser [1983] and Riley et al. [1984]) differentiate between the quantity that is being referred to ('the referent'), the quantity that is being compared to the referred quantity ('the compared quantity') and the difference between these two quantities. Van de Walle et al. (2015) and Clements and Sarama (2009), however, differentiate between the larger quantity, the smaller quantity and the difference between the two (see Figure 7). Although both approaches can be used to generate six different subcategories and although the six categories can be mapped onto each other, this article argues that the formulation used in the original typologies is more useful for two reasons.
Firstly, the original typologies foreground the use of the referent in comparison-type problems. As explained by Roberts (2016b), compare type problems are particularly difficult because:
… the language of comparison is complex in English as comparison requires a referent (something to compare to). The referent is not made explicit … but is inferred from the word order of the sentence. (p. 5)
For example: Joe has 5 marbles. Tom has 3 more marbles than Joe. How many marbles does Tom have? The referent is the number of marbles that Joe has as indicated by 'than Joe'. The referent is not made explicit in Van de Walle et al.'s formulation.
Secondly, in the original typologies the relative difficulty of the compare-type subcategories is linked to the position of the unknown in a similar way to the change-type category. Riley et al. (1984) refer to research that has shown that problems where start set is unknown (for change or equalise problems), or similarly where the referent is known for compare-type problems, are more difficult for children to solve than problems where the start set (change problems) or the referent (compare problems) are known. They explain that the reason for this (p. 177) is that it is more difficult to model problems where the value that needs to be acted on is unknown.
In both the change and the compare problem types, not knowing the value of the set that needs to be acted on increases the difficulty of the problem. In the original typologies, therefore, the more difficult compare-type problems fall into the same subcategories (i.e. referent unknown).
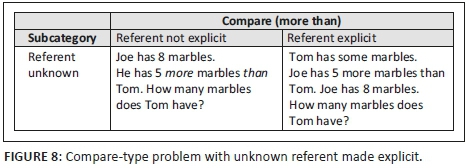
For compare-type problems, the difficulty of having the set that needs to be acted on (i.e. the referent) being unknown is compounded by the complexity of English (as explained by Roberts 2016a). While change-type problems indicate that the start is unknown by stating that 'Tom has some marbles', the compare-type problems do not make this explicit. Figure 8 shows how to rephrase the compare-type problem to make the unknown referent explicit.
In contrast, Van de Walle et al. (2015) attribute the relative difficulty of the different subcategories in their typology to the relationship between the quantities and the operations:
When the larger amount is unknown, stating the problem using the term more is easier for children because the relationships between the quantities and the operation more readily correspond to each other. In the smaller unknown situation, stating the problem using the term fewer is easier for children for the same reason. (p. 194)
In their typology, therefore, the more difficult problems are not in the same subcategory. This, together with the lack of reference to the referent, is why the formulation of the original typologies is used in this article.
Exemplifying the comprehensive typology
Figure 9 provides a comprehensive typology with all 22 subcategories named and exemplified. The typology is structured similarly to one of the typologies in the CAPS document (Department of Basic Education 2011:221-222), with the different unknowns in different rows and the different directions of change or comparison in different columns. The names in the problems are also taken from the examples in the CAPS document. For each of the four categories, the 'position of the unknown' subcategories are ordered, with the first being the one learners find easiest to solve (in that category) and the last being the one they find most difficult to solve (Nesher et al. 1982). To emphasise that change-type problems are 'single set' problems, only one person is referred to in the examples, rather than two, which was the case in both original typologies.
What happened to the typologies in the Curriculum and Assessment Policy Standard?
Finally a note on the problematic typology referred to in CAPS in the Grade 2, Term 1 teacher guidelines (Department of Basic Education 2011:221-222). As explained by Roberts (2016a:117), this table is problematic in many ways, most importantly because 'this typology (incorrectly) maps both "join" and "separate" actions and a common "start-change-result" generalised structure onto the static situation of "compare" problem types'.
During the detailed analysis of older texts for the literature review necessary to refine the framework used in this article, a possible reason for these errors was uncovered, namely the potentially ambiguous formatting of tables. The error of mapping 'join' and 'separate' onto categories besides the change category has occurred in at least one other text. This is potentially because of the lack of differentiation in the formatting between the higher-level heading of 'change', and the subheadings of 'join' and 'separate', together with the columns used to list the different examples of word problems. The table on the right of Figure 10 shows the adaptation by Stigler et al. (1986) of the original table (on the left) as it appears in Carpenter and Moser (1983). The headings 'Join' and 'Separate' have been placed above, rather than below, the change heading, therefore implying that they apply to the combine and compare categories as well.
The error of mapping a common 'start-change-result' generalised structure onto the static situation of compare problem types is possibly because of another ambiguously formatted table, this time in Carpenter et al. (1988:388) (see Figure 11). In this table it is not clear whether the headings 'Result unknown', 'Change unknown' and 'Start unknown' refer to only the 'Join' and 'Separate' categories or whether they also refer to combine and compare problem types - although in the text Carpenter et al. (1988) clarify that the headings only refer to the first two categories.
Research methods and design
The comprehensive typology described in the previous section was used to do an analysis of the prevalence and distribution of additive relation word problems in the Grade 1-3 DBE Mathematics workbooks, against a specific typology of word problems.
Selection of texts
The 2017 versions of the DBE foundation phase Mathematics workbooks were selected. The workbooks were selected because in the two schools forming part of the bigger research project, the workbooks were the primary (and in some cases the sole) teaching text used by the foundation phase teachers in 2017.
Procedure
Electronic version of the 12 (four terms per grade across three grades) DBE workbooks were used to identify all additive relation word problems. Firstly, each page was examined for word problems and a copy of the relevant pages was extracted from the electronic document. As in Stigler et al.'s study (1986:160), a problem had to present two premises and a question in order to be included. Word problems that required two steps were excluded (e.g. I bought 15 sweets. I ate 2. I gave my friend 4. How many sweets do I have left?). Almost all of the two-step problems had money (4 out of 8) or weight as a context (3 out of 8). Only one had sweets as a context. Word problems that did not require a numerical answer were also excluded (e.g. I have a R5 and a R1 coin. My friend has three R5 coins. Who has the most money?).
Some problems used pictures of objects to provide some information about the problem, although the question was still stated in words (see Figure 12).

These were taken as word problems. This differs from the decision made by Stigler et al. (1986), who required each premise and each question to be presented in a verbal form. There were only two pages in which this occurred - one in Grade 1 (two questions) and one in Grade 2 (four questions). The one worked example (in the Grade 3 workbooks) was included as one of the word problems.
Each word problem was captured on an Excel sheet and classified according to the three levels of the comprehensive typology. The initial classification was done by the author. The list of word problems together with the typology was then sent to a colleague who independently classified the 61 problems. Any cases where there were differences were discussed until an agreement was reached.
Results
The frequency of each of the 22 problem types in the comprehensive typology, by grade, is shown in Figure 13. The first interesting thing to note is the very small total number of word problems (61) that appear in the workbooks across the three grades.
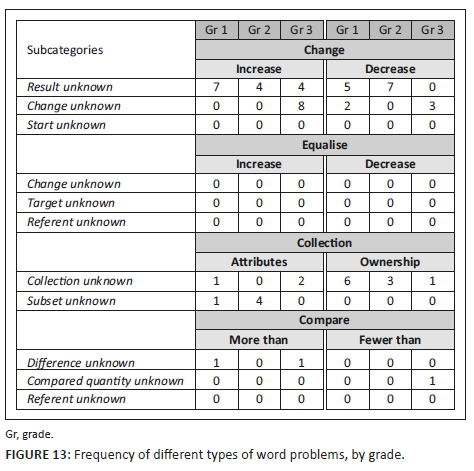
Looking at the distribution of word problems across the four main problem types reveals a greater focus on change-type problems, no equalise-type problems and very few compare-type problems. In fact, only three compare-type word problems appear across all three grades:
· Thandi has 19 bananas. Silo has 10 bananas. How many more bananas does Thandi have than Silo?
· Sipho counts out 87 bottle tops. Andile counts out 38. How many more bottle tops does Sipho count than Andile?
· The Grade 2s have a collection of 360 marbles. The Grade 3s have 216 fewer marbles than the Grade 2s. How many marbles do the Grade 3s have?
It should be noted that there were three additional compare-type problems that were not included in the analysis because they did not require a numerical answer. However, Roberts (2016b) argues that these types of problems are an important step in supporting learners to solve compare type problems. The problems provide two amounts (e.g. Mandla has 5 pencil crayons. Anne has 8 pencil crayons) but instead of asking 'How many fewer pencil crayons does Mandla have than Anne?', learners are asked 'Who has fewer pencil crayons?'. This type of question can only be asked for compare-type problems and therefore there are no similar occurrences for the other problem types.
In terms of the distribution across the grades, the total number of word problems varies across the grades from 23 in Grade 1, to 18 in Grade 2 to 20 in Grade 3, as seen in Figure 14. The number of word problems in each category also varies across the grades, with Grades 1 and 3 having more change and compare-type problems than Grade 2 and the number of collection-type problems decreasing with each grade (see Figure 14).
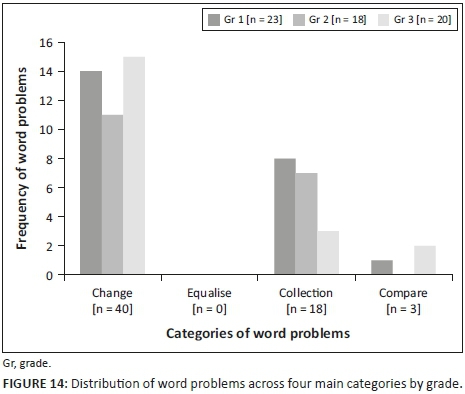
In terms of the distribution across the subcategories, there are a number of interesting things to note. For the change-type problems, there are more increase than decrease-type problems. Result unknown problems are more prevalent than change unknown problems and there are no start unknown problems. Similarly, there are no compare-type problems where the set to be acted on (i.e. the referent) is unknown.
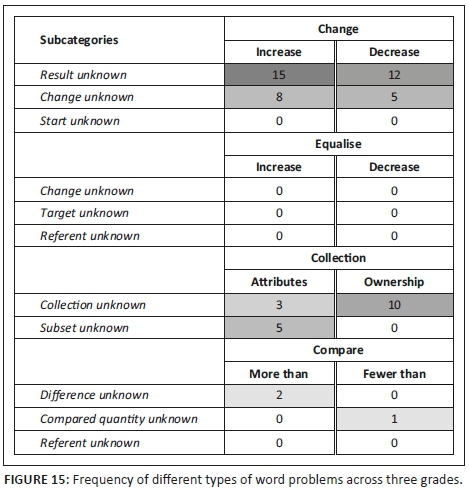
For collection-type problems, both subcategories (different attributes and different ownership) appear in the workbooks. However, all the 'different ownership' problems are in the 'subset unknown' category while the 'different attributes' problems are almost equally spread between the 'collection unknown' and 'subset unknown' subcategories (see Figure 15).
Discussion
In this section each of the four main results are discussed and related recommendations are made. The strengths and limitations of the research are also considered.
Firstly, the analysis of the foundation phase workbooks showed a very small number of additive relation word problems across 3 years of schooling in comparison to textbooks used in other countries. For example, the US Grade 1-3 textbooks analysed by Stigler et al. (1986) have a total of between 347 and 408 word problems while the Soviet textbooks have a total of 275 word problems. Turkish Grade 1-3 textbooks have between 139 (Tarim 2017) and approximately 190 (Olkun & Toluk 2006) word problems, while one set of Brunein textbooks was shown to have 389 word problems (Dhindsa et al. 2014). In comparison, the DBE workbooks only included a total of 61 word problems.
This considerably smaller number of word problems is not problematic if the workbooks are being used as they were designed to be used - namely as supplementary resource for learners to practise what they have been taught in class. However, when they are being used as the sole teaching resource and learners not being exposed to any other word problems, the very small number of problems is a matter for concern. Should the workbooks be revised, an increase in the number of word problems across the three grades is recommended.
Secondly, the distribution of word problems across the four main problem types reveals a similar distribution to other studies - namely a greater focus on change-type problems, no equalise-type problems and very few compare-type problems (Despina & Harikleia 2014; Dhindsa et al. 2014; Olkun & Toluk 2006; Singh 2006; Stigler et al. 1986; Tarim 2017). The complete lack of equalise problems is particularly striking. The only study to classify equalise-type problems was by Stigler et al. (1986), who included only one subcategory of equalise problems (equalise increase, change unknown). Only two of the four textbooks that were analysed in their study had this type of equalise problem. All other studies used Van de Walle et al.'s (2015) typology, which does not include the equalise problem-type.
As argued previously, equalise problems can be used to support learners to move from change-type problems (which they generally find easier to solve), through equalise problems, to the more difficult compare-type problems. The complete absence of equalise problems in the DBE workbooks and in most other studies points to the likelihood that even in classes where the workbooks are not the primary teaching text, learners are not being presented with equalise problems.
The under-representation of collection- and compare-type problems (18 and 3, respectively) is a reason for concern as these two-word problem types provide learners with an opportunity to engage with useful mathematical concepts. Collection-type problems highlight that a set can be separated into subsets. Compare-type problems introduce learners to an alternative conceptualisation of subtraction - as the difference between two quantities rather than as a 'take away sum'. In more advanced Mathematics the notion of the difference is much more prevalent than that of subtraction as 'taking away'.
Thirdly, in terms of the distribution across the grades, the numbers of problems in each grade (23 in Grade 1; 18 in Grade 2; and 20 in Grade 3) are too small and too similar to draw any reasonable conclusions. They do, however, emphasise the very small number of problems learners are presented with in the workbooks, particularly in Grade 2, which does not include any compare-type problems. A more preferable distribution would include more problems in each grade, some equalise problems (particularly in Grades 1 and 2) and a decrease in change-type problems, mirrored by an increase in compare-type problems (which are conceptually more challenging for learners) across the three grades.
Finally, the distribution of word problems across the subcategories shows an under-representation of the subcategories that learners find more difficult to solve. Nesher et al. (1982) reported on the results of a number of studies that determined the relative difficulty of different word problems. These studies showed that, for change-type problems, children find 'result unknown' problems easier to solve than 'change unknown' problems, and they find 'start unknown' problems the most difficult to solve. For collection-type problems, the 'collection unknown' subcategory is significantly easier than 'subset unknown' subcategory. For compare-type problems, 'referent unknown' problems are more difficult than 'compared quantity unknown' or 'difference unknown' problems.
This increase in difficulty is reflected in the comprehensive typology where the easiest subcategory appears first for each problem type and the most difficult one last. In each category the position of the unknown determines the relative difficulty of the subcategory, as can be seen in Figure 5, where the general number sentence for each of most difficult (last) subcategories has the unknown in the first position. Figure 15 shows a decrease in the number of problems, as the difficulty level of the problems increase (darker cells equate to better-represented subcategories). Therefore, the problem types that learners find more difficult to solve are the ones that are less prevalent in the workbooks. This is another reason for concern and a more preferable distribution would be one in which the number of problems in the more difficult subcategories increased with an increase in grade.
Conclusion
This article sets up a comprehensive typology for classifying additive relation word problems and then uses the typology as an analytical framework to explore the distribution of word problems in the DBE foundation phase Mathematics workbooks. The comprehensive typology reintroduces equalise-type problems, which have been excluded from more recent typologies and argues that these are a useful bridge from change-type problems to the more difficult compare-type problems.
The comprehensive typology also distinguishes between two subcategories that were previously grouped together, namely the part-part-whole category (from the work of Carpenter and Moser) and the combine category (from the work of Riley and Greeno). These two subcategories have been renamed 'different attributes' and 'different ownership'. A more recent typology by Van de Walle, which differs from the early typologies in terms of the collection problem type, was considered but not used as the formulation of the subcategories in the compare category does not take into consideration the importance of the referent. The article also provides possible reasons for the problematic typologies that are presented in the CAPS document. The layout and choice of contexts and names in the comprehensive typology is aligned with the typologies in the CAPS document.
The analysis of the DBE foundation phase Mathematics workbook reveals a very limited number of word problems (only 61 across three grades). In particular, there are no equalise problems and only three compare-type problems. This is a reason for concern in the light of the central role played by the DBE workbooks in many no-fee schools. The very limited number of compare-type word problems is particularly concerning because of the consistently poor performance on word problems as highlighted in the 2012, 2013 and 2014 ANA diagnostic reports.
In their analysis of the Grade 3 DBE workbooks as curriculum tools, Hoadley and Galant (2016) conclude that it is not viable to use the current workbooks as a teaching or transmission tool, primarily because of the limitations of conceptual signalling. The findings of this article support this conclusion by showing that the frequency and distribution of the additive relation word problems in the workbooks are not suitable for them to be used as a teaching tool.
Acknowledgements
This publication has been developed through the Teaching and Learning Development Capacity Improvement Programme which is being implemented through a partnership between the Department of Higher Education and Training and the European Union.
Competing interests
The author declares that she has no financial or personal relationships which may have inappropriately influenced her in writing this article.
Funding information
The study was funded by the South African National Research Foundation through the South African Research Chair: Learning Language, Mathematics and Science in Primary School, held by Prof Elizabeth Henning.
References
Carpenter, T.P., Fennema, E., Peterson, P.L. & Carey, D.A., 1988, 'Teachers' pedagogical content knowledge of students' problem solving in elementary', Journal for research in Mathematics Education 19(5), 385-401, viewed 26 February 2018, from http://www.jstor.org/stable/749173 [ Links ]
Carpenter, T.P., Hiebert, J. & Moser, J.M., 1981, 'Problem structure and first-grade children's initial solution processes for simple addition and subtraction problems', Journal for Research in Mathematics Education 12(1), 27-39. https://doi.org/10.2307/748656 [ Links ]
Carpenter, T.P. & Moser, J.M., 1983, 'The acquisition of addition and subtraction concepts', in R. Lesh & M. Landau (eds.), Acquisition of mathematics concepts and processes, pp. 7-44, Academic, New York.
Clements, D.H. & Sarama, J., 2009, Learning and teaching early math: The learning trajectories approach, Routledge, New York.
De Corte, E. & Verschaffe, L., 1987, 'The effect of semantic structure on first graders' strategies for solving addition and subtraction word problems', Journal for Research in Mathematics Education 18(5), 363-381. https://doi.org/10.2307/749085 [ Links ]
Davis, Z., 2012, 'Homomorphisms, counting and the constitution of addition in a Grade 1 lesson', in S. Nieuwoudt, D. Laubscher & H. Dreyer (eds.), Proceedings of the 18th National Congress of the association for mathematical education of South Africa (AMESA), University of the North-West, Potchefstroom, June 25-28, 2012, pp. 100-107.
Department of Basic Education, 2011, Curriculum and assessment policy standards (CAPS) grades 1-3: Mathematics, Curriculum document, DBE, Pretoria.
Department of Basic Education, 2012, Diagnostic report: Annual national assessment 2012, DBE, Pretoria.
Department of Basic Education, 2014, Annual national assessment: 2013 Diagnostic report and 2014 framework for improvement, DBE, Pretoria.
Department of Basic Education, 2015, Annual national assessment 2014 diagnostic report foundation phase: Mathematics and home language, DBE, Pretoria.
Department of Basic Education, 2018, Workbooks, viewed 26 February 2018, from https://www.education.gov.za/Curriculum/Workbooks/tabid/574/Default.aspx
Despina, D. & Harikleia, L., 2014, 'Addition and subtraction word problems in Greek grade A and grade B mathematics textbooks: Distribution and children's understanding', International Journal for Mathematics., viewed 3 March 2018, from http://www.cimt.org.uk/journal/desli.pdf
Dhindsa, H.S., Veloo, P. & Singh, P., 2014, 'The distribution of addition and subtraction word problems in Bruneian elementary mathematics texts', in Proceedings of the 1st international seminar on innovation in mathematics and, mathematics education, pp. 193-208, Yogyakarta State University, Yogyakarta, 26th-30th November 2014.
Galant, J., 2013, 'Selecting and sequencing mathematics tasks: Seeking mathematical knowledge for teaching', Perspectives in Education 31(3), 34-48. [ Links ]
Halliday & Matthiessen, 2013, Halliday's introduction to functional grammar, Routledge, New York.
Hoadley, U. & Galant, J., 2016, An analysis of the grade 3 department of basic education workbooks as curriculum tools, South African Journal of Childhood Education6(1), 1-13. [ Links ]
Mathews, C., Mdluli, M. & Ramsingh, V., 2014, 'The use of workbooks in South African grade 3 mathematics classrooms', South African Journal of Childhood Education4(1), 80-94, viewed 14 March 2018, from http://www.scielo.org.za/scielo.php?script=sci_arttext&pid=S2223-76822014000100006&lang=pt [ Links ]
NEEDU, 2016, Presentation to the portfolio committee on basic education (national assembly), viewed 15 April 2018, from https://pmg.org.za/committee-meeting/23495/
Nesher, P., Greeno, J.G. & Riley, M.S., 1982, 'The development of semantic categories for addition and subtraction', Educational Studies in Mathematics 13(4), 373-394. https://doi.org/10.1007/BF00366618 [ Links ]
Olkun, S. & Toluk, Z., 2006, 'Textbooks, word problems, and student success on addition and subtraction', International Journal for Mathematics Teaching and Learning162, 1-7. [ Links ]
Parmjit, S., Sahari, A. & Moideen, N., 2006, 'An analysis of the distribution of word problems in primary school mathematics textbooks used in Malaysian school', Journal of Science and Mathematics Education in S.E. Asia 29(1), 41-61. [ Links ]
Riley, M., Greeno, J. & Heller, J., 1984, 'Development of children's problem-solving ability in arithmetic', Development of mathematical thinking, Academic Press Inc, Orlando, FL.
Roberts, N., 2016a, 'Additive relations word problems in the South African curriculum and assessment policy Standard at foundation phase', African Journal of Research in Mathematics, Science and Technology Education 20(2), 106-118, viewed 6 April 2018, from http://www.tandfonline.com/doi/full/10.1080/18117295.2016.1189212 [ Links ]
Roberts, N., 2016b, 'Telling and illustrating additive relations stories: A classroom-based design experiment on young children's use of narrative in mathematics', Doctoral dissertation, University of Witwatersrand South Africa. https://doi.org/10.13140/RG.2.1.1092.6964 [ Links ]
Singh, P., 2006, 'An analysis of word problems in school mathematics texts: Operation of addition and subtraction', Journal of Science and Mathematics Education in S.E. Asia 29(1), 41-61. [ Links ]
Stigler, J.W., Fuson, K.C., Ham, M. & Sook Kim, M., 1986, 'An analysis of addition and subtraction word problems in American and soviet elementary mathematics textbooks', Cognition and Instruction 3(3), 153-171. [ Links ]
Tarim, K., 2017, 'Problem solving levels of elementary school students on mathematical word problems and the distribution of these problems in textbooks', Cukurova University Faculty of Education Journal 46(2), 639-648, viewed 23 March 2018, from http://dergipark.gov.tr/doi/10.14812/cuefd.306025 [ Links ]
Taylor, N., 2013, NEEDU national report 2012: The state of literacy teaching and learning in the Foundation Phase Department of Basic Education, Pretoria
Van de Walle, J., Karp, K. & Bay-Williams, J., 2015, Elementary and middle school mathematics - teaching developmentally, 9th edn., Pearson, New York.
 Correspondence:
Correspondence:
Ingrid Mostert
ingridmostert@gmail.com
Received: 16 Apr. 2018
Accepted: 16 July 2018
Published: 27 Mar. 2019














