Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.9 n.1 Johannesburg 2019
http://dx.doi.org/10.4102/sajce.v9i1.622
ORIGINAL RESEARCH
Multiplicative reasoning: An intervention's impact on Foundation Phase learners' understanding
Mike AskewI; Hamsa VenkatI, II; Corin MathewsI; Valerie RamsinghI; Thulelah TakaneI; Nicky RobertsIII
ISchool of Education, University of the Witwatersrand, Johannesburg, South Africa
IISchool of Education and Communication, Jönköping University, Jönköping, Sweden
IIICentre for Education Practice Research, University of Johannesburg, Johannesburg, South Africa
ABSTRACT
BACKGROUND: Given the context of low attainment in primary mathematics in South Africa, improving learners' understanding of multiplicative reasoning is important as it underpins much of later mathematics.
AIM: Within a broader research programme aiming to improve Foundation Phase (Grades 1-3, 7-9-year-olds) learners' mathematical performance, the aim of the particular research reported on here was to improve learners' understanding of and attainment in multiplicative reasoning when solving context-based problems.
SETTING: The research was conducted in a suburban school serving a predominantly historically disadvantaged learner population, and involved teachers and learners from three classes in each of Grades 1-3.
METHODS: A 4-week intervention piloted the use of context-based problems and array images to encourage learners to model (through pictures and diagrams) the problem situations, with the models produced used both to support problem solving and to support understanding of the multiplicative structures of the contexts.
RESULTS: Cleaning the data to include those learners participating at all three data points - pre-, post- and delayed post-test - provided findings based on 233 matched learners. These findings show that, on average, Grade 1 learners had a mean score average increase of 22 percentage points between the pre-test and the delayed post-test, with Grades 2 and 3 having mean increases of 10 and 9 percentage points, respectively.
CONCLUSION: The findings of this study demonstrate that young learners can be helped to better understand and improve their attainment in multiplicative reasoning, and suggest the usefulness of trialling the intervention model more broadly across schools.
Keywords: Foundation Phase; multiplicative reasoning; assessment; raising standards.
Introduction
Learner attainment in primary mathematics in South Africa continues to be low for the majority of children in the state education system, and is described by Fleisch (2013) as the ongoing 'quality challenge' in the context of striking improvements in the extent of physical access to primary schooling. Within this broad challenge, a more specific problem relates to progression in the strategies that children use for arithmetic tasks, with evidence of learners persistently relying on concrete counting methods well into the upper primary grades (Schollar 2008). There is also evidence of a lack of sense-making when solving simple problems, with Hoadley's (2007) research indicating that learners offered random answers set within what she describes as 'guessing exchanges' in which 'the learners offered any number as a response until such time as the correct answer was offered and affirmed by the teacher' (p. 701).
This context of poor performance leads to ongoing interest in interventions that seek to improve learners' understandings of, and outcomes in, primary mathematics. The programme of research under the umbrella of the Wits Mathematics Connect - Primary (WMC-P) project has several research and development initiatives aimed at addressing raising attainment. Prior to the research reported on here, the focus in intervention initiatives within the broader project was primarily on additive reasoning (AR), with only one multiplicative reasoning (MR) intervention trialled in one Grade 6 class (Dlamini, Ventkat & Askew 2014). In this article, we report on a pilot study where the attention turned to teaching and learning MR, that is, to the kinds of reasoning required in situations underpinned by a multiplicative (i.e. a multiplication- or a division-based) structure. Later, in this article, before reporting the findings relating to learning gains seen in the pilot study, we describe the kinds of situations that have been described in the literature as constituting the 'conceptual field' of MR. In the literature on learner responses to MR tasks, of particular note and pertinence here is the widely reported issue of learners reverting to the incorrect use of addition or subtraction operations in situations that require a multiplicative scaling up or scaling down (Hart 1981).
This pilot project's overall aim was to develop, adapt and trial teaching materials through a focused intervention to support a better-connected pedagogy for teaching MR. Thus, specific objectives of the study were to:
-
examine the impact on learner performance of a small-scale, pilot, school-based intervention
-
further understand the teaching and learning of MR.
This article reports on the first of these objectives, focusing in particular on the evidence of learner gains based on results in pre-, post- and delayed post intervention tests.
Theoretical background
Rationale for the focus on multiplicative reasoning
Internationally, it is widely acknowledged that MR is a critical area within primary mathematics and that strengthening attainment in this aspect of mathematics would create a more secure foundation for secondary and tertiary mathematics. Multiplicative reasoning underpins several key aspects of work in number, including rational number, ratio and proportion, and percentages. These are topics that Lamon (2005) points out are not only important for later success, but also are difficult to teach, as they are mathematically challenging and require time for the development of learners' understanding. Further to this, longitudinal research in the United Kingdom shows that raising levels of understanding of MR in secondary school appears to be an intractable problem (Brown, Kuchemann & Hodgen 2010), a result that the literature suggests is likely to hold elsewhere. Thus, a sound grounding in MR in the early years of primary schooling is essential, and research into how to achieve this has implications not only for South Africa but also more broadly.
Multiplicative reasoning situations: Overviewing the literature
Our analysis draws primarily on Vergnaud's (1994) distinction between addition and multiplication as conceptual fields. In Vergnaud's analysis, a key feature of AR is that it involves the transformation of only one variable that can happen in three ways: an initial quantity or variable is changed either through combining or separating off another, like quantity; part-part-whole considerations can be made of a quantity; and two quantities of the same variable can be compared. Although couched in different terms, this analysis is similar to the distinctions set out in the cognitively guided instruction framework of 'root' problems of addition (Carpenter et al. 1999). From this analysis, Vergnaud argues that AR problems are essentially ternary problems in that they involve three numbers, and, importantly, each number represents one variable (e.g. in the problem 'Constance bought 3 apples and then 4 more. How many apples is that in total?', the three numbers involved are three, four and the whole, seven, and each represents the single variable 'number of apples').
Vergnaud also classifies MR problems into three types: simple proportions, Cartesian product of two measures and multiple proportions. Simple proportion problems represent the first category of problems relating to multiplicative situations that are introduced in schools, and were thus suitable for an intervention focused on the Foundation Phase grades (Grades 1-3, 7-9-year-olds). Simple proportion problems involve two variables in a fixed ratio, a typical type of such problem being:
Nomonde bought 3 bags of apples. Each bag contains 4 apples. How many apples did Nomonde buy?
This problem represents a basic multiplicative situation, the variables being bags and apples, here in the fixed ratio of 1:4. Such a context can also be set in two other problem forms, resulting in:
Nomonde bought 12 apples in 3 equal sized bags. How many apples were in each bag?
Nomonde bought 12 apples in bags which contained 4 apples each. How many bags of apples did she buy?
These latter two problems can both be represented by division, with the former depicting a sharing (partitive) situation and solved initially by young children with concrete one-by-one distributing actions, which over time can be compressed through moves from unit counting out to composite sharing actions, and, eventually, to replications of the number of shares as a composite unit. The latter problem depicts a grouping (quotative) situation in which initial concrete actions involve the formation of a group and then replicating the group as a composite unit.
Although simple proportion problems can be solved by repeated addition or subtraction, Vergnaud points out that multiplicative structures 'have their own intrinsic organization which is not reducible to additive aspects' (Vergnaud 1983:128). Restricting understandings of multiplicative situations to repeated addition or subtraction masks the fact that even such seemingly simple problems actually involve four numbers with the 'hidden' number being 1, hidden through being implicit in phrases like 'each bag'. The subtle rate invoked in such problems means that MR problems are primarily distinguished from AR problems in being quaternary - they involve four numbers, not three. The quaternary nature of multiplication becomes clear when setting out, for example, the first problem above in a simple T-table (see Figure 1) to make clear that, unlike additive situations, there are two variables - the number of bags and the number of apples - with a constant ratio between these.

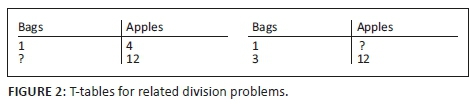
Shifting the position of the unknown in Figure 1 leads to models for the two related division problems above, thus not only linking multiplication and division but also providing the opportunity to make explicit the ratio nature of the problems (see Figure 2).
Kieren (1988) emphasises that the basic action in MR situations is one of replication of the ratio-based composite unit or its inverse. The correspondence relation in MR situations is based on this ratio or rate. For example, in the multiplicative relationship of one bag containing four apples, adding two more bags to the set of bags, results in needing to add eight more apples to the set of apples to keep constant the ratio relationship between the bags and apples. Learners retaining an additive view of correspondence frequently increase the number of apples by two in the latter situation, providing 'six apples' as the quantity matched with three bags. Park and Nunes (2001) report that a small-scale experimental study indicated greater progress for the groups that were explicitly taught about this functional correspondence relationship, in the context of multiplicative situations, than for the groups that were taught the more traditional procedural connection between repeated addition and multiplication (see also Askew 2018).
We posit that learners can be supported into an informal sense of functional correspondence by the incorporation into lessons of 'realistic situations' - with 'realistic' used here in the sense developed by the researchers in the tradition of 'Realistic Mathematics Education' (see, e.g., Beishuizen, Gravemeijer & Van Lieshout 1997) of 'realisable' situations that (1) learners make sense of and (2) having made sense of, can then use informal means to solve. Nunes and Bryant's (2009) review of evidence further suggests the need to include a variety of situational contexts as a base from which to mathematise. The learners' informal means of solution are used as the basis for developing diagrammatic 'models of' multiplicative situations that can then function as 'models for' new situations, as also noted within the MR literature (Streefland 1985).
Two models have been identified as particularly useful in work with young children on simple proportions. Several researchers have argued for the power of array images to help learners develop MR and to distinguish this from AR (Barmby et al. 2009). The two-dimensional nature of the array image reflects, spatially, the two-variable structure of multiplicative situations, in contrast to the one-dimensional number line that reflects the one-variable structure of additive situations. Arrays also embody the commutative nature of multiplication and encourage a view of multiplicative situations as involving composite groups - for example, describing an array as three groups of four or four groups of three encourages and reinforces treating a 'group of three' or a 'group of four' as units in their own right (Fosnot & Dolk 2001).
Symbolic representation of the array image leads to the second model, the ratio table (also known as the T-table), as shown in Figure 1, which both Streefland (1985) and Vergnaud (1994) have argued is particularly useful for emphasising multiplicative relationships. For simple proportions, the T-table's spatial arrangement helps to make explicit the scalar relationship within quantities (reading down the columns of the table) and the functional relationship between quantities (reading across the rows) (Vergnaud 1994:6). The double number line acts as a precursor to the ratio table, with key differences being that the former is presented horizontally and the latter vertically, and with all possible ratio pairs being set out on the double number line (see Küchemann, Hodgen & Brown 2011), whereas the T-table encourages some compression of pairs (e.g. through doubling as you go down with the column). For instance, in the case of the apples problem above, jumps for bags would be shown above the line, jumps for groups of apples below the line, with the intermediate jumps also shown (see Figure 3).

Moving to the vertically presented T-table brings affordances that encourage the learners to look for relationships that circumvent filling in all the possible steps, for example, extending the problem to six bags of apples would involve, on the double number line, drawing the extra jumps for four, five and six bags or scaling up the jump size, whereas learners might note in the T-table that doubling the number of apples in three bags gives the solution to six bags. In each case, however, the key conceptual move in MR is realising the ratio, functional, relationship that exists when reading the figures above and below on the double number line or across the rows in the ratio table (as opposed to coordinating two scalar relationships by working separately along two number lines or down the two columns of the ratio table). See Askew (2018) for a fuller discussion of this move to the functional.
South Africa's Foundation Phase Curriculum and multiplicative reasoning
The overview of literature provides a vantage point for considering the ways in which MR ideas are inscribed into the South African Foundation Phase Curriculum and Assessment Policy Standard (CAPS) document. All three categories of simple proportion problems as outlined above - multiplication, together with division as both sharing and grouping - are exemplified within the CAPS Foundation Phase document across all three grades (Department of Basic Education [DBE] 2011:G1 pp. 45-46, G2 pp. 61-62, G3 pp. 79-80). Furthermore, the curriculum includes examples of division situations involving a remainder that sometimes needs to be rounded up, or down, based on making sense of the context. For example, Grade 1 learners are expected to solve problems like (Department of Basic Education [DBE] 2011):
Stella sells apples in bags of three apples each. She has 14 apples. How many bags of three apples each can she make up? …
Ben wants to take 15 eggs to his grandmother. How many egg boxes that can take six eggs each does he need to pack all the eggs? …
Share 14 sweets among three friends so that they all get the same number of sweets. (p. 45)
Similar problems are suggested for Grades 2 and 3 with the basic problem structure preserved but the number range increased. However, the curricular advice in the 'topics' outline on how to work with such problems tends singularly to emphasise repeated addition as the route into multiplication, across both word problems and context-free calculations, with the recurring appearance of the phrase: 'Repeated addition leading to multiplication'. Details elsewhere in the document's clarification guidelines do elaborate on a broader range of representations, including the array and ratio tables, but also emphasising the use of single number lines to represent repeated addition (e.g. DBE 2011:425) (a one-variable representation, as noted above) and with scant guidance on how to work with and across a range of representations. There are also statements such as learners should: 'practise and understand that multiplication can be done in any order (the commutative law or property)' (e.g. p. 394), but with little detail on how the commutative property could be introduced, such as using the array as a useful model for showing the commutativity property.
Division is largely dealt with as a separate strand to multiplication in the CAPS, and, in particular, strikingly absent is the notion that models such as double number lines, arrays or ratio tables might be used as inscriptions that connect both operations, in spite of the specification that learners should (DBE 2011):
… understand and appreciate the relationship between multiplication and division and that they are inverse operations. (p. 465)
Taken together, and considered in relation to the literature, the CAPS curriculum presents a disconnected list of problem situations, models and procedures, rather than the carefully connected and progressive sequence for building MR that Vergnaud (1994) suggests is possible. These disconnections are of concern, given that the Department of Basic Education diagnostic reports on South Africa's Annual National Assessments (ANAs) (DBE 2012, 2013, 2014) all highlight word problems in general and MR situations in particular as systemic concerns in the light of low learner performance on such items.
The intervention
Design principles
Curricular confusion, coupled with the low learner performance on word problems and on MR tasks more widely that we noted early, added motivation to our decision to develop, in one primary school, an intervention focused on MR across Foundation Phase grades (Grades 1-3). Our conjecture in designing the research and intervention was that if more explicit attention were paid to the ratio aspect of the MR problems met in primary school, then learners would be better prepared for later understandings of proportional reasoning and linear functions (Kaput & West 1994). With this in mind, a pilot project was carried out comprising a 4-week intervention of one lesson per week with a focus on making the simple ratio nature of MR explicit, both to teachers and to learners, through using problems set in contexts such as cooking pots and legs, people and feet, boxes and eggs, and working in the first instance with array models, coupled later with T-tables. The impact of the intervention was investigated through learners being assessed pre- and post-intervention, and then in a delayed post-assessment.
The ways in which the CAPS advice both overlapped and also departed from the literature on teaching MR informed our choice of theoretical framings. In particular, we drew on the focus on MR in terms of Vergnaud's (2009) conceptual fields, which integrate findings from psychology about learning of MR together with disciplinary considerations of the structure and relationships among MR situations, rather than treating MR only as developing the knowledge of multiplication and division facts and procedures. Treating MR as a conceptual field was also useful to us not only because it provided a coherent model of situations that can form the basis of understanding MR but also because it explicitly contrasts MR with AR.
Study design
The broader WMC-P project had worked with classroom interventions in a sequential grade-based model in the Foundation Phase, which is tracking the learner cohort across the Foundation Phase years. One of the partner schools invited us to do some work with them at the phase level (not just year level) on topics that both teachers and learners were having difficulty working with. This quintile 5 school (the category of schools catering for the least poor 20% of pupils1) was a functional suburban Johannesburg school serving a predominantly historically disadvantaged learner population. There were three classes in each of Grades 1-3 and our initial plan was to involve only two classes in each grade, with testing undertaken with all learners in all nine Foundation Phase classes: three classes would thus have provided control data. The school's senior management was, however, keen to offer all the teachers the opportunity to participate - an offer that all nine accepted, so no control data would be collected. While limiting our research, we went with the schools' wishes as this seemed most equitable.
Multiplication, division and word problems, mentioned as separate topics, featured prominently in these Foundation Phase teachers' comments about areas of difficulty. This led us to think about an intervention lesson sequence model that we had developed at a smaller scale in an earlier project (Ekdahl, Venkat & Runesson 2016). The intervention was based on an adapted lesson-study model. A grade-specific pre-test, co-developed by and agreed between researchers and teachers as suitable for the grade, was initially administered to all learners. The test included some AR items interspersed with MR items to prevent learners being 'cued' into the selection of multiplication or division operations. Items requiring the rounding up or rounding down of remainders were included, given that the curriculum included these in its specification. The learner pre-testing was followed by an initial school-based workshop with the nine teachers. Part of this workshop involved the teachers in marking some of the pre-test papers. Discussion of the learners' responses on these tests alerted the teachers to the predominance of errors, particularly learners treating the problems erroneously as simple additions, and thus set the scene for the introduction of the array image and the idea of using problems to elicit and work with models.
The intervention model
Over the 4 weeks following the pre-testing of learners, four lessons, co-operatively planned between the teachers and the research team, were taught, one a week. The intervention lessons were organised around three phases: rapid calculation of multiplication and division facts by working with images of arrays, learners solving context-based problems in pairs and solutions discussed as a whole class, individual practice and consolidation of context-based problems. The contexts chosen for the problems in the lessons differed from those in the test.
After each lesson, the research team and the teachers met in the afternoon to explore and reflect on the responses of the learners and plan the next lesson in light of these (part of these meetings was spent working in grade-level teams, and part spent looking at cross-grade issues). At these meetings, we explored whether or not any of the teachers were teaching additional lessons informed by the intervention: our sense was that they were only teaching the four lessons that we proposed. The post-test was administered the week after the fourth lesson. All intervention lessons were videotaped, as were the meetings with the teachers, and each teacher was interviewed pre- and post-intervention. The data were analysed to explore the impact of the intervention on pedagogy and teacher beliefs and understanding, and to put into context the assessment data reported on here.
The intervention took place towards the end of the school year and the delayed post-test was administered soon after the start of the next school year, before the teaching in the subsequent grade had addressed multiplication and division. Table 1 provides an overview of the design.
Lesson design
Each lesson was designed around introducing learners to the array as an image for multiplication and a focus on using simple ratio problems to elicit models. Lessons started with a 10-min introduction where posters of arrays of dots were shown to the learners who were asked how many dots there were. Discussion of different ways of finding the total that went beyond simply counting individual dots introduced the learners to the language of rows, columns and groups, which was subsequently linked to the symbolic notation for multiplication.
The main part of each of the four lessons was based on adapting the pedagogic approach developed by Askew (2005). Building on the work of Carpenter and colleagues (1999) and Fosnot and Dolk (2001), the pedagogy Askew advocates was closely linked to the principles and approaches outlined in the literature on working with 'realistic' word problems from which to develop the more formal, abstract mathematics.
The main part of the lesson started with the teacher offering learners a 'realistic' word problem to work on. This problem was intended to invite learners to share informal models and solution strategies. Typically, these informal models and strategies involved the use of concrete materials, or learner produced, inscriptions that may, in the initial stages, represent the problem situation iconically. The problems were, in other words, chosen to be 'model-eliciting' problems, in the words of Lesh and colleagues (2013).
After the teacher orally introduced the problem, learners were given time to work on producing a model for the problem, with particular examples of these learner productions selected to share with the class (selected in the expectation of advancing discussion of the mathematics). A second problem was worked on in a similar way, encouraging learners to think about the models just shared, and after the models for the second problem had been looked at, talk with the class focused on the similarities across the two problems. Time permitting, learners practiced individually on further similar problems.
Test design
The pre- and repeated post- and delayed post-tests included all three types of MR simple proportion problems: multiplication, grouping and sharing. Each of the assessment items is briefly described below, with a keyword or phrase arising from the context attached as a reference for later discussion. An explicit array problem was last on the test in order not to cue learners into using arrays in the other test items.
Across all Grades 1-3 tests, the context and the basic format of each problem situation were kept constant but the numbers involved were changed to be in line with the curriculum grade-level expectations (although on a small number of items, the numbers were kept the same across adjacent years, to provide some anchor items to make cross-grade comparisons). Given the small number of MR items, the clusters of three multiplication problems and five division problems were checked for internal consistency by calculating average inter-item correlations on the pre-test performance. An average inter-item correlation between 0.15 and 0.50 suggests that items grouped together appear to be testing the same construct (less than 0.15 and the items are not well correlated and look not to be effectively measuring the same construct, if at all, and an average over 0.50 suggests that some items may be redundant). Across all three grades, the average inter-item correlations on each cluster fell within the ideal range of 0.15-0.5, suggesting that these items were assessing the similar constructs (Y1: 0.25/0.27 [multiplication cluster or division cluster], Y2: 0.26/0.21, Y3: MR 0.17/0.21). As noted above, two AR problems were also included, so that any expectation that the assessment was only about multiplication and division was not set up.
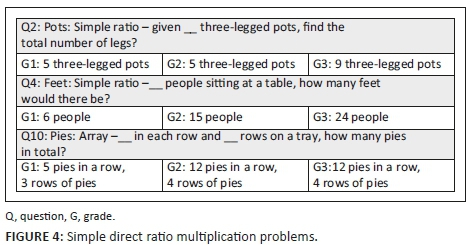
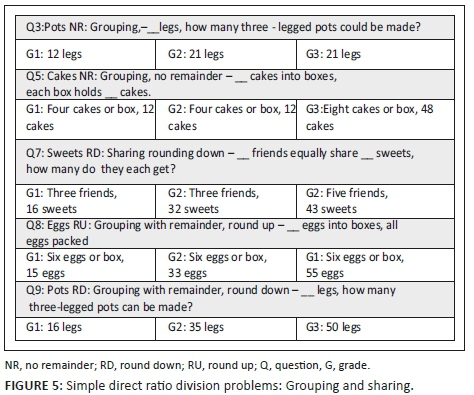
The MR problems on the test are listed in Figures 4 and 5, separated into the questions assessing direct simple ratio multiplication problems and those assessing the inverse division problems.
Given that the Grade 3 curriculum expects learners to deal with simple division problems with fraction answers (e.g. one apple shared between three people), we allowed for answers incorporating fractions in our marking, but only five G3 learners actually attempted to produce a fraction in the pre-test, two in the post-test and none in the delayed post-test (with one of these seven answers providing the correct number of whole sweets, but no answer providing the correct fractional part of 3/5).
The AR problems were:
Q1: Apples: Change increase - a number of apples were picked and then some more, how many altogether? (G1, 17 + 3; G2, 17 + 3; G3, 17 + 33)
Q6: Marbles: Change decrease - a given number fell out of a pocket, how many were there originally? (G1, 12 - 3; G2, 25 - 18; G3, 25 - 18)
Test administration and marking
The pre-, post- and delayed post-tests were administered to each class by one of the research team. Given that the majority of children at the school are learning through the medium of a second language, each question was read out, at least twice, and a brief dialogue engaged in to check that the learners understood the context and what was happening within it, but without leading them to which operation to use. Learners were given time to answer the question and encouraged to use whatever representations they thought could help them figure out an answer. Copying was discouraged by providing each learner with a sheet of plain paper to cover up their work and seating learners as far apart as possible, and the two adults in the room (researcher and class teacher) reminding learners to do their own work. Although we cannot be sure that copying was eliminated, we are confident that it was kept to a minimum.
Each learner's script was marked and results were entered into a spreadsheet as correct, incorrect (with the incorrect answer recorded) or omitted. As very few learners omitted questions (42 instances in 2330 responses across all three grades), in the following analysis, omitted answers are included with incorrect responses rather than analysed separately, on the assumption that if a learner omitted an answer, then they did not know what to do.
Scripts were kept for more detailed analysis and, together with learners' inscriptions from activities engaged in during the lessons, are being analysed qualitatively to probe further the quantitative findings that are here presented.
Ethical considerations
Ethical clearance was provide by the University of the Witwatersrand (number 2011ECE012C).
Findings
Item-level responses by grade
Figures 6-8 show the pre-, post- and delayed post-test results for each grade, combining the scores for individual classes. While there were totals of 126, 102 and 114 learners in each of G1, G2 and G3, respectively, pupil absences near the end of term reduced post-test numbers, bringing the matched sample with performance data across all three test administrations down to G1, n = 79 learners; G2, n = 79 learners; and G3, n = 75 learners. Figures 6-8 are for these matched learners. The mean score for the full cohort of Grade 1 learners on the pre-test was 25% compared to a mean score of 27% for the subgroup of matched learners. In Grade 2, the pre-test mean score for the entire cohort was 43% compared to 44% for the matched group, with the Grade 3 figures being 40% and 43%, respectively. Thus, the mean scores on the pre-test are marginally higher across all three grades for the matched cohort than for the entire cohort. Although this shows that the matched cohort is skewed slightly to under-represent the lower achieving learners, the differences are not so great as to be troublesome.
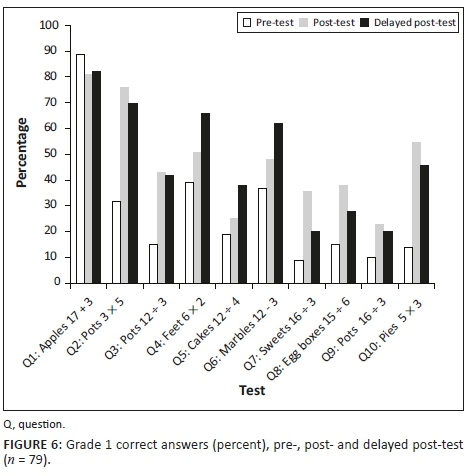
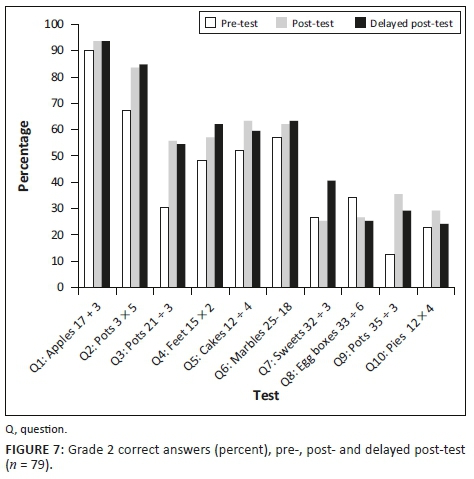
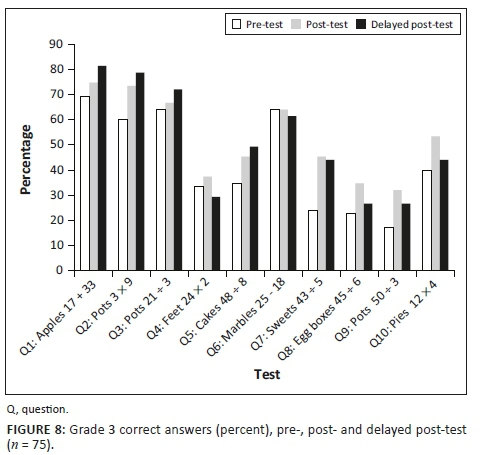
Question 1 and 6 are the two AR questions. At all three assessment points and for all three grades, the results on Q1 are similar (although, interesting, G1 did slightly better on this item on the pre-test than later tests), with similar scores also on Q6 all three times in G2 and G3 (and Grade 1 making a slight improvement, which might be expected given the attention to subtraction in this grade). On the other eight questions, all focused on MR, there are sustained gains on all but two instances across every grade. The similarity in the performance on the AR items compared to the differences attained on the MR items supports the hypothesis that the gains on the MR problems were a result of the intervention, rather than a consequence of test familiarity.
Five MR problems were single-step problems in that the context answer matched the numerical answer (Q2, 3, 4, 5, 10), for example, finding how many three-legged pots could be made from 21 legs. Performance on all these single-step items shows gains from the pre-test to post-test, gains that were largely sustained and, in some instances, even exceeded, in the delayed post-test results. Performance on Q4 looks somewhat anomalous, with G3 performing worse on this question than either G1 or G2. While the calculation in G3 was harder, inspection of the scripts revealed many learners halving rather than doubling 24, an error not prompted in the G2 question through the problem using 15 people.
The remaining three MR problems (Q7, 8, 9) required the numerical answer to be made sense of in the problem context, for example, rounding down to find the number of pots that could be made with 50 legs. The graphs show, as might be expected, that performance was lower on these items than on the single-step ones and post-test gains were not as well sustained in the delayed post-test. The results show, however, that delayed post-test performance remained higher than on the pre-test on all but one item across all three grades (the one anomaly being the G2 'eggs' item).
Pre-test and delayed post-test scores by grade
We turn now to examine results comparing grade and class mean scores on the pre- and delayed post-tests. The means (M) and standard deviations (SD) for the percentage of correct answers on the eight MR questions are presented in Table 2 (figures based on matched learners who took both the pre- and delayed post-tests: n is higher here than for the matched number of learners taking all three tests). The difference between the pre- and delayed post-test means (MD) shows that there were sustained gains for all grades and all classes.
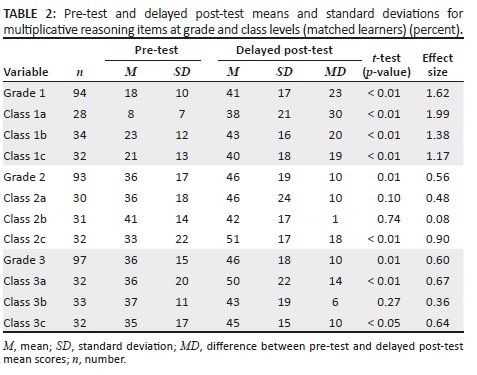
Grade 1 showed the highest sustained gains, with a rise from 18% on the pre-test, to 41% on the delayed post-test, a gain of 23 percentage points. Class 1a demonstrated the largest overall gain of 30 percentage points, but given that the pre-test mean score of the class was only 8%, there was more room for growth. This substantial gain, however, brought the class up from this low starting point to a delayed post-test score of 38%, not far behind the other two G1 class scores of 43% and 40%.
The mean difference gains for Grade 2 and Grade 3 were similar at 10 percentage points in each case. This overall figure does not reflect the range of scores at the class level, particularly in Grade 2. Classes 2a and 2c showed an improvement of 10 and 18 percentage points, respectively. Class 2b, in contrast, showed only a difference of 1 percentage point, from a pre-test mean of 41% to a delayed post-test mean of 42%. Although Class 2b's pre-test mean of 41% was higher than that of the other two classes (36% and 33%), it was not so much higher to make this low gain a result of a ceiling effect.
The Grade 3 class scores also show a range, albeit less dramatic, of performance at the class level, from similar pre-test mean scores of 36%, 37% and 35%. Class 3a showed the greatest growth of 14 percentage points, followed by Class 3c with 10 points and Class 3b moving 6 percentage points from 37% pre-test to 43% delayed post-test.
A two-tailed paired t-test was conducted comparing the pre- and delayed post-test results for grades and classes. At grade-level, the results are all statistically significant at the 1% level, or less. At the class level, the results for all three G1 classes are statistically significant at less than 1%, with the results being more mixed for Grades 2 and 3. In four of these six classes, the results were statistically significant at the 1% level or less, and for a fifth class, the result was statistically significant at the 5% level. In the case of Class 2b, the results were not statistically significant.
Effect sizes (Cohen's d) were calculated at the grade and class level. Grade 1 had the highest effect size of 1.62, with Class 1a having the high figure of 1.99. The effect sizes for Grades 2 and 3 were similar at 0.56 and 0.6, respectively, but these figures again mask a range of effect sizes at the class level. Class 2c, for example, achieved an effect size of 0.9 compared to 0.08 for Class 2b. In Grade 3, Class 3a had the highest effect size of 0.67 and Class 3b had the lowest at 0.36. Any effect size over 0.4 is worthy of note, as an effect size smaller than this is likely to be the result of changes that would come about over time anyway. On this measure, the intervention appears to have had good impact in all three G1 classes and a moderate impact in two out of three classes in each of Grades 2 and 3.
Discussion
The results show that there were sustained, statistically significant gains in mean levels of performance from the pre- to delayed post-test across all three grades and all classes within grades, and these gains, together with the effect sizes, indicate that this model of a short, focused and structured intervention has the potential for contributing to the raising of standards in an area of the mathematics curriculum (MR) that has been identified as a presenting of difficulties not only in South Africa but also internationally. The delayed post-test scores were based on a test administration that followed the long summer break at the beginning of the next year of schooling (late January), that is, the Grade 1 delayed post-test was taken at the beginning of Grade 2, and similarly, the Grade 2 test was taken at the beginning of Grade 3. Given wide evidence that learning 'falls back' over long holiday breaks (Cooper et al. 1996), it was particularly pleasing that gains were sustained over this period. In every grade and class, the delayed post-test scores at the beginning of the next year of schooling were higher than those shown in the same grades on the pre-test that was taken in the October of the previous school year. That is, for example, the Grade 2 mean score on entering Grade 3 was 46%, while the previous October score of the Grade 3 year was 36%. This gain across all the years suggests that more focused teaching of MR earlier in the school year could raise standards in ways that are sustained beyond the immediate teaching period. This is important in a South African context where the phenomena of 'extreme localisation' have been noted (Venkat & Naidoo 2012), in which even very recent learning is not being taken as established, and used to carry learning forward.
While the gains are important, it is also worth noting that only two out of the nine classes had an average score of correct answers of 50% or more on the delayed post-test - Class 2c and Class 3a - with the comparable scores in the other classes being in the range of 38% - 46%. Thus, there is still some way to go before the majority of learners demonstrate proficiency in MR at even the level of 50% correct. Our initial qualitative analyses suggest that the gains were mainly as a result of learners' better interpretation of the mathematical structure of the problems, many shifting from using addition to recognise the multiplicative structure. There is less evidence, however, of learners then using more sophisticated calculation strategies to find answers - G3 learners relied on iconic representations and counting just as much as G1 and G2 learners. Hence, it is likely that the lower gains observed in Grades 2 and 3 are a result of errors in working with larger numbers. This continued reliance on unit counting reflects the broader South African terrain of evidence that we noted earlier in the article and suggests that further research is needed into how to help learners develop more efficient calculating strategies once they have correctly identified the mathematical structure of a problem.
Hattie (2008) argues that 'effect sizes' are the best way of answering the question 'what has the greatest influence on student learning?' and that an effect size of 1.0 is typically associated with advancing learners' achievement by 1 year. Given an effect size of 1.62 in Grade 1, we might be tempted to suggest that the intervention was nothing short of miraculous, but that would be overstating the case given the relatively limited purview of the test involving only eight MR items. While pragmatic from the perspective of working with early primary years' learners, we note that the initial pre-test mean result in Grade 1 stood at 18%, with the delayed post-test mean score of 41%, indicating that there was still considerable room for improvement.
Hattie's own research has shown that 'instructional quality' and 'direct instruction' can have effect sizes of 1.00 and 0.82, respectively. Given the careful attention to the designing and delivery of the lesson with a well-focused set of small learning intentions together with instruction carefully designed to address MR in ways that distinguish it from AR, the effect sizes we obtained are sufficiently encouraging to explore some scaling up of the intervention. Our next step is therefore to broaden the scope of the intervention to a larger number of schools and teachers, building in some control schools, and to explore the nature and magnitude of effects when the research teams are less directly involved in the teaching of the intervention lessons.
Acknowledgements
Competing interests
The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.
Authors' contributions
M.A. was the lead author of the article, and the other authors were involved in the data collection and read, commented and added to drafts of the article.
Funding information
Funding for this research was provided by the First Rand Foundation-National Research Foundation.
Disclaimer
The views expressed in this article are those of the authors and do not reflect and official position of either the University of the Witwatersrand or University of Johannesburg.
References
Askew, M., 2005, Beam's big book of word problems year 1 and 2 (New edition), BEAM Education, London.
Askew, M., 2018, 'Multiplicative reasoning: Teaching primary pupils in ways that focus on functional relations', The Curriculum Journal 29(3), 406-423. https://doi.org/10.1080/09585176.2018.1433545 [ Links ]
Barmby, P., Harries, T., Higgins, S. & Suggate, J., 2009, 'The array representation and primary children's understanding and reasoning in multiplication', Educational Studies in Mathematics 70(3), 217-241. https://doi.org/10.2307/40284574 [ Links ]
Beishuizen, M, Gravemeijer, K. & van Lieshout, E.C.D.M. (eds.), 1997, The role of contexts and models in the development of mathematical strategies and procedures, Freudenthal Institute, Utrecht, Holland.
Brown, M., Kuchemann, D. & Hodgen, J., 2010, 'The struggle to achieve multiplicative reasoning 11-14', in M. Joubert & P. Andrews (eds.), Proceedings of the British Congress for Mathematics Education, University of Manchester, Manchester, April, pp. 49-56.
Carpenter, T.P., Fennema, E., Franke, M.L., Levi, L. & Empson, S.B., 1999, Children's mathematics: Cognitively guided instruction, Heinemann, Portsmouth, NH.
Cooper, H., Nye, B., Charlton, K., Lindsay, J. & Greathouse, S., 1996, 'The effects of summer vacation on achievement test scores: A narrative and meta-analytic review', Review of Educational Research 66, 227-268. https://doi.org/10.3102/00346543066003227 [ Links ]
Department of Basic Education (DBE), 2011, Curriculum and Assessment Policy Statement (CAPS). Foundation Phase Grades 1-3, Department of Basic Education, Pretoria.
Department of Basic Education (DBE), 2012, Diagnostic report: Annual national assessment, Department of Basic Education, Pretoria.
Department of Basic Education (DBE), 2013, The annual national assessment. 2013 Diagnostic report, Department of Basic Education, Pretoria.
Department of Basic Education (DBE), 2014, The annual national assessment of 2014: Diagnostic report, intermediate and senior phases mathematics, Department of Basic Education, Pretoria.
Dlamini, E., Venkat, H. & Askew, M., 2014, 'A modeling and models approach: Improving primary mathematics learner performance on multiplication', in D. Huillet (ed.), Proceedings of 23rd Annual Meeting of the Southern African Association for Research in Mathematics, Science and Technology Education, Pedagogical University & Eduardo Mondlane University, Pretoria, January, pp. 61-68.
Ekdahl, A.-L., Venkat, H. & Runesson, U., 2016, 'Coding teaching for simultaneity and connections: Examining teachers' part-whole additive relations instruction', Educational Studies in Mathematics 93(3), 293-313. https://doi.org/10.1007/s10649-016-9700-0 [ Links ]
Fleisch, B., 2013, 'The post 2015 quality challenge: Lesson from the South African experience of improving literacy and mathematics in a poorly performing system, (Education and Development in the Post-2015 Landscapes)', NORRAG News 49, October, pp. 71-72. viewed 03 November 2016, from http://www.norrag.org/fileadmin/Full%20Versions/NN49.pdf [ Links ]
Fosnot, C.T. & Dolk, M., 2001, Young mathematicians at work: Constructing multiplication and division, Heinemann, Portsmouth, NH.
Hart, K., 1981, Children's understanding of mathematics: 11-16, John Murray, London.
Hattie, J., 2008, Visible learning: A synthesis of over 800 meta-analyses relating to achievement, Routledge, London.
Hoadley, U., 2007, 'The reproduction of social class inequalities through mathematics pedagogies in South African primary schools', Journal of Curriculum Studies 39(6), 679-706. https://doi.org/10.1080/00220270701261169 [ Links ]
Kaput, J.J. & West, M.M., 1994, 'Missing-value proportional reasoning problems: Factors affecting informal reasoning patterns', in G. Harel & J. Confrey (eds.), The development of multiplicative reasoning in the learning of mathematics, pp. 237-292, State University of New York Press, Albany, NY.
Kieren, T.E., 1988, 'Personal knowledge of rational numbers: Its intuitive and formal development', in J. Hiebert & M. Behr (eds.), Number concepts and operations in the middle grades, pp. 162-181, National Council of Teachers of Mathematics, Reston, VA.
Küchemann, D., Hodgen, J. & Brown, M., 2011, 'Using the double number line to model multiplication', in M. Pytlak, T. Rowland & E. Swoboda (eds.), Proceedings of the Seventh Congress of the European Society for Research in Mathematics Education (CERME7), University of Rzeszów, Poland, pp. 326-335, on behalf of the European Society for Research in Mathematics, Rzeszów, Poland.
Lamon, S., 2005, Teaching fractions and ratios for understanding. Essential content knowledge and instructional strategies for teachers, 2nd edn., Routledge, New York.
Lesh, R., English, L., Sevis, S. & Riggs, C., 2013, 'Modeling as a means for making powerful ideas accessible to children at an early age', in S.J. Hegedus & J. Roschelle (eds.), The SimCalc vision and contributions, pp. 419-436, Springer Netherlands, Dordrecht.
Nunes, T. & Bryant, P., 2009, 'Paper 3: Understanding rational numbers and intensive quantities', in T. Nunes & P. Bryant (eds.), Key understandings in mathematics learning, Nuffield Foundation, London.
Park, J.H. & Nunes, T., 2001, 'The development of the concept of multiplication', Cognitive Development 16(3), 763-773. https://doi.org/10.1016/S0885-2014(01)00058-2 [ Links ]
Schollar, E., 2008, Final report: The primary mathematics research project 2004-2007 - Towards evidence-based educational development in South Africa, Eric Schollar & Associates, Johannesburg.
Streefland, L., 1985, 'Search for the roots of ratio: Some thoughts on the long term learning process (Towards a theory): Part II: The outline of the long term learning process', Educational Studies in Mathematics 16, 75-94. https://doi.org/10.1007/BF00354884 [ Links ]
Venkat, H. & Naidoo, D., 2012, 'Analyzing coherence for conceptual learning in a Grade 2 numeracy lesson', Education as Change 16(1), 21-33. https://doi.org/10.1080/16823206.2012.691686 [ Links ]
Vergnaud, G., 1983, 'Multiplicative structures', in R. Lesh & M. Landau (eds.), Acquisition of mathematics concepts and processes, pp. 128-175, Academic Press, London.
Vergnaud, G., 1994, 'Multiplicative conceptual field: What and why?', in G. Harel & J. Confrey (eds.), The development of multiplicative reasoning in the learning of mathematics, pp. 41-59, SUNY Press, Albany, NY.
Vergnaud, G., 2009, 'The theory of conceptual fields', Human Development 52(2), 83-94. https://doi.org/10.1159/000202727 [ Links ]
 Correspondence:
Correspondence:
Mike Askew
michael.askew@wits.ac.za
Received: 08 Feb. 2018
Accepted: 07 Nov. 2018
Published: 25 Mar. 2019
1 . South Africa adopts a pro-poor funding model for its schools where schools are classified by socio-economic status of the surrounding community. The schools in the most affluent areas are referred to as quintile 5, while schools in lower socio-economic status communities are classified as lower quintiles. Quintiles 1-3 receive the greatest public funding per learner and are 'no fee schools', while quintiles 4 and 5 schools may charge parents fees (provided that the learner's family earns in excess of 10 times the annual school fees; and if this is not the case, the family is fee exempt).














