Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.8 n.2 Johannesburg 2018
http://dx.doi.org/10.4102/sajce.v8i2.565
ORIGINAL RESEARCH
Meerkat Maths - A comprehensive maths learning programme for Grade-R
Eurika Jansen van VuurenI; Moritz HerzogII, III; Annemarie FritzII, III
IDepartment of Childhood Development, University of Mpumalanga, South Africa
IIDepartment of Educational Studies, University of Duisburg-Essen, Germany
IIICentre for Education Practice Research, University of Johannesburg, South Africa
ABSTRACT
BACKGROUND: Several studies have shown the influence of mathematical knowledge on both individual opportunities and chances for a self-determined and prosperous life as well as the welfare of nations. Against this background, the contents of maths education in the foundation phase as well as the way in which it is conveyed gain importance. While competence-oriented approaches (e.g. the Curriculum Assessment Policy Statements [CAPS]) state learning goals that all learners should achieve, developmental approaches (e.g. developmental models) describe typical learning trajectories of learners. As both approaches are quite separated, there is a need for bridging the gap between them
AIM: This article aims at revisiting the CAPS critically and comparing contents for early numeracy instruction. A possible alternative to the CAPS is intended
SETTING: In this article, we describe a maths learning programme for Grade-R (Meerkat Maths) that combines and integrates empirical findings and curricular demands. The presented maths training aims at teaching maths in such a way that it suits children's development, raises a positive attitude towards maths and also meets educational expectations
METHODS: Contents of the training programme and the CAPS are compared against the background of empirical research on numerical development and predictors for arithmetic performance
RESULTS: The results reveal that research based math instruction can be conveyed in a formal training programme
CONCLUSION: Keeping in mind the qualifications and training of Grade-R teachers, teacher training is necessarily embedded in the programme. Thus, the described programme is a comprehensive application of recent research for maths classes in the early grades
Introduction
International studies reveal that South African learners still show poorer performances in maths than most of their peers worldwide (Reddy et al. 2016). International comparative studies usually use scales with a fixed mean at 500 points keeping a standard deviation of 100 points to measure learners' competencies. Across the years, South African learners scored an average dramatically below 400 points (Hanushek & Woessmann 2015; Spaull 2013). Thus, they score more than one standard deviation below the worldwide mean; this equals the lack of more than 2 years of schooling (Hanushek & Woessmann 2015). Maths competencies are related to the economic development of the country. Better maths competencies across the population of a nation sustainably lead to higher economic growth (Hanushek & Woessmann 2015). Although the economy of the country increased, the below-average performance of South African learners is stable, not only across the recent Trends in International Mathematics and Science Study (TIMSS) and Program for International Student Assessment (PISA) studies, but it can also be tracked back for the last 50 years (Hanushek & Woessmann 2015).
Poor mathematical knowledge implies enormous individual disadvantages for learners. They earn less, are more often unemployed and have fewer chances to work in the field of their choice (Parsons & Brynner 2005). Moreover, the educational status of parents affects the educational potential of children. Thus, poor maths performance is likely to replicate in the following generation and it is hard to break the cycle.
However, research suggests that additional schooling time does not affect learning outcomes positively. It is not only the time learners spend in the school that determines their progress, but also the knowledge they obtain during this time (Hanushek & Woessmann 2015).
South African policy is aware that poor maths knowledge of learners leads to severe individual and economic problems. As a reaction to the maths performance misery amongst others, Grade-R was established in 1998 and efforts enhanced within the last years (Van Rensburg 2015). Grade-R implies both more total learning time and an earlier school start with the intention to increase pupils' knowledge and performance. In particular, Grade-R was supposed to improve learners' school readiness at their entrance into Grade 1 (Van Rensburg 2015). The term 'school readiness' refers to the experiences and knowledge children gain before they enter school, which are necessary for successful in-school learning.
This is of particular interest for maths learning as the acquisition of mathematical competencies is a complex learning process that sets in long before formal schooling (e.g. Carey 2009; Dehaene 2011). As not all children learn at the same pace - because of individual learning capacities and opportunities - their mathematical prerequisites differ both in quantity and quality (Aunola et al. 2004). It is important to note that the prior knowledge that learners have when they enter school is a good predictor for later learning success (Aunio & Niemvierta 2010).
Regrettably, empirical findings underpin that South Africa's Grade-R has only little effect on learners' school readiness. In particular regarding maths, Grade-R does not substantially improve learners' competencies or school readiness (Reddy et al. 2016; Van der Berg et al. 2013). Regarding school readiness, Van Rensburg (2015) recently revealed that about half of the South African preschoolers are not school ready even after introduction of Grade-R. The sample included schools from all socio-economic backgrounds and even in the richest quintile, 40% of the students lacked important cognitive prerequisites for formal schooling.
The main reason for the failure of the current Grade-R is seen in the insufficient professional education of the majority of the Grade-R teachers regarding content and pedagogical content knowledge (Van Rensburg 2015; Venkat & Spaull 2015). We argue that there is no adequate curriculum yet for Grade-R that meets teachers' skills and learners' development by now.
As Grade-R in South Africa is not yet able to promote learners' early numerical knowledge, the question how this can be done remains urgent (Long & Dunne 2014). Promoting pupils' school readiness involves the contents and their structure (i.e. the curriculum) as well as the expertise and proficiency of the teachers, who convey the contents. This article aims at presenting a comprehensive approach towards an option of better maths education in South Africa. The result of these efforts is a training programme named -Meerkat Maths. With the training programme Meerkat Maths, we aim to make research results applicable for in school teaching. To provide a comprehensive training programme, three questions have to be answered: which contents should be addressed by the training, how should it be structured and how should the training be realised?
Determining contents for mathematical training
The first question to solve, when originating a maths training programme, is how to choose its contents. The aims determine the contents of a training programme. Theoretical considerations might justify the selection of contents. As research indicates several different predictors and precursor skills, mathematical training can and should be derived from research. In the case of mathematics, central precursor skills are necessary as they are required to understand the fundamental arithmetical operations.
Children entering school have a kind of 'learning history' that describes what they learned in their first years (Fritz, Ehlert & Balzer 2013). These early years are of great importance as learners' success in school is highly predicted by their prior knowledge (Aunio & Niemvierta 2010; Aunola et al. 2004). In conclusion, we need to know which abilities and skills are necessary foundations for a successful start in primary school.
Abilities and skills that are important for mathematical learning in school can be divided into predictors and precursors. Predictors are abilities that allow - for a group of learners and within a certain range of confidence - forecasting the development of mathematical concepts. The expected development as derived from the predictors is more likely to happen, yet is not determined. Precursor skills are directly linked to mathematical concepts. They precede important mathematical knowledge and are therefore necessary prerequisites for the learner's development.
General predictors and precursor skills
Within the last decades, research has been able to identify several general predictors and precursors that contribute significantly to learners' conceptual development. Working memory abilities are prominently discussed as predictors for mathematical development. Working memory enables us to retrieve and store information and control attention while working on a maths problem. Visual-spatial abilities are particularly predictive in preschool and early school age regarding mental arithmetic performance (Arndt et al. 2013; Barnes et al. 2014; De Smedt et al. 2009; Kroesbergen & Van Dijk 2015), whereas older children's verbal working memory abilities outrun visual-spatial abilities when it comes to mathematical reasoning (De Smedt et al. 2009). Executive functions, such as inhibition and shifting, seem to predict mathematical development as well (Cowan & Powell 2014; Navarro et al. 2011). Inhibition is the ability to abort an ongoing action and to supress the urge of an action; shifting refers to changing between tasks fast and reliably (Miyake et al. 2000).
One of the oldest predictors discussed is inductive reasoning (Desoete 2015; Klauer & Phye 2008; Piaget 1965). Inductive reasoning contains general cognitive skills that allow finding patterns, regularities and rules that can occur in attributes or relations of items. Typical tasks are classification, seriation and pattern formation (Desoete 2015; Klauer & Phye 2008). In particular, patterns are considered as a central element of mathematical thinking (Devlin 2003). In empiric studies, classification and seriation skills could be identified as predictors for arithmetic achievement (Desoete 2015; Desoete et al. 2009). Furthermore, inductive reasoning predicted arithmetic performance in 6-year-old children, even if controlled for working memory (Nunes et al. 2007).
Language skills are on the edge between general and domain-specific predictors, depending on their relation to mathematics. However, even non-specific language skills predict mathematical development (Desoete 2015; Prediger et al. 2013). Particular attention was drawn to phonological awareness of young children, which showed predictive power in empiric studies (Barnes et al. 2014; Navarro et al. 2011; Passolunghi, Vercelloni & Schadee 2007). Empirical studies showed that the influence of phonological awareness on mathematical concepts is sustainable across the transition from kindergarten (same age as South African Grade-R learners) to Grade 1 and partially even increases (Langhorst, Ehlert & Fritz 2013; Navarro et al. 2011). Prediger et al. (2013) found high correlations between mathematical and reading skills that applied even for tasks that did not require reading competencies. Language skills get more important during the growth of mathematical skills (Dehaene 2011). As formal schooling involves verbal activities, it requires linguistic skills, which affect the acquisition and retrieval of mathematical knowledge in school (Prediger et al. 2013).
Research on domain-specific language skills is still rather rare. For instance, Göbel et al. (2014) revealed how knowledge of single and multi-digit number words at the beginning of Grade 1 is a good predictor of mathematical achievement 1 year later. However, there is still a lack of empiric research on mathematic-specific language skills and knowledge, for example grammatical competencies in prepositions or vocabulary. Indeed, research suggests that grammar skills predict later mathematical performance (Cowan & Powell 2014; Sarnecka 2014).
A general predictor of mathematical development that is often neglected is the emotional aspect of learning. Children's attitudes to mathematics, whether they enjoy maths or are scared of it, affect their learning success enormously (Moore, Rudig & Ashcraft 2015). Children who feel anxious about mathematics show significant poorer performances in maths (Ashcraft & Moore 2009). Some researchers argue that negative attitudes towards mathematics and poor maths skills reinforce each other; maths anxiety leads to avoidance, which leads to poorer performance, which increases the fear to fail in maths and so on (Dowker, Bennett & Smith 2012; Krinzinger, Kaufmann & Willmes 2009; Moore et al. 2015). This relation can be found even in preschoolers. In contrast to this, Thomas and Dowker (2000) report that younger children get affected by positive attitudes towards maths rather than by anxiety. Most interestingly, the relation of maths anxiety and performance could be replicated with preschool teachers (Jenßen et al. 2015). Thus, teachers' attitudes towards mathematics have direct influence on learners' success, which sheds a broader light on the importance of teachers' attitudes.
Domain-specific predictors and precursor skills
While general factors on learning promote all disciplines, domain-specific predictors and prerequisites specifically affect learning mathematics. All children are born equipped with a set of innate abilities to distinguish quantities, the so-called number sense (Dehaene 2011; Feigenson, Dehaene & Spelke 2004). This innate number sense could be identified as a predictor of mathematical development (Desoete 2015). Magnitude comparison is the ability to distinguish large quantities at one glance, as long as their difference is big enough. We distinguish non-symbolic (e.g. dots) from symbolic (numbers) magnitude comparison tasks, which have different predictive powers for mathematics during childhood (De Smedt et al. 2013). In general, symbolic magnitude comparison tasks show higher correlations with mathematics performance. This applies in particular to learners in primary school.
Another innate ability called subitising is to record small quantities up to four at one glance. Empirical research revealed a correlation between subitising and mathematical performance in Grades 1-3 (Desoete et al. 2009; Kroesbergen et al. 2009). Quantities bigger than four can be recorded at once only if they hold a structure that allows for subitising subsets, which can be added mentally afterwards (Starkey & McCandliss 2014). This process, which is known as conceptual subitising or groupitising, does not only require subitising skills, but also addition facts that can be retrieved easily. Thus, it is no surprise that groupitising is a good predictor of mathematical performance (Arndt et al. 2013; Starkey & McCandliss 2014).
Obviously, a central precursor skill for mathematical learning during preschool is counting. Children usually learn to recite the number word sequence (i.e. the number words in the correct order) before they know what the number words mean (Wynn 1990). This means that children at some age can recite the number words up to five, yet cannot give five counters or enumerate them. Children acquire the concepts of integers one at a time (Le Corre et al. 2006). Firstly, they learn to enumerate one while giving varying numbers when asked for two or more. Subsequently, they learn the meaning of two, three and four. According to Le Corre et al. (2006), this process takes more than 1 year, usually starting in the third year of life. In many studies, counting skills are a good predictor for mathematical achievement in school and outrun most other predictors (Desoete et al. 2009; Sarnecka, Goldman & Slusser 2015).
Counting routines facilitate solving small and simple addition tasks (e.g. 5 + 3 = 8) by counting. However, tasks that involve bigger numbers or are more complex (e.g. 8 + 7 = 15; 18 + 7 = 25; 8 - ? = 3) require more sophisticated effective solving strategies like breakdown (8 + 2 + 5 = 15; 18 + 2 + 5 = 25) or separating the place values. These strategies usually build up on a cardinal number concept (Fritz et al. 2013; Resnick 1983). With this concept, also called cardinality, learners perceive numbers not only as positions on a mental number line, but also as representatives of sets. In this way, a number like 5 gains a property of representing five items, or in other words a certain kind of 'fiveness'. When numbers are closely related to sets, they can be decomposed on a conceptual level (Fritz et al. 2013). Cardinality is not acquired on its own; it depends on the instruction (Dehaene 2011).
Precursor skills in Meerkat Maths: Basic cognitive and basic numerical concepts
Meerkat Maths contains several training units that not only cover general cognitive skills, but also introduce numbers and important first number concepts. The contents and structure of Meerkat Maths are derived from research results. Table 1 provides an overview of Meerkat Maths. The general and domain-specific knowledge mentioned above is covered in the first two sections of Meerkat Maths.
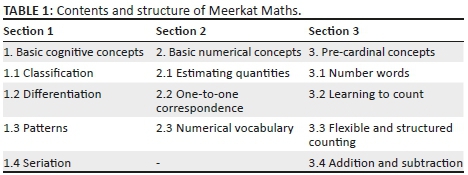
Basic cognitive concepts
The aim of the first section (1.1-1.4) is to provide children with the cognitive concepts they need to develop basic numerical competencies. As described above, these concepts prepare for successful learning in Grade 1. Although the chapters deal with different issues, each chapter's contents are hierarchically based on the preceding chapter's concepts. As research has revealed, all parts of the first section are precursor skills for mathematical development (Desoete et al. 2009).
The first chapter (classification) is about characteristics of objects like shape or colour. This chapter is designed to enable children to learn how to recognise and compare characteristics. They learn how to combine objects that share characteristics in a group.
In the second chapter (differentiation), the children learn about differences in characteristics. These differences allow finding the odd one out. By detecting common characteristics and classifying them to a group, children are able to exclude objects that do not fit. This concept is important to distinguish relevant from irrelevant characteristics when it comes to counting.
Mathematics is referred to as the 'science of patterns' (Devlin 2003). The ability to detect, describe and transfer patterns is a crucial prerequisite for the abstraction that one encounters while learning maths. Thus, in the third chapter (patterns), children learn how to find, describe and continue a given pattern.
Chapter 4 (seriation) enhances the knowledge of patterns and introduces the principle of order within patterns. While patterns are arbitrary and have individual rules, the number word sequence is ordered in a certain way: by number size. In this chapter, the children learn how to seriate - that is, to sort a set of objects by size. This will help them with learning the number word sequence.
Basic numerical concepts
Before children learn numbers and counting, they should learn certain basic numerical concepts. These include the approximate comparison of quantities. These concepts are closely related to special verbal expressions that should be taught with the concepts, yet deserve their own section. In particular regarding younger children, magnitude comparison tasks predict later performance (De Smedt et al. 2013). One-to-one correspondence is a crucial prerequisite for the acquisition of counting skills (Sarnecka et al. 2015). Number-specific language is an important learning factor for the development of arithmetic concepts (Dehaene 2011; Prediger et al. 2013).
In the first chapter (2.1), children train their approximate non-symbolic skills (estimating quantities). All humans have innate neural structures that allow comparing quantities that differ in certain ratios. Usually, ratios of 1:2, 2:3 and 1:3 are possible for children to distinguish. As the ability to compare small sets of objects is known as a predictor of later success in numeracy, children train their core systems in this chapter.
Mathematics requires the precise distinction between amounts. Counting requires the precise assignment of number words to counted items (one-to-one correspondence). Before children learn to use number words for counting, they should learn strategies to develop the ability to compare amounts in two or more sets without counting. The one-to-one correspondence is such a strategy. One object in a set is paired with one object in another set. Remaining objects in one of the two groups indicate the bigger set. This strategy is a precursor skill for counting, when each number word is assigned to an individual object.
The third chapter (numerical vocabulary) focuses on verbal expressions that allow describing and handling quantities and their relations verbally. While children learn to distinguish sets by size, they should learn to express differences in sets verbally. As numerical vocabulary such as 'more', 'many', 'nothing', 'less', 'few' or 'equal' is very important, this chapter serves as a checkpoint before learning the number word sequence.
Structuring the contents of a mathematical training programme
Predictors and precursor skills allow finding crucial abilities and knowledge that promote learning mathematics in school. However, these skills do not provide a structure, how they should be taught. Empirically validated learning trajectories allow structuring the contents in a way that meets learners' typical development. This way, a training programme does not force mathematical knowledge onto a child that is not yet prepared, but rather is suited to the learner's schooling demands.
Fritz et al. (2013) describe a hierarchical model sequence of early numerical concepts with six levels. The level sequence covers the ages from 4 to 8 years. The model is based on a theoretical foundation and was empirically validated in German as well as in four South African languages (Fritz et al. 2014). As Grade-R mostly covers the first three conceptual levels, we content ourselves with a description of these levels. With the MARKO-D-SA (Henning et al., in press) test, a South African diagnostic device based on this model is obtainable.
Developmental model of arithmetic concepts
Usually, children between the ages of 3 and 4 learn how to count and thus acquire the first level. On level I (rational counting concept), children know the number word sequence and are able to count and enumerate a small amount of items. This skill is acquired successively for each number (Le Corre et al. 2006). Typical tasks such as 'give-a-number' and 'how-many' are solvable for them (Wynn 1990). Children on this level know what counting can be used for and how to perform counting. However, their counting routines are not yet flexible and therefore learners on level I can only count forward by one. In addition, they do not yet understand the cardinal aspect of numbers: A number like '5' is seen as a representative for a result of a counting process, not as a representative for a set of five elements (Fritz et al. 2013). As they understand the principle of the one-to-one correspondence underlying the counting scheme, these children can share an even quantity of counters between two persons equally; while doing so, they rely on concrete manipulatives.
After having learned to count, children understand that numbers possess an orientation property: they get bigger. Each number has a predecessor and a successor forming a linear sequence of numbers. Thus, level II (number sequence concepts - line and lists) is characterised by a mental number line representation. To learners on this level, numbers line up on a directional number line (Nuerk, Moeller & Willmes 2015). This mental representation allows comparing numbers: the number that comes later in the number word sequence (and thus is farther right on the number line) is bigger. Children on level II can count backwards and forwards. This enables them to solve simple addition and subtraction tasks by counting (Siegler & Booth 2004). Note that computing by counting is considered a main characteristic and source for maths difficulties (Dowker 2005).
With level III (concept of cardinality), children construct a set-based representation of a number. While on the previous level, numbers were represented by a position on an ordinal number line, on the third level, numbers represent cardinalities (sizes) of certain sets. 'Five' now means the cardinality of a set consisting of five items; 'five' obtains a certain property - a kind of 'fiveness' (Fritz et al. 2013). This concept is seen as an important milestone during the development of arithmetic concepts as it forms the basis for following concepts (Dehaene 2011). The set representation of numbers also allows their decomposition. Five can be decomposed into three and two (or four and one) by splitting up the whole set of five into subsets which add up to five. For example, an addition task like 3 + 5 = 8 can be seen as the merger of the decompositions of 8. A sound and flexible knowledge of number decompositions supports addition task performances (Dowker 2005; Fritz et al. 2013). Besides, ordinal representation is no conceptual basis for number decompositions. The cardinal number concept facilitates the use of efficient computing strategies. Equipped with a cardinal number understanding, learners do not rely on counting as only computing routine, but are able to develop and use sophisticated strategies.
Children are supposed to gain the cardinal number concept during the first half of Grade 1 to have a resilient basis for the arithmetic contents of primary school. Keeping in mind the hierarchical structure of the concept sequence, all learners should acquire level II during Grade-R.- Including level III in Grade-R would clearly overload the Grade-R curriculum. To avoid this, Meerkat Maths Grade-R sticks to the levels I and II. Note that the last chapter (addition & subtraction) is not supposed to train computing by counting. This chapter rather aims at supplying a conceptual basis for a set-based representation of addition and subtraction tasks.
Learning trajectories in Meerkat Maths: Pre-cardinal concepts
Learning the number word sequence and how to count is the first step into numeracy. Therefore, counting completes Meerkat Maths for Grade-R. It includes learning the first 10 number words; applying the one-to-one correspondence principle, the stable order principle (number words are always used in the same order) and the cardinal principle (the last number name indicates the amount in the set); and using counting to do very simple addition and subtraction calculations in a cardinal sense. Counting skills are one of the most powerful predictors for mathematical performance in preschool age (Desoete et al. 2009; Sarnecka et al. 2015).
Children start learning to count with the number words (Sarnecka et al. 2015). They learn the number word sequence like a poem by heart but do not necessarily have a conception about what the words mean. In the first chapter (number words), children learn to recite the number words correctly.
Knowing the number words does not imply being able to count. For this reason, this chapter (learning to count) specifically focuses on learning to count small amounts up to 10. Counting in this chapter means being able to enumerate a set and give the correct number of items when asked for.
In chapter 3 (flexible and structured counting), the learners learn to count more flexibly. The more counting experience the children get, the more flexible they are at reciting the number word sequence including counting forwards and backwards. While doing so, children understand the orientation of the number words: they get bigger. Hereby they build the representation of the mental number line that allows them to increase or decrease amounts by using the orientation of the numbers on the mental number line. Counting is easier and more reliable, when the set is structured. The children are given structured representations of numbers and learn to count in a structured manner and to structure sets before counting.
Applying the knowledge to addition and subtraction tasks is the heart of the last chapter of Meerkat Maths Grade-R (addition and subtraction). The mental number line coupled with the cardinal principle of counting enables children to solve simple addition and subtraction tasks. However, Meerkat Maths uses this skill to link addition and subtraction to cardinal representation (e.g. with concrete manipulatives). Addition and subtraction shall be seen as set-based operations embedded in number decompositions.
Principles for realising mathematical training
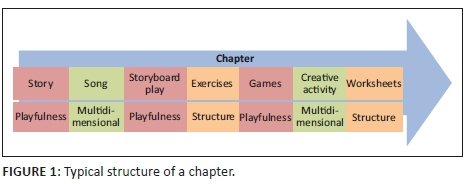
Mathematical training should follow certain principles (Hellmich 2007; Langhorst et al. 2013). In the following section, we will describe the training programme and its features along important principles for early numerical education. A typical structure of a Meerkat Maths chapter is demonstrated in Figure 1.
Development aligned and structured outline
Mathematical training should pay respect to learners' development to avoid too high as well as too low demands on them (Langhorst et al. 2013). The mathematical content should be structured in a way that suits the learners' development. As Meerkat Maths is aligned to the hierarchical model by Fritz et al. (2013), its structure is according to children's development. As seen above, the sections and chapters are clearly structured and build up on each other. Each chapter includes several exercises that are matched to the learners' prior knowledge.
Theoretical basis
Why do we teach the way we teach? This question expresses how every training programme needs to legitimate itself. A theoretical basis explains and justifies the learning steps. Moreover, it organises the content in a way that the following contents can be derived from current contents. The theoretical basis of Meerkat Maths was validated empirically in South Africa (Fritz et al. 2014).
Professional knowledge
The best training programme is likely to fail if the conductors, in this case the Grade-R teachers, are not well educated (Hellmich 2007). As mentioned initially, South African Grade-R teachers often lack important professional knowledge (Van Rensburg 2015). To make a difference where it matters most - in the Grade-R classroom - it is necessary to ensure that certain requirements are met during the implementation of intervention programmes. It is imperative that training programmes consider teachers' specific needs (Guskey 2002) and also their motivation to learn (Selter et al. 2015). In our implementation study (see below), we combine Meerkat Maths with teacher training. In regular sessions, the principles of Meerkat Maths and how it is used are explained to a group of Grade-R teachers in an active manner. By testing the programme, the teachers take the learners' role and reflect their experiences subsequently. This approach is supported by a comprehensive manual.
Multidimensionality
Learning mathematics involves several different skills as described above. Therefore, maths training programmes are supposed to include these skills, too. General cognitive aspects of mathematical learning are taken up in the first section. An important part of Meerkat Maths is the linguistic aspect of mathematical learning. Each chapter starts with a story in which the central mathematical problem is introduced. The ongoing story line leads the learners through the programme and moderates the learning process.- Section 2 includes a complete section regarding mathematical language. In several creativity exercises, children can apply their acquired mathematical knowledge to musical, kinaesthetic or artistic activities.
Playfulness and authenticity of contents
Children ought to develop a positive attitude towards mathematics as it has deep impact on mathematical learning success (DBE 2011; Moore et al. 2015). Playful activities help to develop such a positive attitude (Barnard & Braund 2016). Therefore, Meerkat Maths offers such playful learning opportunities such as songs, games or a storyboard play in which the stories' content is re-enacted. Research has shown that it is of great importance to perceive a domain as useful and valuable for learning outcomes (Harackiewicz et al. 2014). Although the problems that the protagonists solve by using mathematics are not part of the learners' everyday life, they experience the utility of mathematics.
Metacognition
Mathematical instruction should not only convey processes (e.g. solving routines for mathematical problems), but also conceptual foundations and strategy knowledge such as breakdown or decimal structure-based strategies (Langhorst et al. 2013; Long & Dunne 2014). This prevents the development of the so-called inert knowledge (Whitehead 1929). For this reason, Meerkat Maths stresses metacognition and strategy reflection at the end of every exercise.
Adaptivity
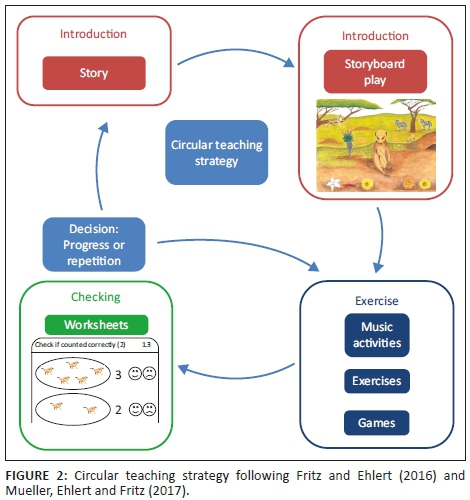
As children learn at different paces, mathematical training programmes should adapt to their learning speed (Langhorst et al. 2013). Meerkat Maths does not include a fixed time schedule for each chapter. The training takes as long as necessary and thus adapts to the learners' individual learning speed. Although it is intended that all children of a class learn together, splitting classes and teaching them at different rates is possible. Figure 2 demonstrates how this adaptiveness is realised in Meerkat Maths.
Integrating research and curricular demands
The training programme aims at supplying a sound conceptual basis for mathematical learning in school. However, learners in Grade-R are supposed to meet certain learning goals as described in the Curriculum Assessment Policy Statements (CAPS) (DBE 2011). The contents and demands of the CAPS have been discussed in the past (Barnard & Braund 2016; Long & Dunne 2014; Spaull & Kotze 2015). Although not all researchers agree with the CAPS, Meerkat Maths covers central topics from the Grade-R curriculum (see Table 2).
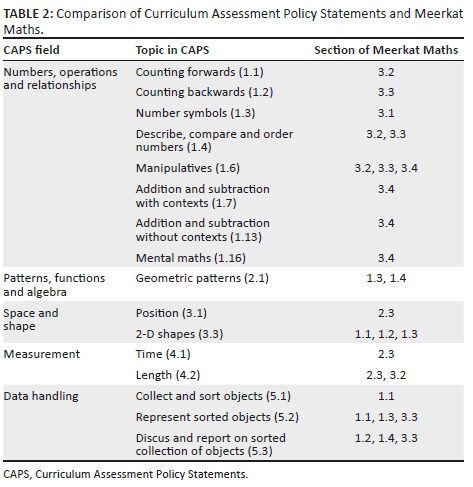
The most crucial field of the CAPS is numbers, operations and relationships, which consists mostly of the mathematical domain of arithmetic in the number range up to 10 (DBE 2011). Children are supposed to learn number concepts, for example to count forwards and backwards (1.1 and 1.2), the number symbols (1.3) and to describe, compare and order numbers (1.4). Operational contents like solving simple addition and subtraction tasks with and without contexts (1.7 and 1.13), solution strategies including manipulatives and mental maths (1.6 and 1.16) are covered, too. The issue of knowledge of coins and notes and dealing with money is the only topic neglected in Meerkat Maths. The section 'basic cognitive concepts' covers the CAPS field patterns, functions and algebra (2.1). Geometry (space and shape) is partly dealt with position and orientation and the corresponding language (3.1) and two-dimensional shapes are included in Meerkat Maths. In the field of measurement, Meerkat Maths addresses time (4.1) and length (4.2) in the section 'basic cognitive concepts', while mass and volume are not included. Meerkat Maths covers collecting, representing and discussing of counted objects (5.1-5.3) as learners' first experiences with data handling in the 'pre-cardinal concepts' section.
Most of the topics mentioned in the CAPS are included in Meerkat Maths (see Table 2). The selection of topics reveals their importance, which does not mean that topics not included are unimportant. Number concepts and elementary arithmetic form the basis for following operations and solving strategies. Their application, for example to value units, is necessary prior knowledge for other competency fields like measurement or data handling. Thus, these topics are stressed in Meerkat Maths. Other topics from the CAPS curriculum were deliberately omitted to avoid overloading the programme for Grade-R. Keeping in mind the developmental design of Meerkat Maths, it does not appear helpful to include topics and domains for which the learners are not prepared.
Discussion: Conditions for successful schooling
The aim of this article was to present a training programme that can meet the learners' development of early numerical concepts. Research has shown the importance of successful mathematical education in school for individual life opportunities as well as social economic development (Hanushek & Woessmann 2015; Parsons & Brynner 2005). These findings demonstrate the value of a resilient basis for learning mathematics. During Grade-R, children are supposed to acquire and internalise numerical knowledge to prevent the development of incoherent, isolated facts that can only be recalled, but lack a conceptual basis (Fritz & Ehlert 2016).
To develop a sound foundation for mathematical learning, children need basic mathematical knowledge that is appropriately structured. This means that the instruction in Grade-R has to address the development of basic numerical concepts. In particular, numerical, conceptual knowledge, for example cardinality and a resilient operation understanding, is a challenge for mathematical education in school.
Emotional aspects of mathematical learning have a great influence on the development of resilient arithmetic concepts. Arithmetic education in Grade-R has to convey a positive attitude towards mathematics to prevent math anxiety. Otherwise learners are likely to avoid mathematics and thus lack basic concepts because of missing learning opportunities. In conclusion, the contents of Meerkat Maths Grade-R demonstrate which aspects (i.e. cognitive and emotional) of early mathematics education deserve particular attention in Grade-R.
Teaching maths should not focus on the expected outcomes, but - in first line - consider the typical development, and how children acquire mathematical conceptual knowledge, including their precursor skills. Research consistently reveals hierarchies within the mathematical development of children during their first years. Precursor skills determine following developments and learners acquire arithmetic concepts successively following a certain hierarchy (Dehaene 2011; De Smedt et al. 2013; Desoete 2015; Desoete et al. 2009; Fritz et al. 2013; Le Corre et al. 2006). Obviously, there is no point in teaching children mathematical content that is not already based on previous knowledge (Figure 3). Teaching has therefore to facilitate cumulative learning by structuring the content according to the hierarchy of arithmetic concepts (Fritz et al. 2013). Fritz and Ehlert (2016) note that unconnected knowledge can even be a learning barrier.
To summarise, meaningful learning means to build up new learning content on previous knowledge and to link them together. In this sense, Ausubel (1968), one of the first cognitive psychologists, stressed the importance of previous knowledge for gaining competencies in a specific domain and thereby building a network of numerical concepts. The learners need to elaborate and deepen these concepts during primary school (Fritz et al. 2013; Rittle-Johnson et al. 2001). In this sense, learning means not to add new knowledge that stands separately from existing knowledge. Learning means to gain knowledge 'that is organised qualitatively, differently through new learning experiences and thus becomes richer, more flexible, and more effective' (Fritz & Ehlert 2016:371). Thus, rather than rote learned facts and procedures, mathematical education should support the learners in creating a flexible and conceptual understanding of numeracy (Long & Dunne 2014).
However, instructions have not only to follow developmental trajectories, but also to pay respect to the learners' individual learning state; otherwise, the new knowledge is likely to be isolated. If newly acquired knowledge is not related to previous knowledge, learners are unable to apply it to new situations (Fritz & Ehlert 2016; Hellmich 2007); it remains 'inert knowledge' (Whitehead 1929).
All these learning processes need time. If we want learners in Grade-R to develop a real understanding of mathematics, we must not overload them. Giving learners the time they need has two dimensions. Generally, a suitable curriculum should not be too packed, but focus on the most important topics that research indicates. On an individual level, all learners have to be given the time they need. This means that teaching mathematics needs to heed the individual learning speed. If learners need more time and more repetition, they should get it. There seems to be no use in forcing learning processes that are not adapted to the learners (Fritz & Ehlert 2016).
Finally, the schools and, even more so, the teachers have to be educated for implementing an appropriate curriculum. Teachers need theoretical background knowledge regarding the development of arithmetic concepts. To apply their knowledge to teaching, they need pedagogical content knowledge. Diagnostic competencies allow them to determine learning states and adapt teaching to the learners (Fritz & Ehlert 2016). Research suggests that Grade-R teachers often lack the necessary knowledge and competencies (Van Rensburg 2015). Thus, a comprehensive mathematical training programme implies training of prospective and in-service teachers, too.
Perspectives
As described, Meerkat Maths is designed in a way that can improve mathematical learning in Grade-R. However, the training programme has to be implemented and evaluated to investigate its efficiency. The focus of an evaluation study usually is to measure how efficient a certain training programme is by comparing the learning success depending on which programme was used. The only criterion is usually the learning outcome of the learners; how the programme can be used in school is mostly neglected (Balzer & Beywl 2015; Petermann 2014). Implementation means to reveal under which conditions Meerkat Maths can be used in schools by Grade-R teachers (Michie et al. 2005). Important questions include the following: does the training programme meet the teachers' competencies (feasibility), does it meet the learners' demands (appropriateness) and can schools afford the programme (costs)? Both aspects - learning outcomes and implementation conditions - are crucial to improve mathematical education successfully.
Therefore, we recently started an implementation study in five primary schools in a rural part of Mpumalanga. The implementation contains teacher training sessions that are run by an academic expert and convey the contents of the section the teachers conduct currently in school. The monthly training programme for these Grade-R teachers considers the matter of feasibility. The training is conducted to enable the teachers who work in Grade-R classes to conduct proper mathematical training. In between the training sessions, schools are visited by the academic expert to support teachers. The appropriateness of the course for the learners is gauged by the reports received from the teachers at the training sessions and during the workshops. Workshops are started with a reflection session and teachers are encouraged to share failures and successes. An evaluation study is planned subsequently.
Acknowledgements
This publication has been developed through the Teaching and Learning Development Capacity Improvement Programme which is being implemented through a partnership between the Department of Higher Education and Training and the European Union.
Competing interests
The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.
Authors' contributions
E.J.v.V., M.H. and A.F. created the training presented, A.F. provided its theoretical basis in advance, A.F. and M.H. supplied the theoretical background, E.J.v.V. and M.H. described the training programme and the integration of research and curricular demands, while its implications were discussed by A.F. and M.H.
References
Arndt, D., Sahr, K., Opfermann, M., Leutner, D. & Fritz A., 2013, 'Core knowledge and working memory as prerequisites of early school arithmetic', South African Journal of Childhood Education 3(1), 1-20. https://doi.org/10.4102/sajce.v3i1.29 [ Links ]
Ashcraft, M.H. & Moore, A.M., 2009, 'Mathematics anxiety and the affective drop in performance', Journal of Psychoeducational Assessment 27(3), 197-205. https://doi.org/10.1177/0734282908330580 [ Links ]
Aunio, P. & Niemivierta, M., 2010, 'Predicting children's mathematical performance in grade one by early numeracy', Learning and Individual Differences 20, 427-435. https://doi.org/10.1016/j.lindif.2010.06.003 [ Links ]
Aunola, K., Leskinen, E., Lerkkanen, M.-K. & Nurmi, J.-E., 2004, 'Developmental dynamics of math performance from pre-school to Grade 2', Journal of Educational Psychology 96(4), 699-713. https://doi.org/10.1037/0022-0663.96.4.699 [ Links ]
Ausubel, B., 1968, Educational psychology, a cognitive view, Holt, Rinehart and Winston, New York.
Balzer, L. & Beywl, W., 2015, Evaluiert - Planungsbuch für Evaluationen im Bildungsbereich, Hep Verlag, Bern.
Barnard, W. & Braund, M., 2016, 'Strategies for the implementation of mathematics in Grade R: Teachers' beliefs and practices', South African Journal of Childhood Education 6(1), a409. https://doi.org/10.4102/sajce.v6i1.409 [ Links ]
Barnes, M.A., Raghubar, K.P., Lianne English, L.,. Williams, J.M. & Landry, H.S., 2014, 'Longitudinal mediators of achievement in mathematics and reading in typical and atypical development', Journal of Experimental Child Psychology 119, 1-16. https://doi.org/10.1016/j.jecp.2013.09.006 [ Links ]
Carey, S., 2009, The origin of concepts, Oxford University Press, Cambridge.
Cowan, R. & Powell, D., 2014, 'The contributions of domain-general and numerical factors to third-grade arithmetic skills and Mathematical learning disability', Journal of Educational Psychology 106(1), 214-229. https://doi.org/10.1016/j.jecp.2013.09.006 [ Links ]
DBE - South African Department of Basic Education, 2011, Curriculum and assessment policy statement grade R: Mathematics. Policy, DBE, Pretoria.
De Smedt, B., Janssen, R., Bouwens, K., Verschaffel, L., Boets, B. & Ghesquière, P., 2009, 'Working memory and individual differences in mathematics achievement: A longitudinal study from first grade to second grade', Journal of Experimental Child Psychology 103, 186-201. https://doi.org/10.1016/j.jecp.2009.01.004 [ Links ]
De Smedt, B., Noël, M.-P., Gilmore, C. & Ansari, D., 2013, 'How do symbolic and non-symbolic numerical magnitude processing skills relate to individual differences in children's mathematical skills? A review of evidence from brain and behavior', Trends in Neuroscience and Education 2, 48-55. https://doi.org/10.1016/j.tine.2013.06.001 [ Links ]
Dehaene, S., 2011, The number sense, Oxford University Press, Cambridge.
Desoete, A., 2015, 'Cognitive predictors of mathematical abilities and disabilities', in R.C. Kadosh & A. Dowker (eds.), The Oxford handbook of mathematical cognition, pp. 915-932, 2 Medicine UK, Oxford.
Desoete, A., Stock, P., Schepens, A., Baeyens, D. & Roeyers, H., 2009, 'Classification, seriation, and counting in grades 1, 2, and 3 as two-year longitudinal predictors for low achieving in numerical facility and arithmetical achievement?', Journal of Psychoeducational Assessment 27(3), 252-264. https://doi.org/10.1177/0734282908330588 [ Links ]
Devlin, K.J., 2003, Mathematics, the science of patterns, Holt, New York.
Dowker, A., 2005, 'Early identification and intervention for students with mathematics difficulties', Journal of Learning Disabilities 38(4), 324-332. https://doi.org/10.1177/00222194050380040801 [ Links ]
Dowker, A., Bennett, K. & Smith, L., 2012, 'Attitudes to mathematics in primary school children', Child Development Research vol. 2012, Article ID 124939, 8 p. https://doi.org/10.1155/2012/124939 [ Links ]
Feigenson, L., Dehaene, S. & Spelke, E., 2004, 'Core systems of number', Trends in Cognitive Sciences 8(7), 307-314. https://doi.org/10.1016/j.tics.2004.05.002 [ Links ]
Fritz, A., Balzer, L., Herholdt, L., Ragpot, L. & Ehlert, A., 2014, 'A mathematics competence test for Grade 1 children migrates from Germany to South Africa', South African Journal of Childhood Education 4(2), 114-133. [ Links ]
Fritz, A. & Ehlert, A., 2016, 'Learnind difficulties', in L. Ramrathan, L. le Grange & P. Higgs (eds.), Education studies for initial teacher development, pp. 365-382, Juta, Cape Town.
Fritz, A., Ehlert, A. & Balzer, L., 2013, 'Development of mathematical concepts as basis for an elaborated mathematical understanding', South African Journal of Childhood Education 3(1), 38-67. [ Links ]
Göbel, S.M., Watson, S.E., Lervag, A. & Hulme, C., 2014, 'Children's arithmetic development it is number knowledge, not the approximate number sense, that counts', Psychological Science 25(3), 789-798. https://doi.org/10.1177/0956797613516471 [ Links ]
Guskey, T.R., 2002, 'Professional development and teacher change', Teachers and Teaching: Theory and Practice 8(3), 381-391. https://doi.org/10.1080/135406002100000512 [ Links ]
Hanushek, E.A. & Woessmann, L., 2015, The knowledge capital of nations, MIT Press, Cambridge, MA.
Harackiewicz, J.M., Canning, E.A., Tibbetts, Y., Giffen, C.J., Blair, S.S., Rouse, D.I. et al., 2014, 'Closing the social class achievement gap for first-generation students in undergraduate biology', Journal of Educational Psychology 106, 375-389. https://doi.org/10.1037/a0034679 [ Links ]
Hellmich, F., 2007, 'Möglichkeiten der Förderung mathematischer Vorläuferfähigkeiten im vorschulischen Bereich', bildungsforschung 4(1), 16 p., viewed from 30 September 2018, http://www.bildungsforschung.org/Archiv/2007-01/mathematik/ [ Links ]
Henning, E., Ehlert, A., Herholdt, R. Balzer, L., Ragpot, L. & Fritz, A. in press., MARKO-D. Mathematics and Arithmetic Diagnostic Instrument, University of Johannesburg, Johannesburg.
Jenßen, L., Dunekacke, S., Eid, M. & Blömeke, S., 2015, 'The relationship of mathematical competence and mathematics anxiety', Zeitschrift für Psychologie 223(1), 31-38. [ Links ]
Klauer, K.J. & Phye, G.D., 2008, 'Inductive reasoning: A training approach', Review of Educational Research 78(1), 85-123. https://doi.org/10.3102/0034654307313402 [ Links ]
Krinzinger, H., Kaufmann, L. & Willmes, K., 2009, 'Math anxiety and math ability in early Primary school years', Journal of Psychoeducational Assessment 27(3), 206-225. https://doi.org/10.1177/0734282908330583 [ Links ]
Kroesbergen, E.H. & Van Dijk, M., 2015, 'Working memory and number sense as predictors of mathematical (dis-)ability', Zeitschrift für Psychologie 223(2), 102-109. [ Links ]
Kroesbergen, E.H., Van Luit, J.E.H., Van Lieshout, E.C.D.M., Van Loosbroek, E. & Van de Rijt, B.A.M., 2009, 'Individual differences in early numeracy', Journal of Psychoeducational Assessment 27(3), 226-236. https://doi.org/10.1177/0734282908330586 [ Links ]
Langhorst, P., Ehlert, A. & Fritz, A., 2013, 'Realising pre-school mathematical education - A development-oriented math programme with special consideration of phonological language', South African Journal of Childhood Education 3(1), 68-99. https://doi.org/10.4102/sajce.v3i1.32 [ Links ]
Le Corre, M., Van de Walle, G., Brannon, E.M. & Carey, S., 2006, 'Re-visiting the competence/performance debate in the acquisition of the counting principles', Cognitive Psychology 52, 130-169. https://doi.org/10.1016/j.cogpsych.2005.07.002 [ Links ]
Long, C. & Dunne, T., 2014, 'Approaches to teaching primary level mathematics', South African Journal of Childhood Education 4(2), 134-153. https://doi.org/10.4102/sajce.v4i2.208 [ Links ]
Michie, S., Johnson, M., Abraham, C. & Lawton, R., 2005, 'Making psychological theory useful for implementing evidence based practice: A consensus approach', Quality and Safety in Health Care 14, 26-33. https://doi.org/10.1136/qshc.2004.011155 [ Links ]
Miyake, A., Friedman, N.P., Emerson, M.J., Witzki, A.H. & Howerter, A., 2000, 'The unity and diversity of executive functions and their contributions to complex "Frontal lobe" tasks: A latent variable analysis', Cognitive Psychology 41, 49-100. https://doi.org/10.1006/cogp.1999.0734 [ Links ]
Moore, A.M., Rudig, N.O. & Ashcraft, M.H., 2015, 'Affect, motivation, working memory and mathematics', in R.C. Kadosh & A. Dowker (eds.), The Oxford handbook of mathematical cognition, pp. 933-952, 2 Medicine UK, Oxford.
Mueller, A., Ehlert, A. & Fritz, A., 2017, 'Inklusiver Mathematikunterricht - Notwendige methodische und organisatorische Veränderungsprozesse', in A. Fritz, S. Schmidt & G. Ricken (eds.), Handbuch Rechenschwäche, pp. 460-477, Beltz, Weinheim.
Navarro, J.I., Aguilar, M., Alcalde, C., Ruiz, G., Marchena, E. & Menacho, I., 2011, 'Inhibitory processes, working memory, phonological awareness, naming speed, and early arithmetic achievement', The Spanisch Journal of Psychology 14(2), 580-588. https://doi.org/10.5209/rev_SJOP.2011.v14.n2.6 [ Links ]
Nuerk, H.-C., Moeller K. & Willmes, K., 2015, 'Multi-digit number processing: Overview, conceptual clarifications, and language influences', in R.C. Kadosh & A. Dowker (eds.), The Oxford handbook of mathematical cognition, pp. 106-139, 2 Medicine UK, Oxford.
Nunes, T., Bryant, P., Evans, D., Bell, D., Garnder, S., Garnder, A. et al., 2007, 'The contribution of logical reasoning to the learning of mathematics in primary school', British Journal of Developmental Psychology 25, 147-166. https://doi.org/10.1348/026151006X153127 [ Links ]
Parsons, S. & Bynner, J., 2005, Does numeracy matter more? National Research and Development Centre for Adult Literacy and Numeracy, London.
Passolunghi, M.C., Vercelloni, B. & Schadee, H., 2007, 'The precursors of mathematics learning: Working memory, phonological ability and numerical competence', Cognitive Development 22, 165-184. https://doi.org/10.1016/j.cogdev.2006.09.001 [ Links ]
Petermann, F., 2014, 'Implementationsforschung: Grundbegriffe und Konzepte', Psychologische Rundschau 65(3), 122-128. https://doi.org/10.1026/0033-3042/a000214 [ Links ]
Piaget, J., 1965, The child's conception of number, Norton, New York.
Prediger, S., Wilhelm, N., Büchter, A., Gürsoy, E. & Benholz, C., 2015, 'Sprachkompetenz und Mathematikleistung - Empirische Untersuchung sprachlich bedingter Hürden in den Zentralen Prüfungen 10', Journal für Mathematik Didaktik 36, 77-104. https://doi.org/10.1007/s13138-015-0074-0 [ Links ]
Reddy, V., Isdale, K., Juan, A., Visser, M., Winnaar, L. & Arends, F., 2016, TIMSS 2015: Highlights of mathematics achievement of Grade 5 South African learners, HSRC Press, Cape Town.
Resnick, L.B., 1983, 'A developmental theory of number understanding', in H. Ginsburg (ed.), The development of mathematical thinking, pp. 109-151, Academic Press, New York.
Rittle-Johnson, B., Siegler, R.S. & Alibali, M.W., 2001, 'Developing conceptual understanding and procedural skill in mathematics: An iterative process', Journal of Educational Psychology 9, 346-362. https://doi.org/10.1037/0022-0663.93.2.346 [ Links ]
Sarnecka, B., 2014, 'On the relation between grammatical number and cardinal numbers in development', Frontiers in Psychology 5, Art. 1132, 4 p. https://doi.org/10.3389/fpsyg.2014.01132 [ Links ]
Sarnecka, B.W., Goldman, M.C.. & Slusser, E.B., 2015, 'How counting leads to children's first representations of exact, large numbers', in R.C. Kadosh & A. Dowker (eds.), The Oxford handbook of mathematical cognition, pp. 291-309, 2 Medicine UK, Oxford.
Selter, C., Gräsel, C., Reinold, M. & Trempler, K., 2015, 'Variations of in-service training for primary mathematics teachers. An empirical study', ZDM - The International Journal on Mathematics Education 47(1), 65-77. https://doi.org/10.1007/s11858-014-0639-2 [ Links ]
Siegler, R.S. & Booth, J.L., 2004, 'Development of numerical estimation in young children', Child Development 75, 428-444. https://doi.org/10.1111/j.1467-8624.2004.00684.x [ Links ]
Spaull, N., 2013, 'Poverty & privilege: Primary school inequality in South Africa', International Journal of Educational Development 33(5), 436-447. https://doi.org/10.1016/j.ijedudev.2012.09.009 [ Links ]
Spaull, N. & Kotze, J., 2015, 'Starting behind and staying behind in South Africa. The case of insurmountable learning deficits in mathematics', International Journal of Educational Development 41, 13-24. https://doi.org/10.1016/j.ijedudev.2015.01.002 [ Links ]
Starkey, G.S. & McCandliss, B.D., 2014, 'The emergence of "groupitizing" in children's numerical cognition', Journal of Experimental Child Psychology 126, 120-137. https://doi.org/10.1016/j.jecp.2014.03.006 [ Links ]
Thomas, G. & Dowker, A., 2000, 'Mathematics anxiety and related factors in young children', paper presented at British Psychological Society Developmental Section Conference, September 2000, Bristol, UK.
Van der Berg, S., Girdwood, E., Shepherd, D., Van Wyk, C., Kruger, J., Viljoen, J. et al., 2013, 'The impact of the introduction of Grade R on learning outcomes', University of Stellenbosch, Stellenbosch.
Van Rensburg, O.J., 2015, 'The school readiness performance of a group of Grade R learners in primary schools in the Gauteng Province of South Africa', South African Journal of Childhood Education 5(1), 106-124. https://doi.org/10.4102/sajce.v5i1.352 [ Links ]
Venkat, H. & Spaull, N., 2015, 'What do we know about primary teachers' mathematical content knowledge in South Africa? An analysis of SACMEQ 2007', International Journal of Educational Development 41, 121-130. https://doi.org/10.1016/j.ijedudev.2015.02.002 [ Links ]
Whitehead, A.N., 1929, The aims of education and other essays, The Free Press, New York.
Wynn, K., 1990, 'Children's understanding of counting', Cognition 36, 155-193. https://doi.org/10.1016/0010-0277(90)90003-3 [ Links ]
 Correspondence:
Correspondence:
Moritz Herzog
moritz.herzog@uni-due.de
Received: 31 July 2017
Accepted: 18 Aug. 2018
Published: 29 Nov. 2018














