Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.8 n.2 Johannesburg 2018
http://dx.doi.org/10.4102/sajce.v8i2.539
ORIGINAL RESEARCH
Pre-service primary Mathematics teachers' understanding of fractions: An action-process-object-schema perspective
Ifunanya J.A. Ubah; Sarah Bansilal
Department of Science, Technology and Mathematics, School of Education, University of KwaZulu-Natal, South Africa
ABSTRACT
BACKGROUND: The concept of rational numbers is one of the learner's first experiences with a Mathematics concept beyond the basic skills operations on whole numbers. The personal knowledge of fractions that teachers bring to the teaching context is important because teachers mediate the conceptions that their learners construct
AIM: This study was set up to apply Action-Process-Object-Schema theory to study primary teachers' understanding of addition and subtraction of fractions
SETTING: The participants of this study comprised 60 undergraduate full-time students, studying to become teachers. The participants were enrolled in a foundational course in Mathematics because they had not passed Mathematics at Grade 12 level. This course was intended to help deepen their understanding of basic numeracy, allowing them to continue with further courses if they wanted to specialise in teaching primary mathematics
METHODS: Data were collected using written responses of the pre-service students to two tasks that focused on operations with fractions. Ten students volunteered to be interviewed of which three are drawn upon in this article
RESULTS: Many of the pre-service teachers coped well with addition and subtraction of common fractions with the same denominator. However, more than 52% struggled to carry out these operations on common fractions with different denominators, showing that their conceptions had not developed into object-level structures
CONCLUSION: It is evident that the incorrect procedures have become embedded in the students mental schema. It is crucial that programmes for upgrading pre-service teachers should include opportunities for teachers to interrogate their personal understandings of the basic mathematics concepts
Introduction
Many learners, as well as teachers, often groan with dismay when they hear the word 'fraction' because it is associated with early experiences in primary school of numbers that did not make sense, where rules without reasons were applied. The introduction of fractions is one of learners' first experiences with a math concept beyond the basic skills of whole number arithmetic (Chinnapan 2006; Cramer et al. 2009; Siegler et al. 2013; Steffe & Olive 2010). 'Fraction' is a word that originated from the Latin fractus, meaning 'broken' (Rothstein, Rothstein & Lauber 2006). This meaning is quite apt, because a fraction represents part of a whole, or more generally any number of equal parts. The well-known saying about the glass being 'half full or half empty' also makes use of fractions. It is important that a child feel comfortable and confident in his understanding of fractions. Knowledge of fractions is a building block for other math skills, and a successful experience of learning a new concept will help the pre-service teachers gain confidence in their ability to teach (Cramer & Wyberg 2009). Consequently, students who possess these essential understandings are able to apply their knowledge and explain their actions, demonstrating strong links between a range of skills and knowledge, and mathematical representations of fractions (Bruce, Chang & Flyann 2013; Wong & Evans 2007).
Fractions are considered an essential skill for future Mathematics success but also a difficult concept to learn and to teach (Hecht, Close & Santisi 2003; Newton 2008; Siegler et al. 2013; Steffe & Olive 2010; Van Steenbrugge, Valcke & Desoete 2010). A survey of the literature shows that there are limitations to learners' knowledge of fractions (Boyce & Norton 2016; Hackenburg & Tillema 2009; Newton 2008; Norton & Wilkins 2009; Reys et al. 2012; Steffe & Olive 2010; Van Steenbrugge et al. 2010; 2014). One reason for this limited knowledge of fractions is that the curriculum tends to rush to symbolisation and operations without developing the strong conceptual understanding that learners must have for fractions (Rey et al. 2012). Fractions require much attention because they present a hurdle as learners attempt to transfer their understanding of whole numbers to a new but related class of numbers (Chinnappan & Forrester 2014; Siegler et al. 2013; Stafylidou & Vosniadou 2004).
Siegler et al. (2013) identified some reasons why fractions are experienced as difficult by many learners. They observed that some learners incorrectly assume that properties of whole numbers apply to fractions. A further problem is that of connecting written fractions with the magnitudes they represent. Hence identifying and ordering the magnitude of different fractions is a challenge for many. A key construct that underpins the learning of fractions is the part-whole relationship (Siegler et al. 2013). Learners need to understand the part-whole relationship between the numerator and the denominator or they may treat these numbers as wholes, that is, the use of whole number arithmetic operations is performed independently on the numerator and on the denominator. Sometimes over-reliance on the part-whole interpretation of a fraction can lead to problems with understanding a fraction such as 4/3. Another source of difficulties with fractions is the confusion between the relations among the fraction arithmetic procedures. Another common type of error in fraction arithmetic is the wrong fraction operation error, which involves using steps that may be correct for a particular fraction operation but that are used in an operation where they are incorrect. For example, Siegler et al. (2013) observed learners maintaining a common denominator in multiplication of fractions with the same denominator, which is correct in the addition of fractions with the same denominator (for instance, 1/5 × 3/5 = 3/5).
There is consensus in the teacher education literature that a strong knowledge of the subject taught is a core component of teacher competence (Baumert et al. 2010). Given that teacher education is a crucial period for obtaining a profound deep and conceptual understanding of fractions (Borko et al. 1992; Ma 1999; Newton 2008; Toluk-Ucar 2009; Zhou, Peverly & Xin 2006), for effective teaching to take place, there is a need to focus on the content knowledge required of pre-service teachers for a profound understanding of fractions. In this study, we use the Action-Process-Object-Schema (APOS) theory to try to understand some deficiencies faced by pre-service primary school teachers. Many studies have been carried out about misconceptions and understanding of fractions by school learners (e.g. Cramer et al. 2009; Hansen et al. 2017), but fewer studies have being carried out on pre-service teachers' understanding of fractions in South Africa. Furthermore, the use of APOS theory in pre-service teachers' understanding of fractions in South Africa has not been done. APOS studies have been conducted on pre-service high school Mathematics teachers' understanding of various concepts, but none on primary school teachers' knowledge (e.g. Bansilal, Brijlall & Trigueros 2017; Ndlovu & Brijlall 2015). In this article we will consider pre-service teachers' misconceptions that permeate from addition and subtraction of fractions using APOS theory.
Literature review
Understanding the notion of fractions
Siegler et al. (2013) point out that the set of whole numbers has many properties that are not true of all numbers in general. Stafylidou and Vosniadou (2004) list some properties of whole numbers that are not shared by the set of fractions. For example the symbolic representation of a whole number is one number symbol, while a fraction is represented symbolically by two numbers separated by a bar. The ordering of whole numbers is supported by the natural numbers' sequence, while this is not true for fractions. There is no unique successor or preceding number for any fraction, as is the case for whole numbers. Furthermore, multiplication of two whole numbers makes the number bigger, whereas with fractions multiplication may make the number bigger or even smaller. It is for these reasons that Siegler et al. (2013) argue that the learning of fractions requires a reorganisation of one's numerical conceptions because children who have not learnt fractions yet assume that properties of whole numbers hold for all numbers. Many authors (Cramer, Post & Del Mas 2002; Hackenberg & Lee 2015; Siegler 2013) have emphasised that one property shared by all real numbers is that they represent magnitudes that can be represented on a number line. Hence an important conceptual idea of fractions is understanding and differentiating between the magnitudes of fractions.
However, helping learners develop these key ideas is not easily achieved as is evident from the numerous studies focusing on students' difficulties with fractions (Cramer et al. 2002; Hackenberg & Lee 2015). The Rational Number Project (RNP) reported great success in helping their students develop an understanding of the key conceptual ideas and identified four types of strategies used in comparisons about the magnitudes of fractions (same numerator, same denominator, transitive and residual) (Cramer et al. 2002). When students compare two fractions with the same numerator, they reason that an inverse relationship exists between the number of parts a unit is partitioned into and the size of each part (e.g. in comparing 3/7 and 3/10, it can be deduced that 3/7 is large because a seventh is larger than a tenth, and three larger pieces must be bigger than three smaller pieces). Reasoning about the order of two fractions with the same denominator (using the same denominator strategy) requires an understanding that the size of each part remains the same but the number of pieces differ (e.g. reasoning that 3/7 is greater than 2/7 because 3/7 has three parts while 2/7 consists of two of those parts). The use of transitive reasoning in ordering two fractions involves considering a third fraction that fits between the two so that the comparison can be made (e.g. in comparing 3/8 and 4/7, the fraction 1/2 can be used to deduce that because 3/8 is less than 1/2, and 4/7 is greater than 1/2, it is clear that 3/8 is less than 4/7). The residual strategy identified by Cramer et al. (2002:115) is evident when students make a comparison based on the size of a 'missing piece' (e.g. when reasoning about 5/6 and 7/8, it is evident that 5/6 needs a sixth to make a whole unit, while 7/8 needs an eighth. Because an eighth is smaller than a sixth, it means that 7/8 is larger than 5/6 (Cramer et al. 2002).
Furthermore, Cramer et al. (2002) find that children taught using the conceptually grounded curriculum approach (RNP) that focused on making connections between different modes of representations, performed much better on fraction tasks than those who were taught using standard curricula. In the RNP approach, children were led to develop an understanding of fractions, magnitude and ideas of equivalence, before being introduced to fraction arithmetic procedures. The approach did not rely on symbolic procedures for deciding on order or equivalence of fractions but inculcated a quantitative sense of fractions. The authors argued that the reason why the project students did so well was because of the extended time they spent in engaging with the key ideas of the fraction concept as well as the meaning of symbols using multiple methods (Cramer et al. 2002).
Hackenberg and Lee (2015:203) use the notion of 'extensive quantity' (something that can be enumerated or measured) to explain the algebraic reasoning of students from a quantitative perspective. The authors cite Smith and Thompson (2008), who argue that in order to conceive of an extensive quantity it is necessary for a student to first understand the key property of a measurement unit, which is being able to subdivide the quantity into a number of measurement units and to then establish some method of counting the number of those units to give rise to a measurement or enumeration of the quantity. Hackenberg and Lee (2015:204) contend that the act of subdividing a length or quantity into equal parts could be done by the operations of partitioning ('marking a part or whole into some number of equal pieces'), disembedding ('removing a part from a whole' mentally, while still preserving the mental picture of the whole as a separate entity) and iterating (repeatedly adding a part, thus accumulating a larger amount). A student who has access to an iterative fraction scheme is able to conceive of a fraction as multiples of unit fractions; hence 3/8 is seen as three multiples of the unit fraction 1/8. With this iterative conception, a student will thus be able to make sense of fractions that are larger than a whole unit, such as seeing 11/8 as 11 multiples of 1/8.
Teachers' knowledge of fractions
Many researchers have investigated what teachers know about Mathematics, teaching Mathematics and how they know it, since Shulman (1987) coined the notion of pedagogical content knowledge. These researchers have generally reported low levels of knowledge about teaching Mathematics, in particular, pre-service teachers' lack of understanding about whole numbers, fractions and fraction operations (Chinnappan & Forrester 2014; Depaepe et al. 2015; Krauss, Baumert & Blum 2008; Son & Crespo 2009; Son & Sinclaire 2010). Chinnappan (2000) examines the understanding of fractions of a group of pre-service primary Mathematics teachers. The participants were required to order fractions using a software tool. The results of the study indicated that while the pre-service teachers had built up robust knowledge about fractions, they did not exhibit skills at using the software to provide pedagogically different solutions to the given problem. Chinnappan suggests that teacher education programs need to analyse the mathematical content and software interface carefully.
Chinnappan and Forrester (2014) distinguish between procedural and conceptual knowledge of fractions by pre-service teachers when examining the impact of an instructional model designed to improve the conceptual understanding of fraction concepts and operations. The authors argue that pre-service teachers come into teacher education programmes with knowledge of fractions and fraction operations that is mainly about procedures, with limited appreciation of the conceptual basis of these concepts and operations. The study recommended that pre-service teachers can be supported, within an existing teacher education programme, in constructing conceptually and procedurally robust content knowledge through the development of appropriate representations of fraction concepts and operations.
According to Hansen et al. (2017), there are many different representations and interpretations of fractions. It is important that teachers are both aware of and understand these interpretations so they can introduce them to children in meaningful ways. Teachers also need to be aware that some interpretations of fractions are conceptually more difficult than others; for instance the part of a whole interpretation as an object split into two or more equal parts. In addition, Charalambous and Pitta-Pantai (2005) observe that the method of teaching fractions as part of a whole was necessary but that it was not appropriate to use this as the only way to teach fractions. They suggest that teachers should develop a deep understanding of the different interpretations of fractions.
Ji-Won and Ji-Eunlee's (2016) study characterise profiles of pre-service teachers' mathematical competence on the topic of fraction multiplication by examining pre-service teachers' understanding of multiplication of fractions in three different contexts. Analyses of 60 pre-service teachers' written responses revealed that there are distinct gradations of competency, ranging from the pre-service teachers who were unable to solve a given problem in any context to those capable of flexibly portraying an understanding of fraction multiplication in three contexts. Their findings offered descriptors of how the pre-service teachers understood fraction multiplication in different contexts and provided information for the design of interventions in teacher education.
A collaborative action research project by Bruce et al. (2013) focused on representing, comparing and ordering fractions and engaged teacher teams in examining student thinking over 3 months. The study revealed that comparing and ordering fractions allows students to develop a sense of fractions as quantity, as well as a sense of the size of a fraction, both necessary prior knowledge components for understanding fraction operations. Although the learning progression is not linear, there are some strongly interconnected components that support students' understanding of subsequent concepts.
A study by Isik and Kar (2012) used a case study analysis of the type of error committed by pre-service elementary Mathematics teachers in Turkey. Seven types of errors were identified: unit confusion; assigning natural number interpretations to fractions; problems using ratio proportions; being unable to establish part-whole relationships; dividing by the denominator of the divisor; using multiplication instead of division; and increasing errors by inverting and multiplying the divisor fraction. Similarly, the study by Tobias, Olanoff and Lo (2012) demonstrate that pre-service teachers tend to 'have a rule-based conception of fraction multiplication and division' (p. 671) and have 'misconceptions that resulted from overgeneralised rules from other number systems, such as multiplication always makes bigger, or result from inability to understanding algorithms for multiplying and dividing fractions' (p. 671).
Theoretical framework
This study is based on APOS theory, which proposes that an individual has appropriate mental structures built up through particular mental mechanisms, to make sense of a given mathematical concept. The mental structures refer to the likely actions, processes and objects required to learn the concept, organised in schemas to make sense of the situations (constituting the acronym APOS). Dubinsky (1991) also identifies mental mechanisms, such as interiorisation, coordination, reversal, encapsulation and generalisation, involved in the mental construction development. An action is physical or mental transformation of a mathematical entity in response to an external stimulus. As an action is repeated and reflected upon, it can get interiorised into an internal mental construction called a process in which the person can think of forming the same kind of action but no longer with the need for external stimuli. The process is encapsulated into an object when the individual becomes aware of the process as a totality and realises that transformations can act on it. At this stage a person can distinguish between and compare objects arising from similar processes. A schema for a mathematical concept is a mental collection of actions, processes, objects and other schemas, which are linked to form a coherent framework for an individual (Dubinsky & McDonald 2001).
Research based on this theory requires that for a given concept the likely mental structures be identified, detected and then suitable learning activities designed to support the construction of those mental structures. One of the major tools used in APOS-based research is genetic decomposition (GD), which is a hypothetical model of mental construction that a student may need to make in order to learn a mathematical concept (Arnon et al. 2014). So, a GD postulates the particular actions, processes and objects that play a role in the construction of a mental schema for dealing with a given mathematical situation. The details of the preliminary GD used in this analysis appear below.
Genetic decomposition for operations on fractions
We draw upon Hackenberg and Lee's (2015) work in terms of fraction schemes to make sense of the action-process-object development of the concept of fractions. The fraction scheme highlighted is an iterative fraction scheme in which fractions are conceived of as multiples of unit fractions (Hackenberg 2007; Steffe & Olive 2010). For example students who have constructed an iterative fraction scheme view 2/5 as 2 times 1/5, and 7/5 as 7 times 1/5, which means these students have constructed fractional numbers (Steffe & Olive 2010). Moreover, students who have constructed iterative fraction schemes can usually solve a problem in which they are given an improper fractional number. For instance to make the whole, students need to view 14/9 as 14 times the amount they need to iterate 9 times to make the whole, which involves operations that students with iterative fraction schemes have constructed.
Prerequisite: Understanding of multiplicative concepts
How students generate and coordinate composite units is the foundation of how we understand students' multiplicative concepts. These multiplicative concepts are the interiorised results of students' units coordinating schemes as they progress from one concept to the next (Hackenberg & Lee 2015).
Prerequisite: Understanding of the concept of fraction
Action
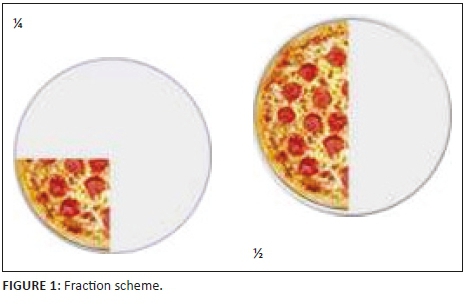
At an action level a person sees a fraction as representing a part of a whole, where the numerator is identified in terms of the number of shaded or selected equal parts while the denominator is the total number of equal parts that the whole has been divided into. At this stage the individual is able to make sense of unitising a fraction by the operation of partitioning or splitting a whole into a certain number of equal parts (Hackenberg & Lee 2015). For example, a learner can identify the figures as representing the fractions given (see Figure 1).
Process
As a learner continues working with the physical representations, the action of the operation of partitioning is interiorised so that individuals can recognise a fraction without having to physically count each part, that is, they are able to carry out the process of partitioning mentally. At a process level a learner is not restricted to a physical representation when working with fractions but can work with the symbolic representation of 3/5 as representing 3 parts out of a whole of 5 parts.
Object
The process of partitioning is encapsulated into an object when the individual is able to conceive the partitioning process as fractional numbers (Steffe & Olive 2010) upon which the multiplicative operations can be carried out. Hence at this stage an individual's conception of fractions will have been extended into an iterative fraction scheme (Hackenberg & Lee 2015), allowing him or her to make sense of the symbol 5/8, say, as being equivalent to 5 × 1/8. This flexible notion of fractions allows the individual to make sense of an improper fraction such as 11/8. The object conception also enables students to distinguish between and compare the results from different partitioning schemes. Hence the iterative fraction conception permits the individual to 'take three level of units and flexibly switch between three-levels-of-units structures' (Hackenberg & Lee 2015:206) - so, for example if a quantity is divided into units of 35, this can be represented as 5 units each composed of 7 subunits, or equivalently as 7 units each composed of 5 subunits. This iterative fraction skill is key to understanding equivalent fractions
Addition and subtraction of fractions
The mental structures for addition and subtraction are similar to each other, so we will describe them with respect to addition, but they can be the same for subtraction as well.
Action
To add fractions, a learner requires diagrams or physical representations to carry out the addition operation. The learner performs a single operation at a time, without thinking beyond the action of the single addition operation; for example, the addition operation 1/4 + 1/4 = 1/2 needs to be represented as fractions using a pizza diagram or any other figure, as shown in Figure 2.
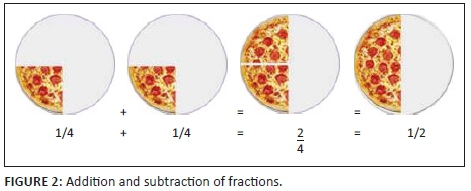
If the fractions have different denominator, say ½ and ¼, then the learner would first transform the fractions into equivalent ones that share a common denominator, so that the action of putting them together can be done. They may require a physical representation to substitute one part of size 1/4, say with two parts of size 1/8, if considering the sum 1/4 + 3/8, for example.
Process
The action of adding two fractions is interiorised into a process when a learner can carry out the addition operation without requiring physical representation. To add fractions with different denominators a learner will first transform fractions mentally or symbolically into equivalent fractions that share a common denominator so that the fractions can be added.
Object
When a learner becomes aware of the process of adding two like fractions as a totality, realises that transformations can act on that totality and can actually construct such transformations (explicitly or in one's imagination), then we say the individual has encapsulated the process of adding fractions into a cognitive object called a 'sum of fractions'. For example, a learner could find multiples of a sum of fractions or explain the properties of the sum of fractions, such as showing that the sum of fractions is commutative. At this stage a learner is able to distinguish between the results of objects arising from similar processes. Hence a learner can perceive the equivalence between the two processes of adding two fractions with different denominators - for example in finding the sum 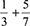 using equivalent fractions
using equivalent fractions 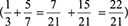 and using the algorithm
and using the algorithm 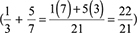 . That is, the one process that uses transformation into equivalent fractions with the same denominator first, before finding the sum, is equivalent to the algorithm for adding fractions with different denominators.
. That is, the one process that uses transformation into equivalent fractions with the same denominator first, before finding the sum, is equivalent to the algorithm for adding fractions with different denominators.
Pseudostructural conception
Sfard and Linchevski (1994) argue that sometimes learners do not progress to connecting the different mathematical relationships so as to build a coherent mathematical object. Instead of developing an object-level (or structural) understanding of a concept, they develop a pseudostructural conception. This occurs when the understanding of a concept is not sufficiently robust to be considered as structural (that is, an object conception). This may be because of some misconceptions that may interfere with the action-process-object hierarchical development of the concept proposed by APOS theory; hence a pseudostructural conception can also arise when incorrect actions are interiorised. Misconceptions are often represented at an action level because of the concepts that were misconstrued at the inception level, that is, the level at which the concept is presented to learners. The manner in which the concept is presented will determine the representation of the concept procedurally through the correct or wrong answers displayed by the learner or spoken by the learner. Usually as students are exposed to further learning opportunities and as they work on the activities, problems relating to errors associated with incorrect actions may get resolved as a natural progression. However, it may happen that an incorrect conception of an action may get interiorised into a process, giving rise to a problem that is much more difficult to address because it has become embedded into the learner's mental schema of the concept. In this study we explore some incorrect notions of addition and subtraction of fractions that appear to have become interiorised into pseudostructural conceptions.
Methodology
The participants of this study comprised 60 undergraduate full-time students, who were enrolled in a 3-year Bachelor of Education degree to become teachers. The 60 participants were enrolled in a foundational course in Mathematics because they had not passed Mathematics at Grade 12 level. This course was intended to help deepen their understanding of basic numeracy, including aspects such as operations on fractions with respect to meaning and use of representation. These students were all primary school pre-service teachers and would take on further primary Mathematics Education courses, having passed the basic course. This study was interpretative in nature as it recognised that individuals with their own varied backgrounds and experiences contribute to the ongoing construction of reality (Wahyuni 2012). Data to gauge pre-service teachers' misconceptions that permeate from addition and subtraction of fractions were obtained from the participants' responses to a written task (see Appendix 1) that was designed to probe their understanding of fractions. Participants who did not get all the items correct were invited for interviews. Ten students volunteered and thereafter met with the first author, who then conducted semi-structured interviews. In this article, we draw upon three of these interviews. The interviewees were probed generally about their understanding of fractions and more specifically about their responses to the written task.
The research question explored in this study is: What are the pre-service teachers' misconceptions that permeate from addition and subtraction of fractions that can be described using APOS theory? The preliminary GD presented in the section 'Genetic decomposition for operations on fractions' served as an analytical tool for the study.
Ethical consideration
We got the approval of the students who happen to be our student before using their script and interview extract in writing the article.
Results and discussion
The results of the activity test, which comprised two tasks with sub questions (see Appendix 1), and the interview extracts will be discussed in the following section.
Task 1
This first task (which appears in Box 1) explored the pre-service teachers' understanding of addition of fractions. The participants' percentage responses with respect to completely correct responses, wrong responses and no response are shown in Table 1.

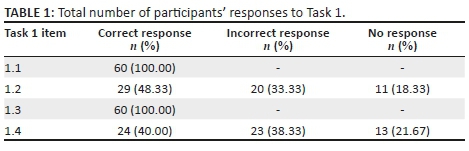
All participants responded correctly to Q1.1 and Q1.3, which involved the addition and subtraction, respectively, of fractions with the same denominator. This could indicate that all participants had developed at least an action conception of addition of fractions. However, the success rate dropped to 48.3% in Q1.2  and approximately 40.0% for Q1.4
and approximately 40.0% for Q1.4 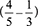 . The difference between the items is that the former items (Q1.1 and Q1.3) involved fractions with the same denominator while the latter involved fractions with different denominators. To add or subtract fractions that have different denominators, one needs to first convert the fractions into equivalent ones that share a common denominator. This involves applying the operation of subunitising the units making up the two fractions. This involves a transformation or operation on the fraction, which according to our GD can be effected only when the person sees the fraction as an object upon which transformations can take place. Drawing upon language used in recent studies (Boyce & Norton 2016; Hackenberg & Tillema 2009; Steffe 2001), forming equivalent fractions with a different denominator from the one given requires a flexible understanding of the iterative fraction scheme.
. The difference between the items is that the former items (Q1.1 and Q1.3) involved fractions with the same denominator while the latter involved fractions with different denominators. To add or subtract fractions that have different denominators, one needs to first convert the fractions into equivalent ones that share a common denominator. This involves applying the operation of subunitising the units making up the two fractions. This involves a transformation or operation on the fraction, which according to our GD can be effected only when the person sees the fraction as an object upon which transformations can take place. Drawing upon language used in recent studies (Boyce & Norton 2016; Hackenberg & Tillema 2009; Steffe 2001), forming equivalent fractions with a different denominator from the one given requires a flexible understanding of the iterative fraction scheme.
Alternatively students may opt to use the lowest common denominator (LCD) addition-subtraction algorithm, requiring that they find the LCD of the two fractions. Some of the students who worked out the addition and subtraction tasks correctly may well have opted for the algorithm so it is not possible to gauge their own understanding of fractions because the students were not interviewed and their working details did not provide sufficient evidence of the method they used. The incorrect responses, however, show that for many of the participants, it was their conception of a fraction that had hampered their progress in understanding the addition of fractions. It is clear that at least 20 participants (33.3%) who provided wrong responses to Q1.2 had not progressed past seeing a fraction as two numbers separated by a line and had not developed a process (or partitive fraction). Of the 20 participants, eight participants wrote down the question but could not solve further, while the other 12 participants displayed a common misconception of using fractions as two separate whole numbers, as illustrated by T57's response in Figure 3.

Participant T57 was interviewed about his approach to addition. See response in Box 2, where T57 stands for Participant T57 and A is the first author of the article.

T57 explained that he got the answer he did considering the sum as two whole number sums: the sum of the two numerators and the sum of denominators. The response of T25, which appears in Figure 2, illustrates similar reasoning.
Siegler et al. (2013) argue that the learning of fractions requires a reorganisation of one's numerical conceptions because children who have not learnt fractions yet assume that properties of whole numbers hold for all numbers. In the case of this common misconception, it is evident that the students such as T57 and T25 incorrectly applied properties of whole numbers in two disconnected procedures applied separately to the numbers appearing above the line and the ones appearing below the line. The responses illustrate that the students have not been able to consider the issue of fractional value or magnitude of fraction, key ideas that form a foundation for further work in fraction operations (Cramer et al. 2002. Moreover, Bailey et al. (2015) argue that learners who do not understand the fractional value are significantly disadvantaged in studying fraction procedures because they cannot predict arithmetical relationships. For example (using Figure 3, in adding 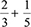 , the result should be greater than
, the result should be greater than 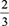 ; thus, the students would think again about the answer of
; thus, the students would think again about the answer of  because
because  is far smaller than
is far smaller than 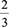 . Similarly, if Participant T25 in Figure 4 understood the concept of magnitude of fractions, he would have reasoned that the difference between two fractions, both of which are less than one, could not be greater than one. The indication of the responses in Figures 3 and 4 is an indication that the pre-service teachers did not understand that the need for a common unit is universal for all addition and subtraction; they could not readily connect their understanding of whole number addition to other number systems, such as fractions. Therefore they were unable to build a central conceptual framework for understanding the principles of addition and subtraction across all number systems.
. Similarly, if Participant T25 in Figure 4 understood the concept of magnitude of fractions, he would have reasoned that the difference between two fractions, both of which are less than one, could not be greater than one. The indication of the responses in Figures 3 and 4 is an indication that the pre-service teachers did not understand that the need for a common unit is universal for all addition and subtraction; they could not readily connect their understanding of whole number addition to other number systems, such as fractions. Therefore they were unable to build a central conceptual framework for understanding the principles of addition and subtraction across all number systems.

We now look in more detail at the interview with Participant T25, which provides more insight into his conception of fractions and the operations of addition and subtraction. In the interview, Participant T25 was asked to explain the idea of a fraction (see Box 3).

The extract in Box 2 shows that T25 does not consider it important for the pieces, and being compared in the fraction, to be equal. His response is a counter indication of an understanding of the part-whole fractional conception (Norton & Wilkins 2009). Boyce and Norton (2016) describe the part-whole conception as the first of five fraction conceptions (schemes), which seem to develop in sequence. Clearly Participant T25, almost 20 years after being introduced to fractions, was still missing a key idea underpinning the part-whole conception: a fraction is the ratio of the number of equal parts in a selected group to the number of equal parts in a larger group.
The interview proceeded to the subject of addition and subtraction of fractions with the same denominator (see Box 4).
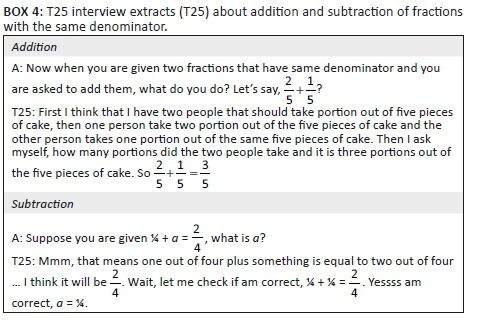
As explained in Box 3, T25 can bring selected parts of a group together and add up (or take away) the number of selected pieces and compare it to the total number of pieces in the bigger group. Hence his action level conception of a fraction allows him to consider adding or subtracting fractions as long as the denominators are the same. However, as seen in Figures 3 and 4, this limited conception does not allow him to work out the sum or difference fractions that do not have the same denominator.
The participant's explanations of addition and subtraction of two fractions which have different denominators appear in Box 5.

The extract in Box 4 shows that, when asked about addition and subtraction of fractions that have different denominators, T25 still tried to explain them in terms of the number of selected pieces divided by a new total of pieces. However, the total number of pieces that T25 referred to was not linked to the actual situation of counting the physical pieces. T25 recognised that his answer 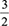 did not make sense but thought it was a problem with the task given and not with his own interpretation. There was no longer one whole but two wholes (represented by the two situations), which T25 could not account for. Hence, because his understanding of fractions remained at the action level, it did not allow him to explain the procedure of adding or subtracting in terms of his number of selected pieces over the total number of pieces conception. Hence he could not progress further than adding two fractions with the same denominator. His explanation about subtraction is consistent with the written response in Figures 3 and 4, being the same as his verbal explanation. Notably, he had no scheme to provide an explanation of subtraction when the first denominator was smaller than the second one and deduced that the answer was zero.
did not make sense but thought it was a problem with the task given and not with his own interpretation. There was no longer one whole but two wholes (represented by the two situations), which T25 could not account for. Hence, because his understanding of fractions remained at the action level, it did not allow him to explain the procedure of adding or subtracting in terms of his number of selected pieces over the total number of pieces conception. Hence he could not progress further than adding two fractions with the same denominator. His explanation about subtraction is consistent with the written response in Figures 3 and 4, being the same as his verbal explanation. Notably, he had no scheme to provide an explanation of subtraction when the first denominator was smaller than the second one and deduced that the answer was zero.
It is clear that the participant's understanding of fractions was embedded within the physical representation of the number of selected pieces divided by the total number of pieces, and the action had not been interiorised. The fraction was not seen as an object upon which transformations can be carried out, and the participants were unable to distinguish between the object arising from the process of addition or subtraction of fractions with the same denominator and the object arising from the process of addition or subtraction of fractions with different denominators. Because the participant did not understand the part-whole relationship between the numerator and the denominator, he treated these numbers as whole numbers. He instead constructed a pseudostructural conception to help him deal with addition or subtraction of fractions with different denominators. However, when subtracting part-whole fractions, they must attend to the unit (the number of pieces the whole has been partitioned into) before subtracting quantities. As learners transition from whole numbers to other number systems, including fractions, explicit attention to and naming of the unit is important so that they develop this understanding. Although unit fractions have not typically been a central focus in fraction teaching in South Africa, according to researchers like Pienaar (2014), students need to be able to think of 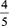 as '4 one-fifth units', which is necessary in an iterative fraction conception (Boyce & Norton 2016). The responses discussed in Figures 3 and 4 are an indication that pre-service teachers did not understand the need for a common unit or for the operation of unitising the two fractions into a common unit.
as '4 one-fifth units', which is necessary in an iterative fraction conception (Boyce & Norton 2016). The responses discussed in Figures 3 and 4 are an indication that pre-service teachers did not understand the need for a common unit or for the operation of unitising the two fractions into a common unit.
Task 2
The second task, presented in Box 6, explored the participants' understanding of multiplication and addition of fractions. The results for the tasks are presented in table 2.
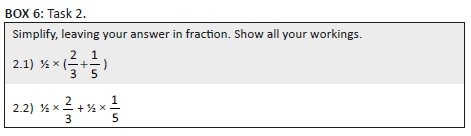
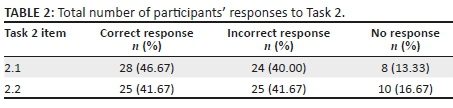
Box 6 shows that 46.7% of the participants solved Q2.1 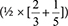 correctly, while 41.7% completed the Q2.2 correctly. The responses revealed similar errors with fraction addition as those identified in the previous task. We look in more detail at the response of Participant T38 (Figure 5), which is followed by extracts from the interview with her.
correctly, while 41.7% completed the Q2.2 correctly. The responses revealed similar errors with fraction addition as those identified in the previous task. We look in more detail at the response of Participant T38 (Figure 5), which is followed by extracts from the interview with her.
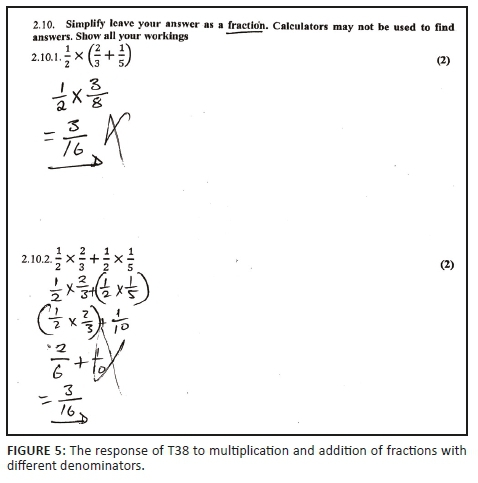
Figure 5 shows that the participant followed the BODMAS (bracket, of, division, multiplication, addition and subtraction) rule by adding the fractions inside the bracket first (this is the correct procedure done by all the participants in the incorrect response group). Her method of adding was incorrect because she applied whole number addition to the two numerators and denominators. Her multiplication was done correctly. The fascinating aspect of this response is that the incorrect method of adding the fractions was done so consistently in the two questions that she obtained the same result for both. Box 7 presents the dialogue between the author and Participant T38 in the interview.

The response from the interview confirmed that the student had used the method of whole number addition applied to the numerators and denominators. The written response of, and interview with, Participant T38 shows how strongly embedded her pseudostructural conception of addition of fractions had become. Hence it is clear that this incorrect method had become interiorised into a pseudostructural 'process' to the extent that she was able to carry out transformations on this 'process' of addition of a fraction by multiplying it by other fractions, using the correct method. In fact she obtained the same answer to both problems using this pseudostructural rule, based on whole number addition. That is, she showed that with her rule in Equation 1 it was true that:

This relationship is true in general for fraction multiplication and addition because the operation of multiplication is distributive over addition. The question that arises is whether this result will hold true in general if the incorrect rule is used. In other words, using this incorrect rule for fraction addition, will multiplication be distributive over this incorrect addition rule? To see this, given fractions 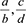 and
and 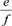 , using the participant's pseudostructural rule, we investigate the product of
, using the participant's pseudostructural rule, we investigate the product of 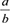 and the sum of the other two fractions,
and the sum of the other two fractions, 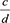 and
and 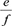 , and get the result for Q2.1 in Equation 2:
, and get the result for Q2.1 in Equation 2:
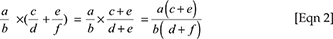
Now if we work out the sum of the products in Q2.2, the result is shown by Equation 3:
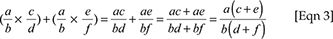
The algebraic verification shows that the participant's consistent application of her pseudostructural rules gives rise to the same incorrect answer of 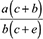 for both Question 2.1 and Question 2.2.
for both Question 2.1 and Question 2.2.
Hence, it can be seen that the correct rule for multiplication is actually distributive over the pseudostructural rule of addition. This distributive property helps us to understand how this incorrect rule has become so widely used and applied. It is closely aligned to whole number addition facts and satisfies certain properties that are satisfied by the correct rule.
Concluding comments
This article studied 60 pre-service teachers' responses to questions involving the basics of fractions. The questions involved operations on fractions with the same denominator and fractions with different denominators, in order to explore their mental constructions of the understanding of operations on fractions using APOS theory. The findings reveal that many teachers were able to answer those items requiring action level engagement with the addition and subtraction of fractions with the same denominator but struggled with those that required higher levels of engagement. Although all the participants answered Items 1.1 and 1.3 correctly, more than 52% of the participants could not respond correctly to Items 1.2 and 1.4, indicating that the participants had not developed object-level conceptions of addition and subtraction of fractions. The analysis of the responses and the interviews showed that a common reason for the non-encapsulation of addition and subtraction of fractions was because of their weak conceptions of what a fraction entails. For many students their notion of fractions was that of a numerator, which represents the number of selected pieces, and a denominator, which represents the total number of pieces. A key idea that was missing from this fraction conception was the notion of the equality of the pieces: a fraction is the ratio of the number of equal parts in a selected group to the number of equal parts in a larger group.
It is likely that for these students their learning experiences neglected the action level of development of the part-whole conception of fractions. The addition of fractions could not make sense beyond working with like fractions. They were able to add fractions with the same denominators by considering the action of putting pieces together, without having to check the sizes of the pieces. However, this conception does not work for addition of fractions with different denominators, because the difference in denominators means that the sizes of the pieces are different, so putting together pieces of different sizes cannot lead to a measurement of a fraction. Instead some students, such as T38, had instead interiorised an incorrect rule for addition (and subtraction) of fractions with different denominators that arose from their idea of portions of a cake. So  was seen as 2 parts out of a total of 3 parts, while
was seen as 2 parts out of a total of 3 parts, while  is seen as one part of another five parts, and adding them means getting three parts out of a new total of eight parts. This resulted in a strongly embedded pseudostructural rule for addition and subtraction. The rule was based on whole number addition and it was shown to satisfy the property of fraction multiplication, being distributive over the incorrect fraction addition rule.
is seen as one part of another five parts, and adding them means getting three parts out of a new total of eight parts. This resulted in a strongly embedded pseudostructural rule for addition and subtraction. The rule was based on whole number addition and it was shown to satisfy the property of fraction multiplication, being distributive over the incorrect fraction addition rule.
There is much concern in the literature about the poor background of primary school learners in basic Mathematics, which hinders them from progressing sufficiently in higher-level Mathematics (Hckenburg & Tillema 2009; Siegler et al. 2013; Steffe 2001). There is also concern that primary school teachers may not have sufficiently strong subject matter knowledge themselves (Mupa & Chinooneka 2015; Van Steenbrugge et al. 2014). This study has shown that some primary school teachers have misconceptions about the basic operations on fractions and can work only in an externally driven manner (action level) on fraction operations. More alarming is the fact that these incorrect procedures have become interiorised by these students, becoming deeply embedded in their mental schema. Hence they may unwittingly teach these incorrect versions to their learners when they start teaching, if these misconceptions are not confronted and resolved. This study recommends that programmes for upgrading pre-service teachers should be carefully structured to allow them to work with basic concepts such as the basic operations in fractions. The quality and target of the learning opportunities afforded to the pre-service teachers should be evaluated, so that such strong misconceptions can be addressed.
References
Arnon, I., Cottrill, J., Dubinsky, E., Oktac, A., Fuentes, S, R., Trigueros, M. et al., 2014, APOS theory. A framework for research and curriculum development in Mathematics education. Springer, New York.
Bailey, D.H., Zhou, X., Zhang, Y., Cui, J., Fuchs, L.S., Jordan, N.C. et al., 2015, 'Development of fraction concepts and procedures in U.S. and Chinese children', Journal of Experimental Child Psychology 129, 68-83. https://doi.org/10.1016/j.jecp.2014.08.006 [ Links ]
Bansilal, S., Brijlall, D. & Trigueros, M., 2017, 'An APOS study on pre-service teachers' understanding of injections and surjections', The Journal of Mathematical Behaviour48, 22-37. https://doi.org/10.1016/j.jmathb.2017.08.002 [ Links ]
Baumert, J., Kunter, M., Blum, W., Brunner, M., Voss, T., Jordan, A. et al., 2010, 'Teachers' mathematical knowledge, cognitive activation in the classroom, and student progress', American Educational Research Journal 45(1), 133-180. https://doi.org/10.3102/0002831209345157 [ Links ]
Borko, H., Eisenhart, M. Brown, C.A., Underhill, R.G., Jones, D. & Agard, P.C., 1992, 'Learning to teach hard mathematics: Do novice teachers and their instructors give up too easily?', Journal for Research in Mathematics Education 23, 194-222. https://doi.org/10.2307/749118 [ Links ]
Boyce, S. & Norton, A., 2016, 'Co-construction of fractions schemes and units coordinating structures', The Journal of Mathematical Behavior 41, 10-25. https://doi.org/10.1016/j.jmathb.2015.11.003 [ Links ]
Bruce, C., Chang, D. & Flynn, T., 2013, Foundations to learning and teaching fractions: Addition and subtraction, Ontario Ministry of Education, Ontario
Charalambous, C.Y. & Pitta-Pantazi, D., 2007, 'Drawing on a theoretical model to study students' understandings of fractions', Educational Studies in Mathematics 64, 293-316. https://doi.org/10.1007/s10649-006-9036-2 [ Links ]
Chinnappan, M., 2000, 'Preservice teachers' understanding and representation of fractions in a JavaBars environment', Mathematics Education Research Journal 12(3), 234-253. https://doi.org/10.1007/BF03217087 [ Links ]
Chinnappan, M. & Forrester, T., 2014, 'Generating procedural and conceptual knowledge of fractions by pre-service teachers mathematics education research group of Australasia', Mathematics Education Research Journal 26,871-896. https://doi.org/10.1007/s13394-014-0131-x [ Links ]
Cramer, K., Behr, M., Post, T. & Lesh, R., 2009, Rational number project: Initial fraction ideas, Originally published in 1997 as Rational Number Project: Fraction Lessons for the Middle Grades - Level 1, Kendall/Hunt Publishing Co., Dubuque, IA.
Cramer, K. & Wyberg, T., 2009, 'Efficacy of different concrete models for teaching the part-whole construct for fractions', Math, Think, Learn 11(4), 226-257. https://doi.org/10.1080/10986060903246479 [ Links ]
Cramer, K.A., Post, T.R. & Del Mass, R.C., 2002, 'Initial fraction learning by fourth- and fifth-grade students: A comparison of the effects of using commercial curricula with the effects of using the rational number project curriculum', Journal for Research in Mathematics Education 33(2), 111-144. [ Links ]
Depaepe, F., Torbeyns, J., Vermeersch, N., Janssens, D., Janssen, R., Verschaffel, L. et al., 2015, 'Teachers' content and pedagogical content knowledge on rational numbers: A comparison of prospective elementary and lower secondary school teachers', Teaching and Teacher Education 47, 82-92. https://doi.org/10.1016/j.tate.2014.12.009 [ Links ]
Dubinsky, E., 1991, 'Reflective abstraction in advanced mathematical thinking', in D. Tall (ed.), Advanced Mathematical thinking, pp. 231-250, Kluwer, Dordrecht.
Dubinsky, E. & McDonald, M.A., 2001, 'APOS: A constructivist theory of learning in undergraduate mathematics education research', in D. Holton (ed.), The teaching and learning of mathematics at university level: An ICMT study, Kluwer, Dordrecht, viewed from http://www.math.kent.eds-edd/ICMIpaperr.pdf
Hackenberg, A. J., 2007, Units coordination and the construction of improper fractions: A revision of the splitting hypothesis, Journal of Mathematical Behavior, 26(1), 27-47. https://doi.org/10.1016/j.jmathb.2007.03.002 [ Links ]
Hackenberg, A.J. & Lee, M.Y., 2015, 'Relationships between students' fractional knowledge and equation writing', Journal for Research in Mathematics Education 46(2), 196-243. https://doi.org/10.5951/jresematheduc.46.2.0196 [ Links ]
Hackenberg, A.J. & Tillema, E.S., 2009, 'Students' whole number multiplicative concepts: A critical constructive resource for fraction composition schemes', Journal of Mathematical Behaviour 28, 1-18. https://doi.org/10.1016/j.jmathb.2009.04.004 [ Links ]
Hansen, A., Drews, D., Dudgeon, J., Lawton, F. & Surtees, L., 2014, Children's errors in Mathematics, Learning Matters, England, London.
Hansen, A., Drews, D., Dudgeon, J., Lawton, F. & Surtees, L., 2017, Children's errors in Mathematics, Learning Matters, England, London.
Hecht, S., Close, L. & Santisi, M., 2003, 'Sources of individual differences in fraction skills', Journal of Experimental Child Psychology 86, 277-302. https://doi.org/10.1016/j.jecp.2003.08.003 [ Links ]
Isik, C. & Kar, T., 2012, 'An error analysis in division problems in fractions posed by pre-service elementary mathematics teachers', Kuram ve Uygulamada Egitim Bilimeiri12(3), 2303-2309. [ Links ]
Ji-Won, S. & Ji-eun, L., 2016, 'Pre-service teachers' understanding of fraction multiplication, representational knowledge and computational skills', Mathematics Teacher Education and Development 18(2), 5-28. [ Links ]
Krauss, S., Baumert, J. & Blum, W., 2008, 'Secondary mathematics teachers' pedagogical content knowledge and content knowledge: Validation of the COACTIV constructs', The International Journal on Mathematics Education 40(5), 873-892. https://doi.org/10.1007/s11858-008-0141-9 [ Links ]
Ma, L., 1999, Knowing and teaching elementary mathematics: Teachers' understanding of fundamental mathematics in China and the United States, Erlbaum, Mahwah, NJ.
Mupa, P. & Chinooneka, T.I., 2015, 'Factors contributing to ineffective teaching and learning in primary schools: Why are schools in decadence?', Journal of Education and Practice 19(6), 125-132. [ Links ]
Ndlovu, Z. & Brijlall, D., 2015, 'Pre-service teachers' mental constructions of concepts in matrix algebra', African Journal of Research in Mathematics, Science and Technology Education 19(2), 156-171. https://doi.org/10.1080/10288457.2015.1028717 [ Links ]
Newton, K.J., 2008, 'An extensive analysis of pre-service elementary teachers' knowledge of fractions', American Educational Research Journal 45(40), 1080-1110. https://doi.org/10.3102/0002831208320851 [ Links ]
Norton, A. & Wilkins, J.L.M., 2009, 'A quantitative analysis of children's splitting operations and fraction schemes', Journal of Mathematical Behavior 28(2-3), 150-161. https://doi.org/10.1016/j.jmathb.2009.06.002 [ Links ]
Pienaar, E., 2014, 'Learning about and understanding fractions and their role in the High School Curriculum', Thesis presented in fulfilment of the requirement for the degree of Master of Education Curriculum Studies at Stellenbosch University. [ Links ]
Rothstein, A., Rothstein, E. & Lauber, G., 2006, Write for Mathematics, Corwin Press, New York.
Sfard, A. & Linchevski, L., 1994, 'Between arithmetic and algebra: In the search of a missing link, the case of equations and inequalities', WALTI 52(3), 279-307. [ Links ]
Shulman, L., 1987, 'Those who understand: Knowledge growth in teaching', Educational Researcher 15(2), 4-14. https://doi.org/10.3102/0013189X015002004 [ Links ]
Siegler, R.S., Fazio, L.K., Bailey, D.H. & Zhou, X., 2013, 'Fractions: The new frontier for theories of numerical development', Trends in Cognitive Sciences 17(1), 13-19. https://doi.org/10.1016/j.tics.2012.11.004 [ Links ]
Siegler, R.S. & Pyke, A.A., 2013, 'Developmental and individual differences in understanding of fractions', Developmental Psychology 49(10), 1994-2004. https://doi.org/10.1037/a0031200 [ Links ]
Smith, J. P., III, & Thompson, P. W., 2008, Quantitative reasoning and the development of algebraic reasoning, In J. J. Kaput, D. W. Carraher, & M. L. Blanton (Eds.), Algebra in the early grades, pp. 95-132, New York, NY: Lawrence Erlbaum
Son, J. & Crespo, S., 2009, 'Prospective teachers' reasoning about students' non-traditional strategies when dividing fractions', Journal of Mathematics Teacher Education12(4), 236-261. https://doi.org/10.1007/s10857-009-9112-5 [ Links ]
Son, J. & Sinclaire, N., 2010, 'How pre-service teachers interpret and respond to student geometric errors', School Science and Mathematics 110(1), 31-46. https://doi.org/10.1111/j.1949-8594.2009.00005.x [ Links ]
Stafylidou, S. & Vosniadou, S., 2004, 'The development of students' understanding of the numerical value of fractions', Learning and Instruction 14, 503-518. https://doi.org/10.1016/j.learninstruc.2004.06.015 [ Links ]
Steffe, L.P., 2001, 'A new hypothesis concerning children's fractional knowledge', The Journal of Mathematical Behavior 20(3), 267-307. https://doi.org/10.1016/S0732-3123(02)00075-5 [ Links ]
Steffe, L.P. & Olive, J., 2010, Children's fractional knowledge, Springer, New York, NY.
Tobias, J.M., Olanoff, D. & Lo, J.-J., 2012, 'A research synthesis of preservice teachers' knowledge of multiplying and dividing fractions, pp. 668-673, Proceedings of the 34th Annual Meeting of PME-NA, PME-NA, Kalamazoo, MI.
Toluk-Ucar, Z., 2009, 'Developing pre-service teachers understanding of fractions through problem posing', Teaching and Teacher Education: An International Journal of Research and Studies 25(1), 166-175. https://doi.org/10.1016/j.tate.2008.08.003 [ Links ]
Van Steenbrugge, H., Lesage, E., Valcke, M. & Desoete, A., 2014, 'Preservice elementary school teachers' knowledge of fractions: A mirror of students' knowledge', Journal of Curriculum Studies 46(1), 138-161. https://doi.org/10.1080/00220272.2013.839003 [ Links ]
Van Steenbrugge, H., Valcke, M. & Desoete, A., 2010, 'Mathematics learning difficulties in primary education: Teachers' professional knowledge and the use of commercially available learning packages', Educational Studies 36(1), 59-71. [ Links ]
Wahyuni, D., 2012, 'The research design maze: Understanding paradigms, cases, methods and methodologies', Journal of Applied Management Accounting Research10(1), 69-80. [ Links ]
Wong, M. & Evans, D., 2007, 'Students' conceptual understanding of equivalent fractions', in J. Watson & K. Beswick (eds.), Mathematics: Proceedings of the 30th Annual Conference of the Mathematics Education Group of Australasia, p. 824-833.
Zhou, Z., Peverly, S.T. & Xin, T., 2006, 'Knowing and teaching fractions: A cross-cultural study of American and Chinese Mathematics teachers', Contemporary Educational Psychology 31(4), 438-457. [ Links ]
 Correspondence:
Correspondence:
Ifunanya Ubah
adaichieify2000@gmail.com
Received: 05 May 2017
Accepted: 31 Aug. 2018
Published: 29 Nov. 2018
Appendix 1: Activity test items.
Task 1

Task 2















