ORIGINAL RESEARCH

 

Foundation phase teachers' use of manipulatives to teach number concepts: A critical analysis

 

 

Lindiwe M. Mntunjani^I; Stanley A. Adendorff^II; Sibawu W. Siyepu^II

^IWestern Cape Education Department, South Africa
^IIFaculty of Education, Cape Peninsula University of Technology, South Africa

Correspondence

 

 

---

ABSTRACT

BACKGROUND: The poor performance of learners in mathematics has long been a matter of concern in South Africa. The Annual National Assessment (ANA) results reveal that the problem starts in the foundation phase with number concepts
AIM: This research sought to ascertain how foundation phase teachers used mathematical resources to teach number concepts as this may be one of the contributors to poor mathematics results
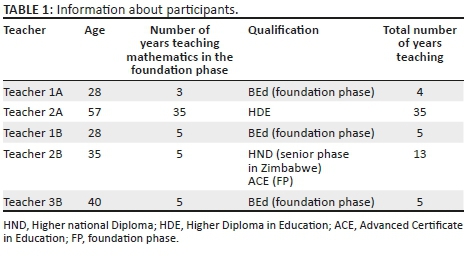
SETTING: The purposively selected participants included five foundation phase teachers teaching Grades 1-3 at two schools in the Western Cape, in South Africa
METHODS: The research was located within the interpretive qualitative research paradigm and used a case study approach. Data were collected through lesson observations and interviews and analysed through the lens of Vygotsky's sociocultural theory
RESULTS: The findings of this study revealed that teaching for understanding was often compromised by teaching to enable learners to pass systemic assessments. Teachers are inclined to rote teaching with drill work in preparation for assessments such as the ANA and the systemic assessment. Consequently, manipulatives are not necessarily used optimally or opportunely
CONCLUSION: This study recommends that teachers should receive the necessary training to use and follow Vygotsky's Zone of Proximal Development and also make an effort to follow the guidelines indicated in the Curriculum and Assessment Policy Statement mathematics document in respect of how and when to use practical mathematical manipulatives

---

 

 

Introduction and background

The use of systemic tests and Annual National Assessments (ANA) to measure learners' performance in Mathematics have put pressure on teachers to reflect on their teaching strategies and look for ways to ensure that all their learners are taught effectively. This article reports on teachers' use of concrete manipulatives (resources), as opposed to virtual manipulatives (Cockett & Kilgour 2013), in teaching number concepts. As a foundation phase teacher, the first author has always understood the importance of using mathematical manipulatives to support learning in the classroom. She is aware that teaching learners mathematics is a step-by-step process, which requires the selection of appropriate manipulatives to support every concept taught. This is supported by many researchers who believe that concrete materials help learners to learn mathematics concepts (Drews 2007:20; Paparistodemou, Potari & Pitta-Pantanzi 2014:3; Van de Walle 2007). Working with concrete materials helps to enable learners to decompose complicated concepts to the level of their understanding and improves performance on mathematical tasks (Martin, Lukong & Reaves 2007:2).

Various descriptions exist of what concrete manipulatives mean. A more comprehensive description is that of Moyer (2001:176) who describes concrete manipulatives as '… objects designed to represent explicitly and concretely mathematical ideas that are abstract. They have both visual and tactile appeal and can be manipulated by learners through hands-on experiences'. The availability and use of concrete mathematical manipulatives should be matched by a good understanding of how and when these manipulatives should be used, as different manipulatives serve different functions at different times and in different grades (Mtetwa 2005:255). For example, flard cards are sometimes used for calculation when their primary purpose is to support the learning of place value (CAPS 2011:247).

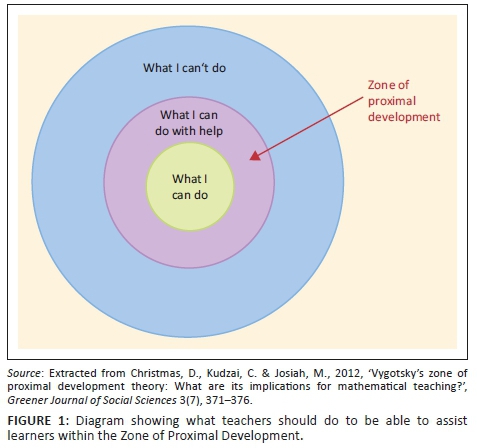
Thus this study explores learners' understanding of number concepts in foundation phase classrooms, in terms of how concrete manipulatives are applied to facilitate conceptualisation and understanding. Number concepts form the foundation for all other mathematical concepts, and proficiency in this area has long been one of the main objectives of teaching and learning mathematics in both school and university (Engelbrecht, Bergsten & Kågesten 2009:928). The aim of this research was to investigate foundation phase teachers' use of various mathematical manipulatives in teaching number concepts in one district of the Western Cape, South Africa. The focus was the question of how these concrete manipulatives were used to promote the understanding of number concepts and support the learning of number concepts. The study examines the use of counters, bead strings, abacuses, base ten blocks, number lines, number charts, number tracks (see Figure 1) and Department of Education (DoE) rainbow workbooks.

 

 

 

Contexts that informed this study

The poor performance of South African learners in mathematics is a major concern (Siyepu 2013:1). Findings based on the results obtained from the Western Cape Education Department from the systemic mathematics evaluation in Grade 3 and Grade 6, conducted every year in September between 2010 and 2013, revealed that the learners at the school at which the second author was a teacher performed poorly in mathematics. Less than half of the learners obtained a pass rate of 50% for mathematics in the years 2010 to 2013. This suggests that the teaching methods used were not actually producing the required results.

There are five content areas to be covered in the foundation phase, as stipulated in the Mathematics Curriculum and Assessment Policy Statement (CAPS 2011:10-11), namely number, operations and relationships; patterns, functions and algebra; space and shape; measurement; and data handling. This study only focused on the content area dealing with number, number operations and relationships.

There are several factors that contribute to the poor performance of learners in mathematics in a South African context. These include the tendency to blame poor teaching approaches, learners who study mathematics in a second language, socio-economic factors, qualifications of parents and lack of qualified mathematics teachers in the foundation phase (Siyepu 2013). Several researchers mention the inadequacy of teaching and learning manipulatives in terms of use and application (Back 2013; Clements 1999; Cope 2015). Apart from the fact that it is hard to find studies that report on the use of manipulatives in foundation phase mathematics classrooms in a South African context, the question is also whether such manipulatives are used optimally. The teaching of number concepts is fundamental in developing learners' understanding of mathematics, and consequently, the use of manipulatives to teach number concepts to enhance learning and facilitate understanding is the focus of this study.

Answers to the following research question are consequently sought: How do foundation phase teachers use mathematical manipulatives to teach number concepts? The rationale for this research is furthermore strengthened by the following pertinent questions, based on the research findings emphasised by Back (2013) in the paper entitled 'Manipulatives in the primary classroom': Do learners experience the use of manipulatives as more pleasant? Were learners more active, more involved and interested when manipulatives were used? Did teachers merely use manipulatives as secondary tools and crutches? Did teachers manage manipulatives in a way that allowed learners to make sense and that advanced mathematical thinking and reasoning? Did teachers afford learners the opportunity to use manipulatives to demonstrate a result or solution to a peer or to support his or her own line of reasoning?

 

Educationists' views of concrete mathematics manipulatives

Performance of learners in mathematics is aligned to understanding of number concepts rooted in the foundation phase. The literature review focuses on pertinent aspects related to the teaching of number concepts as encountered during the course of this study, the different types of concrete manipulatives used in a mathematical classroom and the use of concrete mathematical manipulatives reflected in past research literature.

As previously stated, the number content area forms the foundation for all the other content areas in the foundation phase. In order for teachers to lay a firm foundation for learners, number concepts should be taught and understood well. Subsequently, learners' chances of success in other content areas would increase substantially. Locuniak and Jordan (2008:453) agree that number concepts and working memory in the foundation phase would be a strong predictor of later fluency in calculations.

The selection and effective use of appropriate mathematical resources require careful consideration and planning on the part of the teacher (Drews 2007:21). Drews (2007:19) argues that 'it has been common practice for foundation teachers to view the use of resources as an essential part of teaching and learning mathematics'. Edwards (1998) argues that mathematical understanding is brought on by connections made between the modes of representations. Despite that, practical activity has a clear role in helping learners' mathematical development. Anghileri (2000) cautions against an overuse of concrete material. Anghileri argues that:

it is important that learners do not come to rely on using concrete materials for modelling number but that they develop mental imagery associated with these materials and can then work with 'imagined' situations. (p. 10)

The mere use of manipulatives does not necessarily mean that desired outcomes such as promoting understanding and enhancing knowledge of mathematical concepts will be achieved (Van de Walle, Karp & Bay-Williams 2010:29). Mathematics is not just about completing sets of exercises or following processes that the teacher explains, but rather generating strategies for solving problems, applying those strategies to help solve problems and checking to see whether the answers make sense. As Van de Walle, Karp & Bay-Williams et al. (2014:12) assert, 'mathematics in the classroom should closely model how mathematics is done and used in the real world'.

Many foundation phase classrooms employ concrete mathematical manipulatives such as number charts, number lines, counters, Dienes blocks and Cuisenaire rods. These mathematical manipulatives are designed to represent and develop mathematical concepts. However, it is not always easy for young children to connect concrete objects such as blocks, beans and sticks, with mathematical concepts (Paek 2012:2). The ineffective use of resources often happens when teachers 'tell learners exactly what to do and how to use the resources' (Van de Walle et al. 2010:29). This teaching style does not promote understanding so much as rote learning. Thus, Van de Walle et al. (2010:29) cautions against 'the natural temptation by teachers to take out the materials and [show] children exactly how to use them'. Although learners need the direction of teachers in using resources, too much directing from teachers can be harmful. Too much direction on the use of resources or models can lead to learners depending on them and using them as 'answer-getting devices rather than tools to explore a concept' (Van de Walle et al. 2010:29).

Manipulatives can be helpful to young children when they are used correctly (Boggan, Harper & Whitmire 2010:3). The material may be concrete, but the knowledge that learners need to acquire is conceptual. Therefore, it is important to know what materials to use, when to use them and how to use them in order to help children understand the mathematical concepts being taught (Boggan et al. 2010:3). Specific mathematical resources are designed to represent specific mathematical ideas that are abstract. They can be used as models by both teachers and learners as they hold a visual and tactile appeal and as such are designed primarily for hands-on manipulation (Drews 2007:21).

Contrasting views, referred to as 'inconsistencies … within the manipulation-based literature' by Carbonneau, Marley and Selig (2013:396) of the benefits of concrete manipulatives exist as far as the teaching and learning of mathematics are concerned. Whilst some researchers claim it to have particular benefits (Back 2013; Carroll & Porter 1997; Clements 1999), others do not share the same view and experienced the use thereof to be limiting and overrated (McNeil & Jarvin 2007; Uttal 2003; Uttal, Scudder & DeLoache 1997). It is reported by Uttal et al. (1997:38) that 'research on the effectiveness of manipulatives has failed to demonstrate a clear, consistent advantage for manipulatives over more traditional methods' of teaching. In this regard, they mention the research of Grupe, Huffman and Barry (1996), Hiebert and Carpenter (1992) and Sowell (1989).

In contrast, some of the older studies by Heddens (1986), Picciotto (1998) and Sebesta and Martin (2004) report that the use of manipulatives over a long period of time showed learners made improvements in respect of articulating mathematical thinking, discussion of mathematical concepts and ideas, thinking divergently to find alternate methods to solve problems, ability to use a number of different mathematical symbols when solving problems and making presentations and increase in confidence. More specifically, with respect to number concept development, Clements (1999) found concrete manipulatives to help learners to count; Phillips (1989) found manipulatives to increase learners' understanding of place value; Carroll and Porter (1997) claimed that learners seemed to grasp and remember computational skills more completely if manipulatives were used.

Later studies corroborate older research findings on the benefits of concrete mathematical manipulative, such as the research project by Cockett and Kilgour (2015:47), which investigated whether the use of manipulatives in combination with activity worksheets enhanced 32 learners' understanding and increased engagement, efficiency and enjoyment doing mathematics than only using worksheets. Their research results revealed that learners showed increased engagement when manipulatives were used 'and that their perception of their learning environment improved in the areas of enjoyment, understanding and efficiency'.

Research by Carbonneau et al. (2013:380), titled 'A meta-analysis of the efficacy of teaching mathematics with concrete manipulatives', can be considered a seminal work that importantly compared the use of concrete manipulatives with abstract teaching approaches limited to the use of symbols only. Their findings show 'small- to medium-sized effect' (2013:396) on learning of mathematics when compared with abstract teaching strategies that use mathematical symbols only. Furthermore, the strength of this effect using manipulatives depends upon other teaching variables:

such [as] the perceptual richness of an object, level of guidance offered to [learners] during the learning process, and the development status of [how] the learner moderate the efficacy of manipulatives. (p.391)

 

Vygotsky's sociocultural theory as theoretical underpinning

This study uses Vygotsky's (1978) sociocultural theory and one of its constructs, the Zone of Proximal Development (ZPD), as the lens through which the lessons were observed and interview data were analysed. Vygotsky's sociocultural theory is based on the idea that 'knowledge represents a permanent construction, reconstruction and deconstruction of reality', depending on the experiences of each individual (Alexandru 2012:19). This theory takes into account the important role that society plays in individual development and how learning is largely dependent on the social environment (Hall 2007:94; Siyepu 2013). 'Interactive learning and other informal activities are particularly important contexts in which adults provide children with new information, support their skill development and extend their conceptual understanding' (Ramani & Siegler 2014:2).

The ZPD is one of Vygotsky's (1978) sociocultural tenets (Christmas, Kudzai & Josiah 2012). Vygotsky (1978) defines the ZPD as:

the distance between the actual development level as determined by independent problem solving and the level of potential development as determined through problem solving under adult guidance, or collaboration with the more capable peers. (p. 86)

The ZPD relates to knowledge that a learner is capable of learning with appropriate teaching, support and guidance by a more knowledgeable other (Wright et al. 2006:28). This guidance is also referred to as 'other-regulation' and includes both 'implicit and explicit' mediation involving varying levels of assistance (Lantolf & Thorne 2006:200).

As mentioned before, Vygotsky (1978) believes that interaction with other people and people who know more (more knowledgeable others) will mediate between a learner and what a learner needs to learn (Christmas et al. 2012:372). A more knowledgeable other should provide opportunities for learners to learn mathematics by providing the necessary support and tools and using the ZPD to scaffold the process of learning (Vygotsky 1978).

The ZPD can be divided into four stages (Dunphy & Dunphy 2003:49-50). These stages attempt to explain what happens at the beginning of teaching a concept, during the teaching and after the teaching.

Stage 1 is where learning is assisted by a more knowledgeable other (Dunphy & Dunphy 2003:40-50). This is the stage where the teaching of concepts starts and where learners have little understanding thereof. It is during this stage that teaching and intervention occur in different ways, including modelling, coaching and other methods of scaffolding (Polly 2012:81).

Stage 2 is called self-assisted. This is when a learner is able to perform and carry out tasks independently and is trying to make sense of tasks independently. This does not mean that the performance is fully developed or internalised. It merely means that the control and direction of the performance has been passed on to the learners (from other-regulation to self-regulation).

Stage 3 is where performance is developed and automatised. At this stage, a learner is fully able to perform on his or her own and has advanced from the ZPD into the developmental stage for the task. The task is now achievable without intervention or assistance from the more knowledgeable other.

Stage 4 is where de-automatisation of performance leads to going back through the ZPD and starting from stage 1 again. Dunphy and Dunphy (2003:49-50) observe that 'for every individual, at some stage, there will be a mix of other-regulation, self-regulation, automised and deautomatised processes'. Teachers should also understand that learners will not necessarily move through these stages the same way or at the same time. It is the teacher's responsibility to assist the learner's understanding through the ZPD into the next phase (Vygotsky 1978).

Through their research aimed at improving the mathematics results of some schools, Scott and Graven (2013:7) realised that the ZPD is not a 'physical space' in the learners' prior learning activities. They had thought that the ZPD theory was a way of recognising where learners were in terms of their existing understanding in order to plan activities and ways to mediate the learning processes. They came to realise through their study and interaction with learners that the ZPD was rather more 'fluid than a fixed set of predetermined possibilities' (Scott & Graven 2013:7). They found that the ZPD was largely influenced by learners' interaction with activities which were also dependent on social, emotional, health and other interactional influences. Furberg and Arnseth (2009) agree that:

focusing on the learners' actual interaction during collaborative learning activities enables teachers to describe how learners' making meaning of conceptual representations emerges in a particular setting and is responsive to the characteristics of the setting. (p. 158)

This suggests that learners' performance could vary from activity to activity, day to day and under different contexts, depending on the above-mentioned interactional influences. Learners move through the ZPD in ways which are predictable, as a result of making their own sense of what is provided by the teacher. Bliss, Askew and Macrae (1996:39) add that 'in the school context, the ZPD is not characterised by an invariant task because the negotiation between teacher and learner may change it'. Scott and Graven (2013:7) only came to realise the above through reflection. It was through reflecting on each learner's progress and proficiency that these researchers were able to come to appreciate the emergence of each learner's ZPD (Scott & Graven 2013:6). This is important in teaching, as teachers need constantly to reflect on teaching and learning so as to recognise their learners' ZPD and the direction to follow next.

 

Design and methodology

This research is by nature qualitative and located within an interpretive case study approach. The case study is used as an empirical inquiry that investigates an existing phenomenon in depth and within its real-life context, particularly when the boundaries between phenomenon and context are not clearly evident (Yin 2009:18). Qualitative research is a form of research in which the researchers seek to acquire a thorough understanding of a specific field of study and is aimed at uncovering a specific population's behaviour and the perceptions that underpin it in relation to specific topics or issues (Cooper, Flescher & Cotton 2012; QRCA 2013; Strauss & Corbin 2015).

This research was conducted in two primary schools in a sub-area of the Western Cape, South Africa. Both schools comprise learners from communities considered low socio-economic status. The schools were referred to as school A and school B. School A where the second author teaches is situated in a Xhosa-speaking area and school B in a previously Afrikaans-speaking school in Athlone.

The participants were purposively selected on the basis of their knowledge and experience in the foundation phase and all had mathematical manipulatives (resources) in their classes as per recommendations from CAPS. The first author worked with five foundation phase teachers, two of whom were from the school at which she was teaching at the time of the study, whilst three were from school B. She worked with one teacher per grade, from Grade 1 to Grade 3 in each school. The teachers were selected according to their experience in the grade concerned. Table 1 contains biographical data pertaining to the participants.

 

 

Data were collected through document analysis, non-participatory observation and semi-structured interviews. The five selected teachers' lessons were observed whilst teaching number concepts in their classrooms, using available concrete manipulatives. An observation schedule was used. The researcher (second author) recorded the events that happened during course of the lessons in terms of how the manipulatives were used to enhance learners' understanding in terms of number concepts.

Data analysis was an on-going process whereby the first author extracted meaningful conclusions from the data collected (Patton & Cochran (2002:23). Although document analysis, observation analysis and interview analysis were used, this article only reports on findings based on semi-structured interviews and observation analysis. Parts of the data relevant to the research question were transcribed and analysed (Flick 2011:136). The teachers' use of concrete manipulatives was examined in terms of the following: How were they using mathematical resources in their mathematics lessons? What did they do and what did they say? Which aspects worked well and which did not? And what might the reasons for this be? The aim was to determine whether what the teachers had in their lesson plans was really what happened when observed in their classrooms.

 

Discussion of participant teachers' use of concrete manipulatives

The observation and interview findings are presented as integrated discussions to present a more holistic picture. The focus of analysis involves the following: teachers' teaching strategies in terms of Vygotsky's ZPD, teachers' perspectives on the role and use of concrete mathematical manipulatives and essentially a critique of incidents reflecting how teachers actually went about using these manipulatives.

During the observations, it was established that the teachers were aware of what the CAPS document stipulated about mathematics lessons in the foundation phase. All their lessons started with a whole class activity before the teacher engaged with a small group on the mat, leaving the rest of the learners working independently at their tables. The mat work was identified as stage 1 within Vygotsky's ZPD. This is the stage during which the more knowledgeable other assists by scaffolding the learning process. Teachers engaged learners through asking probing questions and using various manipulatives. The teachers supported the learners through modelling, guiding and discussion in order to achieve the desired learning outcomes.

Stage 2 in Vygotsky's ZPD was visible at the learners' tables after the lessons on the mat. Learners were then given activities to complete independently at their tables. Learners were expected to do the activities on their own but could still ask for help if necessary. Teachers differentiated the learning activities to suit the levels at which the learners were competent. Blue books were used because these books are all the same and do not differentiate amongst learning activities.

Stage 3 of the ZPD, when performance is developed and automatised, took place right at the beginning of the lessons when the teachers allocated activities to the class before taking a small group onto the mat. Learners were allocated activities to complete on their own. These were activities relating to concepts taught and already understood. This stage was more visible in some classes than others. In the Grade 1A and Grade 3B classes, learners constantly came to the mat where the teacher was busy with a small group to ask for assistance with the activities assigned to them. In the rest of the classes, the teachers could go through the whole lesson without interruptions from the other learners.

When asked what the purpose of manipulatives in teaching number concepts was, teachers gave similar responses, namely that manipulatives were important to promote understanding in the foundation phase. Teacher 2A replied:

'If I look at my children, manipulatives are important especially for me because most of my learners whenever I teach a new concept, I have to go through those three stages where it is the concrete stage, the semi-concrete stage and then an activity because if they don't see or feel or look. Like when you are busy with hundreds, tens and units, you have to show them the hundreds cause they might not grasp it. You have to have that manipulative where it says hundreds, tens and units. So for me manipulatives are important. I need manipulatives but there are many other things like we doing eighths now, we doing sixths. Your first group grasps it immediately, they see oh teacher if you cut it into eight each part is called a eighth. But the other children I have to actually cut an orange or an apple so they actually see and they will still tell you that that is one apple'. (Grade 2, female, 58 years old)

Teacher 1B answered:

'Definitely, like with studying also it works if you start with touch, feel, see, smell. So especially with those children that struggle, it's easier for them to take something and say right, so this is one and put it aside, pick up another one, if you put it together it's two. If you take one away it's like minus, so … like … manipulatives are very important cause even with the top learners, they might know what going on but for them to touch and like with the flard cards and like sucker sticks. When explaining any concept, things like counters are amazing, things like sucker sticks, later on when you do flard cards it's amazing how these children need to see it in front of them. You can't just tell them 4+3. They need tactile at this stage'. (Grade 1, female, 28 years old)

The above-mentioned responses and those by other teachers clearly suggest that teachers seem to know the value of mathematical manipulatives, even if it may not always have been in a deeper sense of the word. Teachers also reveal some understanding as to the importance of teaching number concepts development. Words and utterances such as 'definitely', 'have to show them', 'have to have' and 'I need manipulatives' reveal a sense of dependency on manipulatives and a belief that it has a powerful role to fulfil in helping learners to understand, which are in line with Drew's (2007) research findings. The haptic, tactile and visual values of concrete mathematical manipulatives, also mentioned by Moyer (2001), are expressed in terms of words and phrases such as 'it works, but only with touch, feel, see, smell'. The belief in the 'power' of manipulatives is evident in utterances such as, 'things like counters are amazing' and 'it's amazing how these children need to see it in front of them'. The 'power' of manipulatives as a means to remedy misconceptions is verbalised in the following way: for those who 'don't grasp it' and 'those children that struggle'. These beliefs correspond to the findings by Carbonneau et al. (2013) that the use of manipulatives has some positive effects in learning with specific reference to retention and to the views of Cockett and Kilgour (2013) that manipulatives can be used to address learners' individual needs.

Upon probing deeper, it became clear that participant teachers realised the potential didactical value of concrete manipulatives and that using manipulatives was an important component of teaching. This viewpoint matches the claims by Cockett and Kilgour (2015:48) that manipulatives 'facilitate the creation of a learning environment that encourages engagement' and enhance understanding. However, they did not necessarily always use these when the opportunity arose, neither did they use manipulatives optimally, or use them in combination with other related manipulatives. This observation is in accordance with Back's (2013:7) finding that often manipulatives are used as 'adjuncts to blindly following a taught procedure …'. The implication is that this limited use does not necessarily advance mathematical fluency, problem-solving skills or mathematical reasoning at a deeper level. The Grade 3B teacher understood that for concepts to develop faster and more fully, the phase or stage of using resources was crucial. In this regard, she explained that:

'Manipulatives are important for the learners especially concrete material and concrete manipulative. I think that would really make it, it does make a difference because you take them back to the basic, the foundation for them to grasp that concept from the beginning with um your, uhm, blocks and things for them to actually develop that concept. It does, it makes the difference. I think that would be an ideal environment, to work with those manipulatives but we are not working in an ideal environment and there needs to be work in the learners' books'. (Grade 3, female, 40 years old)

Also, this teacher expresses a firm belief in the importance of manipulatives as fundamental in laying the basic foundations in terms of developing, understanding and conceptualising number. This belief is in line with Phillips' (1989) research that the use of manipulatives facilitates understanding of place value. From the explanation of the 3B teacher, it is evident that teachers are compelled to let learners work in their workbooks (notebooks) and this seems to be viewed as cumbersome and a burden as opposed to the 'ideal [learning] environment' created through concrete manipulatives. This view expressed borders on an overemphasis and exaggeration of the qualities of concrete manipulatives these teachers perceive the manipulative inherently possesses.

Observation of lessons indicated that teachers tended only to resort to resources when they saw that the learners did not understand a concept, which may not be the appropriate way to use manipulatives a pointed out by Back (2013) and Cope (2015). Furthermore, lessons observed revealed that manipulatives were used to support written activities. Written activities were all based on the work that the learners did on the mat. The learners were consistently moved from stage 1 (assisted by the more knowledgeable other) of the ZPD to stage 2 (self-assisted). The learners first did the activities with the teacher on the mat and then were given a chance to do the activities on their own. When learners showed signs of not understanding by doing the work incorrectly, teachers assisted them, using manipulatives until they could do the activities independently. Learners in one class (Grade 1A) were instructed to use the number lines in their books to hop from 2 to 6 after the teacher explained and demonstrated how to hop (see Figure 3).

 

 

 

 

The teacher then looked around and saw that some of the learners had made more hops than they were asked. Some learners grasped the concept and others did not. Realising this, the teacher then told the learners to count the hops that were made on the board and then count their hops to see if they had made the correct number of hops. The teacher tried to help the learners who had more hops by counting and demonstrating on the big number line on the board (see Figures 2 and 3).

The teacher gave the learners more problems to solve using the number line so that they could master using the number line (3+3, 0+6, 6+0). They were then asked to complete one more problem on their own. This did not mean that the learners had reached stage 2 of the ZPD, although that was what the teacher wanted. One lesson for the concept of number lines was not enough. It was almost certain that if the teacher had given the same learners more of the same type of computations to do that same day or even the following day, they would not have been able to complete them without her assistance.

The teachers observed had access to the required mathematics teaching manipulatives described in CAPS. Each classroom observed had a number chart, number lines, number tracks and strings of beads. At school B, the teachers had their own learner teacher support material (LTSM) kit which consisted of all the required materials recommended by CAPS. School A had one kit to share amongst the whole school. At school A, teachers did not use the LTSM kit because it was an effort to go fetch the resources they needed from the learner support teacher responsible for them and they did not even know what it contained.

Teachers at both schools used the number lines but did not use them with the concrete bead string as CAPS recommends. Learners were not given enough time to engage and explore with the manipulatives because these were kept in closed boxes. These materials should not be in the boxes in which they originally came. They should be placed in the mathematics corner for anyone who comes into the class to see so that the learners can use them. When learners went back to their tables to work independently, there were no manipulatives available for them to use. If and when they used manipulatives, it was only on the mat with the teacher. At their tables, they only engaged in written work. This was because they had already practised the work on the mat with the teacher and the teacher probably saw no need for manipulatives to be used again. However, if learners need to assist themselves as stage 2 as the ZPD suggests, the required manipulatives should be available for them to do so.

Teachers used mathematics manipulatives to teach computations (number sentences), that is, they used manipulatives to help the learners get to the answers. This points to 'rote learned procedure[s] without a sense of the ways in which the apparatus reflects mathematical structures' (Back 2013:3). Learners were shown how to use number lines as a calculation tool for addition and subtraction. CAPS (2011) indicate that a number line is an abstract resource and should be used together with the bead string. This is to ensure that learners understand concepts related to numbers and make connections between numbers on the number line and the number of objects on the bead string. Using the bead string helps to avoid meaningless or rote learning because learners might be able to make the necessary or expected jumps from number to number and reach the correct answer by merely repeating what they were shown. Teachers then assume that learners understand and move them to the next level of the ZPD, stage 2 where the learners are able to carry out tasks on their own. This creates gaps that cause bigger problems in the higher grades such as not being able to transfer, apply and build on previously taught number concepts.

Vygotsky (1986) believed that in order for learning to take place, understanding the meaning of words is crucial. Language should serve as a tool mediating between the learner and what needs to be learnt: 'meaning cannot be separated from words and words without meaning is an empty sound and no longer part of human speech' (Vygotsky 1986:5-6). The majority of learners in school B were isiXhosa-speaking learners. In teacher 1A's class there were 33 learners, of whom 20 were isiXhosa, 11 were English, one was Sepedi and one was Setswana. In all the participant teachers' classes, learners were taught in English despite the fact that their mother tongue was not English.

Most of the teachers were able to speak English and Afrikaans but not the African languages. This made learning a challenge, especially in the Grade 1 classes, because most of the isiXhosa learners were being taught in English for the first time. By the time they got to higher grades, they would be able to communicate in English, but by then they would have missed out on the basis of mathematics taught from Grade 1. Teachers said that it became an even bigger challenge when learners came from isiXhosa- or Afrikaans-medium schools and only started at an English school in Grade 3. The content to be covered in Grade 3 is much greater than in previous grades and communication lines are effectively closed.

 

Conclusion

There are clear commonalities in terms of how participant teachers view, use and apply concrete mathematical manipulatives. They all exclaimed appreciation for the inherent usefulness of manipulatives because they believe such materials assisted learners' thought processes and also that manipulatives served as catalysts for decomposing intricate concepts to learners' levels of understanding (Martin et al. 2007). From what was observed, no overuse of manipulatives (Anghileri 2000) occurred, but participating teachers had a tendency generally to only use manipulatives when some learners experienced difficulty understanding aspects regarding number concepts, that is, only as 'crutches' (Back 2013). As such there is a discrepancy between what teachers say they believe about and how and when they use manipulatives. Lesson observation and comments from teachers indicate that manipulatives are not necessarily optimally or opportunely used. However, the body language of learners during lesson observation clearly indicated that they were more active and greater interaction with content occurred and, evidently, a deliberate effort was made by teachers to enhance mathematical sense-making. Little to no opportunities were given to learners to use manipulatives to demonstrate a result or solution to peers, or for learners to support their own line of reasoning

From the research findings, it is evident that mathematics teachers in the foundation phase are in need of training of how to use and follow Vygotsky's ZPD and how to make sense of and follow the CAPS mathematics guidelines in respect of when and how to use mathematical manipulatives.

There were instances where teachers used a number of different manipulatives, such as beads, the number line and flash cards jointly to help develop and reinforce the development of a particular number concept or procedures related to number operations such as addition, but that practice was not used consistently. At the same time, however, teachers should heed Anghileri's (2000) caution that learners should not rely entirely on the use of manipulatives, but that learners need to develop mental images that are intertwined with particular manipulatives.

 

Acknowledgements

Competing interests

The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.

Authors' contributions

L.M.M. was responsible for research design, data collection, and analyses. S.A.A. and S.W.S. refined the article, assisted and reworked the article according to the reviewer reports.

 

References

Alexandru, F., 2012, 'The pedagogy of sociocultural diversity', Euromentor Journal 3(4), 17-24.         [ Links ]

Anghileri, J., 2000, Teaching number sense, Continuum, London.

Back, J., 2013, Manipulatives in the Primary classroom, University of Cambridge, viewed 11 September 2016, from http://nrich.maths.org/10461.

Bliss, J., Askew, M. & Macrae, S., 1996, 'Effective teaching and learning: Scaffolding revisited', Oxford Review of Education 22(1), 37-61. https://doi.org/10.1080/0305498960220103        [ Links ]

Boggan, M., Harper, S. & Whitmire, A., 2010, 'Using manipulatives to teach elementary Mathematics', Journal of Instructional Pedagogies 1-6, viewed 12 March 2014, from http://www.aabri.com/manuscripts/10451.pdf

Carbonneau, K.J., Marley, S.C. & Selig, J.P., 2013, 'A meta-analysis of the efficacy of teaching mathematics with concrete manipulatives', Journal of Educational Psychology 105(2), 380-400. https://doi.org/10.1037/a0031084        [ Links ]

Carroll, W.M. & Porter, D., 1997, 'Invented strategies can develop meaningful mathematical Procedures', Teaching Children Mathematics 3(7), 370-374.         [ Links ]

Christmas, D., Kudzai, C. & Josiah, M., 2012, 'Vygotsky's zone of proximal development theory: What are its implications for mathematical teaching?', Greener Journal of Social Sciences 3(7), 371-376.         [ Links ]

Clements, D.H., 1999, '"Concrete" manipulatives, concrete ideas', Contemporary Issues in Early Childhood 1(1), 45-60. https://doi.org/10.2304/ciec.2000.1.1.7        [ Links ]

Cockett, A. & Kilgour, P., 2015, 'Mathematical manipulatives: Creating an environment for understanding, efficiency, engagement, and enjoyment', TEACH Collection 1, 47-54.         [ Links ]

Cooper, R., Flescher, A. & Cotton, F.A., 2012, 'Building connections: An interpretive phenomenological analysis of qualitative research students' learning experiences', The Qualitative Report 17(17), 1-16.         [ Links ]

Cope, L., 2015, 'Math manipulations: Making the abstract tangible', Delta Journal of Education 5(1), 10-19.         [ Links ]

Drews, D., 2007, Do resources matter in primary mathematics? Using resources to support mathematical thinking, primary and early years, Learning Matters, Exeter.

Dunphy, B.C. & Dunphy, S.L., 2003, 'Assisted performance and the zone of proximal development (ZPD); a potential framework for providing surgical education', Australian Journal of Educational & Developmental Psychology 3, 48-58.         [ Links ]

Edward, L.D., 1998, 'Embodying mathematics and science: Microworlds as representations', Journal of Mathematical Behavior 17(1), 53-78.         [ Links ]

Engelbrecht, J., Bergsten, C. & Kågesten, O., 2009, 'Undergraduate students preference for procedural to conceptual solutions to mathematical problems', ERIC 40(7), 927-940. https://doi.org/10.1080/00207390903200968        [ Links ]

Flick, U., 2011, Introducing research methodology: A beginner's guide to doing a research project, Sage, London.

Furberg, A. & Arnseth, H.C., 2009, 'Reconsidering conceptual change from a socio-cultural perspective: Analyzing students' meaning making in genetics in collaborative learning activities', Cultural Studies of Science Education 4, 157-191. https://doi.org/10.1007/s11422-008-9161-6        [ Links ]

Grupe, L.A., Huffian, L.F. & Bray, N.W., 1996, 'Addition strategies in kindergarten children', Paper presented at the Conference on Human Development, Birmingham, AL, 14th March.

Hall, A., 2007, Vygotsky goes online: Learning design from a sociocultural perspective, Sultan Qaboos University, Muscat.

Heddens, J.W., 1986, 'Bridging the gap between the concrete and the abstract', The Arithmetic Teacher 33(6), 14-17.         [ Links ]

Hiebert, J. & Carpenter, T.P., 1992, 'Learning and teaching with understanding', in D.A. Grouws (ed.), Handbook of research on mathematics teaching and learning, pp. 65-97, McMillan, New York.

Lantolf, J.P. & Thorne, S.L., 2006, Sociocultural theory and the genesis of second language Learning, The Pennsylvania State University, Oxford University Press, Oxford.

Locuniak, M.N. & Jordan, N.C., 2008, 'Using kindergarten number sense to predict calculation fluency in second grade', Journal of Learning Disabilities 41, 451-461. https://doi.org/10.1177/0022219408321126        [ Links ]

Martin, T., Lukong, A. & Reaves, R., 2007, 'The role of manipulatives in arithmetic and geography tasks', Journal of Education and Human Development 1(1), 225-228.         [ Links ]

McNeil, N. & Jarvin, L., 2007, 'When theories don't add up: Disentangling the manipulatives Debate', Theory Into Practice 46(4), 309-316. https://doi.org/10.1080/00405840701593899        [ Links ]

Moyer, P., 2001, 'Are we having fun yet? How teachers use manipulative to teach mathematics', Educational Studies in Mathematics 47, 175-197. https://doi.org/10.1023/A:1014596316942        [ Links ]

Mtetwa, D.K.J., 2005, 'Some characteristics of mathematics teaching in Zimbabwean infant and primary school classrooms', International Journal of Early Years Education 13(3), 255-264. https://doi.org/10.1080/09669760500295912        [ Links ]

Paek, S., 2012, The impact of multimodal virtual manipulatives on young children's mathematics learning, Columbia University Press, New York.

Paparistodemou, E., Potari, D. & Pitta-Pantanzi, D., 2014, 'Prospective teachers' attention on geometrical tasks', Educational Studies in Mathematics 86, 1-18. https://doi.org/10.1007/s10649-013-9518-y        [ Links ]

Patton, M. & Cocharn, M., 2002, A guide to using qualitative research methodology, Médecins Sans Frontières, Paris.

Phillips, D.G., 1989, 'The development of logical thinking: A three-year longitudinal study', paper presented to the National Council of Teachers of Mathematics, 12-15 April 2989, Orlando, FL.

Picciotto, H., 1998, Operation sense, tool-based pedagogy, curricular breadth: A proposal, viewed 17 July 2016, from http://www.picciotto.org

Polly, D., 2012, 'Supporting mathematics instruction with an expert coaching model', Mathematics Teacher Education and Development 14(1), 78-93.         [ Links ]

QRCA, 2013, What is qualitative research?, viewed 15 June 2016, from http://www.qrca.org

Ramani, G.B. & Siegler, R.S., 2014, How informal learning activities can promote children's numerical knowledge, Oxford handbooks online, viewed 23 June 2016, from http://www.psy.cmu.edu/~siegler/publications-all.html

Republic of South Africa. Department of Basic Education, 2011, Curriculum and assessment policy statement Grades R-3: English and mathematics, Government Printer, Pretoria.

Scott, D. & Graven, M., 2013, The dialectical relationship between theory and practice in the design of an after-school mathematics club, viewed 23 June 2016, from https://www.ru.ac.za/media/rhodesuniversity/content/sanc/documents/Pythagoras-Stott-174.pdf

Sebesta, L.M. & Martin, S.R.M., 2004, 'Fractions: Building a foundation with concrete Manipulatives', Illinois Schools Journal 83(2), 3-23.         [ Links ]

Siyepu, S.W., 2013, 'The zone of proximal development', South African Journal of Education 33(2), 1-13. https://doi.org/10.15700/saje.v33n2a714        [ Links ]

Sowell, E.J., 1989, 'Effects of manipulative materials in mathematics instruction', Journal for Research in Mathematics Instruction 76, 68-72. https://doi.org/10.2307/749423        [ Links ]

Strauss, A. & Corbin, J., 2015, Basics of qualitative research, 4th edn., Sage, London.

Uttal, D.H., 2003, 'On the relation between play and symbolic thought: The case of mathematics Manipulatives', Contemporary Perspectives on Play in Early Childhood Education 1(6), 97-114.         [ Links ]

Uttal, D., Scudder, K. & DeLoache, J., 1997, 'Manipulatives as symbols: A new perspective on the use of concrete objects to teach mathematics', Journal of Applied Developmental Psychology 18, 37-54. https://doi.org/10.1016/S0193-3973(97)90013-7        [ Links ]

Van de Walle, J.A., 2007, Elementary and middle school mathematics education: Teaching developmentally, 6th edn., Pearson education, Boston, MA.

Van de Walle, J.A., Karp, K.S. & Bay-Williams, J.M., 2010, Elementary and middle school mathematics: Teaching developmentally, 7th edn., Allyn & Bacon, Boston, MA.

Van de Walle, J.A., Karp, K.S. & Bay-Williams, J.M., 2014, Elementary and middle school mathematics: Teaching developmentally, 8th edn., Pearson Education, Boston, MA.

Vygotsky, L.S., 1978, 'Mind in society: The development of higher psychological processes', in M. Cole, V. John-Steiner, S. Scriber & E. Souberman (eds.), pp. 52-57, Harvard University Press, Cambridge, MA.

Vygotsky, L.S., 1986, Thought and language, Ed. A. Kozulin, MIT Press, Cambridge, MA.

Wright, R.J., Martland, J., Stafford, A.K. & Stanger, G., 2006, Teaching number: Advancing children' skills & strategies, 2nd edn., Paul Chapman Publishing, London.

Yin, R.K., 2009, Case study research; Design and methods, 4th edn., Sage, London.

 

 

Correspondence:
Stanley Adendorff
adendorffs@cput.ac.za

Received: 05 Sept. 2016
Accepted: 03 Aug. 2018
Published: 21 Nov. 2018