Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.8 n.1 Johannesburg 2018
http://dx.doi.org/10.4102/sajce.v8i1.505
ORIGINAL RESEARCH
Can mathematics assessments be considered valid if learners fail to access what is asked of them?
Lucy Sibanda; Mellony Graven
Department of Education, Rhodes University, South Africa
ABSTRACT
BACKGROUND: The underperformance of South African learners in literacy and numeracy is a source of concern, especially when learners move from Grade 3 to Grade 4
AIM: This article reflects on the reading and comprehension challenges of English language learners (ELLs) in the Grade 4 2013 mathematics Annual National Assessments (ANAs
SETTING: The study took place in two primary schools that served relatively less affluent sectors of the community in the Eastern Cape. Learners were IsiXhosa speakers learning mathematics in English
METHODS: A sample of 26 out of 106 isiXhosa-speaking Grade 4 learners in the two schools participated in task-based interviews (focused on ANA questions) in which reading and linguistic mediation was provided. While the broader study (from which this article derives) revealed learners' challenges in reading, comprehension, transformation and process skills, here the focus is on findings related to reading and comprehension skills, which are foundational to accessing written assessment items
RESULTS: Interview excerpts show the negative influence poor English reading and comprehension skills had on learner access to questions and their subsequent performance in the ANA
CONCLUSION: The article challenges the validity of assessing ELLs' mathematical competence in English ANAs and draws implications for strengthening ELLs' language and mathematical proficiency in the Foundation Phase
Introduction
In South Africa, the Department of Basic Education (DBE) prioritised the Annual National Assessments (ANAs) where they tested literacy and numeracy skills of learners as part of the Foundations for Learning campaign. The aim was to monitor and track achievement of the goals that were set in the DBE (2011). The ANAs also aimed at giving teachers a better experience of assessing, as well as assisting educational districts in identifying schools that were in need of assistance. Parents were also informed about their children's performance after the results were analysed (DBE 2011, DBE 2012). The results of the ANAs were, however, disappointing because learners were performing poorly throughout the 4-year period (Department of Education [DoE] 2012, 2013b, 2014). The usefulness of the ANAs was criticised by others who argued that the process wasted resources because the outcome of the results was not of value to the education system (Spaull 2015). Furthermore, Spaull (2015) argued that there also was no statistical or methodological foundation that could be used to compare the results over time yet a comparison was made, giving inaccurate outcomes (Spaull 2015). Graven and Venkat's (2014) research with teachers in Gauteng and the Eastern Cape highlighted both reading and language challenges teachers experienced in relation to the ANAs. While teachers in this study bought into the broad aims of the ANAs enabling the strengthening of teaching and learning, they did not experience them as such and found instead that they took time away from teaching. Indeed in 2015, following pressure from teacher unions the ANAs were not written nationally and have since been abandoned.
Most South African learners from Grade 4 study in English although English is the home language for less than 10% of the learners (DBE 2011). Robertson and Graven (2015) note that in South Africa there is an increase in the percentage of learners who use English as the language of learning and teaching (LoLT) as they progress up the grades. About 80% of learners use English as LoLT by Grade 4. This is a marked increase from the 28% using English as LoLT in Grade 3. This implies that the greater number of children learning in South African schools have a double responsibility, that is, to learn the English language in addition to attempting to access English concepts that are used in mathematics.
The Language in Education Policy for 1997 states that home language should be used during the learners' first 3 years of school, as the LoLT (DoE 1997). Therefore, in the Foundation Phase, mother tongue is used as the LoLT and English is studied as an additional language (DBE 2011). Most of the learners thus use a language they are not proficient in to learn mathematics (Setati & Barwell 2008). International and regional learning assessments confirm that when home language differs from the LoLT, there is an adverse impact on test scores (UNESCO 2016). Webb (2011) sees language as the central mediator of learners' knowledge acquisition and comprehension skills as well as their social and psychological development; hence the failure to speak, read and understand the LoLT is problematic.
Desai (2001) notes that children need to be taught in their mother tongue until the end of Grade 6 if they are to have a firmer foundation in the Intermediate Phase. Once they fail to get the basics in the Foundation and Intermediate Phases, they are likely to struggle as they go to higher grades. Le Roux (1993) argues that learners learning a new language usually struggle with vocabulary and new concepts because these are more abstract and not as easily understood as in everyday language. When mother tongue is dropped as the LoLT in Grade 4, the cognitive demands on learners increase as they must learn both the new LoLT and more abstract mathematical language and concepts in that LoLT. Therefore, for Webb (2002), the use of English as LoLT in Grade 4 in South Africa is one factor that contributes to the poor pass rate.
In order to learn in a second language, it is crucial that learners have a high level of proficiency in that second language (Cummins 2000). However, Schlebush (2002) confirms that most South African learners lack the command of English that is needed to comprehend the various concepts, principles and techniques that are required in order to learn different subjects. There is also an assumption that mathematical assessments not only measure mathematical skills but language skills as well (Hakuta 2011).
This article considers the difficulties Grade 4 English language learners (ELLs) experience as they solve mathematics problems, particularly in the context of national assessments where linguistic or other mediation is not allowed. The research question addressed by this article is: What difficulties do Grade 4 ELLs experience as they solve mathematics problems presented in English in the ANAs?
Literature review
In South Africa, Grade 4 represents a crucial stage in learners' language learning. Learners are expected to make several significant changes in their reading as they move from the Foundation Phase (Grades R-3) into the Intermediate Phase (Grades 4-6). Included in these transitions are:
-
shifting from 'learning to read' to 'reading to learn'
-
shifting from reading narrative texts in which the language used is the ordinary everyday interaction language to reading informational texts that comprise dense vocabulary in content subjects at Grade 4 (DBE 2008).
It is assumed that when learners begin Grade 4, they should be able to read independently and fluently (Rault-Smith 2009). The Department of Education (2007a:10-11) identifies a child as a fluent reader if he or she:
-
can identify common sentence forms and knows how to read for comprehension
-
identifies most common words when they see them (up to 200 words)
-
reads easily up to 60 words in a minute
-
understands the meaning of different punctuation
-
starts to understand suggested but not directly expressed meaning
-
can read long and complex texts
-
can read independently.
Thus, Grade 4 learners are expected to access information, start to become critical readers and creative thinkers, work out the meaning of unknown words, and visualise and understand abstract concepts in the LoLT (DoE 2007a). This expectation is inherent in the mathematics in the English ANAs; however, the majority of Grade 4 learners who participated in this study did not meet these requirements (Sibanda 2017). According to the DoE (2007b:25), these learners are expected to read '158 words per minute' yet most of the 26 learners interviewed took close to 60 seconds to read an 11-word question (Sibanda 2016). This is in agreement with the 2011 Progress in International Reading Literacy Study (PIRLS) analysis, which indicates that Grade 4 learners in South Africa are still performing poorly in literacy in comparison to their peers in other countries (Howie et al. 2017). Furthermore, the ANA results confirm South African learners' underperformance in literacy and mathematics at all levels. Howie et al. (2008) also note that there is a very low reading comprehension in South African learners as revealed by a large-scale assessment of reading comprehension of Grade 4 and 5 learners. Sibanda's (2016) study similarly confirms that the majority of learners who participated in the task-based interviews were 'learning to read' rather than 'reading to learn'.
That language proficiency is a factor that is correlated with poor mathematical learning (see Fleisch 2008) and performance on mathematics assessments (see Reddy et al. 2016) is well established. Reports on South African participation in the Third International Mathematics and Science Study (see Howie 1997) and the more recent Trends in Mathematics and Science Study (Reddy et al. 2016) note language as a key contributing factor to low achievement. Similarly, Setati, Chitera and Essien's (2009:66) review of both large-scale and smaller-scale research on the relationship between language proficiency and mathematical proficiency indicates consensus on 'language as a major determinant of success in mathematics learning'.
This is not to say that this is the only factor linked to South African learners' poor mathematical performance; factors such as teaching time, teacher mathematical knowledge for teaching, poverty and so forth are all widely acknowledged in contributing to poor mathematical proficiency (see Fleisch 2008; Graven 2014 for overviews of such local literature). The focus of this article is, however, on the challenge that a lack of proficiency in the LoLT and the language of Grade 4 national assessments of the majority of learners in the study presents for the validity of national mathematics assessments in English.
Learning the English language can present additional challenges for learners whose mother tongue is in a non-cognate language to English. For example, isiXhosa and English are non-cognate languages because they do not originate from the same family of languages. There are differences in the orthography of English and that of the African languages, where in the latter there is a one-to-one correspondence between the graphemes (the smallest meaningful contrastive unit in a writing system) and the phonemes (any of the seen distinct units of sound in a language that differentiates one word from the other). On the other hand, the opaque orthography of English does not have such correspondence (Prinsloo 2009). This can lead to confusion and misreading of words.
Another problem is the inability to recognise sight words (words that are recognised as a whole word without analysing it) during reading. Fourie (2008) notes that word recognition ability is crucial if one is to master written words and read fluently. If this skill of word recognition is missing, learners cannot get any meaning from what they read. It has been noted by Jennings, Caldwell and Lerner (2006) that once learners succeed in recognising sight words, reading becomes easier. According to the DoE (2010), grade-appropriate sight words should constitute 75% of most reading passages and they are core to reading basics. When a learner looks at the word, he or she remembers the forms and recognises the words and this supports fluency of reading and improves reading speed (DoE 2010).
It is also noted by Duke and Pearson (2002) that if learners have knowledge of tenses, vocabulary, participants, as well as the order of what they read, the texts are easily read and understood. It becomes easy for the text features to be identified and hence learners can read with fluency and comprehension. The DoE (2002) emphasises the importance of well-developed reading skills. Reading fluency is a prerequisite to the comprehension of texts in all subjects. However, for mathematical texts, there is the additional challenge of learning mathematics-specific terminology (such as 'numerator', 'denominator' and so forth) in English.
The relationship between mathematics and language
The language of mathematics is complex. The Curriculum Assessment Policy Statement for mathematics defines mathematics as 'a language that makes use of symbols and notations to describe numerical, geometric and graphical relationships' (DBE 2011:8). The mathematics language describes mathematical concepts, which the everyday language cannot describe. Bohlman and Pretorius (2008) note that:
Mathematics texts are also hierarchical and cumulative, such that understanding each statement is necessary for understanding subsequent statements. Overlooking or misunderstanding a particular step has severe consequences for overall comprehension. (p. 43-44)
Hammill (2010) views mathematics as having dense information and a complex structure. According to Bell (2003), when children learn mathematics in English, some factors that contribute to difficulties in comprehension include mathematics vocabulary, as well as specific syntactic structures and discourse patterns found in written text. Setati (2005) also notes that when learning mathematics, one is required to acquire fluency in the mathematics language. Hence it becomes challenging, especially for ELLs who have just begun learning in English, to learn mathematics in English. In the case of ELLs, the challenge of learning mathematical vocabulary is exacerbated by their lack of proficiency in the English language (Barbu 2014). In this respect teachers need to find strategies to support learners as they engage in the complex language of mathematics. Schleppegrell (2012) suggests that mathematics learning should consist of multimodal and multisemiotic activities to support scaffolding in the academic mathematical language.
Relationship between language proficiency and mathematics achievement
Beal, Adams and Cohen (2010) as well as Brown, Cady and Lubinski (2011) note that there is a relationship between English language proficiency and mathematics achievement. Carrasquillo, Kucer and Abrams (2004) also argue that ELLs need high levels of literacy as they go to higher grades in schooling. In a study by Kieffer et al. (2009) in the USA, it was observed that mathematics required that learners be proficient in English and those who were not proficient in English experienced more difficulties in the mathematics assessments in comparison with those who were proficient in English. Confirming this, other researchers (Abedi & Lord 2004; Beal et al. 2010; Han 2011; Jordon, Kaplan & Hanich 2002) note that learners with strong reading skills in English achieved higher results in mathematics than those who had difficulties in reading English. For Henry, Nistor and Baltes (2014), locally and nationwide, learning the LoLT at the same time with mathematics content challenges ELLs' academic learning experiences and this is especially revealed at Grade 4 where ELLs always perform lower than non-ELLs in mathematics in many other countries. Neville-Barton and Barton (2005) also revealed that students who use English as a second language, and use it as LoLT, had a 10% - 15% lower performance in mathematics because they lacked English language proficiency. According to Neville-Barton and Barton (2005), learning challenges, especially in relation to making sense of mathematical vocabulary, depend on one's proficiency in English, and ELLs struggle most with problem-solving.
In summary, large and small scale, local and international research confirms that language proficiency is one of the important factors that determines access to mathematical sense-making and is one of the factors influencing mathematics performance, although several other factors also play a role.
The use of language in multicultural and multilingual contexts
Moschkovich (2016) notes that teaching mathematics to ELLs in a classroom should include the use of many different resources in the classroom. It is important that ELLs also have the opportunity to express their mathematical ideas, yet this is difficult to do in English when one is still learning basic English communication skills (see Robertson & Graven, submitted, for discussion of the challenges of Grade 4 ELLs in engaging in mathematics classroom talk). In South Africa it has been found that using more than one language in order to draw on the learners' home language(s) as a resource for mathematical sense-making is beneficial to learners (Setati 2005; Webb & Webb 2013). Setati's work (e.g. Setati 2005) on code-switching has been particularly noted as beneficial and more recently Webb and Webb (2013) have argued that this is particularly useful when working with problem-solving.
Barbu (2014) argues that when bilinguals switch from English to their home language during mathematical computation, the time necessary for calculations is reduced. Hence he argues that learners should be allowed to use the language they prefer when learning mathematics. Barbu (2014) further argues that when a learner delays in giving a response, it doesn't necessarily mean that he or she doesn't know; but the learner may be code-switching and preparing for an answer in his or her own language. Therefore, he says 'code-switching is an efficient use of ELLs' language skills and should be encouraged' (Barbu 2014:140).
Assessment in multilingual contexts
While mathematics assessment should be used to evaluate or measure the level of mathematical proficiency in learners and allows one to monitor the learning progress in learners, sometimes the assessment fails to measure what it intends to assess and ends up measuring language proficiency. Mathematics assessments, like all other assessments, will be judged as valid if they assess and gain results that provide information on what they intended to assess, whether a particular skill or broader competence. So, if one wants to assess whether learners can perform the skill of adding two-digit numbers, one might design items such as 22 + 34 and 48 + 67. However, when mathematics questions require a lot of reading and interpretation in order to make sense of what is being asked, it is often difficult to tell whether poor learner performance is as a result of reading difficulties, interpretation of terminology difficulties or mathematical understanding difficulties, among others. Abedi and Herman (2010) note that administering assessments that are written in English to learners who are still learning English complicates the learning experience for those learners because they are still not proficient in English. According to Halliday (2010), for an assessment to be fair, the learners' language proficiency should be considered. In ELLs' mathematics classrooms, sometimes the validity of assessments is compromised if learners have a limited English proficiency. This is because their comprehension of assessment questions is low and thus learners struggle to access what is being asked of them. In this case, the results of the assessment cannot tell what learners really know. Hence in South Africa, the fairness of some ANAs has been questioned because of the inaccessibility of the language used in them (Graven & Venkat 2013, 2014; Henning & Dampier 2012).
On the assessment of ELLs, Moschkovich (2012) argues:
When students are first learning a second language, they are able to display content knowledge more easily by showing and telling, rather than through reading text or choosing from verbal options on a multiple-choice test. Therefore, discussions with a student or observations of hands-on work will provide more accurate assessment data than written assessments. (p. 24-25)
This captures the rationale of the use of task-based interviews in the broader study to assess the extent to which language challenges influenced Grade 4 learner access to language-based mathematics assessment items in the ANA and, as a result, their performance on these items. Thus, the research objective was to investigate the difficulties experienced by the Grade 4 ELLs as they solved mathematics problems presented in English in the ANAs.
Theoretical perspective
This study draws on a broadly sociocultural perspective of learning where language and learning are viewed as deeply interconnected. Cummins (1979) identifies two aspects of language proficiency, the conversational (which he also calls the 'basic interpersonal communicative skills' [BICS]) and the academic (which he called 'cognitive academic language proficiency' [CALP]). He distinguishes between these two proficiencies. According to Cummins (1979), BICS, on the one hand, are surface skills of listening and speaking that learners acquire quickly and they use this language for social interaction. For example, isiXhosa speakers in South Africa may pick up English language BICS when conversing with English language speakers at school. On the other hand, CALP is 'the extent to which an individual has access to and command of the oral and written academic registers of schooling' (Cummins 2000:67). Cummins then argues that while BICS are easily acquired in about 2 years of interaction with the native speakers of the target language, academic language takes around 7 years to be attained. Taking our own South African example, an isiXhosa-speaking child at school would need about 7 years of learning English to acquire academic proficiency (CALP) in English. As learners move up the grades, they get to a point where they should be able to manipulate language in cognitively demanding and context-reduced situations that are different from their everyday interactions (Cummins 2013). They need to use the language of mathematics or science (CALP), which is different from everyday language (BICS). Cummins (2017) advises that teachers should avoid conflating the two, BICS and CALP, because it poses challenges to ELLs if attention is not paid to the distinction between the two. That is, teachers should be aware that proficiency in BICS in English should not be confused with proficiency in CALP in English. The isiXhosa-speaking learners in this study had the double challenge of needing to develop CALP in English even while their BICS in English was not fully developed, as they had only been learning English at school as an additional language for a few years and had only just begun using English as the LoLT at the beginning of Grade 4.
Cummins (1994) therefore recommends that, when a child is learning in a second or third language, additive bilingualism be encouraged. This is when the use of the first language is maintained while the second language is used, too. Teachers should therefore incorporate the first language, especially when they are teaching mathematics in English to ELLs. Cummins (1979) also hypothesised that the cognitive academic skills of the first language and the second language are interdependent and, therefore, when a learner develops proficiency in the first language, the development in the proficiency of the second language is supported by this. Thus, the use of both languages in the classroom is beneficial to learners. Cummins (1979) attributed the failure of ELLs in schools to the lack of instruction in their first language, because before learners have developed CALP in the first language they are introduced to another language, the LoLT. Therefore, the learners are likely to face challenges in acquiring literacy in both languages (Cummins 1979).
Cummins (2000) also added that:
a central implication of the framework for instruction of second language learners is that language and content will be acquired most successfully when students are challenged cognitively but provided with the contextual and linguistic supports or scaffolds required for successful task completion. (p. 71)
In addition to that, extensive reading is essential for the development of academic proficiency because academic language is found primarily in written text (Krashen 1993). The less the ELLs read, the less they get access to academic language. Cummins (1999) concludes that instruction within a strong bilingual programme should provide a Focus on Message, a Focus on Language and a Focus on Use in both languages (Cummins 1999). It is important to provide opportunities for collaboration in learning and to talk about text because it assists learners to understand the academic language they encounter as they extensively read the texts (Cummins 2008).
Research methodology
A qualitative case study research approach was used to investigate the experiences of learners in three Grade 4 classes in the 2013 Grade 4 mathematics assessment (in English). As the research aimed to investigate the challenges learners experienced when solving mathematical problems, a case study allowed us the depth required to do this. In this article, we share excerpts from task-based interviews conducted with Grade 4 ELLs. The learners are all home language isiXhosa speakers with little access to English beyond school. The excerpts are all taken from the unpublished doctoral dissertation on which this article is based (Sibanda 2016). The excerpts illustrate how a lack of proficiency in English, where this is the language of learning, teaching and assessment in mathematics, limited these learners' opportunity to demonstrate mathematical proficiency in a selection of ANA questions.
Sample
The study reported in this article was located within the South African Numeracy Chair (SANC) Project, in which the first author was a PhD student and the second author was the chair and supervisor of the research. As the focus was on Grade 4 mathematics ANAs, two teachers participated, each from different schools involved in the SANC project, in the Grahamstown District. The schools were chosen for their close proximity to the university, allowing ease of access. One teacher at Santa Anna School taught one class (Class A), and the other taught two classes at Biko Primary (Classes B and C). All ethical permissions were obtained, and the names of the schools, teachers and learners used in this article are pseudonyms.
As the study sought to explore the experiences of Grade 4 ELLs as they solved a selection of the 2013 Grade 4 mathematics ANA items, interviews were required because written responses to the items did not allow this insight. The 2013 mathematics ANA consisted of 38 items. A sample of 15 items were selected for inclusion in the interviews (see Sibanda and Graven [2015] for discussion of this selection and the analysis of the linguistic complexity index of these assessment items). The majority of learners from the three classes performed poorly in the 15 items. Nine learners were purposefully selected from each class according to their performance in the ANAs: three top, three middle and three low performers.
Data collection
The task-based interview was designed so that the researchers could ask questions that could solicit detailed information on the difficulties that the learners experienced. This interview was informed by Newman's Error Analysis (NEA) (Newman 1977), which provided a framework that assisted in giving an explanation of the struggles the learners faced in the process of solving mathematical problems. Newman highlighted that as children solve mathematical problems, they may experience reading, comprehension, transformation, process skills or encoding problems. According to White (2005), the NEA instrument makes it possible to explore the links between one's ability to read and the ability to understand and work with numbers. During the interview, learners were probed in order to encourage them to proceed through the stages of solving the mathematical problems, in the process uncovering the challenges they experienced. The interviews were audio recorded, which allowed us to record accurately the occurrences of difficulties represented by learners when they hesitated or became silent during responses. Field notes recorded their facial expressions or gestures. Video recording was considered to be too intrusive and was therefore not used.
As part of the interviews, learners were taken through a process of reading, interpreting and solving the problems, which were written in the ANAs in English. The interview involved probing questions to follow up on the learners' responses on the 15 identified questions. All 15 questions consisted of English language text to be read. Learners were prompted or supported with translation at 'break down' points, as will be evident in the transcripts below.
A limitation of the study is that it involves only three classes of learners in township schools where learners share a single home language (isiXhosa), while in Grade 4 they learn through the medium of English. There are of course many other Grade 4 classroom contexts where learners have different linguistic backgrounds. IsiXhosa-speaking learners were assessed in this study because it is the dominant language of learners in the Eastern Cape - the province of this study. It was not the intention of this study to compare the linguistic challenges of the ANAs for ELLs to native English speakers. For that, an entirely different design would be needed. Instead, this study sought to understand the challenges that three classes of isiXhosa-speaking Grade 4 learners faced when responding to a sample of items that required reading and interpretation of English in order to make sense of what was being asked mathematically.
Ethical consideration
All ethical permissions were obtained, and the names of the schools, teachers and learners used in this article are pseudonyms.
Findings and discussion
We have previously argued, and shown, that the linguistic complexity of the majority of the Grade 4 mathematics ANA items is far too high for Grade 4 ELLs, most of whom have only just started to learn mathematics through the medium of English (see Sibanda 2016; Sibanda & Graven 2014). Here we do not focus on the specific linguistic complexity of the items but rather illustrate, through purposefully selected excerpts from the learner interviews, the challenges these learners faced when reading and attempting to comprehend the selected ANA items during the linguistically mediated task-based interviews. From these interviews, three categories of mediation were identified as required by learners for both reading and comprehension (i.e. no mediation needed; some mediation needed and extensive mediation needed). The indicators for extensive and moderate mediation were as follows: 'no mediation required' meant the learners were able to read, interpret and move to solving the problem without any input from the interviewer.
'Extensive reading mediation' meant the assistance that was given to learners whose reading skills were so weak that they struggled to read several words or more, in all the questions.
Medium reading mediation was the assistance given to learners who were not able to read a word or words in half of the questions, and the words were read for them.
Extensive comprehension mediation was done for those learners who failed to understand almost all the questions in the interviews and the interviewer had to explain all those questions.
Medium comprehension mediation meant the assistance that was given to those learners who failed to understand about half of the questions and then demonstrated the subsequent skill after the mediation.
Table 1 shows that learners fell into all three groups in relation to the extent of mediation required to overcome reading difficulties they experienced. On the other hand, learners fell into only two groups (extensive and moderate mediation required) in relation to mediation required to overcome comprehension difficulties. That is, no learner required no mediation in making sense of the 15 questions asked. Learners who were given substantial mediation during reading or comprehension were considered to be those who were unable to read or comprehend 50% to 100% of the questions, respectively, in the interviews.
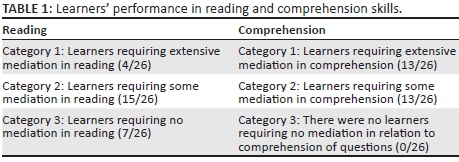
As is evident from the number of learners in each group, the number of learners requiring extensive, moderate or no mediation for reading does not directly align with the number of learners requiring extensive, moderate or no comprehension mediation. So, for example, while there were seven learners requiring no reading support on these items, all learners required either extensive or moderate comprehension support. However, there was some alignment of learners requiring extensive reading support in that all four of these learners also required extensive comprehension support.
Table 1 suggests that all 26 ELLs in this study struggled to access mathematical questions posed in written English, either through comprehension difficulties or a combination of comprehension and reading difficulties. This, in turn, restricts opportunities for learners, who may be able to solve the mathematical problem, were they able to comprehend what is being asked, to demonstrate the mathematical skills that are to be assessed. In the following section, we will provide transcribed excerpts taken from the interviews that will reveal learners' comprehension experiences. To do this we focus on the first and the last of the groups of learners as defined in Table 1 by the extent of reading mediation required. This allows us to illuminate comprehension difficulties for learners across the spectrum of reading difficulties (i.e. from ELLs with extreme reading difficulties and those with basic reading fluency in reading).
It is crucial to note that we do not argue that if learners can access what is required mathematically they will be able to demonstrate the targeted mathematical skill. These excerpts serve to show that access (reading and comprehending what is required) is only the first necessary step for successful performance in written mathematics assessments. It is not sufficient for success. The excerpts have been chosen specifically because they exemplify several of the types of challenges learners in these categories faced. Furthermore, they reveal the way in which mediation, in some cases, enabled learners to demonstrate the mathematical skill, while in other cases mediation did not enable demonstration of subsequent mathematical skills.
There were cases in which learners struggled to read a large number of the words in an assessment item, causing difficulty in understanding or misunderstanding what they were reading (Category 1 readers, see Table 1). In other instances, learners could not read or comprehend to an extent that even with extensive mediation from the interviewer, it was still difficult for them to access the items sufficiently to attempt the problem.
In other cases, learners managed the reading for most questions but struggled to comprehend the questions (Category 2 readers). While seven learners could read with little or no need for reading support (Category 3 readers), all learners needed mediation in comprehending some of the questions. Below, we share the selected learner excerpts taken from the first author's PhD study (see Sibanda 2016 for additional excerpts). Firstly, excerpts from the interviews with two learners who required extensive reading mediation are provided and discussed. Thereafter, two excerpts are provided that show examples from interviews in which the learners required almost no mediation in reading but did require moderate mediation in comprehending an item.
Learners requiring extensive mediation in reading (and subsequent challenges to comprehension)
As indicated above, all ANA items are taken from the 2013 Mathematics ANA article (DBE 2013a). In Category 1, 19 out of 26 learners had great difficulty in reading the items and required extensive assistance in reading. In Box 1 - 7 are excerpts from two learners who needed reading mediation on every question. Some learners failed to independently read several words in all 15 items and as a result struggled to comprehend those items. They reveal some of the reading and comprehension difficulties encountered by such learners. The ANA item is presented, and thereafter the interview excerpt is provided. The interaction with the researcher of the two learners chosen, Bongani (see Box 1 and 2) and Benny (see Box 3), typified the types of responses of most learners in Category 1. Bongani's (and other learners') pauses in speech are indicated by an ellipsis (…).







ANA Item 5.1:
Mrs Mazibe buys an apple for R1,20 and sells it for R1,95. How much money does Mrs Mazibe make by selling 1 apple? (DBE 2013a)
Bongani hesitated before reading the words 'Mazibe', 'buys' and 'apple', and he read the second 'for' in the sentence as first 'fro' and then 'from'. He could not read the word 'does' in the question and once more grappled to read this word in the next question even though the interviewer had modelled reading it in the above question. Bongani's poor reading skills could have affected his comprehension of the question and consequently his ability to respond to the mathematical item. Box 2 shows Bongani's difficulty in comprehending the item that he had struggled to read.
From the excerpt, it is clear that Bongani failed to understand what was required by the question. Although the interviewer explained that 'make' here meant he had to look for the profit, he did not understand what the term meant and therefore could not respond appropriately to the mathematical item in order to attempt to demonstrate the mathematical skill required. In this respect introducing this term as part of the mediation process was not helpful in clarifying what was being asked. Although we are not claiming that Bongani's failure to solve the problem was solely caused by his reading and comprehension challenges, it is important to note that fluent reading is essential for comprehension (DoE 2002), which then allows learners to access the item and interpret the question, which is the first part of the mathematical problem-solving cycle- that is, understand the problem; then come up with a plan; carry out the plan; review and check (Polya 1973). Box 3 is another example of Bongani's challenges in reading the items.
ANA Item 7 (DBE 2013a):
Write a number sentence for the number sentence below. The difference between 1 613 and 859 is seven hundred and fifty-four.
Here Bongani failed to read accurately the words 'sentence' and 'below'. This was manifested clearly by his mispronunciation of the words. As with the previous excerpt Bongani could recognise almost none of the words instantly, and this caused him to read slowly. Bongani also experienced difficulties in reading certain words in other assessment items in the interview, for example 'departures', 'airport', 'answer', 'destination', 'midday', 'use', 'wall', 'symbol', 'correct' 'statement', 'bar', 'graph', 'amongst' and 'baseball'. It is also interesting to note that all the words that Bongani was unable to read were contained in items that were high in linguistic complexity (see Sibanda 2016). Bongani failed to read 14 out of 15 questions fluently. Failure to read four or five words in a single problem translated to virtually no comprehension of the test item. Most of the words he failed to read were those words with sounds that did not match the letters (e.g. 'use') and also words consisting of silent letters (e.g. 'answer', 'does').
In Box 4 we share excerpts from Benny's interview. Benny struggled to read and comprehend, requiring extensive mediation in both.
ANA Item 5.1 (DBE 2013a):
Mrs Mazibe buys an apple for R1,20 and sells it for R1,95. How much money does Mrs Mazibe make by selling 1 apple?
Even after these words were explained, Bongani and Benny remained silent and the interviewer thus moved onto the next item. On this item, Benny was unable to read the word 'buys'. On his first attempt to read it, the sound /u/ was pronounced as it is pronounced in the isiXhosa way, not English. The word 'buys' was not read because he was asked to leave out the words he did not know. When one is reading the word 'buys', sounds of the letters /b/+/uy/+/s/ are made, noting that uy makes the sound 'I', which is taught in the Foundation Phase. Because Benny had not become proficient in matching the sounds and the letters in English he could not read this word. It was evident that his knowledge of English phonics, which is the basis for word recognition (Shanahan 2008) was limited. By learning phonics, learners get to know how sounds and letters are related (and combination of letters such as uy in buy and guy). Benny's difficulty with word sounds, as evident in his reading, lowered his comprehension during reading. In Box 5 a further example of Benny's struggle in reading and how this affected his opportunity to comprehend what was being asked:
ANA Item 11 (DBE 2013a): Draw the reflection of the arrow on the vertical dotted line.
Benny clearly showed weak reading and comprehension skills on Item 11. Initially, he was not able to read the word 'reflection' because he failed to sound the letters. The difference in orthography between isiXhosa and English plays a role here (Prinsloo 2009). This can lead to the learner getting confused and therefore misreading words. He was also unable to read the word 'vertical', as was evident in his inclusion of some letter sounds that were non-existent in the word. He was not able to recognise the words 'vertical' and 'dotted'. He also did not seem to understand these words even when they were read to him. The interviewer introduces the term 'symmetrical' in an attempt to mediate as this is a term used in the curriculum and textbooks but this too is a difficult and unfamiliar term for Benny. It is only after the interviewer rephrases it in more everyday BICS language - 'so that the two sides … look the same' - that Bennie is able to respond (successfully) to the question. Benny thus had the skill of completing a diagram so as to be reflected along a given axis but did not have the language skills to access what the question was asking.
Jennings et al. (2006) note that once learners succeed in recognising sight words, reading becomes easy. Words like 'reflection' and 'vertical', for example, do not need to be sounded when reading them. According to the DoE (2010), such words constitute 75% of most reading passages and they are core to reading basics. When a learner looks at the word, he or she remembers the forms and recognises the words and hence this promotes reading speed (DoE 2010). To Benny, who had not managed decoding most words, these words were difficult to read and it could explain the misreading, hesitations and silences.
Fourie (2008) notes that word recognition ability is crucial if one is to master written words and read fluently. If this skill of word recognition is missing, learners cannot get any meaning from what they read. Considering Benny's case, it took him a longer time than expected to finish reading the question because he could not readily recognise the sight words. Hence there was pressure on his short-term memory, which compromised the recollection and retention of the first words and their meaning at the end of the sentence.
Rault-Smith (2009) suggests that learners moving to Grade 4 should be beginning to read fluently and independently. However, this was not confirmed in this study because the majority of learners who participated in the task-based interviews were still 'learning to read' rather than 'reading to learn'. Instead of reading independently, reading and understanding a text on their own, learners were reading with difficulty, defined as struggling to read over 10% of the words in a text (Treptow, Burns & McComas 2007). Hence, for Bongani and Benny, the text was very difficult to read as they could not read more than four words correctly in a question consisting of 11 words. This resulted in their difficulty understanding the questions.
Learners requiring almost no mediation in reading but moderate mediation in comprehension
Two of the seven learners who required no reading support required extensive mediation in comprehension while the other five learners required only moderate mediation (see Table 1). Here, we share excerpts from two learners' interviews to show that despite fluent reading ability, in the case of unfamiliar words and items of a high linguistic complexity, learners still struggled to comprehend what was being asked of them mathematically.
Excerpts from the interviews with Anathi (see Box 6) and Buhle are discussed below in order to illustrate the difficulties they experienced comprehending the ANA items. Their responses were typical of the comprehension challenges that other fluent readers among those interviewed faced.
The extract given above shows the challenges that Anathi faced as she tried to understand what the question asked. There is evidence from this extract that she had not understood the requirement of the text even though she had claimed to have understood all the words. She did not know the meaning of 'number sentence' and she thought the question instructed her to 'write what is the difference between 1613 and 859'. Hence she could not recognise that the 'difference' was already provided as 754 in the question.
Secondly, while Anathi indicated that she knew what the word 'difference' meant, she did not understand this as a mathematical concept, as, for example, the distance between two numbers on a number line. She rather viewed them as two numbers being different (not the same) from one another. She explained 'difference' as 'what is different numbers, numbers are different'. Anathi took 'difference' to mean 'dissimilar', the everyday meaning.
According to Bohlman and Pretorius (2008), a learner is able to interpret mathematical concepts and information only if he or she has understood the information with coherence. Anathi could read items quite fluently and her comprehension problems seemed to be attributable more to unfamiliar mathematical terms or terms having different meanings from their everyday use. Anathi struggled to find the solution to the problem because she could not understand what was meant by 'making a number sentence'.
Next is an excerpt from the interview with Buhle (see Box 7). We see that his lack of familiarity with mathematical terms in English results in his struggling to make sense of and solve the word problems given to him in question 11.
Buhle struggled to understand the words that seemed to be new to him because he could not instantly recognise them when he read them. The words 'reflection' and 'vertical', are mathematical vocabulary that he was unfamiliar with. When they interact day, learners seldom hear or speak such words. Examples of such words that could not be understood by Buhle are 'departure', 'convert', 'flow diagram', 'destination' and 'amongst'. The words that the learners could not understand were also part of the questions that had high linguistic complexity, and these are difficult for Grade 4 ELLs as illuminated by the broader study.
It is apparent that for both Buhle and Anathi comprehension was hampered by unfamiliar words and mathematical terms in the items. Duke and Pearson (2002) note that if learners have knowledge of tenses, vocabulary and participants, as well as the order of what they read, the texts will be easier to read and understand. Attention is needed to reading comprehension as many South African learners have indicated very poor performance in this aspect (Pretorius & Lephalala 2011). Howie et al. (2008) also note that there is a very low reading comprehension in South African learners, as revealed by a large-scale assessment of reading comprehension of Grade 4 and 5 learners. This study also confirms the findings by the aforementioned researchers.
Concluding remarks and implications
This study utilised a form of linguistic mediation in task-based interviews to investigate the challenges Grade 4 isiXhosa-speaking learners faced when reading and interpreting a selection of 2013 Grade 4 ANA questions in English. This article has shared excerpts from task-based learner interviews focused on a sample of items from the Grade 4 2013 mathematics ANAs in English. The excerpts illustrate how learners were unable to read and/or understand many mathematics words in the questions. This could be because, firstly, the words they failed to read are rarely heard or spoken in the everyday language of these learners, and they were thus unfamiliar with them. In the article we have shown how the English language can present challenges for learners and how some of these challenges emanate from the differences in the orthography of English and that of the African languages; in the latter there is a one-to-one correspondence between the graphemes and the phonemes, whereas in English the opaque orthography does not have such correspondence. These excerpts further revealed that some learners were unable to read because they could not recognise sight words, which are critical for the mastery of written words as well as for fluent reading (e.g. everyday words such as 'buys' would be a word that fluent readers would know by sight).
In addition, the excerpts showed that many of the words and items that learners struggled to read and comprehend had a high linguistic complexity, as was indicated in the broader study (Sibanda 2017; Sibanda & Graven 2014). As an example, words like 'reflection' and 'destination' not only have many letters but are not familiar words to Grade 4 English. This increases the linguistic complexity of the item for these particular learners. This is especially true for Grade 4 ELLs, whose English proficiency is limited in both academic language and everyday language.
Furthermore, the challenges of comprehension also emanated from words within the mathematics register, which are rarely encountered in everyday conversation or take on a different meaning from everyday meaning in the mathematics classroom. Learner difficulties with the word 'difference', which they understood and interpreted in the everyday sense, would provide such an example. However, there is the possibility that basic mathematical concepts (or other concepts of higher cognitive order) may not have been developed in the mother tongue in the previous grades and they now pose challenges in Grade 4.
Discussion of the excerpts shared called into question the validity of the ANAs. The interviews showed that learners' inability to access the reading and language of these questions meant that learners then did not have the opportunity to demonstrate what they may have been able to do mathematically, - were they able to read and understand what the questions were asking providing linguistic mediation supported learners in making sense of what the questions were asking. One might consider that teachers should be able to provide such mediation to learners in assessments. Indeed in the Grades 1 and 2 ANAs teachers read the questions to the learners. However, further research is needed to ascertain where such linguistic mediation should begin and end and to what extent such mediation interferes with learners owning the problem-solving process, which requires that they independently work through interpreting a problem, devising a plan, carrying it out and then reviewing and checking their work.
Taking into consideration the fact that Grade 4 ELLs are still developing their everyday language in the additional language, English, it makes sense that they have not also developed the academic language that they use for learning. It is therefore important for future research to explore possibilities of either delaying learning in English as the LoLT until learners have had sufficient years of exposure to English and have well-developed BICS in English or providing increased access to developing the English proficiency needed for learning in English in Grade 4 in the Foundation Phase. It has been argued and shown that access to mathematics learning and successful interpretation of assessments depends to a large degree on understanding the language of learning, teaching and assessment. Given that this language is English from Grade 4 for the majority of South African learners (even while the majority of these learners do not have English as their mother tongue and have had very limited access to English beyond school) indicates a great unfairness in our education system that disadvantages the majority of learners in our country.
In summary, the study found that most learners were challenged by the language of assessment (being English) and this compromised their access to the questions. Thus, we challenged whether mathematics assessments in English can be considered valid if learners fail to understand the English language of the questions. In order to demonstrate one's mathematical problem-solving capabilities one must first interpret the problem, which when stated as a word problem in English requires English language proficiency.
Acknowledgements
This research was supported by the FirstRand Foundation, Anglo De Beers Chairman's fund, Department of Science and Technology and the National Research Fund.
Competing interests
The authors declare that they have no financial or personal relationships which may have inappropriately influenced them in writing this article.
Authors' contributions
M.G. was the project leader. L.S. was responsible for the project design. L.S. performed the experiments and did the interviews. L.S. and M.G. made conceptual contributions and M.G. assisted with the analysis and interpretation of data. L.S. prepared the samples and performed the calculations. M.G. proofread the manuscript.
References
Abedi, J. & Herman, J., 2010, 'Assessing English language learners' opportunity to learn mathematics: Issues and limitations', Teachers College Record 112, 723-746. [ Links ]
Abedi, J. & Lord, C., 2004, 'The language factor in mathematics tests', Applied Measurement in Education 14, 219-234. https://doi.org/10.1207/S15324818AME1403_2 [ Links ]
Beal, C., Adams, N.M. & Cohen, P.R., 2010, 'Reading proficiency and mathematics problem solving by high school English language Learners', Urban Education 45(1), 58-74. https://doi.org/10.1177/0042085909352143 [ Links ]
Barbu, O.C., 2014, 'Understanding English Language Learners' Needs in Mathematics Education', Journal of Education & Human Development 3(1), 131-144. [ Links ]
Bell, B., 2003, Mother-tongue maintenance and Maths and Science achievement: A contribution towards the formulation of multilingual language-in-education policies for South African schools, viewed 15 December 2014, from http://und.ac.za/und/ling/archieve/bell-01.htm
Bohlman, C. & Pretorius, E., 2008, 'Relationships between mathematics and literacy: Exploring some underlying factors', Pythagoras 67, 2-55. https://doi.org/10.4102/pythagoras.v0i67.73 [ Links ]
Brown, C.L., Cady, J.A. & Lubinski, C.A., 2011, The effects of poverty and language on mathematics achievement for English language learner, Springer, New York.
Carrasquillo, A., Kucer, S.B. & Abrams, R., 2004, Beyond the beginnings: Literacy interventions for upper elementary English language learners, Multilingual Matters Limited, Clevedon, UK.
Cummins, J., 1979, Cognitive/academic language proficiency, linguistic interdependence, the optimum age question and some other matters, Working Papers on Bilingualism. Ontario Institute for Studies in Education, Bilingual Education Project, (ERIC Document Reproduction Service No. ED 184 334), Toronto, Canada.
Cummins, J., 1994, 'The acquisition of English as a Second Language', in K. Spangenberg-Urbschat & R. Pritchard (eds.), Reading Instruction for ESL Students, International Reading Association, Delaware, pp. 32-62.
Cummins, J., 1999, BICS and CALP: Clarifying the distinction, University of Toronto, Opinion Papers (120), viewed 13 June 2013, from http://ezproxy.wou.edu:2100/hww/results/external_link_maincontentframe.jhtml?_DARGS=/hww/results/results_common.jhtml.44
Cummins, J., 2000, Language, power and pedagogy: Bilingual children in the crossfire, Multilingual Matters Ltd, Great Britain.
Cummins, J., 2008, 'BICS and CALP: Empirical and theoretical status of the distinction', in B. Street & N. Hornberger (eds.), Encyclopedia of language and education, 2nd edn., vol. 2, Literacy, pp. 71-83, Springer Science + Business Media LLC, New York.
Cummins, J., 2013, 'BICS and CALP: Empirical support, theoretical status, and policy implications of a controversial distinction', in M.R. Hawkins (ed.), Framing languages and literacies socially situated views and perspectives, pp. 10-23, Routledge, New York.
Cummins, J., 2017, 'BICS and CALP: Empirical and theoretical status of the distinction', in B.V. Street & S. May (eds.), Encyclopedia of language and education: Literacies and language education, 3rd. edn., pp. 59-71, Springer, Cham, Switzerland.
Department of Basic Education, 2008, Foundations for learning campaign: 2008-2011, Government Gazette No. 30880, Pretoria.
Department of Basic Education, 2011, Report on Annual National Assessments Grades 1-6 & 9, Department of Basic Education, Pretoria.
Department of Basic Education, 2012, Report on Annual National Assessments Grades 1-6 & 9, Department of Basic Education, Pretoria.
Department of Basic Education, 2013a, Annual National Assessment 2013 Grade 4 Mathematics Test, viewed 08 May 2014, from https://www.education.gov.za/Portals/0/CD/Curriculum%20doc%20question%20Papers2007/New%202013%20Grade%204%20Mathematics%202013%20Eng.pdf?ver=2013-09-16-145952-000
Department of Basic Education, 2013b, Report on Annual National Assessments Grades 1-6 & 9, Department of Basic Education, Pretoria.
Department of Basic Education, 2014, Report on Annual National Assessments Grades 1-6 & 9, Department of Basic Education, Pretoria.
Department of Education, 1997, Language in Education Policy, Government Printer, Pretoria.
Department of Education, 2002, Revised national curriculum statement, Grades R-9, Department of Education, Pretoria.
Department of Education, 2007a, Teaching reading in the early grades, A teacher's handbook, Department of Education, Pretoria.
Department of Education, 2007b, A guide for grade 4 teachers: Reading and writing English additional language (Quality, Improvement, Development, Support and Upliftment Programme), Department of Education, Pretoria.
Department of Education, 2010, Introduction to the Gauteng primary literacy 105 strategy, Department of Education, Pretoria.
Department of Education, 2011, National Curriculum Statement: Curriculum and Assessment Policy (CAPS), Senior Phase Grade (7-9) Mathematic, Department of Education, Pretoria.
Desai, Z., 2001, 'Multilingualism in South Africa with particular reference to the role of African languages in education', International Review of Education 47, 232-339. https://doi.org/10.1023/A:1017957927500 [ Links ]
Duke, N.K. & Pearson, P., 2002, 'Effective practices for developing reading comprehension', in E. Farstrup & S. Jay Samuel (eds.), What research has to say about reading instruction, 3rd edn., pp. 205-242, International Reading Association, Inc., Newark, DE.
Fleisch, B., 2008, Primary education in crisis: Why South African children underachieve in reading and mathematics, Juta, Cape Town.
Fourie, J., 2008, Study guide: Learning support in the classrooms, Johannesburg, University of Johannesburg.
Graven, M.H., 2014, 'Poverty, inequality and mathematics performance: The case of South Africa's post-apartheid context', The International Journal of Mathematics Education ZDM 46, 1039-1049. [ Links ]
Graven, M. & Venkatakrishnan, H., 2013, 'ANAs: Possibility and constraints for mathematical learning', Learning and Teaching Mathematics 14, 12-16. [ Links ]
Graven, M. & Venkatakrishnan, H., 2014, 'Primary Teachers' experiences relating to the administration processes of high-stakes testing: The case of Mathematics Annual National Assessments', African Journal of Research in Mathematics, Science and Technology Education 18(3), 299-310. https://doi.org/10.1080/10288457.2014.965406 [ Links ]
Hakuta, K., 2011, 'Educating language minority students and affirming their equal rights: Research and practical perspectives', Educational Researcher 40(4), 163-174. https://doi.org/10.3102/0013189X11404943 [ Links ]
Halliday, J., 2010, 'Educational assessment', in R. Bailay, R. Barrow, D. Carr & C. McCarthy (eds.), The SAGE Handbook of Philosophy of Education, pp. 369-384, Sage, Thousand Oaks, CA.
Hammill, L., 2010, 'The interplay of text, symbols, and graphics in mathematics education, Text, symbols, and graphics in mathematics education', Transformative Dialogues: Teaching & Learning Journal 3(3), 1-8. [ Links ]
Han, W.J., 2011, 'Bilingualism and academic achievement', Child Development 82, 1709-1714. [ Links ]
Henning, E. & Dampier, G., 2012, 'Simple language is the answer to 'difficult' assessment tests', Mail and Guardian, viewed 02 May 2013, from http://mg.co.za/article/2012-09-08-simple-language-is-the-answer-to-difficult-assessment-tests
Henry, D., Nistor, N. & Baltes, B., 2014, 'Examining the relationship between math scores and English Language Proficiency', Journal of Educational Research and Practice 4(1), 11-29. [ Links ]
Howie, S., 1997, Mathematics and science performance in the middle school years in South Africa: A summary report on the performance of the South African students in the Third International Mathematics and Science Study, HSRC, Pretoria.
Howie, S., Venter, E., van Staden, S., Zimmerman, L., Long, C., Du Toit, M. & Archer, E., 2008, PIRLS 2006 Summary Report: South African children's reading achievement, Centre for Evaluation and Assessment, University of Pretoria, Pretoria.
Howie, S.J., Combrinck, C., Roux, K., Tshele, M., Mokoena, G.M. & McLeod Palane, N., 2017, PIRLS Literacy 2016 Progress in International Reading Literacy Study 2016: South African Children's Reading Literacy Achievement, Centre for Evaluation and Assessment, Pretoria.
Jennings, J.H., Caldwell, J. & Lerner, J.W., 2006, Reading problems assessment and teaching strategies, 5th edn., Pearson/Allyn & Bacon, Boston, MA.
Jordon, N.C., Kaplan, D. & Hanich, L.B., 2002, 'Achievement growth in children with learning difficulties in mathematics: Findings of a two-year longitudinal study', Journal of Educational Psychology 94(3), 586-597. https://doi.org/10.1037/0022-0663.94.3.586 [ Links ]
Kieffer, M.J., Lesaux, N.K., Rivera, M. & Francis, D.J., 2009, 'Accommodations for English language learners taking large scale assessments: A meta-analysis on effectiveness and validity', Review of Educational Research 79, 1168-1202. https://doi.org/10.3102/0034654309332490 [ Links ]
Krashen, S., 1993, The power of reading, Libraries Unlimited, Englewood, CO.
Le Roux, B., 1993, The black child in crisis, A socio-educational perspective, Van Schaik, Hatfield-Pretoria.
Moschkovich, J., 2012, 'Mathematics, the common core, and language: Recommendations for mathematics instruction for ELs Aligned with the common core', Commissioned Papers on Language and Literacy Issues in the Common Core State Standards and Next Generation Science Standards, Proceedings of 'Understanding Language' Conference, Stanford University, Palo Alto, CA, pp. 17-31.
Moschkovich, J., 2016, 'Hearing mathematical competence expressed in emergent language', Cases for Mathematics Teacher Educators: Facilitating Conversations about Inequities in Mathematics Classrooms 1, 161-170. [ Links ]
Neville-Barton, P. & Barton, B., 2005, The relationship between English language and mathematics learning for Non-Native Speakers, A TLRI Research Report for NZCER, NZCER, Wellington.
Newman, M.A., 1977, 'An analysis of sixth-grade pupils' errors on written mathematical tasks', Victorian Institute for Educational Research Bulletin 39, 31-43. [ Links ]
Polya, G., 1973, How to solve it, A new aspect of mathematical method, Princeton University Press, Princeton, NJ.
Pretorius, E. & Lephalala, M., 2011, 'Reading comprehension in high-poverty schools: How should it be taught and how well does it work?', Per Linguam 27(2), 1-24. [ Links ]
Prinsloo, D., 2009, 'Current lexicography practice in Bantu with specific reference to the Oxford Northern Sotho School Dictionary', International Journal of Lexicography 22, 151-178. https://doi.org/10.1093/ijl/ecp009 [ Links ]
Rault-Smith, J., 2009, Teaching reading: Expect educator series, Macmillan, Northlands.
Reddy, V., Isdale, K., Juan, A., Visser, M., Winnaar, L. & Arends, F., 2016, TIMSS 2015: Highlights of mathematics achievement of Grade 5 South African students, Department of Basic Education/ Human Sciences Research Council, Pretoria.
Robertson, S-A. & Graven, M., 2015, 'Exploring South African mathematics teachers' experiences of learner migration', Intercultural Education 26(4), 278-295. https://doi.org/10.1080/14675986.2015.1071754 [ Links ]
Schlebush, G., 2002, Cognition and language of learning in South Africa: A grade 10 Economics perspective, viewed 23 October 2013, from /www.nova
Schleppegrell, M.J., 2012, 'Academic Language in teaching and learning Introduction to special issue', The Elementary School Journal 112(3), 409-418. https://doi.org/10.1086/663297 [ Links ]
Spaull, N., 2015, 'An overview and interrogation of the Annual National Assessments in South Africa', Presented at the Catholic Parliamentary Liaison Office roundtable discussion, viewed 19 September 2017, from https://nicspaull.com/presentations/
Setati, M., 2005, 'Teaching Mathematics in a Primary Multilingual Classroom', Journal for Research in Mathematics Education 36(5), 447-466. [ Links ]
Setati, M. & Barwell, R., 2008, 'Making mathematics accessible for multilingual learners', Pythagoras 67, 2-4. https://doi.org/10.4102/pythagoras.v0i67.68 [ Links ]
Setati, M., Chitera, N. & Essien, A., 2009, 'Research on multilingualism in mathematics education in South Africa: 2000-2007', African Journal of Research in Mathematics, Science and Technology Education 13(1), 65-80. https://doi.org/10.1080/10288457.2009.10740662 [ Links ]
Shanahan, T., 2008, Phonic: Issues and trends in literacy education, Pearson, Boston, MA.
Sibanda, L., 2016, 'Investigating the nature of the linguistic challenges of the Department of Basic Education (DBE) 2013 Grade 4 Mathematics ANAs and learners' and teachers 'experience of them', Unpublished PhD thesis, Rhodes University, Grahamstown.
Sibanda, L., 2017, 'Grade 4 Learners' Linguistic difficulties in solving mathematical assessments', African Journal of Research in Mathematics Science and Technology Education 21(1), 86-96. https://doi.org/10.1080/18117295.2017.1291476 [ Links ]
Sibanda, L. & Graven, M., 2014, 'Applying a linguistic complexity checklist and formula to the 2013 Grade 4 Mathematics National Assessment', Paper presented at the Proceedings of the 23rd Annual Meeting of the Southern African Association for Research in Mathematics, Science and Technology Education (SAARMSTE), Maputo, 15 January 2015.
Treptow, M., Burns, M.K. & McComas, J.J., 2007, 'Reading at the frustration, instructional, and independent levels: The effects on students' reading comprehension and time on task', School Psychology Review 36(1), 159-166. [ Links ]
UNESCO., 2016, If you don't understand, how can you learn? Policy Paper 24, pp. 1-9, Global Education Monitoring Report, viewed 25 June 2017, from https://en.unesco.org/gem-report/sites/gemreport/files/language_paper_references.pdf
Webb, V., 2002, Language in South Africa: The role of language in national transformation, reconstruction and development, John Benjamins, New York/Amsterdam.
Webb, V., 2011, 'Language and education: Marginalization and failure, or access and success', Paper presented at the 2011 lunch of research project: Paradigms and practices of teaching and learning in Foundation Phase language classroom in Gauteng and Limpopo provinces.
Webb, L. & Webb, P., 2013, 'Teaching strategies in language-diverse mathematics classes: A case study', Educational Research for Social Change 2(2), 31-42. [ Links ]
White, A.L., 2005, 'Active mathematics in classrooms: Finding out why children make mistakes - and then doing something to help them', Square One 15(4), 15-19. [ Links ]
 Correspondence:
Correspondence:
Lucy Sibanda
lcysbnd@gmail.com
Received: 04 Nov. 2016
Accepted: 03 Aug. 2018
Published: 13 Nov. 2018














