Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.8 n.1 Johannesburg 2018
http://dx.doi.org/10.4102/sajce.v8i1.540
ORIGINAL RESEARCH
Weaving in connections: Studying changes in early grades additive relations teaching
Anna-Lena EkdahlI, II; Hamsa VenkatI, II; Ulla RunessonI, II; Mike AskewII
ISchool of Education and Communication, Jönköping University, Sweden
IIWits School of Education, University of the Witwatersrand, South Africa
ABSTRACT
In this article, we present aspects of teaching that draw attention to connections - both within and between examples - in order to explore the potential objects of learning that are brought into being in the classroom space and thus what is made available to learn. Our focus is on exploring differences in teaching over time, in the context of learning study style development activity of additive relation problems in three Grade 3 classes in South Africa. In a context where highly-localised and fragmented instruction has been noted, this study reports on the nature and extent of changes in connections in instruction over time. The application of a coding framework focused on simultaneity and connections in teaching points to a richer range of structural relationships within examples, and more connecting work between examples in the second year in comparison to the first year.
Introduction
The centrality of 'connections' within well-grounded, efficient and flexible mathematical working has been written about extensively in mathematics education (e.g. Hiebert et al. 2005). A key motivation for this body of work is evidence from studies of instruction pointing to teaching that presents mathematics, not as a network of connected ideas, but rather as a collection of isolated facts and procedures. Hiebert, Stigler and Manaster (1999), overviewing the findings from the Trends in International Mathematics and Science [Video] Study looking at 8th grade lessons in the United States, Germany and Japan, pointed to differences in the nature and extent of links between parts of lessons between the three countries. Their American lesson analysis indicated that 40% of the lessons contained explicit connections in instruction between segments of the lesson, and 45% of the lessons contained segments linked by what the authors described as: '…at least one appropriate mathematical relationship (e.g. one segment was dependent on another or extended another)' (Hiebert et al. 1999:198). In Japanese lessons, these figures were 96% and 92%, respectively.
Our study is focused on early grades mathematics instruction in South Africa, a country where low mathematics performance continues to be a concern. Studies of instruction in the early years in South Africa have pointed to practices in which individual examples are treated separately, with repeated return to concrete counting strategies, a phenomenon that Venkat and Naidoo (2012) refer to as 'extreme localisation':
a scenario in which not just episodes, but individual examples within episodes are played out in what appear as ahistorical ways. What we mean by this is that each time a new example enters the scene, the past appears to vanish (including the methods and answers that might have been generated in the very recent past). (pp. 31-32)
Other evidence points to poorly-selected representations and/or teacher talk or gesture disconnected from representations further compounding a lack of connections (Mathews 2016).
Given the importance of connections in contrast to the localisation seen on the ground, this study reports on the nature and extent of changes in connections in instruction over time in a professional development study located in South Africa focused on better-connected additive relations teaching. Hiebert et al.'s (1999:198) description of coherent lessons, as 'achieved by weaving together ideas and activities', reflects our focus, both in the professional development and in the analysis that we present in this article. The intervention model was aimed at supporting more connected handling of examples by teachers. The analysis studied differences in the nature of connections seen in their teaching of additive relations tasks.
Given the 'extreme localization' at the level of examples in South Africa, we needed a finer 'grain size' when looking for connections than the lesson segment level used in the Trends in International Mathematics and Science [Video] Study. Watson and Mason (2006a) have noted that the selection and sequencing of examples can allow mathematical structure and generality to be foregrounded through instruction that treats lesson examples as a connected set. In our analyses, we thus focused on aspects of teaching that explicitly drew attention to connections - both within and between examples - in order to explore differences in the objects of learning that were made available to learn.
Our empirical data is drawn from three Grade 3 teachers in one school who collaborated with the research team in three cycles of an adapted learning study process1 (Marton & Pang 2003) to explore and improve the teaching of additive relations. We emphasised a structural approach to additive relations in all three cycles, which contrasted with the more operational approaches based on counting foregrounded in the South African curriculum. Here we attend to two of the study cycles (February 2013 and February 2014), both of which focused on partitioning and missing number additive relation problems. A coding framework for analysing the teaching of partitioning was developed in our earlier work with the February 2013 dataset (Ekdahl, Venkat & Runesson 2016), and grounded in variation theory (explored below) (Marton 2015) and example spaces (Watson & Mason 2006a). In this article, we apply the earlier coding framework to the 2014 partitioning teaching and extend it to the topic of missing number problems.
Our aim is to present evidence of differences over the two study cycles with respect to connections in teaching within examples and between examples, and to consider the implications of this evidence. We overview the literature base on structural approaches to additive relations, and outline key ideas in variation theory that are used in this article. We go on to share our methodology, data sources and analytical foci, before presenting our findings and analysis. We detail the phenomena underlying the differences that we found, and argue that these different phenomena can be interpreted as improvements in the teaching of additive relations through bringing structural properties into the foreground to a much greater extent in the second cycle.
Literature
Standing in contrast to the view of addition and subtraction as fundamentally proceeding from counting-based operational processes toward truncated and reified structural part-whole relationships (Carpenter et al. 1999), our point of departure is to begin from a base in structural and relational connections. In operational counting approaches, quantities are worked with sequentially, while structural approaches are based in numerical reasoning about part and whole quantities simultaneously. Additive relationships consist fundamentally of a parts and whole relation structure, and appreciating this structure has been described as critical for children's development of arithmetic skills (Fritz, Ehlert & Balzer 2013; Resnick 1983). Structural approaches foreground mathematical properties such as commutativity and compensation from the outset, whereas operational approaches focus on counting at the start and build subsequently into structure. Schmittau's (2003) work, following Davydov's curriculum, presents a key example of a structural approach to part-part-whole relationships. Similarly, Neuman (1987, 2013), from her work studying differences in young students' performance on early addition and subtraction, argues for a structural approach to additive relations.
Within a structural approach, teaching may start with tasks and representations aimed at providing openings for children to discern wholeness, to see different possible parts within the whole, and come to an awareness, on a concrete level, of how these parts are simultaneously related to each other and to the whole. An instance of such a task is Cobb et al.'s (1997) splitting monkeys between two trees in different ways task. Such situations can be represented in iconic diagram and symbolic forms (e.g. part-part-whole bar or triad diagrams, and number sentences).
Neuman (2013) argues that attending to parts and whole and their relationship within examples simultaneously provides a precursor to familiarity with 'families' of connected additive relations problems with one missing value, that is, 4 + _ = 7, _ + 4 = 7, 7 = 4 + _, 7 = _ + 4, 7 - 4 = _, 7-_= 4, _= 7 - 4, 4 = 7-_. A problem like _+ 4 = 7, can be solved by analysing its part-part-whole relationship, leading to the varied relationship formulations listed. The part-part-whole relationship is invariant across all of these number sentences. Connecting within any particular sentence involves working with the part-part-whole relationship. Connecting between these sentences builds awareness of commutativity and inverse relations between subtraction and addition. Part-part-whole models represent the outcomes of actions of composing parts or decomposing the whole and therefore can promote young children's learning of additive relations in terms of structure rather than operation. While part-whole relationships can be seen in concrete or iconic part-whole formats, working with symbolic representations provides efficiencies and generality beyond the specific context, and has therefore been noted as an important aspect of progression in additive working (Gray & Tall 1994).
Connections and simultaneity
The evidence of frequent disconnections in South African mathematics instructional discourse both within the handling of examples (Venkat & Adler 2012) and between examples (Adler & Venkat 2014; Venkat & Naidoo 2012), highlighted in the introduction, forms a key motivation for this article. Key tenets of variation theory (Marton 2015) and empirical findings from Neuman's study (1987, 2013) provide a theoretical base for our study. For example, Neuman (1987) used a task presenting 'splits' of nine stones between two boxes, with children asked how many stones could be in the first box and how many would be in the second box. One pattern of responses was children offering a part (e.g. four stones) for one box, then saying the second box contained nine stones. Neuman suggested that the offer of nine for the second box pointed to an ordinal awareness of number that has not yet been combined with simultaneous awareness of part-part-whole relationships. More generally, in this view, successfully solving new tasks involves discerning the aspects that are necessary to take into consideration at the same time. Creating openings for the simultaneous discernment of aspects critical for learning is therefore a necessary condition for building awareness of what we want students to learn.
Variation theorists argue that discernment of aspects is made possible through experience of variation in those aspects. The idea that variation can structure sense making by drawing attention to the targeted aspects has been advocated by Watson and Mason (2006a), when they present example spaces underpinned by variation in the midst of invariance as a way to promote attention to structure and generalisation. These principles can be applied in this way to missing number problems. If we want students to see 10 - _ = 7 as an additive part-whole equivalence relationship where 10 represents the whole (i.e. the targeted aspect), this discernment is likely to be supported by contrast with missing number problems with the same quantities where 10 does NOT represent the whole: e.g. 10 = _ - 7. Such contrast usually requires both (or multiple) examples to be simultaneously visible (Marton & Pang 2006).
Variation theorists have also argued that alongside choosing example sequences that incorporate certain patterns of differences and similarities, teaching actions must draw attention to their links (Kullberg, Runesson & Mårtensson 2014). Linking actions in primary and secondary mathematics have been described as constituted in combinations of teacher speech and/or gestures (Alibali et al. 2013). This leads to our interest in teachers' linking actions within and between examples, through which connections can be made visible for the learners.
Research design
We draw here on data from a broader study that ran across a one-year period spanning two academic years, conducted in a suburban government English-medium primary school in Johannesburg. The principal, teachers, parents and/or carers and students had given their written consent for participation in the study and videotaping of lessons and planning meetings. The research included three learning study cycles, each comprising three lessons taught by each teacher over a three-week period (February 2013 and October 2013 with the 2013 Grade 3 student cohort, and February 2014 with the 2014 Grade 3 student cohort). In this article, the analytical focus is on the teaching of the three Grade 3 teachers who were involved in the first 2013 study cycle and also the 2014 cycle. All three teachers were experienced Foundation Phase (Grades 1-3) practitioners, with between 13 and 19 years' teaching experience.
The teacher group worked together with the research team, planning, enacting, observing, discussing and evaluating the lessons. The research team designed some tasks and activities, and the teachers themselves initiated others. Most often the researchers suggested a task or activity to the teachers: these were occasionally rejected, but most often revised and adapted by the teachers based on their perceptions of students' needs and abilities. Analyses of student performance on pre-intervention tests and on classroom worksheets were collated and used for each reflection and planning meeting. Short sequences from the recordings, of the lessons together with the research team's first analyses of these and worksheet results, were selected for sharing in the planning and reflection meetings. In the discussions with the teachers, we emphasised a structural approach to additive relations. The use of representations and talk that emphasised connections within examples and between examples figured within the discussion of how examples could be handled.
The key data sources for this article are the nine video-recorded lessons (three from each teacher) from the first cycle in 2013 and a further nine lessons from the cycle in February 2014. All of the whole-class teaching related to partitioning and missing number problems from these 18 video-recorded lessons was transcribed, including teacher talk and gestures, and students' answers whether given individually or collectively. As our focus was on teacher instruction, episodes in the lessons related to students' individual work were not included in the analysis. Transcripts were analysed on a micro-level using the coding framework described in the next section.
The analytic process involved several steps and levels. Firstly, lessons were divided into sections of teaching. Each section focused on teaching of additive relations was marked as ended when the teacher introduced time for working on individual worksheets. Four sections of teaching (three in 2013 and one in 2014) related to partitioning of numbers and six sections (three in 2013 and three in 2014) related to missing number problems were thus delineated for analysis. The notation: Year. Lesson. Section (i.e. 13.3.2 for 2013, third lesson, second section of teaching) is used in Table 1 to overview sections of teaching in 2013 and 2014.
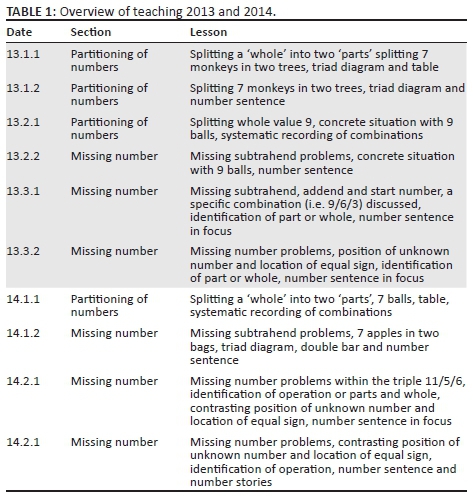
Second, within sections, segments formed the smallest unit of analysis. We marked segments by when the teacher introduced a question related to part-part-whole relations. Evaluations, explanations and discussion associated with that initial question were included in the same segment. A segment was marked as complete when the teacher asked a new question or the discussion focused on another example, aspect or mathematical idea related to the additive relations problem. A segment, in occasional cases, consisted of an introduction of a new representation or an instruction or an explanation without any questions being asked. The segments in each section were numbered consecutively and coded using the criteria developed within the coding framework, detailed next.
Coding framework
In our earlier work we developed a coding framework for considering the nature of simultaneity and connections in the teaching of partitioning (Ekdahl et al. 2016). This framework considered simultaneity and connections at three levels: between representations (SCBR), within examples (SCWE) and between examples (SCBE). These levels provided insights into contrasts in the teaching across the three teachers in the February 2013 study cycle. In exploring for differences in teaching between February 2013 and 2014, a common aspect across all three teachers was a smoother and earlier transition into symbolic representations from concrete situations in partitions teaching in 2014 in comparison to the previous year, with similar, though less marked shifts to symbolic representations in the teaching of missing number problems for two of the three teachers. Given this smooth transition, we focus the current analysis on the SCWE and SCBE categories, with extensions of the earlier indicators for partitioning to missing number problems.
Simultaneity and connections occur in links made in teachers' speech and deictic gestures (McNeill 1992) that emphasise relations within and between examples. An SCWE linking gesture in partition problems could be a hand or a finger moving, in a triad diagram, between the left and right circles and finally to the top circle to emphasise the part-part-whole relation. In missing number problems, linking actions in speech and/or with gestures within examples (SCWE) also pointed to the 'structural' part-part-whole relation, for instance, to the position of the unknown number in the relation or the equality relationship.
Across partitioning and missing number problems, looking at between examples (SCBE) criteria, a range of structural relations can emerge when different examples of missing number problems are juxtaposed and connected, for example: 11 - _ = 3 and 3 = 11 - _. In missing number problems, examples connected with linking speech and/ or gesture can compare the invarying position of the missing value in the relation. The criteria for coding partitioning and missing number problem are described in Table 2.
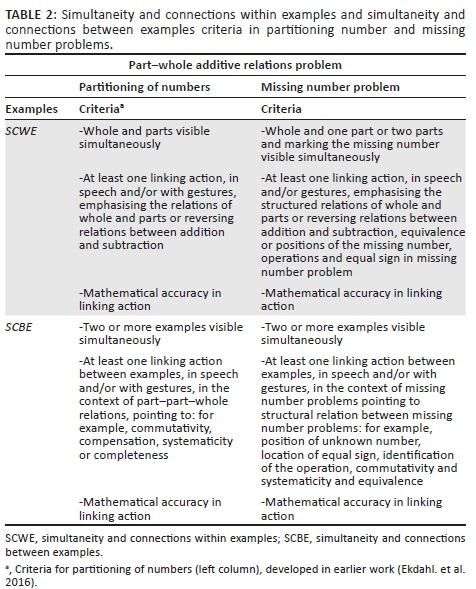
Each segment was examined for occurrences of SCWE and SCBE. For SCWE, we identified the examples handled (each example being an instance of a part-part-whole relation or a missing number problem). We then checked if the whole and the parts were visible simultaneously (partitioning task) or if the missing number problem was treated 'horizontally across the grain' (Watson & Mason 2006b:5), in that the whole and one part or two parts, together with the marking of the missing number, were simultaneously visible. Lastly, we assessed if there was at least one linking action emphasising the structural relationship within the example. Both these criteria had to be met to mark a segment with SCWE.
For SCBE, we noted the examples in each segment, and whether these were erased from the board as each one was completed. We then identified if there was at least one linking action in speech or gesture drawing attention to structural connections between examples. Both these criteria had to be met for the segment to be coded as SCBE.
Across both categories, examples had to be treated with mathematical accuracy to be assessed as SCWE and SCBE, respectively - see Table 2. All 18 lessons were coded in this way, and the number and percentage of segments in each category from each teacher coded as SCWE and SCBE for each section were summarised.
Ethical consideration
Ethical clearance for this project was granted by the University of the Witwatersrand within the Discussing Lessons initiative within the Wits Maths Connect - Primary project. Permissions were also in place from the provincial department of education. The data collection and research procedures were consistent with the principles of research ethics in South Africa. The principal at the primary school and the three teachers had indicated their willingness and voluntary informed consent to participate in the planning and development of the lessons. Also, parents or carers and participating students gave their informed written consent for the students' participation.
Results
Changes in teaching over time pointed to a richer range of structural relationships and connections between examples in the second year, supported by growing attention to part-part-whole relations within examples. Interesting differences between the three teachers in teaching additive relations were also identified in our analysis. Here we summarise the number and proportion of segments meeting the criteria for each category. We also use excerpts of teaching to illustrate changes in teaching over time of each category (SCWE and SCBE).
Simultaneity and connections within examples
In a structural approach to additive relation problems the part-part-whole relation is seen as a base for addition and subtraction (Neuman 2013). Differences in SCWE between 2013 and 2014 were seen in the missing number problem instruction as well as in the partitioning problems. In Table 3, we present a summary of the number and proportion of segments for each teacher meeting the SCWE criteria for each of the two topics across 2013 and 2014.
Taken overall, the results from the coding point to small changes in segments meeting the criteria for simultaneity and connections within examples (SCWE) in the partitioning and the missing number problems teaching. There are, however, some high scores, especially in the missing number problems in the second year. Looking at the scores on an individual teaching basis, the increases seen in teacher A's instruction of partitioning are particularly substantial (from 34% in 2013 to 83% in 2014). This difference is underpinned by teacher A's handling of the partition activity in symbolic form in 2014, writing each partition as a number sentence that foregrounded the whole-part-part relation. Segments in 2013 not meeting the criterion for mathematical accuracy in partitioning and in missing number problems (detailed below) also contributed to her lower 2013 score.
Illustrations of changes in teaching (simultaneity and connections within examples)
Changes in instruction focusing on missing number problems were seen in teacher A's teaching. In 2013, in Section 13.2.2 she handled a series of missing subtrahend problems with a set of nine balls on the board. Missing subtrahend problems involve a missing part. The teacher though, kept both parts of the whole visible. This linking action did not accurately emphasise the structural relation between the whole and given part in the problem.
In contrast, in 2014 the planned activity focused again on different missing number problems representing the part-part-whole relationship. In one example in the early segments of Section 2, the teaching proceeded as per Figure 1.
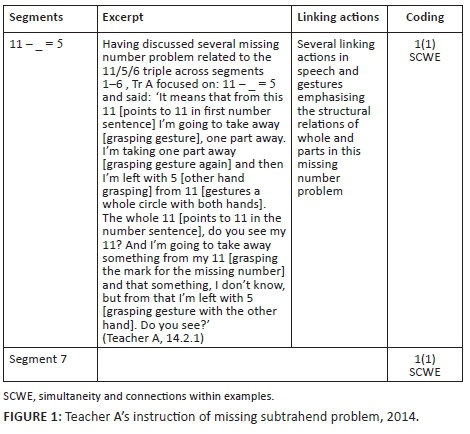
This 2014 teaching excerpt exemplifies coherent linking actions in speech and gestures within this missing number problem. Attention is paid in teacher A's talk and gestures to the structured relation of parts and whole by, for example, marking the whole value with both hands and using 'grasping gestures' separately to focus on the missing part (7) and visible part (5).
Another illustration of change was seen in teacher B's instruction of partitioning in the 2013 cycle where moves to systematicity were seen. In the 2013 cycle (Section 13.2.1), teacher B produced a compensational pattern through listing the first part, independently, as an increasing number sequence (0, 1, 2, 3…) in one column. This was followed by the writing up of a decreasing sequence for the second part (9, 8, 7…). The teacher pointed to each part vertically saying: 'Counting from smallest to biggest' indicating the first column, and for the second column: 'Here we are subtracting'. In this 'vertical' working, the horizontal part-whole constraint was backgrounded and therefore, there were few linking actions within examples. This kind of teaching with isolated focus on one part in a vertical column, without connection to the other part or to the whole value, was not seen in 2014. There was greater prevalence of gestures and speech linking the parts to each other and to the whole value within segments in 2014 in comparison to 2013, achieved predominantly through connections in talk and gestures, for example: '…but altogether they make up? [puts fists together]' or 'But you see these parts, you can put them together to get 7 [pointing horizontally to the produced split].' While teacher B's partitions instruction in 2014 pointed to fewer SCWE-links, segments marked as SCWE often included several linking actions in 2014, compared to 2013 when these links were not flagged in many segments. These multiple occurrences within segments were counted as single presences in our coding methodology.
Simultaneity and connections between examples
Paying attention to the part-part-whole relation is fundamental in a structural approach to additive relation, not only in relation to specific examples, but also between examples. Careful variation in the relational structure within the examples worked on is a precursor for being able to connect different examples. Both of these aspects are considered below.
The results showed more examples being connected in 2014 than was the case in 2013. One phenomenon underlying this result was that in 2013 several examples were erased from the board, resulting inevitably in examples being treated separately. Table 4 summarises the coding for SCBE. It includes the total number and proportions of segments coded as SCBE for each year and for each teacher.
Looking at the overall pattern across partitioning and missing number teaching, the proportions of segments of SCBE increased across both topics. At the individual level, in 2013 teacher A's instruction indicated particularly low levels of attention to connections between examples within both topics. In all three teachers' instruction, the proportion of segments coded as SCBE went up in 2014. The coding reveals that in several sections of teaching in 2013, the examples were treated separately. In 2014, there were increases in the proportions of segments meeting the criteria for SCBE, and via this connecting, bringing general structural properties into view, while also working with the example space more systematically and completely.
Illustrations of changes in teaching (simultaneity and connections between examples)
Several situations where teachers used linking actions between examples to point to systematicity and completeness were seen in 2014, where all possible parts of whole value seven were visible simultaneously and in evidence in all three classes. This was not the case in 2013, when the teachers only hinted at completeness.
As an illustration of changes, we compare the partitioning teaching of teacher B. In her instruction in 2013 (Section 13.2.1), which we elaborated on previously, few actions linking between examples (SCBE) were seen because the part-part-whole relation was backgrounded, resulting in limited attention to different part-part-whole relations for a specific whole value. Systematicity, through generating all the combinations, was therefore not produced. Such limitations were not seen in the same teacher's instruction in 2014. Instead, after having produced a complete commutative set of 7, teacher B introduced a compensational pattern saying: 'You can do it in another way. I can start with my seven and zero…and six and one' [writes 7 and 0, 6 and 1]. 'What are the next numbers.' A complete compensational pattern was then produced. In segment 25, she pointed vertically, asking: 'What is happening on the left side and on the right side…?' and pointed to each horizontal combination saying: '…but you see these parts, you can put them together to get seven like a pattern.' (Teacher B 14.1.1, segment 19-25). So, the instruction paid attention to both the increasing and decreasing patterns through speech and gesture, and to the production of all possible partitions of the whole value 7, thus providing the opportunity to discern the idea of systematicity as part of being able to discern completeness. In 2014 there were also more extended utterances from teachers focusing on completeness, for example: 'Have we finished? - [pointing horizontally and vertically to the compensational pattern of 7]' with more elaborated discussion of possibilities of partition options, for example: 'What if I put 8 here? [pointing to the left column]' (Teacher C 14.1.1). Teacher C also began to address a strategy that could be generalised to other whole values, by asking for 'numbers of combinations' for other whole values.
Specific differences in commutativity teaching were also identified across the two years. While correct linking actions for commutativity were seen in the 2013 instruction, through pointing to 3/4 and 4/3 partitions of seven and saying: 'We swap them' (Teacher B 13.2.1), there was little beyond this kind of noting of commutativity. In contrast, segments involving reasoning about commutativity were seen in 2014 (Figure 2).

In this instruction (Figure 2), the speech and linking gestures were coherent and most segments met the criteria for SCBE as well as SCWE. Also the contrast between 2 + 7 / 7 + 2 and 1 - 6 / 11 - 6 in 2014 brings examples and non-examples of commutativity into focus. Thus, the idea of commutativity becomes an object of attention in its own right. Further, correct and incorrect answers were compared with deliberate introduction of 'planned' incorrect answers for the purpose of contrast (Ekdahl & Runesson 2015).
In 2013, different types of missing number problems were often handled separately with gestures and talk focused on within examples connections (SCWE). Even when sequenced examples had potential for these connections, few linking actions between examples (SCBE) were seen in most sections of teaching (with the exception of teacher C in 13.3.1). For instance, in 2013, following rubbing out of earlier examples of subtraction problems, Teacher B handled four examples with a missing subtrahend (9 - _ = 4; 9 - _ = 5; 9 - _ = 3; 9 - _ = 6). For each example, she followed the same procedure: wrote the number sentence on the board, asked the students to close their eyes, covered the number of balls representing the missing subtrahend and said: 'Open your eyes, how many balls are hidden?'(Teacher B 13.2.2, segments 4-8). In this teaching, linking actions focused on the relations between the numbers within each example. However, while the example sequence showed potential for attention to commutativity and/or inverse relations, no pointing to relations between these missing number problems was seen across these segments. None of segments 4-8 met the criteria for SCBE. Similar trends were seen in all sections of teaching in 2013, contrasting with the 2014 teaching seen in Figure 3.
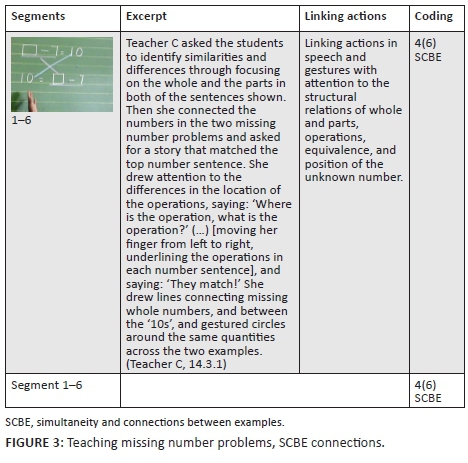
The 2014 excerpt points to important issues for additive relations teaching. When the teacher compared and discussed the two number sentences (e.g. underlining and pointing to _ − 7 in both number sentences), she opened up possibilities for discerning differences and similarities in operations, position of the missing whole number and the location of the equals sign. Equivalence ideas are foregrounded in these segments through SCBE links. These discussions were not seen in the 2013 teaching. Juxtaposed examples involving invariance in the midst of variation were more often discussed in 2014 teaching.
Discussion
We have already noted the key overview shifts in the incidence of SCWE and SCBE in the teaching between 2013 and 2014. In this discussion, we make a case for why we view the differences in teaching underlying these coding shifts, when considered collectively and interconnectedly, as changes in the direction of improvement.
At the within examples level, there were extensions into coherent handling of part-part-whole relationships across partition and missing number tasks, supported by representations and talk or gesture that made the part-whole quantities and relation simultaneously visible. This coherence is important in relation to South African evidence of slippage into inaccuracy in teachers' explanations, with within-example connections laying the ground for between example connections. Additionally, the partitions teaching was much more efficiently, as well as coherently, handled in 2014, with the three teachers using between 11- and 18-min on this topic in 2014, in contrast to 36- and 52-min in 2013, with more correct answers in 2014 student worksheet responses indicating that the more efficient pacing was appropriate.
The increased proportions of segments coded with SCBE are of particular interest. This points to a move towards treating the whole example space as a single object - a move that Watson and Mason (2006a) have noted as important if focus is to shift from the 'immediate doing' of individual examples to attending to the general structure in simultaneity with answering the particular problem.
In partitioning numbers, there was evidence of teaching moves in 2014 that simultaneously addressed connections within and between examples, afforded through the establishing of complete and systematic example spaces. Thus, the teaching not only had more emphasis on connections between examples, but also a wider emphasis.
In spite of the increases seen, the proportions of segments coded with SCBE remained at below 50% for partitioning and missing number problems teaching. Thus, the teaching still has some way to go to bring structural relationships that connect across examples more squarely to the fore. The increases in SCBE in the context of missing number problems are important though, given the evidence in South Africa and internationally of an emphasis on producing individual answers to isolated examples - a point that Schifter (2011) has made about the traditional ways in which additive problems are handled in teaching where the emphasis is on calculation. Schifter calls instead for attention to the general behaviour of operations, and presents examples that depend on connecting between examples rather than focusing on the quantities within examples.
Our data and analysis echo the view that possibilities for seeing structural similarities are enhanced by increased attention to connecting between examples alongside maintenance of coherent attention to the SCWE level. The extent of explicit SCWE attention that is appropriate is contingent on student responses to the example spaces presented: breakdowns in responses to individual examples tend to point to the need for some tracking back into more extended elaboration at the levels of connections between representations and/or within examples. The data analysis presented in this article supports the underlying theoretical position that when responses to individual examples are secure at broad levels in the classroom context, it becomes more important to focus attention on working across the example space rather than working on 'more' examples. The attention shifts in the 'between example' space to structure and what Goldenberg and Mason (2008) describe as 'examplehood', rather than to what Rowland (2008) has described as examples for practice of an operational skill. Thus, we argue that the differences seen in our analysis go beyond quantitatively more connections being made to a distinct, and important, difference in the quality of the mathematics made available to students. Furthermore, it would appear that 're-teaching' of the same topics in a supported teaching development environment has allowed for a broadening of occurrence of coherence and connections in instruction.
A final point to make relates to the coding framework itself. Devised in the context of a micro-analysis of partitioning problems, we - and others - had questions about the extent to which ideas about connections in the context of SCWE or SCBE (and between representations in our earlier work) might have broader applicability and purchase. The extension of the framework and the analysis to missing number tasks suggest that the ideas can be usefully applied more broadly. Our work going forward looks to expand the framework towards a broader and more general application.
Acknowledgements
This article forms part of the work in progress within the Wits Maths Connect - Primary project. It is generously funded by the FirstRand Foundation, Anglo American, Rand Merchant Bank and the Department of Science and Technology and is administered by the National Research Foundation.
Competing interests
The authors declare that they have no financial or personal relationships which may have inappropriately influenced them in writing this article.
Authors' contributions
H.V. was the project leader and together with A.L.E. and U.R. worked with the teacher group in the intervention study. A.L.E. was responsible for data collection and development of the coding framework. The data were analysed by A.L.E., H.V. and U.R. The manuscript was jointly produced by all four authors.
References
Adler, J. & Venkat, H., 2014, 'Teachers' mathematical discourse in instruction: Focus on examples and explanations', in H. Venkat, M. Rollnick, J. Loughran & M. Askew (eds.), Exploring content knowledge for teaching science and mathematics, pp. 132-146, Routledge, London.
Alibali, M.W., Nathan, M.J., Wolgram, M.S., Church, R.B., Jacobs, S.A., Martinez, C.J. et al., 2013, 'How teachers link ideas in mathematics instruction using speech and gesture: A corpus analysis', Cognition and Instruction 32(1), 65-100. https://doi.org/10.1080/07370008.2013.858161 [ Links ]
Carpenter, T.P., Fennema, E., Franke, M.L., Levi, L. & Empson, S.B., 1999, Children's mathematics: Cognitively guided instruction, Heinemann, Portmouth, NH.
Cobb, P., Boufi, A., McClain, K. & Whitenack, J., 1997, 'Reflective discourse and collective reflection', Journal for Research in Mathematics Education 28(3), 258-277. https://doi.org/10.2307/749781 [ Links ]
Ekdahl, A.-L. & Runesson, U., 2015, 'Teachers' responses to incorrect answers on missing number problems in South Africa', in Proceedings of ICMI Study 23, International Commission on Mathematical Instruction (ICMI), June 3-7, Macau.
Ekdahl, A.-L, Venkat, H. & Runesson, U., 2016, 'Coding teaching for simultaneity and connections Examining teachers' part-whole additive relations instruction', Educational Studies in Mathematics 93(3), 293-313. https://doi.org/10.1007/s10649-016-9700-0 [ Links ]
Fritz, A., Ehlert, A. & Balzer, L., 2013, 'Development of mathematical concepts as basis, for an elaborated mathematical understanding', South African Journal of Childhood Education 3(1), 22-38. [ Links ]
Goldenberg, P. & Mason, J., 2008, 'Shedding light on and with example spaces', Educational Studies in Mathematics 69, 183-194. https://doi.org/10.1007/s10649-008-9143-3 [ Links ]
Gray, E. M. & Tall, D.O., 1994, 'Duality, ambiguity, and flexibility: A 'proceptual' view of simple arithmetic', Journal for Research in Mathematics Education 26(2), 116-140. [ Links ]
Hiebert, J., Stigler, J. & Manaster, A., 1999, 'Mathematical features of lessons in the TIMSS Video Study', Zentralblatt für Didaktik der Mathematik 31(6), 196-201. https://doi.org/10.1007/BF02652695 [ Links ]
Hiebert, J., Stigler, J.W., Jacobs, J.K., Givvin, K.B., Garnier, H., Smith, M. et al., 2005, 'Mathematics teaching in the United States today (and tomorrow): Results from the TIMSS 1999 Video Study', Educational Evaluation and Policy Analysis 27, 111-132. https://doi.org/10.3102/01623737027002111 [ Links ]
Kullberg, A., Runesson, U. & Mårtensson, P., 2014, 'Different possibilities to learn from the same task', PNA 8(4), 139-150. [ Links ]
Marton, F. & Pang, M.F., 2003, 'Beyond "lesson study": Comparing two ways of facilitating the grasp of some economic concepts', Instructional Science 31(3), 175-194. https://doi.org/10.1023/A:1023280619632 [ Links ]
Marton, F. & Pang, M.F., 2006, 'On some necessary conditions for learning', The Journal of the Learning Sciences 15(2), 193-220. https://doi.org/10.1207/s15327809jls1502_2 [ Links ]
Marton, F., 2015, Necessary condition of learning, Routledge, London.
Mathews, C., 2016, 'Division means less … Chains of signification in a South African classroom', Extended paper presented at the 13th International Congress on Mathematical Education, Hamburg, 24th-31st July.
McNeill, D., 1992, Hand and mind: What gesture reveals about thought, University of Chicago Press, Chicago, IL.
Neuman, D., 1987, The origin of arithmetic skills. A phenomenographic approach, Acta Universitatis Gothoburgensis, Göteborg.
Neuman, D., 2013, 'Att ändra arbetssätt och kultur inom den inledande aritmetikundervisningen [Changing approach and culture within the introduction of arithmetic; in Swedish]', Nordic Studies in Mathematics Education 18(2), 3-46. [ Links ]
Resnick, L.B., 1983, 'A developmental theory of number understanding', in H. Ginsburg (ed.), The development of mathematical thinking, pp. 109-151, Academic Press, New York.
Rowland, T., 2008, 'The purpose, design, and use of examples in teaching of elementary mathematics', Educational Studies in Mathematics 69, 143-163. https://doi.org/10.1007/s10649-008-9148-y [ Links ]
Schifter, D., 2011, 'Examine the behavior of operations noticing early algebra ideas', in M. Gamoran Sherin, V.R. Jacobs & R.A. Philipp (eds.), Mathematic teaching noticing: Seeing trough teachers' eyes, Routledge, New York.
Schmittau, J., 2003, 'Cultural-historical theory and mathematics education', in A. Kozulin, B. Gindis, V. Ageyey & M. Miller (eds.), Vygotsky's educational theory in cultural context, pp. 225-245, Cambridge University Press, Cambridge.
Venkat, H. & Adler, J., 2012, 'Coherence and connections in teachers' mathematical discourses in instruction', Pythagoras 33(3), 25-32. https://doi.org/10.4102/pythagoras.v33i3.188 [ Links ]
Venkat, H. & Naidoo, D., 2012, 'Analyzing coherence for conceptual learning in a Grade 2 numeracy lesson', Education as Change 16(1), 21-33. https://doi.org/10.1080/16823206.2012.691686 [ Links ]
Watson, A. & Mason, J., 2006a, 'Seeing an exercise as a single mathematical object: Using variation to structure sense-making', Mathematical Thinking and Learning 8(2), 91-111. https://doi.org/10.1207/s15327833mtl0802_1 [ Links ]
Watson, A. & Mason, J., 2006b, 'Variation and mathematical structure', Mathematics Teaching 194, 3-5. [ Links ]
 Correspondence:
Correspondence:
Anna-Lena Ekdahl
anna-lena.ekdahl@ju.se
Received: 07 May 2017
Accepted: 13 Jan. 2018
Published: 13 Mar. 2018
1. Adapted learning study relates to our use of several components of the learning study process. However, some concepts from variation theory used in a typical learning study process were not familiar to the teachers and therefore not used in our adopted model.














