Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.6 n.1 Johannesburg 2016
http://dx.doi.org/10.4102/sajce.v6i1.377
ORIGINAL RESEARCH
Learning from disruptive classroom behaviour in a Grade 2 mathematics lesson
Nicky Roberts; Hamsa Venkat
Department of Education, University of the Witwatersrand, South Africa
ABSTRACT
In this article, Mason's 'discipline of noticing' is used to theorise a reflective process for changing mathematics teaching in a challenging context. The methodological approach was guided by critical reflective processes that produced, firstly, a descriptive 'account-of' an unsuccessful mathematics lesson, followed by layers of analyses drawing on theory and literature that guided our development of 'accounts-for' the classroom interactions. This example of a South African teacher-researcher's self-study on disruptive learner behaviour in her Foundation Phase mathematics class is useful at the practitioner level, in which it details how increasingly critical layers of pedagogic reflection can be used to transform mathematics teaching, and via this route, to improve access to mathematical learning in a challenging context. At the research and policy levels, our findings question the separation of attention to mathematics and learner behaviour, rather than addressing the two in combination.
Introduction
Primary mathematics teaching continues to be in the spotlight in South Africa with research evidence on the causes of poor performance of a learner pointing towards a range of teacher inadequacies. These include gaps in primary mathematics content knowledge (Spaull 2013), gaps at the level of pedagogic content knowledge and teaching (Carnoy, Chisholm & Chilisa 2012) and apparent ill-disciplined teacher (Taylor et al. 2013). Large-scale responses to these issues have relied on constraining teacher decision-making through increasingly prescriptive one-size-fits-all mathematics curricula that stipulate coverage, sequencing and pacing of content (DOE 2002).
Research points to teaching as a complex system of interactions in which constraining one factor has influence on the other components of the system (Stigler & Hiebert 1998). Henning (2011) cautions about large-scale top-down approaches and highlights the importance of Komensky's (or Comenius') (1648) 'didactical triangle' of learner, content and teacher. In placing tight controls on content (what is taught, when it is taught and how it is assessed), these complex interactions tend to be neglected. It is this complexity of interactions that we seek to centrally focus in this article. We do this in the context of an intervention study that sought to improve the learning of additive relations in an urban Grade 2 township classroom in Western Cape, South Africa. We refer to this as a 'challenging context', in which discipline of a learner was an acknowledged problem.
In the broader South African education literature, 'misbehaving learners and disciplinary problems' are identified as being 'a disproportionate and intractable part of every teacher's experience of teaching' (Marais & Meier 2010:41). This is echoed by Moodley (2015) who, writing about Foundation Phase teaching, states that, in a South African context, behavioural difficulties of a learner continue to be a major problem in schools. Yet we have not seen any research that examines disruptive behaviour within mathematics classrooms in South Africa. This suggests that within educational research as well as policy, there is a separation of attention - to mathematical foci or behaviour, rather than the two in combination.
We tell this story, at first level, as part of our pragmatic need to understand the contexts and conditions better under which external initiatives to improve primary mathematics teaching and learning might work. At second level though, we seek to more critically address the silences in national policy and research on the complex human interactions in classrooms within which we sought to focus on mathematical learning. Specifically, we illuminate the disruptions to the strongly mathematical foci that we brought to the intervention and the reflective processes that were required to reinsert this focus. The focus is thus on teachers' learning for teaching in challenging contexts in ways that reinsert attention to mathematics. Aligned with this reflective practice approach, the research question that we set out to answer was: What did I learn from examining a mathematics lesson in a Grade 2 township classroom where discipline of a learner was a problem?
In this article, we draw on Mason's (2002) notion of teacher noticing, which provides both the theoretical base and methodological approach to reflecting on classroom events. We also draw on two literature bases. The first relates to our entry-stage epistemic concerns and is focused on additive relation word problems, which formed the central pillar of our intervention lesson planning. The second relates to South African findings on disruptive classroom behaviour, which we examined midstream in order to understand the extent to which the episodes within the intervention lessons could be categorised and seen as more widely occurring.
Methodological approach
Reflective practice-based approaches to teacher development have a long tradition within pedagogic theorising. The origins of much of this tradition can be traced back to Dewey's (1933) writing:
Thinking begins in what may be fairly referred to as a forked-road situation, a situation that is ambiguous … that proposed alternative. As long as our activity glides smoothly along … there is no call for reflection. Difficulty or obstruction in the way of reaching a belief brings us however to a pause. In the suspense of uncertainty, we metaphorically climb a tree; we try to find some standpoint from which we may survey additional facts and, getting a more commanding view of the situation, decide how the facts relate to one another. (p. 14)
We framed our study in relation to Mason's (2002) 'discipline of noticing', in which the teaching and learning of mathematics are always present. Mason describes the core idea of noticing as 'a collection of practices both for living in, and hence learning from, experience, and for informing future practice' (Mason 2002:29). Drawing on ideas from variation theory (Marton & Booth 1997), he elaborates that 'to notice is to make a distinction, to create foreground and background, to distinguish some "thing" from its surroundings' (Mason 2002:33).
Mason emphasises that noticing happens all the time and is structured into three levels of intensity: ordinary-noticing, marking, and recording. From the perspective of reflective practice that seeks change, ordinary noticing or perceiving is insufficient, and requires a shift in awareness to marking and then to recording. For ordinary noticing or perceiving, 'sufficient memory is established accessibly to be jogged or reconstructed by what someone else says' (Mason 2002:33). Through ordinary noticing of something you have enough experience of the phenomenon to recognise it when someone else describes it. In contrast, for marking 'not only do you notice, but you are able to initiate mention of what you noticed' (Mason 2002:33). This may be in the form of a mental note, or a scribble to self. Marking is a heightened form of noticing as to mark something is to be able to re-mark about it to someone else. Recording is the third level of intensity to noticing, which is fuelled by a desire to make a note of, or record, something (Mason 2002:34). This is a more formal communication, not only with self, but with others.
Mason also makes a useful distinction between 'giving an account-of' and 'accounting-for' some incidents (Mason 2002:54). An account-of 'describes as objectively as possible by minimising emotive terms, evaluation, judgments and explanation' (Mason 2002:54). An account-for includes redescribing the incident to attend to the question of why it occurred. Generating such accounts-for is potentially an unending iterative process, where the level of reasoning can be deepened with each round of exploration. In this article, we provide an initial account-of the lesson and then go on to share our subsequent deeper reflections through processes of marking and recording as we sought to develop accounts-for occurrences within it.
Our methodological approach was therefore guided by reflective processes that produced, firstly, a descriptive account-of the lesson, followed by layers of analyses drawing on theory and literature that guided our development of accounts-for the classroom interactions.
Our empirical base in this article is a 23-min lesson segment (hereafter referred to as the lesson) that took place during the eighth lesson of a ten-lesson research intervention. This segment was selected as illustrative of several episodes of disrupted teaching in the ten-lesson sequence taught by the first author, and representative too, according to the class's normal teacher, of her broader context of teaching with this class. The segment represented a 'forked-road situation' where activity could no longer 'glide smoothly along'.
Drawing from a combination of classroom video, my reflective field notes and subsequent writing on the lesson, we use 'teacher noticing' to analyse how classroom events shifted my awareness away from noticing features of the intended mathematics to considerations of safety, efficacy and containment in the classroom.
In the process of reflecting on shifts in what I noticed, I examined what I marked when I personally reflected on the lesson and what I re-marked on in my informal discussions with colleagues and then recorded in my reflective notes. This was then overlaid with our refection on this account and noticing, which we conducted together as we sought to make sense of the lesson. The reflection was then further deepened by critically reviewing our reflections with colleagues and from a theoretical perspective. In doing so, we aimed to identify and describe my learning from this reflective study process.
Literature bases
Additive relations concepts
Our focus in the broader intervention was on supporting children to expand their additive relations example space for additive relations word problems. The narrative approach adopted is described in Roberts and Stylianides (2013), and detailed analysis of learners generating narratives is presented in Roberts (in press). In this article, we simply present a few definitions, familiarity with which is necessary for engagement with the mathematics that was in focus during the lesson segment detailed in this article.
Mathematics education literature delineates different additive relation problem types. One can distinguish between 'change' problems, such as:
I have 7 red beads, but I lose two of them', and 'compare' problems, such as 'I have 5 red beads. You have 7 blue beads. How many more beads do you have than me? (Carpenter et al. 1999)
We have found a subset of compare-type word problems, which we term 'matching word problems' to be useful in introducing compare problem types. 'Matching word problems' involve scenarios which elicit a one-to-one mapping of each element in one set to each element in the other set: 'There are 7 locks but only 5 keys. How many keys are missing?'
Change and compare problem types can be linked with different kinds of images. For a takeaway image of subtraction, 7 minus 3 is depicted with an image of 7 objects, in which 3 of them are crossed out, as shown in Figure 1.

A compare image of subtraction depicts 7 minus 3 with a row of 7 objects lined up against a row of 3 objects, as shown in Figure 2.

Different situation contexts and different choices of numbers within these scenarios can, in turn, be associated with different calculation strategies for working out answers. A key distinction here is between 'counting back' strategies and 'counting up to' strategies (Thompson 2008). For a 'counting back' calculation strategy, 9 minus 3 is calculated by starting at 9 and counting back 3 counts: 8, 7, 6. The answer is the last number named: 6. For a 'counting up to' calculation strategy 9 minus 7 is calculated by starting at 7 and counting up to 9: 8, 9 to reach nine. The answer is the number of counts: 2.
The intention in the lesson segment was to introduce and discuss ideas related to 'matching word problems' (as a subset of compare problems) that lent themselves to comparison images, and 'counting up to' calculation strategies.
Disruptive classroom behaviour
There is a vast global literature on learner's behaviour in schools and in classrooms. In a South African context, disruptive behaviour is defined as 'inappropriate' to the schooling context (Mabeba & Prinsloo 2000) or learner behaviour that inhibits achievement of the teacher's purposes (Levin & Nolan 1996). In our references to 'disruptive classroom behaviour', we allude similarly to learner behaviour that (in the teacher's view) disrupts lesson progress and impedes learning. Marais and Meyer (2010:44) distinguish 'surface behaviours' from 'more serious disruptive behaviours'. The former include verbal interruptions, off-task behaviours, physical movement and disrespect, it usually 'exist to some extent in all classrooms … and are usually not the result of deep-seated personal problems but normal developmental behaviour of children while the latter refers to violent physical contact (Marais & Meyer 2010:44).
The literature on disruptive classroom behaviour considers various forms of these behaviours, and the underlying reasons for, management of, and responses to such behaviours. How disruptive classroom behaviour is viewed and analysed depends on the theoretical stance adopted. In reviewing this literature, we identified four broad views of disruptive classroom behaviour.
A behaviourist view assumes that disruptive classroom behaviour can be controlled through effective management by the teacher. This is evident in the writing by, for example, Marais and Meyer (2010). An interpretive view considers disruptive classroom behaviour as a means of learner's communication which requires interpretation, Papatheodorou (2005). This view acknowledges that how teachers see and interpret disruptive behaviour is likely to influence their responses and argues that disruptive behaviour cannot ignore the profoundly emotional impacts on both learners and teachers (Wright 2009). In more medicalised views, the locus of responsibility for managing learner's behaviour shifts from the teacher to a specialist (a medical practitioner or specialist in some aspect of special needs). In this view, there are shifts from disruptive behaviour being viewed as 'naughty' to it being viewed as 'defective' (Slee 2010:51). Wright identifies three meta-discourses, which construct children as either 'bad', 'mad' or 'sad' (stemming from criminology, psychiatry and patronage, respectively). Which construct is used to interpret the disruptive behaviour guides the response. From the sociological view, disruptive behaviour is not only a matter of teacher and learner relations but fits into a broader social context in which power and authority are exerted. Disruptive behaviour is interpreted as a reaction to an unequal social order that mitigates against the aspirations of working class children. Slee notes the shift over time from the behavioural view to a more medicalised view and asserts that in spite of this shift: 'the fundamental social relations of exclusion, and the organisational imperatives of categorization, surveillance and control remain' (Slee 2010:41).
Results
This section opens with a description of the context of this intervention study and the lesson. This is followed by our presentation of the deepening layers of reflective analysis, underpinned by the theory of noticing, that were conducted in order to answer the research question.
Context
I worked with Foundation Phase learners and teachers in this school as part of a development project to improve mathematics learning. In the specific research intervention, I took on a lead teacher role to trial a pedagogic approach to teaching mathematics that drew on narrative for mathematical modelling. The usual Grade 2 classroom teacher remained present during the intervention, which took place over 10 consecutive days towards the end of 2013. The focal lesson occurred on the 8th day of the research intervention.
This school was in a township community with low socio-economic status and many social problems. The language of learning and teaching throughout the school was English although the home languages of the learners and teachers include Afrikaans, isiXhosa and a variety of other languages. The school was unusual in the national context in that it is funded partially by the state and partially by a philanthropic trust. As a result, the size of the classes were unusually small (30 children per class), teacher assistants supported classroom teachers and some classrooms had smart-boards.
In the remainder of this section we detail my initial subjective reflections on the context of the intervention and the lesson that formed the basis for our subsequent more objective 'account-of' what happened in the lesson, presented in the next section. We do this to highlight the potential of layers of reflection based on the idea of deliberate noticing.
Frequent physical fighting was a striking attribute defining this class. At the time of the research intervention, the classroom teacher described frequent physical fighting in her class (reporting that there were up to eight fights a day). Six months later (when she was no longer teaching this class) she described the class as follows:
'The class was a challenging class, although there were a few who were eager to learn. [There were] many violent learners who sorted out any issue with hitting or kicking'. (Usual class teacher, written description of the class, May 2014)
There were 29 learners in the class achieving a class mean Annual National Assessments (ANA) result of 53%, below the national Grade 2 average of 59% in 2013. Of these 29 learners, 9 did not progress to Grade 3 in 2014. There was a wide range of special needs for learners in this class, described by the specialist remedial staff and usual classroom teacher as including attention deficit hyperactivity disorder (ADHD), crystal-meth (Tic)-related problems1 and foetal alcohol syndrome (FAS)-related problems, as well as more general social and developmental difficulties.
The major difference for me when I compared this class to Foundation Phase classes I had taught previously was, from the outset, behaviour; managing the class was an area of difficulty and demanded much of my focus. My emotions ran high and I was aware of deliberately masking my feelings to project an outer sense of calm and control. I was in tears at home on more than one occasion and sought out support from colleagues.
Physical fights between learners were uppermost in my mind. In the first lesson of this intervention, a learner was kicked in a karate style in the head during seatwork by another learner. I was shaken by this incident. In my experience, while arguments over pencils were common, they usually resulted in verbal altercations or minor scuffles, rather than serious physical violence. What disturbed me was the nature and speed of the karate kick to the head. I imagined that the attacked child could have been seriously hurt and worried that my classroom was not safe. What had I done wrong? How could I watch every member of the class, and simultaneously be available to respond to mathematics questions? In the second lesson two learners had a fist fight, repeatedly punching each other in the chest and face. They did not stop until I physically restrained both of them and removed them into the corridor. I felt that my class was not safe and I was quite on edge. This day was most upsetting for me. Two fights in two days, and I was clearly not in control of the classroom space, which was obviously unsafe. At first I wanted an immediate consequence and strict follow-up on the fights. I felt I needed to assert myself and mete out some consequence or punishment.
How was I to respond to this learner conflict? I aimed to remain completely calm. I resolved not to lose my temper, not to take their behaviour as a personal attack on me. I chose to discard suggestions to use corporal punishment or to shout or raise my voice at the learners. I knew I needed a reasonable, defensible and consistent consequence for inappropriate behaviour.
Following discussion with colleagues I chose to draw my own and my learners' attention to, and label, the classroom management issues in the third lesson. I spent some time discussing inappropriate behaviour (the learners provided examples such as fighting, calling out and not listening). We agreed that learners would be kept in at break time to catch up on wasted mathematics time. As a result, I introduced a break-time ritual of releasing children one table at a time based on the time we had wasted on managing behaviour during lessons. I aimed to defuse other fights and keep things as calm and as mathematics-focused as possible. I knew I needed to spend time building a relationship with each child. This rational advice did help to manage, or at least mask, my emotional reactions.
Planned mathematics for the lesson
Just prior to the lesson, learners had been encouraged to pose problems requiring subtraction, and had generated their own 'takeaway' word problem example. An example of this prior work is depicted in Figure 3.

They had represented solutions to these problems using takeaway images and counting back strategies on empty number lines.
In the lesson I intended to start off with some whole class mat work recapping this and then encourage learners to work in their seats on 'matching' word problems (a subset of the compare word problems defined above). I planned to ask learners to pose word problems for a particular number sentence, allow a volunteer learner to draw their explanation of how they solved the problem and to invite another learner to depict this on a number line. I planned to use 9 minus 7, as this lent itself to a counting up from 7 to 9 calculation strategy. I expected that the learners would use a counting-back calculation strategy from 9 to 7, draw takeaway images of subtraction and show 7 hops back from 9 on an empty number line. I also expected that I would need to introduce a matching word problem, model a compare image of subtraction, and 'counting up from 7' strategies on an empty number line.
Layers of analysis
In this section, we provide our analysis of what took place in the lesson. We have found it helpful to distinguish the following layers of analysis:
-
Layer 1: Recording the mathematics episodes;
-
Layer 2: Marking the (lack of) mathematics;
-
Layer 3: Recording classroom management episodes;
-
Layer 4: Describing accounts of the classroom management episodes;
-
Layer 5: Refining the recordings;
-
Layer 6: Responding to collegial feedback;
-
Layer 7: Theorising what this represents.
To develop an 'account-of' the lesson, I reviewed and transcribed the lesson video recording. I then separated episodes in the transcript focused on mathematics from episodes focused on classroom management. The resulting transcript episodes were used to develop the accounts-of the lesson at Layer 1 (the mathematics), Layer 2 (marking the lack of mathematics learning), Layer 3 (the behavioural incidents) and Layer 4 (the qualitative descriptions of my responses). Layers 5-7 were developed through deepening layers of critical reflection on 'account-for' the lesson.
Layer 1: Recording the mathematics episodes
This section provides a brief, but vivid, account-of the mathematics during the lesson. It stresses the mathematics and deliberately ignores the classroom management episodes. The classroom management episodes were both frequent and numerous and are our focus in the Layer 3 analysis below. What had happened regarding the teaching of mathematics during the lesson?
When I had greeted the class and the learners were settled, I wrote 9 − 7 on the smart board. I asked Gavin2 to read the number sentence, 9 minus 7, and listened to some learner discussion on how to calculate this. I demonstrated a counting-back takeaway calculation for 9 minus 7 using my fingers.
I then asked Derek to draw a picture on the board to explain how to calculate 9 minus 7. Derek drew a takeaway image for subtraction (Figure 4) and was helped by some learners calling out to keep track of the numbers involved.

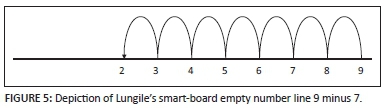
I asked Lungile to show 9 minus 7 on a number line. Lungile drew 7 hops back from 9 (Figure 5). Some learners supported this by counting to help Lungile keep track of the numbers involved.
I then introduced a new subtraction problem context: 'There are 9 porridge bowls, but only 7 lids. How many lids are missing?' Thandi was able to answer this correctly, and I asked her how she did this, and what the number sentence would be. No other learner responded when asked how they worked out the problem.
I presented to the learners an alternative 'matching' picture for 9 minus 7 (see Figure 6).

With my prompting, some learners chant counted the 9 bowls, and chant counted the 7 lids as I drew this image. I referred back to Derek's picture of 9 minus 7. I asked learners to compare the two images: the takeaway image; and the matching image. I asked learners to find what was different between the two pictures. I then demonstrated an alternative way for working on a number line for the calculation 9 minus 7. However, this was not completed due to the numerous disruptions that occurred within this episode.
I was overcome by a sense of helplessness and abandoned the lesson in the 23rd minute: 'I am giving up. I can't do this. I am sorry Grade 2 but we can't learn like this. Let's rather just stop this lesson. We are wasting your time and mine like this' (Video transcript, 23rd minute).
Layer 2: Marking the (lack of) mathematics learning
Why had this happened? Why did I find this lesson so tough to teach? This type of approach had well worked before, what was different now?
Most striking to me about this lesson was the lack of mathematics learning in it. I recorded the following to formalise what I had re-marked on to colleagues:
It had been very unproductive both from a learning and a teaching perspective. I was disappointed with myself and frustrated by my learners. I was grateful that I had at least noticed that the lesson was not progressing productively and had acted to abandon it. What struck me about the account was there was not much mathematical talk. I felt that my mathematical teacher talk deteriorated in quality over the episode as my approach and became increasingly in a transmission mode of teaching. (Reflective notes, December 2013)
I thought that I should look for points at which the mathematics in the lesson had gone wrong, or where I felt that I could have acted differently:
My teacher talk started to dominate with longer teacher utterances and fewer learner utterances over the lesson episode. I was surprised that I had not asked for, or referred to, stories of subtraction which the learners had generated in the previous lesson. I was also surprised that I did not make it clear that the number sentence for the bowls and lids problem was also 9 minus 7, so the relationship between the take-away and matching images may not have been clear to learners. I did not allow for discussion on what was the same, what was different and how the images related to each other. I also did not elaborate on the new label of 'a matching picture'. (Reflective notes, December 2013)
On the whole I felt that the classroom management episodes 'hidden' in the mathematical recording above would help to explain what had happened. I needed to 'metaphorically climb a tree' to get 'a more commanding view of the situation' (Dewey 1933:14). As a result, I turned my attention to the classroom management episodes.
Layer 3: Recording classroom management episodes
What happened that drew my attention away from the mathematics?
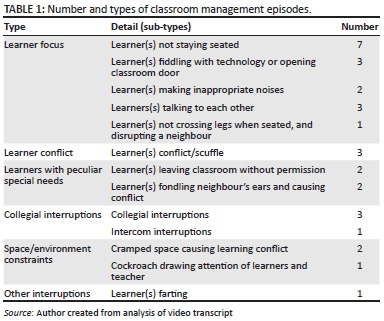
There were a total of 31 'classroom management episodes' which interspersed the 'mathematical episodes' in the 23-min lesson. A crude analysis of utterances (lines of text in the transcript) showed that in total only a third of the utterances were mathematical, with 66% attending to classroom management. Within each episode, we considered different types of actions, behaviours or events that drew my attention away from the mathematics. I classified each interruption by type. The types emerged as labels used to structure my noticing in the transcript data. For some interruption types, it became necessary to distinguish sub categories.
The list and frequency of types and subcategories (Table 1) made me feel embarrassed and uncomfortable about my teaching. How had all this happened under my watch? The analysis helped us to know what it was we were talking about when we were grappling with 'disruptive learner's behaviour' in the lesson. However, in order to change my classroom management approaches we felt I needed to examine key incidents that exemplified each interruption type and report on my response to them.
Layer 4: Describing accounts of the classroom management episodes
I returned to the video recording to review each interruption subtype and pay particular attention to my reactions to each one. In doing so, I shifted from using quantitative methods of timing, counting and labelling episodes to more qualitative descriptions of what had happened. This was still at the level of extended account-of the lesson; I was still grappling with the lesson and examining its constituent parts.
I wrote detailed qualitative descriptions drawn from the transcript as accounts-of classroom management types and shared these with the second author. We illustrate this part of the analytical process by summarising one example relating to an episode coded as 'Learners with particular special needs'. Eleven children in this class were considered to have particular special needs.3 In my reflective notes, I wrote descriptions of my observations and concerns about six of these children.
Adrian was one of the six children and was the child involved in the incident detailed as 'Leaving the classroom without permission'. The following excerpt provides some sense of this episode:
Teacher: 'But I first want everybody looking here and be quiet. Adrian sit down. Adrian sit down. Gift come and sit on the mat please.' [Adrian ignores teacher and walks towards the door]
Teaching Assistant: 'Miss you know what Adrian is going to do? He is going to walk out of the class now.' [Adrian opens the classroom door]
Teacher: 'Adrian where are you going?' [Adrian leaves the room ignoring the teacher]
Teacher: 'Can you go and get him please?' [directed at the Teaching Assistant]
Teacher: 'Ok let us keep focused on our work, and Adrian can be dealt with outside.'
[Teaching Assistant leaves the classroom to get Adrian]
(Video transcript, 10th minute)
Reviewing my teacher talk during this episode revealed to me that I managed to remain calm and defuse the situation, thereby enabling the lesson to continue as I had consciously planned. I followed up on Adrian's behaviour with him, the usual teacher and specialist staff at another time. His leaving the class was apparently habitual. I thought it is important to consider my possible alternative reactions to this incident: shouting or raising my voice at Adrian; following him; trying to physically bar the door for his escape; deliberately disrupting the lesson to show my frustration with his behaviour to other learners; meting out a punishment. However, I do not think such alternatives (some of which I have used in other contexts) would have been effective. I suspected his behaviour may have been seeking out attention from me (albeit my negative attention). This incident seemed to be reflective of a bigger problem relating to this particular child.
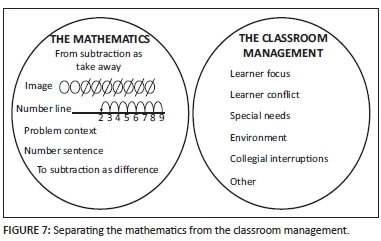
At this level of analysis, my awareness of the lesson was structured into two disjoint sets: episodes relating to mathematics and episodes relating to managing learner's behaviour. I split the latter into the seven subcategories and was able to exemplify each one as shown in Figure 7.
Layer 5: Reflecting on the video transcript analysis
What did this video transcript analysis indicate? Reflecting back across the classroom management episodes and considering them in relation to our prior experiences with Foundation Phase classes it struck us that no single episode was completely foreign. What was most starkly different in this case was the number and frequency of the classroom management episodes. We felt that a few of the interruptions could have arisen in our other teaching contexts and would have required attention. Thirty-one interruptions in 23 min were rare in our experiences with young children.
My initial reaction was to view the non-mathematical episodes as 'disruptions' or 'interruptions' to mathematics. As we worked with the data to provide an account-of, and then account-for the disappointing lesson, my views shifted slightly:
Separating the mathematics from the classroom management was necessary to be able to better understand what transpired. However it was simply not possible to maintain this separation in the lived reality of teaching a classroom of children. Attention to both classroom management and mathematics are fundamental requirements of effective teaching. (Reflective notes, May 2014)
It was at this point that we were able to start to move beyond what was being examined to articulate what this lesson revealed for us. As such we documented several adjustments which we planned to make for the third intervention cycle in support of the development project:
1. Establish classroom rules and agree consequences for inappropriate behaviour in the first lesson, with the intention to make use of keeping children in during break, and utilise the school disciplinary hearing process if necessary.
2. Reduce the planned length of whole class plenary sessions, aiming to do more of our work with small groups rather than whole class teaching.
3. Set a wide variety of differentiated tasks (on work-cards) for seatwork which we think will keep learners motivated during individual seatwork to allow for more small-group mat work.
4. Involve the teaching assistant more closely in the mathematics of the tasks.
5. ake use of a separate 'maths hub' venue (that had been introduced in the school) to engage with smaller groups, while the teaching assistant supervises the rest of the class in their normal classroom venue.
6. Implement voluntary after-school maths clubs to help motivate learners with regard to mathematics and encourage a culture of productive learning.
7. Support the school in their shift to become a full-service school, where there will be more professional and specialist personal available to attend to special needs of learners.
8. Extend the length of time which we plan to work with a class for a focused intervention. (Reflective notes, April 2014)
With some concrete plans on how to improve classroom management in place, I was now able to re-examine the mathematics. I felt that I had been too ambitious in what I attempted in the lesson. The shift from change to compare problem types was a big move for these children. Working with four representations (the number sentence, the problem context, an image or drawing and a number line) was unrealistic. I wondered what would be lost if I dropped the number line representation. Although the number line provides a cognitive tool with longevity, I questioned whether its introduction was sensible at this point.
Layer 6: Responding to collegial feedback
I had experienced the lesson and moved from my ordinary noticing to marking specific aspects of the lesson. I had remarked on these to my colleagues and recorded my analysis where I had tried to work with an account-of, before moving towards an account-for the lesson. I had shared this with close colleagues. We had adjusted my approach and I had experienced more success with a similar intervention in the same school (Roberts in press). This gave me the confidence to present my analysis of the lesson in a broader collegial forum.
In the collegial discussion, my attention was drawn to several issues which, for me, had not been substantive. They were so much a part of what I was attempting, and which had worked successfully in other contexts, that I did not see them. Colleagues questioned several of my pedagogical choices: My expecting all the learners to sit on the mat; my allowing learners to write on the board in a plenary session; my using story telling in English in a class of second language speakers. They argued that the choices I had made were clearly not engaging the learners, who were bored, cramped and understandably disruptive. What the learners were attending to seemed to be highly variable and unstable. They probably needed a frequent shifting of attention to keep concentrating on what I intended. I could have given them a greater sense of involvement through making choices for themselves (choosing which numbers or which presentation to use). The learners' disruptive behaviour thus came to be viewed as a reflection of my poor pedagogic choices.
At the same time, the importance of the context of this lesson as being part of a research intervention was highlighted. I was not the usual classroom teacher. I did not have time to build long-term and trusting relationships with each child. In this case, I had stepped into an existing classroom culture characterised by disruptive learning behaviours.
Collegial feedback motivated me to delve deeper, to be more critical. While I had acknowledged that the lesson was poor, I had focused my attention on what the learners were doing and how I had responded to them. I had not examined my own pedagogical decisions clearly enough as key and contributing factors to the situation. I realised that I had accounted for the poor mathematics in the lesson by focusing on what distracted me from it - the disruptive learner behaviour. But what I had thought of as an account-for the lack of mathematical learning was in fact an account-of the interruptions. I was seeking to describe (and could not yet explain) the learner's inappropriate behaviour, instead of focusing on my own inappropriate behaviour (to describe, explain and hence change my pedagogy).
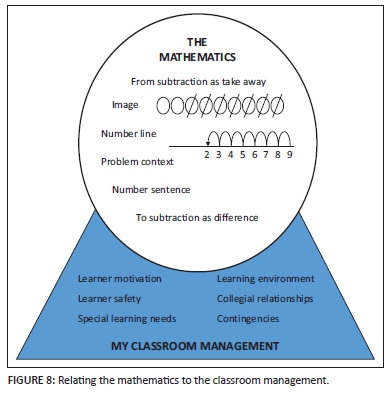
Yet, the substance of what I was grappling with - and the process of analysis - was of interest. I was reassured that this was valuable work, but aware that it was not yet complete. I was now thinking about classroom management as supportive of the mathematics, as shown in Figure 8.
At this point, I revisited the literature on disruptive classroom behaviour, from which the summary was distilled.
Layer 7: Theorising what this represents
The collegial engagement brought me to reflect on what this lesson - and so this article - meant to me. I grappled with its significance and sought to generalise from it. What was this an example of? What did this represent for me?
Was this an example of a typical challenging Grade 2 mathematics classroom? It was certainly an authentic example, and literature confirms that disruptive learner behaviour (even if this lesson is an extreme case) is a major issue in many South African Foundation Phase classrooms.
The layered reflection process brought clarity in terms of my theoretical lenses on behavioural problems. In thinking about my responses - at all the layers of analysis presented to this point - it is clear that in the immediacy of the moment (during the lesson, and immediately following it) my responses were dominated by a behaviourist view. I wanted to assert my authority and have some control of the children. I was grappling for approaches to classroom management that I could use to restore classroom order. My language reflected a separation between mathematics and classroom management, and I was aiming to focus my, and my learner's, attention on each with clear consequences agreed for what would happen if behaviour was not supportive of the mathematics. Planned Adjustment 1 (detailed above) is consistent with this view.
As the analysis deepened, however, I could identify evidence of an interpretive view of behaviour. In particular, my emotional response to the experience was undeniable. This was verbally expressed to close colleagues and written in my reflective notes (Layer 2). While - at the time - I was not aware of seeing children as communicating to me through their behaviour, later I recognised that I had labelled them as either mad, bad or sad. When I was seeing them as bad I wanted them punished, when I was seeing them as mad, I was seeking out specialist interventions, and when I was seeing them as sad I was patronising them and attributing their behaviours to their challenging socio-economic contexts. Labelling behaviour is quite distinct from labelling children. The learners' reasons for behaving in particular ways ought to be less substantive than what their behaviour communicates about my classroom practice.
I also see evidence of my thinking being influenced by the medicalised view. My coding of learner behaviours as 'special needs' reflects much of this view. In most of my responses, I was grappling for a diagnosis and recommending some specialist intervention and support. This is clearly evident in Planned Adjustment 7.
The sociological view was least evident to me when looking back at my written responses. However, the social context of learners and the desperateness of their situations, together with the awareness that the school was not working for many of them, was a frequent source of collegial discussion. This bigger social context seemed to be too big a problem to grapple with, and one where I had very limited head room to affect change. I think this may be why it did not feature in my written recordings.
I had not noticed and questioned most of my pedagogical decisions in relation to the teaching of mathematics until quite far down this process. I know that teachers I work with tend to resist changing their pedagogy, yet I myself was stubbornly holding on to my preferred pedagogic choices (despite them not working in this context). It was only at Layer 6 and Layer 7 of analysis that I moved towards an account-for the interruptions, which forced my attention back to the pedagogic forms in which mathematical aims are couched. It seemed that only when re-examining aspects of the account-for (which were embedded in my initial accounts-of) that my underlying assumptions and stance towards learners' behaviour was shifted from viewing disruptive behaviour as wilful contravention of my intended classroom practices to communicating learner feedback about those practices. To attend to my pedagogy (my own behaviour), over which I had the most control, I had to background each learner's behaviour (and their underlying reasons for this).
Conclusion
In addressing the research question, the main learning for me was not in the specific adjustments to my teaching and my personal growth. Rather it was in seeing anew previously taken-for-granted assumptions about South African Grade 2 classrooms. Firstly, I had assumed that the content, pacing and sequencing of my lesson was reasonable for the Grade 2 learners in this classroom, as this approach had worked well in the other contexts. Secondly, I had assumed that the learners would feel safe at school and that physically fighting would be rare. However, I learnt that in a context of distrust and frequent violence, significant time, effort and emotional engagement is required to collectively create a secure space in which mathematics can then be made possible to learn. This meant that there was far less instructional time available for mathematics-focused activity, and my mathematics expectations on pacing had to be adjusted significantly. I had to transform my 'knowledge for teaching mathematics' (KfTM) for this more challenging context.
Spending time on creating and maintaining a productive classroom culture in a disruptive classroom environment is not easy, but required investments of time and emotional energy in order to establish trusting relationships which could sustain shifts towards productively working on mathematics. Teachers require specialised KfTM in challenging contexts. We have provided a few adaptations regarding content, pedagogy and organisation which we have now used to better respond to this challenging context. We have described a process of a teacher learning for teaching mathematics in challenging contexts, by using the discipline of noticing to develop accounts of and accounts for their pedagogy.
Through this process, we have been reminded that learning and teaching are emotionally charged and psychologically illuminating experiences (Wright 2009). In the didactic triangle, the behaviour of particular learners in this challenging context offered the teacher an opportunity for professional growth to expand her KfTM which required critical interpretation of the mathematics content and how they approached it.
In summary, the layered critical reflection process supported a cycle of noticing moves that began and ended (for now) with pedagogic attention to mathematical learning. Classroom management has come to be integrated within the lesson planning in content and pedagogic terms, rather than being viewed as an interruption to mathematical working. The didactic triangle of teacher, learners and the mathematics content of a particular lesson are brought into focus.
This reflective cycle is centrally attuned to becoming more responsive, and thereby more effective, as mathematics teachers in classroom situations where disruptive learner behaviour, is a feature. The literature suggests that these contexts are relatively widespread, and our sense is therefore, that both our processes of moving towards a more responsive pedagogy and our findings are broadly useful. While the policy context is not the key focus of this article, our findings also raise questions about how prescriptions for coverage, sequence and pacing could be playing out in contexts like the classroom described in this article - how these demands may be experienced in the complex systems of classroom interactions, and how teachers may be accountable for any sense of a lack of efficacy in this mix?
Acknowledgements
The development project on which this article draws was the Focus on Primary Maths project (2012-2014), which was funded by Apex Hi, as administered by Tshikululu Social Investments.
Competing interests
The authors declare that they have no financial or personal relationships which may have inappropriately influenced them in writing this article.
Authors' contributions
N.R. was the project leader of the Focus on Primary Mathematics project which coincided with her PhD study. She was the teacher of this lesson and the main author of this article. H.V. was her PhD supervisor and a reference group member for the development project. She supported N.R with her writing, structuring and theorising for this article.
References
Carnoy, M., Chisholm, L. & Chilisa, B. (eds.), 2012, The low achievement trap: Comparing schooling in Botswana and South Africa, HSRC, Pretoria.
Carpenter, T., Fennema, E., Franke, M., Levi, L. & Empson, S., 1999, Children's mathematics: Cognitively guided instruction, Heineman, Portsmouth.
Department of Education (DOE), 2002, Revised national curriculum statement grades R-9 (Schools) Mathematics (pp. 1-120). Department of Education, Pretoria, South Africa.
Dewey, J., 1933, How we think: A restatement of the relation of reflective thinking in the education process, Heath and Co., London.
Henning, E., 2011, 'Topping up on top down', Education As Change 15(1), 1-2. http://dx.doi.org/10.1080/16823206.2011.602183 [ Links ]
Levin, J. & Nolan, J., 1996, Principals of classroom management: A professional decision-making model, Ally & Bacon, London.
Mabeba, M.Z. & Prinsloo, E., 2000, 'Perceptions of discipline and ensuing discipline problems in secondary education', South African Journal of Education 20, 34-41. [ Links ]
Marais, P. & Meier, C., 2010, 'Disruptive behaviour in the foundation phase of schooling', South African Journal of Education 30, 41-57. [ Links ]
Marton, F. & Booth, S., 1997, Learning and awareness, Erlbaum, Mahwah.
Mason, J., 2002, Researching your own practice: The discipline of noticing, Routledge, New York.
Moodley, V., 2015, 'An investigation into the feasibility of the positive behaviour support model for Limpopo's primary schools (Grade R-3): Preliminary findings', in E. Walton & S. Moonsamy (eds.), Making education inclusive, pp. 94-112, Newton on Tyme, Cambridge Scholar Publishers, Cambridge.
Papatheodorou, T., 2005, Behaviour problems in the early years: A guide for understanding and support, Routledge Falmer, New York.
Roberts, N., in press, 'Learners exemplifying for themselves: Grade 2s telling additive relations stories', in H. Venkat & M. Graven (eds.), Improving primary mathematics education, teaching and learning: Research for development in resource constrained contexts, Palgrave Macmillan, Basingstoke.
Roberts, N. & Stylianides, A.J., 2013, 'Telling and illustrating stories of parity: A classroom-based design experiment on young children's use of narrative in mathematics', ZDM Mathematics Education 45(3), 453-467. http://dx.doi.org/10.1007/s11858-012-0474-2 [ Links ]
Slee, R., 2010, Bad behavior, in L. Graham (ed.), (De)Constructing ADHD, pp. 41-61, Peter Lang Publishing, New York.
Spaull, N., 2013, 'Poverty & privilege: Primary school inequality in South Africa', International Journal of Educational Development 33, 436-447. http://dx.doi.org/10.1016/j.ijedudev.2012.09.009 [ Links ]
Stigler, J. & Hiebert, J., 1998, 'Teaching is a cultural activity', American Educator 22(4), 4-11. [ Links ]
Taylor, N., Draper, K., Muller, J. & Sithole, S., 2013, NEEDU National Report 2012 Summary: National Education Evaluation and Development Unit.
Thompson, I., (ed.), 2008, Teaching and learning early number, 2nd edn., Open University Press, Birkshire.
Wright, A.-M., 2009, 'Every child matters: Discourses of challenging behaviour', Pastoral Care in Education: An International Journal of Personal, Social and Emotional Development 27(4), 279-290. http://dx.doi.org/10.1080/02643940903349344 [ Links ]
 Correspondence:
Correspondence:
Nicky Roberts
nickyroberts@icon.co.za
Received: 30 Nov. 2015
Accepted: 27 Mar. 2016
Published: 29 July 2016
Note: Note to readers: We pay particular attention to our use of voice in this article to narrate what happened as well as our shifting thoughts about what happened. Writing in the first person is the voice of the first author who was both the teacher of the lesson and a doctoral researcher. Writing in the second person is the voice of both authors.
1 This is not referring to Crystal-meth addition by children, but the apparent social and development difficulties associated with children born to mothers' who use Crystal-meth during pregnancy.
2 Not the learner's real name. Pseudonyms are used throughout this article.
3 Identification of special needs was conducted in collaboration with the usual class teacher and the learning support coordinator at the school.














