Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.5 n.3 Johannesburg 2015
http://dx.doi.org/10.4102/sajce.v5i3.375
ORIGINAL RESEARCH
Online supplementary mathematics tuition in a first-year childhood teacher education programme
Kathleen Fonseca; Nadine Petersen
Department of Childhood Education University of Johannesburg, South Africa
ABSTRACT
This study reports on an intervention that was aimed at improving the content knowledge of first-year intermediate-phase education students at a South African university. The study gives some insight into preservice teachers' perceptions of an online programme for the development of mathematics common content knowledge for teachers of mathematics in the intermediate grades. The effectiveness of the intervention programme was analysed according to Shapiro's evaluation criteria for intervention research. The findings show that there has been a positive shift in preservice teachers' common content knowledge but that there is much room for further development. The student teachers found the programme to be of great benefit with regard to the development of their mathematics knowledge as well as their confidence as future teachers of mathematics. The findings highlighted their disturbingly limited knowledge of mathematics content knowledge and pointed to the responsibility of teacher education departments at universities to implement sufficient maths content courses that will address the status quo of poor mathematics teaching in South African primary schools. The authors conclude that the students need to spend much more time on 'catching up' before they become teachers.
Introduction
Given the high value placed on scarce skills in South Africa, such as engineering, medicine, finance and accounting, most top-performing learners will go into professions other than teaching, which is assumed to be less lucrative. The challenge for teacher training institutions then is that the applicant pool for B.Ed. degrees tends to comprise young people with relative poor content knowledge of mathematics (Spaull & Kotze 2015). International studies have indicated for a long time now that prospective foundation and intermediate-phase mathematics teachers have poor conceptual knowledge of maths and often do not know the concepts that underlie operations and procedures (Ball 1990; Ma 1999). Most students know rules and procedures but lack conceptual understanding and reasoning skills (Wilson, Floden & Ferrini-Mundy 2001) as described, amongst others, by Sharma (2015) and Bugden and Ansari (2015). In a study conducted at five South African universities, it has been reported that prospective teachers enter university programmes with reasonable procedural knowledge of mathematics but poor conceptual knowledge (Bowie 2014). In a study at our university too, we have found that most preservice teachers enter the primary school teacher education programmes with limited basic mathematics content knowledge (MCK),1 which negatively impacts mathematical pedagogical content knowledge (MPCK).2 Therefore, we argue that it is necessary to improve student teachers' content knowledge (Kajander 2005; Sowder 2007), especially the content they will have to teach when they enter the profession. Teacher training institutions are faced with limited human resources and a large amount of catch-up work is required in order to prepare student teachers with a 'profound understanding of fundamental mathematics' (Ma 1999). Both international (Schmidt, Blömeke & Tattoo, 2011a; Schmidt, Cogan & Houng 2011b) and local (Bowie 2014) studies have shown that there is great variation amongst teacher training institutions with regard to the type and number of mathematics courses needed to be completed in mathematics teacher preparation programmes. Some programmes place more emphasis on university-level mathematics and others have included compulsory school content courses. Youngs and Qian (2013) have argued that it is not the number of mathematics courses taken during teacher preparation programmes but the mathematical content topics in these courses that is strongly associated with preservice teachers' MCK.
The paper reports on a pilot project of an online mathematics 'co-curricular' enrichment course and how this course advanced common content knowledge of the first cohort of intermediate-phase student teachers in 2014. The programme was added to the existing curriculum and therefore described as 'co-curricular'. It also reports on the value of the course according to the students themselves, by drawing on their qualitative responses to open-ended questions in a survey. The initiative was funded partly through the Faculty of Education and partly through Numeric (a not-for-profit community engagement partner of the faculty). Numeric utilises the coursework and materials, as well as the interactive platform of the Khan Academy (http://www.khanacademy.org).
The development of mathematical knowledge for teaching
As teacher educators who prepare preservice teachers for the foundation phase and as mathematics specialists for the intermediate phase, we believe that a strong basis of fundamental mathematics knowledge is vital. Our emphasis on the development of sound mathematical content knowledge is informed by the research findings on the strong correlation between teachers' ability to teach and their MCK (Ball, Hill & Bass 2005; Chapman 2005). In the intermediate-phase teacher education programme, based on the current entrance requirement for mathematics, less than 10% of the total first-year student cohort of 120 students qualifies to specialise in mathematics. More students need to qualify as mathematics teachers for the intermediate phase and not enough meet our institution's goals for graduating sufficient numbers of qualified mathematics teachers for the primary school. Recent research into teacher provision (Green, Adendorff & Mathebula 2014) also indicates that primary schools tend not to recruit and deploy subject specialisation candidates, especially in the intermediate phase. Many intermediate-phase teachers will thus be required to teach mathematics, regardless of their subject specialisation. We argue that it is imperative to improve the MCK of all first-year students because if their limited competence is not addressed during their preservice education, these students will be ill-equipped to teach maths after graduating and the status quo in South African mathematics education will persist. Thus, we wish to make the point that mathematics knowledge for teaching should be compulsory for all primary school teachers. It is from this position that we decided to institute an online intervention programme, aiming to improve students' mathematical competence. We reasoned that such an intervention could increase the number of intermediate-phase students who choose mathematics as specialisation from the second year of their programme, whilst all others could also benefit. We also aimed at increasing the mathematics competence knowledge of those who qualify with other specialisations, in the event that they have to teach mathematics.
Teaching in general is informed by various knowledge domains (Shulman, 1986, 1987). Many factors impact the development of preservice mathematics teachers' professional knowledge or mathematical knowledge for teaching (MKT). As a construct, MKT consists of two main domains, namely subject matter knowledge (with subdomains, common content knowledge, specialised content knowledge and knowledge at the mathematical horizon) and pedagogical content knowledge (with subdomains, knowledge of content and students, knowledge of content and teaching and knowledge of curriculum) (Ball, Thames & Phelps 2008). In the paper our attention is on MKT, especially common content knowledge. Common content knowledge refers to the mathematics knowledge that is not unique to teaching only; it is the type of mathematical knowledge that every well-educated person is competent in. Ball et al. (2008) argue the teaching of mathematics suffers and valuable time is lost when teachers lack common content knowledge.
In the last decade, the aim of mathematics education research has been to find out which national and institutional policies have most influenced the development of preservice professional knowledge. There has also been a keen interest in studying the influence of affective factors (e.g. self-efficacy beliefs, attitudes, maths anxiety) on the development of preservice teachers' MCK and MPCK (Bandalos, Yates & Thorndike-Christ 1995; Bekdemir 2010; Hembree 1990; Hine 2015; Trujillo & Hadfield 1999; Uusimaki & Nason 2004). One large-scale study, the Mathematics Teaching for the Twenty-First Century and Teacher Education and Development Study-Learning to Teach Mathematics, is the first cross-national comparative study (n = 15 countries) that measured the MCK and MPCK of preservice teachers in their final year of their study (Tatto et al. 2012). This study reported on the mathematical knowledge gains (MCK and MPCK) of both primary and secondary preservice teachers in their final year of study. Findings suggest that there were great differences across countries, with higher performing countries (e.g. Singapore, Chinese Taipei) having substantially greater MCK and MPCK than the lower performing countries (e.g. Chilli and Botswana).
A number of authors, in turn, did follow-up studies to explore factors associated with the development of preservice teachers' MCK and MPCK. These studies looked at cognitive factors (MCK, MPCK and general pedagogical knowledge-GPK), individual predictors (e.g. gender effects, language effects, prior knowledge and motivation effects) and institutional predictors (sequencing and delivering of curriculum and practicum involvement). For the purposes of the paper, we briefly discuss two of these studies that highlighted the effects of preservice teachers' prior mathematical knowledge on the development of their MCK.
Qian and Youngs (2013) reported on data of five of the Teacher Education and Development Study-Learning to Teach Mathematics countries, namely Chinese Taipei (Taiwan), Philippines, Singapore, Spain, Switzerland and the USA (Qian & Young 2013). They explored whether the number and type of mathematics content courses and mathematics methods courses that the elementary preservice teachers had completed had an impact on the development of their MCK and MPCK. Qian and Youngs (2013) found that preservice teachers' MCK scores in the USA and Spain were lower compared to the students from the other three countries, irrespective of the amount of university-level mathematics courses they took. Significant in their analysis was that preservice teachers from the USA and Spain entered their mathematics courses with weaker levels of prior school mathematics knowledge than students from Singapore, Chineses Taipei and Switzerland. They established a correlation between the preservice teachers' previous mathematical achievement (at school) and their MCK (Qian & Young 2013). The results of this inquiry are significant for us because it indicates that teacher educators need to decide what mathematics content should be taught and how deeply the content should be explored.
Laschke (2013) conducted a similar study by looking at which of the individual predictors of Taiwanese and German preservice teachers were associated with the development of their MCK. The individual predictors they considered were social aspects (e.g. gender, parent education, home language), prior knowledge (e.g. high school achievement, level of mathematics lessons), motives (e.g. intrinsic, pedagogical and extrinsic) and constraints (female and money related). Findings from this study suggest that the prior mathematical achievement of Taiwanese preservice teachers had a greater impact on the development of their MCK than that of their German counterparts. Laschke (2013) explained that this finding was in line with the hypothesis that 'mathematical competence plays a significant role in university entrance' in Taiwan. Prospective mathematics teachers in this country studied mathematics for 12 years and attended schools where mathematics was taught at an advanced level, whereas the German students entered university courses with varied prior mathematical achievements (Laschke 2013). This author concluded that students with higher prior knowledge perform better at university. The implication for teacher education is that it would be preferable to recruit prospective mathematics teachers from a pool of school graduates with a stronger domain-specific knowledge of mathematics. This is probably easier in countries such as Singapore and Switzerland where the teaching profession is highly regarded and where there are very selective recruitment criteria for teacher education. As Quian and Youngs (2015) argue, 'Singapore is able to recruit teachers from the top one-third of each age cohort with regards to academic ability'. Switzerland too recruits high academic achievers; those students in the top 20% of their age cohort (ibid). This may not be a feasible option for South Africa because top mathematics students tend to choose careers in the sciences such as engineering and medicine and also accountancy. Thus, we have to put other measures in place to either select prospective mathematics teachers and/or to develop the MCK of students who may not have the required levels of mathematics knowledge on entry to their programmes. Zerpa, Kajander and Van Barneveld (2009) argue that:
assessing preservice teachers' initial levels of conceptual and procedural knowledge as well as their levels of high school mathematics may help determine how much preparation via a mathematics methods course or other courses are needed to improve pre-service teacher's conceptual mathematical knowledge. (p. 72)
Improving mathematics knowledge
A number of teacher education institutions have competency tests and student support courses in place to address preservice teachers' lack of mathematics content they need to teach (Afamasaga-Fuatai'I, Falo & Meyer 2008; Mays 2005). In two Australian universities, New South Wales institute of Teachers and Charles Sturt University, preservice teachers who enrol at the university without the appropriate mathematics competence have to pass a basic skills test covering Grade 6 mathematics topic such fractions, decimals, division by two-digit numbers, place value and order of operations. A pass is pegged at 90%, and if students after four opportunities do not reach this level, they are compelled to enrol in an enrichment course. The course is aimed at improving their mathematical competence as well as assisting them in developing their professional identity as a mathematics teacher and equipping them as teachers of both conceptual and procedural knowledge (Meany & Lange 2012). The designers wanted to give preservice teachers the opportunity to develop mathematical conceptual understanding. Research on this initiative (Meany & Lange 2012) showed that 66% of students struggled to pass the Basic Skills Test the first time, with some having to attend five 1-hour tutorials. Those who continued to find the course challenging were referred to web sites and also their respective universities' learning support services. After having received some form of support, all preservice teachers were able to reach the 90% pass mark required. A major finding of this research was that preservice teachers with weak MCK will in all likelihood not be unable to teach the very basic mathematical concepts required of them.
A similar study was conducted by Mays (2005). In this study, preservice teachers had to complete a diagnostic test on the mathematics knowledge they will have to teach. The purpose of the diagnostic test was not only to assess preservice teachers' knowledge but also to remediate common errors and misconceptions. The level of mastery was pegged at 80%, and only 17 out of 159 preservice teachers achieved the mastery level (Mays 2005). A remediation course for these students was in the form of a unit on mathematical misconceptions.
The inquiry
This intervention comprised a pre- and posttest, using a Grade 7 level test for mathematical competence assessment. Because there was no control group and because the participants were not selected randomly, the study may be described as a 'nonexperiment'. The effects of the intervention will be described by the four characteristics of Shapiro's (1987) evaluation criteria for intervention research. The four characteristics are treatment effectiveness (amount of change as a result of intervention), social validity (effectiveness of the intervention as perceived by participants), treatment acceptability (enjoyment of intervention programme by participants) and treatment integrity (whether all participants receive equal opportunities and treatment).
The intervention was administered after the baseline pretest to an intact intermediate-phase student-teacher group in the second half of their first year of study at the university (n = 108). The pretest was designed to assess concepts in mathematics at a Grade 4-7 level. Thereafter, Numeric, in collaboration with university lecturers, designed the intervention programme to cover mathematics curriculum content up to and including Grade 7, reasoning that at minimum prospective foundation- and intermediate-phase teachers need to have basic mathematics competence at Grade 7 level at least. The intervention consisted of students engaging with up to 150 online Khan Academy exercises covering topics that span arithmetic and prealgebra over a 10-week period from July to October 2014 (see http://www.khanacademy.com). Students were required to attend weekly supervised Khan Academy sessions (1.5 hours per session) in a computer laboratory on the Soweto campus of the university, with the expectation that they would complete at least 2 hours of independent study on Khan Academy outside of class. Table 1 provides an overview of the spread of topics, the number of videos on each topic and the number of exercises students had to complete in each topic area. To encourage students' attendance and engagement with the online materials, this intervention contributed 15% of the final course mark. The posttest was administered at the end of the 10 weeks. The baseline and end-line tests were identical, save for the actual numbers used on the questions. The purpose was to create two highly comparable tests at different time points so as to measure any increase in mathematical proficiency as a result of the intervention. We also used open-ended survey questions for student self-reporting on their experience of the intervention.
Representation of data:
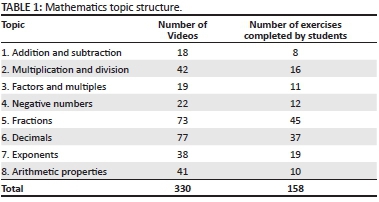
Khan Academy exercise 'mastery'
The average student mastered 137 exercises and watched 37 Khan Academy videos over the course of 10 weeks. In order to be considered to have 'mastered' a given exercise, students must complete seven questions correctly in a row. If they answered one question wrong, the exercise resets. In this way, Khan Academy encourages 100% mastery as opposed to the traditional 50% pass mark approach.
Whilst the target number of exercises was set at 150, students were encouraged to go beyond this target, with class prizes awarded to students who achieved the highest number of exercises mastered. The maximum number of exercises mastered by a single student was 231 (Figure 1).
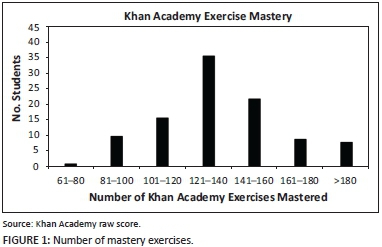
Baseline versus end-line scores
The average score on the baseline test was 37% [with a standard deviation (SD) of 11%]. The average score on the end-line test was 51% (with an SD of 13%). This constitutes an absolute shift of 14% upward, or roughly 1.16 SD from the mean. Figure 2 shows the distribution of baseline test scores (striped bars) compared with the distribution of endline test scores (solid black bars).
Survey: students' perceptions of the Khan Academy course
The student self-reporting survey consisted of a number of open-ended and closed questions. A, 5-point Likert scale was used for the open-ended questions. These questions included ones that asked students to respond to aspects such as the difficulty level of the exercises, usefulness of videos and improvement in mathematics competency levels. We present a synopsis of these data below.
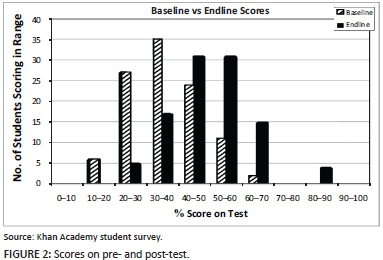
Difficulty level of exercises
Students were asked how they rated the difficulty level from (1) being easy, (2) easy-to-moderate, (3) moderate, (4) moderate-to-hard and (5) hard. Based on their responses, the overall difficulty rating for the course was 3.3 out of 5, indicating that the course was challenging but manageable (Figure 3).
The following were some of the student responses on the open-ended questions about the difficulty level of the course:
The Khan Academy is very convenient and useful. It's a very creative way to get students to pass Maths. It's easy to understand.
Khan academy helped me to improve my maths skills and gave me easier methods of solving problems. Videos were very useful and mastery challenge too, although it was challenging.
Usefulness of videos
Students were expected to spend 2 hours per week outside of class on the Khan Academy exercises and videos. These videos are instructional videos, where the mathematical concepts are explained and students have to complete an associated exercise. The average time spent watching videos was 5 hours per student over the 10-week period. Of the students, 84% indicated that they found the videos either 'useful' or 'very useful' (Figure 4).
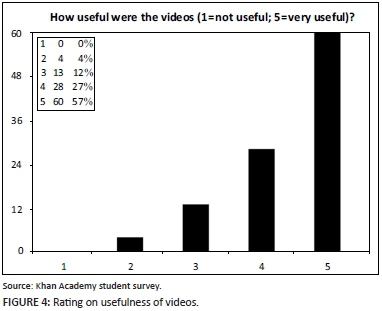
Some of the students' responses were:
The course was useful because of the videos.
Videos were very useful and the mastery challenges as well.
Khan Academy was very useful to me and I have learned a lot from it, even though I don't want to major in mathematics. I really enjoyed doing the activities given to me and the coaches were very good and well prepared on what they were doing.
Khan Academy course duration
Students indicated that they need more time working on the Khan Academy exercises. In all, 64% indicated that they preferred for the course to last the full semester of 14 weeks.
Students indicated that they needed more time working through the exercises. The exercises were time bound and they thus felt that they could have completed more modules (Figure 5).
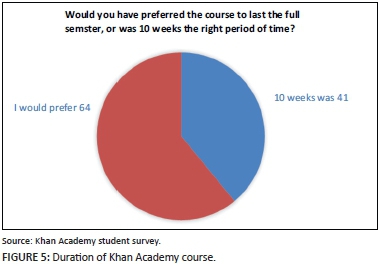
The following are excerpts from students:
If we were given time for all this semester it was gonna be good and we would have completed all the exercises.
The Khan Academy was very useful to me because I learned too many skills that I will apply throughout the four years and further. One important thing I enjoyed learning is how to explain maths, which is going to be needed as a teacher.
It has created confidence in me because I can teach certain topics in various ways.
Khan Academy was very useful to me and it changed my negative attitudes towards mathematics.
Improvement on mathematics competence
Students were asked whether they think that their maths has improved as a result of the course. They rated their improvement from (1) no improvement, (2) slight improvement, (3) moderate improvement, (4) moderate-to-large improvement and (5) large improvement. Of the students, 78% indicated that the improvement of their maths ranged between moderate-to-large and large (Figure 6).
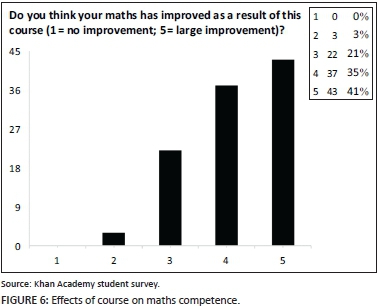
This program helped me a lot with maths concepts that I didn't understand before.
The program helped me with a lot of things that I was failing in class but now I can do them with confidence. It changed the way I need to look at maths as being difficult. The good tutors helped.
Khan Academy was very useful to me I could not understand some of the things in class. Now I'm a little bit better in maths as I hate it.
I really learned a lot from Khan Academy even though I hated maths and I have always failed it but I managed to make sense of many things.
Choosing mathematics as a major in the second year
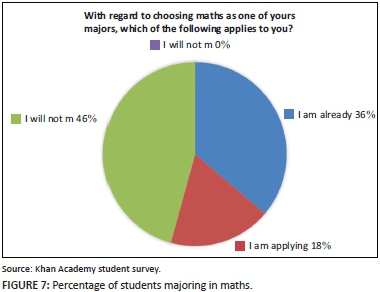
Of the 108 students in the course, only 38 were scheduled in major in mathematics at the outset of the course. At the end of the course, 14 students applied to change one of their majors to mathematics (Figure 7).
Discussion
The evaluation process of this intervention study was guided by Shapiro's (1987) four criteria for effectiveness.
Treatment effectiveness
We examine the intervention's treatment effectiveness based on the actual effects of the preservice teachers' participation on the development of their common content knowledge. The main finding of this pilot study shows that the intervention substantially improved the preservice teachers' common content knowledge, with a very large 1.16 SD. This shift is significant at the p < 0.001 significance level. An end-line score of 51% (refer to Table 2) is still not an acceptable level and further work needs to be carried out in order to improve preservice teachers' MCK, especially their common content knowledge.
Preservice teachers were very involved in the mastery exercises and instructional videos with an average of 137 mastery exercises completed and 37 videos watched. There seems to be a strong correlation between prior knowledge (pretest) and number of mastery exercises completed in the participants. The participant with the highest pretest score of 73% managed to complete the maximum number of mastery exercises (231) and obtained an end-line score of 84%. This is likely because of the level of prior knowledge, which resulted in the participant completing the exercises at a faster pace and could thus complete more exercises. On the other end, the participant with a very low pretest score of 25% (not the lowest, lowest 17%) could only complete 67, the lowest number of mastery exercises in this study. This could be because of the number of times a particular exercise was reset because of a lack of conceptual understanding before moving on to a new exercise. The study found that the average preservice teacher spent one fifth of the time on watching the instructional videos and four fifths on mastering the exercises. This implies that preservice teachers with low prior mathematical knowledge need appropriate time to master new knowledge and skills. One of the biggest obstacles to student achievement is that these students started at a very low level of mathematical knowledge as indicated by the average score of 37% on the baseline test. However, the findings suggest that the intervention was effective based on the 1.16 shift in the SD from the mean. We are also clear that it is not possible to undo or remedy the lack in primary school mathematics in the 10 weeks of the intervention The low level of mathematics knowledge is likely because of the poor quality of their primary and secondary school mathematics education (refer to Table 2, Spaull & Kotze 2015) and the socio-economic status of their school communities as measured by school quintile, with Quintile 1-3 being nonfee-paying schools. Learners from lower socio-economic school communities (Quintiles 1-4) are often exposed to teachers who are not qualified to teach mathematics and who have lower MKT (Hill, Rowan & Ball 2005) and whose teaching emphasises procedures without conceptual understanding and answers without mathematical justification (Lubienski 2002).
Spaull and Kotze (2015:21) argue:
The trajectory lines, one for Quintile 5 and one for the average of Quintiles 1-4, show that in Grade 3 there already exist large differences in performance (approximately three grade levels) and that by the time children enter Grade 9, this gap in performance has grown to about four grade levels. The linear trend in performance between these two groups suggests that if the same number of students in Quintiles 1-4 in Grade 9 continued in schooling until Grade 12 (i.e. no drop out between these two periods), they would be functioning at approximately 4.5 grade levels lower than their Quintile 5 counterparts (1.4 standard deviations lower).
Social validity
Social validity refers to the effectiveness of the Khan Academy programme as perceived by the preservice teachers. Students responded positively towards the intervention course. They indicated that the exercises were challenging but manageable. Responses like the following were given:
Khan Academy was very useful to me and I have learned a lot from it, even though I don't want to major in mathematics. I really enjoyed doing the activities given to me and the coaches were very good and well prepared on what they were doing.
The course was found to be useful because of the instructional videos and mastery exercise and it is perceived to be a very creative way of learning mathematics. According to the students, the course improved their maths skills and they gained new methods to solve problems. Of the students, 78% reported that the improvement ranged between moderate-to-large and large. They also reported that the programme assisted them in understanding mathematics in their course work.
This program helped me a lot with maths concepts that I didn't understand before.
The program helped me with a lot of things that I was failing in class but now I can do them with confidence. It changed the way I need to look at maths as being difficult. The good tutors helped.
The fact that 15 of the 108 students (14%) applied to change one of their majors to maths is a strong indicator of the increased enthusiasm and confidence students feel as a result of the intervention.
Treatment acceptability
Treatment acceptability reports on whether the preservice teachers enjoyed the intervention procedure. Preservice teachers reported that they enjoyed the intervention, the instructional videos and the involvement of the course tutors:
Khan Academy was very useful to me and I have learned a lot from it, even though I don't want to major in mathematics. I really enjoyed doing the activities given to me and the coaches were very good and well prepared on what they were doing.
However, they did feel that more time was needed and that they would have preferred for the course to continue for the full semester. According to a meta-analysis conducted by de Boer, Donker and van der Werf (2014) on the effects of education intervention on students' academic performance, the appropriate length for an effective intervention study is 10 weeks, because interventions longer than 10 weeks have a slightly smaller effect on students' performance.
Treatment integrity
Treatment integrity refers to whether all preservice teachers who participated in the intervention received the same opportunities like access to the computer laboratories and effective coaches/ tutors. Preservice teachers indicated that the coaches were skilled and very effective. The average attendance of the participants was 89%.There were some challenges as reported by the preservice teachers with regards to attendance; some found it challenging to attend these sessions because of financial constraints such as transport money because the sessions were not conducted on the same day as their lectures. All preservice teachers were given the same treatment and support.
Limitations and implications
The limitation of this study is that we did not analyse the knowledge gains within the different mathematical topics; factors and multiples, negative numbers, fractions, decimals, exponents, arithmetic properties and four basic mathematical operations. Because of the online nature of the course, it is also difficult to identify specific errors and misconceptions of specific content domains.
Implications for the Department of Childhood education would be to monitor and improve mathematics competency levels from year to year in order for preservice teachers to exit the programme with the requisite mastery competence.
They would also be required to review and assess the appropriateness of the tutoring of at-risk students. Methodology lecturers should also review their methods courses to accommodate the lack in MCK.
Conclusions
It is evident to us that poor MCK of preservice teachers on entering teacher education programmes, especially the content knowledge they will have to teach to the learners, is not unique to the UJ Department of Childhood Education or South Africa. Preservice teachers in this study performed similarly in this intervention to their counterparts in other countries such as the USA, Australia, New Zealand, Germany, England and Canada. However, it is evident that as a department, we need to put unique interventions in place to remediate this lack in mathematical content knowledge of the pool of teacher education entrants.
Whilst not all preservice teachers would be specialising in mathematics, we argue that is important for all students teaching in the intermediate phase to have a firm understanding of the basics of mathematics. Thus, we do not consider this intervention as the whole solution to the low level of preservice teachers' primary school mathematics in the UJ Department of Childhood Education. It merely highlights the fact that we need to pay attention to preservice teachers' prior mathematical knowledge in order to make informed decisions about the type of mathematics content courses and methodology courses those of us in teacher education offer as learning opportunities.
On this basis, we conclude that this is an initiative worth investigating further. It is our contention that this intervention for childhood teacher education students can and does enhance the student experience of both the teaching and learning of mathematics.
Competing interests
The authors declare that they have no financial or personal relationships which may have inappropriately influenced them in writing this article.
Authors' contributions
K.F. (University of Johannesburg) and N.P. (University of Johannesburg) contributed equally to the writing of this article.
Acknowledgements
The authors acknowledge the valuable contributions of the preliminary raw data from the online programme supplied by Mr Andrew Einhorn of Numeric.
References
Afamasaga-Fuatai'I, K., Falo, N. & Meyer, P., 2008, 'Assessing primary preservice teachers' mathematical competence', in M. Goos, R. Brown & K. Makar (eds.), Proceedings of the 31st Annual Conference of the Mathematics Education Research Group of Australia, © MERGA Inc.
Ball, D., 1990, 'The mathematical understandings that prospective teachers bring to teacher education', The Elementary School Journal 90(4), 449-466. [ Links ]
Ball, D.L., Hill, H.C. & Bass, H., 2005, 'Knowing mathematics for teaching: Who knows mathematics well enough to teach third grade, and how can we decide?' American Educator 29(3), 14-46. [ Links ]
Ball, D.L., Thames, M.H. & Phelps, G., 2008, 'Content knowledge for teaching: What makes it special?' Journal of Teacher Education 59(5), 389-407. [ Links ]
Bandalos, D.L., Yates, K. & Thorndike-Christ, T., 1995, 'Effects of math self-concept, perceived self-efficacy, and attributions for failure and success on test anxiety', Journal of Educational Psychology 87(4), 611-623. [ Links ]
Bekdemir, M., 2010, 'The pre-service teachers' mathematics anxiety related to depth of negative experiences in mathematics classrooms while they were students', Educational Studies in Mathematics 75(3), 311-328. [ Links ]
Bowie, L., 2014, Initial Teacher Education Research Project: Report on mathematics courses for intermediate phase student teachers at five universities, JET Education Services, Johannesburg.
Bugden, S. & Ansari, D., 2015, 'Probing the nature of deficits in the "Approximate Number System" in the children with persistent Developmental Dyscalculia', Developmental Science.
Chapman, O., 2005, 'Constructing pedagogical knowledge of problem solving: Preservice mathematics teachers', in H.L. Chick & J.L. Vincent (eds.), Proceedings of the 29th Conference of the International Group for the Psychology of Mathematics Education, 2, pp. 225-232.
de Boer, H., Donker, A.S. & van der Werf, M.P.C., 2014, 'Effects of the attributes of educational interventions on students' academic performance: A meta-analysis', Review of Educational Research 84(4), 509-545. [ Links ]
Green, W., Adendorff, M. & Mathebula, B., 2014, '"Minding the gap" A national foundation phase teacher supply-demand analysis 2012-2020', South African Journal of Childhood Education 4(2), 1-23. [ Links ]
Hembree, R., 1990, 'The nature, effects, and relief of mathematics anxiety', Journal for Research in Mathematics Education 21(1), 33-46. [ Links ]
Hill, H.C., Rowan, B. & Ball, D.L., 2005., 'Effects of teachers' mathematical knowledge for teaching on student achievement', American Educational Research Journal 42(2), 371-406. [ Links ]
Hine, G.S.C., 2015, 'Strengthening pre-service teachers' mathematical content knowledge', in Teaching and learning uncapped. Proceedings of the 24th Annual Teaching Learning Forum, The University of Western Australia, Perth, January 29-30, 2015.
Kajander, A., 2005, 'Moving towards a conceptual understanding in the preservice classroom: A study of learning fractions', in Proceedings of the Teacher Education for the Schools We Need Conference, University of Toronto, Toronto.
Laschke, C., 2013, 'Effects of future mathematics teachers' affective cognitive and socio-demographic characteristics on their teacher education in Germany and Taiwan', International Journal of Science and Mathematics Education 11, 895-921. [ Links ]
Lubienski, S., 2002, 'A closer look at Black-White mathematics gaps: Intersections of race and SES in NAEP achievement and instructional practices data', Journal of Negro Education 71, 269-287. [ Links ]
Ma, L., 1999, Knowing and teaching elementary mathematics. Teachers' understanding of fundamental mathematics in China and the United States, Lawrence Erlbaum Associates Inc, Mahwah, NJ.
Mays, H., 2005, 'Mathematical knowledge of some entrants to a preservice education course', in M. Coupland, J. Anderson & T. Spencer (eds.), Making mathematics vital Proceedings of the 20th biennial conference of the Australian Association of Mathematics Teachers, pp. 43-52, AAMT, Adelaide.
Meany, T. & Lange, T., 2012, 'Knowing mathematics to be a teacher', Mathematics Teacher Education and Development 14(2), 50-69. [ Links ]
Schmidt, W.H., Blomeke, S. & Tatto, M.T., 2011a, Teacher education matters: A study of middle school mathematics teacher preparation in six countries, Teachers College Press, New York, NY.
Schmidt, W.H., Cogan, L. & Houang, R., 2011b, 'The role of opportunity to learn in teacher preparation: An international context', Journal of Teacher Education 62(2), 138-153. [ Links ]
Shapiro, E.S., 1987, 'Intervention research methodology in school psychology', School Psychology Review 16(3), 290-305. [ Links ]
Sharma, M.C., 2015, 'Number sense: A window into dyscalculia and other mathematics difficulties', in S. Chinn (ed.), The Routledge international handbook of dyscalculia and mathematical learning difficulties, pp. 277-291, Routledge, London.
Shulman, L., 1986, 'Those who understand: Knowledge growth in teaching', Educational Researcher 15(2), 4-14. [ Links ]
Shulman, L., 1987, 'Knowledge and teaching: Foundations of the new reform', Harvard Educational Review 1-22.
Sowder, J., 2007, 'The mathematical education and development of teachers', in F.K. Lester (ed.), Second handbook of research on mathematics teaching and learning, pp. 157-199, IAP, Charlotte, NC.
Spaull, N. & Kotze, J., 2015, 'Starting behind and staying behind in South Africa. The case of insurmountable learning deficits in mathematics', International Journal of Educational Development 41, 13-24. [ Links ]
Tatto, M.T., Schwille, J., Senk, S.L., Ingvarson, L., Peck, R. & Rowley, G., 2008, Teacher Education and Development Study in Mathematics (TEDS-M): Policy, practice, and readiness to teach primary and secondary mathematics. Conceptual framework, Teacher Education and Development International Study Center, College of Education, Michigan State University, East Lansing, MI.
Trujillo, K.M. & Hadfield, O.D., 1999, 'Tracing the roots of mathematics anxiety through in-depth interviews with elementary teachers', College Student Journal 33(2), 11. [ Links ]
Uusimaki, L. &Nason, R., 2004, 'Causes underlying pre-service teachers' negative beliefs and anxieties about mathematics', in M.J. H0ines & A.B. Fuglestad (eds.), Proceedings of the 28th conference of the International Group for the Psychology of Mathematics Education, Vol. 4, pp. 369-376, Bergen University, Bergen, Norway.
Wilson, S.M., Floden, R.E. & Ferrini-Mundy, J., 2001, Teacher preparation research: Current knowledge, gaps, and recommendations, Center for the Study of Teaching and Policy, University of Washington, Seattle, WA.
Youngs, P. & Qian, H., 2013, 'The influence of university courses and field experiences on Chinese elementary candidates' mathematical knowledge for teaching', Journal of Teacher Education 64(3), 244-261. [ Links ]
Zerpa, C., Kajander, A. & Van Barneveld, C., 2009, 'Factors that impact preservice teachers' growth in conceptual mathematical knowledge during a mathematics methods course', International Electronic Journal of Mathematics Education 4(2), 5. [ Links ]
 Correspondence:
Correspondence:
Kathleen Fonseca
kfonseca@uj.ac.za
Received: 20 Nov. 2015
Accepted: 23 Nov. 2015
Published: 03 Feb. 2016
1 MCK 'includes not only basic factual knowledge of mathematics but also conceptual knowledge of structuring and organising principles of mathematics as a discipline' (Blömeke & Delaney 2012:225)
2 Mathematics pedagogical content knowledge is a blending of the MCK and a knowledge of how to make this content accessible to the students.














