Teacher characteristics and student performance: An analysis using hierarchical linear modelling

 

 

Paula Armstrong^*

Research on Socio-Economic Policy (ReSEP). Department of Economics, Stellenbosch University

 

 

---

ABSTRACT

This research makes use of hierarchical linear modelling to investigate which teacher characteristics are significantly associated with student performance. Using data from the SACMEQ III study of 2007, an interesting and potentially important finding is that younger teachers are better able to improve the mean mathematics performance of their students. Furthermore, younger teachers themselves perform better on subject tests than do their older counterparts. Identical models are run for sub-Saharan countries bordering on South Africa and for Kenya, and the strong relationship between teacher age and student performance is not observed. Similarly, the model is run for South Africa using data from SACMEQ II (conducted in 2002), and the relationship between teacher age and student performance is also not observed. It must be noted that South African teachers were not tested in SACMEQ II, hence it was not possible to observe differences in subject knowledge amongst teachers in different cohorts and it was also not possible to control for teachers' level of subject knowledge when observing the relationship between teacher age and student performance. Changes in teacher education in the late 1990s and early 2000s may explain the difference observed in the later data set in the performance of younger teachers relative to their older counterparts.

Keywords: Hierarchical linear modelling, education production function, teacher training, teacher characteristics, SACMEQ III, teacher characteristics and student performance

---

 

 

Introduction

The relationship between teacher characteristics (both qualifications and demographic characteristics) and student performance is important for education policy. Ensuring that teachers who are best suited and most able to enhance student performance are employed is a key responsibility for policy makers. Wayne and Youngs (2003) explain that there is a large body of literature on teacher characteristics and education outcomes. The focus of the studies vary between questions about teacher quantity and turnover, and issues surrounding teacher quality. In many countries (South Africa included) certain qualifications need to be obtained before teachers are permitted to enter the teaching force. Much of the literature surrounding teacher characteristics and student performance is comprised of analyses of the relationship between these and other qualifications. Attempts have been made to identify trends in the quality of teachers, and the question of whether characteristics of teachers in different parts of the schooling system differ is often investigated (ibid).

The relationship between teacher characteristics and student performance is surprisingly elusive, however. Researchers have found it difficult to find aspects of teacher training that correlate with student performance in a statistically significant way (Chingos & Peterson 2011). Conflicting or indeterminate results occur often. For example, Summers and Wolfe (1977) found a negative relationship between teacher score and student performance in the United States (US). Anderson (2000) finds a positive association between teachers using an interactive approach to teaching in mathematics and language and the performance of their students. She also finds evidence of a positive relationship between hours spent teaching and performance in both subjects.¹ Angrist and Lavy (2001) find positive estimates of the relationship between in-service teacher training on mathematics, English language and Hebrew language skills in secular primary schools in Jerusalem.

Contrary to the results obtained by Summers and Wolfe, Ferguson (1998) found a positive correlation between student performance and teacher test scores.² Indeed, the relationship between teacher performance on tests in the subject they teach and student performance in that subject has also been tested extensively. Positive associations between teacher test score and student performance are observed across a range of subjects in some studies (Ehrenberg & Brewer 1995; Hanushek 1992; Rowan, Chiang & Miller 1997); while others find a negative impact of teacher test scores on student outcomes (Murnane & Phillips 1981). It seems then that the evidence regarding the impact of teacher content knowledge on student outcomes is mixed. Results obtained for formal teacher qualifications were also mixed, with the majority of studies returning indeterminate results. Amongst those that did return results, both negative and positive impacts were observed (Wayne & Youngs 2003). The existing research therefore leaves us with few answers to questions about the relationship between teacher qualifications and student performance. Indeed, are teacher qualifications important at all?

Another study that finds a relationship between observable teacher characteristics and student performance was conducted by Slater, Davies and Burgess (2009). Using data from the United Kingdom for 7 000 students (aged sixteen) writing the General Certificate of Secondary Education (GCSE) Keystage 4 examinations,³ the authors investigate whether observable characteristics of teachers correlate with measures of teacher effectiveness. The observable characteristics available are teacher gender, age, educational attainment and teaching experience, and the authors find that none of these characteristics have a statistically significant association with teacher effectiveness.

Another study that finds a statistically significant relationship between teaching experience and student performance is that of Clotfelter, Ladd and Vigdor (2007). The authors find a positive and statistically significant impact of teacher experience on student performance in both mathematics and English.⁴ The size of the coefficients indicate that the majority (or more than half) of the returns to teaching experience occur within the first two years of teaching. Hanushek (2009:171) concurs on the impact of teachers on student performance: "By many accounts, the quality of teachers is the key element to improving student performance." The impact of being taught by a good teacher is quantified by Hanushek (2011). Hanushek estimates that students who perform a standard deviation above average (as measured by performance on high school tests) earn between 10% and 15% more per annum than average - an estimate he deems conservative as it is measured in the early years of their careers, before they have reached their full earning potential - but concedes that this result does not account for the possibility that higher performance at high school level probably results in higher educational attainment. The home background and motivation of the student obviously contribute significantly to the level of success that students are able to achieve, but rigorous research has isolated the impact of effective teaching on student performance. Hanushek (ibid) reports that studies have consistently shown that high-performing teachers (performing 1 standard deviation above the mean, or at the 84^th percentile of the distribution) result in student grades that are at least 0.2 standard deviations higher at the end of a school year. Although these gains diminish over time, it is estimated (although somewhat less conclusively) that the long-term benefit of being taught by an effective teacher is 70% of the immediate gain, and so consecutive years of high-quality teachers result in student outcomes markedly higher than they would have been had students been taught by teachers at the 50^th percentile of the distribution. It is clear then that teacher quality and teacher effectiveness have a considerable effect on the lifetime earnings of students.

How then should we measure teacher quality? To what extent are we 'missing the point?' An important aspect of teacher quality and teacher effectiveness to consider is the extent to which the education received by teachers is appropriate for enabling them to teach.

The National Council of Teachers of Mathematics (NCTM) in the United States describes teachers' knowledge of their students as being central to their ability to influence their performance (NCTM 2000). Broadly speaking, this means that teachers are able to identify the "preconceptions and background knowledge that students typically bring to each subject" (NBPTS 20i2:vi) - what Hill et al (2008:373) essentially refer to as 'pedagogical content knowledge' (PCK). Although its importance in improving student outcomes is widely acknowledged, very little exists in the way of empirical evidence and understanding of this relationship. Hill et al (ibid) believe that this results from two factors. Firstly, there is an absence of studies that are able to prove that teachers possess such knowledge; and secondly, measures to assess programmes that aim to develop this knowledge and its impact on student achievement have not yet been developed. In the absence of such measures, it may be difficult to measure the aspect of teacher quality that truly affects student performance.

In a South African context, Fleisch (2004) finds inconclusive results regarding the relationship between higher levels of teacher resources and student performance. However, Fleisch explains the importance of understanding the absence of the relationship. Indeed, if education policy aims to improve the state of education through changes in teacher policy, then caution must be exercised when considering this policy. Qualitative research on what happens in schools is required in order to understand how teachers may best be utilised to improve education outcomes. Other South African research by Crouch & Mabogoane (2001) finds a strong correlation between teacher qualifications and student performance on matric (Grade 12) examinations. As a result these authors suggest the possibility of upgrading teacher qualifications as a means to improve student outcomes.

This research aims to investigate which characteristics of South African teachers, both demographic and in terms of qualifications and teaching experience, impact on student performance. The first part of the paper defines the research question and introduces the data set that will be used in the analysis, SACMEQ III. The second part briefly discusses the methodology - hierarchical linear modelling (HLM) - and presents the results obtained from the model. The paper concludes with a discussion of the possible driving factors behind these results.

 

Research question and data

Defining the research question

This research aims to investigate whether teacher characteristics (both demographic and human capital) are significantly associated with student performance. Substantial evidence shows that South Africa's educational performance is weak. The question we attempt to answer in this chapter is whether this weak performance can be explained by observable teacher characteristics. In order to measure the impact of these characteristics, the fact that students share teacher characteristics with other students in the same class means that the assumptions that would render ordinary least squares (OLS) regression coefficients accurate (that is, that students are drawn from a random sample) are violated. The multi-level nature of the data requires that this element be controlled for and modelled in the investigation. A full discussion of this is available in a working paper discussing this research (Armstrong 2014b). Students being taught by the same teacher not only share teacher characteristics, but are also more likely to be more similar to one another than to students taught by different teachers. Hierarchical linear modelling (HLM) is therefore the appropriate technique to use (Arnold 1992).

The subsection that follows explains the data used to conduct the analysis, namely the third study conducted, in 2007, by the Southern and Eastern African Consortium for Monitoring Educational Quality (SACMEQ).

Data: SACMEQ III

The paper makes use of data collected by the third study conducted by SACMEQ in 2007. SACMEQ was launched in 1995 with the objective of conducting research and providing training that enables policy makers to monitor and improve their education systems (Moloi & Strauss 2005). SACMEQ undertook three major surveys (referred to as SACMEQ I, II and III) in 1995, 1998 and 2007 respectively. Fifteen countries participated in SACMEQ III, namely Botswana, Kenya, Lesotho, Malawi, Mauritius, Mozambique, Namibia, Seychelles, South Africa, Swaziland, Tanzania (Mainland and Zanzibar), Uganda, Zambia and Zimbabwe (Spaull 2011).

SACMEQ III involved administering three tests to Grade 6 students: a reading test, a mathematics test and a health test (aimed largely at measuring the level of knowledge about HIV/AIDS). In South Africa, 9 038 Grade 6 students in 392 schools were tested, along with 498 mathematics teachers, 498 reading teachers, and 492 health teachers (totalling 1 488). All the teachers completed a health test, and reading and mathematics teachers completed a test in the subject that they taught (Spaull 2011:5).

The data obtained from SACMEQ III comprise the most extensive nationally representative sample available for the South African education system.⁵ Importantly, the testing was only conducted in English and Afrikaans. It is therefore highly likely (if not certain) that a significant proportion of the students writing the tests were disadvantaged in terms of understanding the mathematics questions, given that neither English nor Afrikaans was their first language. The extent to which English is spoken outside of school is controlled for at the student level, but the data set did not contain the corresponding variable for Afrikaans. It is worth noting, however, that the aforementioned language disadvantage applies to the majority of students tested in South Africa (Moloi & Strauss 2005:67).

Importantly, in any analysis of performance in education making use of cross-sectional data that does not contain a pre-test score, unobservable characteristics of students (such as motivation or intelligence) which influence their performance on mathematics tests are therefore not controlled for. It is also important to bear in mind that the impact of teachers on students' education is cumulative. The results observed in Grade 6 therefore reflect the impact of teachers throughout students' educational 'career' and cannot be attributed only to the teachers by whom students are taught in that year. Having said that, we do not have a pre-test score and we are therefore not able to control for students' ability or level of performance before their exposure to their current teacher.

A full explanation of the variables included in the model, as well as the descriptive statistics of these variables, can be found in a University of Stellenbosch Department of Economics working paper on this research (Armstrong 2014b).

 

Hierarchical linear modelling: A method for multi-level data

Social science contains countless examples of hierarchical data structures. This means that although variables capture characteristics of individuals, these individuals also exist within larger groups, and a set of variables describe the groups (Raudenbush & Bryk 2002:xix). A classic example of hierarchical data structure is education data. Students are grouped according to the schools they attend, so individual or learner-level variables describe individual students, and school-level variables describe schools. Although school-level variables may be independent of the students (for example, the type of buildings or the geographical location of the school), school-level variables may also represent aggregated learner-level data (for example, the racial or gender composition of the school, or the average socio-economic status of the students attending the school). The school probably consists of smaller groups such as classrooms, each of which have their own characteristics, captured by classroom-level variables. Schools may also form the smaller groups contained within school districts.

We are interested in understanding how teacher characteristics are related to student performance. Students are grouped within classrooms, which in turn are grouped within schools. In education the context in which students are educated is immensely influential in determining their performance. In other words, for individual students, characteristics of the school classroom significantly influence the level of learning that occurs, and therefore their performance on standardised tests (Luke 2004). Relationships and occurrences at this level affect what happens at the individual level. In South Africa the context in which learning takes place differs dramatically across the school system, and so the variables describing characteristics at the classroom and school level reflect large differences between schools within the country. We are interested in how these differences at the higher level impact on lower-level performance (Luke 2004). For example, how do differences in school management characteristics translate into differences in the performance of students on standardised mathematics and language tests? How is teacher training related to student performance in mathematics and language tests?

The research question is whether or not teacher characteristics are significantly correlated with student performance. The variables at the teacher level in the model are grouped according to four categories: demographic characteristics, education and experience characteristics, effort characteristics, and school/classroom characteristics.

Demographic characteristics: Teacher gender may beimportant in explaining student performance if male and female teachers differ significantly from each other in terms of their ability to teach. Teacher female is included to control for whether a teacher is female and whether this bears a statistically significantly relation to mean student mathematics performance. Teacher age is controlled for using dummy variables for ten-year bands, and the impact of teachers' age is measured relative to the youngest group of teachers (19 to 29 years of age). Significant coefficients on these variables may indicate either inherent differences in the ability of teachers to improve student performance associated with teacher age, or potentially differences in the training received by teachers trained at different times in South Africa.

Education and experience: Experience⁶is included to capture the number of years that teachers have been teaching. Literature on teacher experience suggests that beyond the initial years of teacher experience, the impact of having taught for longer periods of time becomes smaller. Teaching experience is rarely found to be significantly associated with student performance (Koedel 2007). It is included in this analysis as dummy variables capturing experience in five-year bands. Dummy variables capturing teachers' level of educational attainment are included to investigate the relationship between education and student performance. Given the restructuring of teacher training with the closing of teacher training colleges in 2000, it is important to investigate the extent to which the attainment of a university degree impacts on student performance.

Days of training captures the time teachers spent participating in in-service training courses. In-service training programmes are perceived by researchers to be largely ineffective in affecting student performance (NEEDU 2013).

Teacher training is captured by dummy variables reflecting whether teachers received less than one year, one year, two years, or three years of teacher training.

Teacher maths score⁷is included to control for teachers' own mathematical content knowledge. The model is run including as well as excluding teacher maths score. This is done in order to ensure that the association between teacher training variables and student performance is separated from that of student performance and teachers' own performance in mathematics. Finally, dummy variables controlling for whether teachers are trained to teach (that is, pedagogical training) and whether they are trained specifically to teach maths are included.

Effort characteristics: Parents sign homework is included as a dummy variable to capture the extent to which teachers ensure that students complete their assigned work. The variable is intended to proxy for teachers' interest in students' progress. Dummy variables controlling for the frequency of testing are included to measure teacher 'engagement' with students' progress. Marking of tests is time-consuming and often tedious work for teachers. It is assumed that higher frequencies of testing indicate higher levels of effort. Important to note is that both variables are self-reported by teachers. It is likely therefore that the extent to which these activities occur is over-stated.

School and classroom characteristics: A number of variables included in the teacher-level model are in fact school-level characteristics, but in the case of the SACMEQ data, in a significant number of schools only one classroom was sampled. The classroom is therefore completely identified by the school and so for these variables (with the exception of Classroom socio-economic status, or SES) no variation occurs at the level of the school. The school-level variables, namely Rural, Private school and Average class size, are therefore included to control for differences that are observed between students attending schools with these characteristics and those attending schools where these characteristics are absent.

 

Results

The multi-level nature of education data means that there are characteristics of both students and their teachers associated with student performance.

Table 1 below presents the results from the multi-level model.⁸ Model 1 contains the results for the full teacher model including teacher maths score, while model 2 excludes teacher maths score.

 

 

The results obtained are discussed for the model excluding teacher mathematics score, as this model is run for a greater number of observations. The results obtained for both specifications are largely similar, however. Coefficients that differ markedly from each other will be discussed where relevant.

Teacher demographic characteristics: Whether a teacher is female does not have a statistically significant relation to student performance. An interesting result obtained is the association between teacher age and mean student performance. The coefficients on age indicate that relative to the reference group - teacher age 19 to 29 years old; the youngest group of teachers in the sample - the mean mathematics score of students taught by teachers from all other age groups is lower. Furthermore, with the exception of the coefficients on SES and less than one year of teacher training, the coefficients on teacher age groups are the largest among the teacher-level characteristics. Indeed, the mean mathematics score of students taught by teachers who are 30 to 39 years old, 40 to 49 years old, 50 to 59 years old, and older than 60 are respectively 0.378, 0.474, 0.618 and 0.360 standard deviations below that of students taught by teachers belonging to the youngest age group.⁹ The size of the coefficient for the group of teachers aged 50 to 59 years old is slightly higher than that of the other age groups, but other than this coefficients for different age groups seem consistent.¹⁰ This may say something about teacher training, given the movement away from teacher training colleges in 2000. This is discussed in greater depth later.

Teacher education and experience: Some interesting results are observed for variables capturing teacher qualifications. The mean performance of students being taught by teachers who have obtained a university degree is 0.111 standard deviations higher than that of students taught by a teacher who has not obtained a university degree. Important to acknowledge at this stage is that the positive association between teachers having a university degree and student performance is likely driven to some extent by the fact that better educated teachers are able to secure employment in well-performing schools. This selection effect means it is likely that variables controlling for SES - a key predictor of school performance - do not capture all aspects of schools' socio-economic contexts.

In terms of teaching experience, coefficients for two of the dummy variables are statistically significant - Experience 6 to 10 years and Experience 31 to 35 years. The coefficients on these variables indicate that relative to students being taught by teachers with five or less years of teaching experience, students being taught by a teacher with six to ten years of teaching experience perform on average 0.181 standard deviations better, and students being taught by teachers with between thirty-one and thirty-five years of teaching experience perform 0.323 standard deviations above other students. Interestingly, in model 1 (which controls for teachers' performance on their mathematics tests), teachers' mathematics test performance results are statistically significantly positively related to mean student mathematics performance. As teachers' maths scores are z-scored, the coefficient of 0.105 indicates that an improvement of 1 standard deviation in teacher maths performance results in an improvement of 0.105 standard deviations in mean mathematics performance amongst students.

Teacher effort: None of the teacher effort variables included in the model are significantly associated with mean mathematics performance. This may be due to the fact that these variables are self-reported by teachers. The frequency of testing as well as whether parents are required to sign homework may well be over-reported.

School and classroom characteristics: The large and statistically significant coefficient observed for classroom SES is to be expected. The coefficient of 0.627 indicates that a 1 standard deviation increase in classroom SES is associated with a 0.627 standard deviation increase in mean mathematics performance. The statistically significant negative coefficient for Average class size (of the school) isintuitive, suggesting that larger classes are associated with weaker performance. The size of the coefficient is very small, however. Increasing class size by one student is associated with a decrease in mean student performance of 0.006 of a standard deviation. Despite the fact that it is statistically significant, it is not economically significant. It is too small to indicate any real relationship between the variables.

 

Discussion and conclusion

The results presented above are important in the context of South Africa's education system. Teachers are an important resource in education and it is necessary to understand how best to utilise them.

The results for the hierarchical linear model (HLM) reveal that younger teachers are better able to increase the mean performance of students. In order to test whether this is a trend observed amongst teachers across different countries, or whether this is a trend particular to South Africa, the identical HLM model was run for three other countries in the SACMEQ III data set - two of South Africa's neighbouring countries, Botswana and Zimbabwe, and a high-performing East African country, Kenya. The coefficients on the teacher age variables are presented in Table 2.

 

 

The pattern for lower mean mathematics performance amongst students being taught by older teachers appears in Kenya. The magnitude of these coefficients is comparable with those observed in South Africa. In fact, in Kenya the coefficient for teachers aged 50 to 59 years old is almost double that of South Africa's. However, this is the only coefficient that is statistically significant, whereas in the case of South Africa, the coefficients for all teacher age groups are statistically significant relative to the reference group of teachers aged 19 to 29 years old.¹¹

This discussion investigates why this may be the case. As described earlier, the studies conducted by SACMEQ in 2000 and 2007 included teacher tests. Due to union objections to teachers being tested, South African teachers participated only in the teacher test conducted in 2007, and were allowed to opt out of being tested.

Interestingly, teacher performance on the mathematics test appears to differ according to age in the same way that teachers' ability to elicit test performance from their students does. Figure 1 presents the distribution of teacher performance on mathematics tests for teachers of different ages.

 

 

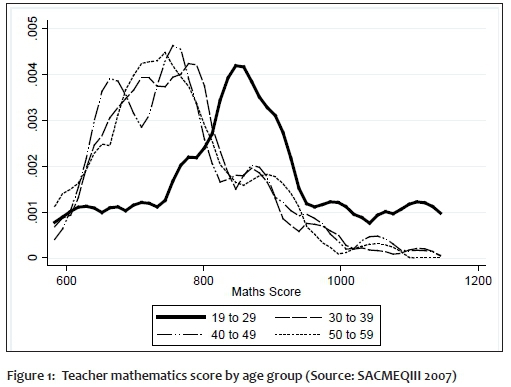
The kernel density curves demonstrate that younger teachers perform at a significantly higher level in the mathematics test than teachers in older age groups. Similar results are obtained with regards to teacher performance on language tests. Figure 2 presents the distribution of language performance results amongst teachers in different age groups. As seen in the mathematics test, teachers in the age group 19 to 29 perform better than their counterparts in older age groups in the language test.

 

 

Similar analysis was conducted for Botswana, Kenya and Zimbabwe. The differences in the performance of teachers of different ages are not as marked as they are in South Africa. It therefore seems that this is a phenomenon particular to South Africa.

A basic ordinary least squares (OLS) regression was run to investigate whether the difference in performance between teachers is statistically significant. The results are presented in Table 3.

 

 

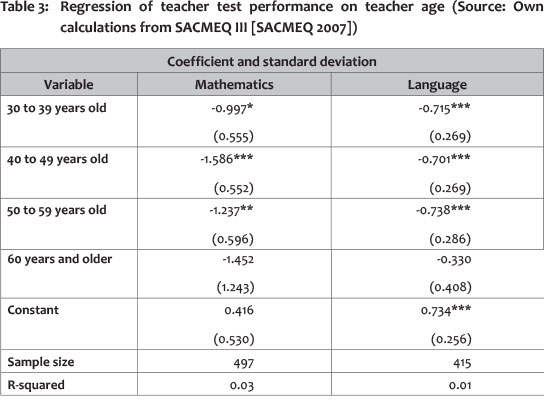
It therefore appears that older teachers are outperformed by younger teachers in both mathematics and language. The performance of students taught by younger mathematics teachers is also stronger than that of students taught by older teachers. It is important to investigate the possible reasons for this pattern. Similar estimates were found by using data from the Progress in International Reading Literacy Study (PIRLS) 2006 on reading and literacy amongst students of a similar age. Shepherd (2013:31) used weighted least squares regression to investigate the determinants of student reading and literacy, and found a large, positive and statistically significant coefficient for teachers who are 30 years old or younger. Interestingly, this is only observed amongst teachers of students who wrote the PIRLS test in an African language and who were therefore in the historically black part of the schooling system. Amongst students writing the test in English or Afrikaans the coefficient was somewhat smaller, negative and statistically insignificant (ibid). Interestingly, when the model is run for Quintiles 1 to 4 for South Africa in the SACMEQ III data set, the coefficients diminish in size, and although still statistically significant, they are significant at a lower level.

More than one explanation may exist for the differential ability of younger teachers to elicit stronger performance from their students. Younger teachers may relate better to their students because they are closer in age to them than their older counterparts. Another possibility is that changes to teacher training may have left teachers trained under a new system better equipped to teach. We are able to test these hypotheses using data from the second SACMEQ survey, conducted in 2000. As previously mentioned, no teacher tests were conducted for South African teachers in 2000. Other than that, the questionnaires of the 2002 and 2007 were almost identical, making it possible to compare the two surveys, and therefore the same model can be run for SACMEQ II data. If younger teachers are inherently better at teaching (and not as a result of different teacher training), then we expect to see similar coefficients to those observed using the SACMEQ III data for teacher age variables in similar models from different time periods.

The full HLM model was run using SACMEQ II data. Table 4 presents the coefficients on the teacher age variables obtained when data from the 2000 study were used.

 

 

The coefficients in Table 4 are quite different from those obtained from the 2007 data of the SACMEQ III survey. In fact, only the teachers aged 50 to 59 differ significantly from the youngest group of teachers, and in this case they seem to elicit better performance from their students. According to this data then, the statistically significant negative coefficients observed for teachers older than 29 years of age (relative to the youngest group) are not explained by an inherent ability of younger teachers to positively influence mean student performance. It is possible then that differences in teacher training may explain the differences in the student performance according to the age of their teacher.

Teacher training is one of the few characteristics that may explain the positive, relatively stronger performance of students taught by younger teachers. Changes in teacher training in the South African education system occurred in the late 1990s and early 2000s - the period during which the youngest cohort of teachers were trained. The following section discusses these changes.

Differences in teacher training

An obvious avenue to pursue in understanding the differences observed in the performance of teachers of different ages is to investigate the extent to which the training received by teachers differed across years. A potential source of differences in teacher training is the shift from teacher training colleges as the institutions responsible for training teachers to the incorporation of teacher training within universities. Chisholm (2009) explains that teacher training colleges expanded predominantly in the 1960s. The apartheid state located the majority of teacher training colleges in the 'homeland' areas, with the objective of staffing the colleges with the graduates. Enrolment in the teacher colleges was high due to the fact that opportunities in the formal economy were restricted for non-white South Africans, and entering a teacher training college was one of very few ways that people living in the homelands could enter higher education.

Teacher training colleges were expensive to run and were heavily subsidised by the state (Chisholm 2009). Due to a movement towards decreasing unit costs and enhancing productivity within the higher education sector, teacher colleges were offered the option of remaining open as independent institutions (if they were able to enrol 2 000 full-time students in 1999), or becoming integrated as part of universities or universities of technology. Teacher training colleges were formally incorporated into universities and universities of technology from January 2001. Irving (2012) explains that changes to teacher training in South Africa have been abrupt and dramatic. The closure of teacher colleges and the relocation of teacher training to universities was a considerable change and required adjustment.

Teachers trained after the incorporation of teacher training colleges into universities or universities of technology would therefore have been 25 years old in 2007 when SACMEQ III was conducted,¹² and allowing for some violations of the assumptions (explained in footnote 12), the age group of 19 to 29 years old (the reference group in the analysis conducted above) captures teachers who are likely to have completed their teacher training at universities or universities of technology.¹³

If we assume that teacher training does in fact influence teacher performance, then it appears that teachers trained at universities and universities of technology are better able to teach than are teachers trained at teacher training colleges. If this is the correct interpretation of the results obtained in Table 1, it has important implications for the teacher training landscape in South Africa. South African teacher unions have since 2002 called for the reopening of teacher training colleges (Chisholm 2009). The South African Democratic Teachers Union (SADTU) - the biggest union, representing two-thirds of teachers (Wills 2014:4) - is of the opinion that teacher shortages (particularly in the areas of mother tongue and Foundation Phase education) result in excessively large class sizes that interfere significantly with the ability of union members to provide quality education. Indeed, at SADTU's 2006 National Conference, there was a recommendation for setting a maximum acceptable class size of thirty students - a number that requires substantial increases in teacher supply in order to be achieved (Chisholm 2009). This resulted in SADTU's 2007/08 call for the reopening of teacher training colleges.

A second argument in favour of reopening teacher training colleges has to do with the quality of teacher training provided by universities and universities of technology.

Patterson and Arends (2008) are of the opinion that primary and secondary school teaching are not given the attention they require in the higher education system. The authors also consider university fees for studying to teach primary education high enough to exclude candidates from the teaching profession. Finally, university education is considered by teachers already teaching in schools as excessively theoretical and abstract relative to what is required to be taught at primary school (ibid). Teachers and lecturers trained in teacher training colleges feel that universities and universities of technology lack the 'hands-on' practical guidance that colleges provided. They are of the opinion that principals and experienced teachers do not have the same opportunities for involvement in training future teachers as had been available in teacher training colleges (Chisholm 2009).

For various reasons, therefore, there is a strong belief that reopening teacher training colleges may improve the quality (and quantity) of teachers in general, and primary teachers in particular. The evidence above suggests that this may not be the case.

Other sources of differentials by teacher age

Other explanations for differences in the performance of older and younger teachers have less to do with the structures within which teacher training takes place, and more with the nature of teaching itself. Anecdotal evidence from teachers suggests that younger teachers are better able to engage and build rapport with their students because they are closer in age to students and because successful teaching requires high levels of energy. Younger teachers are also likely to be more familiar with the current curriculum and may therefore be more familiar with the content they are required to teach to students (Education Forum 2006). An unflattering view of the performance gap between older and younger teachers is the supposed tendency or willingness of younger teachers to 'cheat' or 'teach to the test' in order to appear to be performing well, compared to older teachers who would probably be more intent on ensuring that students receive a broader, more complete education, rather than to focus on what is prescribed by the curriculum (Education Forum 2006). Literature on differences in performance of teachers by age is scarce in the area of primary education. Very little empirical evidence exists of such disparities, which renders the results obtained in this paper quite important.

Another possible explanation for the stronger educational performance observed in 2007 amongst students taught by younger teachers is that South Africa experienced high levels of economic growth between 2004 and 2007 (IDC 2013). Previous research (Armstrong 2014a) shows (admittedly anecdotal) evidence that relative to candidates enrolling for degrees other than in education, those enrolling for Bachelor of Education degrees perform relatively poorly in Grade 12 mathematics and language. In periods of high economic growth, where employment opportunities are likely to be created, it is plausible that more able teachers from older cohorts may have left the teaching profession to pursue relatively more attractive professions (from a wage perspective) in the non-teaching part of the labour market (Armstrong 2014a). It is possible then that the stronger performance of younger teachers may simply reflect a comparison with a relatively weaker cohort of older teachers.

This research finds that younger teachers are better able to elicit performance from students in mathematics at a Grade 6 level. Similar results are found by Shepherd (2013) using different data, also at a Grade 6 level, but for performance in reading literacy. More must be done to fully understand this finding and to further investigate the reasons for differences in the ability of teachers of different ages to affect student performance. Differences in the training received by teachers at universities and universities of technology and that received by teachers trained at teacher training colleges need to be understood. How exactly do these differences translate into student learning? Are there unobservable characteristics according to which teachers differ and which are correlated with age? If so, what should be done to ensure that students have access to teachers with these characteristics?

Policy implications

The finding that students taught by younger teachers on average outperform those taught by older teachers is an important one. Importantly, as mentioned previously, this needs to be explored in greater detail. A possible explanation for this finding is that teachers trained at universities and universities of technology seem to outperform their peers trained at teacher training colleges, both in terms of student performance and performance on teacher tests. If this result is driven by the institution where teachers were trained and the type of training they received, then it is important to ensure that teacher training remains the responsibility of universities and universities of technology, and to resist reopening teacher colleges - a call supported by the widely held belief that these were more appropriate places of training.

 

References

Anderson, J.B. 2000. Factors affecting learning of Mexican primary school children. Estudios Economicos, 15(1):117-152.         [ Links ]

Angrist, J.D. & Lavy, V. 2001. Does teacher training affect pupil learning? Evidence from matched comparisons in Jerusalem public schools. Journal of Labor Economics, 19(2):343-369.         [ Links ]

Armstrong, P. 2014a. Teacher wages in South Africa: How attractive is the teaching profession? Stellenbosch Economic Working Papers WP07/14. Stellenbosch: Department of Economics, Stellenbosch.         [ Links ]

Armstrong, P. 2014b. The impact of teacher characteristics on student performance: An analysis using hierarchical linear modelling. Stellenbosch Economic Working Papers WP25/14. Stellenbosch: Department of Economics, University of Stellenbosch.         [ Links ]

Arnold, C.L. 1992. Methods, plainly speaking: An introduction to hierarchical linear models. Measurement and Evaluation in Counselling and Development, 25:58-90.         [ Links ]

Chingos, M.M. & Peterson, P.E. 2011. It's easier to pick a good teacher than to train one: Familiar and new results on the correlates of teacher effectiveness. Economics of Education Review, 30:449-465.         [ Links ]

Chisholm, L. 2009. An overview of research, policy and practice in teacher supply and demand 1994-2008. Cape Town: HSRC Press.         [ Links ]

Clotfelter, C.T., Ladd, H.F. & Vigdor, J.L. 2007. Teacher credential and student achievement: Longitudinal analysis with student fixed effects. Economics of Education Review, 26:673-682.         [ Links ]

Crouch, L. & Mabogoane, T. 2001. Not magic bullets, just tracer bullets: The role of learning resources, social advantage and education management in improving the performance of South African schools. Social Dynamics: A journal of African studies, 27(1):60-78.         [ Links ]

Education Forum. 2006. Teacher age and performance. Retrieved from http://education-forum.ipbhost.com/index.php?showtopic=8063 (accessed 30 May 2014).

Ehrenberg, R.G. & Brewer, D.J. 1995. Did teachers' verbal ability and race matter in the 1960s? Coleman revisited. Economics of Education Review, 14:1-21.         [ Links ]

Ferguson, R.F. 1998. Can schools narrow the Black-White test score gap? In: C. Jencks & M. Phillips (Eds.). The Black-White test score gap. Washington, DC: Brookings Institution. 318-374.         [ Links ]

Fleisch, B. 2004. Does higher education expenditure generate higher learner achievement? A study of historically disadvantaged schools in Gauteng. South African Journal of Education, 24(4):264-269.         [ Links ]

Hanushek, E. 2009. Teacher de-selection. In: D. Goldhaber & J. Hannaway (Eds.). Creating a new teaching profession. Washington, DC: The Urban Institute Press.         [ Links ]

Hanushek, E. 2011. Valuing teachers. Education Next, 11(3):40-45.         [ Links ]

Hanushek, E.A. 1992. The trade-off between child quantity and quality. Journal of Political Economy, 100:85-117.         [ Links ]

Hill, H.C., Loewenberg Ball, D. & Schilling, S.G. 2008. Unpacking pedagogical content knowledge: Conceptualising and measuring teachers' topic-specific knowledge of students. Journal for Research in Mathematics Education, 39(4):372-400.         [ Links ]

IDC (Industrial Development Corporation). 2013. South African Economy: An overview of key trends since 1994. Retrieved from http://www.idc.co.za/reports/IDC%20R&I%20publication%20-%20Overview%20of%20key%20trends%20in%20SA%20economy%20since%201994.pdf (accessed 29 September 2015).

Irving, M. 2012. Teacher labour markets in South Africa and Botswana: A comparative analysis. Prospects, 42:389-402.         [ Links ]

Koedel, C. 2007. Teacher quality and educational production in secondary school. Working paper for the National Centre on Performance Incentives. Nashville, Tennessee.

Luke, D.A. 2004. Multilevel modelling. Thousand Oaks, CA: Sage Publications.         [ Links ]

Moloi, M. & Strauss, J. 2005. The SACMEQ II project in South Africa: A study of the conditions of schooling and the quality of education - South Africa Working Report. Retrieved from http://www.sacmeq.org/education-south-africa.htm (accessed 5 May 2014).

Mullens, J.E., Murnane, R.J. & Willett, J.B. 1996. The contribution of training and subject matter knowledge to teaching effectiveness: A multilevel analysis of longitudinal evidence from Belize. Comparative Education Review, 40(2):139-157.         [ Links ]

Murnane, R.J. & Phillips, B.R. 1981. What do effective teachers of inner-city children have in common? Social Science Research, 10(1):83-100.         [ Links ]

NBPTS (National Board for Professional Teaching Standards). 2012. NBPTS early childhood generalist standards. 3rd Edition. Arlington: NBPTS.         [ Links ]

NCTM (National Council of Teachers of Mathematics). 2000. Principles and standards for school mathematics. Reston, VA: NCTM.         [ Links ]

NEEDU (National Education Evaluation and Development Unit). 2013. National Report 2012: The state of literacy teaching and learning in the Foundation Phase. Pretoria: NEEDU.         [ Links ]

Patterson, A. & Arends, F. 2008. Teacher graduate production in South Africa. Cape Town: HSRC Press.         [ Links ]

Raudenbush, S.W. & Bryk, A.S. 2002. Hierarchical linear models: Applications and data analysis methods. London: Sage Publications.         [ Links ]

Rowan, B., Chiang, F.-S. & Miller, R.J. 1997. Using research on employees' performance to study the effects of teachers on students' achievement. Sociology of Education, 70:256-284.         [ Links ]

Shepherd, D. 2013. A question of efficiency: Decomposing South African reading test scores using PIRLS 2006. Stellenbosch Economic Working Papers WP20/13. Stellenbosch: Department of Economics, Stellenbosch University.         [ Links ]

Slater, H., Davies, N. & Burgess, S. 2009. Do teachers matter? Measuring the variation in teacher effectiveness in England. Centre for Market and Public Organisation (CMPO) Working Paper Series No 09/212. Bristol: CMPO.         [ Links ]

SACMEQ (Southern and Eastern African Consortium for the Measurement of Educational Quality). 2000. SACMEQ II Data. Retrieved from http://www.sacmeq.org/sacmeq-data (accessed 27 January 2011).

SACMEQ. 2007. SACMEQ III Data. Retrieved from http://www.sacmeq.org/sacmeq-data (accessed 12 May 2013).

Spaull, N. 2011. Primary school performance in Botswana, Mozambique, Namibia and South Africa: A comparative analysis of SACMEQ III. SACMEQ III Working Paper No 8. Retrieved from http://www.sacmeq.org/reports.htm#working_papers (accessed 7 April 2013).

Summers, A.A. & Wolfe, B.L. 1977. Do schools make a difference? American Economic Review, 67:639-652.         [ Links ]

Wayne, J. & Youngs, P. 2003. Teacher characteristics and student gains: A review. Review of Educational Research, 73(1):89-122.         [ Links ]

Wills, G. 2014. The effects of teacher strike activity on student learning in South African primary schools. Stellenbosch Economic Working Papers WP01/14. Stellenbosch: Department of Economics, Stellenbosch University.         [ Links ]

 

 

* Email address: paula.louise.armstrong84@gmail.com
1 Anderson notes that this variable is self-reported (Anderson 2000:145) and may well be over-reported. However, if this is the case, it is likely that the coefficient on these variables is a lower bound of the effect of time on task of student performance.
2 Important to note is that Ferguson's study aggregated data to the district level. Hanushek, Rivkin and Taylor (1996:616) explain that aggregating data to a 'higher' level (that is, school, district or state level) increases the likelihood of obtaining positive results.
3 Keystage 4 examinations are compulsory examinations that determine entrance to post-secondary education. They are written at age 16. Keystage 3 examinations are written at the beginning of the Keystage 4 programme, during the year that students turn 14 (Slater, Davies & Burgess 2009:4). Keystage 3 examinations are often used as a 'pre-test' measure in education research, or an as indication of prior attainment.
4 Teacher experience is captured by categorical variables denoting 1 to 2 years of experience, 3 to 5 years of experience, 6 to 12 years of experience, 13 to 20 years of experience, 21 to 27 years of experience, and more than 27 years of experience. They therefore control for non-linear returns to teaching experience (Clotfelter et al 2007). The returns observed are higher for mathematics than they are for English - a finding largely in line with what is found in the literature about teaching experience and student performance.
5 Mullens, Murnane and Willett (1996:140) explain the need for longitudinal data in assessing the impact of teachers on student learning. In the majority of studies investigating this topic in the developing world, longitudinal data are not available and so researchers have no choice but to use cross-sectional data. Cross-sectional data can only tell us about the level of student achievement and not about the progress that takes place (that is, the actual learning). However, data on changes in achievement are necessary to truly evaluate the effectiveness of teachers.
6 Teaching experience and teacher age may have conflating effects on student performance. However, the model was run without controlling for teaching experience, and this made very little difference to the age coefficients. Experience and age were asked separately in the teacher questionnaire. Both have been retained, as they control for different characteristics, and both are necessary for the sake of this analysis.
7 Teacher maths score is missing for ninety-eight teachers in the SACMEQ III data set. Where possible, missing data were replaced with the mean mathematics score of teachers within the same school. Teachers from schools where no teachers wrote the mathematics tests were excluded from the model in which teacher maths score was included as an explanatory variable. This meant that twenty-nine teachers were dropped from this sample.
8 A working paper (Armstrong 2014b) contains the results from the student-level model as well as the descriptive statistics of the variables included in the model.
9 A possible explanation for the difference in the ability of younger teachers to elicit superior performance from their students is the fact that they themselves have a better grasp of the mathematical content that they are required to teach. An important part of understanding the differences illustrated by the coefficients above is investigating whether younger teachers are better at maths or whether they are better teachers. This is tested by interacting teacher test score with the dummy variables controlling for age. However, the coefficients are small and statistically insignificant. It therefore does not appear that this effect works through superior mathematical content knowledge amongst younger teachers.
10 The model was re-run with different cohorts of teachers as the reference group. The results indicate that although the differences in the coefficients are smaller in size amongst groups older than the youngest group, the ability to elicit stronger performance from students does differ by teacher age, with younger teachers out-performing their older colleagues. This is confirmed by an F-test.
11 The coefficient for South African teachers aged 60 and older is not statistically significant. However, this group is comprised of just four teachers.
12 With the data available there is no way of knowing at what age teachers were trained. The age of 25 is based on the assumption that teachers started higher education directly after finishing secondary school, and that teachers left secondary school at the grade-appropriate age of 18, therefore turning 19 during their first year of tertiary education. In many instances these assumptions are most definitely violated. It is likely, for example, that individuals took longer than the prescribed amount of time to complete tertiary education, and that individuals started teacher training after having completed other courses of study.
13 Seventy-three per cent (73%) of the teachers in this age group are younger than 25 years old.