ARTICLES

 

Learning support pedagogy for children who struggle to develop the concepts underlying the operations of addition and subtraction of numbers: The 'Calculia' programme

 

 

Annemarie Fritz-Stratmann^{I, *}; Antje Ehlert^II; Gabriele Klüsener^III

^IUniversity of Duisburg-Essen, University of Johannesburg
^IIUniversity of Potsdam, University of Johannesburg
^IIIUniversity of Duisburg-Essen

 

 

---

ABSTRACT

This paper argues for teaching pre-service teachers about remediation strategies for learners who encounter problems in mathematics in the early grades. The premise is that all teachers should be equipped with theory-based practical knowledge to support learning. A few teaching sessions to develop the concepts that underlie the mathematical operations of addition and subtraction are introduced in this paper. An empirically validated, comprehensive model of cumulative arithmetic competence development from the ages of four to eight years forms the basis for the construction of the suggested teaching unit. The model distinguishes five competence levels of arithmetical conceptual development, and proposes that concepts build on one another hierarchically. A 'part plus part is equivalent to whole' model was constructed based on this hierarchical structure and the understanding that the concept of addition is a dynamic process. The teaching examples include exercises for all children, not only ones who struggle. Possibilities for adapting the exercises to the individual development level of slower or faster learners are also included. All exercises are accompanied by a reflection on the procedure and strategies applied in order to support meaningful and sustainable learning and to give student teachers the opportunity to use knowledge of mathematical cognition theory during their pre-service years.

Keywords: mathematics remediation, elementary school, foundation phase, conceptual development, remedial programme, Germany, mathematical cognition, pre-service teacher education

---

 

 

Introduction: Early development of mathematical concepts

In teacher education programmes students learn not only mathematics content and how to teach mathematics to certain age groups; they also learn how children develop concepts. We argue that it is important for pre-service teachers to know the psychology of learning mathematics in order for them to be able to help children who may encounter problems. Therefore, the question we ask in this article is: How can a remedial programme based on a conceptual model of mathematical knowledge development in young children be utilised in a structured remedial programme for individuals and groups in the early grades?

We begin the article by sketching some background regarding the conceptual development of mathematics, followed by a description of the model of development that we utilise. We then discuss a few elements of a programme that is designed to assist young learners with the mathematical operations of addition and subtraction by focusing on the concept of parts making up a whole number.

Studies from the past three decades have provided substantial evidence that children have some innate mathematical knowledge long before acquiring the ability to speak. Many cognitive developmental psychologists and other authors refer to this ability (see, for example, Carey 2009; Dehaene 1997; 2011; Feigenson, Dehaene & Spelke 2004; Fritz, Ehlert & Balzer 2013; Henning & Ragpot 2014). These studies suggest that the brain is equipped with core cognitive systems that are crucial for subsequent learning processes. Two core systems that allow first representations of numerosities are: (1) an analogue magnitude system of representation (AMS); and (2) an object-file system of representation, known as the object tracking system (OTS) (Feigenson, Carey & Spelke 2002; Feigenson et al 2004). The analogue magnitude system of representation allows imprecise and approximate comparisons where quantities are not represented as single, discrete units. The second system serves to precisely track and distinguish a small set of distinct individual elements (Feigenson et al 2002; Piazza 2010; Xu 2003; Xu & Spelke 2000). The upper set size limit for this is three elements.

Based on these two core systems, children increasingly develop mathematical competences, which are still numerically imprecise. Resnick (1992:403) speaks of proto-quantitative schemes which evolve intuitively, but in which quantities cannot yet be described by means of numerical quantifications:

[...] comparisons of amounts are made and inferences can be drawn about the effects of various changes [...] on amounts, but no numerical quantification is involved.

Resnick (1992) distinguishes between three types of proto-quantitative schemes, namely a compare-scheme, an increase-decrease scheme, and a part-part-whole scheme. According to her, children aged two years can compare two quantities and label the result of the comparison as being smaller or larger (compare-scheme). At the age of three to four years, the increase-decrease scheme becomes available, which enables children to evaluate changes in quantities according to their direction (more/ larger or less/smaller). An understanding of the part-part-whole concept, whereby quantities can be divided into parts which together are equal to the original quantity, develops at the age of about four.

If, however, the aim is to represent quantities precisely, knowledge of the number word line and the relevant representations, which children take many years to learn, is necessary (Baroody 1992; Fuson 1992; Gelman & Gallistel 1978; Goswami 2008). Learning the number words and the counting principles requires the construction of a new representational scheme, which is not innate but is a prerequisite for acquiring explicit knowledge about numerical concepts.

This early knowledge, acquired at preschool age, is an essential condition for the successful development of mathematical abilities that are further developed at school. Results from longitudinal studies attribute an influential and predictive importance to previous mathematical knowledge for learning mathematics in primary school (Aunola, Leskinen, Lerkkanen & Nurmi 2004). A low level of number competences six months prior to the beginning of school enrolment predicted difficulties in learning mathematics at school with high reliability (Krajewski & Schneider 2009), whereas children with good prior mathematical knowledge had a better chance to use the learning opportunities at school for further development.

This demonstrates the value of starting mathematical instruction before children enter primary school. The following model of progressive conceptual stages serves as a validated foundation for the 'Calculia' programme, the English version of a validated German remediation and development programme, 'Kalkulie' (Gerlach, Fritz, Ricken & Schmidt 2007), which is used in kindergarten and primary school classes in Germany. The programme includes pre-numerical skills development exercises as well as component parts of inductive reasoning, such as pattern recognition and categorisation. Calculia exercises emphasise multilayered ideas and various strategies of addition and subtraction. Parts of the addition instruction are introduced in this paper. The programme combines conceptual and strategic instruction. This means that the part-part-whole concept is stimulated by way of a variety of strategies.

 

Conceptual model for the development of early numerical concepts and arithmetic skills

The main reason for using a conceptual model for investigating children's mathematical performance is that conceptual reasoning is the first step they take to recognise a problem. The strategies they use to solve the problem thus originate from their conceptual knowledge (and the reasoning that it elicits). Children create arithmetic (mathematics) exercises conceptually as individuals and then use strategies to suit the exercises that they have conceptualised. This principle if often ignored in pedagogy. Many teachers are satisfied with the teaching of operations (procedural knowledge), perhaps not realising that these may obscure the conceptual knowledge that has to precede it. If children do not learn to see mathematics conceptually, they may struggle from the early grades onwards, because although they may learn procedures from instruction and even 'master' these, this does not guarantee that they understand what they are doing. If they do not develop concepts, they run the risk of not progressing beyond procedures and may start struggling when these alone no longer suffice. If they do not receive assistance timeously, they may forever struggle with maths in school.

The findings of research about the mathematical performance prognosis of children who experience challenges early in their learning path show the importance of support at an early stage (at preschool and primary school) to counteract negative developmental pathways in a preventive and compensatory way. We describe a model for the development of numerical concepts and arithmetic skills in children between the ages of four and eight years, and then discuss how the Calculia intervention is based on this model.

Our starting point for the composition of such a model (Fritz et al 2013; Fritz & Ricken 2009) is the assumption that key concepts of mathematical understanding (specifically, the understanding of number concepts) develop hierarchically and that children develop more sophisticated cognitive structures in a step-by-step manner.¹ Each step is marked by the configuration of specific concepts that build on each other in a cumulative way. Such an empirically validated model can assist in establishing which numerical concepts a child has already developed, which numerical concepts are currently about to emerge, and which numerical concepts are likely to develop next. In this way, the model can be utilised to ascertain children's learning level and to adapt instruction and learning support to their specific needs.

It is important to emphasise the difference between concepts and strategies related to numbers and operations. While strategies are ways to handle and use mathematical operations more effectively, concepts refer to the fundamental ideas and understandings which constitute the meaning that numbers and operations have for learners. This can be illustrated by the subtraction task 7 - 3 = 4, which can appear in different contexts and - as clarified below - in different conceptual stages. A decrease in a specified amount - for example 'Seven children are in a room, three leave. How many children stay in the room?' - may be found on an earlier conceptual level as a part-part-whole context such as 'There are seven children in a room, three of them are girls. How many boys are there in the room?' At an even more advanced level, the context may be that there is an unknown difference between two amounts; for example, 'Seven girls and three boys are in a room. How many more girls than boys are there?' Each of these tasks can be solved with any subtraction strategy, be it counting on, counting down, remembering from long-term memory ('fact retrieval'), or any other suitable strategy. But the choice of an appropriate operationalisation of the given problem-solving situation depends on the underlying number concepts that are initialised in a child's mind, which are described here. Thus, where strategies help children to solve an arithmetic task, concepts lead them to create a correct arithmetic task from a given situation.

The developmental model that we have referred to will be presented briefly, including only the first four levels that are relevant to the teaching unit which we subsequently describe.

Level I: Count number

The first major concept in dealing with numbers is to see the meaning of number words as representations of quantities and to understand number words as counting tools. This is not as easy as it seems, starting with the number words. These are arbitrary in every language; they bear no correspondence to the counted objects, nor do these words and signs give any indication of the related quantity. How can children nevertheless gain a gradual understanding of counting and of how to deal with numbers skilfully and effectively (and thus also conceptually)?

In studies with young children (thirty to forty-eight months of age), Wynn (1990; 1992) and Le Corre, Van de Walle, Brannon and Carey (2006) showed that children can first recite the number word sequence like a rhyme, without being able to count or count out even a single object (Fuson 1982). The authors gave the children exercises of counting or counting out small quantities of toys. Although all children were able to confidently recite the number word sequence at least up to six, there were children who were not able to give any number of objects, not even one object, when requested to do so (the 'o-knowers'). They always grabbed some toys at random. Only gradually, step by step, did they learn the meaning of 'one, and then the meaning of 'two', 'three' and 'four' as a way of counting out discrete objects (Le Corre et al 2006; Wynn 1990; 1992). This development takes place within a one-year period up to the age of approximately three and a half years. However, at this level, only concretely perceivable, distinct objects or elements (for instance, sounds) can be counted, and only if the recital of the number word sequence starts at 'one'. The counting process ends with the last number word recited, or when the last item of the collection is reached.

Level II: Mental number line

The number word line is gradually represented as an ordinal mental line, with succeeding numbers continuously increasing. This is a mental 'image', which is represented in education settings by a material line from left to right (for children using Western alphabets and who read from left to right). Four- to five-year-old children compare numbers according to their position on the number word line: '9 is larger than 5, because it appears later in the line.' This construction of an ordinal number line allows a precise identification of proceeding and succeeding numbers on the one hand, and the precise numerical addition and subtraction of quantities by moving forward and backward along the mental number line on the other hand (Case & Okamoto 1996). Understanding the concept of adding and subtracting with the help of the number word line enables children to solve simple mathematical problems as they develop a concept of increase that 'advises' them conceptually to perform the task of moving on the number line: 'You have 3 lollies and you get 2 more.' All quantities are counted out individually, starting with one. The solution does not represent a sum; rather, it remains a point on the number word line.

Level III: Cardinality and decomposability

In the next step of development, children learn that, when counting out a quantity, the last-mentioned number word represents the amount of counted elements within the quantity. If, for example, seven objects have to be counted, each object is assigned a number word and all objects together will be integrated into a total quantity with the number attribute seven ('sevenness'), independent of what (representation) is counted out or from where (irrelevance principle) (Piaget 1965). A new cardinal understanding of numbers develops, where numbers are understood as abstract composite units of all counting steps and elements that occurred up to this number (Steffe, Cobb & Von Glasersfeld 1988). At the same time, a first understanding evolves that once composed together, numbers can be decomposed again. The expanded understanding of numbers as cardinal entities that can be composed and decomposed can now also be applied to operational understanding. Children begin to understand the connection between a partial quantity, another partial quantity, and the total quantity (for example, 2 and 3 together are equivalent to 5).

Level IV: Class inclusion and embeddedness

The knowledge of quantities and their relationships increasingly differentiates as children develop conceptually. They begin to understand that numbers are composite units consisting of all objects in a quantity, and that they can be composed and decomposed in different ways (Huttenlocher, Jordan & Levine 1994).

Consequently, transformations between partial quantities are possible without a change in the total quantity. The quantity '5' can be decomposed into the two partial quantities '1' and '4'. By shifting (or transforming) one element from one partial quantity to the other, the partial quantities '2' and '3' are formed. Quantities can be 'composed' in different ways through decomposition and transformation. Each number is understood as a composition of any combination of smaller numbers, so that each number can be decomposed systematically (for example, '5 = 5 + 0'; '5 = 4 + 1'; '5 = 3 + 2', and so forth). The indicator of this understanding is children's ability to find different decompositions for numbers (Baroody 2006; Hunting 2003; Steffe et al 1988).

The relationship between the three quantities (part-part-whole) is fixed, and if two quantities are known, the third can be deduced. With this understanding, problems that require finding any of the three quantities become solvable. This applies to all types of tasks, regardless of whether an additive or a subtractive task is given: the sum, the exchange, or the start quantity is missing. When they understand the part-part-whole concept, it becomes possible for children to see addition and subtraction problems as conceptually complementary; thus they can convert subtraction tasks into addition tasks ('9 - 5 =?' becomes '5 + ? = 9'). Moreover, effective procedures for solving different problems become possible (for example, strategies of decomposition) (Baroody 2006; Carpenter & Moser 1983).

Diagnosing the developmental level: Assigning strategies to levels

With the help of the MARKO-D test of early mathematical competence, which is based on the developmental model discussed above (Fritz, Balzer, Ehlert et al 2014; Ricken, Fritz & Balzer 2013), the performance of a child can be assigned to a specific level. Furthermore, the arithmetic strategies used by children provide an indication of their underlying conceptual understanding. As we have noted already, the tasks are the outflow of conceptual understanding, which leads to an individual child's procedural knowledge implementation.² Based on the analysis of a child's solving procedures, his or her performance can be located within the conceptual development model.

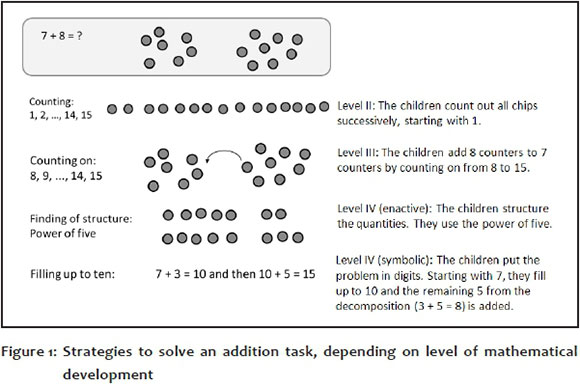
The following task clearly illustrates the practical importance of the different levels:

Grade 1's are asked to solve the problem '7 + 8 = ?' The problem is stated verbally (in written or spoken language). As additional support, they receive two sets of seven and eight counters, respectively. The following strategies can be observed, which we allocated to the various levels of the model:

 

 

Introduction and elaboration of the addition and subtraction concepts: Teaching sessions of the Calculia programme

In this section, we present an example of teaching sessions from the Calculia programme. Each session builds on the previous one, first introducing the conceptual basis of addition and then of subtraction. The tasks given in the respective sessions are not specific to a certain grade level at school, because we want to focus on learners' conceptual levels, which may differ from the expected level in a given grade.

Simple addition tasks of the type 'Naledi has 3 marbles. She gets another 3. How many marbles does she have now?' can generally be solved correctly by most children during their first days at school (Riley, Greeno & Heller 1983). They complete the task by counting out the quantity. The basic idea of addition is that one quantity is added to another quantity, and that the two quantities together make a whole (a sum), which is equivalent to both partial quantities put together. This idea is rarely understood by children, because they have not yet formed a concept of parts that together form a whole. But more importantly, the underlying process is hidden by the counting-all strategy. This applies equally to the concept of subtraction. In this case, a whole (the quantity we call the 'minuend') is given and has to be decomposed into two partial quantities. Both partial quantities are, again, equivalent to the whole (which is decomposed, but does not 'disappear'), as can be seen from the fact that the two parts can be interchanged.

It should be stressed once more that tasks or problems of addition and subtraction can be solved on earlier conceptual levels, which implies that performance per se is not a reliable indicator of the level of conceptual development. Nevertheless, it is crucial for children to achieve a conceptual foundation of the part-part-whole-concept, not as a strategy, but as a basic idea or concept of number which they can utilise in different ways with more or less sophisticated conceptual tools. The operation of addition (and its inversion, subtraction) is always embedded in a part-part-whole scheme; therefore, real understanding cannot be gained without developing this concept.

 

 

The operations of addition and subtraction can be seen as dynamic processes between a part, another part, and a whole. Once this idea is formed, the relationship between the three quantities can be treated flexibly. In this sense, conceptual knowledge of addition and subtraction is essential for:

• the understanding of the two operations as complementary tasks (8 - 5 = 3; 3 + 5 = 8);

• effective completion of complement tasks (5 + ? = 8; ? + 3 = 8; 8 - ? = 3); and

• modelling semantic tasks (word problems), where the sum, exchange or initial quantity (in other words, one of the 'summands') is missing.

Furthermore, a conceptual understanding of addition (and subtraction) is certainly also a prerequisite for learning effective calculating strategies such as flexible decomposition (see for example, Figure 1: 7 + 8 = 7 + 3 + 5), which requires conceptual understanding beyond the use of the strategy itself.

The following teaching sessions contain a systematic structure for introducing the conceptual underpinnings of the operation of addition as a part-part-whole process (and vice versa, the flexible decomposition of a whole quantity into two partial quantities as subtraction operation). Basic exercises to help children, especially low-performing children, to operationalise a conceptual task are presented. These exercises, or 'work' tasks, are based on the conceptual tools expected to be utilised and are designed with a specific succession in mind. The idea is to facilitate an understanding of the reasoning behind the addition operation as a (conceptual) task that flows from conceptual understanding, ranging from Level I up to Level IV. A time frame of at least three months is required for the implementation of these exercises. The exercises build on each other; hence it is recommended that they be kept in the order in which they are presented.

In order to give a summary description of the teaching sessions, we will only give a brief overview of Level I before moving on to exercises dealing with conceptual Level II. Level 1 contains the strategy of one-to-one correspondence, one of the earliest strategies used, particularly by children who are unable to count. One-to-one correspondence is the concept that enables children to precisely compare two quantities with each other and determine whether they are of the same cardinality (whether one is smaller or larger) without having to count out the single elements, and thus without any use of numbers. In the exercises on Level I, children are shown pictures of two kinds of objects, for example bees and flowers, and are asked to connect two objects of different kinds.

Exercise 1: Part + part - producing the whole with counters

Addition exercises are given as part-part-whole conceptual exercises from the outset. To prevent children from building up wrong, ineffective representations, they are taught right from the start that the operation of addition is a combination of three quantities: a partial quantity and another partial quantity, which are jointly equivalent to the whole quantity. Although children may not have reached a cardinal understanding of number, they are able to do this exercise, which helps them to form this important number concept. For this purpose, children are provided with a laminated A₄ worksheet (Figure 3), which serves as a template on which they complete the addition exercises that follow with the help of counters (such as bottle tops). (Notice: All three quantities remain visible together throughout the work!)

 

 

Instruction:

'Put 3 red counters in the bottom left field and 2 red counters in the bottom right block. How many blue counters do you have to put in the top block to have the same amount of counters in the top block as in both bottom blocks together?'

After the children have placed the counters, they areinstructed: 'Check your answer and put the red counters with the blue ones. Are the quantities the same?'

 

 

More exercises are given orally by the teacher. All the children work to complete the exercises:

• 2 red counters and 4 red counters

• 3 red counters and 5 red counters

• 4 red counters and 3 red counters

• 5 red counters and 2 red counters

• 6 red counters and 3 red counters

• 7 red counters and 1 red counter

Right from the start, all exercises or work should also be expressed as word problems (see examples below). These exercises are also completed on the part-part-whole block, to train the modelling of problems.

• '3 meerkats are playing in front of the burrow. Another 2 join them. How many meerkats are there altogether?'

• '7 meerkats are playing in front of the burrow. Another meerkat joins them. How many are playing together now?'

• '3 meerkats stand guard in front of the burrow. Another 3 meerkats come out of the burrow and stand guard too. How many are standing guard now?'

These practice tasks are performed for approximately one week. It is important that the teacher verifies whether the children check their answers correctly during the execution of the tasks. The teacher is beginning to train them 'in action' for what she/he aims for conceptually - that they perform the tasks in their mind.

In order to introduce some variety, the children can give each other simple tasks or word problems. Here the teacher should choose the pairs of children working together, because they benefit from working on a comparable performance level. There is a risk that high-performing children may overstrain low-performing children by choosing too large partial quantities that they cannot handle.

Exercise 2: Part + part - producing the whole with digits

After gaining sufficient experience of performing addition tasks with the help of counters, a first attempt at writing down these tasks in digits is introduced. For this, the children receive a worksheet and oral instructions, such as: '3 counters and 2 counters are given to you.' The children can put the counters on the part-part-whole worksheet, then fill in the digits in the digit worksheet or immediately process the task in digits.

 

 

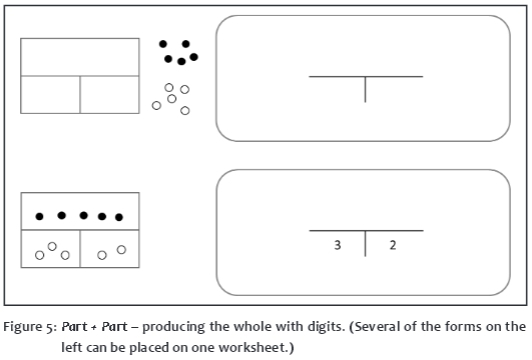
Once the exercise tasks with digits are understood, word problems can also be formulated, as in Exercise 2.

Exercise 3: Finding all the parts of a whole

With the help of the addition exercises, the children will have learned that the relationship between a part, another part, and a whole is determined by the constituent parts. In reverse, this means that one whole can be divided into two parts (part and part). The next exercise develops the understanding that one whole can be divided into different partial quantities, which in turn prepares children to understand the concept of subtraction, which often requires time to consolidate. The exercise requires children to find all possible parts of a given whole.

Instruction:

Each child receives a worksheet containing a whole and a corresponding number of counters in two colours.

'In this worksheet, you can see a 5 in the roof. Try to find out how the 5 can be broken up into two parts. The counters can help you to do this. Take all 5 counters in your hands, shake them, and throw them on the table. After that, fill in the line to show how many red and how many blue counters you can see. Write it down with digits (number symbols) next to it.'

 

 

Reflection:

The children are encouraged to see if there are doublings in the lines. They should mark these doublings. Furthermore, they have to check whether they have found all the possible decompositions. Missing decompositions are noted. It is important to ask here: 'How can you be sure that all variants of decompositions (all the different pairs) have been found?' The children explain different ways of doing the exercise and assembling the counters, thus solving the problem of decomposed parts identification.

Exercise 4: Finding an order

After the children have found a variety of decompositions, they are required to arrange them systematically. This provides them with an overview of all possible decompositions and allows them to check whether they have found all of them. The system can later be used to show the complementarity of addition and subtraction.

As a first step, all decompositions are recorded in a table on the class writing board. Then the children are asked to reflect on how to organise them. The aim is to create the picture ('number house') illustrated in Figure 7. The systematic structure can be achieved by turning over one counter after another to build 'stairs'. High-performing children discover the system by themselves, whereas low-performing children may need support. Besides teaching all possible decompositions of a given number, these exercises also deepen the concept of cardinality.

 

 

Reflection:

The children are encouraged to figure out the structures and rules when elaborating the system. What is important here is that they look closely at the changes within the single lines.

Exercise 5: Operation signs + and =

The children verbalise the tasks they carry out with the counters; for example: '5 and 3 are 8 together.' At first, no operation signs have been introduced yet. The children know the operation signs, but often use them without fully understanding their meaning. The equal sign in particular, which stands for the equivalence of the quantities on either side of the sign, is not thoroughly grasped as a concept of equal number value yet. The children's previous experience with the part-part-whole blocks, where they had to double-check the equivalence between both partial quantities and the whole quantity, can now be used as a basis for introducing the '=' sign.

The '+' sign is introduced with the help of the 'number house', which the children already know from the 'finding an order' exercises.

Instruction:

The children write down the decompositions of the number 5, organised as addition tasks. In doing so, they use the same procedure as in 'finding an order'. After having filled in the decompositions in the 'number house', they read them out in the following way: Ί plus 4 equals 5.'

Reflection:

The children are encouraged to identify similarities and differences between addition exercise tasks; for example, between '2 + 4' and '4 + 2'. In this way, the rules of addition can be elaborated (the commutative property). In addition, specifics are discussed; for example, the children describe what they have noticed in the task '3 + 3'.

Exercise 6: The operation of subtraction

Only when the addition operation as part-part-whole process is understood completely and the children have had sufficient experiences with this practice task, can the subtraction operation (and its underlying conceptual scheme) be introduced. The subtraction operation can be presented as a word problem; for example, 'At a party, there were eight cakes on a table. Then two were eaten. How many cakes are left on the table?' With the help of introductory word problems, the children start to understand the meaning of 'minus': a whole quantity is reduced or decomposed. This involves two parts: one part that is 'gone' or 'removed', and one part that is left.

The reduction can be described using different words (for example, to 'remove', to 'leave', to 'swim away', to 'fly away', to 'eat up', to 'break', to 'sell', to 'hide', and so forth). For this reason, it is of vital importance that the children be given enough time to develop this understanding, and especially to provide them with enough examples of mathematical subtractive situations and the verbs that capture subtraction.

After the term 'minus' has been sufficiently explained, exercises with counters follow: 'Place eight counters, remove three.' The children then verbalise the task: 'Eight counters are given. Three are removed and five are left.' They can illustrate the task on their part-part-whole material: 'Place all eight counters in the top block with blue counters; then three red counters in the left block below (this is the part that goes away); and then five red counters in the right block (this is the part that is left behind).' In this way, the children experience the subtraction task as decomposition, in the same way that they experienced addition as a composition. They form concepts and do not just follow the procedures of the operations.

An extended period of practice is required for children to gain a contextual understanding of the content on both a word and a practical action level. Once these exercises have been successfully completed, the teacher may introduce the minus sign.

Instruction:

The children decompose numbers and write the decompositions down systematically as a subtraction exercise. They are expected to apply the same systematic approach as in the 'finding an order' addition exercises. Afterwards, single decompositions are read out in the following way: 'Six minus two equals four.' In case of uncertainty about the equal sign, the teacher can stick to the scale (see Figure 8).

 

 

 

 

Reflection:

The reflections in Figure 10 offer examples of how the teacher may encourage the children to describe the systematics they have noticed. Are they able to write the exercise task down in a different order?

 

 

Exercise 7: Complementarity of addition and subtraction

There should be a major focus on having children experience addition and subtraction as complementary mathematical operations. Introducing word problems are also particularly suitable here. The children are introduced to mathematical problems that contain both an addition and a subtraction task: 'Six children are in one classroom. Another four children enter. How many children are in the classroom now? Ten children are in the classroom now. Four children leave. How many children remain in the classroom?' Pictures illustrating addition and subtraction tasks can further show the connection between addition and subtraction. Especially low-performing children can use their part-part-whole material and counters to clarify the relationships between the quantities and the connection between addition and subtraction.

Instruction:

A complex consolidation of the complementarity of addition and subtraction is achieved by completing the decomposition 'stairs': 'Write down the tasks as an addition and a subtraction task in each line.'

 

 

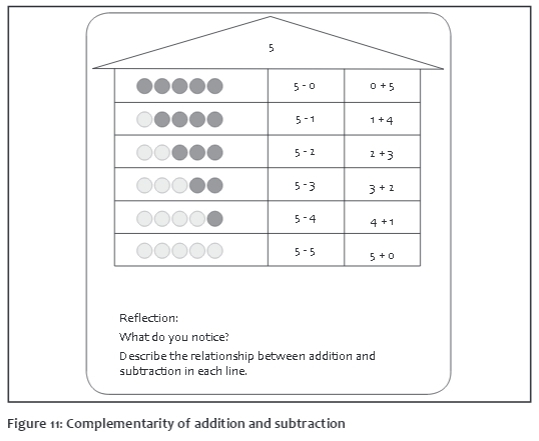
Reflection:

The children describe what they noticed while completing the addition and subtraction tasks. This may be, for example, regularities or rules of change. The aim of the reflection is to find out how addition and subtraction tasks relate to each other. It is therefore important that children use their own words to describe their observations and the rules they have found. They can discuss their findings in class and explain them to each other.

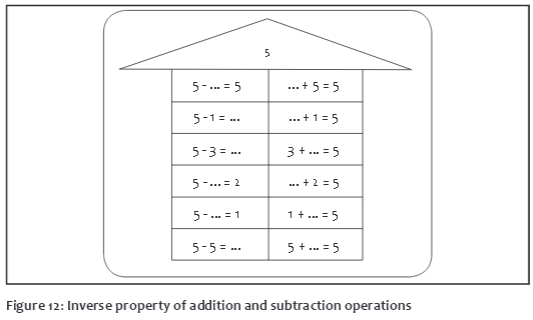
Exercise 8: Inverse property of addition and subtraction

Based on this knowledge, the children can now be seen as competent on Level IV of the model. On this level, part-part-whole tasks can be completed flexibly by the adaptive use of addition and subtraction. Because every subtraction task is also an addition task (and contrariwise), children can use the inverse operation most suitable to the context. This leads to an integrated concept of addition and subtraction, which allows them to switch operations flexibly. The understanding of the inverse property of addition and subtraction is enhanced by:

• plus and minus complement exercises

• orally given complement tasks

• verbalising part-part-whole word problems

 

 

These tasks can be completed by means of word problems, such as: Ά woman has ten oranges. She shares some with her daughter. Now she has three oranges left. How many oranges did she give to her daughter?' Low-performing children can go back to the part-part-whole blocks at any time.

Productive tasks: Exercises for all children

It is not a new idea that children's mathematical abilities and cognitive development (among other things) differ, even though they are taught in the same class. This also applies to their strategies to solve mathematical problems, and thus to the conceptual elicitation that goes with a certain strategy as well. In the problem '7 + 8 = ?', one would probably observe all the strategies described in the introduction to this article being applied in a Grade 1 class, indicating a remarkable degree of performance heterogeneity. Given that not all children in a class are on the same performance level or learn at the same pace, it is not fair to give them all the same exercises or the same amount of time to solve exercises. Doing so overburdens slow learners and they may not come to a deep understanding; whereas fast learners may not be challenged enough and may become bored after some time. One goal of teaching is therefore to create a learning environment that promotes the individual development of all children. In order to close the gap and benefit all children individually, so that they may all progress in learning, the various individuals should be offered different exercises with differing degrees of difficulty. This means that task formats should be chosen in such a way that they allow children to work at different levels. In this way, all children can work on the exercises at their own performance level, gain experience, and achieve learning progress in the end. Such exercises are called 'productive exercises'. According to Scherer (2013), productive exercises:

• are complex: the task formats can be completed on different levels, and children can develop various concepts and mathematical principles.

• allow for natural differentiation: learners with different prerequisites for learning can learn on their individual level and at their own pace.

• are constructivist: the task formats encourage investigative learning and productive practise; they can be solved with different strategies and allow children to make more mathematical discoveries.

• are reflective: when children's methods are identified and compared in class, it allows them to reflect together on the range of experiences, the various activities, and the strategies used. In this way, low-performing children can profit from different approaches to finding solutions.

Most of the exercises presented in this paper can be used as productive exercises. They are intentionally designed to be suitable for low-performing children, but can be adjusted to suit high-performing children as well. This can be done by extending the number range to 20, using more reflections on general rules of addition and subtraction, or encouraging children to design their own exercises based on the basic exercises.

 

Conclusion

In this article we presented ideas for teaching sessions that facilitate a step-by-step understanding of the mathematical operations of addition and subtraction. These sessions may extend across almost half a school year, but must be constantly aligned with other mathematical areas of the curriculum. All the exercises discussed here must be intensified by using a variety of tasks with different numbers. Low-performing children need considerably more time to practice and have to try out various activities for each quantity, such as the decompositions for every number within the number range up to 10. Sometimes they have to try out the same decompositions several times, which may require considerable patience of the teacher. High-performing children, however, display a much faster learning pace, as they generalise their experiences faster and are able to transfer them to a more abstract level. These children can proceed to more challenging exercises. In addition, they may be introduced to a number range up to 20, where they are able use the same materials as their slower learning classmates but work with larger numerals.

If low-performing children are given enough time and exercises, they are likely to acquire a conceptual understanding of the operations and to discover effective strategies as well as relationships between numbers, which provide a solid and sustainable basis for further learning. It is therefore important not to accelerate such children's learning process, but to teach them this basal conceptual knowledge, which forms the root of successful future mathematical learning, even beyond the contents of primary school. These concepts are not only needed to perform calculations, but also to operationalise other concepts into mathematical tasks. They form the basis for secondary school mathematics; for example equations, which rely on a thorough understanding of basic concepts such as the part-part-whole concept.

Providing all exercises in the form of productive exercises with different performance requirements allows for natural differentiation within a class of learners. All children work on the same exercise formats, but high-performing children discover new challenges that are acknowledged in the classroom. In this manner, an atmosphere is created that does not overstrain low performers or demand too little of high-performing children, while at the same time allowing the instruction of major mathematical concepts in the primary school curriculum. Furthermore, differences in the children's mathematical performance are less apparent to them, since they all work on similar exercises. This may have a positive effect on them, especially the lower performing children, because there is less emphasis on their slower pace of learning. In this way, anxiety and serious learning barriers can be counteracted.

The ideas discussed in this article can be incorporated into pre-service teacher education programmes and students can practice these teaching strategies in their practicum work at schools before they start their teaching careers. They can do this under the watchful eye of experienced teachers as well as their lecturers. They can utilise their knowledge of the 'mathematical' mind of the developing, learning child reflectively - not implementing teaching methods so much as testing their own knowledge of how children learn and how they may be given suitable learning support.

 

References

Aunola, K., Leskinen, E., Lerkkanen, M-K. & Nurmi, J-E. 2004. Developmental dynamics of math performance from preschool to grade 2. Journal of Educational Psychology, 96(4):699-713.         [ Links ]

Baroody, A.J. 1992. The development of kindergartners' mental-addition strategies. Learning and Individual Differences, 4(3):215-235.         [ Links ]

Baroody, A.J. 2006. Why children have difficulties mastering the basic number facts and how to help them. Teaching Children Mathematics, 13(1):22-31.         [ Links ]

Carey, S. 2009. The Origin of Concepts. Oxford: University Press.         [ Links ]

Carpenter, T.P. & Moser, J. 1983. The development of addition and subtraction problem-solving skills. In T.P. Carpenter, J. Moser & T. Romberg (Eds.), Addition and subtraction: A cognitive perspective. Hillsdale, NY: Lawrence Erlbaum. 9-24.         [ Links ]

Case, R. & Okamoto, Y. 1996. The role of central conceptual structuresin the development of children's thought. Monographs of the Society for Research in Child Development, 61(1-2): serial no 246. Chicago, IL: University of Chicago Press.         [ Links ]

Dehaene, S. 1997. The Number Sense. Cambridge: Oxford University Press.         [ Links ]

Dehaene, S. 2011. The Number Sense: How the Mind Creates Mathematics (Revised and expanded edition). New York: Oxford University Press.         [ Links ]

Feigenson, L., Carey, S. & Spelke, E.S. 2002. Infants' discrimination of number vs. continuous extent. Cognitive Psychology, 44(1):33-66.         [ Links ]

Feigenson, L., Dehaene, S. & Spelke, E.S. 2004. Core systems of number. Trends in Cognitive Science, 8(7):307-314.         [ Links ]

Fritz, A. & Ricken, G. 2009. Rechenschwache. Munich: Reinhardt (UTB).         [ Links ]

Fritz, A., Balzer, L., Ehlert, E., Herholdt, R., Ragpot, L. & Henning, E. 2014. A mathematics competence test for grade 1 children migrates from Germany to South Africa. South African Journal of Childhood Education, 4(2):14-133.         [ Links ]

Fritz, A., Ehlert, A. & Balzer, L. 2013. Development of mathematical concepts as basis for an elaborated mathematical understanding. South African Journal of Childhood Education, 3(1):38-67.         [ Links ]

Fuson, K.C. 1982. An analysis of counting-on solution procedure in addition. In T.P. Carpenter, J.M. Moser & T.A. Romberg (Eds.), Addition and subtraction: A cognitive perspective. Hillsdale, NY: Lawrence Erlbaum. 67-81.         [ Links ]

Fuson, K.C. 1992. Research on learning and teaching addition and subtraction of whole numbers. In G. Leinhardt, R. Putnam & R.A. Hattrup (Eds.), Analysis of arithmetic for mathematics teaching. Hillsdale, NY: Lawrence Erlbaum. 53-187.         [ Links ]

Gelman, R. & Gallistel, C.R. 1978. The child's concept of number. Cambridge, MA: Harvard University Press.         [ Links ]

Gerlach, M., Fritz, A., Ricken, G. & Schmidt, S. 2007. Kalkulie:Diagnose- und Trainingsprogramm für rechenschwache Kinder. Trainingsprogramm: Bausteine 1-3. Berlin: Cornelsen.         [ Links ]

Goswami, U. 2008. Cognitive development. The learning brain. New York: Psychology Press.         [ Links ]

Henning E. & Ragpot L. 2014. Pre-school children's bridge to symbolic knowledge: First framework for a cognition lab at a South African university. South African Journal of Psychology, DOIM0.1177/00812463145199. Retrieved from sap.sagepub.com (accessed 12 August 2014).

Hunting, R.P. 2003. Part-whole number knowledge in preschool children. Journal of Mathematical Behavior, 22(3):217-235.         [ Links ]

Huttenlocher, J., Jordan, N.C. & Levine S.C. 1994. A mental model for early arithmetic. Journal of Experimental Psychology: General, 123(3):284-296.         [ Links ]

Krajewski, K. & Schneider, W. 2009. Early development of quantity to number word linkage as a precursor of mathematical school achievement and mathematical difficulties: Findings from a four-year longitudinal study. Learning and Instruction, 19(6):513-526.         [ Links ]

Le Corre, M., Van de Walle, G., Brannon, E.M. & Carey, S. 2006. Revisiting the competence/performance debate in the acquisition of the counting principles. Cognitive Psychology, 52(2):130-169.         [ Links ]

Piaget, J. 1965. The child's conception of number. New York: Norton (originally published 1941).         [ Links ]

Piazza, M. 2010. Neurocognitive start-up tools for symbolic number representations. Trends in Cognitive Sciences (Special Issue: Space, Time and Number), 14(12):542-551.         [ Links ]

Resnick, L.B. 1992. From protoquantities to operators: Building mathematical competence on a foundation of everyday knowledge. In G. Leinhardt, R. Putnam & R.A. Hattrup (Eds.), Analysis of arithmetic for mathematics teaching. Hillsdale, NY: Lawrence Erlbaum. 373-430.         [ Links ]

Ricken, G., Fritz, A. & Balzer, L. 2013. MARKO-D - Mathematik und Rechnen - Test zur Erfassung von Konzepten im Vorschulalter. Gottingen: Hogrefe.         [ Links ]

Riley, M.S., Greeno, J.G. & Heller, J.H. 1983. Development of children's problem-solving ability in arithmetic. In H.P. Ginsburg (Ed.), The development of mathematical thinking. New York: Academic Press. 153-196.         [ Links ]

Scherer, P. 2013. Natural differentiation in the teaching of mathematics to children starting school. South African Journal of Childhood Education, 3(1):100-116.         [ Links ]

Steffe, L.P., Cobb, P. & Von Glasersfeld, E. 1988. Construction of arithmetical meanings and strategies. New York: Springer Verlag.         [ Links ]

Wynn, K. 1990. Children's understanding of counting. Cognition, 36(2):155-193.         [ Links ]

Wynn, K. 1992. Addition and subtraction by human infants. Nature, 358:749-750.         [ Links ]

Xu, F. & Spelke, E.S. 2000. Large number discrimination in 6-month old infants. Cognition, 74(1):B1-B11.         [ Links ]

Xu, F. 2003. Numerosity discrimination in infants: Evidence for two systems of representations. Cognition, 89(1):B15-B25.         [ Links ]

 

 

* Email address: fritz-stratmann@uni-due.de
1 See also the article by Fritz, Balzer, Ehlert et al (2014), in which this model was used in research to migrate a mathematics competence test from Germany to South Africa.
2 It is widely known that children struggle with so-called 'word problems' in maths. We believe that this is partly due to their inability to select a task, because they lack the conceptual knowledge to do so.