Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.4 n.2 Johannesburg 2014
ARTICLES
Approaches to teaching primary level mathematics
Caroline LongI; Tim DunneII
ICentre for Evaluation and Assessment, University of Pretoria. Email address: Caroline.Long@up.ac.za
IIUniversity of Cape Town
ABSTRACT
In this article we explore approaches to curriculum in the primary school in order to map and manage the omissions implicit in the current unfolding of the Curriculum and Assessment Policy Statement for mathematics. The focus of school-based research has been on curriculum coverage and cognitive depth. To address the challenges of teaching mathematics from the perspective of the learner, we ask whether the learners engage with the subject in such a way that they build foundations for more advanced mathematics. We firstly discuss three approaches that inform the teaching of mathematics in the primary school and which may be taken singly or in conjunction into organising the curriculum: the topics approach, the process approach, and the conceptual fields approach. Each of the approaches is described and evaluated by presenting both their advantages and disadvantages. We then expand on the conceptual fields approach by means of an illustrative example. The planning of an instructional design integrates both a topics and a process approach into a conceptual fields approach. To address conceptual depth within this approach, we draw on five dimensions required for understanding a mathematical concept. In conclusion, we reflect on an approach to curriculum development that draws on the integrated theory of conceptual fields to support teachers and learners in the quest for improved teaching and learning.
Keywords: curriculum design, teaching mathematics, conceptual fields, teaching approaches, dimensions of understanding, exceptional teachers, assessment
Introduction
The theoretical question explored hereis how the particular approach taken to teaching mathematics in the primary school impacts on the effective learning of mathematics.1 The focus of school-based research has generally been on whether the 'curriculum has been covered', and whether this coverage has been achieved to the appropriate 'cognitive depth' (Reeves & Muller 2005, among others). In our view, the above constructs of breadth and depth do not adequately address the challenges of teaching mathematics from the perspective of the learner. A teacher may well have covered the curriculum in that the ninety or so topics in the Intermediate Phase curriculum2 have been addressed in class, but the important question is essentially whether the learners have engaged with the underlying mathematical structures in such a way that they build the foundations for more advanced mathematics, or whether, in contrast, the concepts as acquired are likely to lead to a frustrating outcome, such as the inability to make the transition to advanced mathematics.
In this paper we firstly discuss three approaches that may be taken singly or in conjunction in the teaching of mathematics in the primary school. The approaches identified by Webb (1992) are the topics approach, the process (or operational) approach and the conceptual fields approach. Each of the approaches is described, presenting both the advantages and the limitations. Secondly, weillustrate the conceptual fields approach, which integrates both a topics and a process approach, in the planning of an exploratory instructional design. And thirdly, to ensure that multiple dimensions of a concept are included, we draw on five dimensions required for the understanding of a mathematical concept elaborated by Usiskin (2012).
The distinction between the characteristics of a 'good' teacher,3 which include both a deep understanding of mathematics and an ability to engage with the learners' interests, and a 'really good' teacher, who looks for opportunities to 'seize the teachable moment' (Benson 2002), is a theme that runs throughout this article. We note here that, for most of the time, teachers may be adequately engaging with learners in the pursuit of learning mathematics. However, every now and then teachers may find that both insights into the curriculum and connections to learners' current interests converge to constitute a 'teachable moment' that is not easily forgotten.
Common perception is that many teachers lack 'mathematical knowledge'. The predominant view of mathematics teaching in South Africa is somewhat bleak, with increasing regulation of the curriculum occurring during this century (see Chisholm, Volmink, Potenza, Muller, Vinjevold, Malan et al 2000). Gaps in teacher knowledge have been reported based on the 2007 SACMEQ test results (Taylor, Van den Berg & Mabogoane 2012; Venkatakrishnan & Spaull 2014) and recurrently reported in the media, even very recently (Jansen 2014). Based on test outcomes it is further observed that there are two distinct populations in the education system (Spaull 2013b). The next step appears to be that the two populations should be provided with differentiated educational experiences (Hugo 2014).
We question the validity of the above chain of reasoning, well intentioned though flawed, and warn against findings from a particular set of educational encounters being used to support educational policy. Decisions such as advocating a restricted curriculum may appear to be an answer, as is proposed by the 'back to basics' movement. The argument put forward in this article points to the importance of an approach that aligns the structure of mathematics itself with children's learning. With Vergnaud (1997), we assert that mathematics is encountered by individuals in many and varied situations. Furthermore, people respond with the schema they have available. In order to expand the schema (concepts-in-action) to generalizable mathematical concepts, scaffolding is required.
Approaches to teaching mathematics
In the planning of any curriculum, decisions are made concerning the philosophy of mathematics, the mathematics knowledge appropriate to the phase, the approach to teaching mathematics, and the subsequent assessment. The explicit expression of the underpinning philosophy, the mathematical knowledge, and the related teaching directives vary from country to country. The degree of control exerted centrally by the national education departments also varies. For example, in some education systems, such as that of the Netherlands,4 broad statements and objectives are provided at the mega level for both socio-political and educational purposes, but, at the micro level, the details and interpretation of these statements for school purposes and the classroom work scheme are left to the teachers and textbook writers (Thijs & Van den Akker 2009). The approach adopted by CAPS in the Intermediate Phase of the South African education system (RSA DBE 2011) is to prescribe the detail, even with regard to the day-to-day, minute-by-minute teaching of a particular topic. Here the curriculum product is located at the micro level. The National Curriculum Statement (RSA DoE 2003), the forerunner to the current CAPS, was objectives-based, with the interpretation occurring at the textbook and individual school level. The rationale for the change is that our teachers are deemed not capable of interpreting an objectives-based curriculum, or of transforming these objectives into instructional units (Dada, Dipholo, Hoadley, Khembo, Muller, & Volmink 2009). This argument for prescribing the detail at the curriculum level is not warranted, as the textbook writers generally provide the detail for the teachers. We note here that the process of engaging with the demands of the curriculum and the textbook or workbook and transforming these demands into instructional units is necessary for good teaching. The teacher needs relative autonomy to interpret the learning requirements for the specific classroom.
The view of mathematics, the principles informing the proposed learning experiences and the design of assessment tasks are not always made explicit within the current broad framework provided by the Department of Basic Education.
A national curriculum may be underpinned by the assumption that mathematics knowledge may be separated into distinct topics, and that behaviours, for example, knowing, applying and reasoning, are distinct and may be attributed a priori to a test item without regard for a learner's cognitive level (Webb 1992) or without the necessary attention to previous educational experience (Bloom, Engelhart, Furst, Hill & Krathwohl 1956). The CAPS document may be characterised as prescribing a topics approach, evident in the week-by-week and hour-by-hour prescriptions, though it must be noted that this approach may be read somewhat differently in the 'General Aims', which propose attention to critical thinking (RSA DBE 2011:4-5).
A second approach to mathematics knowledge is the process approach, in which problem-solving approaches and higher order thinking skills are identified. This approach is somewhat aligned to problem-solving. Some elements of Curriculum 2005 drew on a problem-solving approach. The assessment aligned with such an approach may draw on interviews and observations to identify actions and processes and to make thought processes explicit, rather than the routine paper-and-pencil tests.
The third approach may be described as a conceptual fields approach. A conceptual field is generated by specific structural criteria; for example, the multiplicative conceptual field is identified by common multiplicative structures. The key elements of the field include problem situations and operations of thought and symbolic representations, but in addition, this field approach considers the interrelationships "between problems and situations and [the] student's thinking in addressing them" (Webb 1992:667). The assumption underlying conceptual fields is that different problem situations may be described mathematically by a limited number of statements and symbols. The strength of this approach is that it can be used "to map what a student knows within a knowledge domain and to track the maturation of concepts within that domain" (ibid). In this approach, extensive work is required to specify the elements from both a mathematical perspective5 and a cognitive perspective; for example, by specifying the increasing complexity of multiplicative structures (see Greer 1992, 1994; Vergnaud 1983). This third conception is evident in the New Zealand Primary School curriculum (NZ MoE 2009).
A topics approach
The advantage proposed by a topics approach and which underlies the design of CAPS (2011) and its operationalisation, is that if teachers follow the curriculum and 'teach' the topics in the week-by-week order prescribed, some proficiency in mathematics will be attained, or at least that element of proficiency that is assessed by the Annual National Assessment (ANA).6 This sentiment has been echoed in the media: "Teachers must be taught that the workbooks structure the curriculum per week of teaching time, allowing them to ensure that the full curriculum is covered" (Spaull 2013a:32, authors' emphasis).7
A second and related perceived advantage may be that the order and progression of the topics are carefully planned, so that conceptually preceding concepts are presumably taught prior to the more advanced topics. In the current CAPS document at the Intermediate Phase, fractions are taught in Grade 4 and Grade 5, and only in Grade 6, when the fraction concept is presumed to be in place, is the decimal fraction
concept introduced. The teacher, if aware of this logic underpinning the curriculum and if knowing that an understanding of decimal fractions depends on knowledge of both place-value and fraction, will ensure that the teaching of decimal fractions is linked to the prior understanding of place-value and fractions. She may, in Grades 4 and 5, in anticipation of the decimal fractions to be taught in Grade 6, ensure that common fractions with denominators of multiples of ten are covered, and that the relationship for example of one tenth (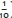 ) to ten hundreds (
) to ten hundreds (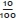 ) is understood. Here links with measurement - notably the length of a decimetre, one tenth of a metre (
) is understood. Here links with measurement - notably the length of a decimetre, one tenth of a metre (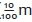 ), and ten centimetres, ten hundredths of a metre (
), and ten centimetres, ten hundredths of a metre (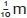 ) - may provide a context in which to develop these concepts and demonstrate equivalence of fractions. This traditional approach may be subverted, and the fact that children have experience with the decimal system through familiar monetary currency may be used to build understanding of the decimal system independently of, or in parallel with, developing fraction concepts.
) - may provide a context in which to develop these concepts and demonstrate equivalence of fractions. This traditional approach may be subverted, and the fact that children have experience with the decimal system through familiar monetary currency may be used to build understanding of the decimal system independently of, or in parallel with, developing fraction concepts.
Both of the above perceived advantages of the topics approach are premised on the assumption that teachers already have knowledge of the underlying mathematical principles and properties and have a clear understanding of the challenges the learner will face in higher grades. In the case of the examples described, it is assumed that teachers know the central properties of rational numbers, namely that for each point on the number line there are an infinite number of names and that between any two rational numbers there is always another rational number (in fact, infinitely many). These properties of rational numbers render them conceptually distinct from natural numbers and not merely an extension (Kieren 1976; Vamvakoussi & Vosniadou 2007). Many of the errors made by learners are due to the confusion of the properties permitted in the natural number system and the properties permitted in the rational numbers.
The disadvantage of the topics approach may therefore be that the designers, planners and officials responsible for teacher education assume that an explicitly topics-based curriculum can bypass the necessity for advanced mathematics knowledge. Where there are deficits, or an absence of advanced mathematics knowledge, the workbooks, however well intentioned, will not 'structure the curriculum' without input from the teacher. The good teacher makes sense of the mathematics herself before transforming the curriculum, or the workbooks, into valuable instructional experiences for the learners. In fact, it is in the process of transforming the curriculum or the textbook into teaching units that the teacher consolidates her own understanding. It is the teacher in interaction with the learners, keeping in mind their current proficiency and the various paths to abstract concepts, that promotes learning.
A process approach
Somewhat juxtaposed to the topics approach is a process approach, which may in some senses be aligned with a problem-solving approach. The theoretical informants of this approach are extensive, from Piaget and collaborators, who proposed that conceptions and competences are attained through activity (Piaget 1952; Piaget & Inhelder 1969); to Dewey, who proposed that the thoughtful methods employed in problem-solving may be likened to the work of advanced mathematicians (1910, cited in Hiebert, Carpenter, Fennema, Fuson, Human, Murray, Olivier & Wearne 1996); and then to Polya (1957), who conducted extensive research into identifying phases of problem-solving. In this process approach, the focus is more directly on the learner and the development of his or her skills in engaging with problems. These problems may of course be the task of adding 12 and 12, or multiplying 24 by 3. Though all mathematics requires solving a problem, for example '5 χ 12', the task is more often situated in some context that includes more than the mathematical context, for example, 'Explain why 5 time periods of 12 minutes is the same as one hour'.
Underpinning the theoretical informants of this approach is the view of the learner as an intelligent individual who engages with the world he or she encounters - and we note that this view includes the teacher, who solves problems outside of the classroom daily, if not minute by minute. The comprehension of new subject matter is "a function of knowledge construction and transformation, rather than [merely] acquisition and accumulation" (Loyens & Gijbels 2008, cited in Renkl 2009). This view does not imply that a constructivist position is adequate; the metaphor applied here is that of a journey towards the inherently existing mathematical structure.
The advantage of this process approach, when the lessons have been well conceptualised and planned, is that having learners engage with contextually relevant and therefore meaningful problems will propel their curiosity, exploration, and the discovery of new learning (Hiebert et al 1996). Underpinning any fertile problem situation will be the teacher's awareness of the specific mathematics knowledge and skills required and the pre-empting of these skills and concepts, so that the required learning is within the learners' "zone of proximal development" (Vygotsky 1962:102). In the 5 x 12 minutes example above, addition and multiplication skills are required along with an understanding of time (hours and minutes).
A disadvantage of course arises when the teacher unthinkingly presents a whole class with a problem that is either out of the learners' general zone of proximal development or that is not conceptualised for learning purposes. The teacher may not be acutely aware of the actual levels of mathematical proficiency of individuals within the group. The related problem here is that attention to the core mathematical skills such as the operations may not yet be at a level of sufficient mastery to solve a particular problem, although these skills may be built concurrently. A second failing of this process approach has been that the teacher underestimates the extent and degree of planning and of both indirect and direct teaching that underpins such an approach.
The process approach, like the topics approach, requires an advanced understanding of the mathematics, with particular attention to the conceptual precursors and the mathematical concepts that are to follow. In addition, an explicit sense of the relationships between the different elements of the curriculumis crucial. In particular,in the Intermediate Phase, the selection of problem contexts should harness and orchestrate the conceptual connections between multiplication and division, fractions and decimal fractions, ratio and proportion, percent, and the early conceptions of probability.
A conceptual fields approach
The conceptual fields approach8 draws primarily on the work of Vergnaud (1983; 1988), in which he responds to both the complexity of mathematics knowledge and the gradual acquisition of this knowledge by learners by positing a complex conceptual framework. His theory of conceptual fields provides
[...] a framework that is mathematical, by making explicit the structural links across concepts, and by tracing the filiations and thresholds along the mathematical path from early arithmetic to advanced mathematics. From a cognitive perspective, the concepts-in-action and theorems-in-action provide the building blocks, which teachers may use to help learners transform current thinking into generalisable concepts and actions.
(Long 2011:ii)
One of the challenges of mathematics education noted by Vergnaud (1988) is that arguably every mathematics concept is rooted in situations and problems, and in consequence a single concept may be applied to multiple problem situations; at the same time one specific situation or problem may require many distinct mathematics concepts. The reality from a cognitive perspective is that related concepts do not develop in isolation (as in separate steps in a sequence), but simultaneously and in conjunction with other concepts.
Building on the notion of a conceptual field we note that addition and subtraction are not inherently separate, but rather related concepts. The notion of the additive conceptual field encourages the learning of the related concepts in contexts that ensure that their meaning is understood (Vergnaud 1997). Addition and subtraction concepts9 are used in many problem contexts. Vergnaud notes that the permissibility of addition "is the first essential characteristic of number"; it is essentially because one "needs to combine quantities and magnitudes and find the measure of the whole, knowing the measures of the parts, that humans invented and developed the concept of number" (ibid:15).
The additive conceptual field may be described as follows:
The additive conceptual field comprises the contexts and situations for which additive structures (addition and subtraction) are required. These structures include counts and measures and situations of comparison, with the related concepts of order and equality, and situations of combination or separation, including concatenation or partition, addition or subtraction, and subsequent comparison of like or unlike extents.
(Adapted from Long 2011:100, drawing on Vergnaud 1997)
It is quite plausible that a broad underlying theme underpinning the Intermediate Phase mathematics curriculum may be described as enabling a transition from the additive conceptual field to the multiplicative conceptual field. Research in this area (Hart 1984; Long 2011; Zaskis & Liljedahl 2002) provides evidence that errors emerge in solving mathematical problems when additive reasoning is applied incorrectly where it would be appropriate to apply multiplicative reasoning. Following this logic, it is imperative that, in the Intermediate Phase, attention be given to understanding the connections between addition and multiplication, but at the same time to also create awareness that the distinctive multiplicative operations are not repeated addition (Devlin 2008); rather, multiplication provides an alternative operation that leads to the same result as repeated addition in a special case.
The multiplicative conceptual field is conceptualised as
[...] all situations that can be analysed as simple and multiple proportion problems and for which one usually needs to multiply or divide. Several kinds of concepts are tied to those situations in addition to the thinking required to master them.
(Vergnaud 1988:141)
In the Intermediate Phase we identify concepts spanning the natural number system (multiplication and division), as well as the trio of concepts (fraction, ratio, rate) that are essential to developing the concept of rational number. The development of proficiency in the multiplicative conceptual field, as with the additive conceptual field, begins in the early grades and continues throughout high school and further (Long 2011).
The disadvantage of a conceptual fields approach may be that it requires more advanced mathematical knowledge than the topics approach. A second challenge may be that more attention is required with regard to the learners' existing understanding. These 'disadvantages' have a counterpoint in the satisfaction and confidence that come from a better understanding of mathematics and its antecedents, and in the engagement with learners' current resources, potentially the springboard for advanced mathematics.10
In summary, we note that the transitions to be made in the Intermediate Phase in terms of conceptual development are firstly from working within the natural number system to embracing the rational number system (Usiskin 2005), and, concurrently, developing multiplicative structures through an understanding of multiplication and division. In fact, one might argue that, from a conceptual fields perspective, it is the transition from additive reasoning within the additive conceptual field to multiplicative reasoning within the multiplicative conceptual field that is the precursor to an emerging understanding of rational number, whose characteristics include density within the number line and an infinity of representations (Vamvakoussi & Vosniadou 2007).
An illustrative example
We propose that the two major transitions required in the Intermediate Phase are firstly acquiring an understanding of multiplication and its inverse in division, and then of several other mathematical concepts (fraction, ratio, proportion, percentage and probability) introduced during this phase which build on an understanding of multiplication and division. Based on this proposition, we present an exploratory instructional design that incorporates these transitions. In following a conceptual fields approach, we note with Vergnaud (1988) that conceptual understanding builds on situations that demand the particular mathematical concepts, the invariant schemas, and the representations, signs and symbols. The situations within which the concepts are embedded perform two functions, firstly of illustrating the concept, and secondly of extending the concept when the problem that is posed is slightly more difficult than current proficiency.
Here we also bring in the 'really good' teacher who, by being alert, may every so often alight on a particularly fruitful 'teachable moment' which caters not only for the mathematical concepts appropriate to the phase of teaching, but equally importantly also for the interests of the learners. The problem situation illustrated below is appropriate for an urban context, but may be adapted for a rural context.11
The context and problem situation
Context 1: Gautrain route between Johannesburg Park Station and Pretoria Station
The recent implementation of the Gautrain project12 in Gauteng has solved a problem for some commuters travelling between Johannesburg and Pretoria. Prior to using the train, many commuters travelled up to two hours by car to get to work, and two hours home again. The time it takes to travel by train from Johannesburg Park Station to Pretoria Station is 40 minutes. During the morning peak hours, from 05:24 until 10:00, the train leaves Park Station every 12 minutes. The same time schedule applies during the afternoon and evening peak hours, from 16:00 to 20:30. During off-peak hours, from 10:00 to 16:00, the train leaves every 20 minutes.
A variety of questions that call for the operations of addition (and subtraction) or multiplication (and division) may be posed. Learners may also set their own problems.
Some examples:
- How many trains leave Park Station from 05:24 to 10:00 (inclusive) every weekday?
- If the train has four coaches and each coach can carry 60 passengers, how many people can travel on a four-car train on a single journey?
- How many people can travel from Johannesburg to Pretoria during the morning peak hour in one day?
We note that the count of trains will equal one plus the number of time intervals when time is loosely specified by two endpoints.
At a higher level, questions that require fraction concepts, ratio and rate, and percentage may be asked. The development of a concept of speed is critical here (see Thompson 1994).
- What is the average speed of the train if it takes 30 minutes to travel 60 km?
- The top speed of the train is 160 km/h. How much faster is the train than a car at the permitted speed limit of 120 km/h?
Context 2: Waiting for the bus
A student is leaving Pretoria to travel to Johannesburg. She arrives at the Gautrain bus stop at 15:00 to find the following information:
The question is: How long will she have to wait for the bus? What action should she take to find out? Starting at 06:06, calculate the next four departure times.
The student compares this timetable with one she might see in Cape Town, or in other cities around the world. Look on the Internet for a bus timetable in other cities. What are the major differences between the timetables? What is the longest time she might have to wait for the Gautrain bus?
The learners may be informed that the logistics team of the Gautrain project are handling these calculations all the time in order to offer an efficient service. They might also be asking questions about how money should best be spent to improve the general travel experience. It is not out of the bounds of expectation that a problem identified by a member of the public and for which that person offers a solution, could inform the logistics team. This member of the public may be a school child!
Mathematical skills and concepts
The contexts described above may be used to illustrate a variety of concepts within the additive conceptual field and to extend the learners' concepts to applying the operations of multiplication (and its inverse, division).
In addition to additive and multiplicative structures and the related concepts of fraction, ratio, rate and percent, the learners would need to understand the concepts of both analogue and digital time, as well as 24-hour time. Within the time concept, it would be essential to know the number of minutes in an hour and to work with the base of 60.
For the question, 'How many trains leave Park Station from 08:00 until 10:00?', some learners may add 12 + 12 + 12 ... and so on. They may be told or asked whether they could use their knowledge of the 12 times table to tackle the problem more efficiently. The problem may be changed into a ratio or rate problem: there are five trains per hour.
The same concepts and skills are required to solve the bus problem. We note that different levels of skill may be used to solve the problem and each learner or group of learners may be extended or guided to a more advanced and therefore more economical skill. For example, in the bus problem, the repeated addition of 24 may be employed. Another learner may decide that adding in half hours and then subtracting 6 minutes for each half hour may be possible. A more advanced strategy may be to realise that for every two hours of off-peak time three busses depart - here the ratio concept is being evoked. The type of problem may be expanded to include percentage as the explicit form of the ratio.
Though the problems within the multiplicative conceptual field appear to be infinitely variable, the essential structure underlying the problems can be encapsulated by identifying distinct measure spaces (dimensions) and then identifying the unknown, as illustrated in Table 1 (see Long 2011, drawing on Vergnaud 1983). Note that in this particular example the variables are the number of carriages and the number of people.

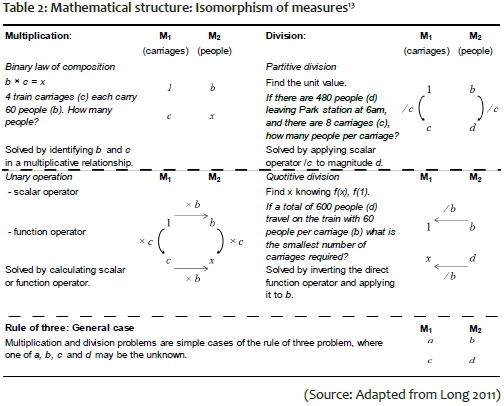
Extension of the concepts into multiple dimensions of understanding
The train and the bus contexts in their present form may appear somewhat unstructured, especially when compared with a page of calculations involving addition of two-digit numbers or involving multiplication by 12. In order to ensure that multiple facets of the concepts, for example 'adding two-digit numbers' or 'calculations involving hours and minutes', are covered, we propose drawing on the five dimensions required to fully understand a mathematical concept (Usiskin 2012). Usiskin labels these elements the skills-algorithm dimension, property-proof dimension, use-application dimension, representation-metaphor dimension, and history-culture dimension of understanding. By applying these five dimensions to the problem context described above, we envisage the following explicit clarifications.
Skills-algorithm dimension
An understanding of place value and skill are required to support fluency in calculations. For this particular problem context, the number 12 and its multiples may be the focus. The learners may be provided with practice sheets that require identifying patterns when adding 12s (twelves), with the requisite practice for consolidation. The concept of multiplication may be compared with addition, noting the efficiency of multiplication. Because we are dealing with time, the number 60 is critical. Depending on the current proficiency levels, questions relating to division may be asked, for example, 'How many time periods of 12 minutes are there in one hour (60 minutes)?' or 'How many numbers divide into 60 without a remainder?' The idea of factors may be introduced. We note here that skills and algorithms are underpinned by concepts, and that conceptual and procedural knowledge are entwined.
Property-proof dimension
The properties of operations involving number are few when compared with the hundreds of number facts that must be learned. These properties, for example the associative property, commutative property and distributive property can be used to guide the operations that are performed. Attention to these properties in the current project will enable the generalisation of skills to other situations. Justification of the algorithms for the above properties may elicit further depth of understanding.
The relevance of the mathematics properties exhibited within the additive and multiplicative conceptual fields is that the foundations are laid for the algebraic conceptual field still to be encountered. The real value of solid teaching of grounded concepts in the Intermediate Phase is in the preparation for the phases to come.
Use-application dimension
The focus of the project is on the use of mathematics and its application to a real-life problem, as illustrated earlier. Apart from the time contexts here, some everyday contexts (for example, the selling and buying of eggs) may provide a rich context. The utility of a solution is the driving motivation for positing the question. The important feature of the context must be that, through engagement, learners generate ideas and relationships that may be formalised in mathematics.
Representation-metaphor dimension
This dimension relates to how mathematics concepts are represented through symbols, drawings, diagrams and graphical representation. Here we offer an array, or an area metaphor such as a rectangle, or a volume metaphor of a cuboid. In order to pre-empt the algebra that is to come, inequalities and equations may also be introduced in such a way that they may be represented graphically.

The drawing of timelines covering 24 hours, representing the times that the train will depart from Park Station, may be an aid to understanding the problem by providing a visual representation of the problem. Here a clock face may also be divided into five sections, each representing 12 minutes, to introduce fractions of an hour.
History-culture dimension
The ancient Babylonians chose 60 as the base for their number system. The evidence that this number was a very good choice is that we continue to use base 60 for our time units and angle measures. Its mathematical properties include partitions and hence division into two, three, four, five, six, ten, twelve, fifteen, twenty, thirty and sixty equal parts (Eves 1980). Another interesting historical fact is that the number 12 was the chosen base rather than 10 because it has more factors. This information may appear superfluous, especially if one has to cover the 90 or so topics in the curriculum; however, by having learners engage with the differences between the hexagesimal (base 60) and the decimal system (base 10), their curiosity may be sparked and other bases may be explored.
In summary, the five dimensions are overlaid or embedded in a conceptual fields approach, of which only some essential features have been presented here.14 Greater elaboration of this approach may be found in Long (2011).
Discussion
The conceptual fields approach
In our view, a conceptual fields approach, following Vergnaud (1988), coheres favourably with mathematical knowledge and problem-solving requirements, and is also economical in that the conceptual structure underlying all elements of the conceptual field is identifiable (see Table 1). By contrast, a topics approach will address each topic independently, with no explicit connections (see Long 2011, drawing on Webb 1992).
An advantage of presenting a context is that the many concepts find meaning within the context. The organisation of lesson sequences around a problem context such as the Gautrain example above may be critiqued from a perspective asserting that we are moving away from the scientific and abstract mathematical concepts. We, along with Vergnaud, note that the origins of mathematics lie in problems. The power of mathematics is that it transforms intuitive and implicit knowledge for solving a class of problems into explicit and generalised knowledge that applies to other problems. The aim therefore is to build from intuitions to explicit and general concepts and theorems by having learners engage with more challenging applications and to lead them to more abstract concepts in the process. Here we note the distinction between the predicative form of mathematical knowledge, comprising linguistic and symbolic expressions that are clearly defined and have been authorised by the collective of the creators of mathematical knowledge,15and the process form, which is found in action on the physical and social world (Vergnaud 2009).
Learners and teachers
The argument presented for the current week-by-week topics approach and the highly structured minute-by-minute lesson plans, as required by the Gauteng Provincial Literacy and Mathematics Strategy (GPLMS), is based on the view that tightly orchestrated instructional practices should be put in place in order to improve the education in poorer schools, the implication being that the resource capacity of teachers, schools and districts is somewhat limited (Fleisch & Schoer 2014).
The critical question however is whether a topics approach, with the associated invariant order and pacing, is the best for learners. Reports from the GPLMS are that 30% of the learners are being left behind (in respect of CAPS), and the teachers are disturbed by this situation. Even if such reports are, for the time being, only anecdotal, we argue that whichever approach is adopted for mathematics teaching, the essential requirement for the teacher is extended knowledge of the subject matter, and that it is this extended knowledge, supported by the theory of conceptual fields informing the many routes to the acquisition of proficiency, that will remedy the situation. A curriculum statement of any kind has to address supporting the elaboration of such extended knowledge amongst teachers. Where such knowledge is alleged to be absent or minimal, a sequenced list of topics and detailed process specifications cannot be expected to cover the fundamental deficit being implied or claimed.
Teaching materials
The argument that teachers do not have time to create their own materials may be valid. However, in the interests of professional development, this skill is to be encouraged, even if initially only to identify mathematically rich contexts in their environment. However, there should also be a concerted effort by publishers and people working in mathematics education to contribute to a bank of project ideas that are appropriate for different contexts. The argument that planning context-specific educational experiences - for example, requiring rural children to engage with rural problems - limits children is not justified when we take seriously the aim of mathematics education proposed by Vergnaud, which is the development of increasing abstraction from situations and contexts with which the children are already familiar. We note here that well-designed materials incorporating dimensions of understanding and a conceptual fields approach are in existence (see the University of Chicago Schools Mathematics Project); however, it is argued here that it is of critical importance that such resources be developed for the South African context and that teachers be engaged in this process.
Assessment and the approach to learning and teaching mathematics
We note here that assessments such as the Annual National Assessment (RSA DBE 2010) have the power to impact on the approach taken by teachers in the classroom (see Schoenfeld 2007). As stated previously, we make the distinction between a good teacher and a 'really good' teacher. A good teacher does everything that is expected, but every now and then a set of ideas comes together and she understands that to inspire her learners and instil a love of learning is half the battle won. In this instant she becomes a 'really good' teacher!
Assessment is a key tool, and assessment resources that embody diagnostic beliefs and insights could complement the teaching resource. However, the lack of alignment between the approach to teaching mathematics at the Intermediate Phase and the type of systemic assessment that is administered may well impact negatively.
Comment on the curriculum
Assuming that the aim of mathematics education expressed here, namely to develop from initial intuitions to more explicit and general concepts that lead learners to greater abstraction and induction into mathematics, is justified, we ask to what extent the approach to teaching as currently advocated within the CAPS curriculum serves this purpose. The question arises whether a national curriculum should specify the day-to-day decisions to the level of detail currently specified from a substantive knowledge perspective (specified content) and from a technical-professional perspective (specified classroom practice) (Thijs & Van den Akker 2009).
The advantage of leaving the finer detail of curriculum distributed across diverse educational communities is that the decisions are distributed among many talented people. Here we consider both substantive knowledge issues, such as the diverse meanings of the fraction symbols, and technical aspects pertaining to how much time should be allocated to a particular section of the curriculum. By having central control there is the danger that if the particular design has not drawn sufficiently from the most talented and knowledgeable people in the country, a suboptimal outcome inescapably affects all. This sentiment has been expressed by Andrich (2009), commenting on the adoption of a national curriculum across the states and territories that constitute the Australian Federation:
When the various jurisdictions [provinces] are in control of their respective curriculums, even with a consensus on principles behind these curriculums, there is a greater opportunity to experiment and take risks, and a greater opportunity to have an excellent curriculum and a greater opportunity to make a mess. If the latter occurs, it might be confined to one or two jurisdictions. Excellent curriculums can be adopted by other jurisdictions, and those with problems can be avoided. However, in the case of a single national curriculum, a mess will affect the whole country.
(Andrich 2009:24)
Andrich elaborates further, warning that it is
[... ] imperative that the curriculum, syllabuses, illustrative lesson plans, programs of teaching and learning, materials for the assessment of learning and relevant professional development be so well prepared that even if the national curriculum is not mandated, schools will see them as so good that they will take them up voluntarily.
(ibid)
Conclusion
The various views of mathematics implied in a national curriculum and in teaching approaches impact directly on teachers. A teacher may have an implicit view of mathematics and her approach to teaching will reflect this view in one way or another. Engagement with different views of mathematics through professional development may extend her understanding and reflect in teaching and learning, especially if supported by a coherent set of materials which may be adapted for a specific context.
We acknowledge that both theidentification of topics and the presentation of progressively more complex topics are important, but advocate that it is the understanding of this progression that enables effective teaching. A conceptual fields approach requires a deeper insight into the underpinning mathematical concepts, and also presents a route to mathematics proficiency through transforming implicit concepts-in-action to explicit and generalisable concepts. The addition of dimensions of understanding, as elaborated by Usiskin (2012), may extend teachers' presentation of particular topics. This enriched view of mathematics teaching and learning may maximise children's opportunities.
The common perception that the mathematics education situation is bleak and that many teachers lack 'mathematical knowledge' may be subverted by introducing an approach which draws on learners' and teachers' existing schemas and where mathematics concepts may be generated in anticipation of formal and abstract systems.
Acknowledgement
We thank the various reviewers for their insightful comments. Thanks also to Anna Vaskova for assisting with technical details.
Competing interests
We declare that we have no financial or personal interest(s) that may have inappropriately influenced the writing of this article.
Authors' contributions
The article is based on the PhD thesis of Caroline Long. The paper was conceptualised in rough form by Caroline Long and the ideas found form in discussion with Tim Dunne. The editing, polishing and fine tuning was the responsibility of both authors.
References
Andrich D. 2009. Review of the curriculum framework for curriculum, assessment and reporting purposes in Western Australian schools, with particular reference to years Kindergarten to Year 10. Perth: University of Western Australia. [ Links ]
Benson J. 2002. What makes a good mathematics teacher?. UCSMP Newsletter, 30(4). [Retrieved 6 October 2014] http://d75gtjwn62jkj.cloudfront.net/30.pdf.
Bloom BS, Engelhart MD, Furst EJ, Hill WH & Krathwohl DR. 1956. Taxonomy of educational objectives: The classification of educational goals. Handbook I: Cognitive domain. New York, NY: David McKay Company.
Chisholm L, Volmink J, Potenza E, Muller J, Vinjevold P, Malan B et al. 2000. A South African Curriculum for the Twenty First Century. Report of the Review Committee on Curriculum 2005. Pretoria.
Dada, F., Dipholo, T., Hoadley, U., Khembo, E., Muller, S., & Volmink, J. 2009. Report of the task team for the review of the implementation of the National Curriculum Statement. [Retrieved 6 October 2014] http://www.education.gov.za/LinkClick.aspx?fileticket=kYdmwOUHvps%3d&tabid=358&mid=i26i.
Devlin K. 2008. It's still not repeated addition! Mathematical Association of America (MAA). [Retrieved http://www.maa.org] http://www.maa.org/external_archive/devlin/devlin_0708_08.html (accessed).
Eves HW. 1980. Great moments in mathematics (before 1650). Washington, DC: MAA.
Fleisch B & Schoer V. 2014. Large-scale instructional reform in the Global South: insights from the mid-point evaluation of the Gauteng Primary Language and Mathematics Strategy. South African Journal of Education, 34(3):1-12.
Greer B. 1992. Multiplication and division as models of situations. In: DA Grouws (ed). NCTM Handbook of Research on Mathematics Teaching and Learning. New York, NY: Macmillan Publishing Company. 276-295.
Greer B. 1994. Extending the meaning of multiplication and division. In: G Harel & J Confrey (eds). Multiplicative Reasoning. Albany, NY: State University of New York. 41-49.
Hart K. 1984. Ratio: Children's strategies and errors. Windsor: NFER-Nelson.
Hiebert J, Carpenter T, Fennema E, Fuson K, Human P, Murray H, Olivier A & Wearne D. 1996. Problem-solving as a basis for reform in curriculum and instruction: The case of mathematics. Educational Researcher, 25(4):12-21.
Hugo W. 2014. Underperforming schools and turnaround strategies that work or fail - a literature review and framework for South African interventions. Education Excellence Consortium.
Jansen L. 2014. Dire state of SA's grade 6 maths teachers. Pretoria News, 7 August 2014. [Retrieved 7 October 2014] http://www.iol.co.za/news/south-africa/kwazulu-natal/dire-state-of-sa-s-grade-6-maths-teachers-1.1731759.
Kieren TE. 1976. On the mathematical, cognitive and instructional foundations of rational number. In: R Lesh (ed). Number and measurement: Papers from a research workshop. Columbus, OH: ERIC/SMEAC. 101-144.
Kuiper W & Berkvens J (eds). Balancing curriculum freedom and regulation across Europe. CIDREE Yearbook2013. Enschede: SLO.
Lamon SJ. 2007. Rational numbers and proportional reasoning: Toward a theoretical framework for research. In: F Lester (ed). Second handbook of research on mathematics teaching and learning. Charlotte, NC: NCTM. 629-666.
Long C. 2011. Mathematical, cognitive and didactic elements of the multiplicative conceptual field investigated within a Rasch assessment and measurement framework. Unpublished PhD thesis. Cape Town: University of Cape Town. Available from http://hdl.handle.net/%2011180/1521.
Millwood R. 2012. Learning theories. HoTEL EU Project. [Retrieved 6 October 2014] http://cmapspublic3.ihmc.us/rid=1LGVGJY66-CCD5CZ-12G3/Learning%20Theory.cmap.
NZ MoE (New Zealand. Ministry of Education). 2009. New Zealand curriculum: Mathematics standards Grades 1-8. Wellington: Learning Media Limited.
Piaget J & Inhelder B. 1969. The psychology of the child. New York, NY: Basic Books.
Piaget J. 1952. A child's conception of number. London: Routledge & Kegan Paul Ltd.
Polya G. 1957. How to solve it: A new aspect of mathematical method. Princeton, NJ: Princeton University Press.
Reeves C & Muller J. 2005. Picking up the pace; variation in the structure and organisation of learning school mathematics. Journal of Education, 37:103-130.
Renkl A. 2009. Why constructivists should not talk about constructivist learning environments: A commentary on Loyens and Gijbels. Instructional Science, 37:495-498.
RSA DBE (Republic of South Africa. Department of Basic Education). 2011. Curriculum and Assessment Policy Statement: Intermediate Phase. Pretoria: Department of Education.
RSA DBE. 2010. Annual National Assessment. Pretoria: Department of Education.
RSA DoE (Republic of South Africa. Department of Education). 2003. Revised national curriculum statement Grades R-9 (Schools) Mathematics. Pretoria: Department of Education.
Schoenfeld AH. 2007. What is mathematical proficiency and how can it be assessed? In: AH Schoenfeld (ed). Assessing mathematical proficiency. Cambridge: Cambridge University Press. 3-15.
Sfard A. 1995. The development of algebra: Confronting historical and psychological perspectives. Journal of Mathematical Behaviour, 14:15-39.
Spaull N. 2013a. Absentee teachers are a thorn in our side. Mail & Guardian, 10 March. [Retrieved 15 March 2014] http://mg.co.za/article/2013-03-10-absentee-teachers-are-a-thorn-in-our-side.
Spaull N. 2013b. Poverty & Privilege: Primary School Inequality in South Africa. International Journal of Educational Development, 33:436-447.
Taylor N, Van der Berg S & Mabogoane T. 2012. What makes schools effective? Report of South Africa's National School Effectiveness Study. Cape Town: Pearson Education.
Thijs A & Van den Akker J. 2009. Curriculum in development. Enschede: Netherlands Institute for Curriculum Development (SLO).
Thompson P. 1994. The development of the concept of speed and its relationship to the concept of rate. In: G Harel & J Confrey (eds). The development of multiplicative reasoning in the learning of mathematics. Albany, NY: State University of New York. 179-234.
Usiskin Z. 2005. The importance of the transition years, Grades 7-10, in school mathematics. UCSMP Newsletter, 33 (Winter 2005). 4-7.
Usiskin Z. 2012. What it means to understand school mathematics? Paper presented at 12th International Congress on Mathematical Education (ICME-12), Seoul, South Korea, 10 July 2012. [Retrieved 15 September 2013] http://www.icme12.org/upload/submission/1881_f.pdf.
Vamvakoussi X & Vosniadou S. 2007. How many numbers are there in a rational number interval? Constraints, synthetic models and the effect of the number line. In: S Vosniadou, A Baltas & X Vamvakoussi (eds). Reframing the conceptual change approach in learning and instruction. Oxford: Elsevier. 265-282.
Venkatakrishnan H & Spaull N. 2014. What do we know about primary teachers' mathematical content knowledge in South Africa? An analysis of SACMEQ 2007. Stellenbosch Economic Working Papers, No 13. [Retrieved 15 October 2014] http://www.ekon.sun.ac.za/wpapers/2014/wp132014/wp-13-2014_2.pdf.
Vergnaud G. 1998. A comprehensive theory of representation for mathematics education. Journal of Mathematical Behaviour, 17(2):167-181.
Vergnaud G. 1979. The acquisition of arithmetical concepts. Educational Studies in Mathematics, 10(2):263-274.
Vergnaud G. 1983. Multiplicative structures. In: R Lesh & M Landau (eds). Acquisition of mathematics concepts and processes. New York, NY: Academic Press. 127-174.
Vergnaud G. 1988. Multiplicative structures. In: J Hiebert & M Behr (eds). Number concepts and operations in the middle grades. Hillsdale, NJ: National Council of Teachers of Mathematics. 140-161.
Vergnaud G. 1997. The nature of mathematical concepts. In: T Nunes & P Bryant (eds). Learning and teaching mathematics: An international perspective. Hove: Psychology Press. 5-28.
Vergnaud G. 2009. The theory of conceptual fields. Human Development, 52: 83-94.
Vygotsky LS. 1962. Thought and language. Cambridge, MA: MIT Press.
Webb NL. 1992. Assessment of students' knowledge of mathematics: Steps toward a theory. In: DA Grouws (ed). Handbook of research on mathematics teaching and learning. New York, NY: Macmillan Publishing Company. 661-683.
Zaskis R & Liljedahl P. 2002. Arithmetic sequence as a bridge between conceptual fields. Canadian Journal of Science, Mathematics and Technology Education, 2(1):93-120.
1. We do not attempt to 'measure' effective learning; rather, we explore what effective learning might mean. In the full study (Long 2011), Rasch measurement theory was applied to an empirical study.
2. The Curriculum and Assessment Policy Statement (CAPS) is the official policy statement prescribing teaching and learning (http://www.education.gov.za/Curriculum/CurriculumAssessmentPolicyStatements)
3. We have omitted reference to the 'poorly resourced' teacher, as it is our view that people are inherently creative and are able to draw on these resources with enabling conditions in place.
4. Recent developments in Europe indicate some shifts with regard to the regulation of education inputs in terms of the curriculum and outputs in terms of systemic assessment (Kuiper & Berkvens 2013).
5. We note here that the University of Cape Town includes the underlying mathematical concepts in the course for Foundation Phase teachers.
6. This claim is unsubstantiated. There is research literature to show that where there is inadequate engagement with the conceptual underpinnings, there may initially be an improvement, but without the prerequisite professional development for teachers, they will inevitably hit a ceiling (Lamon 2007).
7. The notion that teachers are subordinate to workbooks, as implied in 'must be taught', works against the notion of a professional teacher.
8. For elaboration of the theory of conceptual fields in a South African study focusing on the multiplicative conceptual field, see Long 2011.
9. These problem contexts comprise concepts such as taking away, finding the difference, how much more?, how much less?, etc.
10. For elaboration of the theory of conceptual fields, see Vergnaud 1979, 1983, 1988, 1997, 1998, 2009; and Long 2011.
11. Here we note that contrasting problem contexts relating to the amount of water needed for domestic purposes and for farming may provide an appropriate context.
12. The decision to spend money on the high speed train rather than improving the existing Metrorail is political and economic. The larger issues may form a context for serious engagement with the numbers.
13. There are three basic uses of multiplication, that is, area, rate factor and scaling (Usiskin 2012). Here we deal with rate factor, which is equivalent to Vergnaud's isomorphism of measures.
14. Greater elaboration of this approach may be found in Long 2011.
15. Term borrowed from Sfard (1995).














