Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.4 n.1 Johannesburg 2014
An error analysis in the early grades mathematics - A learning opportunity?
Roelien Herholdt; Ingrid Sapire
JET Education Services, University of Witwatersrand. Email: rherholdt@jet.org.za; ingrid.sapire@wits.ac.za
ABSTRACT
Error analysis is the study of errors in learners' work with a view to looking for possible explanations for these errors. It is a multifaceted activity involving analysis of correct, partially correct and incorrect processes and thinking about possible remediating strategies. This paper reports on such an analysis of learner tests. The tests were administered as part of the evaluation of an intervention project that aimed to teach mathematical problem solving skills to grade 1-4 learners. Quantitative error analysis was carried out using a coding sheet for each grade. A reliability coefficient was found for each test, as were item means and discrimination indexes for each item. The analysis provided some insight into the more common procedural and conceptual errors evidenced in the learners' scripts. Findings showed similar difficulties across intervention and control schools and highlighted particular areas of difficulty. The authors argue that this analysis is an example of large-scale error analysis, but that the analysis method could be adopted by teachers of grades 1-4.
Keywords: Mathematical error analysis, mathematical pedagogy, elementary school, foundation phase, assessment, mathematics
Background: Teachers learning from child assessment in national tests
South African learners are now required to write annual national tests, which have become known colloquially as 'the ANAs'. The teachers are meant to use the test results to inform their teaching. The Department of Basic Education (DBE) published the outcomes of its qualitative analysis of the results in the Annual national assessment: 2013 Diagnostic report and 2014 framework for improvement (DBE 2014). In the diagnostic section of this report the analysis appears to be what KetterlinGeller and Yovanoff (2009:3) term "skills analysis", i.e. the analysis of learners' item level responses to determine their mastery of specific mathematical reasoning skills. However, in the introduction to the section 2014 ANA framework for improvement, the diagnostic analysis is described as the investigation of "common errors" and "misconceptions" of learners. This description matches what is generally termed "error analysis" (Ketterlin-Geller & Yovanoff 2009:4). The diagnostic analysis conducted by the DBE did not investigate whether error patterns differed across different language (and cultural and socio-economic) groups. In its report the DBE specifies that all schools are expected to customise the broad framework provided by the DBE into grade and subject specific improvement plans (DBE 2013). The ultimate aim is to improve learner achievement by focusing on remedial interventions targeting common errors and misconceptions evident in learners' responses to the national tests (DBE 2013). Two questions immediately come to mind if this is the status quo: 1) How are teachers to analyse ANA and other test scripts productively, and 2) how are they to use the tests to inform their teaching? Error analysis is central to answering both of these questions.
Error analysis, also referred to as error pattern analysis, is the study of errors in learners' work with a view to finding explanations for these reasoning errors. This multifaceted activity can be traced back to the work of Radatz in 1979. Not all errors can be attributed to reasoning faults; some are simply careless errors (Yang, Sherman & Murdick 2011), identified as "slips" (Olivier 1996:3), which can easily be corrected if the faulty process is pointed out to the learner. Slips are random errors in declarative or procedural knowledge, which do not indicate systematic misconceptions or conceptual problems (Ketterlin-Geller & Yovanoff 2009). Error analysis is concerned with the pervasive errors (or 'bugs') which learners make, based on their lack of conceptual or procedural understanding (Ketterlin-Geller & Yovanoff 2009). These authors explain that such mathematical errors occur when someone who makes this type of error believes that what has been done is correct - thus indicating faulty reasoning. Such errors are systematic (Allsopp, Kuger & Lovitt 2007) and persistent and occur across a range of school contexts (Nesher 1987). Yang et al (2011) point out that systematic errors might be the result of the use of algorithms that lead to incorrect answers or the use of procedures that have not been fully understood.
Error analysis, however, does not just involve analysis of learners' correct, partially correct and incorrect steps towards finding a solution, but also implies the studyof best practices for remediation (McGuire 2013). This would require of the teacher a good knowledge of mathematical content, as well as a good grasp of learners' levels of mathematical understanding (McGuire 2013). In the Data Informed Practice Improvement Project (DIPIP) key aspects of error analysis were found to span three of the domains of teacher knowledge as described by Ball, Thames and Phelps (2008) and Ball, Hill and Bass (2005), viz. common content knowledge, specialised content knowledge and pedagogical content knowledge (Shalem & Sapire 2012). Similarly, McGuire (2013) argues that the ability of teachers to remediate common learner errors and misconceptions underlies Shulman's (1986) definition of pedagogical content knowledge. Hill, Ball and Schilling (2008) further include the ability to anticipate learner errors and misconceptions in their understanding of pedagogical content knowledge. Hill et al's (2008) division of pedagogical content knowledge into knowledge of content and students, knowledge of content and teaching, and knowledge of curriculum is useful to explain that activities such as error analysis, which require pedagogical content knowledge, involve more than just pedagogy; they involve a well-grounded understanding of the learner and how a learner learns.
When Shulman (1986) first proposed his theory of teacher knowledge, in relation to pedagogic content knowledge, he suggested that a teacher's knowledge of learners' levels of understanding contributes to an awareness of the process of learning mathematics as well as knowledge of the mathematical concepts that learners struggle to grasp. Authors such as Sousa (2008) and Ashlock (2006) focus on the contribution of error analysis and other efforts to grasp learners' levels of mathematical understanding to the teacher's own knowledge of the underlying cognitive processes involved. From the above, it is clear that error analysis is interwoven with teachers' content and pedagogical content knowledge, as well as teachers' knowledge of mathematical cognition and conceptual development. On the whole, error analysis helps teachers to understand some of the thinking of the learners. This, in turn, may assist teachers to adjust their pedagogy as well as classroom and assessment practices, which may ultimately lead to improvement of learner achievement (Franke & Kazemi 2001). Borasi (1994), for example, has documented the positive effects on learner achievement of an integrative teaching approach which made use of error analysis.
Several researchers (Riccomini, 2005; Sherman, Richardson & Yard, 2005; Yang et al, 2011) reached the conclusion that error analysis is an important skill for teachers teaching mathematics to non-native speakers of English. Even though there is no agreement between researchers (see Carey, 2004; Gelman & Butterworth, 2005) as to whether or not language is the cause of mathematical difficulties for learners learning in a language other than their home language, Yang et al (2011) highlight the need for a curriculum that supports systematic mastery of mathematical vocabulary, conceptual development and comprehension. We argue that this finding makes error analysis even more relevant to the South African context, where the majority of the learners learn mathematics in a language other than their home language from grade 4 onwards.
Unfortunately, research has shown that teachers are often not equipped to design and implement teaching interventions based on the errors made by learners (see Riccomini 2005). Russell and Masters (2009) note in their paper presented at the annual meeting of the American Education Research Association that during error analysis, teachers may neglect the conceptual understanding of learners in favour of procedural correction. Ketterlin-Geller and Yovanoff (2009:6) further point out that teachers might find it difficult to distinguish between "slips" and "bugs". These are legitimate and real concerns regarding the diagnostic value of error analysis and should be considered and addressed within teacher training programmes.
The error analysis described in this article was done using learner tests developed by the project management team (not the researchers) and administered as part of the programme evaluation of an intervention concerning the teaching of mathematical problem solving skills in grade 1 to 4 classrooms. The tests were administered in three languages, i.e. isiZulu, siSwati and English, according to the school's medium of instruction in the specific grade. The majority of the grade 1 to 3 learners wrote the tests in their home language, whereas all the grade 4 learners wrote the tests in English. English is the home language of only a very small minority of the learners in the sample. The research was conducted in two provinces in South Africa. Although it presents an example of large-scale error analysis, the methodology could be adopted by teachers and used by them to perform error analysis using the work of the children they teach. Thus, as practitioner researchers, teachers could inform their own practice.
Methodology
A quantitative error analysis was done after the development of an error analysis coding sheet for each grade. The coding sheets were used by markers to code every item in the test according to the types of answers given by learners. The codes were developed by the mathematics expert in the evaluation team and refined after initial coding of a sample of scripts to include as many of the varieties of errors made by learners as possible. The criterion for inclusion of an error was what the expert deemed to be 'incorrect mathematical reasoning'. A team of nine markers was trained on the use of the coding sheets. Markers were recruited from the ranks of teachers, district officials and graduate students specialising in mathematics. Coding was quality assured by the project manager. After marking the first set of tests, any issues that emerged were discussed and agreement was reached on consistent implementation of the codes. After that each marker coded her or his first pack of actual tests; this was again followed by a discussion of issues that emerged during the coding activity. Coding and discussion was an iterative process that continued until all tests had been coded. A minimum of 10 percent of all tests was moderated by the senior marker.
Data capture and analysis
The coded responses and biographical data of the learners were captured by a team of capturing specialists. The data were captured using a 'restricted entry method' in order to ensure complete accuracy in the data capturing process. Consistency checks and verification procedures were included to further ensure the accuracy of the data captured. The data preparation and analysis followed using SPSS Statistics data analysis software (version 21). Each of the learner datasets was imported into SPSS. The data were then 'cleaned', which involved screening for invalid cases, duplicates, outliers and missing data. Reliability analysis was carried out on each grade level test, providing a reliability coefficient for each test as well as item means and discrimination indexes for each item. Items were screened to ensure that each one contributed to test reliability. Items with a negative effect on test reliability were flagged and considered for deletion prior to the analysis.
A detailed analysis of results was carried out utilising SPSS Statistics. Learner performance was analysed with respect to group (intervention or control group), type of support received (group A or B), province, school, language of instruction and age of learner. Overall means were calculated for the whole test, as well as for word problem type items only. Using the coding, descriptive statistics were used to analyse the learner errors in conjunction with learner material given to the teachers in the intervention schools. Qualitative notes were added to the findings using a random sample of learners' scripts taken from the greater sample of coded tests.
Findings: The process
The error analysis methodology employed for the purpose of the evaluation report is instructive in itself. In developing the error codes, it became clear that even though the mathematics expert and the selected markers were relatively good at predicting the types of errors learners were likely to make, they often did not list all the possible errors. This lead to the need to add additional codes after the coding of an initial sample of scripts was completed. The markers did not anticipate finding certain types of errors, such as reversals and rotations of numerals and digits within numbers, in the higher grades (i.e. grades 3 and 4), but these errors were found to be quite prevalent.
Since markers were recruited from a pool of teachers, district officials (i.e. mathematics curriculum advisors) and graduate students qualified as specialists in mathematics teaching with relevant experience in teaching mathematics and references from reputable sources, accuracy of marking was expected to be high. This was, however, not the case, at least not in the initial stages of marking. Intensive training and discussions were needed before a high level of agreement between markers was reached. The processes of quality assurance, discussions of issues and training became iterative and were judged to be essential for maintaining high levels of consistency in the marking. This indicates the relative unfamiliarity of error analysis to teachers, teaching students and district officials; the indication was confirmed through anecdotal discussions with markers.
It was found that the quality of data that can be expected from error analysis is limited by the overall quality of the test construction, as well as by the quality of specific test items. It stands to reason that poor functioning test items would yield less valuable data regarding learners' performance than items that function well. For the purposes of this article we adopted the definition of a good test item as found in Gregory (2000), i.e. an item that measures the construct that it is supposed to measure, that discriminates well between weak and strong learners and that is free from bias. In this analysis, a curriculum-based scholastic achievement test was used, which highlighted another factor that influenced the data that could be extracted through error analysis, namely, the effect the conceptual model that underpins the South African curriculum has on the selection of knowledge to be tested in a curriculum based test. For example, addition, subtraction, sharing and grouping, halving and doubling are just a few of the concepts taught in the first school year according to the Curriculum and Assessment Policy Statements (DBE 2011). This leads many of the scholastic tests developed by the DBE (and others) to include only one or two items per concept or skill. Such tests do not adequately capture the conceptual development of learners, nor do they elicit all the common errors associated with a specific construct. In psychometrics this is termed construct under-representation (Downing & Haladyna 2004) and it limits the validity of diagnostic inferences made from the specific measure. We, however, argue that despite the often very apparent limitations of the tests used in South African schools, error analysis could still be considered a worthwhile and beneficial activity, even if it just makes the teacher aware of the limitations of the specific test or test item in yielding valuable data and the need for further investigation through e.g. the use of cognitive diagnostic tests.
Findings: Learner errors
The findings of the error analysis are presented in a series of tables, each of which represents a step in the error analysis process. The first step in analysing a learner test would be to determine the difficulty level of each of the items. This shows (based on the results) which items learners found more difficult and less difficult. In a well-constructed test the progressive difficulty of items would be indicative of the phases of mathematical conceptual development through which learners pass. In this case, as in many other examples of scholastics tests in South Africa, the tests did not contain a sufficient number of items to systematically test learners' conceptual development in any one construct. The test rather covered a wide variety of concepts and skills at just one juncture (or very seldom two) in conceptual development, e.g. the grade 1 test only contained two addition items (the first, 6 + 2 + 2 = □ and the second 9 + 8 = □). In a test designed to reflect conceptual development, item difficulty levels could be used by teachers to set priorities in order to plan the progressive development of concepts effectively. Note that the number of test items per grade differs, but that for each grade difficulty level 1 is the most difficult item.

In terms of mathematical curricular content areas, there was a spread of difficulty levels across all of the content areas in all grades.2 For example, the shaded cells are those items in which learners achieved over 40 percent as a raw score in the test. Achievement in the different learning areas does worsen from grade 1 to 4, but in all grades there were 'easier' and 'more difficult' items from each content area. It can be deduced that there are still many areas of weakness in learners' performance across the curriculum and much can still be learnt from the errors evidenced in these tests. We argue that the vast spread of areas of difficulty might be the result of a curriculum requiring the teaching of a vast variety of concepts and skills from grade 1 onwards, as opposed to devoting more intensive teaching to the basic concepts that form the foundation for mathematical understanding and development.
The second step is to focus on the 'correct methodologies' of the test-takers. This is a positive step that gives insight into what is working rather than leaping straight into what is not. The addition of this step incorporated skills analysis with error analysis. In this study it was seen that not all learners showed their working (in spite of being encouraged to do so) and as a result it was not always possible to identify methodologies learners used or the conceptual level on which learners functioned. However, limited information on which items learners were able to do well does become clear when one focuses on questions learners got right. Evidence from the error analysis revealed, as is to be expected, that learners were using unit and group counting methods, vertical and horizontal algorithms and diagrammatic representations to find the solutions to questions involving operations.
The third step involves the identification of whether a 'correct' methodology was used, but in such a way that it lead to a final answer that was incorrect. This can be seen as a 'step in the right direction' and gives insight into work which can be honed, not necessarily starting from scratch. Ashlock (1994) termed this category of error "defective algorithms".
The fourth step is to identify the extent to which questions were not attempted, since this reveals areas of weakness in which no knowledge appears to be present and full attention to these topics is required.
The fifth and final step is to identify the most commonly occurring errors per item. One can go into great detail here, which would yield a rich overview of learner errors, the underdeveloped concepts on which they are based (where relevant) and ideas for how to address these errors. This step is left to the end, since it is the most complex and it builds on the earlier steps. A focus on learner errors also reveals that some of the children's thinking cannot be classified according to some or other predetermined category as decided by the team expert. These errors we coded as "other incorrect answer". A prevalence of such errors could be a sign of general confusion, which does indicate a need for further clarification of the topic by the teacher. It could also indicate a need for the child to be assessed with alternative tools, preferably a standardised diagnostic instrument that can produce a very detailed description of the level of conceptual development of the child.1 Other alternative assessment methods, such as talk-through-the-problem approaches, are also very useful in gathering further information regarding the conceptual understanding of a specific learner.
Some of the learner errors are shown here by way of example, since it is not possible to record all of the errors noted in the full report. These examples are taken from the qualitative sections of the report where learners' work was shown with a view to raising questions as to the curriculum requirements.
Examination of the grade 1 learners' scripts showed that very little tangible 'workings' were done on the part of learners. The working processes were frequently done with some manipulatives or drawings of little sticks or circles (serving as counters). This indicates that these learners are still relying on count all and count on/ back strategies in problem solving, despite a curriculum requiring grade 1 learners to exhibit understanding of place value by the end of the second term. In the opinion of the authors, this is an example of where the conceptual model underpinning the South African curriculum does not take cognizance of the research in the field of mathematical cognition.
An example of learner's work from the grade 1 script shown below in figure 1 illustrates the mechanical use of unit counting with little or no understanding. We argue that this is an expected result when the teaching of operations commences before learners have mastered ordinality and cardinality of number, which would enable them to grasp the part-part-whole principle (see Ehlert & Fritz, 2013; Ricken & Fritz, 2009). This type of application of procedures without the necessary conceptual understanding is also mentioned by researchers such as Wisniewski (1990) as a cause of systematic errors.

In this example, which is most disturbing, the learner has drawn units (in the form of circles) all over the paper. This learner only answered one question correctly in the test. There is no logic or reasoning apparent in the illustrations, though presumably the learner has been led to believe that illustrations of units are meaningful and may earn some credit in a test paper or, at the very least, should be shown. The excerpt from this learner's script shows a response to the question "Calculate: 6 + 2 + 2 = □". The working shows 6 circles and two symbols beneath the circles which could possibly be numerals to represent the twos; the drawings have some relation to the question, but no further working and no solution to the question is given.
Excerpts from grade 2 learners' work add to the insight gained from the grade 1 scripts into learners' use of unit counting in their solution of mathematical operations. The excerpts illustrate that many learners drew counts (either with sticks or circles), but these did not necessarily correspond to the answers then given or the questions being answered. This raises the question of whether learners truly understand the mathematical concepts needed to perform operations or are they merely going through the motions of some or other method they has been taught?
The extract shown in figure 2 is an example of unit counting that has not worked although it got 'close'. One needs to think about the frustration which must surely be felt by a learner who has taken such care to draw so many units (not clustered in any systematic manner according to place value, which is possibly why the count went wrong in the end). The question needs to be asked - has this learner had the opportunity to master the principles of cardinality and decomposition of number before being faced with the concepts of class inclusion and embeddedness or was this learner merely taught a method to solve addition problems? It is clear from the learner's responses that the learner is still making use of counting all or counting on strategies at the end of his/her grade 2 year.
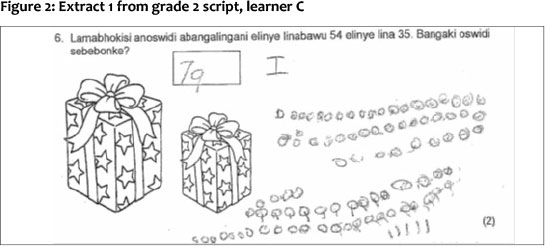
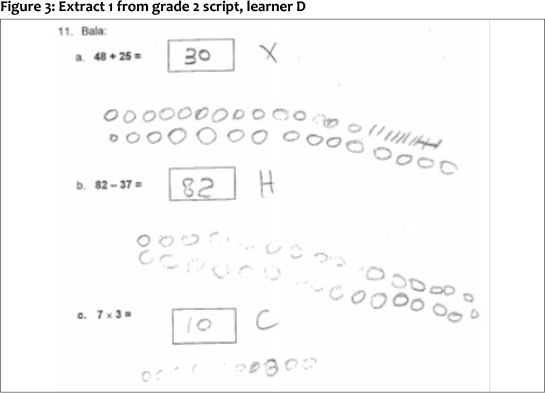
The next two extracts shown in figures 3 and 4 consist of three different examples of calculation in grade 2 level addition, subtraction and multiplication as specified in the curriculum. There is no consistent use of counting and the counting does not always lead to the correct solution. The answers vary in the extent to which they correspond to the working shown - some do have connections, but others seem to come out of the blue or are related to the question itself (for example performing the incorrect operation on the numbers in the question).

Examples taken from learners' scripts in grade 3 begin to give insight into the use not only of unit counting, but also of numeric vertical and horizontal algorithms. From these examples we can see how evidence of learner errors in the numeric calculations lends itself well to meaningful explanations which teachers can use to guide the learners in the correct use of place value when doing calculations in higher number ranges.
The first pair of extracts shown in figure 5 illustrates horizontal working or breaking down of numbers in some way. Errors arise in both extracts. There is logic that can be identified in these methodologies and an observer can work out the learners' reasoning shown in this working. To give meaningful explanations, a teacher would have to take time to get into the heads of the learners and work out their mathematical reasoning. The teacher could then start to address the errors that have resulted from the learners' working. Working horizontally has, to an extent, enabled learner H to get very close to the correct answer in the addition question, but not so in the subtraction question. Learner I, although having given horizontal working, demonstrates the well-known errors which learners make when operating on numbers that involve regrouping if the learners do not understand place value and how to work with it. The question arising from these extracts is: What would be required to consolidate the learners' understanding of decomposition of number in order to move them beyond their current level of understanding?

The second pair of extracts in figure 6 gives insight into learners' incorrect use of the vertical algorithm. Here it is evident quite quickly what has gone wrong; a teacher could meaningfully engage with these learners to explain how and where their calculations went wrong and how to address the errors identified. The same errors involving poor use of place value and regrouping using place value can be seen as in figure 5, but because of the structure of the algorithm, what the learners have done is clear and a teacher can pinpoint the errors and address them. When addressing these errors, teachers can devise explanations which are meaningful to the learners on how to use place value to regroup and add or subtract correctly.

The extracts in figure 6 also give evidence of unit counting by all three learners in the multiplication question. In the case of learner L, the learner's working is inaccessible and meaningless in all three of the questions and the answers given bear no resemblance to the circles drawn by way of working in the spaces provided for learners' work. In the case of the unit counts used by learners J and K, there is some order which can be interpreted, but the working still did not yield the correct answers.
The next extract shown in figure 7 present an example of grade 4 learners' work. The extracts show that unit counting at this level is not helpful. Both of these extracts are from the same learner's script. In the first extract, the learner clearly and neatly shows his or her working using the vertical algorithm for subtraction, but makes several errors. The numeric calculation does not appear functional as a working model; rather it is more of a written record for working that has been done on the side using unit counting. The understanding of place value and the way in which it is used when subtracting from a 3-digit number (regrouping and breaking down) is evidently not yet in place (only required by CAPS the third term of grade 4); the learner did not manage the 'borrowing'. This learner cannot even compute 15-8 and 12-7 mentally and has used circles and crossing out (unit counting) to do these calculations. It should be noted that 12-7 should actually have been 11-7, since the tens were broken down when 15-8 was computed. Again, is this evidence of teaching a method of problem solving before the learner is conceptually ready? In spite of these complications, based on learners' errors, the teacher could identify the need to teach decomposition and place value before proceeding with vertical algorithms.

The progression of extracts from the grade 1 to the grade 4 scripts has been presented to indicate how error analysis can be used as a starting point for answering two questions: At what level of conceptual understanding is the learner functioning; and what actions are needed from the teacher to assist the learner to progress to the next level of conceptual understanding? In the process of attempting to answer the above questions, other important questions arise. Are teachers teaching methods of problem solving at the expense of conceptual understanding? Does the curriculum expect learners to perform at levels for which the learners are not conceptually ready? Does the current structuring of our tests allow for in-depth error analysis? These questions provide evidence of how error analysis can assist teachers to think critically about teaching practices.
Discussion
It is not possible to reduce the error analysis findings easily. The details of the spread of errors discussed in the project report could not be included here. This, however, does not mean that the details regarding errors are deemed unimportant. Quite the opposite.
Across the grades, the percentages of learners whose answers could not be coded according to any particular mathematical reasoning were high. Such answers are probably indicative of general lack of understanding/knowledge of the content covered in the particular item. These percentages were highest in grade 4 and followed a similar pattern across the control and intervention groups in all grades. This means that many of the learners who wrote the tests did not exhibit identifiable mathematical reasoning when answering, which makes it difficult to address the misconceptions underlying their errors. This further indicates the need for standardised diagnostic mathematics tests, as well as teacher training in the use of alternative methods of assessment (e.g. talk-through-the-problem approaches), which could illuminate the conceptual understanding of learners.
The analysis of the percentages of learners who did not attempt to answer each item goes further to providing insight into areas of difficulty. The pattern of learners who 'did not attempt to answer' the questions was similar for control and intervention groups, revealing common areas of difficulty which need attention. Highest percentages of questions not attempted in grades 3 and 4 related to fraction concept - in which diagrammatic wholes were provided. This is interesting when considered in the light of the findings of quite a few researchers - that teachers also tend to struggle with fractions (Ball, 1990; Mok, Cai & Fung, 2008; Yim, 2010). Across all grades there were very slightly higher percentages of learners who avoided the geometry items.
An analysis of the 'partially' incorrect answers gives insight into content/skills that could be developed in learners. Across all of the grades these partially correct answers indicate that learners were aware of the correct operation that needed to be done, but did not complete the operation correctly. This indicates some conceptual understanding, despite the presence of procedural error(s). This can at least be seen as a step in the right direction, with the learners having skills that need to be honed rather than taught from scratch. Errors in the formation of numerals should be noted - in several questions the inability of learners to write numerals correctly was seen (particularly in grades 1 and 2) and this should be addressed as a matter of urgency, since learners cannot progress if they cannot even write their numerals correctly. The two grades in which there was the greatest evidence of answers indicating partial understanding were grades 2 and 3.
There were errors evident in all of the mathematical content areas covered in the test and they were prevalent in these areas to such an extent that they all warrant attention. Of particular concern is the very poor performance on items in which the measurement of time was involved. Learners (across both groups) did not seem able to tell the time using analogue clocks or to refer to a calendar in a meaningful way. Many of the errors made by learners in both the control and intervention groups are common errors made not only by South African learners, but also by learners internationally. These errors (often based on misconceptions) are seen by some as a natural part of the learning process (Nesher 1987). The majority of these errors are of a conceptual nature, although many procedural errors were also noted. It is important that teachers are made aware of such errors and how to address them, since they would then be empowered to enable their learners to grow out of these misconceptions and reach a full and correct understanding of the foundational mathematical concepts assessed in this test.
Many of the errors point to a learner's use of a problem solving method despite a lack of conceptual understanding. Whether this is the result of poor or no conceptual teaching, teaching of concepts and skills for which learners are not yet ready or an unreasonably fast pace required by the curriculum, is open to debate.
Conclusion
The ANA tests now written annually in South Africa will go no further than quantifying and monitoring the problem which we already know exists in our schools (one of the said purposes of the ANA, but not the only one) unless the scripts are taken up and used by teachers for self-evaluation purposes. This study clearly shows how much can be learnt if learners' scripts are analysed with regard to learner errors, even when limitations are imposed by less than ideal test construction and a fast paced curriculum that often requires learners to master skills for which they are not conceptually ready.
An analysis of learner errors does require mathematical content and pedagogical content knowledge on the part of teachers, but it would also serve to broaden teachers' knowledge of mathematical cognition and concept development. We would recommend that teachers pick up their learners' test scripts (including the ANA scripts) and start to sift through them, question by question, noting both correct methodologies and errors learners make and that teachers then follow up (at their own pace, but with due diligence) any methods or errors which they themselves cannot explain. In this way, one step at a time, teachers' mathematical content and pedagogical content knowledge will be developed. Teachers will also be able to adapt their teaching to address the errors which they note are prevalent in their learners' work and work towards the goals they set for themselves on an annual basis regarding the achievement of their learners. Teachers may even become aware of which items in their assessments and tests yield better data regarding learners' difficulties, which in turn may lead to improvement in teachers' assessment practices.
We further recommend that the DBE (and other stakeholders) take a more rigorous approach to the error pattern analysis in the ANA and other testing programmes. This would include investigating whether the common errors made by learners are similar across language and cultural groups. It further entails that in their reporting, the descriptions of common errors are supported by research findings and reference is made to the cognitive developmental research which should underpin mathematics teaching. In short, in an effort to avoid over emphasis on procedural correction to the detriment of conceptual understanding, learner errors must not just be superficially described, but must be embedded in the knowledge of why, when and how learners learn mathematics and make the mistakes they often make. We would hazard to say that such an in-depth analysis of learners' responses to test items would probably lead to a reconsideration of the test construction processes followed in the ANA and other curriculum based tests that are used for diagnostic purposes as well as of the content and pace required by the curriculum.
Acknowledgments
The authors express their appreciation to: JET Education Services for the funding and resources made available for the completion of this paper; the 5000 learners in 40 schools that agreed to participate in the broader study of which this paper is an extension - without your willing participation and kindness this paper would not have been possible; Maureen Mosselson for the endless hours of editing and advice; and professor Elbie Henning for her advice on conceptual development and the teacher - learner interplay.
References
Allsopp, D.H., Kuger, M.H. & Lovitt, L.H. 2007. Teaching mathematics meaningfully: Solutions for reaching struggling learners. Baltimore: Paul H. Brooks. [ Links ]
Ashlock, R.B. 1994. Error patterns in computation. 6th edition. New Jersey: Prentice Hall. [ Links ]
Ashlock, R.B. 2006. Error patterns in computation: Using error patterns to improve instruction. 9th edition. New Jersey: Pearson. [ Links ]
Ball, D.L. 1990. Pre-service elementary and secondary teachers' understanding of division. Journal for Research in Mathematics Education, 21(2):132-144. [ Links ]
Ball, D.L., Hill, H.C. & Bass, H. 2005. Knowing mathematics for teaching: Who knows mathematics well enough to teach third grade, and how can we decide? American Educator, 29(1):14-46. [ Links ]
Ball, D.L., Thames, M.H., & Phelps, G. 2008. Content knowledge for teaching: What makes it special? Journal of Teacher Education, 9(5):389-407. [ Links ]
Borasi, R. 1994. Capitalizing on errors as "springboards for inquiry": A teaching experiment. Journal for Research in Mathematical Education, 25(2):166-208. [ Links ]
Carey, S. 2004. Bootstrapping and the origin of concepts. Daedalus, 133(1):59-68. [ Links ]
Department of Basic Education. 2011. Curriculum and assessment policy statement: English mathematics foundation phase grades 1-3. Pretoria.
Department of Basic Education. 2013. Annual National Assessments 2013: 2013 diagnostic report and 2014 framework for improvement. Pretoria.
Downing, S.M. & Haladyna, T.M. 2004. Validity threats: Overcoming interference with proposed interpretations of assessment data. Medical Education, 38(3):327-333. [ Links ]
Ehlert A., & Fritz, A. 2013. Evaluation of maths training programme for children with learning difficulties. South African Journal of Childhood Education, 3(1):101-117 [ Links ]
Franke, M.L. & Kazemi, E. 2001. Learning to teach mathematics: Focus on student thinking. Theory into Practice, 40(2):102-109. [ Links ]
Gelman, R & Butterworth, B . 2005. Number and language: how are they related? Trends in Cognitive Science, 9(1):6-10. [ Links ]
Gregory, J. 2000. Psychological testing: History, principles and applications. 3rd edition. Boston: Allyn and Bacon. [ Links ]
Hill, H.C., Ball, D.L. & Schilling, S.C. 2008. Unpacking pedagogical content knowledge: Conceptualizing and measuring teachers' topic-specific knowledge of students. Journal of Research in Mathematics Education, 39(4):372-400. [ Links ]
Ketterlin-Geller, L.R. & Yovanoff, P. 2009. Diagnostic assessments in mathematics to support instructional decision making. Retrieved from http://pareonline.net/getvn.asp?v=14&n=16 (accessed on 19 April 2014).
McGuire, P. 2013. Using online error analysis items to support pre-service teachers' pedagogical content knowledge in mathematics. Retrieved from http://www.citejournal.org/vol13/iss3/mathematics/article1.cfm (accessed on 19 April 2014).
Mok, C.A.I., Cai, J. & Fung, F.T.A. 2008. Missing learning opportunities in classroom instruction: Evidence from an analysis of a well-structured lesson on comparing fractions. The Mathematics Educator, 11(2):111-126. [ Links ]
Nesher, P. 1987. Towards an instructional theory: The role of students' misconceptions. For the Learning of Mathematics, 7(3):33-39. [ Links ]
Olivier, A. 1996. Handling pupils' misconceptions. Pythagoras, 21:10-19. [ Links ]
Radatz, H. 1979. Error analysis in mathematics education. Journal for Research in Mathematics Education, 10(3):163-172. [ Links ]
Riccomini, P.J. 2005. Identification and remediation of systematic error patterns in subtraction. Learning Disability Quarterly, 28(3):233-242. [ Links ]
Russell, M. & Masters, J. 2009. Formative diagnostic assessment in algebra and geometry. Paper presented at the annual meeting of the American Education Research Association. San Diego, California.
Shalem, Y. & Sapire, I. 2012. Teachers' knowledge of error analysis. Johannesburg: Saide. [ Links ]
Sherman, H.L., Richardson, L.I. & Yard, G.J. 2005. Teaching children who struggle with mathematics: A systematic approach to analysis and correction. New Jersey: Pearson. [ Links ]
Shulman, L.S. 1986. Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2):4-14. [ Links ]
Shulman, L.S. 1987. Knowledge and teaching: Foundations of the new reform. Harvard educational Review, 57(1):1-22. [ Links ]
Sousa, D.A. 2008. How the brain learns mathematics. California: Corwin Press. [ Links ]
Wisniewski, L.A. 1990. A comparison of subtraction error patterns between students with learning disabilities and nondisabled peers. Dissertation Abstracts International, 52(2):506. [ Links ]
Yang, C.W., Sherman, H. & Murdick, N. 2011. Error pattern analysis of elementary school-aged students with limited English proficiency. Investigations in Mathematics Learning, 4(1):50-67. [ Links ]
Yim, J. 2010. Children's strategies for division by fractions in the context of the area of a rectangle. Educational Studies in Mathematics, 73(2):105-120. [ Links ]
Endnotes
1. See volume 3(1) of this journal, which comprises a number of articles on the topic of a suitable diagnostic tool for South African children, as well as Ketterlin-Geller and Yovanoff (2009) for a description of the benefits of diagnostic assessment in structuring remedial teaching plans.
2. In this table we refer to curriculum discourse and not to the concepts that were tested by the various items. This, therefore, is a table of item difficulty according to content area. These are not conceptual categories. The tables giving learner errors (conceptual/procedural) were also given in the project report.














