Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.3 n.2 Johannesburg 2013
A learning pathway for whole numbers that informs mathematics teaching in the early years
Cally KühneI; Ana-Paula LombardII; Trevor MoodleyIII
IUniversity of Cape Town, Schools Development Unit. Email: cally.kuhne@uct.ac.za
IICape Peninsula University of Technology. Email: LombardA@cput.ac.za
IIICape Peninsula University of Technology. Email: MoodleyT@cput.ac.za
ABSTRACT
This paper reports on the development of a Learning Pathway for Number (LPN) with the aim of facilitating the teaching and learning of whole number in the early primary grades (Grades R - 4) within the South African educational context. The development of the LPN was based on the Dutch Learning/Teaching Trajectory for Whole Number (Van den Heuvel-Panhuizen, 2001). This paper describes a case study that presents the development of the LPN with three teacher groups (teachers from a school improvement project, teachers from high-performing schools and pre-service student teachers). The LPN is a conceptual framework based on five learning/teaching principles, namely the context, level, activity, interaction and the guidance principles. The benefit of this pedagogic tool adapted and refined for the South African context is that it provides a longitudinal view, highlighting milestones in the learning of number with the aim of deepening learners' conceptual understanding of number over time. This case study reveals the importance of a devise that enables teachers to reflect on their mathematics content and pedagogy and bridges the theory-practice divide. It also highlights the critical issue of language and the use of appropriate terminology and activities in the classroom.
Keywords: early years, early number, learning trajectory, South Africa
Introduction
It is well documented that Mathematics performance in primary and secondary schools in South Africa is unsatisfactory (TIMMS, 1999, Howie, 1997 & 2004; Carnoy & Chisholm, 2008; Taylor, 2011; Department of Basic Education, 2012) and that limitations on teachers' mathematical content and pedagogical knowledge (Department of Basic Education, 2007; National Planning Commission, 2011) appear to contribute learner underachievement in Mathematics (Carnoy & Chisholm, 2008). Furthermore, there is limited support for teachers when it comes to the national curriculum subject for Mathematics in terms of understanding how children learn concepts and how these concepts link across the curriculum and grades (Department of Basic Education, 2009). Within the context of the South African Foundation Phase (FP), limitations in teachers' knowledge applies to the Mathematical domain of Number, Operations and Relationships (Department of Basic Education, 2011). Additionally, most South African teachers do not organise and sequence number concepts and activities in terms of conceptual development, but rather do so in a manner based on "concrete to abstract" notions and generic teaching approaches (Kühne, Van den Heuvel-Panhuizen, Lombard, Ensor & Cranfield, 2005). Kühne (2004) states that teachers do not have a good understanding of the stages in number concept development and that they rarely distinguish between, or elaborate on, these stages. Moreover, teachers do not share a common discourse and understanding of children's number development and they express their understanding generally within the context of their own classroom experience.
Learning pathways
One of the approaches to augmenting teachers' knowledge is the use of learning pathways or 'teaching-learning path that consists of the significant steps in learning a particular topic; each new step in the learning path builds on the earlier steps' (National Research Council, 2009). Learning pathways make explicit the content that is needed to provide suitable instructional tasks, with specific goals, so that the child moves through a developmental progression of thinking in that particular mathematical domain. Such learning pathways have been described as 'learning/ teaching trajectories' (Van den Heuvel-Panhuizen, 2001), 'learning trajectories' (Clements & Sarama, 2004; 2009), 'mental structures' (Gelman & Brenneman, 2004), 'instructional sequences' (Clements & Sarama, 2004), 'growth points' (Gervasoni, 2005), 'building blocks', (Clements & Sarama, 2004) and 'learning frameworks' (Wright et al., 2006). For example, Clements and Sarama define "learning trajectories" as follows:
Descriptions of children's thinking and learning in a specific mathematical domain, and a related conjectured route through a set of instructional tasks designed to engender those mental processes or actions hypothesized to move children through a developmental progression of levels of thinking, created with the intent of supporting children's achievement of specific goals in that mathematical domain (Clements & Sarama, 2004:83).
Since the concepts of number, operations and relationships constitute the major component of the Foundation Phase (FP) Curriculum Assessment Policy Statement (CAPS) (Department of Basic Education, 2011), it can be argued that the greatest value gained in mathematical achievement is when 'most of [our] instructional time is spent on deep learning of small numbers' (Clements & Sarama, 2004:187).
The use of a number trajectory can serve as a tool for connecting theory and practice and guide instruction in a sequential way. Sarama and Clements (2009) suggest that learning trajectories have three main parts: a mathematical goal that includes the big ideas of mathematics; a developmental path that maps the typical learning route that children follow in the acquisition of particular mathematics knowledge and skills; and instructional tasks or activities for each level of children's thinking in a developmental progression. Learning trajectories or learning pathways can help to overcome the aforementioned difficulties because they can assist teachers to understand the developmental progressions in learning mathematics and can give suggestions to teachers to build enriched learning environments that are developmentally appropriate and effective. By means of a learning pathway, teachers can recognise that there are stages in number concept development, and that progression between these stages takes place (Kühne, 2004). In fact, over time teachers can internalise and own this learning pathway, which provides a lens through which their interactions with individual learners, small groups and the whole class can be viewed and guided (Bobis, Barbara, Clarke, Thomas, Wright & Gould, 2005).
In order to support South African teachers' professional development in the domain of number, a Learning Pathway for Number (LPN) (Van den Heuvel-Panhuizen, Kühne, & Lombard, 2012) was developed, which was inspired and based on the Dutch Learning/Teaching Trajectory for Whole Number (Van den Heuvel-Panhuizen, 2001a). The LPN relates to the South African Mathematics curriculum and highlights the main features of children's number development in the early years of schooling (Grade R - 4). The rationale for developing this LPN was that if teachers have insight into how the learning of number concepts takes place over time then they would be better able to make informed decisions about planning, teaching and assessment of whole number within the diverse South African context.
Background to the Learning Pathway for Number (LPN)
The development of the LPN was part of the South African project, Count One Count All (COCA) that was funded by the South Africa-Netherlands Research Programme on Alternatives in Development (SANPAD). The University of Cape Town's School of Education's Schools Development Unit (SDU), the Freudenthal Institute (Utrecht University) and the Cape Peninsula University of Technology (Mowbray Campus) collaborated on this project between 2004 and 2007.
Teaching principles
The underlying teaching principles of the LPN have been adopted from the grounding principles of Realistic Mathematics Education (RME) (Van den Heuvel-Panhuizen, 2000 & 2001b; Van den Heuvel-Panhuizen & Drijvers, in press). Five principles for teaching underpin the theory of the LPN, namely: the context, level, activity, interaction and guidance principles. A brief description of each principle follows:
1. The context principle applies to the idea that teaching of mathematics is based on the assumption that the learning of mathematics requires contexts that are meaningful for learners.
2. The level principle relates to the context principles. The idea that learning mathematics requires that children pass through various levels of understanding of a particular concept: from the ability to invent informal context-related solutions, to the creation of various levels of short cuts and schematisations, to the acquisition of insight into the underlying principles and the discernment of even broader relationships (Van den Heuvel-Panhuizen, 2000). Through an awareness of the level principle, teachers will be able to gauge the child's understanding and guide them to higher levels through careful scaffolding and use of mathematical models. Relevant contexts and activities can then be designed which will steer children to the required mathematical goal.
3. The activity principle is grounded in the idea of mathematics as a human activity and implies that learners should be directly involved in the learning-teaching process. This necessitates that learners should be directly involved in processes that support their understanding as they engage with mathematical ideas and activities. This principle directly relates to the interaction and guidance principles.
4. The interaction principle is related to the aspect of social learning and the significant role of interaction between teacher and learners. The socio-constructivist theory of learning as a social activity (Vygotsky, 1978, Woolfolk, 2010) is a strong feature of the LPN. Effective learning takes place when there is discussion and questioning about thoughts and strategies. This involves both listening and speaking. By reflecting on the thoughts and strategies of others, the learner can move to higher levels of mathematical understanding. As children interact with each other and the teacher, the teacher gains insights into the child's level of understanding and is able to use that knowledge to advance the child's understanding.
5. The guidance principle implies that the teacher and the instructional programme should contain situations for learning, which have the potential to work as a lever in shifting children's understanding. It is important that the teacher holds the perspective of the LPN to guide the learning process and assist children to make meaning of the learning situations by reflecting on their understanding.
Aim and structure of the LPN
The LPN gives a detailed description of learning and teaching whole number in the early primary grades. By offering a longitudinal overview of the learning process and the milestones in the development of number concept, the LPN provides teachers with a coherent conceptual educational map for didactical decision-making when teaching number in the Foundation Phase. Clements and Sarama (2009:17) suggest that 'learning trajectories have three parts: a goal (that is, an aspect of a mathematical domain children should learn), a developmental progression, or learning path through which children move through levels of thinking, and instruction that helps them move along that path'. Understanding the different levels of development and the extent of a child's knowledge in each level means that teachers are able to understand what is coming next and what came before in a child's development. Knowing children's learning progression may be an empowering competence for teachers. The intention of the LPN is to give teachers this knowledge so that they can create learning opportunities in the early grades and a firm foundation for further development so that children will succeed in mathematics in the higher grades. It is hoped that the LPN might pave the way for a new framework for teacher professional development in mathematics education by bridging the divide between theory and classroom practice.
The LPN describes the different aspects of whole number development in four distinct but related stages:
Stage 1: Emergent number concept
- first attempts to deal with numbers
- growing number concept
- number knowledge up to 5 and 10 (and beyond)
- emergent counting-and-calculating up to 5 (and beyond)
Stage 2: Counting-and-calculating (counting-based calculating)
- number knowledge up to 20 (and beyond)
- operations up to 10 (and beyond)
Stage 3: Calculating (number-based calculating)
- number knowledge up to 100 and 1 000 (and beyond)
- operations up to 20 and 100 (and beyond)
Stage 4: Advanced calculating
- number knowledge up to 10 000 (and beyond)
- operations up to 1 000 (and beyond).
The four stages comprise the development of whole number that begins with the preschool stage of emergent and growing number concept, and describes the progress that most learners will make en route to the stage of advanced calculating that is usually reached in Grade 3 or 4. In the latter stage, learners are able to operate with numbers up to 1 000 (and beyond) and can make adequate decisions about the most suitable calculation form for a particular operation. For example, one problem may be more suited for mental calculation, while another is more suited for a written form or the use of a calculator. In addition, some problems may be more suited to approximate calculation (estimation) than for calculating a precise answer. Choosing which form is more efficient or suitable depends on the context and complexity of the operation, and the nature of the numbers involved. However, the learner's ability level can also be a determining factor in choosing a particular calculation form.
Overall, the underlying structure of the long-term development of the learning process for whole number reflected in the four stages identified in the LPN is the transition from counting-based strategies to non-counting-based strategies. The LPN describes this development within and across these stages and explains how the stages differ from each other and how they are connected to each other. Of course, not all children develop at the same pace. Therefore, the stages have to be considered with flexibility.
In the LPN, for each stage, descriptions are given of children's strategies and related knowledge and suggestions for classroom assessment tasks. The description of each stage outlines the main features and aspects of children's early number knowledge. Concepts are sequenced progressively and the stages that learners will pass through their way to reaching the Mathematics Number, Operations and Relationships Content Area as presented in the Curriculum and Assessment Policy Statement (CAPS) in the early primary grades.
Workshops based on the LPN
As discussed previously in this paper the LPN was elaborated in four stages, which were adapted from the Dutch learning-teaching trajectory for use in a South African context, i.e. as a tool for continuing teacher professional development and in line with content strands of the national curriculum for FP Mathematics. Initially a framework for the LPN was developed, which identified core milestones concepts in the development of whole number. The stages were outlined and explained and concept strands were identified, for example counting, calculations, estimation, etc. The figure below is taken from the Dutch TAL - Children Learn Mathematics: A learning-teaching trajectory with intermediate attainment targets for calculation with whole numbers in primary school (Van den Heuvel-Panhuizen, 2001a:14). The figure illustrates the basis from which the LPN framework was developed to show the progression from children's counting-based solution strategies to calculations with number and algorithms.
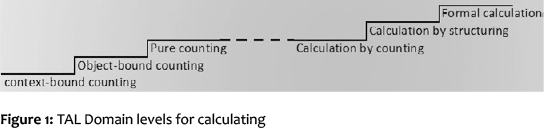
This framework guided the work with a group of Foundation Phase teachers in a school improvement project (project teachers) as the project team (researchers) expanded on each level and elaborated on the stage of development, while assisting with curriculum planning and lesson development. The project schools were geographically closely located and these teachers received two classroom-mentoring sessions per quarter over a two-year period that were specifically intended to support teaching and learning in the classroom. The medium of instruction and home language of the teachers and learners in these schools is isiXhosa. The workshops were conducted in English, but all classroom interaction between the teacher and children was in isiXhosa. The strategies used by the researchers to address this will be discussed in the next section. Parallel to this a second group of teachers trialled classroom activities and collated samples of children's work (reference group teachers) to support the development of the LPN. In addition to this, the development of the mathematical strands/content was incorporated into an initial-teacher development (student teachers) Mathematics methods course.
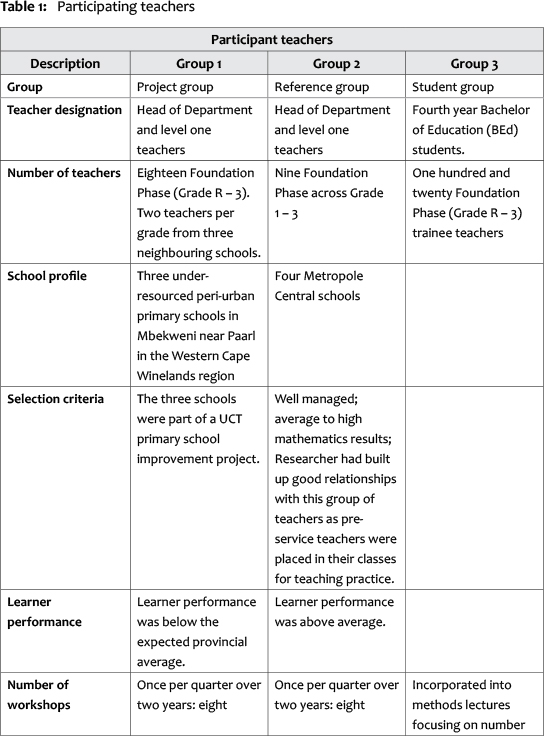
In this section, we describe our experiences in the development of the LPN with these three groups of teachers, and discuss the focus of the workshops that were held. All groups of teachers were given an overview of the purpose, principles and stages of the LPN. Over the two-year period eight workshops were conducted with each of the teacher groups with the average duration per workshop being two hours (one per quarter). The workshops were collaborative and involved application of the content in classrooms and lesson plans. After each workshop a report was written by the facilitator, and these notes/reflections on the content selected and classroom implementation were used to inform further development of the LPN content and future teacher workshops. The table below presents the three different groups of teachers who participated in the development of the LPN.
Workshops with teacher group 1: Project group of teachers
The workshops highlighted the specific features of the development of number across the four stages in the LPN between Grade R and Grade 4 and provided 'a conceptual educational map' (Van den Heuvel-Panhuizen et al., 2012:8) for approaching the teaching and learning of number. Participants were introduced to the notion of teaching conceptually and progressively. During the workshops teachers would engage in discussions and group activities that required that they do the following: map grade specific content along the developmental pathway, and identify specific content for their specific grade in terms of the LPN levels and link this to the national curriculum for their grade; select grade appropriate tasks and present challenging learning opportunities to nurture learners' progress in conceptual understanding; identify the individual learners' solutions in terms of count or number-based strategies; give learners appropriate feedback; and use appropriate teaching and learning materials to model the concepts and ideas they wanted to convey to their learners. Furthermore, these sessions assisted teachers to plan and sequence learning tasks and to address the needs of learners across the spectrum of number development, and also to develop in teachers a common language in discussing the teaching and learning of number (Van den Heuvel-Panhuizen et al., 2012:8).
During the workshops teachers discussed the application of the content that was presented, and they were required to develop lessons based on the concepts presented in the LPN framework. For example, teachers across Grades 1 to 3 would discuss the core concepts linked to counting. They would then discuss how best to present this in each grade, and finally they would select the most appropriate apparatus use in their lesson (this could include an abacus, string of beads or number line). In this way, the theory was grounded in the classroom and the LPN principles and stages of development formed the basis for the workshops. This approach was an attempt to expose teachers to a conceptual approach to curriculum planning, which focused on the big ideas rather than on discrete isolated activities and fragmented lessons.
The workshop sessions followed a set format: the researchers selected a concept and presented the teachers with a relevant section from the LPN. Small groups of teachers discussed these excerpts (vignettes of classroom situations or samples of learners' work) in terms of what they understood by the concept and the way it was presented. For example, when introducing oral counting, the four stages of counting in the LPN were presented to the group, along with a series of questions such as 'What do you understand by the term oral counting? Do you recognise any of the characteristics described in each of the stages of oral counting?' These examples of the discussion of oral counting illustrates how teachers were encouraged to reflect on specific aspects of number, and thus were made aware of the use of specific strategies for teaching number (for example rhymes in the learning of number sequence). This discussion led to an understanding of the importance of oral counting as a prerequisite for resultative counting (counting a collection of object with the aim of determining how many objects there are). In this manner, teachers' perceptions of teaching number sequence broadened as a conceptual progressive approach (Van den Heuvel-Panhuizen et al., 2012).
Teachers had not encountered mathematical terminology such as subitising (the ability to immediately recognise the number of objects in a small group or array of up to five, without counting) and numerosity (the 'how-much' or cardinality of a collection). Teachers were not familiar with these words in isiXhosa or English. Consequently, an intervention was designed in isiXhosa for later workshops to overcome this problem. Consensus was reached with regard to the generation of isiXhosa terms that best described the concepts and common understandings were achieved. Throughout the workshops, teachers were asked to reflect on specific terminology and revisit the process of finding consensus about a particular term, or concepts and the related words. In this way the group of teachers generated isiXhosa terms that they recognised and understood.
In addition, the LPN described the use of specific structured apparatus to be used in a teaching/learning situation with the intention of presenting models for various mathematical problems. For example, strings of 100 beads grouped in tens, presents the underlying structure of the base ten (decimal) number system. The string of beads provides a 'longitudinal' model for the number line. For example, in the early grades children use a five or ten-structure beaded necklace to practice on and discuss counting activities. Gradually the string of beads is replaced with an empty number line, which is used with children for supporting additions and subtractions (Van Den Huivel-Panhuizen, 2000). Apparatus were given to the teachers at the first workshop with the intention of modelling the use of these resources in demonstration lessons. The resources were intended to facilitate the link between theory and practice and provide tools that teachers could use in a process of scaffolding a concept with children. In subsequent workshops, the practice-theory link was emphasised and the appropriate selection and application of apparatus in mathematics lessons was highlighted. Discussions with teachers about the apparatus focused on children's thinking and were linked to classroom activities and the development of appropriate lessons. Teachers were also encouraged to reflect on the LPN principles and relate these to their own practices of teaching number, for example, to reflect on the different levels of competence and understanding children demonstrate during activities. The LPN addresses learners' needs at different levels of number development by providing problems that can be solved through the use of strategies based on different levels of understanding (Van den Heuvel-Panhuizen et al., 2012:8-9).
The workshops also provided a basis for sharing how individual teachers could restructure their teaching approaches to make learning more meaningful by considering classroom contexts and scaffolding learning activities in the transition of learners' everyday understandings to more formal and generalised abstract ways of working with number. Teachers therefore had to review their own theories of teaching and consider the view of learning as set out in the LPN activity and interaction principles. These LPN principles promote active learner involvement in the teaching-and-learning process as individual learners progress to higher levels of understanding through deliberate engagements with peers and the teacher.
Workshops with teacher group 2: Reference group of teachers
Initially teachers from nine primary schools wereinvited to participate in the development of the classroom activities, vignettes and collect samples of learners work for inclusion in the LPN. However, over a period of several months these groups had dwindled down to nine teachers from four schools. The teachers who withdrew expressed a keen interest in the work but were under pressure at their schools and felt that their participation in the workshops would be too time consuming. These teachers had a good relationship with one of the researchers who worked with them at their schools during the pre-service student practice teaching blocks. It was assumed that the teachers had a sound knowledge of teaching mathematics and would therefore be able to seamlessly transfer that understanding to the ways of thinking as expressed in the LPN. The focus of the workshops with these teachers was on the concepts (the content of the mathematics) and how this was organised in the LPN - the difficulty level, the scope and sequencing, the appropriateness for each stage (with grades and ages in mind), the required prior-knowledge, and the separation into skills, concepts, and classroom application.
The procedure followed with this group was firstly to give a brief overview of the purpose, principles and use of the LPN. Teachers were asked to note which number concepts children found difficult and which ones they considered to be most important for FP learners. Teachers were also asked to contribute classroom incidents and examples of how they integrated the use of particular content and apparatus in their classrooms, and to present any other relevant aspects of the teaching and learning of number, which they found interesting in the LPN. Most teachers found number-based counting and calculating to be challenging for children since the move to context-free calculations was seldom organised and clearly mapped out. The information generated from the workshops with this group informed the development of the LPN and guided the planning of workshops with the project group of teachers. For example, the appropriate use of resources and the role this plays in the development of number-based calculation strategies was particularly challenging for this group. Across the two groups of teachers there was a consistent reliance on the use of apparatus as the key focus of the lesson, which is concerning given Ball's view (1992:47) that 'although kinaesthetic experience can enhance perception and thinking, understanding does not travel through the fingertips and up the arm'. Ball (1992) suggests that Mathematics teachers need much more assistance in both how to select appropriate manipulatives to model a specific mathematical concept and how to assist learners to make the necessary connections between the use of the manipulative and the mathematical concept. Ball adds that often teachers overestimate the value of manipulatives because they have an image of what mathematical concepts or processes the materials represent. Consequently, during the workshops with the reference group of teachers, more attention was given to the appropriate selection of resources to advance learners' conceptual understanding of number.
Secondly, the researchers presented exemplars that were typical of learners' solutions, for example drawings or jottings used to solve a number or word problem. Discussion followed and the intention was to develop an awareness of how the individual learner's work can be used to identify the level of understanding and position in the continuum of the learning trajectory. This group of teachers were also unfamiliar with terminology used to describe calculation strategies such as these decomposition terms: 'stringing' (linked to the ordinal aspect of number and involves keeping the first number intact and splitting the second number into tens and ones); 'splitting' (linked to the cardinal aspect of number and involves building up and breaking down numbers into tens and ones up to 100 and beyond) and 'varying' (the use of a range of number knowledge and facts). These terms were discussed and teachers took time to engage with and use the terms comfortably. Subsequently, the teachers were asked to generate their own examples of solving problems by using these strategies. Subtraction, division and multiplication were specifically selected as teachers indicated that learners had most difficulty with these.
This group of teachers were given copies of stages 1 - 4 in the LPN and asked to reflect upon the different stages in terms of the content, pacing and activities. Teacher responses included for example, that the explicit "how to teach" of the four operations was not clear. This was similar to the teachers from the poorly resourced schools who expected to get step-by-step instructions and 'recipes' for what to teach. This was discussed and teachers were encouraged to think about the operations in terms of various contexts (for example manipulatives and word problems), rather than a series of 'steps' on how to teach.
Through workshop participation, conceptual progression in counting and calculating was highlighted with appropriate activities such as the initial use of concrete objects and drawings, followed by the use of different types of number lines and finally the use of context-free calculations.
Workshop with Teacher Group 3: Pre-service student teachers
Interactive workshop-style lectures were presented to students during their Mathematics methods course. Specific concepts were selected from the LPN, for example counting. This concept was introduced to students as a continuum across the stages. The students had already been exposed to the Mathematics content and issues of theory and practice in their first and second years of study. However, the transfer of earlier processes to the concepts offered by the LPN was not seamless and students had to be guided through the principles and content of the LPN.
Once again, new vocabulary had to be introduced, such as the descriptions of the various strategies; 'stringing', 'splitting' and 'varying'. Students were given examples of learners' work from both teacher groups (from poorly-resourced and well-performing schools), for discussion in groups. Unfamiliar terminology was extracted and illustrated in the learner examples. Students analysed the learners' work in terms of prior knowledge, understanding and implications for further teaching.
Students were made aware of the appropriate use of different forms of relevant apparatus in developing the conceptual understanding of number. For example, the linear models that are introduced in the LPN through the use of strings of beads grouped in tens. Later, these are abstracted to structured, semi-structured and unstructured number lines. Students designed activities using appropriate apparatus to foster conceptual understanding and progression in the learning and teaching of number. In this manner, student teachers were encouraged to consider how learners would progress conceptually by considering learners' prior knowledge and predicting future knowledge in relation to the development of mathematical concepts in number. This was unlike typical pre-service teacher experiences during teaching practice sessions, where concepts are traditionally taught in isolation.
The stages of the LPN also enhanced the pre-service student teachers' approach to addressing the diverse levels of understanding number within a specific classroom context. Finally, the mathematical knowledge of most pre-service student teachers was in itself limited. The LPN provided the group with a sense of the benefits of a conceptual approach to the teaching of mathematics.
Conclusion
The iterative process described in this paper, of engaging with teachers as part of the development of a pedagogic and teacher professional development tool, provided valuable insights and multiple perspectives on the longitudinal overview of the learning process and core milestones in the development of number concepts. The value of the LPN as a pedagogic tool is that number concepts are sequenced progressively and the stages that learners will pass in the development of number concepts are clearly indicated with descriptions and examples of learners' work that teachers can recognise because they have been taken from familiar contexts. In addition, the content of the LPN is aligned with the FP CAPS Mathematics content area Number, Operations and Relationships, and is therefore a relevant tool for the professional development of mathematics teachers in the South African context.
This development process revealed several important findings. Firstly, the authors overestimated the ability of the teacher groups to engage with pedagogical content knowledge. It seemed that the mathematical terminology was difficult to understand and therefore generated an aversion towards the reading of theory. All three groups preferred to be given tips and ideas on activities that could be used for teaching number without making an effort to understand their purpose and place in the sequence of teaching progressively and conceptually. The focus of the workshops was therefore on relating number concepts to practical classroom activities.
Secondly, the authors had preconceived assumptions about the knowledge bases of each of the three teacher groups. After engaging with the principles of the LPN, the project group of teachers were able to bridge the theory practice divide to some extent, contrary to prior expectations. The reference group of teachers were not as knowledgeable as expected in terms of pedagogical theory related to number. In particular, they were uninformed about the systematic use of resources in the transition from informal counting-based strategies to formal operations. After exposure to the LPN stages and principles, teachers said they felt more confident and able to select and use appropriate resources to advance learners' understanding of number along the continuum from concrete representations to abstract ideas. This was also evident in the lessons and learner tasks. It was expected that the student teachers would lack the knowledge and experience to design and implement conceptually progressive teaching and learning activities. However, after being exposed to the LPN principles, they were (to some extent) able to sequence learning activities developmentally. Therefore, although this group of teachers came from well-resourced schools, they were unaccustomed to thinking about the purpose of using resources appropriately in developing learners' conceptual understanding. Consequently, there was little planned transition from concrete counting activities to abstract calculations.
As the process developed, our assumption that the teachers' knowledge about teaching mathematics was at a high level because their learners achieved high results proved to be untrue; the one does not automatically follow the other. A teacher queried why this level of reflection and theory, if covered at colleges and universities, did not filter into the classroom. She was particularly motivated to be part of the development of the LPN as she recognised the value of dealing with concept strands and Mathematics content that underpins the topics that Foundation Phase teachers are required to teach. She also said that her own understanding of the connections between content was clearer and she was now able to lead discussions with her Intermediate Phase colleagues about issues and planning for teaching from Grade R to 6.
I found Stage 3 and the number-based theory difficult. Before we worked with you I did not understand what the "commutative property" and "inverse operations" were or that these were linked to addition and subtraction (Reference group teacher).
This was the continuing theory-practice dilemma, which resulted in several informal debates among the workshop leaders and fellow academics. It re-enforced the importance of the LPN as a document that could bring the two closer together.
Thirdly, all teacher groups gained confidence by engaging with unfamiliar concepts and terminology, which broadened their pedagogical knowledge bases. The authors also observed that the acquisition of a repertoire of common terminology, through workshop participation, encouraged teachers to discuss the teaching of number at higher levels in terms of the practice being informed by theory. This process highlighted some unforeseen issues. For example, the small group discussions generated much debate about 'what to call things' when working with the classroom examples and vignettes. Following a workshop on counting a Grade 1 teacher, from the project group of teachers, said 'I have never heard of subitizing or acoustic and resultative counting. Now that I understand I can use this with my kids and not just ask them to say the numbers and then say them again and again'. This was due to a lack of common understanding of the mathematics terminology. The process also raised the major issue of the language used in teacher education, and the use of specialised (mathematics) terminology in African home language classrooms. We found that it was critical to find appropriate terminology in isiXhosa for the complex terms that are presented in the LPN.
A fourth issue was that although teachers were given apparatus to take back to their classrooms, they were disappointed that they had not been given 'recipes' in the use of them. Although the workshops focused on the fact that apparatus does not embody the mathematics the teacher wants to convey, and that learners do not understand concepts simply by using concrete materials, teachers genuinely believed that if they were using apparatus they were presenting mathematical ideas. Teachers from the three groups strongly expressed the desire for more examples of how to use the apparatus in the classroom, rather than reflecting on what mathematical ideas they would be able to scaffold with certain materials. Fuson (1992) emphasises that
Mathematics teachers need to intervene frequently as part of the instruction process to help students focus on the underlying mathematical ideas and to help build bridges from the students' work with the manipulatives to their corresponding work with mathematical symbols or actions.
A fifth insight was that teachers require a higher level of assistance than expected when selecting and presenting mathematics problems to learners. The main issues in this regard are the mathematics content, the method of presentation, the expected interaction with the learners, and the range of possible potential solutions (oral, written and concrete). Although the LPN presents a trajectory for the development of number concepts and activities for teaching and learning, this should be presented over a longer period with more sustained support at the classroom level so that teachers are able to integrate this kind of knowledge and practice, and make links between the curriculum and their classroom activities. Teachers expressed difficulty in determining the level at which learners solve problems, and how to interpret learner products. For example at one of the workshops teachers discussed two learners' solutions to the problems they had been given (Van Den Huivel-Panhuizen et al., 2012:41-42).
Learner A was asked to find out how many wheels nine bicycles have. She drew the picture on the left below (Figure 2). When the teacher asked how she got her answer, she said, 'Well I know a bicycle has only two wheels. So, I drew it and counted all the wheels.' Learner B was asked to solve this problem: There are thirteen learners, how many hands are there altogether? His solution (Figure 3) shows how he counted by grouping. When he finished his work, his teacher asked him, 'How did you find the answer so quickly?' He answered, 'Easy, I know everyone has two hands, so I counted in twos, like at the top of my drawing.'
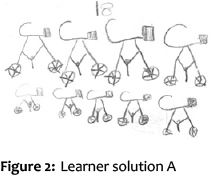
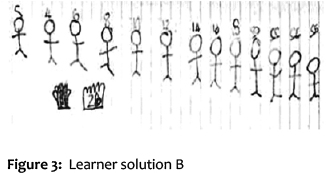
Apart from illustrating differences in counting strategies, these classroom examples also show that the teacher was purposeful in the counting tasks she gave learners. These samples of learner solutions were used to illustrate how one learner used a counting-based strategy to solve the problem while the other learner used a number-based strategy to solve the problem. These learner products also provide examples of how the teacher intentionally selected counting tasks and contexts to elicit learner solution strategies that reveal the level at which they are operating - in terms of the LPN stages. Comments from reference group teachers during the workshop discussions included:
Teacher 1: 'How do we "get to the next level" (in terms of learning number)'.
Teacher 2: 'I have difficulty in drawing the line between "telling how to do it" and letting learners work by themselves.'
Teacher 3: 'It is very difficult not to tell children what to do. We discuss the difference between "telling" and facilitating at our school now.'
Teacher 3: 'It is necessity to have specific examples to use in any teacher development so that it is clear how these are examples of the different stages.'
Finally, we believe that if the gap between theory and practice in these schools could be reduced, then valuable insights might be gained in bridging the theory-practice divide. The LPN provided the impetus and structure around which content and pedagogy could be discussed. Based on our observations there is the potential for the existence of a community of practice, with a focus on support for pedagogy, amongst diverse groups of teachers who are willing to engage in such processes.
Acknowledgement
The authors would like to thank Marja van den Huevel-Panhuizen for her assistance and contributions to this paper, which was written as part of the European Union Primary Education Sector Policy Support Programme: Strengthening Foundation Phase Teacher Education Materials Development Project (Cape Peninsula University of Technology, Mowbray campus). Marja was the COCA Project Leader based at the Fruedenthal Institute at the University of Utrecht in the Netherlands and lead author of the Learning Pathway for Number in the Early Primary Grades (2012).
References
Ball, D. 1992. Manipulatives and the reform of mathematics education. American Educator:14-18, 46-47. [ Links ]
Bobis, J., Barbara, C., Clarke, D., Thomas, G., Wright, R. & Gould, P., 2005. Supporting teachers in the development of young children's mathematical thinking: Three large scale cases. Mathematics Education Research Journal 16(3):27-57. [ Links ]
Carnoy, M. & Chisholm, L. 2008. Towards Understanding Student Academic Performance in South Africa: A Pilot Study of Grade 6 Mathematics Lessons in Gauteng Province: A Report Prepared by the Human Sciences Research Council (HSRC) with Stanford University (in Partnership with a Consortium of South African Universities and JET Education Services), HSRC, South Africa
Clements, D.H. & Sarama, J.S. 2009. Early Childhood Mathematics Education Research Learning Trajectories for Young Children. New York: Routledge; p. 17. [ Links ]
Clements, D.H. & Sarama, J.S. 2004. Learning trajectories in mathematics education. Mathematical Thinking and Learning 6(2):81-89. [ Links ]
Cobb, P. & Bowers, J. 1999. Cognitive and situated learning perspectives in theory and practice. Educational Researcher 28(2):2-15. [ Links ]
Count One Count All (COCA). 2004. South Africa-Netherlands Programme on Alternatives in Development (SANPAD). The design and evaluation of a learning pathway for number in the Foundation Phase and the development of associated INSET requirements: Project Proposal, unpublished.
Department of Basic Education (DBE). 2012. Report on the Annual National Assessment: Grade 1 to 6 & 9. Retrieved from http://www.education.gov.za/LinkClick.aspx7fileticket=YyzLTOk5IYU%3D&tabid=298 (accessed 25 January 2012).
Department of Basic Education (DBE). 2011. Curriculum and Assessment Policy Statement, Final Draft, Foundation Phase Mathematics Grade R - 3. Pretoria: DBE. [ Links ]
Department of Basic Education (DBE). 2009. Ministerial Committee Report on a National Education Evaluation and Development Unit (NEEDU). Pretoria: DBE. [ Links ]
Department of Basic Education (DBE). 2007. The National Policy Framework for Teacher Education and Development. Pretoria: DBE. [ Links ]
English, L.D. 2003. Reconciling theory, research and practice: a models and modelling perspective. Educational Studies in Mathematics 54:225-248. [ Links ]
Even, R. & Schwarz, B. 2003. Implications of competing interpretations of practice for research and theory in mathematics education. Educational Studies in Mathematics 54:283-313. [ Links ]
Fuson, K. 1992. Research on learning and teaching addition and subtraction of whole numbers. In D. Grouws (Ed.), Handbook of Research on Mathematics Teaching and Learning. New York: MacMillan. [ Links ]
Gelman, R. & Brenneman, K. 2004. Science learning pathways for young children. Early Childhood Research quarterly 19(1):150-158. [ Links ]
Gervasoni, A. 2005. Using growth points to describe pathways for young children's number learning. Proceedings of the 29th Conference of the International Group for the Psychology of Mathematics Education, 217-224. Melbourne: PME.
Howie, S.J. 2004. A national assessment in mathematics within an international comparative assessment. Perspectives in Education 22(2): 149-162. [ Links ]
Howie, S.J. 1999. Third International Mathematics and Science Study Repeat (TIMMS-R). Executive summary. Pretoria: Human Sciences Research Council; 29 p. [ Links ]
Howie, S.J. 1997. Mathematics and science performance in the middle school years in South Africa: A summary report on the performance of the South African students in the 3rd International Mathematics and Science Study. Pretoria: Human Sciences Research Council (HSRC). [ Links ]
Kühne, C. 2004. Teacher's Perceptions of Whole Number Acquisition and Associated Pedagogy in the Foundation Phase. Unpublished master's dissertation (Teaching), University of Cape Town, South Africa.
Kühne, C., Van den Heuvel-Panhuizen, M. & Ensor, P. 2005. Learning and Teaching Early Number: teachers' perceptions. In H.L. Chik & J.L.Vincent (Eds.), International Group for the Psychology of Mathematics Education (PME), Proceedings: 29th Conference (3):217-224. Melbourne: PME. [ Links ]
Kühne, C., Van den Heuvel-Panhuizen, M., Lombard, A.P., Ensor, P. & Cranfield, C. 2005. A Learning Pathway for Number as a Guide to Instructional Programme Design. South African Association for Research in Mathematics, Science and Technology Education (SAARMSTE), 13th Annual Conference, 10-13 January 2005, Windhoek, Namibia.
National Planning Commission (NPC). 2011. Diagnostic Overview. Pretoria: NPC. [ Links ]
National Research Council (NRC). 2009. Committee on Early Childhood Mathematics. Cross. In C.T, T.A. Woods & H. Schweingruber (Eds.), Mathematics learning in Early Childhood: Paths towards excellence and equity. Center for Education Division of Behavioural and Social Sciences in Education. Washington, DC:The National Academies Press.
Nieveen, N., McKenney, S & Van den Akker, J. 2006. Educational design research: The value of variety. In J. van den Akker, K Gravemeijer, S McKenney & N. Nieveen (Eds.), Educational Design Research, 229-240. London: Routledge. [ Links ]
Sarama, J. & Clements, D.H. 2009. Early childhood mathematics education research: learning trajectories for young children. New York: Routledge. [ Links ]
Taylor, N. 2011. Priorities for Addressing South Africa's Education and Training Crisis: A Review commissioned by the National Planning Commission. Joint Education Trust (JET) Education Services. South Africa.
Van den Heuvel-Panhuizen, M. 2003. The didactical use of models in realistic mathematics education: An example from a longitudinal trajectory on percentage. Educational Studies in Mathematics 54(1):9-35. [ Links ]
Van den Heuvel-Panhuizen, M. (Ed.). 2001a. Children Learn Mathematics. A learning-teaching trajectory with intermediate attainment targets for calculation with whole numbers in primary school. Utrecht: Freudenthal Institute, Utrecht University/SLO. Published in 2008. Rotterdam/Tapei: Sense Publishers. [ Links ]
Van den Heuvel-Panhuizen, M. 2001b. Realistic mathematics education in the Netherlands. In J. Anghileri (Ed.), Principles and Practices in Arithmetic Teaching: Innovative approaches for the primary classroom (pp. 49-63). Buckingham/ Philadelphia: Open University Press. [ Links ]
Van den Heuvel-Panhuizen, M. 2000. Mathematics Education in the Netherlands: A guided Tour. Freudenthal Institute CDROM for ICME9. Utrecht: Utrecht University. [ Links ]
Van den Heuvel-Panhuizen, M., Kühne, C. & Lombard, A.P. 2012. The Learning Pathway for Number in the Early Primary Grades. Pretoria: MacMillan. [ Links ]
Vygotsky, L. 1978. Mind in Society. Cambridge, MA: Harvard University Press. [ Links ]
Wood, E. & Bennett, N. 2000. Changing theories, changing practice: Exploring early childhood teachers' professional learning. Teaching and Teacher Education 16:635-647. [ Links ]
Woolfolk, A. 2010. Educational Psychology. London: Pearson. [ Links ]
Wright, R.J., Martland, J. & Stafford, A.E. 2006. Early Numeracy: Assessment for Teaching and Intervention. London: Paul Chapman. [ Links ]














