Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
South African Journal of Childhood Education
versión On-line ISSN 2223-7682
versión impresa ISSN 2223-7674
SAJCE vol.3 no.2 Johannesburg 2013
South African research in mathematical cognition and language in childhood: Towards an expanded theoretical framework
Elizabeth Henning
University of Johannesburg Institute for Childhood Education. Email address: ehenning@uj.ac.za
ABSTRACT
The article proposes that cognitive developmental psychology and cognitive neuroscience theory need to feature more prominently in the theoretical frameworks for South African research on language in mathematics learning in the early years of school. I argue that, considering the state of mathematics learning in the foundation phase and the conundrum around the language of learning and teaching debate in the country, we need more integrated theoretical work for equally integrated analyses of learners and learning, moving beyond the practice of drawing from mostly single theories, such as bilingual education theory, or sociocultural theory. The article explains the reasoning behind the proposition for an expansion of the theoretical work in this field, claiming that policy decisions about language of learning and teaching depend on empirical research that includes theories from the cognitive sciences as framework.
Keywords: theoretical framework; mathematics education research; language and conceptual development; mathematical cognition; conceptual development; South African education; language in mathematics learning; educational neuroscience
Introduction
The language of learning mathematics the thesis of this conceptual essay is that South African researchers in mathematics education may benefit from a theoretical lens that includes, but also goes beyond theories describing learner classroom performance and teacher practice. I suggest such a lens, which focuses on the psychology (and to a lesser degree the biology) of learning. Despite the long tradition of research in the language of learning and teaching in South Africa (see Henning, 2012), none of it has provided conclusive evidence of what the impact of various policies on the medium of instruction may have been on learning in the foundation phase in general and on learning mathematics specifically. The national school curriculum in South Africa (DBE, 2011), on the other hand, does not explain which theories of mind and of learning have guided the design of the maths curriculum, the annual national testing of learners, or the language policy. Recently the National Education Evaluation and Development Unit (NEEDU) report (DBE, 2013a) gave sobering empirical evidence of the serious situation concerning the language of literacy and mathematics education in the foundation phase. Research that is required to show the type of impact of the medium of instruction (or the language of learning and teaching [LoLT]) would have to be longitudinal, or cross-sectional comparative research, involving large numbers of learners in in-depth diagnostic testing. The cost and the logistics of such research make it almost impossible to entertain the idea, especially if one considers the many languages in schools and their various dialectical forms (see the NEEDU report about the dialecticalisation of South African languages). Children in rural parts of the eastern Free State, for example, may not use the same oral form of Sesotho as is used in Soweto.
Notwithstanding this huge challenge, I would argue that research in the language of mathematics learning and teaching is now more important than ever. The main reason for saying this is that the role of language in early learning is currently under the spotlight in South Africa, not only in academia, but also in the public and in the policy arena, if judged by the media attention to the topic. Furthermore, there is a universal agreement in education circles that early achievement in school is an indicator of later performance in mathematics (Dehaene, 2011). When one considers the results of the annual national assessment (ANAs) tests (DBE, 2013b) and the NEEDU report against the backdrop of the policy on the medium of instruction in the foundation phase, one has to wonder about the logic and the feasibility of the policy. I also wonder about the assumptions inscribed in the policy: One such assumption is probably that children learn cognitive academic language easily and that they translate their newly acquired lexicon and syntax as easily to a language with a very different form; the added assumption being that a Bantu African language can be translated into a Germanic Indo-European language by the time a child reaches Grade 4. No wonder that many of the schools referred to in the NEEDU sample (DBE, 2013a:35) opt for English terminology and different hybrids of code-switching practices in teaching foundation phase mathematics. One extreme case is a school in Mpumalanga where all 11 official languages are represented by learners. The authors of the report note (DBE, 2013a:33):
The mismatch between LOLT and home language renders visible the fact that a large number of learners are schooled in a language that is different to the one that they speak at home. At many schools, the learner population is widely divergent in home background and HL.
Although I understand what may be the ideology of the policy, namely that the country's languages should be treated as equal and that policy makers believe that children learn best in their home language, I will argue that it is, when viewed from research in the cognitive sciences, a much more complex issue than is popularly thought. The central issues of the universality of languages and the compositional semantics of language (Levinson, 2003; Clarke, 2003; Bowerman & Choi, 2003; Evans & Levinson, 2009; Bowerman & Levinson, 2001; Spelke, 2003) are not discussed in the public spaces where bilingual education and initial mother tongue instruction literature (mostly from North America) is cited as evidence of the feasibility of the policy. Briefly, the policy requires that all children must have the opportunity to start school in their home language (which is not always easy to determine in multilingual areas, as is evident from our own research) and that they learn a first additional language, which is, for most of the children who speak an African language at home, English. Then, by the fourth grade, they are all, supposedly, taught in English, while they continue to study their home language as part of the language and literacy curriculum.
The exception is for Afrikaans learners, who continue with home language education throughout their school career and, of course, also learners who use English as their first language and who never have to switch their language of learning. In this policy the assumption is that young children who learn concepts in an African language can translate all concepts and operations they have learnedin the mathematics curriculum to English by the time they enter fourth grade and that these translations will aptly capture their conceptual development at that stage. The assumption thus means that they will have stored the terminology and the syntax in their long-term memory and that they will be able to extract these and translate them when they have to learn and be assessed in English.
There is, however, a second reason why I argue that research in the language of mathematics learning is now more important than ever: there are many new studies about the psychology and the neuroscience of learning that see language (verbal symbols) as a foundational component of cognition, specifically mathematical cognition (Spelke, 2010; Dehaene, 2011; Fias, Van Dijck& Gevers, 2012; Brysbaert, 2005; Fayol & Seron, 2005). It would be foolhardy not to take notice of this trend in cognitive psychology and other disciplines. In developmental psychology labs in many parts of the world the evidence has been coming out in the last 30 years that early mental representation of concepts depend on both sensorimotor experience and on the symbols of language (Boroditsky, 2012; Carey, 2009, 2003, 2010; Gallistel, 2012; Gopnik, 2001; LeCorre & Carey, 2007) and that mental magnitudes, "the neural realization of computable numbers (which are) used to represent the foundational abstractions of space, time, number, rate and probability" (Gallistel, 2012:11) are at least bi-focal; neural representation of magnitude information is not only analogical, but also verbal-symbolic. In other words, data that are sensed from the world are stored in spatial representational co-ordinates (non-verbally) and in categories (verbally) as well. The linguistic code for the stored data from the world can be seen as part of a neural imprint. Imagine if the verbal imprint is made in Tshivenda to begin with, and then requires translation to English. The cognitive load simply becomes unbearable for some children at a time when mathematics cognition is accelerated by Grade 4; they spend much of their mental energy on finding the way in a mix of neural connections. Early findings in contemporary neuroscience is telling us something.
With these two reasons in mind, namely 1) the current knowledge of language of instruction in the country and 2) the trends in cognitive science, I forward a central argument for the article, asking the question: How can researchers of language in mathematics learning insert developmental cognitive psychology and cognitive neuroscience in the theoretical framework of their research? I will attempt to answer the question by briefly pointing to research in these two intersecting fields that have valence for language in learning. I argue that the scholarly community, policy makers and practitioners may ultimately benefit from research framed in this way. It will not be possible to exhaust the vast literature and I will thus pinpoint only some of the authors that I have encountered in my search for a platform from which I try to understand language and mathematics learning in the conceptual development of young children.
Beyond singular theories in educational research
I choose to use the term "network" to describe interrelated theories. The word implies connections of different nodes of knowledge. The conventions in the academy have been to focus on a specific theoretical framework to demarcate the theoretical position of an inquiry, and to design research accordingly with a specific analytical warrant. Based on such a notion of research, a study should be "tight", "cohesive" and "coherent" and the theoretical focus should be very specific. Although "opposing" theories are tolerated because they show the researcher's scientific openness and stance to the work, the actual analysis is conducted from a very specific framework with its own discourse and methods. For instance, were we to look at children's conceptual development as a sociocultural phenomenon, employing current, new-Vygotskian theories of cognitive apprenticeship and discourse, such a proposed by Rogoff (1990), we aim to find phenomena such as those described by the scholars of the International Society for Cultural and Activity Research community - usually work with a strong discursive flavor, such as the classroom studies of Hardman (2010). If we were only to look at learning from a cognitive developmental position, we would see behavioural data and findings from the labs of cognitive developmental psychologists such as Spelke (2010), Carey (2010), Feigenson (2012) Fayol and Seron (2005), Brysbaert (2005) and others, who show by way of experiments how concepts and language develop. If we were to see learning only from a neuroscience perspective (such as some of the work in the edited volumes by Dehaene and Brannon, (2012) and some of the authors in the edited volume by Campbell (2005). It would illuminate some aspects of the physiology of learning, depending on the type of imaging that is utilised. Lastly, if we were to look at children's learning as an outcome of pedagogy, we would study teachers and classrooms.
I thus suggest a theoretical network consisting of four fields (Figure 1), the knowledge of which need not be more extensive than what one could learn in a standard South African Honours- or MEd degree programme. Of the four fields, I will only discuss some of the ideas of two of them, namely cognitive developmental psychology (with some reference to language development) and cognitive neuroscience.
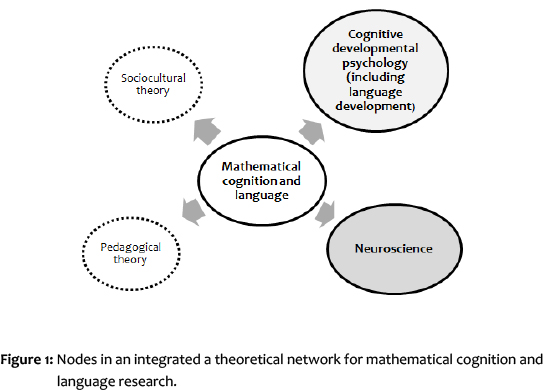
An integrated theoretical framework may give researchers the skills, for example, to express ethnographic findings, using terms from experiments in developmental psychology to explain some cultural phenomenon. The research conducted in the Max Planck Institute for Evolutionary Anthropology in Leipzig (Tomasello, 2003), the Max Planck Institute of Psycholinguistics in Nijmqegen (Levinson, 2003; Bowerman, 2003; Haun et al., 2011) and the Max Plank Research Group, Comparative Cognitive Anthropology are examples of how anthropology and neuroscience and linguistics go hand in hand in research. The close relationship of researchers who work with behavioural data emanating from psychology labs and the work of cognitive neuroscientists is well known too.
Developmental cognitive psychology and language
The field of research on child development, language and cognition is vast. I will only highlight some of the theorists that I have encountered and try to show how their work can be cohered into a network for new researchers.1 To learn about human cognition and language, students could begin with a study of what makes our species different, and what links us to other species, when we look at our minds and brains from the perspective of evolution theory. I introduce three cognitive psychologists first, realising that their work spans more than this descriptor.
I have found in my teaching of new researchers that the introduction of a single author's work, with some reference to others, is more helpful than thematic integration of many authors when the field is as vast as cognitive developmental psychology. This could be because the uptake of the discourse is enabled more easily in this way. Each author has her/his own style and readers have to get acquainted with the form of writing as well as its content - and so it makes sense to get to know the discursive style of the authors one at a time. The three authors that I will discuss briefly are Derdre Gentner, Susan Carey and Elizabeth Spelke. Like other psychologists in this field, they work on those elements of humanness that make the species unique; language and symbolisation are two of these.
Dedre Gentner: language for cognitive stability
Gentner, from Northwestern Universityin the USA, summarises the essence of the network that I am proposing (2003:196) by listing topics of cognitive skills that distinguish humans. I refer only to the ones related to the research question of this article:
- The ability to learn and use external symbols (such as language and mathematical and musical notation) to represent numerical, spatial, or conceptual information
- Our language abilities are equally outstanding. They include our ability to learn a generative, recursive grammar, as well as a set of semantic conceptual abilities
- The ability to learn symbols that lack any iconic relation to their referents
- The ability to learn and use symbols whose meanings are defined in terms of other learned symbols, including even recursive symbols such as the set of all sets
- The ability to invent and learn terms for abstractions as well as for concrete entities
- The ability to invent and learn terms for relations as well as things (my cursive and parenthesis)
Gentner's thesis in this chapter is "what makes humans smart" is -
1. Our exceptional ability to learn by analogy;
2. The possession of symbol systems such as language and mathematics; and
3. A relation of mutual causation between them whereby our analogical prowess is multiplied by the possession of relational language. By "relational language" she means language that can refer to relationships between concepts, many of which are of concepts of space, time and number as well as rate and probability (Gallistel, 2012; 2012) and of causality.
The representation processing of space time and number (the "big three" in cognitive neuroscience), some would argue (Lourenco & Longo, 2012:225), "happens on cues that are part of a general magnitude system", where verbal cues and spatial cues intersect. The mental use of "relational" language is distinctly that of humans.
In her thesis, Gentner comes to the heart of what one should study to become a researcher of mathematics learning and language in the foundation phase. She says it succinctly in an argument that has three parts: Firstly, she says, "(w)e learn because we can see relationships - we develop relational concepts, which are essential for higher order thinking". On this view, one can say that one concept, such as one for spatially observed "distance" relates to another concept, such as "number" (how far is it?), to another one - "place/space" (where is it?) and to another concept - "time" (how long does it take to get there?), for example. According to Gallistel (2012), Dehaene (2012) and Brannon & Merrit, (2012), time, space and number are closely connected in neural terms, and so, seeing relationships and labelling these with linguistic terms comes naturally to human beings after they have acquired verbal language.
Secondly, Gertner (2003) emphasises that we learn by analogy and that relational knowledge is developed through analogical reasoning, a topic that has been researchedincreasingly in studies of core knowledge (Elizabeth Spelke's term for innate capability) research as reported by Carey (2009) and others who inquire into the two innate number systems of infants:
1. Analogue magnitude, or approximate number sense (ANS); and
2. Specific object tracking number sense (up to three objects) of pre-linguistic humans and some animal species and communities that have very few number words (Izard et al., 2013).
Importantly, the third part of her thesis argues that language "serves both to invite learning relational concepts and to provide cognitive stability once they are learned" (Gentner, 2003:196). I would suggest that research programmes should investigate the issue of "cognitive stability" in the multilingual maze (Henning, 2012) in which many young children in South Africa have to find their way in the first grade.
Another part of Gentner's work that could feature in an integrated network of theories is the notion of analogy development and how it can be seen with relational language in cognitive activity. She refers to Quine's (1960) "career-of-similarity hypothesis" and describes how
Quine (1960) proposed that over development children move from perceiving only 'brute' perceptual similarity to perceiving more sophisticated likenesses- 'theoretical' similarity. The career of similarity has wide ramifications. Virtually every cognitive process, from categorization to transfer, is influenced by explicit or implicit similarity comparisons. (Gentner, 2003:197).
And so, in learning the (verbal) language of mathematics, new terms are compared with known terms, selecting from the known repertoire of words and phrases those that will best capture new understanding and that will form relationships. This is also what Tomasello (2003) argues about the ontogenetic evolution of language and a child's selection of terms that will reflect her understanding in a specific environment (such as a classroom). I see this activity of giving a name to an emergent concept as one of the bridges for a child to advance from core/innate knowledge to an expansive, semiotically rich language representing richer conceptual understanding of number and other mathematical phenomena. A child may think: What is the same in this word and that word and in this object/action and that object/action? The "career of similarity" is the cognitive activity of an emergent language knower who is also an emergent concept knower and who decides which terms fit her concept best from the smorgasbord she may have in her environment and vice versa at any given time. For this, she is also dependent on her environment - what words and sentences do teachers, peers and families use - which words are used to depict certain concepts - and in which relations do they do so? Thus, for instance, when number sequence becomes a clear concept, with it will come words such as words of "time" (before or after an event of movement of objects) to be able to say, (in one of Piaget's experiments of cardinality and ordinality) "which marble fell down a pipe first" (Piaget 1991:41-47). The child selects the words to describe time. By the same token she also uses these words to describe "space/place", answering the question of which number is before or behind another one in a string, and then, lastly, the questions of "quantity/ number" - how far are the blue and the red marbles apart in a string and what is the quantity of the marbles that have gone into the hidden container? The depth of the understanding of similarity is shown in the experiments captured in Piaget's last book, written in 1980 - the year he died (Piaget & Garcia, 1991).
In this short introduction to a part of Derdre Gentners (2003:223) work it is evident that from her thesis for language in learning that she believes "language is neither a lens through which one forever sees the world, nor a control tower for guiding cognition, but a set of tools with which to construct and manipulate representations". She takes a semi-Whorfian position but does not ascribe to the strong hypothesis that reality is shaped by language (Whorf, 1956). I find this to be a very sober stance in the new-Whorfian literature. Her work on language and cognition has expanded in the last decade, with Gentner et al. (2013), Christie et al. (2012) and Feist et al. (2012) exploring spatial language.
Elizabeth Spelke: compositional semantics and the meaning of "new wholes" from "parts"
The second developmental cognitive psychologist that I would suggest for a network of theories for studies in child cognition and language is Elizabeth Spelke. Her extensive oeuvre cannot be covered here and I will point only briefly to some of the trends in her recent work, which she conducts with researchers in her own lab at Harvard but also in collaboration with the cognitive neuroscientist psychologists like Stanislas Dehaene. The aspect of her work that has specific relevance for the topic of this essay is her view of language as cognitive tool. I include this lengthy quotation to do justice to her own formulation, which I will not try to paraphrase:
Natural languages, however, have a magical property. Once a speaker has learned the terms of a language and the rules by which those terms combine, she can represent the meanings of all grammatical combinations of those terms without further learning. The compositional semantics of natural languages allows speakers to know the meanings of new wholes from the meanings of their parts. Although a child lacking the concept 'left of the blue thing' cannot learn it, she does not need to. Having learned the meanings of left, blue, and thing, she knows the meaning of the expression left of the blue thing. Thanks to their compositional semantics, natural languages can expand the child's conceptual repertoire to include not just the pre-existing core knowledge concepts but also any new well-formed combination of those concepts (Spelke, 2003:394).
Here Spelke aligns herself with what Gentner (2003) has said about language as a cognitive tool that is used to relate concepts with each other and to bring ideas together in an expanding lexicon and in syntax, drawing on (compositional) semantics and developing a grammar. Spelke also alludes to how core knowledge is extended because it is linked to newly developed concepts through the relational connection with language and in language structures, such as sentences, morphological changes and so forth. On this view, language forms the bridge to symbolic learning long before school starts. She carefully suggests that the compositionality of language semantics makes human cognition flexible. When a child knows something, such as the depth of a stair on a staircase, she will easily learn language about gravitation and depth and build more knowledge about material, physical staircases and with it more language to symbolise and connect her knowledge of physics. This statement has a strong Vygotskian undertone, of words meeting concepts and vice versa and theoretical knowledge developing from that intersect (Vygotsky, 1978; 1992).
Spelke also engages with the new interest in Whorf's (1956) work, carefully taking the stand that it is possible to research cultural conceptual difference in language, such as the work of Bowerman and Choo (2001; 2003) Levinson (2009, 2003) and Tomasello (2003). She suggests that there is merit in a new Whorfian research programme. I quote from her work in some length again:
If the compositionality of natural language semantics gives rise to uniquely flexible human cognition, then the thesis that language produces new concepts cannot be ruled out on logical grounds, and both this thesis and the possibilities that follow from it become open to empirical test. One much-discussed possibility that can be pursued in this context is Whorf's thesis that the members of different cultures and language groups have different repertoires of concepts. Note that no evidence or arguments in this chapter support Whorf's thesis. If the combinatorial properties of language that produce new concepts are universal across human languages, then uniquely human conceptual capacities will be universal as well. Questions about the existence of cultural differences in human conceptual capacities therefore hinge in part on questions about the origins and nature of compositional semantics. How does compositional semantics work? Is there a single, universal compositional semantics that applies to all languages, or do languages vary in their combinatorial properties? How do children develop the ability to use the compositional semantics of natural languages (Spelke 2003:307)?
She admits to not being able to answer these questions, which Levinson (2009, 2003) does with great conviction, saying that there is no universality in languages, despite the arguments of Pinker (1994) and others who maintain this. I have to add that Dehaene (2011:263) regards the Whorfian hypothesis as "overblown" and says that their experiments "argue forcefully for the universality of the number sense and its presence in any human culture, however isolated and educationally deprived" and that
(p)rogess on the conceptual scale of arithmetic depends on the mastery of a toolkit of mathematical inventions. The language of numerals is just one of the cultural tools ...
Susan Carey: conceptual change and "bootstrapping"
Her research on conceptual development (Carey, 1985; 2009) paved the way for many researchers who work with behavioural data but also for researchers utilising neuroimaging. Carey's ideas about conceptual change and of "bootstrapping" have received wide attention. The book, The Origin of Concepts (Carey, 2009), although dense to read, is a recommended text for aspiring researchers of conceptual development. She utilises a wide lens, looking at children's emergent concepts of mind and agency, their language and concepts of number and concepts of the living world. Her take on core cognition (core knowledge, according to Spelke) is explicit and rich in reference and descriptions of experiments that have been conducted in her lab. But, what distinguishes Carey's work, for me, is her view of the theory of conceptual change and with it, her take on the idea of "bootstrapping". She weaves though the literature on conceptual development and language development in concert and then explains learning (symbolic learning largely) with the heuristic of what she calls "conceptual systems". This, in turn, she links with language and discourse of such systems of knowing. In doing so, although she does not state this explicitly, she inserts compositional language semantics into the picture of what constitutes early conceptual development with the help of language - when children move away from core knowledge to symbolic knowledge.
Like the other cognitive developmental psychologists in the current discourse, echoes of her ideas can be found in the work of developmental work with a psycholinguistic turn, such as the work of Levinson (2001), Bowerman (2001, 2003), Clarke (2003) and Slobin, who explains linguistic expression as follows:
Language evokes ideas: it does not represent them. Linguistic expression is thus not a straightforward map of consciousness or thought. It is a highly selective and conventionally schematic map (Slobin, 1979:6).
This contrasts with Levinson (2003:28) who asserts unequivocally that there is no place for "simple nativism" in views on language development and concepts, which he argues happen in co-evolutionary mode. He has strong words for "simple nativists":
Learning a language is on this view simply a matter of learning the local projection, that is, finding the local phonetic clothing for the pre-existing concepts. Or as Li and Gleitman (2002:266) put it: 'Language has means for making reference to the objects, relations, properties, and events that populate our everyday world. It is possible to suppose that these linguistic categories and structures are more or less straightforward mappings from a pre-existing conceptual space, programmed into our biological nature: Humans invent words that label their concepts.' Hence, they hold, 'the grammars and lexicons of all languages are broadly similar.' The view just sketched is simply ill informed.
Levinson (2003:33) suggests a co-evolutionary view on the development of language and concepts, giving a now well-known example of why he has this view:
There are languages with no or very few number words, and without a generative system of numerals - it seems unlikely that the speakers of such a language would ever entertain the notion 'seventy-three', let alone that of a logarithm, and certainly their fellows would never know if they did.
Carey's own view, like that of Gopnik and Meltzhoff (1997) Gopnik and Nazzi (2003) and Gopnik (2001), is that children use language and express and encounter concepts and form concepts because they use hypothesis-testing algorithms, whereby when "the representations most consistent with available data are strengthened - those hypotheses are accepted" (Carey, 2009:475). This view is also known as the "theory" theory of cognitive development (Gopnik, 2001), meaning that young children continually theorise their world and continue to use those theories that are most feasible. When they start to use language the words may serve first as placeholders only for eventual conceptual change. Carey (2009:475) explains:
In Quinian bootstrapping episodes, mental symbols (concept representations) are established that correspond to newly coined or newly learned explicit symbols. These are initially placeholders... As is true of all world learning, newly learned symbols must necessarily be initially interpreted in terms of concepts already available. (My emphasis and parenthesis)
Carey's thesis is complex and although studying her work about concepts and conceptual change may require much perseverance, it is, in my view, essential reading for researchers in child cognitive development. She problematises the interplay of language as explicit symbol system for symbolic learning and as a placeholding and bootstrapping device for conceptual change. She shows how the primary explicit symbol system, language, gradually becomes more than the initial "placeholder" of understanding - it "becomes" the concept. In Vygotskian parlance, language serves as main semiotic mediator and thus also as important concept builder (Kozulin, 1990).
Neuroscience for educational research: Instruction in mathematics is crucial
In this section, I will not discuss individual leading authors because the field is fairly new and my knowledge likely to be too limited to afford such a choice. I begin with a reference to the same topic with which I started the paragraphs on Gentner's work in the previous section - the human ability to be cultural. In the introduction to his book, Reading in the Brain, Dehaene (2009:3) writes:
Our ability to read brings us face-top-face with the singularity of the human brain. Why is Homo sapiens the only species that actively teaches itself? Why is he unique in his ability to transmit a sophisticated culture? How does the biological world of synapses and neurons relate to the universe of human cultural inventions? Reading, but also writing, mathematics, art, religion, agriculture and city life have dramatically increased the native capacities of our primate brains.
As in his seminal work on number sense (Dehaene, 1997; 2011) the author reminds us that writing, reading and mathematics are cultural inventions for which initiation into the cultural is essential. And the early initiation, when children enter the world of cultural symbols in mathematics and in alphabet, is crucial. The authors that I have referred to in the previous section attest to the fact that some form of teaching has to take place in order for a culture of mathematical knowing to be established (in schools and in communities); in this instruction verbal language symbols play an important part. Cognitive neuroscience affirms this in thousands of studies: Mathematics has to be instructed carefully and systematically, especially at the outset of the child's mathematical enterprise, for concepts to develop smoothly.
Furthermore, most researchers would agree that mathematical learning is hierarchical (Fritz, Ricken & Balzar, 2013) and that young children make new knowledge, based on the knowledge they already have (including core knowledge). This is, of course, also a tenet of constructivist epistemologies in the tradition of Jean Piaget and Ernst von Glasersfeld (Henning, 2013b), with one difference being the role of core knowledge. The Piagetian constructivist view of the learning in infanthood has been proven wrong in many studies, starting with the work of Wynn (1992, 1996), who showed that infants have a concept of number, distinguishing up to three objects. Many studies have since confirmed this (Dehaene, 2011:xix).
The number line: magnitude or metaphor?
In cognitive neuroscience there are currently many questions and as research progresses some of these are answered, but they also spawn new questions. For me one of the more interesting research agendas is the role of language in working memory and with that the notion of an analogue mental/(neural) number line. In everyday Western educational parlance there is much talk about "the number line". It is seldom noted by educational practitioners that it is a metaphor that has somehow taken on the material qualities of its signifier. Since Sir Frances Galton first hypothesised in the late 1800s that numerosities are perceived spatially along a mental line (Burr et al., 2012:177), the idea has been embraced by education. A group of researchers in Belgium study this specific issue, trying to find out how verbal language features in working memory of number, time and space and what this implies for the analogue (mental) "number line". They address the question of whether working memory is in spatial mode or in linguistic mode, or in both when dealing with the processing of number. Fias, Van Dijck and Gevers (2012:139) argue that although "high level cognition is grounded in sensorimotor experience" and that
it is also true that humans are a communicative species that uses language to communicate thoughts and cognition with their conspecifics, the essential characteristic of language being that it summarizes information in structured and labeled categories. Hence humans are also exposed to knowledge in a format that is abstracted away from direct physical reality (Fias et al., 2012:139).
On this view, they say that information is not represented in spatial analogue only, but also in a verbal-symbolic system. In other words, data from the world are stored in both spatial representations (non-verbally) and in categories (verbally). When studying young children's learning of mathematics there are bound to be cues related to the functioning of working memory, especially when children slowdown in their responses and appear to think, or applying executive functions (Fitzpatrick, 2012), to which they resort for solutions. In neuroimaging labs these moments are reflected in images that capture processes in milliseconds.2 Fias et al. (2012) further emphasise:
While the idea of a mental number line was originally conceived of as a metaphor, it took on another life and was viewed ... not simply as a metaphor, but a mental representation of numerical magnitude, considered to be homeomorphic to the representation of physical space. We provide pointers to an alternative framework that proposes serial position in the working memory as an important determinant of the interactions between number and space (Fias et al., 2012:135).
Huang et al. (2013) argue in the same vein - that verbal memory and verbal presence in working memory and executive functioning feature strongly in the processes of cognising number and in calculating along/around the spaces of what is assumed to be a mental number line. In our own work (Ragpot & Henning, 2013), we show that the grade 1 children's sensorimotor experience of "the number line" can be altered spatially on cues that are not necessarily from left to right: In a task for first grade children the round number line/curve of an analogue clock was "dismantled" or straightened by placing a removable strip of tape around the clock face with the numbers written on it. The strip was then be removed and placed in a straight line. In this way it was shown that the larger numbers are on the left side of the perceptual base (from 7-11) and the small numbers (1-5) are on the right side, contrary to the iconic notion of small numbers on the left and large ones to the right. This militates against the popular notion in primary maths education that a "number" line starts only from one side. The numbers on the vertical axle of a quadrant or a thermometer and so forth do the same. Issues about the mental number line are not straightforward. Dehaene (2011) and others (Ansari, 2010; Devlin, 2010) note that in languages that read from right to left the line is presented in the same direction, from right to left, but even that is not conclusive.
Categorical and spatial coding: relations in maths cognition
Considering the various views on mental representation and what the role of verbal language codes may be in neural activity it is thus important to take cognisance of what some theorists refer to as a "dual coding theory that claims that information is coded in an analog system and in a verbal-symbolic system". Fias et al. (2012:138) also refer to
Kosslyn et al. (2006) who distinguished between categorical (verbal) and spatial representations. The coordinate system codes for spatial position in a quantitatively precise way and the categorical system defines space in more qualitative and conceptually distinct classes (for instance above and below).
The most poignant examples of expression of qualitative conceptual understanding in the diagnostic maths competence tests that we conduct with young children has been their response to terms for "before", "after" "more" than "less" and "fewer" in different SA languages. These are instances of categorical coding in language.
Much is still to be learned about number and space and what is known in the literature as the SNARC3 effect and its mental coding. Fias et al. (2012:139) conclude:
... the associations between number and space are not absolute but depend on contextual aspects of the stimuli, the responses, and the task. This might suggest that the SNARC effect does not depend on long-term associations between numbers and space, as implied in the mental number line hypothesis, but rather on temporary representations.
For the moment this view appeals to me and explains, to some extent, why so many children struggle with tasks they have to perform on a material number line and the verbal descriptions of it. And yet, the number line is a universal feature in textbooks, workbooks and other resources for education. The view also helps to clarify why children "shut down" in test situations, when the task is overshadowed by extraneous factors. But more than anything, it highlights how difficult it is to judge what the best option would be for South African children. I am left with the question, which is an empirical one that can only be answered in large-scale field trials, of what the best option would be for the language of instruction for mathematics.
My sense is that we pay too little attention to the eye-opening innovations in research in the (developmental) psychology of learning mathematics, specifically with regard to the two mental presentations that come into play - the verbal qualitative categories of mathematics, such as in words pertaining to place and position (prepositions and adverbs) and the spatial coordinates of mental magnitude, the "physically realized symbols in the brain" (Gallistel, 2012:11). These type of debates can only come to the fore if researchers have a wider gaze on learning mathematics and learning language in tandem and finding their relational (Genert, 2003) connections.
Conclusion: theoretical frameworks and empirical questions
Although the interest in the role of language in conceptual development is as old as the discipline of psychology itself and before that was philosophised by many, the current work has brought something new into the arena - brain imaging. The important role that neural, verbal representation plays has gained prominence in both cognitive psychology and, more recently, in neuroscience (Spaepen et al., 2011) and in the discipline known as evolutionary anthropology (Tomasello, 2003; 2006). The implications for research on learning (and teaching) are described by scholars in the internationally established field of Mind Brian and Education (Sousa, 2010), such as Devlin (2010:166) who pinpoints one of the problem areas in multilingual contexts of schooling:
(M)ental storage of numbers and access to them appears to be by way of the symbolic names used during the initial learning process. If so, this has two significant implications for learning arithmetic:
1. Children being taught mathematics in a language other than the one in which they learned the basic number facts (in particular number names and the multiplication tables) are likely to be at a disadvantage).
2. Asian children enjoy a considerable advantage over their counterparts growing up in the West. The basic number words in Chinese, Japanese and Korean are a single syllable and combine in a way parallel to the symbolic rules of the decimal number system.
The issue of language and learning is examined from many other perspectives, with one area crystalising more and more, namely the role of language in the extension of core (innate) knowledge to advanced (symbolic) knowledge. This is one of the elusive issues in the field of early mathematical learning. Elizabeth Brannon (2012:245), when referring to the development of space, time and number concepts in pre-verbal children says that "education and language transform these foundational intuitions" and refers to how it has been shown in Butterworth's work (2012:249) that "preverbal numerical concepts give rise to symbolic mathematical abilities", but it is not yet clear how this happens, although there are a number suggestions. The one that appeals to me most is Fayol and Seron's (2005:15) idea that the bridge may be children's hands. Citing Butterworth (1999) the note that "in all human cultures children use their fingers to count before they are taught arithmetic at school". They also refer to their own work in which they conclude the predictive power of perceptive-tactile skills for future mathematics learning with symbols. The symbolic abilities that develop with instruction include verbal abilities and some of them seem to be playing a far more important role than was previously realised. The language with which mathematics is conceived is also its tool for its expansion. Translation, for all we know, may compromise young learners.
With the coming of new brain imaging technologies, described by one of the leaders in the field (Posner, 2010), it is now possible to see some functions of the brain in scans that show change in milliseconds. What the pioneering studies have done for understanding human learning and language is acknowledged by all who venture into studies of the brain-in-action (Posner, 2010). At the same time there is also a new vigilance because many new findings have been appropriated by the media and by organisations with a commercial interest - hence the abundance of "brain gymnastics" materials and training courses (Sousa, 2010). Sousa (2010) and Fischer and Heikinnen (2010) and many others warn that many of these are based on superficial, popular interpretations of findings that come out of brain imaging labs. All serious researchers in the field warn against this.
Neuroimaging is a difficult brief, because the methodologies require much time and facilities for working with individual children and testing larger groups in reliable ways in laboratories that are expensive to set up. There is, for instance, the move to conduct neuroscientific research in which children's brain activity is imaged while they are performing small tasks of reading, attending, enumerating, or calculating in situ. Although this research is in its infancy, it is already of some value for researchers, schools and families. It helps adults to reposition their view with regard what constitutes literacy (Dehaene, 2009; Wolf, 2010), language development (Williams, 2010; Boroditsky, 2012) and subjects such as mathematics and specifically numeracy and geometry (Dehaene, 2011; Gallistel, 2012; Butterwroth, 1999; Izard et al., 2012). Neuroimaging for educational purposes shows some surprising results, such as how much of mathematics in young learners is processed by way of linguistic symbols.
In responding to the question that prompted this article, I have tried to show that theoretical frameworks that include the work of developmental cognitive psychologists and cognitive neuroscientist may be required for future research in foundation phase education in South Africa. My concluding remark is that studies that omit these frameworks may not yield findings that can explain why the majority of learners in this country's schools are not learning mathematics successfully when they need to lay the first conceptual foundations.
My hypothesis is that we have not investigated learners diagnostically, with instruments that draw on recent theories in the two domains that I have discussed, considering, especially, the recent developments in research on "attaching meaning to arbitrary symbols" (Piazza, 2012:267). Whatever research we may conduct, theoretical frameworks are, however, only lenses for the main questions, which remain empirical:
- How does language feature in individual children's learning of mathematics in grade 1?
- How does learner competence across different ages and in different languages compare on the same test?
- What are the characteristics of oral communication in classrooms when children are initiated into the culture of mathematical life in grade 1?
- How does a standardised test for mathematical competence measure the level of conceptual development of South African children?
- Are the discourses in classrooms conducive to mathematical concept development, or are they preparing children to "do operations" and to automise lower levels calculations?
Endnotes
1. There are few postgraduate courses in Education in South Africa where the strands of theoretical fields I include are given equal weighting.
2. In classrooms we want children to respond on memory cues that include these rapid brain actions in question and answer sessions. Researchers may notice that teachers and peers are inclined to interrupt and detract from this working/thinking, especially when young children are "subjected" to group work. This is a questionable tool, likely to be based on early interpretations of English translations of Lev Vygotsky's work.
3. Dehaene (2012:119) says about the SNARC effect (Spatial-Numerical Association of Response Codes), which he accidentally discovered while studying parity judgments: "The results (of more than hundred papers) reveal that cross-domain associations are much more varied than anyone ever expected: number is associated with space, but also with temporal duration, object size, grip size, saccade side, finger location... Furthermore, these interactions are often, but not always, reciprocal, thus entwining space, time and number into a tangled know of interrelated concepts."
References
Ansari, D. 2010. The computing brain. In D.A. Sousa (Ed.), Mind, brain and education. Neuroscience implications for the classroom; 201-226. Bloomington, IN: Solution Tree Press. [ Links ]
Boroditsky, L. 2012. How languages construct time. In S. Dehaene & E.M. Brannon (Eds.), Space, time and number in the brain. Searching for the foundations of mathematical thought; 333-341. Amsterdam: Elsevier. [ Links ]
Bowerman, M & Choi, S. 2003. Space under construction: Language-specific spatial categorization in first language acquisition. In D. Gentner & S. Goldin-Meadow (Eds.), Language in mind advances in the study of language and thought; 387-428. Cambridge, Massachusetts: MIT Press. [ Links ]
Bowerman, M, & Levinson, S.C. (Eds.) 2001. Language acquisition and conceptual development. New York: Cambridge University Press. [ Links ]
Brannon, E.M. & Merritt, D.J. 2012. Evolutionary foundations of the approximate number system. In S. Dehaene & E.M. Brannon (Eds.), Space, time and number in the brain. Searching for the foundations of mathematical thought; 207-224. Amsterdam: Elsevier. [ Links ]
Brysbaert, M. 2005. Number recognition in different formats. In J.I.D. Campbell (Ed.), Handbook of mathematical cognition, 23-42. New York: Psychology Press. [ Links ]
Butterworth, B. 2012. Foundational numerical capacities and the origins of dyscalculia. In S. Dehaene & E.M. Brannon (Eds.), Space, time and number in the brain. Searching for the foundations of mathematical thought; 249-265. Amsterdam: Elsevier. [ Links ]
Carey, S. 2009. The origin of concepts. Oxford: Oxford University Press. [ Links ]
Carey, S. 2011. Concept innateness, concept continuity, and bootstrapping: A response to commentaries on the origin of concepts. Behavioral and Brain Sciences, 34:113-167. [ Links ]
Carey, S. 2010. Beyond fast mapping. Language Learning and Development, 6(3):184-205. [ Links ]
Carey, S. 2004. Bootstrapping and the origins of concepts. Daedalus, 133(1):59-68. [ Links ]
Carey, S. 1985. Conceptual change in childhood. Cambridge, MA: Bradford/MIT Press. [ Links ]
Christie, S. & Gentner, D. 2012. Language and cognition in development. In M.M. Spivey, K. McRae & M. Joanisse (Eds.), The Cambridge Handbook of Psycholinguistics; 653-673. Cambridge: Cambridge University Press. [ Links ]
Clark, E.V. 2003. Languages and representations. In D. Gentner & S. Goldin-Meadow (Eds.), Language in mind advances in the study of language and thought; 17-24. Cambridge, MA: MIT Press. [ Links ]
Dehaene, S. 2011. The number sense. (How the mind creates mathematics). Oxford: Oxford University Press. [ Links ]
Dehaene, S. 2009. Reading in the brain. London: Penguin Viking. [ Links ]
Dehaene, S. & Cohen, L. 2011. The unique role of the visual word form area in reading. Trends Cogn Sci, May:255-262.
Devlin, K. 2010. The mathematical brain. In D.A. Sousa (Ed.), Mind, brain and education. Neuroscience implications for the classroom. Bloomington, IN: Solution Tree Press. [ Links ]
Evans, N. & Levinson S.C. 2009. The myth of language universals: Language diversity and its importance for cognitive science. Behavioral and Brain Sciences, 32(5):429-492. [ Links ]
Fayol, M. & Seron, X. 2005. About numerical representations. Insights form neuropsychological, experimental, and developmental studies. In In J.I.D. Campbell, Handbook of mathematical cognition; 23-42. New York: Psychology Press. [ Links ]
Feigenson, L. 2012. Objects, sets and ensembles. In S. Dehaene & E.M. Brannon (Eds.), Space, time and number in the brain. Searching for the foundations of mathematical thought; 12-22. Amsterdam: Elsevier. [ Links ]
Feist, M.I. & Gentner, D. 2012. Multiple influences on the use of English spatial prepositions: The case of "in" and "on". In C. Boonthum-Denecke, P.M. McCarthy & T.A. Lamkin (Eds.), Cross-disciplinary advances in applied natural language processing: Issues and approaches; 305-323. Hershey, PA: IGI Global.
Fias, W., Van Dijk, J-P. & Gevers, W. 2012. How is number associated with space? The role of working memory. In S. Dehaene & E.M. Brannon (Eds.), Space, time and number in the brain. Searching for the foundations of mathematical thought; 133-148. Amsterdam: Elsevier. [ Links ]
Fischer, K.W. & Heikkinen, K. 2010. The future of educational neuroscience. In D.A. Sousa (Ed.), Mind, brain and education. Neuroscience implications for the classroom. Bloomington, IN: Solution Tree Press. [ Links ]
Fitzpatrick, C. 2012. What if we considered a novel dimension of school readiness? The importance of classroom engagement for early child adjustment to school. Education as Change. Journal of Curriculum Research, 16(2):333-353. [ Links ]
Fritz, A., Ricken, G., Balzer, L., Willmes, K. & Leutner, D. (in press). Key numerical concepts at pre-school and early primary-school age: An integrative five-level model of cumulative arithmetic skills development. Early Childhood Research Quarterly.
Gelman, R., Butterworth, B. 2005. Number and language: how are they related? Trends in Cognitive Sciences, 9:6-10. [ Links ]
Gentner, D. 2003. Why we're so smart. In D. Gentner & S. Goldin-Meadow (Eds.), Language in mind advances in the study of language and thought. Cambridge, Massachusetts: MIT Press. [ Links ]
Gentner, D., Ozyurek, A., Gurcanli, O. & Goldin-Meadow, S. 2013. Spatial language facilitates spatial cognition: Evidence from children who lack language input. Cognition, 127(3):318-330. [ Links ]
Gentner, D. & Goldin-Meadow, S. (Eds.), 2003. Language in mind advances in the study of language and thought; 195-236. Cambridge, MA: MIT Press. [ Links ]
Gopnik, A. 2003. The theory theory as an alternative to the innateness hypothesis. In L. Antony & N. Hornstein (Eds.), Chomsky and his critics. Blackwell: Oxford.
Gopnik, A. 2001. Theories, language, and culture: Whorf without wincing. In M. Bowerman & S.C. Levinson (Eds.), Language acquisition and conceptual development; 45-69. New York: Cambridge University Press. [ Links ]
Gopnik, A. & Nazzi, T. 2003. Words, kinds and causal powers: A theory theory perspective on early naming and categorization. In D. Rakison & L. Oakes (Eds.), Early category and concept development: Making sense of the blooming, buzzing confusion; 303329. New York: Oxford University Press. [ Links ]
Hardman, J. 2010. Variation in semiotic mediation across different pedagogical contexts. Education as Change, 14(1):91-106. [ Links ]
Haun, D.B.M., Rapold, C.J., Janzen, G. & Levinson, S.C. 2011. Plasticity of human spatial memory: Spatial language and cognition covary across cultures. Cognition, 119:70-80. [ Links ]
Henning, E. 2013a. Forging a research community of practice to find out how South African children make their world mathematical. South African Journal of Childhood Education, 3(1):141-155. [ Links ]
Henning, E. 2013b (in press). Teachers' understanding of mathematical cognition in childhood: Towards a shift in pedagogical content knowledge? Perspectives in Education.
Henning, E. 2012. Learning concepts, language, and literacy in hybrid linguistic codes: The multilingual maze of urban grade 1 classrooms in South Africa. Perspectives in Education, 30(3): 69-77. [ Links ]
Huang, Y.T, Spelke, E.S. & Snedeker, J. 2013. What exactly do number words mean? Language Learning and Development, 9:105-129. [ Links ]
Huang, Y.T., Spelke, E.S. & Snedeker, J. 2010. When is four far more than three? Children's generalization of newly acquired number words. Psychological Science, 21(4):600-606. [ Links ]
Izard, V., Pica, P., Spelke, E.S. & Dehaene, S. 2008. Exact equality and successor function: Two key concepts on the path towards understanding exact numbers. Philosophical Psychology, 21(4):491-505. [ Links ]
Kozulin, A. 1990. Vygotsky's psychology: A biography of ideas. Cambridge, MA: Harvard. [ Links ]
LeCorre, M., Carey, S. 2007. One, two, three, four, nothing more: An investigation of the conceptual sources of the verbal counting principles. Cognition, 105(2):395-438. [ Links ]
Levinson, S.C. 2003. Language and mind: Let's get the issues straight! In D. Gentner & S. Goldin-Meadow (Eds.), Language in mind advances in the study of language and thought; 25-46. Cambridge, MA: MIT Press. [ Links ]
Lourenco, S.F. & Longo, M.R. 2012. Origins and development of general magnitude representation. In S. Dehaene & E.M. Brannon (Eds.), Space, time and number in the brain. Searching for the foundations of mathematical thought; 225-244. Amsterdam: Elsevier. [ Links ]
Piaget, J. 1980. Language within cognition. Schemes of action and language learning. In M. Piatelli-Palmerini (Ed.), Language and learning, 163-183. Cambridge, MA: Harvard University Press. [ Links ]
Piaget, J. & Garcia, R. 1991. Toward a logic of meanings. (Edited by P.M. Davidson & J. Easley). Hillsdale, NJ: Lawrence Erlbaum Ass. [ Links ]
Piazza, M. 2012. Neurocognitive start-up tools for symbolic number presentation. In S. Dehaene & E.M. Brannon (Eds.), Space, time and number in the brain. Searching for the foundations of mathematical thought; 267-285. Amsterdam: Elsevier. [ Links ]
Pinker, S. 1994. The language instinct. New York: Morrow. [ Links ]
Posner, 2010. Neuroimaging tools and the evolution of educational neuroscience. In D.A. Sousa (Ed.), Mind, brain and education. Neuroscience implications for the classroom; 8-27. Bloomington, IN: Solution Tree Press. [ Links ]
Quine, W.V.O. 1960. Word and object. Cambridge, MA: MIT Press. [ Links ]
Ragpot, L. & Henning, E. (Under review). Scriptwriting a teacher education documentary film on how children make their world mathematical. Teaching and Teacher Education.
Rogoff, B. 1990. Apprenticeship in thinking. Cognitive development in social context. New York: Oxford University Press. [ Links ]
Slobin, D.I. 1979. Psycholinguistics. (2nd Edition). Harlow, GB: Longman. [ Links ]
Sousa, D.A. 2010. How science met pedagogy. In D.A. Sousa (Ed.), Mind, brain and education. Neuroscience implications for the classroom; 1-9. Bloomington, IN: Solution Tree Press. [ Links ]
Department of Basic Education (DBE). 2013a. National Educational Evaluation and Development Unit. National report 2012: The state of literacy learning teaching in the foundation phase. Pretoria: DBE. [ Links ]
Department of Basic Education (DBE). 2013b. ANA Report 2012: Diagnostic Report.Retrieved from www.education.gov.za/LinkClick.aspx?fileticket...tabid=424&mid (accessed on 2 July 2013).
Department of Basic Education (DBE). 2011. The Curriculum and Assessment Policy Statement. Foundation Phase. Retrieved from http://www.education.gov.za/Curriculum/CurriculumAssessmentPolicyStatements/CAPSFoundationPhase/tabid/671/Default.aspx (accessed on 2 July 2013).
Spaepen, E., Coppola, M., Spelke, E.S., Carey, S. & Goldin-Meadow, S. 2011. Number without a language model. Proceedings of the National Academy of Sciences, 108(8):3163-3168. [ Links ]
Spelke, E.S. 2010. Innateness, choice, and language. In J. Bricmont & J. Franck (Eds.), Chomsky Notebook (pp. 203-210). New York: Columbia University Press. [Originally published in French: Spelke, E.S. 2007. Inneisme, liberte et langage. In J. Bricmont & J. Franck (Eds.), Cahier n° 88: Noam Chomsky; 197-201. Paris: L'Herne. [ Links ]].
Spelke, E.S. 2003. What makes us smart? Core knowledge and natural language. In D. Gentner & S. Goldin-Meadow (Eds.), Language in mind advances in the study of language and thought; 277-312. Cambridge, MA: MIT Press. [ Links ]
Tomasello, M. 2003. The key is social cognition. In D. Gentner & S. Goldin-Meadow (Eds.), Language in mind advances in the study of language and thought; 47-58. Cambridge, MA: MIT Press. [ Links ]
Tomasello, M. 2006. Acquiring linguistic constructions. In D. Kuhn & R. Siegler (Eds.), Handbook of Child Psychology. New York: Wiley. [ Links ]
Vygotsky, L. 1978. Mind in society .The development of higher psychological processes. M. Cole, V. John Steiner, S. Scribner, & E. Souberman (editors and translators), Cambridge, MA: Harvard University Press.
Vygotsky, L. 1992. Thought and Language. (Edited and revised by A. Kozulin, 6th Edition). Cambridge, MA: MIT Press. [ Links ]
Whorf, B. 1956. Language, thought, and reality: Selected writings of Benjamin Lee Whorf (Edited by J.B. Carroll). Cambridge, MA: MIT Press. [ Links ]
Williams, D.L. 2010. The speaking brain. In D.A. Sousa (Ed.), Mind, brain and education. Neuroscience implications for the classroom; 85-112. Bloomington, IN: Solution Tree Press. [ Links ]
Wolf, M. 2010. Proust and the squid. The story and science of the reading brain. New York: Harper Perennial. [ Links ]
Wynn, K. 1996. Infants' individuation and enumeration of actions, Psychological Science, 7:164-169. [ Links ]
Wynn, K. 1992. Addition and subtraction by human infants. Nature, 358:749-750. [ Links ]














