Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.3 n.2 Johannesburg 2013
Assessing early numeracy: Significance, trends, nomenclature, context, key topics, learning framework and assessment tasks
Robert J. Wright
Adjunct Professor, Southern Cross University, Australia. Email address: rwrigh15@bigpond.net.au
ABSTRACT
This article describes a comprehensive and novel approach to assessment in early numeracy. Topics include the significance of early numeracy, developing a nomenclature for early numeracy, and describing the context for the development of this approach to assessment. The largely unrealised importance of numerals and numeral sequences in early numeracy, the significance of counting and its distinction from saying a number word sequence, the important topics of structuring numbers in the range 1 to 20 and conceptual place value, the Learning Framework in Number and its use in profiling children's early numeracy knowledge, and important assessment tasks are explored.
Keywords: assessment, counting, early arithmetic, learning framework, number, numerals
Introduction
The purpose of this article is to describe a comprehensive and novel approach to assessment in early numeracy. In doing this, the author describes a range of relevant topics. These include the significance of early numeracy, developing a nomenclature for early numeracy, describing the context for the development of this approach to assessment, the largely unrealised importance of numerals and numeral sequences in early numeracy, the significance of counting and its distinction from saying a number word sequence, the important topics of structuring numbers in the range 1 to 20 and conceptual place value, the learning framework in number and its use in profiling children's early numeracy knowledge, and important assessment tasks.
Significance: the compelling case for early numeracy
Several researchers have studied the extent to which children's achievements around the time of school entry can predict their achievements in reading or mathematics several years later (see for example Daraganova & Ainley, 2012; Jordan, Kaplan, Ramineni & Locuniak, 2009). From these kinds of studies, it seems that the extent of a child's knowledge and learning around the time of starting school, or in the first year of school is a very strong indicator of the child's levels of achievement around five or more years later. Studies such as these serve to underline that learning of basic literacy and mathematics in preschool and in the first year of school is very important. The study by Duncan et al. (2007) is particularly interesting. The study used six longitudinal data sets to estimate the links between three key elements of school readiness -school-entry academic, attention, and socio-emotional skills - and later school reading and mathematics achievement. The authors found that:
Across all six studies, the strongest predictors of later achievement are school-entry math, reading, and attention skills. A meta-analysis of the results shows that early math skills have the greatest predictive power, followed by reading and then attention skills. By contrast, measures of socio-emotional behaviors, including internalizing and externalizing problems and social skills, were generally insignificant predictors of later academic performance, even among children with relatively high levels of problem behavior (Duncan et al., 2007).
Thus early mathematics skills were found to be the strongest predictor of later success in mathematics and reading (Duncan et al., 2007).
Richie and Bates (2013) tested the effects of mathematics and reading achievement at age seven on attained SES (socio-economic status) by age 42 and found that "mathematics and reading ability both had substantial positive associations with adult SES, above and beyond the effects of SES at birth, and with other important factors such as intelligence" (Richie & Bates, 2013:1). Geary, Hoard, Nugent and Bailey (2013) found that students' basic maths skills in numbers, counting and low-level arithmetic by first grade predict their success in math by the time they reach fifth grade and advised that educators should ensure that young students understand numerals and quantities. Aubrey, Dahl and Godfrey (2006:27) found that "children who bring into school early mathematical knowledge do appear to be advantaged in terms of their mathematical progress through primary school". They concluded that "without active intervention, it is likely that children with little mathematical knowledge at the beginning of formal schooling will remain low achievers throughout their primary years and, probably beyond" (Aubrey, Dahl & Godfrey, 2006:27). In a similar vein, Princiotta, Flanagan, and Germino-Hausken (2006) found that achievement gaps in the kindergarten year are still prevalent in fifth grade, and Aunola, Leskinen, Lerkkanen and Nurmi (2004) found that growth in mathematics performance across preschool to Grade 2 was faster among those who entered preschool with an already high level of mathematical skills. There are a good number of earlier studies and reports with similar findings (see for example Cockcroft, 1982; Stevenson & Newman, 1986; Zill & West, 2000). Thus collectively, there is a weight of evidence that fostering early learning of mathematics is a crucial goal for parents, schools and education jurisdictions.
Some trends in early number instruction in the last 20 years
Since the mid-1990s, there have been significant developments in approaches to instruction in number and early arithmetic. These include better ways to assess children's early number knowledge and the teaching of topics at more advanced levels. Prior to these developments, early number instruction typically was preceded by a focus on pre-number topics such as sorting, matching, ordering and classifying, usually of about six-months' duration. These topics were regarded as constituting essential pre-requisite knowledge for early number learning. This was followed by a study of number, first in the range 1 to 10, and then extended to 20. This study of number would focus on numbers, where each number constituted a unit of study in its own right. Studying the number six for example, would involve a focus on the additions to six in order; 5 + 1, 4 + 2 ... 1 + 5, and each addition would be constructed with materials such as Cuisenaire rods or counters. Cardinal and ordinal forms of numbers were also considered to be important. Thus counting six items constituted the cardinal aspect and putting items in order from first to sixth gave rise to the ordinal aspect of number. At least in Australia, what has been summarised above, was regarded as the standard and a time-honoured approach to the teaching of number, and this approach was enshrined in mathematics curriculums, syllabi and programmes of the day.
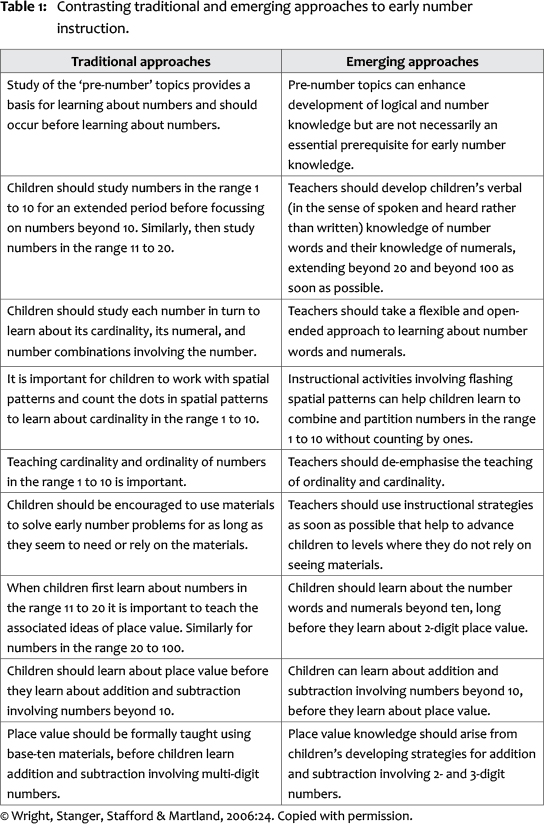
Several studies in the 1990s (for example, Aubrey, 1993; Wright, 1991; 1994; Young-Loveridge, 1989; 1991) provided a basis for profound change to the focus and scope of assessment and instruction in number and early arithmetic. These studies highlighted key factors such as a wide range among school entrants, in their knowledge of early arithmetic and significant numbers of school entrants with knowledge beyond what was typically taught in the first year of school. As well, the notion that pre-number topics constitute essential prerequisites for learning early number was increasingly under challenge (Hiebert, Carpenter & Moser, 1982). Table 1 summarises the differences between traditional and newer approaches to number instruction in the first two years of school (see Wright, Stanger, Stafford & Martland, 2006).
Context - on-going cycles of research and development
My work done with colleagues over the last 25 years has focused on research and development related to the assessment and teaching of number and early arithmetic (NEA). (This could also be referred to as whole number arithmetic). Alongside of this work has been extensive programmes of teacher professional development related to NEA. Thus our work on developing approaches to assessing and teaching NEA, for the most part has been conducted in partnership with teachers and school systems with whom we are engaged in research and development projects. The initial focus of this work was in the first two years of school but in the last 15 years this has extended to the first five years of school. Our work in the 1990s focused on the development and implementation of a programme known as Mathematics Recovery (e.g. Wright, 2000; 2008; Wright, Martland & Stafford, 2006) and from its initial development in New South Wales, this programme of professional learning has been used very widely by school systems in major Anglophone countries (e.g. USA, UK, Canada, and Ireland) as well as in Australia and New Zealand. The programme has also been adapted for use in several other countries (e.g. Mexico). In New South Wales in the 1990s, MR was adapted as a systemic initiative known as Count Me In Too and this programme in its own right made a significant impact elsewhere in Australia, in New Zealand and other countries. Over the last 10 years, the author and colleagues have worked in collaboration with a large Australian school system to extend our earlier work to the range of the first five years of school.
Working with teachers
In all of our development projects we work with teachers in the following way:
(a) Firstly, teachers learn to use assessment schedules involving a distinctive approach we call Videotaped, Interview-Based Assessment (VIBA) (Ellemor-Collins & Wright, 2008);
(b) Teachers then conduct pre-assessments, typically with about 12 low-attaining students;
(c) Teachers implement an intensive programme of one-to-one instruction with two or more students; and
(d) Teachers conduct post-assessments with the same 12 students. Another important feature is that teachers will participate in an on-going series of half- or full-day meetings focusing on professional development and training related to instruction.
Thus, our work over the last 20 years constitutes an extensive period of research, development and implementation. Collectively, this work can be regarded as an extensive and on-going programme of design research (Gravemeijer & Van Eerde, 2009; Gravemeijer & Cobb, 2006).
Developing a nomenclature of early arithmetical learning and teaching
For at least 20 years, the author and his colleagues have been providing major professional development programmes related to assessing and teaching number and early arithmetic (NEA). Many of the teachers with whom they have worked find that they have to learn what is almost a new language and this language can be seen to consist of a set of technical terms in the sense that many of these terms are specific to the field of early arithmetic instruction. A system of technical terms belonging to a particular field of professional endeavour or science is referred to as a nomenclature. One only has to look at professional and research writing in the field of early literacy to see that this field has an extensive nomenclature. A great advantage of developing a nomenclature is that it introduces an element of precision to discussions among professionals in this area. In our work with teachers over the years, we have continued to develop this nomenclature for assessment and instruction in early number. In virtually all cases, we find that teachers have little difficulty in learning the nomenclature and find it to be extremely useful. Below, some of the key terms in our nomenclature are introduced and described. Sources setting out this nomenclature in extensive detail are readily available (see for example, Wright, 2008; Wright, Martland & Stafford, 2006; and Wright, Stanger, Stafford & Martland, 2006.)
Forward number word sequence (FNWS)
This refers to a sequence of number words, for example the number words from fifteen to twenty-three said or considered in a forward direction. Thus, we might say that a student said the FNWS from fifty-seven to seventy-two. We regard saying a FNWS as different from counting, in the sense of counting to determine the number of objects in a collection. Where we would use the term FNWS, some authors use the term "verbal counting" or "rote counting". From our point of view, the term "rote counting" is unsuitable because in our experience of closely observing many students in the activity of saying FNWSs, this activity is far from rote and thus the term "rote counting" tends to sell this activity too short.
Backward number word sequence (BNWS)
This refers to a sequence of number words, for example the sequence from twenty-three to fifteen, that is, the sequence is said or considered in a backward direction. Just as with saying FNWSs, saying BNWSs is far from a rote activity. Over the years, they have learned much about students' ability to say FNWSs and BNWSs (see for example, Wright, Martland, Stafford & Stanger, 2006).
Number, number word and numeral
All three of these terms are important in our nomenclature and it is important to use each of these terms correctly in number and early arithmetic. A number wordis the name of a number. In this nomenclature, the term "number word" usually refers to a spoken and heard number name, but it might also refer to a written and read number name. In the sense of spoken and heard, we can regard a number word as an oral symbol for a number, that is, oral in the sense of being transmitted by speech. A numbercan be regarded as an abstract quantity. If you think of the number of fingers on two hands, you are thinking of a number but in order to convey what you are thinking of, you need to use a symbol for a number such as an oral symbol, that is, a number word, or a written symbol "10", that is, a numeral. Thus, a numeralis a written symbol for a number. Examples of numerals (as they occur in early arithmetic) are: "6"; "10"; "3 407". I have labelled the area of arithmetic that we are concerned with in this paper as early arithmetic and this could also be referred to as whole number arithmetic. Thus, we are concerned with the numbers 0, 1, 2, 3, etc. and the four basic operations of arithmetic: addition, subtraction, multiplication and division. To return to an earlier point above - number words and numerals are the symbols for numbers. One can say and hear a number word, one can read and write a numeral, but one cannot do these things with numbers. Each number is a conception, that is, an idea in one's mind. The distinction between number words and numerals on one hand, and numbers on the other hand is that of signifier (number words, numerals) and signified (numbers). A final point is that, as adults, we seem to "look through" numerals and see numbers. For example, when we consider a number sentence such as 12 + 5 = 17, we are not concerned per se, with the numerals. We "look through" the numerals and think of the three numbers to which the number sentence refers. But in the case of young children first encountering early arithmetic, the situation is very different. In many cases, the children struggle to read numerals. We know for example, that many young children have significant difficulty learning to read "12". So whereas the adult sees "12 + 5 = 17" and thinks of the numbers, the young child may be focused on trying to make sense of the numerals in this number sentence. Thus, how young children eventually come to have a strong facility with reading numerals is important in early arithmetic.
The importance of numerals in early number instruction
In the previous paragraph, I have gone to some length to explain the distinction between numerals and numbers. This relates to our view that numerals have a significant role in early arithmetic instruction that is largely unrecognised. For example, we advocate for instruction, extensive use of both numeral sequences and individual numerals. Extensive details of approaches to instruction that focus on developing children's facility with numerals are readily available (see for example, Wright, Martland, Stafford & Stanger, 2006; and Wright, Stanger, Stafford & Martland, 2006). As well, we think that children should be given every opportunity to learn about numerals as early as possible, and certainly before they start formal schooling. Large numbers of teachers with whom we have worked make significant use of our instructional activities in which numerals and numeral sequences are prominent.
As well, there is significant support for early instructional emphasis on numerals from at least three sources. Firstly, Tolchinsky (2003), who conducted an extensive study from a semiotic perspective, of what children know about numerals before being taught, advised that:
From the very beginning, a child's notational knowledge should be taken into account and expanded - as a referential communicative tool, allowing and enhancing use of numerals in a diversity of contexts and functions, be they numerals in phone books, diaries, lists, dates, birthdays, number of children present or absent from class, counting children in a group but also groups in a class, and classes in a school, counting glasses on a table and calculating the remaining number of glasses to be bought, prices to be compared, currency to be used, measures to be compared and ordered and so forth .... Whatever the project to be developed in preschool or first grade, written representations should be included without any limit concerning magnitudes. Magnitude should not be a limiting factor (2003:141).
Secondly, according to Mix, Huttenlocher and Levine (2003), who work from a perspective of early cognitive development:
Research with preschoolers has revealed that children have an informal understanding of many basic concepts before they enter school. Working with concrete materials serves to help children bridge the gap between conventional symbols and their pre-existing concepts. This suggests that educators should place greater emphasis on the connections between symbols and experiences rather than simply providing the experiences themselves (2003:130).
And further, they advised that:
Because the mappings between spoken count words and single-digit numerals are so straightforward, learning them may set the stage for reading in a way that letter-sound pairings cannot, by introducing the idea that a written symbol can stand for a spoken word (2003:139).
Thirdly, Geary et al. (2013) studied the extent to which mathematical cognition and a range of other factors (e.g. intelligence, working memory, in-class attentive behaviour), measured during the first year of school predicted their functional numeracy at thirteen years of age. They identified as the key predictor - specific beginning-of-schooling numerical knowledge in the first year of school. They described this specific numerical knowledge as the ability to conceptualise a numeral as a symbol for a quantity and understand systematic relationships between numbers. By way of contrast, skill at solving math problems by counting, did not correlate with later ability.
Counting
We use the term "counting" in a particular sense. We label a child's activity as counting when they use a number word sequence (FNWS or BNWS) in a context that involves associating number words with some sense of quantity. Thus, the number word sequence is used in a situation in which quantity is implicated. We describe a progression of stages in which counting is used in increasingly more sophisticated ways. This progression draws extensively on the work of Steffe and colleagues (Steffe, Cobb & Von Glasersfeld, 1988; Steffe, 1992).
Perceptual counting
This involves counting objects that are perceptually available - typically seen but perhaps heard or touched. Perceptual counting usually occurs in situations where the child's task is to figure out how many objects are in one or perhaps two collections where the objects are available in the child's visual field.
Tasks involving screened objects
We also use the term counting in situations where the child's task is to figure out how many items in two collections, where the collections are screened from the child's view and the child is told how many items in each collection. We refer to this as an additive task, because the task is arithmetical in nature but involves collections of objects rather than formal spoken or written arithmetic. In a similar vein, we could present a subtractive task involving a screened collection of objects. The task might be to figure out how many taken away or how many remaining when the number taken away is stated (given).
Figurative counting
Steffe and colleagues (1988; 1992) observed that, when presented with an additive task such as 5 + 3 involving two screened collections, some children would invariably count from one - "one, two, three, four, five - six, seven, eight!". This is referred to as Figurative Counting (see for example Wright, Martland & Stafford, 2006).
Advanced counting-by-ones
In the context of additive and subtractive tasks as referred to above, children advance from figurative counting to the four advanced counting-by-ones strategies:
(a) Counting-up-from is used to solve additive tasks;
(b) Counting-up-to is used to solve missing addend tasks;
(c) Counting-down-from is used to solve what we call removed items tasks or take away tasks; and
(d) Count-down-to is used to solve what we call missing subtrahend tasks. In the period before children learn to add and subtract in the range 1 to 20 without counting, they frequently use the four advanced counting-by-ones strategies (see Wright, Stanger, Stafford & Martland, 2006).
Structuring numbers 1 to 20
As children progress in terms of their facility with counting, FNWSs, BNWSs and numerals they also begin to add and subtract without counting - first in the range 1 to 10 and then to 20. Ascribing number to regular spatial configurations such as dice patterns can provide an important base for children coming to regard numbers in the range 1 to 10 in a unitary sense, for example a square-wise pattern of four dots is regarded as "a four" rather than "four ones". This can extend to ascribing number to standard configurations on a ten-frame and also to building finger patterns for the numbers one to five and then extending this to ten. We think of these standard configurations on ten frames as taking two main forms - five-wise, where 8 for example appears as 5 in one row and 3 on the other, and pairwise where 8 appears as 4 in each row (see Wright, Ellemor-Collins & Tabor, 2012).
Large numbers of teachers with whom we have worked make extensive use of these ten frames and particularly the five-wise frames. Children first learn to ascribe number to five-wise and pairwise patterns for numbers 1 to 10. The frames are also used to teach children the partitions of 10 (9 + 1, 8 + 2, ...). Ten-frames are particularly useful for developing non-counting strategies in the range 1 to 10 and similarly, the arithmetic rack is particularly useful for this topic in the range 1 to 20 (Wright et al., 2012). We regard the development of non-counting strategies in the range 1 to 20 as a distinct and important domain of early arithmetical learning. This domain can be labelled addition and subtraction in the range 1 to 20. But we prefer the label of Structuring Numbers 1 to 20. Working in this domain involves students mentally structuring numbers, for example, 16 might be structured as an eight plus an eight, or a ten, plus a five, plus a one. Our view is that being able to mentally structure numbers in this way, enables children to add and subtract in the range 1 to 20 with good facility and this provides a basis for mastering the basic facts for addition and subtraction (tables or number bonds). An extensive discussion of the topic of Structuring Numbers 1 to 20 is available (see Ellemor-Collins & Wright, 2009; Wright, Ellemor-Collins & Tabor, 2012).
Conceptual place value
For at least 35 years, place value has been regarded as an important instructional topic in early arithmetic. Indeed, place value rose to prominence in the 1970s, to address a perceived problem of children having difficulty in learning the standard written algorithms (vertical or column algorithms) for addition, subtraction, multiplication and division. Children made errors with the algorithms which seemed to indicate that they did not skilfully interrelate ones, tens, hundreds when calculating with algorithms. This led to the development of place value as a distinct domain of instruction we refer to as traditional place value. Its main purpose was to support learning of the standard algorithms. We argue that in current times compared with 30 years ago, learning of the standard algorithms is less important. Much more important is the development of facile mental strategies for adding, subtracting, multiplying and dividing. Most importantly, children should develop facile mental strategies prior to instruction in standard algorithms. Facile mental strategies, as well as being very important in their own right, can support the learning of the traditional algorithms. Thus, traditional place value arose as a topic to support the learning of standard algorithms but it does not necessarily support the development of facile mental strategies. We have developed an instructional domain that we regard as important as a basis for calculation with multi-digit numbers. We label this topic conceptual place value and it involves learning to increment and decrement numbers by ones, tens, hundreds, thousands and so on. An extensive discussion of the topic of Conceptual Place Value is available (see Ellemor-Collins & Wright, 2011; Wright, Ellemor-Collins & Tabor, 2012).
A learning and assessment framework for number and early arithmetic
The Learning Framework in Number (LFIN) appears in summary form in Table 2. LFIN provides a means of mapping students' knowledge of number and early arithmetic on four domains: Counting; Forward Number Word Sequence; Backward Number Word Sequence; and Numeral Identification. See Wright, Martland and Stafford (2006) for an extensive discussion of LFIN.

Table 3 shows profiles of five children on LFIN. With appropriate training, practitioners find this profile approach not only easy to understand but extremely powerful as a model of the progression of early number learning for all learners.

Profile 1
The first profile shows a child who:
(a) Cannot correctly count a collection of 15 counters (SEAL = 0);
(b) Can say the number words forward from one to at least ten but has difficulty with tasks such as "What comes after six?" (FNWS = 1);
(c) Cannot say the numbers from ten back to one (BNWS = 0); and
(d) Has difficulty identifying (reading) at least some of the numerals in the range 1 to 10 (Num. Id = 0).
Profile 2
The second profile shows a child who:
(a) Can count a collection of 15 counters but cannot solve additive tasks involving two screened collections (SEAL = 1);
(b) Can say the number words from one to at least ten and say the number after for numbers in the range one to ten without dropping back (FNWS = 3);
(c) Can say the numbers from ten back to one but cannot say the number before for some of the numbers in the range 1 to 10 (BNWS = 1); and
(d) Can read the numerals in the range 1 to 10 but has difficulty with reading some of the numerals in the range 11 to 20 (Num. Id = 1).
Profile 3
The third profile shows a child who:
(a) Can solve additive tasks involving two screened collections but counts from one when doing so (SEAL = 2);
(b) Can say the number words from one to at least thirty and say the number after for numbers in the range one to thirty without dropping back (FNWS = 4);
(c) Can say the numbers from ten back to one and can say the number before for numbers in the range 1 to 10 but not for some of the numbers in the range 1 to 30 (BNWS = 3); and
(d) Can read the numerals in the range 1 to 20 but has difficulty with reading some of the numerals in the range 21 to 100 (Num. Id = 2).
Profile 4
The fourth profile shows a child who:
(a) Can count-on to solve additive tasks involving two screened collections (SEAL = 3);
(b) Is facile with forward number word sequences in the range one to 100 (FNWS = 5)
(c) Can say backward number word sequences and say the number before a number in the range one to thirty (FNWS = 4); and
(d) Can read the numerals in the range 1 to 100 but has difficulty with reading some 3-digit numerals (Num. Id = 3).
Profile 5
The fifth profile shows a child who:
(a) Can skilfully add and subtract in the range one to 20 without resorting to counting by ones (SEAL = 5);
(b) Is facile with forward number word sequences in the range one to 100 (FNWS = 5);
(c) Is facile with backward number word sequences in the range one to 100 (BNWS = 5);
(d) Can read 1-, 2- and 3-digit numerals (Num. Id = 4).
Assessing domains of early arithmetical knowledge
In this section, the author describes assessment tasks that are used for each of the following six topics:
- Forward number word sequences
- Backward number word sequences
- Numeral identification
- Structuring numbers 1 to 20
- Conceptual place value
More extensive descriptions of these tasks appear in the Wright et al. books (see the list of references).
Topic 1: Forward number word sequences (FNWSs)
We use two main types of tasks to assess facility with FNWSs:
1.1 Saying sequences: Start counting from one and I will tell you when to stop (stop at 32).
Similarly, Start counting from n (e.g. 38, 62, 86) and I will tell you when to stop. Apart from the first task (1 to 32) we typically use sequences of between 8 and fifteen number words. Lower level tasks are in the range 1 to 30 and 1 to 112. Higher-level tasks include crossing a centuple (a multiple of 100, i.e., 100, 200, 300, etc.), 1 000 and 1 100.
1.2 Saying the number word after: I'll say a number and you tell me what comes after it. 6, 3, 9, 4 etc.
According to the student's ability, work with two or three of the following ranges: 1 to 10; 10 to 30; 30 to 100, 100 to 1 000, etc. In each range, the numbers are asked in pseudo-random order.
Topic 2: Backward number word sequences (BNWSs)
Assessing BNWSs corresponds closely with assessing FNWSs. We use two main types of tasks:
2.1 Saying sequences: Count backwards from ten. Start counting backwards from 23 and I will tell you when to stop (stop at 16).
Similarly, Start counting backwards from n (e.g. 46, 58, 92) and I will tell you when to stop. As for FNWSs, we typically use sequences of between 8 and fifteen number words and lower level tasks are in the range 1 to 30 and 1 to 112. Higher-level tasks include crossing a centuple (a multiple of 100, i.e., 100, 200, 300, etc.) 1 000 and 1 100. Surprisingly common is for children to err when crossing a decuple (a multiple of 10), for example, 35, 34, 33, 32, 31, 20, 29, 28. Another somewhat frequent error is to omit a double-digit number such as 44 or 66.
2.2 Saying the number word before: I'll say a number and you tell me what comes before it. 5, 3, 8, 4, etc.
According to the student's ability, work with two or three of the following ranges: 1 to 10; 10 to 30; 30 to 100, 100 to 1 000, etc. As for FNWSs, in each range the numbers are asked in pseudo-random order.
Topic 3: Facility with numerals:
The main task we use is identifying numerals, that is, naming or reading numerals.
3.1 Numeral Identification.
These tasks are very straightforward. The teacher simply displays a numeral card and asks the child to say what number it is. The numerals are presented in pseudo-random order. Lower level tasks are in the range 1 to 10 and 11 to 20. This extends to 100, 1000 and so on. For beyond 100, include numerals with a nought or a one in the tens (416, 804), and with a nought in the ones (780). Many children have particular difficulty identifying 12. They read it as 20 or 21. An alternative task is the task we call recognising numerals. For example, the numerals from one to ten are arranged on the table in pseudo-random order. The teacher asks the child to point to the number eight and so on.
Topic 4: Counting
We use two main categories of tasks for assessing counting. For earlier stages of counting, we use tasks involving counting visible collections and in later stages we use additive and subtractive tasks involving screened collections:
4.1 Counting visible collections
There are two main tasks and these tasks are complementary. One task involves presenting a collection of say 8, 13 or 18 counters - all of one colour - to the child and asking them to count the collection. The complementary task involves presenting a large collection of counters, say 50 counters of one colour and asking the child to get say 8, 13 or 18 counters from the collection. The child who cannot solve these tasks is labelled as emergent. The child might attempt to count the counters but either does not coordinate the number words with the counters or makes an error with the number word sequence.
4.2 Additive tasks
Additive tasks involve two collections, say 8 red counters and 5 blue counters. The collections are displayed momentarily in turn and then screened, and the teacher tells the child how many in each collection. I have 8 red counters under here and 5 blue counters under here. How many counters are there altogether? The number in the first collection - the stem number - is larger than the number in the second collection the count number - which is usually in the range 1 to 5. This is because, in both assessment and instruction, we regard it as generally unproductive for children to make long counts to solve arithmetical tasks. The stem number is typically in the range 1 to 10 or to 20 but could be beyond 20, assuming that the child has the corresponding knowledge of the FNWS in order to count-on to solve the task.
In practice, we typically would present subtractive tasks as well as additive tasks. Nevertheless, it is instructive to consider hypothetically, how children at different stages of counting might respond to an additive task such as the one described above. The emergent child cannot proceed so the teacher unscreens both collections. The child attempts to count the visible counters from one, but does not count them correctly, making either a coordination error or a number word sequence error. The perceptual child, like the emergent child cannot proceed and again the teacher removes both screens. But in this case the child correctly counts the counters. The figurative child correctly solves the task but in doing so, counts from one, to account for the first collection and then continues their count to account for the second collection. The Stage 3 or 4 child (Initial or Intermediate Number Sequence) solves the task by counting up from 8 - "eight . nine, ten, eleven, twelve, thirteen!" Finally, the Stage 5 child uses a non-counting strategy such as partitioning 8 into 5 and 3, summing the two 5s, and then adding on 3. In practice, additive tasks such as this have the purpose of eliciting a counting-up-from strategy. In that case, the student solves the task by making 5 counts up from 8.
4.3 Missing addend tasks
In this case, the teacher briefly displays and then screens, say, 7 red counters. Here are 7 red counters. The teacher then places 4 green counters under the screen without allowing the student to see them. I have put some more counters under the screen and now there are 11. How many more counters did I put under the screen? Missing addend tasks have the purpose of eliciting a counting-up-to strategy. In that case, the student solves the task by counting from 7 up to 11 and keeping track of the counts (4 counts). Note that, as for the additive task, the count number (4) is in the range 1 to 5.
4.4 Removed items tasks
In this case, the teacher briefly displays and then screens say 8 red counters. The teacher then removes 3 counters and briefly displays and then screens them. I had 8 red counters and I took 3 away. How many counters are left? Removed Items tasks have the purpose of eliciting a counting-down-from strategy. In that case, the student solves the task by making 3 counts back from 8. Again, the count number (3) is in the range 1 to 5.
4.3 Missing subtrahend tasks
In this case, the teacher briefly displays and then screens say 17 blue counters. The teacher then removes 2 counters without allowing the student to see them. I had 17 counters. I took some away and now I have 15 counters. How many counters did I take away. Missing subtrahend tasks have the purpose of eliciting a counting-down-to strategy. In that case, the student solves the task by counting from 17 down to 15 and keeping track of the counts (2). Again, the count number (2) is in the range 1 to 5.
Topic 5: Structuring numbers 1 to 20
5.1 Finger patterns
A preliminary set of tasks on this topic focuses on assessing facility to build finger patterns for numbers, firstly in the range 1 to 5 and then in the range 6 to 10. We want to know if the student can build a finger pattern for example, for four by raising fingers simultaneously. As for earlier tasks, these tasks are posed in pseudo-random order.
5.2 Spatial patterns
Another preliminary set of tasks involves ascribing number to flashed spatial patterns that is, regular configurations of dots such as dice patterns.
5.3 Key combinations and partitions
We use an extensive set of tasks to illicit students' facility with key combinations and partitions in the ranges 1 to 10 and 1 to 20. These tasks are posed orally and we are interested to see the student answer very quickly and without counting. Key combinations include: the small doubles (1 + 1, 2 + 2, ... 5 + 5); the 5-plus facts (5 + 1, 5 + 2, ... 5 + 5); the 10-plus facts (10 + 1, 10 + 2, ... 10 + 10); and the large doubles (6 + 6, 7 + 7, ... 10 + 10). Key partitions are the partitions of 5, 10 and 20. For example, I will say a number and you say what goes with it to make 5. 3?
5.4 Addition and subtraction
These tasks involve numbers in the range 1 to 20 and are written in horizontal format. Again, we are interested to see if the student answers very quickly and without counting. We organise the tasks into four hierarchical levels and at each level, a sample of additions and subtractions is posed.
Level 1: Parts in the range 1 to 5, for example 4 + 2, 5 + 1, 7 - 4, 6 - 4
Level 2: Whole in the range 1 to 10, for example 3 + 6, 6 + 2, 9 - 2, 7 - 1
Level 3: Parts in the range 1 to 10, for example 9 + 2, 7 + 8, 12 - 4, 16 - 9
Level 2: Whole in the range 1 to 20, for example 13 + 6, 7 + 12, 17 - 15, 18 - 6
Topic 6: Conceptual place value
Assessment of conceptual place, covers a range of tasks some of which involve the use of materials such as bundling sticks or a base-ten material consisting of ten-strips (strips of 5 black and 5 grey dots) and hundred squares (a square consisting of 10 ten-strips).
6.1 Incrementing by tens on the decuple
The teacher places a bundle of ten sticks under a screen and asks how many sticks there are. The teacher then places a second bundle under the screen and asks how many (20). This proceeds up to 12 bundles (120).
6.2 Incrementing by tens off the decuple
The teacher places four sticks under a screen and asks how many sticks there are (4). The teacher then places a bundle of ten sticks under a screen and asks how many (14). The teacher then places a second bundle under the screen and asks how many (24). This proceeds up to 84 sticks.
6.3 Decrementing by tens off the decuple
The teacher places out 147 sticks arranged as one large bundle consisting of 10 bundles of 10 (100), four bundles of ten and seven sticks. The teacher screens the 147 sticks, removes one bundle, and asks how many sticks now (137). The teacher continues removing one bundle at a time from beneath the screen and asking how many sticks (127, 117 . 77) until 77 sticks remain under the screen.
6.4 Ten more, ten less
The teacher displays a numeral card and asks the student to say the number that is ten more (or ten less) than the displayed number. We use a progression of numbers which is likely to present increasingly more challenging tasks. For example, what is ten more than 70, 90, 49, 66, 572, 407, 497, 999; what is ten less than 70, 49, 66, 103, 572, 407, 1005. Tasks where the teacher asks what number is 100 more or 100 less are also used.
Concluding remarks
As described earlier in this article, my colleagues and I have worked for more than 20 years to understand better the learning and teaching of number and early arithmetic. Further, we have spent a good deal of time providing significant and ongoing professional learning experiences in several countries; for classroom teachers, specialist teachers, and instructional leaders and coaches. Through this work with classroom teachers and others, I have come to the realisation that early years teachers have both a great need and a great capacity to learn more about the teaching of number and early arithmetic. Thus, it is urgent and important for schools and educational jurisdictions to find ways to significantly advance teachers' pedagogical knowledge in this area. And I believe that the approaches to teachers' professional learning that we have progressively developed over more than 20 years are particularly apt. We have seen many times that undertaking such professional learning can be very rewarding and fulfilling for teachers. I urge relevant professionals - researchers, teacher educators, principals, etc. to find ways to incrementally trial and implement with teachers, the approaches to instruction in number and early arithmetic that are set out in our four books (e.g. Wright et al., 2006; 2012). My view is that appropriate professional learning is the pathway to profoundly strengthening children's learning of basic arithmetic, and that through strengthened pedagogy, virtually all young children can achieve at significantly higher levels.
References
Aubrey, C. 1993. An investigation of the mathematical knowledge and competencies which young children bring into school. British Educational Research Journal, 19(1):27-41. [ Links ]
Aubrey, C., Dahl, S. & Godfrey, R. 2006. Early mathematics development and later achievement: Further evidence. Mathematics Education Research Journal, 18(1):27-46. [ Links ]
Aunola, K., Leskinen, E., Lerkkanen, M.K. & Nurmi, J.E. 2004. Developmental dynamics of math performance from preschool to grade 2. Journal of Educational Psychology, 94(4):699-713. [ Links ]
Cockcroft, W. 1982. Mathematics counts: Report of the committee of inquiry into the teaching of mathematics in schools. London: HMSO. [ Links ]
Daraganova, G. & Ainley, J. 2012. Children's numeracy skills. In B. Maguire & B. Edwards (Eds.), The longitudinal study of Australian children annual statistical report 2011, 79-89. Australian Institute of Family Studies: Melbourne.
Duncan, G.J., Dowsett, C.J., Claessens, A., Manuson, K., Huston, A.C., Klebanov, P., Pagani, L.S., Feinstein, L., Engel, M., Brooks-Gunn, J., Sexton, H. & Duckworth, K. 2007. School readiness and later achievement. Developmental Psychology, 43:1428-1446. [ Links ]
Ellemor-Collins, D. & Wright, R.J. 2008. How are your students thinking about arithmetic? Videotaped interview-based assessment. Teaching Children Mathematics, September, 106-111.
Ellemor-Collins, D. & Wright, R.J. 2009. Structuring numbers 1 to 20: Developing facile addition and subtraction. Mathematics Education Research Journal, 21(2):50-75. [ Links ]
Ellemor-Collins, D. & Wright, R.J. 2011. Developing conceptual place value: Instructional design for intensive intervention. Australian Journal of Learning Difficulties, 16(1):41-63. [ Links ]
Geary, D.C., Hoard, M.K., Nugent, L., Bailey, D.H. 2013. Adolescents' functional numeracy is predicted by their school entry number system knowledge. PLoS ONE, 8(1): e54651. doi:10.1371/journal.pone.0054651. [ Links ]
Gravemeijer, K. & Van Eerde, D. 2009. Design research as a means for building a knowledge base for teachers and teaching in mathematics education. The Elementary School Journal, 109(5):510-524. [ Links ]
Gravemeijer, K. & Cobb, P. 2006. Design research from a learning design perspective. In J. Van den Akker, K. Gravemeijer, S. McKenney & N. Nieveen (Eds.), Educational design research. Abingdon, UK: Routledge. [ Links ]
Heibert J., Carpenter, T. & Moser, J. 1982. Cognitive development and children's solutions to verbal arithmetic problems. Journal for Research in Mathematics Education, 13(2):83-98. [ Links ]
Jordan, N.C., Kaplan, D., Ramineni, C. & Locuniak, M.N. 2009. Early math matters: Kindergarten number competence and later mathematics outcomes. Developmental Psychology, 45(3):850-867. [ Links ]
Jordan, N.C., Kaplan, D., Ramineni, C. & Locuniak, M.N. 2009. Early math matters: Kindergarten number competence and later mathematics outcomes. Dev Psychol, 45:850-867. [ Links ]
Mix, K., Huttenlocher, J. & Levine, S. 2002. Quantitative development in infancy and early Childhood. Oxford: Oxford University Press. [ Links ]
Princiotta, D., Flanagan, K.D. & Germino-Hausken, E. 2006. Fifth grade: Findings from the fifth-grade follow-up of the early childhood longitudinal study, kindergarten class of 1998 -99 (ECLS-K) (NCES 2006-038). US Department of Education, Washington, DC: National Center for Education Statistics. [ Links ]
Ritchie, S.J. & Bates, T.C. 2013. Enduring links from childhood mathematics and reading achievement to adult socioeconomic status. Psychological Science, May:23(7):1301-1308. [ Links ]
Steffe, L.R. 1992. Learning stages in the construction of the number sequence. In J. Bideaud, C. Meljac & J. Fischer (Eds.), Pathways to number: Children's developing numerical abilities, 83-88. Hillsdale, NJ: Lawrence Erlbaum. [ Links ]
Steffe, L.P., Cobb, P. & Von Glasersfeld, E. 1988. Construction of arithmetic meanings and strategies. New York: Springer-Verlag. [ Links ]
Stevenson, H.W. & Newman, R.S. 1986. Long-term prediction of achievement and attitudes in mathematics and reading. Child Development, 57:646-659. [ Links ]
Tolchinsky, L. 2003. The cradle of culture and what children know about writing and numbers before being taught. Mahwah, NJ: Lawrence Erlbaum. [ Links ]
Wright, R.J. 1991. What number knowledge is possessed by children entering the kindergarten year of school? Mathematics Education Research Journal, 3(1):1-16. [ Links ]
Wright, R.J. 1994. A study of the numerical development of 5-year-olds and 6-year-olds. Educational Studies in Mathematics, 36:35-44. [ Links ]
Wright, R.J. 2000. Professional development in recovery education. In L.P. Steffe & P.W. Thompson (Eds.), Radical constructivism in action: Building on the pioneering work of Ernst von Glasersfeld, 134-151. London: Falmer. [ Links ]
Wright, R.J. 2008. Mathematics Recovery: An early intervention program focusing on intensive intervention. In A. Dowker (Ed.), Mathematics difficulties: Psychology and intervention, 203-223. San Diego, CA: Elsevier. [ Links ]
Wright, R.J., Ellemor-Collins, D. & Tabor, P. 2012. Developing number knowledge: Assessment, teaching and intervention with 7- to 11-year-olds. London: Sage.
Wright, R.J., Martland, J. & Stafford, A. 2006. Early numeracy: Assessment for teaching and intervention (2nd Edition). London: Sage. [ Links ]
Wright, R.J., Martland, J., Stafford, A. & Stanger, G. 2006. Teaching number: Advancing children's skills and strategies (2nd Edition). London: Sage. [ Links ]
Wright, R., Stanger, G., Stafford, A. & Martland, J. 2006. Teaching number in the classroom with 4- to 8-year-olds. London: Sage. [ Links ]
Young-Loveridge, J. 1989. The development of children's number concepts: the first year of school. New Zealand Journal of Educational Studies, 24(1):47-64. [ Links ]
Young-Loveridge, J. 1991. The Development of children's number concepts from ages five to nine, Volumes 1 and 2. Hamilton, New Zealand: University of Waikato. [ Links ]
Zill, N. & West, J. 2000. Entering kindergarten: A portrait of American children when they begin school. Findings from the condition of education, 2000. (ERIC Document Reproduction Service No. ED448899).














