Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.3 n.1 Johannesburg 2013
Evaluation of maths training programme for children with learning difficulties
Antje Ehlert; Annemarie Fritz
Psychology Department, Faculty of Educational Sciences, University of Duisburg-Essen, visiting professor at Centre for Education Practice Research, Faculty of Education, University of Johannesburg Soweto Campus, e-mail address: antje.ehlert@uni-due.de Annemarie Fritz, e-mail address: fritz-stratmann@uni-due.de
ABSTRACT
In the German school system, children are seen as educationally impaired when they are more than two grades behind in their performance in several areas of learning, and this has been the case for several years. A special problem is the fact that support measures are often effective only to a limited extent, or only for a short period.
The study at hand focuses on the question of whether educationally impaired children with large deficits in mathematics can be supported successfully by means of a highly adaptive support measure (MARKO-T), and whether the effects of this support can be maintained over a certain period. For this, 32 educationally impaired third-graders with math deficits were supported individually with MARKO-T twice a week, over a period of ten weeks. As control group, 32 similarly impaired third-graders were paralleled according to the mathematical and cognitive achievements of the training group. Two further control groups, each with 32 unimpaired first-graders, were paralleled according to their mathematical and cognitive achievements, respectively. The results showed that the very poor mathematical performance of the educationally impaired children could be significantly improved with this support programme. Four months after the end of the training, significant support effects could still be established when compared to the educationally impaired control group. The comparison with the two control groups demonstrated that the developmental curve of the children with learning difficulties increased in a way that was comparable to that of the unimpaired first-graders.
Keywords: educationally impaired children, evaluation of MARKO-training, training effects, control group training, maths training programme
Introduction
The acquisition of mathematical competences is a complex process of learning that sets in long before formal schooling (e.g. Anteil & Keating, 1983; Kobayashi, Hiraki, Mugitani & Hasegawa 2004; Starkey, Spelke & Gelman 1990; Wynn, 1992, Resnick, 1989, Gelman & Gallistel 1978, Fuson, 1992, Piaget & Szeminska, 1975). The relevance of this early acquisition of mathematical competences has been substantiated by numerous especially longitudinal studies. These studies verified empirically that there is a medium to high correlation between pre-school and primary school mathematical performance (Aunola, Leskinen, Lerkkanen & Nurmi 2004), and that the pre-school performance predicts the mathematical performance ability during primary school. Examples used to determine pre-school performance are, for instance, to what extent children are able to complete number rows. To determine this, three cards with digits between 0 and 20 are given (i.e. 4 - 5 - 6), on which one digit was missing: the first, the middle, or the last (Chard, Clarke, Baker, Otterstedt, Braun & Katz, 2005, also in Lembke & Foegen, 2009). In Jordan, Glutting & Ramineni (2010), the children counted to ten, counted stars in illustrations by pointing at the counted object, judged the counting skills of a finger puppet, determined precursory and successive numbers, and compared figures. For example, they were asked 'Which is smaller: 8 or 6?' and had to calculate number questions, such as: 'Paul has 5 oranges. Maria takes 2 of his oranges away. How many oranges does Paul have now?' Koponen, Aunola, Ahonen & Nurmi (2007) had the children identify the third and seventh object of a row, count a quantity of objects and match the counted number to a digit and had them draw quantities that contained two objects more, or one or two less than the presented quantity. Overall, the studies serve to ascertain that before school begins, children know more than merely the number-word-line and the counting out of quantities. They are capable of performing rather complex mathematical operations and already understand the relations between quantities and numbers.
The question is whether this is really the case for all children entering school for the first time. Schipper (1998) investigated this question in critical re-analyses. On the one hand, he could confirm that many children entering school displayed high levels of competence. On the other hand, he detected a high variance in the children's performances at school start. Even though many children entering school already possess significant arithmetic competences according to various studies, this is by no means the case for all children. The heterogeneity in performance amounted to up to three years. The reasons for this heterogeneity are manifold. The children's chances to deal with quantities and numbers in pre-school (before they start school) are seen as essential. The child's cognitive prerequisites are another factor (Geary, Brown & Samaranayake, 1991) as is the performance of his or her working memory (Logie, Gilhooly & Wynn et al., 1994; Tronsky, 2005; luculano, Moro & Butterworth, 2011). In summary, it can be stated that children who start school with a high basic level of mathematical competence will maintain good performance (Aunola et al., 2004). They may even go on to improve more than under-performing children. However, under-performing pupils tend to remain among the weakest performers, even at the end of fourth grade. Different longitudinal studies (for instance Stern, 1994) emphasises that later academic success depends largely on subject-specific prior knowledge. Thus, mathematically precursory competences have significant influence on academic performance (Helmke & Weinert, 1997). They are the prerequisites for understanding school mathematics.
Problems in learning numeracy
Dyscalculia and numeracy problems
Children with numeracy problems or dyscalculia - we will discuss the difference later - usually start school already with a less accomplished level of prior knowledge. The problems do not to arise during school; they begin before. In addition, they increase if the lessons do not begin at the children's respective level of knowledge. Below, we focus on the difficulties faced by weaker mathematicians, by limiting our attention to the field of arithmetic. First, we need to distinguish the different types of difficulties that they face and how these can be differentiated terminologically.
Dyscalculia is diagnosed according to the classification criteria of the ICD-10 (International Classification of Diseases; Dilling, Mombour & Schmidt 2004), when a child's performance in numeracy in a standardised arithmetic test ranks among the bottom 10% of the distribution. Secondly, intelligence should not be significantly below average (i.e., IQ > 70). Finally, a discrepancy between the expected numeracy skills, based on the performance in an intelligence test, and weak numeracy performance, should exist (Ehlert, Schroeders & Fritz, 2012). Another criterion states that the children's problems 'exist from the start' and already affect the acquisition of the basic arithmetic operations. This definition applies to 4 - 6% of all children who are likely to have dyscalculia (Koumoula, Tsironi, Stamouli, Bardani, Siapati, Graham-Pavlou et al., 2004; Von Aster, Schweiter & Weinhold, Zulauf, 2007).
However, problems with numeracy occur far more frequently. Current results from the TIMSS (Bos, 2013) show e.g. that, in Germany, the mathematic performance of 19.3% of children in grade 4 does not meet the minimum requirements (data for other countries from TIMSS: Japan 6.8%; Australia 29.8%, Iran 66.8%). This means that almost 20% of German primary school children only possess a rudimentary knowledge of mathematics at the end of the fourth grade.
What are the mathematical difficulties these children experience and what are the obstacles they do not seem to be able to negotiate by themselves? What all these children have in common is that they hang on to counting strategies and do not develop them further into effective strategies of decomposition and fact retrieval (Geary, 1990; Hanich et al., 2001). Without the necessary support, it is left to chance, whether they abandon finger counting, or verbal counting. When solving arithmetic problems and word problems, they lack the ability to choose between various problem-solving strategies (Hanich et al., 2001; Jordan & Montani, 1997; Barrouillet, Fayol & Lathulière, 1997; Ostad, 1997, 1998, 2000; Gross-Tsur, Manor & Shalev, 1996) and approaches for modelling the tasks. They commit many more errors, when they retrieve arithmetic facts from long-term memory (Hanich et al., 2001; Jordan & Montani, 1997; Ostad, 1997, 2000; Barrouillet et al., 1997; Fayol, Barrouillet & Marinthe, 1998; Geary, 1990). In children with dyscalculia, these problems are more comprehensive and persistent, but are not entirely different.
Numeracy problems as a symptom of general learning problems
The definition of dyscalculia, according to ICD-10, demands a discrepancy between IQ and mathematical performance and thus excludes children with a low IQ. By definition, children are also excluded from being diagnosed with 'dyscalculia' if, on top of a weakness in arithmetic, they exhibit further comprehensive learning difficulties. Within the German school system children are defined as 'educationally impaired', when they are more than two grades behind in their performance in several areas of learning. This definition applies when this has been the case for several years and the situation cannot be compensated for by support measures in the short term (Kanter, 1973). The deficitsin performance should not be caused byinsufficient learning opportunities or inappropriate schooling. The performance deficits should not be caused by insufficient learning opportunities or inappropriate schooling, though. A further criterion, often mentioned, is 'impaired intelligence' (IQ < 85). However, as an isolated factor, this is not enough to diagnose a learning difficulty (Klauer & Lauth, 1996). There is no comparable term to be found internationally for the German category Lernbehinderung (learning difficulty). The international parlance expressed in the ICD-10 (F 81.3 and F 81.9) 'mixed disorder of scholastic skills' and 'developmental disorder of scholastic skills,' and as well as the term 'Mild Mental Retardation' do overlap, to a large extent, with the German term Lernbehinderung.
Although a formal distinction is made, according to this definition, between children with weakness in arithmetic, empirical findings indicate that these children do not differ with regard to the appearance and extent of their difficulties in numeracy. So far, only a few studies exist for the area of mathematics. One such study compared the solutions of arithmetic tasks of arithmetically weak pupils, who did or did not fulfil the discrepancy criterion (Jimenez Gonzalez & Garcia Espinel, 1999; 2002). No significant differences could be found between the two groups of arithmetically weak children, neither in the frequency of solutions nor in the choice of solving strategies. A separate comparison of arithmetically weak children, who did, or did not fulfil the discrepancy criterion, could further demonstrate that both groups of children had the same mathematical concepts at their disposal. Thus, both groups showed a comparable grasp of mathematical concepts, independent of their IQs. This suggests that children of the same age, without an arithmetic weakness, are on a higher developmental level (Ehlert et al., 2012).
The criteria, given for a comprehensive mathematical learning difficulty, describe comprehensive learning deficits of more than two years, which cannot be remedied by short-term interventions. Thus, it must be assumed that difficulties in numeracy, which started at an early stage, have now become entrenched. Furthermore, longitudinal studies indicate that the differences in performance of children with, and those without, learning difficulties, become more pronounced in the course of development. This, in turn, implies that the performance gap between the two groups continues to increase. In order to support children with such pronounced learning deficits, we need a sophisticated way of diagnosing the learning difficulties that may accompany the learning process. This should provide detailed information regarding the progress, or a lack thereof, in learning. In addition, long-term support measures are needed which considers individual learning processes. Both measures will be discussed in more detail in the following section.
Criteria for support
Diagnostics is of special significance in terms of the support required by children who experience difficulties with numeracy. In order to plan an intervention that is in line with the child's state of development, a sophisticated analysis of the initial situation of mathematical learning is required. This should give a comprehensive description of the child's current state of mathematical development, before the support starts.
Nevertheless, in order to support a child successfully, it is not enough to limit diagnostics to the assessment of the initial learning situation and the determination of individual support requirements. A key factor for the success of the intervention is monitoring the support process to continuously adapt the training to the individual's learning speed as well as the individual's learning progress. Analyses of training studies show (Strathmann & Klauer, 2008; Strathmann, Klauer & Greisbach, 2010; Strathmann & Klauer, 2010) that a child's development is not always marked by progress in learning. During the training, learning can also come to a halt, or there can even be a regression in learning. This phenomenon necessitates diagnostic monitoring that accompanies the learning process so that appropriate reactions to the learning process are possible.
The development and implementation of diagnostically monitoring the learning process, however, is fraught with a number of problems (Klauer, 2011). If the learning process is to be represented in a theoretically correct manner, there ought to be different tasks in each test, yet, all of these have to be at the same level of difficulty, and have to assess the same latent trait. Only if this is the case, is it possible to guarantee that the learning curve is represented accurately, and that an improved performance is not due to re-testing, or because of variations in the difficulty of the tasks. Especially in mathematics, it is difficult to generate such test items as, for example, the number range limits the amount of possible tasks. One possible solution under discussion is the modelling of competence level models and the implementation of a probabilistic test theory (Klauer, 2011).
The basic idea here is to break down a complex mathematical competence into partial competences, to put these in a hierarchical order, and then to develop tasks that require the respective partial competence for their solution. After that, one tests psychometrically (e.g. with the Rasch model; Rasch, 1960) to determine whether the tasks, and the partial competences represented in them, really build upon one another hierarchically, as expected. Based on such an empirically validated competence level model, one can then determine, diagnostically, on which level of the competence scale the child currently operates, and which arithmetic concepts he or she has already developed. This provides a grid for the observation and evaluation of levels of competence.
By means of Item Response Theory (IRT), the item difficulties and person abilities can be estimated on a common scale (see also Fritz et al in this journal). The probability of solving a task depends on the individual's ability, and the score achieved (items solved correctly) can be used to locate a person with his/her ability at this scale. If the difficulty of the task is lower than the ability of the learner, it is likely that they will solve the task. Conversely, if the difficulty of the task is higher than the skill of the learner, it is rather unlikely that he or she will solve the task.
If a test, such as this, that is based on a valid model is available, then the performance of each child can be located in the mathematical model, at any point in time, during the intervention. It is possible to determine whether the child shows an improvement in ability and progress in acquiring the next level of competence. Diagnosing the learning process does not then simply represent the learning curve, but also checks whether the child continues to progress in the developmental model, under the influence of the intervention.
Aside from an accompanying diagnosis of the learning process, the training should be designed broadly to allow for a long-term support intervention mechanism that follows the development of the children, and does not merely focus on imparting a limited number of competences. Furthermore, the training should show sustainable effects. This means that if knowledge or skills were actually developed during the training, these should still be evident after several months.
A precursory overview of existing support or training programmes for the primary school age reveals that although there are some evaluated programmes such as, the MAthematics Strategy Training for Educational Remediation (MASTER) by Van Luit, Kaskens & Van the Krol, 1993 (see also Van Luit & Naglieri 1999, and Kroesbergen & Van Luit, 2002), or Tier 2 intervention by Bryant, Bryant, Gersten, Scammacca & Chavez (2008), these do not contain a diagnostic component to accompany the support process. Only the programme Tier 2 intervention is designed to adapt to the individual's developmental process. Only one such programme is based on a mathematical stage model of early arithmetical learning and plans training over six stages of early arithmetic learning (Mathematics Recovery Programme by Wright, Martland & Stafford, 2000). However, this programme has not been evaluated or validated.
Below we present a support programme that takes into account all discussed aspects of a comprehensive intervention programme for children with early arithmetic problems.
The training programme: MARKO-T
The training programme suggested here, MARKO-T (Gerlach, Fritz & Leutner, 2013), is based on a developmental model, which posits that mathematical concepts of acquired sequentially. This model is presented in an article by Fritz, Ehlert & Balzer (in this issue). Although the model distinguishes six levels, for training purposes only five of these levels have been developed so far.
• Level I Count Number: The acquisition of the number- word line begins at the age of two to three. On realising the one-to-one correspondence, number words are successively allocated to quantities of objects (Fuson, 1988), so that children can confidently count and count out smaller quantities.
• Level II Mental number line: The children understand that numbers along the number- word line become 'larger'. By counting, they can now precisely carry out additions in a limited number-range and determine precursory and successive numbers in the number- word line.
• Level III Cardinality and Decomposability: Numbers are understood as a combined unit, consisting of some elements. Therefore, they can be decomposed and put together again. Numbers become connected to the cardinality of the relevant quantity; the number- word line is understood to be a sequence of increasing cardinality. The part-part-whole relation is grasped through actions.
• Level IV Class inclusion and embeddedness: The children grasp the inclusion relations of numbers. Each number contains the quantity of the precursory numbers. Thus, numbers become decomposable into different partial quantities. The part-part-whole relation is further elaborated on and can now be applied to word- problems that enquire after the exchange quantity, as well as the final, or initial quantity.
• Level V Relationality: The children understand that the distance between two consecutive numbers is always the same. One aspect of this number concept is that the sequence of the number-word line is now both seriated and embedded. Each word of the sequence is now an ideal identical iterable one, and each word is now both a sequence word, and a cardinal word, that can refer to all of the words, up to, and including itself. Therefore, each next word presents a cardinal number that is one larger than (using the cardinal as well as the sequence meaning) the earlier word.
The individual levels are arranged in an hierarchical order and build upon one another. On each level, a particular mathematical concept is acquired. In their entirety, the mathematical concepts are captured by a common dimension. On average, preschool children acquire one mathematical concept per year and thus develop one level further.
Scope of application
MARKO-T is a training programme that is accompanied by diagnostics for children aged between five and eight years old. It can be used for the targeted support of children with arithmetic weaknesses or retarded development during the transition from kindergarten to primary school, or in the first years of primary schooling or in schools for children with special-needs.
Training structure
The programme contains five training modules with a total of 57 training units. The training modules are aligned to the five levels of the model (Level I to V). Each of the five modules provides tasks that can be solved on the basis of the respective concept.
In terms of content, each mathematical concept is acquired in small steps.
• Module I comprises 10 training units and contains comparisons of quantities, the one-to-one allocation, learning and consolidating the number-word line, as well as, counting and counting out smaller quantities.
• Module II is composed of 15 training units. This module focuses on the understanding that the number-word line follows a fixed order in which the numbers increase. With this knowledge, numbers can be compared regarding their position, and first arithmetic operations can be carried out.
• The requirements of Module III are also tied into 15 training units. The children work out that numbers are composed entities (units), that is, they represent the number of elements in a quantity. Each number stands for a specific cardinality; this cardinality increases successively in the number- word line. Numbers can therefore be compared according to their cardinality. As numbers are composed entities (units), they can be decomposed and recomposed. The number range is opened up to 20 and with the help of material that provides structures, decompositions and addition tasks, that use the power of 5 or the power of 10, can be practiced.
• The 10 training units of Module IV, which deals with the part-part-whole concept, help the children to grasp that numbers contain other numbers. Tasks such as 'Give me 5, 3 of which should be red' illustrate the determined connection between partial quantity - partial quantity - total quantity. Systematic number decompositions are practiced; decomposition and addition tasks are solved mentally.
• With the last Module V, the children acquire the relational aspect of numbers in 7 training units. The relational number concept makes differences and distances between numbers precisely definable. In the first task of this module, numbers are represented on the number line and differences between numbers are determined (e.g. 'by 2 more/larger than'). Based on this understanding, comparing tasks become solvable: 'Marko and Rollo together have got 6 balls, M has got 2 more than R. How many has M got, how many has R got?'
The individual training units are each structured identically and consist of a greeting that is followed by a check of whether the constructs of the last training session are still known. Then the contents of the current training session is introduced and practiced. The session ends with a closing reflection and an overview on the next training unit.
Structure and principles
The tasks are embedded into problem contexts and are child-oriented and interactive. Dung beetle Marko is the child's learning partner. Marko is continuously faced with problems that form the starting point for solving the tasks together. This way, the child repeatedly has to explain contents, approaches, or strategies, and has to focus and reflect on, or explain correct and false or ineffective procedures (which Marko then uses). By articulating their own, as well as, Marko's strategies, the metacognition of children is stimulated and enhanced. The child is thus made aware of mathematical strategies that can be used for the further development of mathematical understanding.
At the same time, the beetle can be employed to model problem-solving approaches. The performance requirements, within the training, are gradually raised to the child's individual limits of performance. Successfully dealing with requirements, bordering on one's own performance limits, also supports the development of success-oriented motivation. The fact that the child's learning progress is verbalised at the end of each lesson also supports the experience of competence.
With dung beetle Marko tasks can also be done competitively, which provides a 'natural' way of automatising strategies, since it is focused on speed. In this way, the mathematical knowledge and skills are consolidated and become readily available.

Diagnostics
After having analysed the individual's learning abilities, a training programme aims to design learning conditions that facilitate individualised learning progress. As was explained in detail above, a sophisticated description of the initial learning situation, as well as, a diagnostic assessment of learning process is needed.
In MARKO-T, the diagnostics of the initial level of competence is done by means of a diagnostic instrument called the MARKO-D. A series of MARKO tests have been designed, namely; the MARKO-D0 (Ricken, Fritz & Balzer, 2013) for pre-school age and the MARKO-D1 (Fritz, Ehlert, Ricken & Balzer, in prep.) for the first grade. The MARKO-D instrument allows a child's performance to be assessed according to social norms or according to criterion norms:
Assessment by social norm: The child's performance can be assessed based on the percentile ranking scale and T-value scale. The child's performance is compared by reference to the peer group.
Assessment by criterion norm: regarding the IRT approach, the child's performance can additionally be assessed qualitatively with reference to the level of competence. As it cannot necessarily be assumed that a child will solve all tasks of a level of competence without error, a 75% criterion was introduced. This criterion states that at least 75% of all items of a competence level have to be solved successfully, before the level is seen as being understood. Regarding levels of competence, a child's performance profile can look like this: Level 1: 100% - Level II: 90% - Level III: 60% -Level IV: 30% - Level V: 0%. This profile means that the child's performance is allocated to Level III. The concepts of Level I and II are understood and the child is about to develop an understanding of cardinality (concept of Level III). He/she can occasionally solve part-part-whole tasks from Level IV, but the acquisition of Levels IV and V are future steps in his/her development.
Since MARKO-D and MARKO-T are based on a common model of mathematical development, the diagnostics of the MARKO-D can be used to deduce the individual support needs as well as the learning goals for the MARKO-T programme. The individual entry level for a child into the training programme can thus be determined by means, of not only a descriptive, but also a prescriptive diagnostics. The support programme begins with consolidating the concept of the level the child is currently on (Level III in the example above). After that, the support focuses on facilitating the acquisition of the concept needed for the next developmental level.
At the beginning of each training unit, the contents of the last session are checked in the sense of a status diagnostics (see Figure 2). If the child can solve the tasks without difficulty, the training continues. If significant problems occur, the previous training unit is repeated. In addition, the problematic requirements are trained once more and thus the conceptual contents are revised in detail. Conversely, a rapid individual developmental speed can be adjusted. At certain points of the training, the possibility exists to skip training units in case of a very high success rate.

In order to adapt the training to the individual learning speed and learning progress of the child, his or her learning process is additionally checked by 'diagnostic windows' during the practicing phase (Leutner, 1992, 1993, 2004). Only when the specific goals of each training unit are achieved, work on new tasks, with a higher requirement structure, will begin. This is to ensure that conceptual understanding is built systematically and that mathematic competence is acquired successively. Tasks at the next level or of a more complex nature will only be presented and worked on when the necessary requirements, in terms of mathematical understanding, have been acquired and secured.
On the following page is an overview of the structure of a training unit (Figure 3).

Evaluation
The effectiveness of the MARKO training was empirically verified by comparing it with two other training programmes. 137 children with poor mathematical performance and average or below normal IQ were randomly assigned to one of three training conditions. One group was trained mathematically with the MARKO-T, another group received working memory training, and the third group was trained with regard to their social competencies. Forty-five normally developed children acted as control group and received no training. Each child in the three training groups received about sixteen training sessions within a period of eight weeks. Significant effects of the MARKO training could be established in the short, as well as, the long term, that is, directly after the training and ten months following the end of the training session (Ricken, Fritz & Balzer, 2012).
Research question
If we now look at learning disabled children with a history of more than two years of school failure, and considerable difficulties with numeracy, the following question arises: Is it possible to develop the mathematical competencies of these students successfully and maintain the training effects, over a certain period, after the end of the training programme?
Considering the fact that a performance deficit is acquired early on, increases, in comparison to children in regular schools, in the course of school attendance, raises another research question: To what extent can the adaptive mathematical training intervention programme help prevent a further increase in this performance gap? In other words, is the increase in performance of learning disabled children, achieved as a result of the training programme, the same as that of normally developed children?
Study
Design of the study
In order to pursue the research questions, a training study was designed. In this study, third graders, who attended special school for students with learning disabilities, were trained twice weekly utilising the MARKO-T, over a period of 10 weeks. Due to their severe learning difficulties, these children had been referred to a special remedial school.
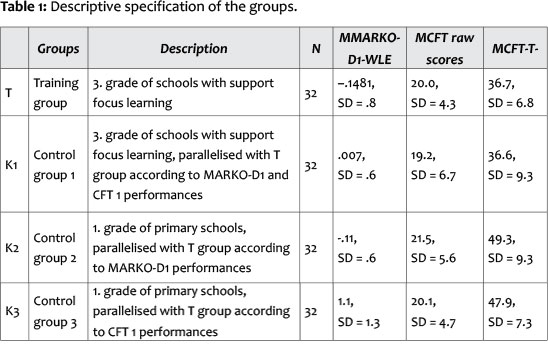
To verify the training effects and to analyse the mathematical learning curve, three parallelised control groups were formed in addition. The children of the first control group (K1) also attended the third grade of a special school for learning disabled children and exhibited similar learning difficulties. Their mathematical and cognitive performance did not differ from that of the children who had been trained. To be able to compare the performance development of the children in the training group, with the performance development of normally developed children, two further control groups were established. The children in these control groups attended the first grade in regular primary schools and were significantly younger than the children in the training group. One of these two control groups (K2) exhibited similar mathematical performances to the trained third graders with learning difficulties. The children in the third control group (K3) showed similar cognitive abilities to the training group in a cognitive performance test. This performance parallelisation was done based on the raw scores obtained in an intelligence test.
Overall, the study comprised three measuring times: pre testing, post testing, and a follow-up four months after the end of the training sessions. At the first and third measuring time, all children of all control groups were tested. At the second measuring time, only the trained children were tested.
Sample
• Master sample: The two groups of children with learning difficulties were chosen from a sample comprised of 82 children. All 82 pupils (age: M = 114.7 months, SD = 8.9) attended special-needs schools with a support focus on learning and were in the third grade. The children in the normally developed control groups were selected from a sample comprising 110 children (age: M = 85.7 months, SD = 5.2). Both the first graders and the third graders attended schools in the Ruhr area.
• Study sample: 32 children, with poor mathematical performances, and a learning disability, were selected randomly from the master sample for the training group (M = 114.2 months, SD = 9.6, 10 girls, 22 boys, 3. grade). For the control group K1, another 32 children (M = 114.7 months, SD = 7.3, 12 girls, 20 boys, 3. grade), who exhibited similar mathematical and cognitive performances to the training group, were picked for the control group K1. Further 2 x 32 children were chosen from the first grades of a primary school, with the aim of forming two parallelised control groups. One group was parallelised according to the mathematical performances (control group K2: M = 86.4 months, SD = 5.3, 14 girls, 18 boys, 1. grade), the other group was parallelised according to the cognitive performances. This cognitive control group was formed according to raw scores in the intelligence test (control group K3: M = 84.6 months, SD = 4.3, 17 girls, 15 boys, 1. grade).
• Drop-out of the study samples: Two girls dropped out of the study at the end of the school year, one of them from the training group, and one from control group K1. Both families moved to other towns and the distances were too large to continue tracking their performance.
Group performances within the parallelisation
The children of the training group (T) and the parallelised control group (K1), exhibited cognitive performances in the area of learning disability; the mean was MCFT-IQ = 81, (T-IQ-Band: 70 to 93 and K1-IQ-Band: 66 to 94). Both groups showed similar mathematical (t(1, 62) = -.925, p = .359) and cognitive performances (t(1, 62) = .602, p = .550, comparison of the achieved raw scores).
The children of control group K2 exhibited similar mathematical performances to those of the training group (t(1, 62) = -.212, p = .832), despite being 2 years younger, and thus having attended two years less of schooling. They displayed age average cognitive performances, MCFT-IQ = 99 (K2-IQ-Band: 85 to 113).
The children of the third control group K3 showed similar cognitive performances (based on raw score) to those of the training group (t(1, 62) = -.028, p = .978). In terms of the normalised performance scales (e.g. IQ scale), however, their performances were age average, MCFT-IQ = 97 (K2-IQ-Band: 86 to 107), as they were two years younger. Both control groups K2 and K3 did not differ in their performances (t(1, 62) = .657, p = .514).
Materials and procedures
The described tests were used at each measuring time.
• Mathematical competences: The mathematical competences were assessed with the MARKO-D1, a test for the assessment of mathematical concepts in the first grade (Fritz, Ehlert, Ricken & Balzer, in prep.). This test is based on the developmental model of mathematical concepts by Fritz and Ricken (2008) (described above), and allows for the assignment of mathematical performances to a level of competence. The test is an individual test that takes about 35 minutes.
• Cognitive competences: The cognitive competences were assessed with the CFT 1 with the scales classification, similarities, and matrices (Catell, Weiß & Osterland, 1997). The methodis regarded as culture and language free; it uses figural material and assesses the general fluid ability of the child. The test was done in a group session with about 5 children lasting about 20 minutes.
Evaluation method
To determine a mathematical competence value for each measuring time, all performances of the children were Rasch-scaled, that is, the mathematical performances at all measuring times were mapped in one model. This was possible because the items of MARKO-D1 are one-dimensional and therefore mapable on one scale (see article by Fritz, Ehlert & Balzer, in this journal). As only a small sample is involved in this study, which does not suffice to appropriately model a competence level model, further 420 first-graders of the normalisation sample of MARKO-D1 were added to the sample. This was a normally distributed sample, Kolmogorov-Smirnov test: p = .555. The following multi-matrix-design resulted accordingly.
Largely, a sufficiently high variance is reached for the comprehensive model calculated, s2 = 1.714. The items show infit values in the range of 1 ± 0.2. The WLE person separation reliability is 0.915 and the EAP/PV reliability amounts to 0.909. In conclusion, this means that the items meet the criteria of the Rasch model (see Adams & Wu, 2000; Rost, 2004; Wright & Linacre, 1994) and represent a one-dimensional construct. For the following analyses, the mathematical competence values will be used.
Results
Appropriateness of the training
Although the MARKO training is highly adaptive and thus adaptable to the learning prerequisites and learning speed of the children, it has to be assumed (see Klauer, 2002) that not all children will benefit in the same way from the training programme. The performance of the children can be impaired additionally by attention or concentration disorders, behavioural or emotional disorders. For this reason, tests were conducted, immediately after the training session, to determine which children had not learned anything from the intervention.
Overall, three children did not demonstrate a learning gain at the second measuring time in MARKO-D1. They came from different schools and had been trained by different coaches. Coaching problems can be eliminated, as all coaches had trained a minimum one to five or more children successfully. We cannot be sure why no training success resulted for these children. In the following evaluation, these children will not be considered.
Effects on the development of mathematical concepts directly after the training session
The remaining 28 children, of the training group, achieved on average a competence value of M = -.12 (SD = 0.8) in MARKO-D1 at t1. After completion of the training, the children improved their mathematical competences, M = 1.35 (SD = 1.0). The t-test confirmed the difference between t1 and t2, t(1, 27)MARKO-D1-WLE = -13.709, p < .001. The performance increase in MARKO-D1 is equivalent to an effect size of d = 1.7. That means qualitatively that the children were on Level III at t1. They were about to develop the cardinal number concept. Directly after the training sessions, most children could be assigned to Level IV. They had understood the concept of cardinality and were acquiring the part-part-whole concept. However, in terms of content, they were no longer at the beginning of this level, but right in the middle of it. Thus, the children had improved by at least one level of competence during the training weeks.
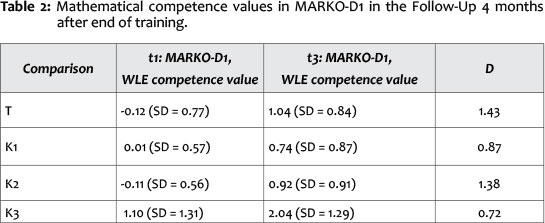
Effects on the development of mathematical concepts in the Follow-Up, 4 months after completion of the training sessions
The performances of the groups in the Follow-Up were analysed by means of an analysis of variance, with repeated measures with the performances of MARKO-D1 at the measuring times t1 and t3, as within subject factor ('measuring time'), and the group assignment as between subject factor ('group assignment'). For the first analysis, training group versus control group K1, the untrained learning disabled children showed a significant main effect for the factor measuring time, F(1, 57) = 87.431, p < .001, part.eta = .61, as well as a significant main effect for the factor group assignment, F(1, 57) = 4.425, p < .05, part.eta2 = .07, four months after completion of the training. The students from the training group thus exhibited a clearer increase in performance than the performance parallelised pupils from control group K1. The increase in the training-group amounted to d = 1.43. The effect size of the performance gap between the groups, changes in favour of the training group (dt1 = -.32, dt3 = .35). The children of the training group had a higher mean at t3 than those of the control group K1, although they had started with a lower mean at t1. Mostly, these results illustrate that their learning curve increases more significantly than that of control group K1.
The analysis of variance for the training group versus control group K2, the first graders parallelised according to mathematical performance, indicates a significant main effect for the factor measuring time, F(1, 58) = 122.664, p < .001, part.eta2 = .68, and no significant main effect for the factor group assignment, F(1, 58) = .383, p = .538. This means that the learning curve of the children of the training group shows a similar increase to that of the control group K2. If we, additionally, compare the effect size of the performance gap per measuring time, that is, at t1 and at t3, between the two groups, we can see that the effect size again changes in favour of the training group: the children of this group have a higher mean than the control group K2 at t3 (dti = .00, dt3 = .14).
The last analysis, training group versus control group K3, the first graders parallelised according to cognitive performance (IQ raw scores), shows a significant main effect for the factor measuring time, F(1, 58) = 81.742, p <. 001, part.eta2 = .59, and again no significant main effect for the factor group assignment, F(1, 58) = .904, p = .346. Thus, the learning curve of the children of the training group again demonstrates a similar increase to that of control group K3.
To sum up, it can be concluded that the training group acquires a significant learning advantage from the training sessions. Furthermore performance comparisons between training group and first graders, show that the learning-disabled children made the same learning progress as the normally developed children. An analysis of this conclusion is presented in the following table:
Learning gains in mathematical basic skills
In the following, the learning gains of the individual (various) groups will be compared. Descriptively, the children of the training group show the largest performance increase in the Follow-up after four months (see Figure 5). On the other hand, the children of the control group K1 show the smallest learning gain. If we compare the performance increase of the training group with that of control group K1, the difference becomes empirically significant, t(1, 57) = 2.103, p < .05, the difference being to the order of d = 0.5.
The differences in increase between training group and control group K2, t(1, 58) = 0.619, p = .538, d = 0.2, as well as, between training group and control group K3, t(1, 58) = 0.951, p = .346, d = 0.2, are not significant, yet slight effects exist. These need to be discussed against the backdrop of the small sample.
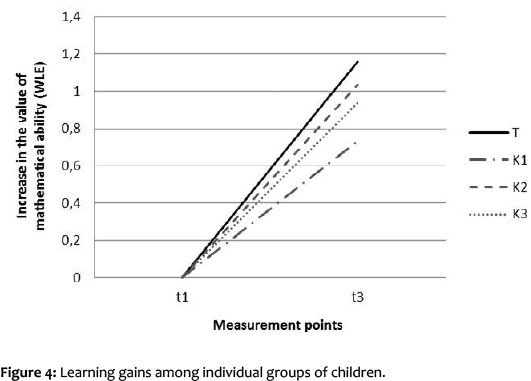
If we examine the performance of the training group at the three measuring times we have for this group: t1, M = -0.12 (SD = 0.77); t2: M = 1.35 (SD = 1.0); t3: M = 1.04 (SD = 0.84), it becomes clear that after a sharp increase in learning at t2, the performances drop again after completion of the training at t3. In other words, the training group shows a learning gain that far exceeds the learning gain of normally developed children immediately after the training intervention. After the end of the training sessions, their performance drops again. Notwithstanding this decrease, their performance at t3 is now equivalent to the learning gain of normally developed children. In contrast, the learning curve of untrained learning-disabled children shows a further drop in performance compared to normally developed children.
Discussion
The present study aimed to determine whether children with learning difficulties can be supported with a highly adaptive mathematical training program and whether these training effects can be maintained over a certain period of time. Furthermore, the question was raised whether the slower development process of the children could be improved by the training intervention programme and whether the children would show a learning increase equivalent to that of normally developed children.
For this, 32 third-graders from special schools for learning disabled children were trained twice weekly in basic arithmetical skills over a period of 10 weeks. In order to validate the effects, three control groups were formed. The pupils of the first control group also attended schools for learning disabled children. They exhibited similar mathematical and cognitive performances to the training group but did not receive any training. The other two control groups attended the first grade in regular schools. They were chosen to have similar performance outcomes to the children in the training group, regarding their mathematical and cognitive performance.
The results prove that the performance of the learning-disabled children could be improved significantly with the adaptive training programme, the MARKO-T. From the first to the second measuring time, they developed, on average, by one level. This result shows that the mathematical skills of children with learning disabilities can be successfully developed or improved if the training is individually adapted to their learning prerequisites and their learning speed.
Even four months after completion of the training sessions, significant training effects existed, in comparison with the children of the control group who also had learning disabilities. Similarly, the comparison with the other two control groups, the first-graders, showed that from t1 to t3, the development curve of the children with learning difficulties rose comparably to that of the children without learning difficulties.
However, the results also showed that four months after the training programme, the learning gain had decreased again. Therefore, it remains to be discussed why, after the initially excellent learning progress made by the children of the training group, the acquired knowledge did not remain permanently consolidated. A possible explanation must take into account the fact that the training group consisted of children in their third school year. That means that in their school lessons, the mathematical subject matter is that of the third grade, in a reduced form. Yet this arithmetical content, with tasks focused on multiplication and division, requires a conceptual understanding that the children definitely do not yet possess. According to our assessment, they are still working on understanding the concept of cardinality.
As a result, the learning requirements of the school lessons and the prerequisites of the children do not fit and the children cannot link the contents of their school lessons to their previous knowledge. Since the newly acquired knowledge from the training sessions could not be applied and exercised in their daily lessons, their regression can be explained in terms of their forgetting what they had learned. It is difficult to maintain learning gains when one assumes that, after the successful ten weeks training programme, the acquired knowledge was not reinforced during normal school lessons in the following four months, and could therefore not be consolidated or internalised.
Again it should be stated that, despite the process of developmental regression among the learning-disabled children four months after completion of the training sessions, there was no difference regarding the increase in learning between them and the first-graders who started this study with a comparable initial mathematical understanding. Both groups demonstrated a comparable mathematical knowledge at measuring time t3. This can also be said for the comparison with the first-graders who had begun the study with comparable cognitive competences, yet, obtained higher IQ values, due to their younger age. Thus, the training had a positive influence on the normally ever-widening and the ever-increasing performance gap between children with and without learning disabilities. By contrast, it could be shown by reference to the untrained group of children with learning disabilities that, without the mathematical training the performance gap of children with a learning disability increased further. They showed considerably less learning improvement, continually acquiring less knowledge than the children without learning difficulties.
In conclusion, the results of this study indicate that the deployed training successfully supports children with learning disabilities. For the sake of sustainability, further criteria should be taken into account, which should, in any case, be applied to all training programmes: children with special learning disabilities can be trained with considerable effect. However, additional focused training units can help maintain and develop the performance on the acquired level. Furthermore, the learning prerequisites should match the requirements in class. Based on the new learning curve, the additional training units should be provided precisely when a regressive trend in mathematical development looms. At this stage, support should be provided, when required, according to the learning curve.
Finally, we should like to emphasise, that the MARKO training programme is not only designed to be used for children with learning disabilities, but also, for the focused support of pre-school children with a developmental delay, or mathematically weak children, in the first years of primary school.
References
Adams, R.J. & Wu, M.L. 2002. PISA 2000 Technical Report. Paris: OECD Publications. [ Links ]
Antell, S.E. & Keating, D.P. 1983. Perception of numerical invariance in neonates. Child Development 54:695-701. [ Links ]
Aunola, K., Leskinen, E., Lerkkanen, M.-K. & Nurmi, J.-E. 2004. Developmental Dynamics of Math Performance from Preschool to Grade 2. Journal of Educational Psychology 96:699-713. [ Links ]
Barrouillet, P., Fayol, M. & Lathulière, E. 1997. Selecting between competitors in multiplication tasks: An explanation of the errors produced by adolescents with learning disabilities. International Journal of Behavioral Development 21:253-275. [ Links ]
Bos, W. 2013. Erste Ergebnisse aus IGLU. TIMSS 2011, IFS. Retrieved from http://www.ipn.uni-kiel.de/abt_erzw/ws12_k/pp_070113.pdf (accessed 4 March 2013).
Bryant, D.P., Bryant, B.R., Gersten, R., Scammacca, N. & Chavez, M.M. 2008. Mathematics intervention for first- and second-grade students with mathematics difficulties. Remedial and special education 29:20-33. [ Links ]
Cattell, R.B., Weiß, R.H. & Osterland, J. 1997. CFT 1. Grundintelligenztest Skala 1. Göttingen: Hogrefe. [ Links ]
Chard, D.J., Clarke, B., Baker, S., Otterstedt, J., Braun, D. & Katz, R. 2005. Using Measures of Number Sense to Screen for Difficulties in Mathematics: Preliminary Findings. Assessment for Effective Intervention 30(2):3-14. [ Links ]
Dilling, H., Mombour, W. & Schmidt, M.H. 2004. Internationale Klassifikation psychischer Störungen. ICD-10 Kapitel V (F). Diagnostische Kriterien für Forschung und Praxis. Bern: Huber. [ Links ]
Ehlert, A., Schroeders, U. & Fritz, A. 2012. Kritik am Diskrepanzkriterium in der Diagnostik von Legasthenie und Dyskalkulie. Lernen und Lernstörungen 1:169-184. [ Links ]
Fayol, M., Barrouillet, P. & Marinthe, C. 1998. Predicting arithmetical achievement from neuro-psychological performance: A longitudinal study. Cognition 68:B63-B70. [ Links ]
Fritz, A. & Ricken, G. 2008. Rechenschwäche. München: Ernst Reinhardt. [ Links ]
Fritz, A., Ricken, G., Balzer, L., Willmes, K. & Leutner, D. (submitted). Key numerical concepts at pre-school and early primary-school age: An integrative five-level model of cumulative arithmetic skills development. Early Childhood Research Quarterly.
Fritz, A., Ehlert, A., Ricken, G. & Balzer, L. (in prep.). MARKO-D1 - Mathematik- und Rechenkonzepte im ersten Schuljahr - Diagnose. Göttingen: Hogrefe. [ Links ]
Fuson, K.C. 1992. Research on whole number addition and subtraction. In D. Grouws (Ed.), Handbook of research on mathematics teaching and learning, 243-275. New York: Macmillan. [ Links ]
Geary, D.C. 1990. A componential analysis of an early learning deficit in mathematics. Journal of Experimental Child Psychology 49:363-383. [ Links ]
Geary, D.C., Brown, S.C & Samaranayake, V.A. 1991. Cognitive addition: A short longitudinal study of strategy choice and speed-of-processing differences in normal and mathematically disabled children. Developmental Psychology 27:787-797. [ Links ]
Gelman, R. & Gallistel, C.R. 1978. The child's understanding of number. Cambridge, MA: Harvard University Press. [ Links ]
Gerlach, M., Fritz, A. & Leutner, D. 2013. MARKO-T - Mathemati-k und Rechenkonzepte im Vorschulalter - Training. Göttingen: Hogrefe. [ Links ]
Gross-Tsur, V., Manor, O. & Shalev, R.S. 1996. Developmental dyscalculia: Prevalence and demographic features. Developmental Medicine and Child Neurology 38:25-33. [ Links ]
Hanich, L.B., Jordan, N.C., Kaplan, D. & Dick, J. 2001. Performance across different areas of mathematical cognition in children with learning difficulties. Journal of Educational Psychology 93:615-626. [ Links ]
Helmke, A. & Weinert, F. 1997. Entwicklung im Grundschulalter. Beltz: Weinheim. [ Links ]
luculano, T., Moro, F. & Butterworth, B. 2011. Updating Working Memory and arithmetical attainment in school. Learning and Individual Differences 21:655-661 [ Links ]
Jimenez Gonzalez, J.E. & Garcia Espinel, A.I. 1999. Is IQ achievement discrepancy relevant in the definition of arithmetic learning disabilities? Learning Disabilities Quarterly 22:292-299. [ Links ]
Jimenez Gonzalez, J.E. & Garcia Espinel, A.I. 2002. Strategy choice in solving arithmetic word problems: Are there differences between students with learning disabilities, G-V poor performance and typical achievement students? Learning Disabilities Quarterly 25:113-122. [ Links ]
Jordan, N.C. & Montani, T.O. 1997. Cognitive arithmetic and problem solving: A comparison of children with specific and general mathematics difficulties. Journal of Learning Disabilities 30:624-634. [ Links ]
Jordan, N.C., Glutting, J. & Ramineni, C. 2010. The importance of number sense to mathematics achievement in first and third grades. Learning and Individual Differences 20:82-88. [ Links ]
Kanter, G.O. 1973. Sonderpädagogische Maßnahmen für Lernbehinderte in einer prospektiven Bildungsplanung, Zeitschrift für Heilpädagogik 24(4):273-284. [ Links ]
Klauer, K.J. & Lauth, G.W. 1996. Lernbehinderungen und Leistungsschwierigkeiten bei Schülern. In F.E. Weinert (Ed.). Enzyklopädie der Psychologie, Themenbereich D, Serie I Pädagogische Psychologie, Psychologie des Unterrichts und der Schule, 701-738. Göttingen: Hogrefe. [ Links ]
Klauer, K.J. 2002. Wie viele haben denn nun wirklich vom Training profitiert? Eine noch nicht eindeutig zu beantwortende Frage. Psychologie in Erziehung und Unterricht 49(3):210-218. [ Links ]
Klauer, K.J. 2011. Lernverlaufsdiagnostik - Konzept, Schwierigkeiten und Möglichkeiten. Empirische Sonderpädagogik 3(3):207-224. [ Links ]
Kobayashi, T., Hiraki, K., Mugitani, R. & Hasegawa, T. 2004. Baby arithmetic: One object plus one tone. Cognition 91(2):B23-B34. [ Links ]
Koponen, T., Aunola, K., Ahonen, T. & Nurmi, J.-E. 2007. Cognitive predictors of single digit and procedural calculation skills and their co-variation with reading skill. Journal of Experimental Child Psychology 97:220-241. [ Links ]
Koumoula, A., Tsironi, V., Stamouli V., Bardani, I., Siapati, S., Graham-Pavlou, A., Kafantaris I, Charalambidou E, Dellatolas G, Von Aster, M. 2004. An epidemiological study of number processing and mental calculation in Greek schoolchildren. Journal of Learning Disabilities 37:377-388. [ Links ]
Lauth, G.W. 2000. Lernbehinderungen. In J. Borchert (Ed.), Handbuch der Sonderpädagogischen Psychologie (S. 21-31). Göttingen: Hogrefe. [ Links ]
Kroesbergen, E.H. & Van Luit, J.E.H. 2002. Teaching multiplication to low math performers: Guided versus structured instruction. Instructional Science 30:361-378. [ Links ]
Lembke, E. & Foegen, A. 2009. Identifying early numeracy indicators for kindergarten and first-grade students. Learning Disabilities Research & Practice 24:12-20. [ Links ]
Leutner, D. 1992. Das Testlängendilemma in der lernprozeßbegleitenden Wissensdiagnostik. Zeitschrift für Pädagogische Psychologie 6:233-238. [ Links ]
Leutner, D. 1993. Das gleitende Testfenster als Lösung des Testlängendilemmas: Eine Robustheitsstudie. Zeitschrift für Pädagogische Psychologie 7:33-45. [ Links ]
Leutner, D. 2004. Instructional-design principles for adaptivity in open learning environments. In N.M. Seel & S. Dijkstra (Eds.), Curriculum, plans and processes of instructional design: international perspectives (S. 289-307). Mahwah, NJ: Lawrence Erlbaum. [ Links ]
Logie, R.H., Gilhooly, K.J. & Wynn, V. 1994. Counting on working memory in arithmetic problem solving. Memory and Cognition 22:395-410. [ Links ]
Ostad, S.A. 1997. Developmental differences in addition strategies: A comparison of mathematically disabled and mathematically normal children. British Journal of Educational Psychology 67:345-357. [ Links ]
Ostad, S.A. 1998. Developmental differences in solving simple arithmetic word problems and simple number-fact problems: A comparison of mathematically normal and mathematically disabled children. Mathematical Cognition 4:1-19. [ Links ]
Ostad, S.A. 2000. Cognitive subtraction in a developmental perspective: Accuracy, speed-of-processing and strategy-use differences in normal and mathematically disabled children. Focus on Learning Problems in Mathematics 22:18-31. [ Links ]
Piaget, J. & Szeminska, A. 1975. Die Entwicklung des Zahlbegriffs beim Kinde. Stuttgart: Klett. [ Links ]
Rasch, G. 1960. Probabilistic models for some intelligence and attainment tests. Copenhagen: Nielsen & Lydiche. [ Links ]
Resnick, L.B. 1989. Developing mathematical knowledge. American Psychologist 44:162-169. [ Links ]
Ricken, G., Fritz, A. & Balzer, L. 2012. MARKO-D - Mathematik- und im Vorschulalter -Diagnose. Göttingen: Hogrefe. [ Links ]
Rost, J. 2004. Lehrbuch Testtheorie - Testkonstruktion. Bern: Huber. [ Links ]
Sas, H., Wittchen, H.-U. & Zaudig, M. 2003. Diagnostisches und Statistisches Manual Psychischer Störungen (DSM-IV-TR): Textrevision. Gottingen: Hogrefe. [ Links ]
Schipper, W. 1998. "Schulanfänger verfügen über hohe mathematische Kompetenzen" - Eine Auseinandersetzung mit einem Mythos. In A. Peter-Koop (Ed.). Das besondere Kind im Mathematikunterricht (S. 119-140). Offenburg: Mildenberger. [ Links ]
Starkey, P., Spelke, E.S. & Gelman, R. 1990. Numerical abstraction by human infants. Cognition 36:97-127. [ Links ]
Stern, E. 1994. Wie viele Kinder bekommen keinen Mohrenkopf? Zur Bedeutung der Kontexteinbettung beim Verstehen des quantitativen Vergleichs. Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie 24:79-94. [ Links ]
Strathmann, A.M. & Klauer, K.J. 2008. Diagnostik des Lernverlaufs. Eine Pilotstudie am Beispiel der Entwicklung der Rechtschreibkompetenz. Sonderpädagogik 38:5-24. [ Links ]
Strathmann, A.M. & Klauer, K.J. 2010. Lernverlaufsdiagnostik: Ein Ansatz zur längerfristigen Lernfortschrittsmessung. Zeitschrift für Entwicklungspsychologie und pädagogische Psychologie 42(2):111-122. [ Links ]
Strathmann, A.M. & Klauer, K.J. 2010. Lernverlaufsdiagnostik: Ein Ansatz zur längerfristigen Lernfortschrittsmessung. Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie 42:111-122. [ Links ]
Strathmann, A.M., Klauer, K.J. & Greisbach, M. 2010. Lernverlaufsdiagnostik. Dargestellt am Beispiel der Entwicklung der Rechtschreibkompetenz in der Grundschule. Empirische Sonderpädagogik 2:64-77. [ Links ]
Tronsky, L.N. 2005. Complex multiplication: Strategy use, the development of automaticity with practice, and working memory involvement. Memory & Cognition 33:927-940. [ Links ]
Van Luit, J.E.H. & Naglieri, J.A. 1999. Effectiveness of the MASTER Program for Teaching Special Children Multiplication and Division. Journal of Learning Disabilities 32(2):98-107. [ Links ]
Van Luit, J.E.H., Kaskens, J. & Van der Krol, R. 1993. Speciaal rekenhulpprogramma vermenigvuldigen en verdelen [Special remediating programme multiplication and division]. Doetinchem, The Netherlands: Graviant. [ Links ]
Von Aster, M.G., Schweiter, M. & Weinhold Zulauf, M. 2007. Rechenstörungen bei Kindern. Vorlaufer, Pravalenz und psychische Symptome. Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie 39:85-96. [ Links ]
Wright, B.D. & Linacre, J.M. 1994. Reasonable mean-square fit values. Rasch Measurement Transactions 8(3):370. [ Links ]
Wright, R., Martland, J. & Stafford, A. 2000. Early numeracy: Assessment for teaching and intervention. London: Chapman. [ Links ]
Wynn, K. 1992. Addition and subtraction by human infants. Nature 358(6389):749-750. [ Links ]














