Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.3 n.1 Johannesburg 2013
Natural differentiation in the teaching of mathematics to children starting school
Petra Scherer
University of Duisburg-Essen. E-mail address: petra.scherer@uni-due.de
ABSTRACT
This article presents a number of carefully selected activities for the mathematics classroom in the early grades. The motivation for their selection is the development of concepts rather than the learning of the procedural skills of arithmetic. As the teacher is faced with a great heterogeneity of children starting school, the concrete learning environment should fulfil several requirements. On the one hand, the environment has to represent core mathematical principles, and, on the other hand, they have to be suitable for all learners in an inclusive classroom. The concrete formats themselves serve a specific conceptual purpose, while, at the same time, addressing, in an integrated way, the needs of a variety of learners with different levels of competence.
Keywords: arithmetic, heterogeneity, low achievers, natural differentiation, investigative learning, operative principle
Introduction
Since mathematics plays an important rolein the world, mathematical literacy represents a central objective in early childhood education (The Organisation for Economic Co-operation and Development, 2009). For the fulfilment of mathematical literacy standards, certain minimum requirements have been developed in many countries (cf. National Council of Teachers of Mathematics, 2000; Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2005) and substantiated in the curricula (see Curriculum and Assessment Policy Statements cited in Van den Heuvel-Panhuizen et al., 20i2:2ff.; Ministerium für Schule und Weiterbildung des Landes Nordrhein-Westfalen, 2008). The formulated objectives are designed to apply to learners of all levels of abilities, for high achievers as well as for low achievers. Moreover, as learning mathematics takes place within the mathematics lessons, but also outside school, and before formal education begins, children entering school for the first time start with an existing mathematical knowledge. In practice, children entering school are heterogeneous with respect to their knowledge of maths. On the one hand, there are learners who have a wide range of everyday mathematics experience, and, on the other hand, there are some with extreme difficulties. In this article, concrete learning environments will be presented that can contribute to the development of arithmetical knowledge and competencies of first graders across the spectrum.
Constructivism and teaching concepts
There is consensus of the validity of the constructivist approach's ability to define 'knowing' (Von Glasersfeld, 1995a) and learning in a social environment (cf. Wittmann, 200i). For mathematics education, investigative learning and productive practice are seen as the main elements of this paradigm (cf. ibid.). Productive work is understood in contrast to the mere reproduction of knowledge. The former should enable learners to think, to construct and to extend their knowledge (cf. Winter, 1984; Wittmann, 1990), while being engaged in empirically observable activities and internalising actions and images. In this way, mathematics can, eventually, become a mental activity with numbers extending far beyond the horizon of being mere empirical entities, or used as 'manipulatives' (Flexer, 1986; Von Glasersfeld, 1995b). With respect to heterogeneous learning groups, several studies and experiences in general have confirmed that investigative learning combined with productive practice is appropriate for all learners - especially for low achievers and children with special needs (cf. Ahmed, 1987; Moser Opitz, 2000; Scherer, 1997; Scherer, 1999; Scherer & Moser Opitz, 2010:49ff.; Trickett & Sulke, 1988; Van den Heuvel-Panhuizen, 1991).
Nevertheless, there is still a need for a change in attitude towards low achieving children. This means, for instance, that the teacher has to trust the children to solve complex problems (cf. Cobb et al., 1991:174; see also Peltenburg & Van den Heuvel-Panhuizen, 2012). According to this view, all learners should be confronted with complex learning environments. Investigative learning and productive practice are usually aligned with holistic approaches that require all learners to see relationships between numbers, shapes, and so forth, in order to understand mathematical structures (Trickett & Sulke, 1988:112). With regard to low achievers, holistic approaches are avoided too often in favour of splitting up a subject matter into small fragments. In this regard, Donaldson (1978) distinguishes between the mastering of all individual patterns or relationships of a system, on the one hand, and understanding the nature of a system, on the other hand. However, splitting a subject into little fragments does not contribute to solving certain difficulties, such as understanding the structure of our number system. As a consequence, for instance, from the very beginning of the first year of schooling the numbers up to 20 should be offered and dealt with, instead of introducing the numbers sequentially (cf. Scherer, 2005).
As mentioned above, one crucial requirement is differentiation. Learning tasks on different levels of difficulty, determined by the teacher, bears the risk that some learners are overextended, misjudged or kept at a specific inappropriate level. Research shows that learning environments following the concept of a natural differentiation (ND) can reduce this risk (cf. Wittmann, 2001; Scherer & Krauthausen, 2010). The teaching units presented in this contribution show this ND in action, which means that the learners can choose their level of working by themselves, and that it is not predetermined. At the same time, ND makes it easier for the teacher to organise the learning processes. All learners work on the same task or problem and there is no need for the teacher to present different worksheets to children of different levels.
In the following section, three examples for mathematics teaching will be presented and discussed, aiming to show how holistic teaching can happen in practice. Firstly, different types of games, which are suitable for early childhood, can be introduced in the early weeks in order to help the children adjust to formal education. Secondly, activities for orientation with numbers up to 20 are introduced in an integrated way. These activities form the basis for later calculations, which will be described in the last section.
Games for transition to formal education
Although games are often used in mathematics classrooms, too often the main reason is to motivate children to do mathematical tasks. You will find drill-and-practice activities arranged as a playful activity. They are, in fact, not true games. By contrast, there are many authentic mathematical games available to teachers, such as strategy games, aiming at improving thinking and anticipating actions. Empirical studies demonstrate the importance and meaning of playful learning environments for early childhood education (e.g. Ainley, 1990; Hughes, 1986; Van Oers, 2010). As an example, the following three games can be used for children entering school. These address different levels of ability and work as follows:
'The robbers and the treasure'
'The robbers and the treasure' is a dice-game, where the dice 'decide' who the winner is. This type belongs to the so called 'stochastic games'. This type of game gives learners of different mathematical levels the opportunity to win a game and the game's outcome is not bound to the competence of a specific child.
For the game, the plan in Figure 1, representing the number line up to 20, can be used and the following story is told:

The narrative: Two robbers live in a forest, each of them in a big cave. The path between these two caves is covered with 20 sequentially numbered stones. One day the robbers discover an old, big sack hidden behind a rock. With great difficulty they are able to get it out and to open it. They see a glittering gold nugget. Immediately, a fight breaks out and each of them claims that he owns the treasure because he has discovered it first. After a time, when they are both exhausted and have both fallen to the ground, they agree that the dice should decide who will get the treasure, and they agree to play according to the following rules:
We will place the treasure (piece) on stone 10. We then throw the dice alternately and move the piece towards our particular cave according to the number shown on the dice. The one who gets the treasure to his cave first is the winner. Because stone 10 is closer to the cave of field 1, the other robber (who moves the treasure to cave 20; see below 'plus-robber') starts throwing the dice (cf. Wittmann et al., 1994:68; also Scherer 2005:129).
In the game, two children or two groups of children take the role of the robbers (if necessary another child/group takes the role of a referee). One child goes forward (adding), and, therefore, he/she can be called the 'plus-robber'; the other child - goes backwards (which entails subtracting) - and is called the 'minus-robber'. The game ends, when one of the players can move the treasure to field 1 or 20 or beyond that.
This game leads to a holistic view of the number line, and with that the individual competencies of a child can be considered. This game allows natural differentiation, which means that it can be played on different levels that are not determined in advance:
• Children might move the treasure step by step (steps of 1);
• Children might move the treasure in bigger steps (steps of 2);
• Children might get the next field simultaneously; and
• Children can get to the right field by calculating in advance, which leads to the Vygotskian Zone of Proximal Development (Scherer, 2005:131).
These different levels not only depend on a learner's individual competency, but also on the specific situation within the game. It might happen that a child calculates in the area up to 10 but places the treasure one-by-one in the area from 10 up to 20. Moreover, it depends on the operation (addition is often considered to be much easier than subtraction) and on the specific tasks (it might be easier to calculate 7 + 2 than 7 + 6). But the transition from one level to another is fluent and can be observed by the teacher during play. The teacher can also encourage learners to name the next target field in advance.
For further challenges, the teacher might pose questions during the game, such as 'The treasure is placed on the stone 17. What must the dice show to win the game?' With growing acquaintance with the number line, the fields can be covered with counters and the learners can then be required to name them from memory - initially, every second field; later on, all fields, except the points of orientation 5, 10, 15, 20; finally, all fields (cf. Scherer, 2005:131).
This game is mainly an orientation exercise, but the transition to calculating is fluent. The teacher can record the course of the game in form of just the addition tasks, or reconstruct the course game (by mentioning intermediate results) (ibid.). In addition to this, an extension with numbers up to 100 can be offered (cf. Wittmann & Müller, 1990:80f.).
The NIM-game
The following version of the so-called NIM-game is limited to numbers up to 20 (cf. Scherer, 2005; Wittmann, 2001) and is played on the number line up to 10 or up to 20 (Figure 2; for other versions of this traditional game (see Bouton, 1902; Shriki, 2009)).

The rules of the game are the following:
1. Two children play with red and blue counters on a game-board with 20 fields arranged in a line (numbered if needed).
2. Alternately, the players place one or two counters on the board serially; the first player starts at field 1 and has to reflect, whether he/she places one or two counters. Then the other player places one or two counters.
3. The player who has reached field 20 wins the game.
Children start to play this game without knowing the strategy in general, and in this way different levels of working and playing are made possible. It is not necessary to know all the numbers, although knowing this facilitates discovering the winning strategy. Even children who have difficulties with identifying the number symbols are able to discover a winning strategy.
Usually, the children soon realise the first step of the winning strategy: 'If the partner has placed his counter on field 18, I have to place two counters.' Next, field 17 can be identified as a winning position: 'If I have placed my counter on field 17, the other player has just two possibilities which both do not lead to success. If he places one counter, I will place two. If he places two counters, I will place one.' In both cases the game will be won. This can then be discussed and illustrated on the blackboard as shown in Figure 3. Usually, children argue for their own position in order to win a game.
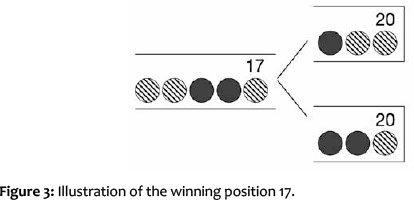
So the 'new' objective for children is to reach field 17 (it may be helpful to turn down the fields 18 to 20 to fade out their attention), which leads to field 14 as the next winning position, and so on. At last, it becomes clear that field 2 is a winning position (Figure 4) and that the first player has the possibility of winning, if he/she starts with two counters laid out.

The children may discover the strategy spontaneously by trying out a strategy and different hypotheses. The teacher, however, can also discuss first discoveries and reflect on the first winning positions with the children (see Figure 3). After having identified the strategy in general the rules of the game can be varied (see also Scherer, 2005:139):
• Variation of rule (1): Variation of the game-board connected with an extension of the space if you started playing it up to 10: you can play up to 12, 20 or up to 100.
• Variation of rule (2): The player is allowed to place 1, or up to 3 (or more) counters.
• Variation of rule (3): The player loses the game when placing his or her counter on field 20.
With all these variations, learners should be able to develop a winning strategy. They have to discover distinctions, but also similarities with the original version (and not just memorise the original winning positions, which actually would not work). They orientate themselves to their position on the number line and combine different number aspects: cardinality in choosing one, two or more counters, or identifying the number of fields to reach a winning position; and ordinality in identifying the number of a field. This integration occurs in a spontaneous way.
Children entering school can play this game when dealing with numbers up to 10 or up to 20, but it is appropriate for older children as well, to foster flexible thinking.
Triangle memory game
Triangle memory is originally an African game named a 'Tarumbeta'. It is played in the sand with beans (cf. Zaslavsky, 1999:111f.). The adaption used in German textbooks (cf. Müller & Wittmann, 1997) is played on a game board with numbers arranged in the form of a triangle (see Figure 5a). Compared with the original version, the ordering of the fields is changed (see Figure 5b). Usually, you start with four or five lines, which means with 10 or 15 fields, but you can extend this game to 45 fields or higher. According to the number of lines and fields the game becomes more difficult.

The general rules and objectives of the adapted game remain the same: One child - performing as a referee (or chief) - is sitting at the top of the game board and is responsible for seeing to it that everyone plays according to the rules. Opposite to him/her is another child, the blindfolded candidate (or challenger). Two other children - assistants (or players) - sit to the right and the left of the candidate. They have to place counters on the board, and the candidate has to name the next field, which means, before one of the assistants places his counter, the candidate has to predict the right number of the field. The assistants alternately place one counter according to a special rule. They begin in the first line (field 1), then they go to the next line, and each of them goes from outside, inwards. If a line is filled, they go to the next line. The assistant sitting left of the candidate starts with field 1. The candidate has to predict the order of numbers according to this special arrangement. If he or she fails, another child becomes the candidate and the next round starts with changing roles.
The learners have to remember the numbers and reconstruct the field. Those who have internalised the number line in a rather mechanistic way, are fixed to the specific arrangement of a line and, for instance, have difficulties dealing with a phone display or other everyday situations, since there might be different arrangements of numbers. The game can contribute to a higher flexibility and supports the orientation with numbers up to 10, 15 or higher (see also Scherer, 2005:140).
Orientation with numbers up to 20
Beyond competencies in calculation, learners should master basic requirements, especially when dealing with iconic representations, and should orientate their position in the relevant number area (see also Van den Heuvel-Panhuizen et al., 2012:26f.). It is important to give learners enough time and suitable experiences to build up mental images of numbers and operations. A crucial point for classroom practice is the use of appropriate manipulatives and representations (cf. Flexer, 1986). The teacher has to choose materials that represent the mathematical structure in an adequate way (like for instance the field of 20 or 100), and flexible representations that can be extended (cf. Wittmann, 1994). Besides the availability of adequate material, the concrete processes of using effective structures and reflection of number relations are of major importance.
A pupil who is unable to identify structures or patterns and to make use of them will not 'see' the eight dots in Figure 6 as '5 and 3' or '6 and 2', but count them again and again one by one. This pupil will have difficulties building up mental images and developing effective calculation strategies, and will persist doing calculations by counting the dots one by one. But calculating by counting the dots one by one will fail in the long term, eventually when dealing with numbers up to 100, and will lead to further arithmetical difficulties.

Many different activities are necessary in order to develop the ability of subitising, as, for example, creating, structuring and describing patterns (cf. Scherer, 2005:141ff.; Thornton, 1978). These activities should be combined with flash exercises,1 'How many?' (cf. Wittmann & Müller, 1990:73ff.). For enhancing the flexibility, not only the decimal structure, including the sub-structure of five (Figure 7; cf. 'power of five' Flexer, 1986) should be used, but also less familiar structures (Figure 8). Such activities not only influence the competences with numbers up to 10 directly, but support insight for working with larger numbers.


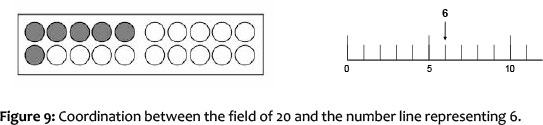
Another crucial issue is the coordination between several models and representations and between inactive, iconic, and symbolic levels (intramodal and intermodal transfer, see Bruner, 1969; see also Van den Heuvel-Panhuizen et al., 2012:32ff.). Adequate activities, not only for school beginners, but even in the higher grades, with numbers up to 1 000 or beyond, should facilitate both types of transfer. Since it might be difficult for the children to see a similar or even the same structure (cf. Lorenz, 1992), the transfer from one representation to another is an important activity (cf. Figure 9). Having internalised the mathematical structures and number relations, activities on the symbolic level are done more insightfully (see also Menne, 2000).
Calculation activities with numbers up to 20
For the systematic instruction of addition and subtraction with numbers up to 20, the above mentioned solid foundation is of major importance. As pointed out for the use of materials, the emphasis on structures and the relationship between numbers is important for calculation activities. The 'operative principle' (Wittmann, 1985) should be a central principle for instruction.
One of the main topics for first graders, the 'addition table', bears the risk that learners may just try to memorise all tasks without any insight and without making the appropriate the connections. For numbers up to 20, this strategy might still be successful, due to the limited number of facts to be remembered, but this does not lead to the extension of knowledge to larger numbers. Unfortunately, this limitation of knowledge might not be easily identified by a teacher.
When solving tasks related to the addition table, numerous number properties and relations should be discussed. For example, with a task such as 4+3 also the commutative property, the 'exchange task' 3+4 should be reflected as well as the 'neighbour tasks' 4+2, 4+4, 3+3 and 5+3. Moreover, analogous tasks, that indicate the extension to larger numbers and further topics, are of major importance. Learners should gain insight into the connection between 4+3 and 14+3, not only on the symbolic level, but also on the iconic level (Figure 10). These relations form the foundation for further topics and relations (4+3, 14+3, 24+3 etc.) and should build up a child's general knowledge (cf. Winter, 1984:7f.).

For realising natural differentiation, operative series of tasks can be used: One set of tasks is given, and the learners have to work them out as well as continue with the series. Before starting to calculate, the learners should reflect on the given tasks' patterns and relationships, and think about how to make use of these patterns for calculation, how to minimise the calculations. Of course, this should not be done in a mechanistic way but with insight and reflective discussions.
Example:
5 + 1 =
5 + 3 =
5 + 5 =
5 + 7 = How to proceed?
The levels of processing may vary individually:
• Learners work out the given tasks (by mental calculation or with the help of manipulatives and representations);
• Learners create further tasks; that means they identify and continue the pattern (the number of further tasks is flexible); moreover, they have the possibility of representing the addends at the >1+1-table< (cf. Wittmann & Müller, 1990:42ff., material that represents all tasks of the addition table and illustrates pattern and relationships by colour, Figure 11);
• Learners work out the self-created tasks;
• Learners describe and justify the given pattern (where appropriate supported by iconic representations); and
• Learners describe and justify the pattern of the results (where appropriate, supported by iconic representations).
While collecting and reflecting on the solutions that they have found, children might learn from each other and gain more insight into mathematics. The earlier these structures are discussed and reflected upon in the classroom, the more likely they are to be transferred to larger numbers and future topics.
A final optional assignment involves the solving of open-ended problems that give the learners the freedom to choose tasks or methods of calculation. This type of task may help to clarify existing misconceptions, but at the same time, it enables the learner to show his or her capabilities (make use of arithmetic structures and properties, systematic work, etc.) This type of activity incorporates natural differentiation as well. It includes tasks on different levels that are neither fixed nor determined by the teacher.
Open-ended problems can be offered with the task format 'number triangle': Number triangles can be worked on with counters or with number symbols and follow the rule (see Wittmann & Müller, 2004:144f; Scherer & Krauthausen, 2010): The sum of two adjacent interior fields is written down in the exterior field.
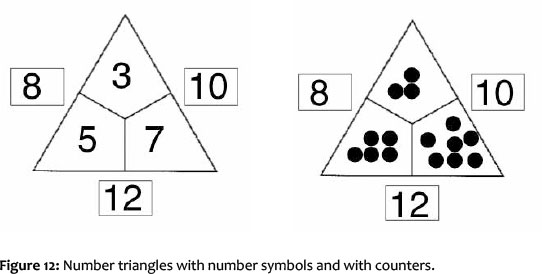
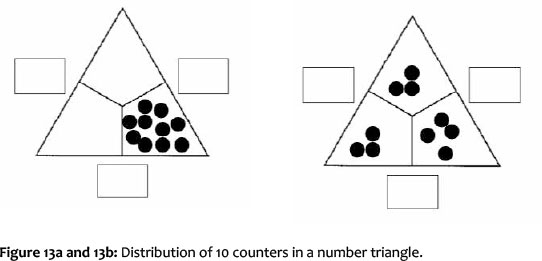
For example, an open-ended task could be to Find number triangles with 10 counters! (cf. Scherer, 2005:183f). The learners have to look for a decomposition of 10 in three addends. Usually, this happens at the beginning, by considering possibilities unsystematically. At the same time, it also allows for a more systematic approach. This could be encouraged by the teacher through inquiries about strategies and solutions ('How did you find a new or a next solution?'). Finally, learners may find several (or all) solutions in the range of an extreme distribution (Figure 13a) and nearly a uniform distribution (Figure 13b). In the on-going process, the calculations can become symbolic tasks.
With these open-ended tasks, the danger of overtaxing learners can be avoided as they can choose tasks on their individual level of ability. These open-ended tasks can be realised in every form of the learning environment. It has been found that children often approach open-ended problems with more motivation because the results are assessed not only as right or wrong, and therefore, reduce the fear of failure (cf. Grossmann, 1975).
Conclusion
Substantial or complex teaching units such as those presented in this article are not only appropriate for the 'good' learners. Children who have difficulties in calculating will also be able to discover and use adequate strategies and relations between numbers (cf. Scherer, 1999). Learning environments, like the ones suggested here, can contribute to the development of both the content-related competencies and the process-related ones (cf. National Council of Teachers of Mathematics, 2000; Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2005) and should lead to successful learning processes in mathematics. Moreover, the illustrated structures and patterns form the necessary basis for understanding the nature of mathematics (see also Van den Heuvel-Panhuizen et al., 2012:6f.).
Since tasks of different difficulty are presented in a natural way, natural differentiation can be realised and all learners can contribute to the same (general) task. The danger of overtaxing the weaker learners and undertaxing the more able ones can be reduced considerably (cf. Scherer, 1999; Wittmann, 1990:159). Giving freedom to learners to test their limits can support both motivation and self-confidence without overtaxing them. Low achievers are often underestimated or misjudged, and teachers often restrict their opportunities to succeed by failing to adopt a more open-ended approach to problem solving (see also Peltenburg & Van den Heuvel-Panhuizen, 2012). Providing learners with appropriate support, entails making certain demands and aiming at long-term learning processes instead of focusing only on short-term success.
The teacher must have considerable patience, since these processes will initially be time-consuming. It will take time for leaners, in the higher grades, to change strategies if they have been accustomed to working with more reproductive methods. But the time invested is more likely to yield dividends and will be far more effective than pure quantitative extension of training. Over the long-term, this affords school beginners a greater chance to develop active learning styles.
The quality of teaching is of great importance, especially for low-achievers:
Good teaching that emphasises the structure of a subject is probably even more valuable for the less-able student than for the gifted ones, for it is the former, rather than the latter, who is most easily thrown off the track by poor teaching (Bruner, 1969:9).
As illustrated above, the concept of natural differentiation, in accordance with a constructivist perspective, represents a sustainable concept for teaching and learning mathematics in the primary grades, as well as, for education in general (cf. Wittmann, 2001).
Endnote
1 The concept of 'flash exercises' (Wittmann & Müller, 1990:73ff.) aims at automatising certain basic elements of arithmetical knowledge.
References
Ainley, J. 1990. Playing games and learning mathematics. In L.P. Steffe & T. Wood (Eds.), Transforming children's mathematics education: International perspectives, 84-91. Hillsdale, NJ: Erlbaum. [ Links ]
Ahmed, A. 1987. Better Mathematics. A Curriculum Development Study. London: HMSO. [ Links ]
Bouton, C.N. 1902. Nim, a game with a complete mathematical theory. Annals of Mathematics 2(3):35-39. [ Links ]
Bruner, J. 1969. The process of education. Cambridge, MA: Harvard University Press. [ Links ]
Cobb, P., Wood, T. & Yackel, E. 1991. A Constructivist Approach to Second Grade Mathematics. In E. von Glasersfeld (Ed.), Radical Constructivism in Mathematics Education, 157-176. Dordrecht: Kluwer. [ Links ]
Donaldson, M. 1978. Children's minds. London: Fontana/Croom Helm. [ Links ]
Flexer, R.J. 1986. The power of five: The step before the power of ten. Arithmetic Teacher 34(3):5-9. [ Links ]
Grossman, R. 1975 Open-ended lessons bring unexpected surprises. Mathematics Teaching 71:14-15. [ Links ]
Hughes, M. 1986. Children and number: Difficulties in learning mathematics. London: Blackwell. [ Links ]
KMK Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, (Ed.). 2005. Bildungsstandards im Fach Mathematik für den Primarbereich Beschluss vom 15.10.2004. München: Wolters Kluwer. [ Links ]
Lorenz, J.H. 1992. Anschauung und Veranschaulichungsmittel im Mathematikunterricht. Mentales visuelles Operieren und Rechenleistung. Göttingen: Hogrefe. [ Links ]
Menne, J. 2000. Jumping ahead: an innovative teaching programme. In J. Anghileri (Ed.), Principles and Practices in Arithmetic Teaching, 95-106. Buckingham: Open University Press. [ Links ]
Moser Opitz, E. 2000. 'Zählen - Zahlbegriff - Rechnen' Theoretische Grundlagen und eine empirische Untersuchung zum mathematischen Erstunterricht in Sonderklassen. Bern: Haupt. [ Links ]
MSW - Ministerium für Schule und Weiterbildung des Landes Nordrhein-Westfalen, (Ed.). 2008. Grundschule. Richtlinien und Lehrpläne. Mathematik. Frechen: Ritterbach. [ Links ]
Müller, G.N. &Wittmann, E.C. 1997. Die Denkschule - Teil 1. Leipzig: Klett Grundschulverlag. [ Links ]
NCTM - National Council of Teachers of Mathematics. 2000. Principles and Standards for School Mathematics. Reston, VA.: NCTM. [ Links ]
OECD - The Organisation for Economic Co-operation and Development. 2009. Learning mathematics for life. Retrieved from http://www.oecd.org/pisa/pisaproducts/pisa2003/44203966.pdf (accessed 29 September 2012).
Peltenburg, M., & Van den Heuvel-Panhuizen, M. 2012. Teacher perception of the mathematical potential of students in special education in the Netherlands. European Journal for Special Needs Education 27(3):391-407. [ Links ]
Scherer, P. 1997. Productive or reproductive exercises - what is appropriate for low attainers? In C. van den Boer & M. Dolk (Eds.), Naar een balans in de reken-wiskundeles - interactie, oefenen, uitleggen en zelfstandig werken, 35-49. Utrecht: Freudenthal Instituut. [ Links ]
Scherer, P. 1999. Entdeckendes Lernen im Mathematikunterricht der Schule für Lernbehinderte - Theoretische Grundlegung und evaluierte unterrichtspraktische Erprobung. 2nd ed. Heidelberg: Edition Schindele. [ Links ]
Scherer, P. 2005. Produktives Lernen für Kinder mit Lernschwächen: Fördern durch Fordern. Band 1. Horneburg: Persen. [ Links ]
Scherer, P. & Krauthausen, G. 2010. Natural Differentiation in Mathematics - the NaDiMa project. Panama-Post 29(3):14-26. [ Links ]
Scherer, P. & Moser Opitz, E. 2010. Fördern im Mathematikunterricht der Primarstufe. Heidelberg: Spektrum. [ Links ]
Shriki, A. 2009. Nim. Not just a game, but so much mathematics! Mathematics Teaching 213:42-44. [ Links ]
Thornton, C.A. 1978. Emphasizing thinking strategies in basic fact instruction. Journal for Research in Mathematics Education 9(3):214-227. [ Links ]
Trickett, L. & Sulke, F. 1988. Low attainers can do mathematics. In D. Pimm (Ed.), Mathematics, teachers and children, 109-117. London: Hodder and Stoughton. [ Links ]
Van den Heuvel-Panhuizen, M. 1991. Ratio in special education. A pilot study on the possibilities of shifting the boundaries. In L. Streefland (ed.), Realistic Mathematics Education in Primary School. On the occasion of the opening of the Freudenthal Institute, pp. 157-181. Utrecht: Freudenthal Institute. [ Links ]
Van den Heuvel-Panhuizen, M., Kühne, C. & Lombard, A.P. 2012. Learning Pathway for Number in the Early Primary Grades. Northlands, South Africa: Macmillan. [ Links ]
Van Oers, B. 2010. Emergent mathematical thinking in the context of play. Educational Studies in Mathematics 74(1):23-37. [ Links ]
Von Glasersfeld, E. 1995a. A constructivist approach to teaching. In L.P. Steffe & J. Gale (Eds.), Constructivism in education, 3-15. Hillsdale, NJ: Erlbaum. [ Links ]
Von Glasersfeld, E. 1995b. Sensory experience, abstraction, and teaching. In L.P. Steffe & J. Gale (Eds.), Constructivism in education, 369-383. Hillsdale, NJ: Erlbaum. [ Links ]
Winter, H. 1984. Begriff und Bedeutung des Übens im Mathematikunterricht. Mathematik lehren 2:4-16. [ Links ]
Wittmann, E.C. 1985. Objekte - Operationen - Wirkungen: Das operative Prinzip in der Mathematikdidaktik. Mathematik lehren 11:7-11. [ Links ]
Wittmann, E.C. 1990. Wider die Flut der 'bunten Hunde' und der 'grauen Päckchen': Die Konzeption des aktiv-entdeckenden Lernens und des produktiven Übens. In E.C. Wittmann & G.N. Müller (Eds.), Handbuch produktiver Rechenübungen, Band 1, 152-166. Stuttgart: Klett. [ Links ]
Wittmann, E.C. 1994. Teaching aids in primary mathematics: Less is more. In L. Bazzini & H.-G. Steiner (Eds.), Proceedings of the Second Italian-German Bilateral Symposium on the Didactics of Mathematics Vol. 39, pp. 101-111. Bielefeld: IDM. [ Links ]
Wittmann, E.C. 2001. Developing mathematics education in a systemic process. Educational Studies in Mathematics 48(1):1-20. [ Links ]
Wittmann, E.C. & Müller, G.N. 1990. Handbuch produktiver Rechenübungen. Band 1: Vom Einspluseins zum Einmaleins. Stuttgart: Klett. [ Links ]
Wittmann, E.C. & Müller, G.N. 2004. Das Zahlenbuch. Mathematik im 1. Schuljahr (Lehrerband). Leipzig: Klett Grundschulverlag. [ Links ]
Wittmann, E.C., Müller, G.N., Berger, A., Fischer, M., Hoffmann, M. & Jüttemeier, M. 1994. Das Zahlenbuch. Mathematik im 1. Schuljahr (Lehrerband). Stuttgart: Klett. [ Links ]
Zaslavsky, C. 1991. Africa counts: Number and Pattern in African Culture. Boston: Prindle, Weber & Schmidt. [ Links ]















