Realising pre-school mathematical education - a development-oriented math programme with special consideration of phonological language processing aspects

 

 

Petra Langhorst^I; Antje Ehlert^II; Annemarie Fritz^III

^IBerlinger Platz 6-8, 45127, Essen (Germany), visiting researcher at the Centre for Education Practice Research, University of Johannesburg Soweto Campus, e-mail address: petra.langhorst@uni-due.de
^IIPsychology Department, Faculty of Educational Sciences, University of Duisburg-Essen and Centre for Education Practice Research, Faculty of Education, vising researcher at the Centre for Education Practice Research, University of Johannesburg, Soweto Campus, e-mail address: antje.ehlert@uni-due.de
^IIIPsychology Department, Faculty of Educational Sciences, University of Duisburg-Essen and visiting professor at the Centre for Education Practice Research, Faculty of Education, University of Johannesburg, Soweto Campus, e-mail address: fritz-stratmann@uni-due.de

 

 

---

ABSTRACT

Mathematical development processes begin long before school starts and the importance of previous mathematical knowledge for later school achievements is beyond dispute. For a suitable pre-school education, the focus of interest must be to find out which early learning processes prepare children best. In this article, the acquisition of the key concepts of numeracy is presented in a developmental model, which served as framework for a supportive programme for 4-8 year-old children. The research into this intervention shows how development-oriented support of key arithmetic concepts can be constructed and taught systematically. The immediate and sustainable effect of the programme Mina and the Mole on the mathematical competencies of children has already been demonstrated in an evaluation study of 248 children aged 5-7. Considering the strong language-orientation of the programme, the present study focused on aspects of phonological awareness and of phonological working memory. It was evident that these phonological language processing aspects correlated with mathematic skills. Furthermore, it was found that the dominant linguistic focus of the training did not constitute a disadvantage - even linguistically weak children significantly improved their mathematical skills. Moreover, children with poor or average phonological performance could profit from the supportive programme also regarding their phonological language processing.

Keywords: key concepts of numeracy, phonological language processing, improved mathematical skills

---

 

 

Introduction: The role of prior knowledge

Ever since the discussion of the PISA studies on school performance (a.o. Baumert et al., 2001), educational activities in the pre-school area have come more and more the focus of attention. Not only has a connection been proven between achievements at the beginning of school and later achievements, but also between the duration of the kindergarten time and achievements in secondary school (Ehmke, Siegle & Hohensee, 2005). Those students who demonstrated higher-level competencies in mathematics in PISA 2003 had attended pre-school institutions for a longer period of time. The importance of the education in kindergarten for the early development of mathematical competence is emphasised (Prenzel et al., 2004).

Research has also shown the predicative importance of previous mathematical knowledge for later success in learning mathematics. Grube & Hasselhorn (2006) found that the extent of the previous knowledge is the key determining factor for mathematic understanding, and that intelligence does not explain any specific part of an increase in performance that cannot already be explained by previous knowledge. In longitudinal studies, Krajewski & Schneider (2006) found a distinct correlation between specific quantity- and number-related prior knowledge and mathematical achievements during and at the end of the primary school period. Low quantity-number competencies allowed the reliable prediction of future difficulties in learning mathematics at school already half a year before the onset of formal education. Aunola et al. (2004), in a Finnish longitudinal study, found that children who had low quantity-number understanding before starting school developed significantly slower in school. These findings illustrate the necessity of preventing, and compensating for, delays in development.

Since the aim of maths education in the pre-school years is to enable all children acquire a sound and school-oriented mathematical knowledge, it is necessary to understand the process of acquiring numeracy. We argue that the approach of effective early mathematical education means focusing on the development of mathematical competencies, specifically of number concept.

 

Development of mathematical concepts

Based on two innate core systems, the abilities to approximately represent and distinguish quantities develop early on (Feigenson, Dehaene & Spelke, 2004): Firstly, the analogue-magnitude-representation-system allows global comparisons in which larger quantities are not represented as discrete units. The second core system, the object-file-representation-system, facilitates the precise quantitative representation of successively given distinct small quantities of up to three elements. These two core systems for recognising and comparing quantities are active before the onset of language use.

These early numerical systems of cognition are followed later on by the acquisition of the number word line, as well as protoquantitative notions that are void of numerically precise number relations. Resnick (1992) describes three protoquantitative schemes. She explains that by means of the 'scheme of comparing', children begin to assess two quantities as 'more' or 'less' already at the age of two. The 'increase/ decrease-scheme' of adding and subtracting allows them to understand and express non-numerical quantity set operations as a process at the age of about 3 to 4 years. The vital protoquantitative 'part-whole-scheme' is developed at the age of about four. This concerns the basic understanding of relations between a whole and its parts without precise quantification (cf. ibid.). A study on the development of the part-whole concept (Langhorst, Ehlert & Fritz, 2012) showed that about two thirds of the four-year-olds and almost 80% of the 5-year-old pre-school children could manage non-numerical part-whole context tasks without visual materials.

While non-numerical quantity knowledge and counting skills at first develop independently, the acquisition of counting principles brings about the integration of both areas. Through their connection with the understanding of ordinal relations and the linking of the number knowledge with the 'increase/decrease-scheme' precise quantity and number operations become possible gradually (a.o. Resnick, 1983; Fuson, 1988). For the system of symbolic number representation key concepts, such as cardinality and the part-whole concept need to evolve in due course. These key concepts do not develop by themselves: they require instruction (Dehaene, 1997). They represent the milestones of knowledge acquisition when acquiring numeracy (Krajewski & Schneider, 2006; Fritz & Ricken, 2008). In the following, the developmental model of Fritz & Ricken (2008) describes which individual components form the basis of these concepts.

Developmental model for the acquisition of numeracy

The developmental model of Fritz & Ricken (2008) consists of five distinguishable levels of ability and is used to assess for 4 to 8-year-olds (see in detail article of Fritz, Ehlert & Balzer in this journal). It is based on theoretical suppositions and empirical findings (a.o. Piaget & Szeminska, 1965; Resnick, 1983; Fuson, 1988; Wynn, 1990; Case & Okamoto, 1996). The operationalisations of the five levels were developed in several studies and tested in various item versions with approximately 3 000 children. In each instance the construction of the model could be replicated.

• Level I Count number:The acquisition of the number word line begins at the age of two to three. At first, children recite the number words without linking each number word to a specific meaning. Gradually, they construct the meaning of numbers as tools for counting. Upon understanding the one-to-one correspondence the number words are successively linked to quantities of objects (Fuson, 1988). It takes about one year to achieve the confident counting out of four objects, then the counting process is seen as achieved (Wynn, 1990).

• Level II Mental number line: Based on representations of a mental number line (Resnick, 1983) children develop the ordinal concept that the number word line has a fixed order which indicates getting 'larger'. 4- to -5 year-old children are able to compare quantities according to their position on the number word line. Children can identify precursory and successive numbers and add and subtract numerically precisely by moving forward and backward on the counting line (Case & Okamoto, 1996). All quantities are counted out individually, always beginning at 1.

• Level III Cardinality and Decomposability: The number word line is understood as a sequence of increasing cardinality. Numbers are composite units that represent the specific cardinality of a quantity with the number of its elements (Steffe, Cobb & Von Glasersfeld, 1988). In additive operations, quantities do not have to be counted out individually any longer as cardinal knowledge is now connected to a first understanding of the composition of quantities and of their decomposition into individual units. The first summand can now be seen as partial quantity of the total quantity.

• Level IV Class inclusion and Embeddedness: Children grasp the inclusion principle that each number contains the quantity of the precursory numbers (Piaget & Szeminska, 1965). By the part-whole concept the child can understand that a number is composed of all elements of its quantity and can be decomposed in different ways (Resnick, 1983; Fuson, 1992). Far more efficient strategies are elaborated and can be applied to word problems that enquire after the exchange quantity, as well as the final, or initial quantity.

• Level V Relationality: With the relational number concept (Stern, 1998) children develop the understanding that the distance between two consecutive numbers is the same: numbers in the number word line increase steadily by 1. Distances between the numbers are congruent and thus can be precisely defined. Tasks such as 'which number is 3 bigger than 4?' become solvable. More complex word problems in which the relations between numbers have to be modelled with only the relational quantity given can now also be solved.

 

Realising suitable mathematical education for a pre-school age

Having described the construction of key arithmetic concepts for numerically precise calculations the question arises how early mathematical education can be realised in a technically- and developmentally adequate, and educationally child-oriented way (Fthenakis et al., 2009). For this, we have generated criteria for pre-school mathematics education.

Development-oriented and systematic conceptualisation

We propose that early mathematics education should not be seen as a short-term intervention but rather as developmentally oriented and systematically constructed. The aim should be to let children acquire the key concepts gradually.

Such support is found in countries where pre-school education is run on a curriculum. In the US this has been the case for a number of years. Griffin (2008) could, for example, show that in the programme Number Worlds, which contains module-like curricula for children from 4 years up to grade 8, children who were supported with it on a daily basis had a more developed number knowledge when they started school. Similarly, Clements & Sarama (2007) stated advances in performance of the 4- to 5-year-olds immediately after they had been supported daily for half a year with the course-like programme Building Blocks. Big Math for Little Kids (Ginsburg, Balfanz & Greenes, 2003) is another structured programme that is carried out on a daily basis for years. The immense effectivity of early systematic support can also be seen in Australia. A comparative survey of the mathematical skills of German and Australian children, at the beginning and after completing their last year of kindergarten, showed superior achievements of the Australian children who are exposed to an obligatory pre-school year that consists of daily exposure to mathematical preparation (Clarke, Clarke, Grüßing & Peter-Koop, 2008).

Early mathematical education should be based on theoretically well-grounded and verifiable concepts (Royar, 2007) that represent the development of competencies. In Germany, the theory-based supportive concepts 'Mengen, zählen, zählen' ('MZZ', Krajewski, Nieding & Schneider, 2008a, 'Sets, Counting and Number') and the 'Förderprogramm zur Entwicklung des Zahlkonzepts' ('FEZ', Peucker & Weißhaupt, 2005, 'Development programme for number concept') have proved to be effective. They were devised for the last year of kindergarten in order to systematically build specific preparatory skills. Both programmes follow a developmental structure, but their support units are limited to a few weeks only.

Activities integrated in games and daily routines

Considering that children interact with their environment through playing and learning processes, the realisation of mathematical education should be oriented towards the child's environment (Fthenakis et al., 2009). Fun activities embedded in everyday situations are seen as appropriate learning instances; they foster positive attitude towards mathematics (Hellmich, 2007).

Such a playful approach is strongly advocated in the Netherlands where early mathematics is learned from the age of three in interaction with adults (Van Oers, 2004). As for addressing mathematics-related topics in picture books and stories, Van den Heuvel-Panhuizen (2012) has highlighted the added potential for learning mathematics in a study with 5-year-old Dutch children.

Research findings also show the effectiveness of such a playful support that does not follow fixed sequences and pre-set tasks. However, it should be noted that these programmes only seem to be effective when they focus on contents that aim at specific precursory skills. A study with Swiss kindergarten children showed that a programme that used games ('Spielintegrierte Förderung', 'SpiF', Hauser & Rechsteiner, 2011, 'Advancing through play integration') brought about learning progress that was similar to the German programme 'Mengen, zählen, zählen' ('MZZ').

Early intervention for weaker children

In addition to the mathematical education of all children, one has to consider the specific compensatory early intervention. Hasselhorn (2010) sees early intervention as a preventive measure to improve the competencies of potential at-risk children, or to prevent unfavourable individual developments. Intervention programmes that focus explicitly on early preventive intervention of potential at-risk children showed long-term effects. In the Netherlands, the programme 'Additional Early Mathematics' (Van Luit & Van de Rijt, 1995), which supports basic mathematical skills and strategies for simple arithmetic problems, was devised for 4- to 7-year-old children with delayed development. In a study, the at-risk children who were supported showed better performance than the control group both in the short- and long-term and caught up with their classmates (Van de Rijt & Van Luit, 1998). A longitudinal study in Germany analysed the successful support of potential at-risk children through adaptation of individual support plans (Grüßing & Peter-Koop, 2008). The selected children displayed increased performance regarding their quantity- and number-related knowledge just before they started school.

The demand for sustainability in early mathematical intervention is of vital importance. If support measures really helped develop skills or knowledge, these should still be traceable after several months (Hasselhorn, 2010). Metacognition, diagnostic integration and adaptivity are seen as key criteria for the realisation of suitable support.

The support should be devised in a way that it focuses not only on the imparting of knowledge, but also enabling the metacognitive reflection of the learning process. Pre-school children already have the capacity to think about their own learning and share these thoughts with others (Hasselhorn & Gold, 2006). This necessitates the verbalisation of strategies and the reflection upon their applicability and effectivity (Gerlach, Fritz, Ricken & Schmidt, 2007). Furthermore, support is particularly effective when it is accompanied by diagnosis and the programme is adapted to the development and learning progress of the children (Walter, 2009). If a support programme lacks adaptability to the learning requirements it may fail to achieve any effect (Langhorst, Hildenbrand, Ehlert, Ricken & Fritz, 2013).

Fulfilling these requirements concerning suitable mathematical diagnostics and support imposes high demands on the professional knowledge of the kindergarten teacher and requires appropriate qualification (Hellmich, 2007). Teachers also need to have learning support materials that speak to the needs of the children.

 

Mina and the Mole - a mathematics development programme

Based on the developmental model of Fritz and Ricken described above, Gerlach & Fritz (2011) have conceptualised a development-oriented programme for children aged 4 to 8. The programme, Mina and the Mole is aligned to the five levels of the model. The support accompanies the development of the children and can be adapted to their specific learning needs and rates of learning.

Contents of the programme

The aim of the programme is to teach basic arithmetic concepts. The training consists of six consecutive modules that are constructed in a systematic way. Entry into the programme can begin with each module; this depends on the developmental requirements of a learner. Each module consists of several topics. So, it can be used with different aspects of the five concepts over a long time. The modules contain the following key concepts (Gerlach & Fritz, 2011):

• Module 0 contains content for younger children or children with delayed development. It focuses on basic skills with elementary pre-numeric contents such as recognising and naming objects, and comparing and sorting them by their characteristics. Here, children make numerically imprecise comparisons of quantities, they estimate quantities and they also identify ascending sequences, for example, ordered by size.

• Module 1 supports the acquisition of the key competence of correct one-to-one matching of number word and counting object, as well as the development of a first concept of numerosity by matching number and quantity. Here, the number word line, the determination of quantities by counting-out, and the comparison of numbers through their position on the mental number line are supported.

• Module 2 deepens the understanding of the concept of numerosity by connecting the number word line and the quantity. Quantities are compared in different ways: by perception, by counting, and by one-to-one correspondence. Quantities are adjusted and divided as well.

• Module 3 works both on adding and subtracting as well as on achieving the concept of decomposability through counting operations on quantities. Operations are carried out based on the part-whole concept and numbers are decomposed in various ways. Furthermore, an understanding of compensation (the whole does not change when an element is shifted from one subset to another) and of covariance (if elements are added to or subtracted from a subset, the whole changes accordingly) is introduced based on perceptive material.

• Module 4 extends 'calculating' and relates specifically to subset operations. Tasks of embeddedness, on inversive relations between addition and subtraction, and of increasing flexibility of the part-whole understanding are all practiced in this module.

• Module 5 deals with the comparison of quantities to determine differences and the relations between numbers. Although, generally, children only develop a firm grasp of the relational number concept in the second grade, rather complex comparison tasks are dealt with here, at a very elementary level, through appropriate choice of context and concrete actions.

Mathematics through stories

The programme is embedded in a cycle of stories. The kindergarten teacher introduces each new module of content by telling a story, which leads the children into an imaginary forest and meadow world. There they meet the protagonist of all stories, the little bee, 'Mina', who has many adventures and meets a lot of other animals. While reading the story, the teacher also uses a bee hand puppet and shows the children a book with suitable illustrations that accompany the story.

Each of the 27 stories poses a mathematical problem the children have to solve. The stories challenge the children to think independently. In module 3, for example, the children need to help two squirrel brothers work with quantities: 'Fred and Rick have gathered 6 acorns. They want to give 4 to their grandma - how many will they have left?' (see Figure 1). In another story, children assist a rabbit, 'Paul', with solving a subset problem (principle of compensation): Paul has got 6 carrots, 4 are in one box, 2 in another box. Mina puts one carrot from the one into the other box but Paul complains: 'Now I have got fewer carrots, since you took one carrot out of my box - or?' (see Figure 2). In module 5, the children are confronted with particular challenges with tasks on relationality, or on the determination of differences. Here, moles need help with looking after their children: 'There are 7 mole children, one more girl than boys -how many girls are there? or Each boy eats 8 worms, each girl eats 5 - how many more are 8 than 5?'-

 

 

 

 

By embedding mathematical problems in stories about real-life topics such as friendship, conflict and reconciliation, sharing fairly, celebrating birthdays or starting school, children are inspired think about these problems for fun and they realise that mathematics can be fun and useful. In general, children want to hear stories and love to pick the same story books with the familiar characters again and again. In the math programme one story is read out repeatedly and used in several support units to introduce the different parts of one content area.

Systematic imparting of contents

The various contents are always addressed in the same way. As described above, a story first introduces the respective problem and solutions are looked for. Set off by the adventures of the bee Mina, the children are then given concrete stimuli for the exploration of the mathematical problem, with a focus on verbalisation and reflection within an instructional setting. For this purpose, the kindergarten teachers are provided with 48 instruction cards with concrete instructions for this deepening group exercise. On the cards the texts are predefined, the cards say exactly what the teacher should say to the children. The exercises with the children are described precisely. So the cards can be regarded as a firm guide for the work with the children.

Supported by these instructions, the teacher can focus much better on a targeted approach. The suggestions for suitable strategies and for the reflection phases serve as content-oriented support for systematic imparting. The stimuli can also be modelled differently by the teachers or developed during the discussion with the children. In the same way children are given room for discovering solutions independently and in different ways (cf. article by Scherer in this journal).

For learning in heterogeneous groups, the task cards also often contain various strategic levels of ability, i.e. simpler or more elaborate strategies, last ones for requiring a higher level of conceptual knowledge.

Example

The following shortened version of a story is used as starting point for the exploration of the topics 'counting principles' and 'quantity concept':

Mina meets the caterpillar Mathilda. Mina boasts "I am already really good at counting!" So Mathilda asks her: "How many humps have I got?" Mina starts to count: "1, 2, 3, 4, 5, 6 and so on." (She does not look at the humps, though). She has no idea how to find out through counting how many humps Mathilda has exactly. So, she answers vaguely: "You have about 5 or 100 humps?!" Then she flies away quickly so that the caterpillar cannot ask further. Now she needs the children's help.

Following the story, the children are encouraged to compare notes, discuss and bring in ideas: 'how can the bee find out "how much" something is?' First, the children's individual counting experiences are referred to. The children realise that this is not about simply reciting the number word line anymore, but rather about identifying the number of elements of a quantity. The story book offers follow up prompts, such as: 'Can you count Mathilda's humps or Mina's stripes or the leaves? How many are there?' (see Figure 3).

 

 

In the guided group exercise, many objects (leaves, conkers, and stones) are counted-out in monitored counting processes. The children are supposed to learn about the concept of numerosity through one-to-one correlation: one number word for one counting object. Here, they can touch the objects, move them to one side or finally learn to count with their eyes only. For this phase, the teachers use the instruction card: 'I now put some leaves into the middle. Who can count the leaves?' (...) 'Please touch each leaf when counting'.' (...), 'Please count out loud'.' (...), 'Move each counted leaf to one side while counting'.' (see Figure 4). In this way, the rule that the last word indicates the number of the total quantity (last-word-rule) is acquired. By verbalising as well as monitoring, comparing and evaluating the actions and strategies, these are more consciously perceived. The use of the hand puppet makes it easier for many children to verbalise their actions.

 

 

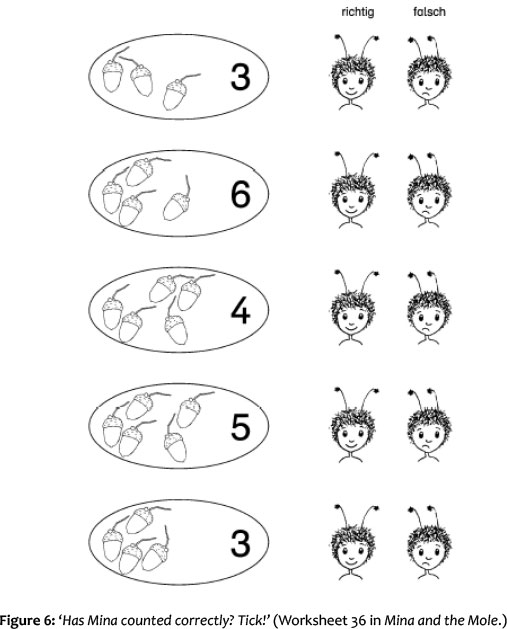
This common exercise with all children is followed by various games (see Figure 5) and a wide range of activities specifically aimed at consolidating the determination of quantities through counting-out. Many counting opportunities should be used so that the children can transfer their counting skills onto new counting tasks ('How many swings do we have on our playground?; How many apples have we got left?; How many rabbits are on the field?'). In the next units the children can be supported differently according to their individual abilities. A work sheet on which the number-quantity-allocation can be checked works well with children with different levels of ability. If a result is correct, the children tick the laughing bee; if it is incorrect they tick the sad-looking bee (see Figure 6). This task is not obligatory for all children.

 

 

 

 

Optional support offers

After initially imparting the contents with a structured approach, they are then supplemented by learning through playing and everyday situations. A variety of ways of learning appropriate to the mathematical requirements of the contents are used for the systematic consolidation of each of the 48 topics. The teachers can expand the units depending on the learning rate and interests of the children. The extensive accompanying handbook offers a wide variety of activities (activity games, games with music, board games or parlour games). Numerous suggestions for songs, rhymes and counting-out rhymes (see Figure 7) or finger games supplement content and offer easy access to mathematical problems through playing. The handbook also suggests materials for a math-corner, which should make for autonomous work and play. A series of tips for everyday life suggests ways of integrating the contents into the kindergarten routine. Furthermore, there is an option to make use of different work sheets. Thus, the kindergarten teachers can pick and choose from different tasks and devise the distinct units flexibly regarding the learners' needs.

 

 

Mina and the Mole is not only seen to support mathematical targets. The programme also offers a wide range of interdisciplinary learning opportunities: the stories can be used for language support and as starting points for topics or projects in science, music or education (Who lives in the forest, who lives at the pond?', Food and living of mole, bee, squirrel).

Diagnostic integration

It is an advantage to be able to orient oneself to a developmental model that shows when individual concepts are acquired and how these build upon each other. The support of the programme Mina and the Mole can be given adaptively, fitting to the diagnosed learning level: The children's skills can be assessed diagnostically with the MARKO-D-Test (Ricken, Fritz & Balzer, 2013), which can assign a child's level of performance to a particular level of development. This has the advantage of being able to determine exactly where the support should start. The child's skills will first be consolidated on his/her level, which will then form the basis on which to impart the competencies of the next level.

Sustainable effectiveness of the math programme

In an evaluation study, the short- and long-term effects on the mathematical abilities of 134 pre-school children of a six month-support with the programme Mina and the Mole have been successful (Langhorst et al., 2013). In order to establish the pre-school mathematical abilities, the MARKO-D (Ricken, Fritz & Balzer, 2013) was used both for the pre-test (before start of training) and the post-test (six months after the training towards the end of the last kindergarten year) analysis. For the follow-up test (eight months after finishing the training in the first grade), the school mathematical abilities were established with the MARKO-D-1-Test (Fritz, Ehlert, Ricken & Balzer, in prep.). A control group was not given any particular mathematical support.

The results showed significant increases in performance for all supported children immediately after theintervention. Kindergarten children whose teachers used the material of the Mina and the Mole programme profited from a marked support effect directly after the end of the training. They had a better starting base for their mathematical learning development. Since these children had been supported with the materials at least up to module 3, they had a better grasp of the level III concepts of cardinality and decomposability, which are particularly important for this moment of transition to primary school. The long-term effects eight months after finishing the support programme were also significantly stronger for the experimental group than for the control group. Even after attending school for half a year and having math classes almost daily, the advance in performance of the training children was still significant. The intervention appears to provide children with sustainably favourable learning prerequisites.

 

Mathematics and Language

Language can be seen as a key medium for teaching and learning mathematics. At a pre-school age, mathematics is exclusively imparted through language. The programme Mina and the Mole also has a strong focus on language, since mathematical topics are presented in stories and possible solutions and strategies are worked out and reflected verbally. We will now take a closer look at the connection between linguistic competencies and learning mathematics.

Phonological awareness

In this article, specific language aspects will be dealt with. The focused is on the formal aspects of spoken language, i.e. phonological awareness. According to various studies, this is the most important precursory skill in the development of learning to read and write and is seen as key predictor for academic reading and writing competence (Goswami & Bryant, 1990; Schneider & Näslund, 1993; Scarborough, 1998).

Phonological awareness is the ability to analyse and manipulate the phonetic structure of spoken language without taking heed of the meaning of the linguistic material (Tunmer & Hoover, 1992) Two different areas are discerned (Skowronek & Marx, 1989; Anthony et al., 2003): phonological awareness in the broader sense entails the perception of larger phonetic entities such as syllables in words or the sound of a rhyme. It develops spontaneously before school since it does not require the ability to writing. Phonological awareness can already be supported in 4- to 5-year-olds with exercises that differentiate between syllables or those that require learners to recognise rhymes (Goswami & Bryant, 1990). The phonological awareness in the narrower sense entails the conscious use of phonemes (e.g. recognising onsets, phoneme segmentation). This ability to analyse and synthesize phonemes is only acquired at school age in the concrete exploration of written language and enhanced when learning graphemes at school.

A poorly developed phonological awareness is seen as a risk factor. In a study with 4- to 5-year-olds, a close connection with the reading performance three years later was detected. The pupils with reading deficits had also shown significantly poorer performances in their phonological awareness (Bryant & Bradley, 1985). Similarly, pupils with proven reading and writing difficulties showed poorer performances in phonological awareness than their peers without problems in this area (Klicpera, Gasteiger-Klicpera & Schabmann, 1994; cf. also Ziegler & Goswami, 2005).

Phonological information processing

Phonological awareness is one of the processes of phonological information processing. This encompasses three dimensions (Wagner & Torgesen, 1987). Apart from phonological awareness, there are the two components of phonological recoding: phonological recoding in the working memory (verbal memory capacity) enables the short-term storage of sounds and sound units in the working memory, for example in tasks of auditory retentiveness. These entail serial reproduction activities among others when repeating numbers forward or when repeating pseudo words (nonsense words). Another component of phonological information processing is the phonological recoding in the long-term memory when accessing the semantic lexicon. It describes the speed of information, bounded to language (rapid automised naming/RAN), with which written symbols are recoded verbally (grapheme-phoneme-correspondence).

Phonological awareness and phonological working memory

It can be argued that phonological awareness, as a processing mechanism of the sound structures of linguistic information, is tied to processes and abilities of the phonological memory. According to Baddeley et al. (1998), phonetic material cannot be handled without its participation. Regarding Baddeley's (2003) working memory model, a controlling and coordinating component can be assigned to the three mentioned dimensions of phonological information processes: the phonological loop as sub system of the working memory. This is used for the short-term storage and processing of phonological information.

Anthony et al. (2002) recommend including phonological working memory in studies of phonological awareness. However, just how close the relation between phonological awareness and phonological working memory really is, is still being debated (Alloway et al., 2005). Yet, it is difficult to outline them independently as both are components of phonological information processing and both take on the processing of phonological information. Phonological memory feats are necessary, since the word always has to be remembered before it can be used phonetically. Some authors argue that they reflect a common underlying construct (Bowey, 1996; Metsala, 1999; Passolunghi & Siegel, 2001). Cutting and Denckla (2001) also found a significant connection between memory span and phonological awareness.

Other authors state that although phonological awareness and phonological loop are both subject to the efficiency of phonological processes, they are embedded in separate cognitive systems (Gathercole, Willis & Baddeley, 1991; Hecht, Torgesen, Wagner & Rashotte, 2001; Alloway, Gathercole, Willis & Adams, 2004). Alloway et al. (2005) view phonological memory feats as separable from phonological awareness, yet they found a correlation of r=.57 in the performances of 4- to 5-year-old children in this regard. What is more, in their study, the number span forward that actually serves to check the phonological loop turned out to be the predictor for phonological awareness.

This article shares the view of a positive connection between the performances of the phonological loop and the phonological awareness. Especially at a pre-school age, respective demands are made purely verbally and thus without written language. These must therefore be retained in the phonological loop until the cognitive processing is done. Even if there are two distinguishable constructs on the theoretical level, a large overlapping in performance can be assumed.

Connection between mathematics and phonological working memory as well as phonological awareness

In a longitudinal study by Hecht et al. (2001), the causes for the connections between mathematical and linguistic performances are supposed to lie in the described phonological information processing. That means, mathematical performances are also dependent on the conscious processing of phonological information as well as on efficient phonological memory processes.

Grube & Hasselhorn (2006) proved a correlation between phonological working memory and numeracy for German children at the end of the second and third grade, while Grube (2006) also established this influence for the advanced calculations of second- and fourth-graders. In a study with Canadian primary school children (Rasmussen & Bisanz, 2005) it was stated that the phonological loop represented the best predictor for achievements in verbal mathematical problems from the beginning of the first school year. De Smedt et al. (2009) found the phonological loop to be a useful measure for predicting the mathematical performance of Belgian second-graders.

Phonological awareness is also seen as a determinant for the development of mathematical competencies at primary school age (Alloway et al., 2005; Grube & Hasselhorn, 2006; Passolunghi, Vercelloni & Schadee, 2007). In the above-mentioned longitudinal-study by Bryant & Bradley (1985), the phonological awareness of English pre-school children correlated not only with their reading achievements but also with later mathematical achievements at school. Navarro et al. (2012) asserted that good phonological awareness led to better results in the Utrecht Early Numeracy Test (UENT) in a study with 4- to 7-year-old Spanish children. Krajewski et al. (2008b) found a correlation of r=.50 between phonological awareness at pre-school age and the mathematical achievements towards the end of the first grade in German children. The authors found that the acquisition of basic numerical competencies depends on the phonological awareness. According to their study, the support of phonological awareness should facilitate the acquisition of basic numerical skills, such as counting skills. It is important for the acquisition of mathematical precursory skills. But phonological awareness did not account for the differences in the higher quantity-number-competencies or mathematic achievements at school (cf. ibid.). Phonological awareness thus has a mediating role between working memory sub systems and early numerical competencies (Krajewski & Schneider, 2009).

Phonological awareness in different languages

It is interesting to see whether phonological awareness is subjected to influences of different languages. Children are first able to operate with syllables, rhymes and individual phonemes of words (Goswami & Bryant, 1990; Anthony et al., 2003). For this phonological awareness in the broader sense, only 'a verifiable insight that one's native or non- native language can be broken down into sounds and sound combinations' (Jannuzi, 1998:8) is necessary. As children implicitly have this ability already at pre-school age, it can be assumed that achievements on this level of mere phonetic analysis of spoken words do not depend on differences in various languages. Studies with English and German children showed that the complexity of syllables in both languages can be equated (Seymour, Aro & Erskine, 2003). Goswami, Ziegler & Richardson (2005) also pointed out a similar development of phonological awareness in the broader sense in English and German 'pre-readers'. As for phonological awareness in the narrower sense, however, German children far outmatched the English ones in the area of phoneme awareness, which can be attributed to the fact that there is a far clearer phoneme-grapheme-correspondence in the German language (cf. ibid.). Costard et al. (2007) also refer to differences between English-speaking and German-speaking children because of the comparably less phonetically accurate and thus more complex orthography of English. Since this conscious use of the smallest linguistic entities only develops with acquisition of written language at school age, it is not in the focus of our considerations.

 

Study

Against the background of this conceptual framework of mathematical concept development and a specific intervention programme, we conducted an inquiry into the effects of the Mina and the Mole programme.

In this discussion of the study, we first look at the connection between the performance of phonological awareness in the broader sense, as well as the phonological working memory, and the mathematical performance of the children. The evaluation then focuses particularly on the influence of these phonological language processing achievements on the increase in mathematical ability. We posed the following questions:

• Considering the strong language-orientation of Mina and the Mole, can linguistically weak children also improve on their mathematical performance?

• Can children benefit from the strong language-orientation of the programme with regard to their phonological language processing?

 

Design of the study and procedure

The study was based on a quasi-experimental design with a treatment- and a control group. The treatment group was supported regularly in small groups of 6 to 12 preschool children for a period of six months from January until the end of June 2010. The kindergarten teachers regularly attended further development sessions for the preparation and implementation of the programme at the University of Duisburg-Essen. They were instructed and supervised in advanced training courses once a month, but they carried out the programme independently. The teachers worked with the children in weekly support units of 45 minutes. In addition, they supported the children on a day-to-day basis with the optional tasks of the programme. In doing so, the teachers differentiated between the developmental pace of the children.

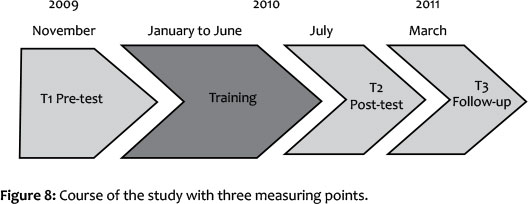
In a pre-/post-/follow-up design, the mathematical, linguistic and cognitive performance of the children was verified by trained external test administrators: in November 2009, about a year before school start, in July 2010, after finishing the training, and in March 2011, after the first school semester (cf. Figure 8).

 

 

Sample

A total of 14 kindergartens from socially and regionally different areas of the city of Essen participated in the study with 248 pre-school children. Eight kindergartens implemented the programme with 134 children. Six kindergartens, with 118 children were willing to have the pre-test carried out in their institutions, but were not interested in the intervention programme. It became necessary for the evaluation to reduce the experimental and control group by individual groups of children. Two institutions (N = 40) had to be excluded from the experimental group, since the kindergarten teachers did not or only occasionally took part in the training sessions. Thus, the experimental group was reduced to N = 94 children. Furthermore, interviews with the control group showed that two institutions (N = 34) ran their own mathematical support programme independently of the study. For this reason, another two groups of children had to be excluded from the analysis and the control group was reduced to N = 78 children. In addition, the study had to register a drop-out. At the follow-up, 15 children had moved house to an unknown address, seven children were deferred from starting school, and 13 children could not be reached after entering to primary school.

 

Instruments

• Pre-school mathematical ability:Based on the developmental model, the diagnostic test MARKO-D (Ricken, Fritz & Balzer, 2013) was used for the pre- and post-test. According to the number of correctly solved tasks, a level is allocated. The test shows a reliability of Cronbachs alpha = .91.

• Academic mathematical ability: For the follow-up, the test MARKO-D-1 (Fritz, Ehlert, Ricken & Balzer, in prep.; see also Fritz, Ehlert & Balzer in this journal) was used. This test for the first grade is also based on the developmental model. The items of MARKO-D and MARKO-D 1 overlap, with the first grade test containing more items on the higher levels and fewer items on the lower ones. The reliability determined by means of the described sample is Cronbachs alpha = .91.

Components of phonological information processing

Tasks related to phonological awareness:

In order to ascertain phonological awareness, the standardised testing procedure 'BISC' ('Bielefelder Screening zur Früherkennung von Lese-Recht-schreibschwierigkeiten', Jansen et al., 2002, 'Screening for literacy') and its sub-test 'segmenting syllables' (10 tasks) were used. Differentiating and identifying syllables are among the most powerful auditory functions, according to Kiese-Himmel & Reeh (2009). Here, spoken words had to be partitioned into pronounced syllables with the help of clapping at each syllable (e.g. Au-to-bahn). The tasks related to phonological awareness show a reliability of Cronbachs alpha = .86.

Tasks related to phonological working memory:

The performance of the phonological working memory is among others operationalised through the memory span for number lines (rehearsal process, cf. Hasselhorn, Grube & Mähler, 2000). Therefore, tasks of repeating number lines (2-9, 3-8-6-, 3-4-1-7, etc.) were required here. Phonological working memory performance can furthermore be ascertained through the reproduction of pseudo words (nonsense words) - for this, tasks of repeating senseless syllable sequences of increasing length are used (Baddeley et al., 1998). The differentiation of phonologically aware and less aware children through the repetition of pseudo words has been proven for various languages in several studies (cf. Girbau & Schwartz, 2007). Here, pseudo words such as e.g. 'queck', 'yib-sott', 'rub-loh-piz', etc. were used. The reliability of the phonological working memory performance is Cronbachs alpha = .77.

 

Results

Ascertaining the mathematical performance data

The mathematical performance was ascertained with two different test procedures (MARKO-D and MARKO-D1) at three measurement points in time. In order to be able to compare the development in performance, the mathematical assessments were represented on a one-dimensional Rasch scale (cf. article of Fritz, Ehlert & Balzer in this journal). Since both test procedures overlap with a large number of items, these overlapping items serve as anchor items, similar to studies with a multi-matrix design. The calculated Rasch model shows the following reliabilities: WLE Person separation - Reliability = .934 (WLE = Weighted Likelihood Estimator) and EAP/PV - Reliability = .927. Almost all items show infit values between 0.8 and 1.2, only three items had infit values between 1.2 and 1.3. All in all, this means that the items fulfil the criteria of the Rasch model (cf. Wright & Linacre, 1994; Adams & Wu, 2002; Rost, 2004) and capture a one-dimensional construct. For the following analyses, the WLE value will be used to estimate the competence at individual level.

Analysis of the phonological scales

As discussedin an earlier section, thereis a theoretical distinction between phonological awareness, and the function and performance of the phonological loop. How clearly these two performance areas overlap is still a matter of discussion in the literature, and so far, there has been no apparent consensus. Here, we presuppose two different constructs that have a large overlap in performance. This overlap will be verified in order to analyse the existing connection between the performances and determine a possible multi-collinearity.

An analysis of correlation shows mostly medium-high relations between the two scales: r = .135, p < .05 and r = .357, p < .01. Only between the scale segmenting syllables (phonological awareness) and repeating number lines forward (phonological loop) there is no significant connection.

In a next step, a factor analysis of the scales of the phonological loop and phonological awareness was conducted. The factor analysis confirmed the existing multi-collinearity. This means that the explaining variables correlate highly. In the analysis of the main components all scales comprised one factor. Thus, there is a high overlap of the various performances. This factor thus obtained will be called phonological language processing in the following, regarding the individual scale requirements described under the section above 'Instruments'.

Based on this result, the items of phonological language processing will be subject to a Rasch analysis items in order to be able to revert to a common test theory, the item-response theory for further data analysis. Since the phonological language processing performance was also measured at three measurement time points, ability scores will be calculated for each measurement time point by means of a multi-matrix design. All in all, the Rasch model exhibits satisfactory reliabilities: WLE Person separation -reliability = .858 (WLE = Weighted Likelihood Estimator) and EAP/PV - reliability = .854. All items show infit values between 0.8 and 1.2. The dichotomous items thus capture a one-dimensional construct so that the WLE value for the estimation of competence on individual level can be used in the following to verify the hypotheses in the research questions.

Influence of phonological language processing on the mathematical abilities and their increase

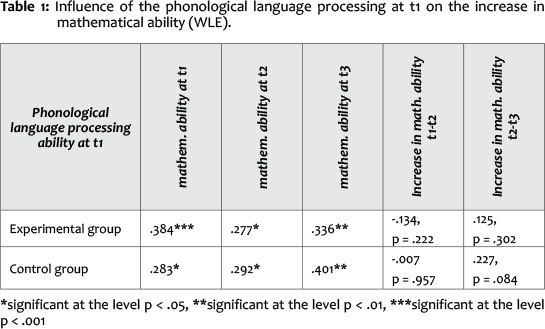
When examining the connections between phonological language processing performance at t1, and the mathematical abilities measured at the three different measurement time points, and the increase in mathematical abilities, it becomes obvious that the phonological language processing ability and the mathematical abilities correlate at all measurement points in time. However, there are no connections between the phonological language processing ability at t1 and the increase in mathematical ability between the measurement time points t1 and t2as well as t2 and t3 (see Table 1).

 

 

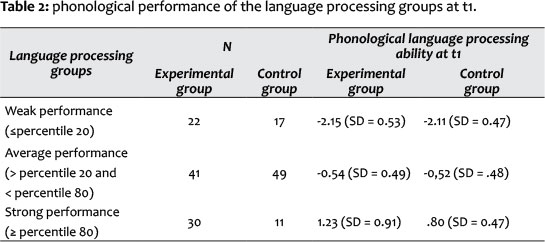
In a next step, we will now analyse whether the extent of phonological language processing leads to differences in the increase of mathematical ability during the intervention phase. For this, phonological language processing groups are formed. All children whose phonological language processing ability lies at < the 20^th percentile are assigned to a phonologically weak language processing group, according to their inclusion in the experimental group or the control group. If their language processing ability lies at > the 80^th percentile, the children are assigned to a phonologically strong language processing group. The other children form the average language processing group (see Table 2).

 

 

By means of a variance analysis with repeated measurement, with mathematical ability at the individual measurement time points as inner-subject-factor ('measurement time point') and the phonological language processing group assignment as between-subject-factor ('group assignment'), the influence of the extent of the phonological performance on the mathematical development will now be analysed. For the experimental group, there is a significant effect for the factor measurement time point directly after completion of the training, F(1, 82) = 131.473, p < .001, part. eta² = .62, yet there is no significant effect for the factor group assignment, F(2, 82) = 0.945, p = .393, part.eta2 = .02. Thus, the children of the experimental group show a significant increase in performance regarding their mathematical development from t1 to t2, while the belonging to a phonological language processing group does not have a significant influence on the mathematical development. This means that significant supportive effects can be observed even for those children with weak phonological language processing performance.

Influence of the programme on the development of phonological language processing

As the supportive programme Mina and the Mole represents a strongly language-oriented intervention, it has been assumed that the learning support does not only have a positive influence on mathematical concept acquisition, but also on phonological language processing. We will check in a last step to what extent the programme also supports phonological language processing.

For this, the phonological language processing increase of the experimental and control group children between the measurement time points t1 and t2 is compared. There are slight effects in favour of the experimental group of the weak phonological language processing group (t(33) = .856, p = .398, d = .29), although there are no significant differences to the control group. However, it must be stressed that the children within the average language processing group do differ (t(74) = 2.006, p < .05, d = .46). The children of the experimental group here achieve a higher phonological language processing increase than the children of the control group, M_Ex= .86 (SD = 1.3), M_Ex= .34 (SD = 1.0). In the strong language processing group, there are no differences between the phonological language processing increase of the children, t(34) = -.927, p = .927, d = -0,03.

 

Discussion

In this article, we introduced the learning support programme, Mina and the Mole, which is based on an empirically verified developmental model. The short- and long-term effects of the programme on the mathematical abilities of children aged 5 to 7 have already been proved in an evaluation study. Since the programme is strongly language-oriented, the present study examined the phonological language processing performance of children in more detail. Here, new research aspects were particularly interesting. On the one hand, the question of whether the language-oriented approach might be detrimental to the mathematical support effects with linguistically weak children, and, on the other hand, the question whether children might even benefit from such a language-oriented mathematical programme regarding their phonological language processing performance.

In this study, a connection was found for 5- to 7-year-old children between mathematical abilities and phonological language processing performance, which consisted here of a combined scale of performances of phonological awareness and phonological working memory. The children showed mathematical abilities that were consistent with their respective phonological language processing performances. This means that children with lesser language processing performances also showed lesser mathematical abilities whereas strong language processing performances were connected with well-developed mathematical abilities. This result confirms the findings of numerous other studies.

Considering the strong language-orientation of the programme Mina and the Mole, can linguistically weak children also increase their mathematical performance?

There were no connections between phonological language processing ability and an increase in mathematical ability. In order to examine a possible influence of phonological language processing on an increase in mathematical ability performance-related immediately after the intervention phase, all children were assigned to three groups according to their phonological language processing performances - weak, average, or strong - at the first measurement time point. It was found that all children of the experimental group showed a significant increase in their mathematical abilities independent of which phonological language processing group they belonged to. This means that the extent of the phonological language processing performance did not have a significant influence on the increase in mathematical ability. Regarding the programme, we come to the positive conclusion that its strong language-orientation does not constitute an obstacle for the children: children with weak language processing performances improved their mathematical abilities as significantly as children with average or strong language processing performances did.

Can children profit from the strong language-orientation of the programme also regarding their phonological language processing?

Apart from the conclusion that the language-orientation of Mina and the Mole is not a disadvantage for the acquisition of mathematical understanding, the study furthermore showed that the programme could even have a supportive effect on the phonological language processing performances of the children. Although the programme does not offer explicit exercises that systematically support phonological awareness in the broader sense or the phonological working memory, language has a considerable share in it, in the stories, in the picture book, in the instructions, when playing, reflecting, and working with it in every-day-life. In addition, mathematical contents are often presented in connection with language through games, songs, or counting-out rhymes in the programme. As a consequence, unspecific secondary effects were expected from the programme in the experimental group. The analysis in this regard of the three performance groups showed that the children from the experimental group with the average phonological language processing performances (performances between > percentile 20 and < percentile 80) displayed a significant increase in performance in their phonological language processing immediately after the programme. Thus, these children could also benefit considerably from the mathematics training regarding their phonological skills. Even for the children of the experimental group with the weak phonological language performances slight effects could be shown and therewith tendencies for the success of the programme. Although the kindergarten teachers did not focus on consciously imparting linguistic aspects when doing the training, the accompanying verbalization of learning mathematics seems to be advantageous for the average and weak children and to lead to an improvement of their phonological language processing performances. With a view on further learning, the phonological secondary effect of the programme could be an enriching opportunity to prevent and compensate difficulties when learning to read and write for weak and average children.

Finally, another important purpose of the programme should be noted. As we pointed out, the supportive programme Mina and the Mole offers effective opportunities for children to acquire and improve basic arithmetic competencies at pre-school age. But since the training targets four to eight year old children, it is not only suitable for education in kindergarten but also for the support of mathematical weaker children in grade one and two at primary school. For an on-going development support, the training can be started with younger kindergartners and pre-schoolers, and can be continued in primary school. So pupils can go on with their mathematical learning, using the familiar training materials. Such a continuous, cooperative work with the programme undoubtedly makes the education of both institutions more effective. Thus, the programme could contribute a successful and smooth transition from kindergarten to primary school.

 

References

Adams, R. & Wu, M. 2002. PISA 2000 Technical Report. Paris: OECD. Retrieved from http://www.oecd.org/dataoecd/42/20/1841899.pdf (accessed 4 July 2012).

Alloway, T.P., Gathercole, S.E., Willis, C. & Adams, A.-M. 2004. A structural analysis of working memory and related cognitive skills in young children. Journal of Experimental Child Psychology 87:85-106.         [ Links ]

Alloway, T.P., Gathercole, S.E., Adams, A.-M., Willis, C., Eaglen, R. & Lamont, E. 2005. Working memory and phonological awareness as predictors of progress towards early learning goals at school entry. British Journal of Developmental Psychology 23(3):417-426.         [ Links ]

Anthony, J.L., Lonigan, C.J., Driscoll, K., Phillips, B.M. & Burgess, S.R. 2003. Phonological sensitivity: A quasi-parallel progression of word structure units and cognitive operations. Reading Research Quarterly 38(4):470-487.         [ Links ]

Anthony, J.L., Lonigan, C.J., Burgess, S.R., Driscoll, K., Phillips, B.M. & Cantor, B.G. 2002. Structure of preschool phonological sensitivity: Overlapping sensitivity to rhyme, words, syllables, and phonemes. Journal of Experimental Child Psychology 82:65-92.         [ Links ]

Aunola, K., Leskinen, E., Lerkkanen, M.-K. & Nurmi, J.-E. 2004. Developmental Dynamics of Math Performance from Preschool to Grade 2. Journal of Educational Psychology 96(4):699-713.         [ Links ]

Baddeley, A.D. 2003. Working memory and language: An overview. Journal of Communication Disorders 36(3):189-208.         [ Links ]

Baddeley, A.D., Gathercole, S.E. & Papagno, C. 1998. The phonological loop as a language learning device. Psychological Review 105(1):158-173.         [ Links ]

Baumert, J., Klieme, E., Neubrand, M., Prenzel, M., Schiefele, U., Schneider, W., Stanat, P., Tillmann, K.-J. & Weiß, M. (Eds.) 2001. PISA 2000. Basiskompetenzen von Schülerinnen und Schülern im internationalen Vergleich. Opladen: Leske + Budrich.         [ Links ]

Bowey, J.A. 1996. On the association between phonological memory and receptive vocabulary in five-year-olds. Journal of Experimental Child Psychology 63(1):44-78.         [ Links ]

Bryant, P. & Bradley, L. 1985. Children's reading problems. Oxford: Blackwell Publishers.         [ Links ]

Bryant, P.E., MacLean, M., Bradley, L. & Crossland, J. 1990: Rhyme and Alliteration, Phoneme Detection, and Learning to Read. Developmental Psychology 26(3):429-438.         [ Links ]

Case, R. & Okamoto, Y. 1996. The role of central conceptual structures in the development of children's thought. Monographs of the Society for Research in Child Development, 61(1-2, Serial No. 246). Chicago: University of Chicago Press.

Clarke, B., Clarke, D., Grüßing, M. & Peter-Koop, A. 2008. Mathematische Kompetenzen von Vorschulkindern: Ergebnisse eines Ländervergleichs zwischen Australien und Deutschland. Journal für Mathematik-Didaktik 29(3/4):259-286.         [ Links ]

Clements, D.H. & Sarama, J. 2007. Effects of a Preschool mathematics Curriculum: Summative Research on the Building Blocks Project. Journal for Research in Mathematics Education 38(2):136-163.         [ Links ]

Costard, S., Springer, L. & Schrey-Dern, D. 2007. Störungen der Schriftsprache: Modellgeleitete Diagnostik und Therapie. Stuttgart: Thieme.         [ Links ]

Cutting, L.E. & Denckla, M.B. 2001. The relationship of rapid serial naming and word reading in normally developing readers: An exploratory model. Reading and Writing: An Interdisciplinary Journal 14:673-705.         [ Links ]

Dehaene, S. 1997. The number sense: How the mind creates mathematics. New York: Oxford University Press.         [ Links ]

De Smedt, B., Janssen, R., Bouwens, K., Verschaffel, L., Boets, B. & Ghesquiere, P. 2009. Working memory and individual differences in mathematics achievement: A longitudinal study from first grade to second grade. Journal of Experimental Child Psychology 103(3):186-201.         [ Links ]

Ehmke, T., Siegle, T. & Hohensee, F. 2005. Soziale Herkunft im Ländervergleich. In M. Prenzel, J. Baumert, W. Blum, R. Lehmann, D. Leutner, M. Neubrand, R. Pekrun, J. Rost & U. Schiefele (Eds.), PISA 2003. Der zweite Vergleich der Länder in Deutschland - Was wissen und können Jugendliche?, 235-268. Münster: Waxmann.         [ Links ]

Feigenson, L., Dehaene, S. & Spelke, E. 2004. Core systems of number. Trends in Cognitive Sciences 8(7):307-314.         [ Links ]

Fritz, A., Ehlert, A., Ricken G. & Balzer, L. MARKO-D-1 (in prep.). Mathematik- und Rechenkonzepte für die 1. Klasse - Diagnose. Göttingen: Hogrefe.         [ Links ]

Fritz, A. & Ricken, G. 2008. Rechenschwäche. München: Reinhardt.         [ Links ]

Fthenakis, W.E., Schmitt, A., Daut, M., Eitel, A. & Wendell, A. 2009. Natur-Wissen schaffen. Band 2: Frühe mathematische Bildung. Troisdorf: Bildungsverlag EINS.         [ Links ]

Fuson, K.C. 1988. Children's counting and concepts of number. New York: Springer.         [ Links ]

Fuson, K.C. 1992. Research on learning and teaching addition and subtraction of whole numbers. In G. Leinhardt, R. Putnam & R.A. Hattrup (Eds.), Analysis of arithmetic for mathematics teaching, 53-187. Hillsdale, NY: Erlbaum.         [ Links ]

Gathercole, S.E., Willis, C. & Baddeley, A.D. 1991. Differentiating phonological memory and awareness of rhyme: Reading and vocabulary development in children. British Journal of Psychology 82(3):387-406.         [ Links ]

Gerlach, M., Fritz, A., Ricken, G. & Schmidt, S. 2007. Kalkulie. Diagnose- und Trainingsprogramm für rechenschwache Kinder. Berlin: Cornelsen.         [ Links ]

Gerlach, M. & Fritz, A. 2011. Mina und der Maulwurf. Frühförderbox Mathematik. Berlin: Cornelsen.         [ Links ]

Ginsburg, H.P., Balfanz, R. & Greenes, C. 2003. Program Overview: Big Math for Little Kids (Pre-Kindergarten and Kindergarten). Palo Alto, CA: Dale Seymour Publications.         [ Links ]

Girbau, D. & Schwartz, R.G. 2007. Non-word repetition in Spanish-speaking children with Specific Language Impairment (SLI). International Journal of Language & Communication Disorders 42(1):59-75.         [ Links ]

Goswami, U. & Bryant, P.E. 1990. Phonological skills and learning to read. Hillsdale, NY: Erlbaum.         [ Links ]

Goswami, U., Ziegler, J.C. & Richardson, U. 2005. The effects of spelling consistency on phonological awareness: A comparison of English and German. Journal of Experimental Child Psychology 92(4): 345-365.         [ Links ]

Griffin, S. 2008. Number Worlds: A prevention/intervention math program for Grades PreK-8. Columbus, OH: SRA/McGraw-Hill.         [ Links ]

Grube, D. 2006. Entwicklung des Rechnens im Grundschulalter: Basale Fertigkeiten, Wissensabruf und Arbeitsgedächtniseinflusse. Pädagogische Psychologie und Entwicklungspsychologie: Bd. 52. Münster: Waxmann.         [ Links ]

Grube, D. & Hasselhorn, M. 2006. Längsschnittliche Analysen zur Lese-, Rechtschreibund Mathematikleistung im Grundschulalter: zur Rolle von Vorwissen, Intelligenz, phonologischem Arbeitsgedächtnis und phonologischer Bewusstheit. In I. Hosenfeld, F.-W. Schrader (Eds.), Schulische Leistung. Grundlagen, Bedingungen, Perspektiven, 87-105. Münster: Waxmann.         [ Links ]

Grüßing, M. & Peter-Koop, A. 2008. Effekte vorschulischer mathematischer Förderung am Ende des ersten Schuljahres: Erste Befunde einer Längsschnittstudie. Zeitschrift für Grundschulforschung 1(1): 65-82.         [ Links ]

Hasselhorn, M. 2010. Möglichkeiten und Grenzen der Frühförderung aus entwicklungspsychologischer Sicht. Zeitschrift für Pädagogik 56(2):168-177.         [ Links ]

Hasselhorn, M. & Gold, A. 2006. Pädagogische Psychologie. Erfolgreiches Lernen und Lehren. Stuttgart: Kohlhammer.         [ Links ]

Hasselhorn, M., Grube, D. & Mähler, C. 2000. Theoretisches Rahmenmodell für ein Diagnostikum zur differentiellen Funktionsanalyse des phonologischen Arbeitsgedächtnisses. In M. Hasselhorn, W. Schneider & H. Marx (Eds.), Diagnostik von Lese-Rechtschreibschwierigkeiten. Tests und Trends, Jahrbuch der pädagogischpsychologischen Diagnostik, N.F. Band 1, 167-181. Göttingen: Hogrefe.         [ Links ]

Hauser, B. & Rechsteiner, K. 2011. Frühe Mathematik: Geführtes Spiel oder Training? 4 bis 8 - Schweizerische Fachzeitschrift für Kindergarten und Unterstufe Mai 2011(5):28-30.

Hecht, S.A., Torgesen, J.K., Wagner, R.K. & Rashotte, C.A. 2001. The relations between phonological processing abilities and emerging individual differences in mathematical computation skills: A longitudinal study from second to fifth grades. Journal of Experimental Child Psychology 79(2):192-227.         [ Links ]

Hellmich, F. 2007. Möglichkeiten der Förderung mathematischer Vorläuferfähigkeiten im vorschulischen Bereich. Bildungsforschung, 4(1). Retrieved from http://www.bildungsforschung.org/index.php/bildungsforschung/article/view/61/64, accessed 5 August 2012.

Jannuzi, C. 1998. Key concepts in FL literacy: Phonemic awareness. Literacy Across Cultures 2(1):7-12.         [ Links ]

Jansen, H., Mannhaupt, G., Marx, H. & Skowronek, H. 2002. Bielefelder Screening zur Früherkennung von Lese-Rechtschreibschwierigkeiten. Göttingen: Hogrefe.         [ Links ]

Kiese-Himmel, C. & Reeh, M. 2009. Sequentielle Informationsverarbeitung bei Kindern mit und ohne auditiver Verarbeitungs- und Wahrnehmungsstörung. HNO 57(12):1285-1290.         [ Links ]

Klicpera, C., Gasteiger-Klicpera, B. & Schabmann, A. 1994. Wieweit unterscheiden sich durchschnittliche Leser mit Rechtschreibschwierigkeiten von Kindern mit Lese- und Rechtschreibschwierigkeiten? Verlauf, Art der Rechtschreibfehler und Lernvoraussetzungen. Zeitschrift für Kinder- und Jugendpsychiatrie 22(2):87-96.         [ Links ]

Krajewski, K. & Schneider, W. 2009. Exploring the impact of phonological awareness, visual-spating working memory, and preschool quantity-number competencies on mathematics achievement in elementary school: Findings from a 3-year-longitudinal study. Journal of Experimental Child Psychology 103(4):516-531.         [ Links ]

Krajewski, K., Nieding, G. & Schneider, W. 2008a. Kurz- und langfristige Effekte mathematischer Frühförderung im Kindergarten durch das Programm 'Mengen, zählen, Zahlen'. Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie 40(3):135-146.         [ Links ]

Krajewski, K., Schneider, W. & Nieding, G. 2008b. Zur Bedeutung von Arbeitsgedächtnis, Intelligenz, phonologischer Bewusstheit und früher Mengen-zählen-Kompetenz beim Übergang vom Kindergarten in die Grundschule. Psychologie in Erziehung und Unterricht 55(2):100-113.         [ Links ]

Krajewski, K. & Schneider, W. 2006. Mathematische Vorläuferfertigkeiten im Vorschulalter und ihre Vorhersagekraft für die Mathematikleistungen bis zum Ende der Grundschulzeit. Psychologie in Erziehung und Unterricht 53(4):246-262.         [ Links ]

Langhorst, P., Ehlert, A. & Fritz, A. 2012. Non-numerical and numerical understanding of the part-whole concept of children aged 4 to 8 in word problems. Journal für Mathematik-Didaktik 33(2):233-262.         [ Links ]

Langhorst, P., Hildenbrand, C., Ehlert, A., Ricken, G. & Fritz, A. 2013. Mathematische Bildung im Kindergarten - Evaluation des Förderprogramms 'Mina und der Maulwurf' und Betrachtung von Fortbildungsvarianten. In M. Hasselhorn, A. Heinze, W. Schneider & U. Trautwein (Eds.), Diagnostik mathematischer Kompetenzen. Tests und Trends - Jahrbuch der pädagogisch-psychologischen Diagnostik, N.F., Bd. 11, 113-134. Göttingen: Hogrefe.         [ Links ]

Metsala, J.L. 1999. Young children's phonological awareness and non-word repetition as a function of vocabulary development. Journal of Educational Psychology 91(1):3-19.         [ Links ]

Navarro, J.I., Aguilar, M., Marchena, E., Ruiz, G., Menacho, I. & Van Luit, J.E.H. 2012. Longitudinal study of low and high achievers in early mathematics. British Journal of Educational Psychology 82(1):28-41.         [ Links ]

Passolunghi, M.C. & Siegel, L.S. 2001. Short-term memory, working memory, and inhibitory control in children with difficulties in arithmetic problem solving. Journal of Experimental Child Psychology 80(1):44-57.         [ Links ]

Passolunghi, M.C., Vercelloni, B. & Schadee, H. 2007. The precursors of mathematics learning: Working memory, phonological ability and numerical competence. Cognitive Development 22(2): 165-184.         [ Links ]

Peucker, S. & Weißhaupt, S. 2005. FEZ - Ein Programm zur Förderung mathematischen Vorwissens im Vorschulalter. Zeitschrift für Heilpädagogik 56(8):300-305.         [ Links ]

Piaget, J. & Szeminska, A. 1965. Die Entwicklung des Zahlbegriffs beim Kinde. Stuttgart: Klett.         [ Links ]

Prenzel, M., Heidemeier, H., Ramm, G., Hohensee, F. & Ehmke, T. 2004. Soziale Herkunft und mathematische Kompetenz. In PISA-Konsortium Deutschland (Ed.), PISA 2003. Der Bildungsstand der Jugendlichen in Deutschland - Ergebnisse des zweiten internationalen Vergleichs, 273-282. Münster u.a.: Waxmann.         [ Links ]

Rasmussen, C. & Bisanz, J. 2005. Representation and working memory in early arithmetic. Journal of Experimental Child Psychology 91(2):137-157.         [ Links ]

Resnick, L.B. 1983. A developmental theory of number understanding. In H. P. Ginsburg (Ed.), The development of mathematical thinking, 109-151. New York: Academic Press.         [ Links ]

Resnick, L.B. 1992. From protoquantities to operators: Building mathematical competence on a foundation of everyday knowledge. In G. Leinhardt, R. Putnam & R.A. Hattrup (Eds.), Analysis of arithmetic for mathematics teaching, 373-429. Hillsdale, NY: Erlbaum.         [ Links ]

Ricken, G., Fritz, A. & Balzer, L. 2013. MARKO-D. Mathematik- und Rechenkonzepte im Vorschulalter - Diagnose. Göttingen: Hogrefe.         [ Links ]

Rost, J. 2004. Lehrbuch Testtheorie - Testkonstruktion. Bern: Huber.         [ Links ]

Royar, T. 2007. Mathematik im Kindergarten. Kritische Anmerkungen zu den neuen 'Bildungsplänen' für Kindertageseinrichtungen. Mathematica Didactica 30(1):29-48.         [ Links ]

Scarborough, H.S. 1998. Early identification of children at risk for reading disabilities: Phonological awareness and some promising predictors. In B.K. Shapiro, P.J. Pasquale & A.J. Capute (Eds.), Specific reading disability: A view of the spectrum, 75-119. Timonium, MD: York.         [ Links ]

Schneider, W. & Näslund, J.C. 1993. The impact of early metalinguistic competencies and memory capacities on reading and spelling in elementary school. Results of the Munich Longitudinal Study on the Genesis of Individual Competencies (LOGIC). European Journal of Psychology and Education 8:273-288.         [ Links ]

Seymour, P.H.K., Aro, M. & Erskine, J.M. 2003. Foundation literacy acquisition in European orthographies. British Journal of Psychology 94(2):143-174.         [ Links ]

Skowronek, H. & Marx, H. 1989. Die Bielefelder Längsschnittstudie zur Früherkennung von Risiken der Lese-Rechtschreibschwäche: Theoretischer Hintergrund und erste Befunde. Heilpädagogische Forschung 15(1):38-49.         [ Links ]

Steffe, L. P., Cobb, P. & Von Glasersfeld, E. 1988. Construction of arithmetical meanings and strategies. New York: Springer.         [ Links ]

Stern, E. 1998. Die Entwicklung des mathematischen Verstandnisses im Kindesalter. Lengerich: Pabst Publisher.         [ Links ]

Tunmer, W.E. & Hoover, W.A. 1992. Cognitive and linguistic factors in learning to read. In P.B. Gough, L.E. Ehri & R. Treiman (Eds.), Reading Acqusition, 175-214. Hillsdale, NY: Erlbaum.         [ Links ]

Van den Heuvel-Panhuizen, M. 2012. Mathematics education research should come more often with breaking news. Lecture given on the occasion of receiving the Svend Pedersen Lecture Award 2011. Retrieved from http://www.mnd.su.se/polopoly_fs/1.76181.1329229188!/ menu/standard/file/svendPedersenLecture_120205.pdf (accessed 4 July 2012).

Van de Rijt, B.A.M. & Van Luit, J.E.H. 1998. Effectiveness of the Additional Early Mathematics program for teaching children early mathematics. Instructional Science 26(5):337-358.         [ Links ]

Van Luit, J.E.H. & Van de Rijt, B.A.M. 1995. De rekenhulp voor kleuters: The Additional Early Mathematics Program. Doetinchem: Graviant.         [ Links ]

Van Oers, B. 2004. Mathematisches Denken bei Vorschulkindern. In W. Fthenakis & P. Oberhuemer (Eds.), Frühpädagogik international. Bildungsqualität im Blickpunkt, 313-329. Wiesbaden: Verlag für Sozialwissenschaften.         [ Links ]

Wagner, R. & Torgesen, J. 1987. The nature of phonological processing and its causal role in the acquisition of reading skills. Psychological Bulletin 101(2):192-212.         [ Links ]

Walter, J. 2009. Theorie und Praxis Curriculumbasierten Messens (CBM) in Unterricht und Förderung. Zeitschrift für Heilpädagogik 60(5):162-170.         [ Links ]

Wright, B.D. & Linacre, J.M. 1994. Reasonable mean-square fit values. Rasch Measurement Transactions 8(3):370.         [ Links ]

Wynn, K. 1990. Children's understanding of counting. Cognition 36:155-193.         [ Links ]

Ziegler, J.C. & Goswami, U. 2005. Reading acquisition, developmental dyslexia, and skilled reading across languages: A psycholinguistic grain size theory. Psychological Bulletin 131(1):3-29.         [ Links ]