Development of mathematical concepts as basis for an elaborated mathematical understanding

 

 

Annemarie Fritz^I; Antje Ehlert^I; Lars Balzer^II

^IPsychology Department, Faculty of Educational Sciences, Duisburg-Essen University and Centre for Education Practice Research, Faculty of Education, University of Johannesburg Soweto Campus, e-mail address: fritz-stratmann@uni-due.de
^IISwiss Federal Institute for Vocational Education and Training

 

 

---

ABSTRACT

A common theme of models of conceptual growth is to establish the hierarchical structures of abilities that can be interpreted along developmental lines. Integrating the literature on the development of mathematical concepts and skills in children, a comprehensive 6 level model for describing, explaining and predicting the development of key numerical concepts and arithmetic skills from age 4 to 8, is proposed. Two studies will be presented. In the first study, 1095 preschool children completed a mathematics test (MARKO-D0) based on a 5-level model. The test fitted with a one-dimensional Rasch model. The extension of the model to a sixth level was verified in a new study: 312 first-graders took part in a mathematics test based on the six levels (MARKO-D1). In order to check whether the data of both samples adhered to the principle of unidimensionality, the data of MARKO-0 and MARKO-1 were used in a common analysis for comparative purposes. The applicability of these findings for a qualitative diagnostics and an adaptive training will be discussed.

Keywords: development of mathematical concepts, numeracy, arithmetic, assessment, adaptive training, Rasch model

---

 

 

Introduction

The acquisition of complex cognitive skills such as reading, writing and calculating depends on a variety of 'building block systems' (Spelke, 2000:1233). Studies from the past three decades indicate that the brain is equipped, from birth, with domain-specific core knowledge systems, which allow for initial representations and reasoning about particular kinds of events and entities such as objects, persons, places and numerosities (Spelke, 2000).

Based on the efficiency of the core knowledge systems for numerosities children acquire first solid mathematical concepts. When children start school, they already have a 'history' of mathematical learning and are equipped with profound mathematical knowledge. In several longitudinal studies the scope and complexity of this knowledge have been shown to be key factors for the development of mathematical knowledge, and mathematical competences, at school age. Children with sound prior knowledge have a good chance of successfully using what is offered at school for their development. Children with poor previous knowledge, however, face the risk of developing difficulties in learning math (cf. Krajewski, 2003; Aunola, Leskinen, Lerkkanen & Nurmi, 2004; Landerl & Kaufmann, 2008).

Developmental models of reading and writing have promoted the diagnostics and instruction methods for these skills, as well as the support of children who have difficulties with acquiring them (e.g., Ehri, 1995). Similarly, there is no empirically validated model for the development of mathematical competences available, and the accompanying training of mathematical knowledge, at a pre-school age, is also still in its early stages. To improve this situation, it is necessary to construct a developmental model with which the performance of kindergarten children can be described qualitatively and which forms the basis for the development of adaptive training programmes.

 

Modelling mathematical development

In the past, several models for the development of mathematical competences in early childhood up to the complete acquisition of the number concept (cf. Fuson, 1988; Piaget, 1965), or even to the understanding of the positional notation system (e.g. Case, 1992; Steffe, Cobb & Von Glasersfeld, 1988), have been presented. The construction of the models is based, in each case, on systematic observations and empirical studies. Yet none of these models has been empirically tested and validated as a comprehensive and rigorous model.

A comparison of the models and research findings indicate that the theories about the key concepts that constitute early mathematical (especially numerical) knowledge and skills, do not differ substantially. There are, however, differences in the terminology, conceptualisation and differentiation of the various concepts. This leads to the question of whether these concepts can be combined into one model consistently.

With this objective in mind, theoretical assumptions and empirical findings were viewed and a hypothesis on a developmental sequence was formulated. The fundamental assumption was that the key numerical concepts develop step by step, that they are based on one another, becoming slowly more elaborate and abstract as the child develops. This idea also forms the basis of the competence-level models, which are used in large-scale assessments such as the PISA study (Programme for International Student Assessment, OECD, 1999). These models assume that a complex construct is measured and that component skills, which are based on one another, are structured hierarchically.

It is assumed that competences in one field of knowledge form a continuum in which steps or levels can be distinguished. Each step is marked by a specific concept that requires certain 'cognitive processes and activities of a special quality' (Klieme, Avenarius & Blum et al., 2003:15, translated by the authors). A hierarchical model of competence allows for a description of the performance of a child, according to a specific level in the model. If it can be asserted that the levels are arranged in a hierarchical order and are at the same time dependent on one another, then establishing which level a child has reached will amount to knowing which concepts he or she has already acquired.

 

Development of non-numerical mathematical concepts

Before children learn number-words through language and understand the meaning of numbers, they have already acquired a 'large store of non-numerical quantity knowledge' (Resnick, 1989:162). Several studies suggest that children possess primary numerical abilities. The human brain is equipped with an inborn mechanism or, at least, with very early abilities to represent quantities (Butterworth, 1999; 2005; Dehaene, 1997; Carey, 2009; Feigenson, Dehaene & Spelke, 2004; Xu, Spelke & Goddard, 2005). Recent infant studies provide evidence for these assumptions, which are further specified, both from a developmental, and a neuropsychological perspective. Feigenson et al. (2004), distinguish between two early core systems of representation: an analogue magnitude system of representation (referred to in Dehaene & Brannon (2011) as the approximate number system or ANS) and an object file system of representation (or in Dehaene & Brannon (2011), object tracking system, also OTS).

Core system 1: Approximate representation of numerical magnitude

This system allows imprecise and approximate comparisons where quantities are not represented as single, discrete units. Habituation studies demonstrate that 6-month-old infants can already distinguish illustrations of quantities, if the quantities differed markedly in a ratio of 1 : 2 (4 vs. 8 and 8 vs. 16 objects, but not 4 vs. 6 or 8 vs. 12) (Brannon, 2002: Brannon, Abbot & Lutz, 2004; Lipton & Spelke, 2003; Xu, 2003; Xu & Spelke, 2000). During their development, the 'distance effect' decreases; thus, 10-month-old infants can already distinguish quantities in a ratio of 2 : 3 (Xu et al., 2005). The capacity to compare quantities by estimating improves as children develop. However, comparisons based on such analogue magnitude representations are only ever possible by approximation (Dehaene, 1997).

By means of the simple comparison of two quantities regarding their disparity, McCrink and Wynn's (2004) research with 9-month-old infants illustrates that the infants already have a basic understanding of simple arithmetic problems such as 5 + 5, and form expectations about the results. Non-symbolic, approximate number representations are central to human knowledge of mathematics and constitute the basis for all subsequent numerical concepts (Feigenson et al., 2004).

Core system 2: Precise representations of distinct entities

The second system refers to the precise representation of small quantities (object tracking system). Spelke (2000:1233) sees the basis for this understanding in the core knowledge of objects, which enables children to -

build representations of objects as complete, connected, solid bodies, that persist over occlusion, and maintain their identity through time (e.g. Baillargeon, 1993; Spelke & Van de Walle, 1993) (Spelke, 2000:1233).

In Wynn's (1992b) famous, often cited experiment, a toy was presented, then occluded, then a second toy was shown and then also occluded. When the occluder was removed, the children saw either two or just one object. The fact that they looked at the unexpected result significantly longer, indicates that they kept track of each object over the time, and maintained distinct representations. This system is constrained, since it only serves to track and distinguish between no more than three individual elements.

A conceptual understanding of adding and subtracting can also be established in the handling of limited quantities: children comprehend additive or subtractive changes of quantities within this number range (Koechlin, Dehaene & Mehler, 1997; Wynn, 1992b). This means that an understanding of significant numerical concepts, such as comparing, adding and subtracting of quantities, is possible even before the acquisition of language.

Mathematical development based on the core systems

How important is core knowledge for the further development of mathematical competency? As Spelke states (2000:1233),

First, core systems continue to exist in older children and adults, giving rise to domain-specific, task-specific, and encapsulated representations like those found in infants. Second, core systems serve as building blocks for the development of new cognitive skills.

Two lines of development can be shown, both frequently discussed in literature: on the one hand (assuming the imprecise performance of the core concepts) the increasing elaboration of mathematical concepts in numerically imprecise contexts, and on the other hand, the development of numerically precise representations. The acquisition of number-words and digits enables the children to count precisely and to perform computations without constraints. The achievement of the verbal number-words is a prerequisite for achieving explicit knowledge about numerical concepts. However, this development does not simply evolve from the core knowledge. Learning the number-words and the counting principles requires the construction of a new representational format. This format is due to the integration of the core system-representations with the requirements of the (numerically) precise handling of numbers.

Let us consider the first developmental line of numerically imprecise concepts. Before children have command over language, they are capable of tracking increasing and decreasing changes in amount. On acquiring language, they are able to evaluate changes in quantities verbally (more/less), without having to be numerically precise. Resnick (1992:403) maintains that,

comparisons of quantities are made and inferences can be drawn about the effects of various changes on quantities, but no numerical quantification is involved.

Resnick speaks of proto-quantitative schemes, which develop intuitively. After the compare and increase/decrease schemes, children understand the part-part-whole scheme, that is, that quantities can be divided into parts and that these parts are equal to the original quantity, at about the age of four. In a series of studies it has been demonstrated that questions about the exchange of quantities in addition and subtraction problems, as well as questions about compensation and covariance, can be solved correctly at pre-school age, if the tasks are phrased in a numerically imprecise fashion (Irwin, 1996; Langhorst, Ehlert & Fritz, 2012; Sophian & McCorgray, 1994; Sophian & Vong, 1995). This also applies if the possible answers are limited to whether a quantity had increased, decreased, or remained the same.

At pre-school age, children can solve approximate arithmetic problems of all four basic arithmetic operations in a number range up to 60, when these problems are embedded in tasks requiring comparisons (Barth, LaMont, Lipton & Spelke; 2005; Barth, La Mont, Lipton, Dehaene et al., 2006). For the adding tasks, for example, the children were successively shown two point sets, which were then hidden behind an occluder. The sum of both occluded point sets had to be compared to a new, visible point set, concerning the question of which point set was the larger of the two. In all these studies, the ratio of the two sets is crucial for the probability of arriving at a correct solution. The significance of these studies lies in the fact that the operations (addition, subtraction, multiplication, and division) have to be done mentally.

The examples illustrate how ever more elaborate arithmetic concepts are constructed. The acquisition of the concepts is supported by the individual's cognitive development, experiences of daily life, language, and so one. But, these representations are essentially based on the representations of the core systems.

 

Development of pre-numerical mathematical concepts

The representations of the core systems are constrained; they are imprecise, or only allow for the representation of small quantities, if these are presented in succession. Precise numerical representations, however, only occur when each number is linked to a specific quantity, which determines the relationships between numbers that can effectively be modelled. It can be assumed, in keeping with the acquisition of the number-words and the gradual grasp of the meaning of number-words, that a new representational system is constructed when each number is associated with a specific quantity. While this is related to core knowledge, it does not simply arise from the 'core knowledge systems' (this means, it needs more than core knowledge, to develop a precise numerical system).

These considerations help to understand that the meaning of numbers is acquired in succession and that this takes children many years to learn (e.g. Spelke, 2000; Goswami, 2008; Carey, 2009; Wynn, 1992a). In studies with 2½- to 4-year-old children, Wynn (1990; 1992a) and Le Corre, Van de Walle, Brannon & Carey (2006) proved that children learn the number-word line during language acquisition, yet, this does not provide them with a representation system for the precise cardinal value of the quantities. They only recite the number words like a rhyme, but are not able to count or count out a single object (cf. Fuson, 1982). It seems that the children learn the meaning of one, then that of two, then that of three in sequence, as a means of counting out objects. As soon as they understand the meaning of 4, they also know the meaning of the other numbers in 'their' number-word chain, and can use them to count, and count out quantities. It seems that at this stage they have grasped the principle of the one-to-one correspondence of number words and objects. This development takes place within a one-year period up to the age of approximately 3½ years.

Simultaneously, with the sequential acquisition of the meaning of number words, arithmetic operations in the small number range become feasible (Jordan, Levine & Huttenlocher, 1994; Levine, Jordan & Huttenlocher, 1992). Here, the core knowledge seems to connect to the precise number concept, but it is not clear how the analogue magnitude and the object tracking systems integrate with the symbolic number system to determine precise quantities.

In a study of our own on 4- to 8-year-old children (Langhorst, Ehlert & Fritz, 2012), we provided evidence for the separate development of both systems, the core knowledge and the symbolic number system. We were able to demonstrate that skills in the numerically imprecise domain are not simply substituted by skills from the precise domain. Understanding numerical concepts in the imprecise domain continues to precede the capability to handle relevant tasks in a mathematically precise fashion (Irwin, 1996; Resnick, 1992; Sophian & McCorgray, 1994; Sophian & Vong, 1995; Langhorst et al., 2012).

In the following discussion, our own model of competences and its empirical validation for learning arithmetic in the age range of 4 to 8 is presented. Central questions for the modelling were: which precise mathematical concepts are fundamental for understanding mathematics from a psychological, as well as didactical, point of view, and how do these concepts build on one another? Our intention was to report on a study on the empirical adequacy of the model.

 

Model for the development of numerical concepts at the age of 4 to 8 years

Level I: Count Number

The first major concept in dealing with numbers is to understand number-words as count- numbers which involves the ability to count and count out small quantities. The count number concept enables children to link each number-word in succession to individual objects or their fingers - the manifestation of one-to-one correspondence. Only concretely perceivable objects can be counted by allocating one object to one number word. The counting process ends with the last number-word recited, or when the last item of the collection is reached (Steffe et al., 1988:337). The count-number is tied to the counting process - 'an awareness of plurality drives the counting activity' (Steffe, 1992:87) - but it is not connected to the quantity. The number ceases to exist for the child once the counting episode is completed. Therefore, the children start to count again when they are asked how many objects they have counted, and the recital of the number-word sequence has to start at 'one'.

In this sense, Cobb & Wheatley (1988:3) argue that,

numbers are transitory entities that have to be made and remade by actually counting and do not exist independent to the activity of counting.

In this way, small collections of objects are countable. The children can also count out a specific number of elements from a larger quantity. This can be ascertained with tasks such as 'Give me 5 discs!' The child, who will then give us 5 objects, does not yet understand the cardinal value of the number; the child does not understand 5 as 'fiveness'.

With the count number concept as a basis, an understanding of the relationship between numbers develops next. The numbers are represented as a mental number line (Case, 1992; Resnick, 1983).

Level II: Mental number line

Counting at level I is tied to the recital of the number-word line and the successive assignment of number-words to discernible and countable objects. In this way, a qualitative representation of numbers occurs, but it is unspecific and does not give any clues as to the relationships between the numbers. A change of the representation of numbers occurs only gradually. The children construct a mental number line, in which the numbers are aligned as gradually increasing quantities. The mental number line constructed in this way is at first nothing more than an ordinal representation of the number-word line.

That is, numbers correspond to positions in a string, with the individual positions linked by a 'successor' or 'next' relationship, and a directional marker on the string specifying that later positions on the string are larger (Resnick, 1983:111).

The distances between the numbers remain as yet unreflected.

 

 

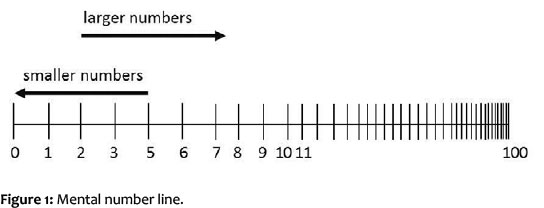
Even though Resnick (1983) stresses the point that the mental number line at this level is called a 'primitive representation of numbers', Fuson (1988) suggests, (speaking rather of a mental number list here) that this representation, nonetheless, provides the children with the basis on which the relationships between numbers become precisely determinable. The construction of a linear number line enables the children to identify preceding and succeeding numbers. As the numbers on the line become progressively larger, the numbers that appear later on the line are greater. Thus, succeeding numbers are larger, while preceding numbers are smaller. With this knowledge, numbers can be compared to each other according to their position on the number-word line. Children can now correctly answer the question: 'which number is larger, 4 or 5?'

This allows children to solve a considerable number of arithmetic problems (Case & Okamoto, 1996; Siegler & Booth, 2004). The concept of adding and subtracting is familiar to the children and could already be applied to numerically imprecise quantities (Resnick, 1992; Resnick & Singer, 1993). With the precise mental number line, simple problems of adding and subtracting can be solved. Simple problems refer to tasks of the kind: a + b = ? or a - b = ?, i.e. tasks that can be solved counting forward. When adding, both partial quantities will first be counted out completely and then the sum will be determined by counting out the two combined partial quantities completely, beginning always from 1. In subtracting the initial quantity is counted out, then the partial quantity to be subtracted is determined and moved aside, and then the remaining quantity is counted out, beginning from 1. For this, the children need the aid of materials or fingers. All quantities have to be counted out individually ('counting-all strategy' or 'count from first') (Briars & Larkin, 1984, Carpenter & Moser, 1983; Riley, Greeno & Heller, 1983). Even though the problems first have to be illustrated clearly with the help of materials at this level, verbally presented number-word problems can be solved by moving forward or backward along the mental number line, while here, too, the partial quantities have to be counted out individually on the fingers (Riley, Greeno & Heller, 1983; Stern, 1992).

Findings (e.g., Case & Okamoto, 1996; Siegler & Booth, 2004) show that understanding the number line concept is crucial for the mathematical development at primary school age, as it forms the basis on which the relationships between numbers are explored further.

Level III: Cardinality and Decomposability

In the development of numerical concepts, the acquisition of the cardinal number concept, that is, the understanding that a number-word also represents a quantity with a specific number of elements, is seen as the first major step (Piaget, 1965; Piaget & Szeminska, 1975). According to Dehaene (1997), an understanding of cardinality is neither innate nor does it unfold automatically, so instruction is required.

Real cardinal understanding requires the mental integration of the counting steps, or the elements of the counted quantity to a whole. This whole is symbolised by a number-word. If, for example, 7 objects have to be counted, each object is assigned a number-word, and all objects together will be integrated into a total quantity with the number attribute seven ('sevenness'). In this way, the number becomes a composite unit (Steffe et al., 1988), in which the 7 distinct objects are combined into one quantity. According to Piaget (1965), and Steffe et al., (1988), the quantity concept is achieved by means of the synthesis of a seriation feat and a classification feat: this constitutes an abstract construction feat in which concepts of ordinal sequences and cardinal quantities are integrated; the number-word line corresponds to the sequence of ascending cardinal units where the quantities follow a fixed order (quantity seriation). Accordingly, both an ordinal and a cardinal correspondence can be established simultaneously between two quantities. This acquired understanding becomes obvious when numbers and quantities can be compared with each other through the number of elements: 4 is less than 5 because the quantity 4 consists of fewer elements than the quantity 5.

Upon understanding number as quantity, attention is disengaged from the counting situation to the cardinal situation, in which the number-word stands for all elements. Therefore, a quantity with the value of 7 retains this quantitative characteristic, independently of where (irrelevance principle) and what (representation) is counted out (Piaget, 1965). Once it is understood that a number is a composite unit that consists of individual elements, it also becomes clear that numbers can be decomposed again.

Therefore, the acquisition of the cardinal number concept is the key prerequisite for the acquisition of effective calculating strategies. Addition problems now become solvable by counting the second quantity onto the first, without having to count the first quantity. Children who have acquired the cardinal number concept no longer rely on the 'counting-all strategy', they rely instead on the 'counting-on strategy' (Fuson, 1992). The first sum is understood as cardinal unit embedded in the whole, and the second sum can be counted on. The cardinal principle brings a first understanding that the first addend forms a part of the whole (Fritz & Ricken, 2008). As the concept of subtraction is understood, subtraction problems also become solvable by subtracting a partial quantity as a unit from the original quantity. This expanded understanding of numbers as cardinal entities, which can be composed and decomposed, can now also be applied to operational understanding: On an action level, the children begin to understand the connection between partial quantity - partial quantity and total quantity (2 and 3 together are 5). Thus, problems become solvable when they have to count from the second partial quantity to the total quantity, for example, 'I want 10 discs, I already have 4. How many are missing?'

Level IV: Class inclusion and Embeddedness

The acquisition of the part-part-whole concept is seen as the most important conceptual leap in the first years of school (cf. Fuson, 1988; Gerster, 2003; Resnick, 1983). According to Fuson, this is a complex conceptual feat that is acquired over a longer period of time. One part of it is that quantities slowly begin to be represented mentally by symbols (number-words), which can be decomposed and composed in different ways (Huttenlocher, Jordan & Levine, 1994).

Based on comprehending cardinality, the child understands that each number represents a specific quantity, which is composed of a number of elements: 'One five' can be taken as 'five ones' (Olive, 2001). According to Piaget & Szeminska (1975), understanding this 'additive composition' is a prerequisite for the child to understand class inclusion. This means that the connection between the partial quantities contained in a quantity, and the total quantity, can be reflected. As a unit of units, 5 can, for example, be seen as part of 7. If 5 is taken away from 7, 2 remain. The relationships between partial quantities and the total quantity are considered by Fuson (1992:95), as partial quantities that are 'equivalent to the sum'. An understanding of the relationships between partial quantities and the total quantity develops, in which the relationships between the partial quantities and the total quantity are seen as determined. With the part-part-whole scheme, the relationships between number triads are specified:

In the triad 2, 5, 7, for example, 7 is always the whole; 5 and 2 are always the parts. Together, 5 and 2 satisfy the equivalence constraint for the whole: 7. The relationship among 2, 5 and 7 holds whether the problem is given as 5 + 2 = ?, 7 - 5 = ?; 7 - 2 = ?, 2 + ? = 7, or ? + 5 = 7 (Resnick, 1983:115).

There is a fixed relationship between three quantities. If two quantities are known, the third one can be deduced. With this capability, problems that require any of the three quantities become solvable.

Consequently, transformations between partial quantities are possible, without a change in total quantity. The quantity '5' can be decomposed into the partial quantities '1' and '4'. By shifting (transformation) one element from one partial quantity to the other, the partial quantities '2' and '3' are formed. Quantities can be 'composed' in different ways through decomposition and transformation. The indicator of this understanding is the children's ability to find different decompositions for numbers (Baroody, 2006; Hunting, 2003; Steffe et al., 1988).

In understanding the part-part-whole concept, it becomes possible for the children to see addition and subtraction tasks as complementary, and to carry out solution procedures based on derived facts (compensation and covariance). In summary, the part-part-whole concept can be understood as the prerequisite for an integration of several algebraic principles, such as the commutative law, the complementarity of addition and subtraction, and the understanding that (natural) numbers are composite units (Stern, 1998).

Studies related to the acquisition of the part-part-whole (PPW) concept (Clarke, Clarke, Grüßing & Peter-Koop, 2008; Fischer, 1990; Irwin, 1996; Resnick, 1992; Sophian and McCorgray, 1994) have demonstrated that the concepts of part-part-whole, compensation and covariance, are already available in pre-school children, if problems do not require numerical precision. Children are only able to recognise the compensation principle in tasks like '5 + 2' and '4 + 3' numerically precisely, after some months of schooling (Baroody, Wilkins & Tiilikainen, 2003). It seems that experiences with a large variety of formal addition problems are necessary before children start to compare the results of different problems.

Riley & Greeno (1988), classified PPW word-problems of addition and subtraction and investigated their level of difficulty. The results revealed that problems that require the production of the final sum can be solved by nearly 100% of the first-graders correctly (this problem corresponds to Level II in our model). Problems that ask for the exchange of quantities or partial quantity, on the other hand, can only be solved by at most 50% of the pupils in first grade. Obviously the understanding of this concept develops in the first year of schooling. Children find problems that ask for the initial quantity even more difficult (approximately 30 to 39 %). In our analysis we found problems of that kind on level V. A replication of this study with German children led to similar results (Stern, 1998).

Level V: Relationality

The crucial concept of this level is called 'operational cardinal number concept' by Piaget (1965). For him, it reflects a deep understanding of the complex concept of the natural number and requires the grasp of cardinality, of ordinality, and of the relationship between these two concepts. The number-word line is understood as a sequence of cardinal units, in which each number in turn is an independent countable unit:

Therefore, each next word presents a cardinal number that is one larger than (using the cardinal as well as the sequence meaning), the earlier word. This cardinal sequence thus comprises both class inclusion (embeddedness within the next number) and seriation. Mastery of both latter concepts was the requirement for understanding a truly operational cardinal number for Piaget (1965) (Fuson, 1992:100).

Realising that numbers do not only represent concrete quantities, but also counting acts, that can be counted themselves, is the key cognitive process at this stage. In this way, 'composite units, whose elements symbolise counting acts' emerge (Steffe et al., 1988:338). Thus, a further level of abstraction is reached, based on which the number line concept can be further differentiated until a precise, metrical number line concept is developed, which allows the correct representation of one-, two- and later also multi-digit numbers, based on which the place-value-system concept is acquired (Campbell, 2005; Moeller, Nuerk & Willmes, 2009; Nuerk, Weger & Willmes, 2001; Nuerk & Willmes, 2005; Nuerk, Moeller, Klein, Willmes & Fischer, 2011).

Nevertheless, to reach a full understanding of the place-value-system, several further realisations are required. The number line concept states that intervals between successive numbers are of the same size (+1). Thus, numbers can also stand for a class of congruent intervals, and indicate a segment on the number line, or a relationship between two quantities (numerable-chain level; Fuson, 1992).

 

 

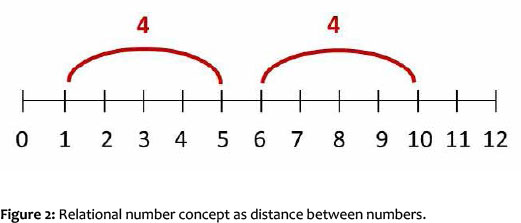
Based on this knowledge, the children now have a kind of scale at their disposal that enables them to compare quantities, and to determine the differences precisely.

 

 

On earlier levels, children are able to compare quantities regarding their cardinality, yet, these comparisons are limited to imprecise indications of direction (larger/smaller; more/less). Only the relational number concept provides the children with a scale on which they can count on a specific number of counting steps, from a random starting point. Thus, the number does not stand merely for a specific quantity anymore, but also for a distance or a number of counting steps on the number line.

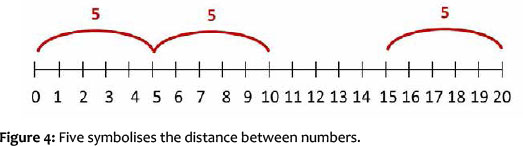
This also means that the same number of counting steps, or equally long distances on the number line, have the same cardinality. The child now understands that the distance between 0 and 5 is equivalent to the distance between 5 and 10; and vice versa, that the number 5 indicates the distance between the numbers 0 and 5 as well as the distance between the numbers 15 and 20. Similarly, when a number is doubled or halved, identical partial quantities or sequences are created. This realisation can only be used for simple doublings and decompositions (halving), on level 5.

 

 

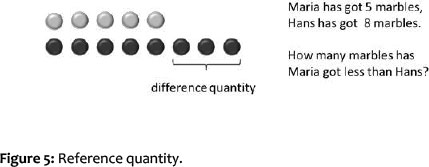
With the construction of a number as scale, or distance on the number line, relationships between numbers can also be modelled on the next higher level of abstraction. With this number concept, which Stern (1998) calls the relational number concept, relationships between quantities can be modelled. Comparison problems of the following kind are typically used to assess this relational number concept level: 'Maria has got 5 marbles. Hans has got 8 marbles. How many marbles has Hans got more than Maria?' (difference quantity unknown) or 'Maria has got 4 marbles. She has got 3 marbles less than Hans. How many marbles has Hans got?' (reference quantity unknown).

In order to solve comparison problems of this kind, the child has to be able, for example, to interpret '3 marbles less' as reference quantity, which first has to be found by determining the difference between the given partial quantity (4 marbles) and the difference quantity (3 marbles less). Such problems have a solution frequency among first-graders of between 16% and 28 % (Riley & Greeno, 1988; Stern, 1992). This means that the understanding of this concept is to be expected not earlier than in grade two.

 

 

Level VI: Units in Numbers (bundling and unbundling)

The PPW concept conveys the realisation that numbers are composite units, which can be flexibly decomposed into different partial quantities, on the one hand (8 into 1 and 7, 2 and 6, 3 and 5, 4 and 4, etc.), and into several partial quantities, on the other hand (8 into the partial quantities 1 - 3 - 4). In each case, the sum of the partial quantities is equivalent to the total quantity.

With the concept of relationality, the child realises that the distances between the numbers on the continued number-word line are always the same. Therefore, segments of the same size, or bundles, can be formed on the number line (e.g. 3 x 4). These bundles become new, abstract composite units. In the multiplication task 3 x 4, for example, 3 bundles of 4 elements each are formed, that is, 3 bundles of 4. Depending on the task, bundles of 2, 3, 4, and so on, can be formed. A bundle of 10 elements, or 10 counting steps on the number line, becomes a bundle of 10. The bundles themselves become countable units of a higher order.

 

 

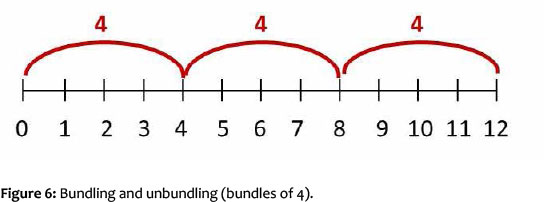
Conversely, a number can obviously also be decomposed into partial quantities of the same size, or, if presented as a segment on the number line, into partial segments (bundles) of the same size (12 : 4). In keeping with the PPW understanding that quantities can be flexibly decomposed into different or several partial quantities, a quantity can be decomposed into several partial quantities of the same magnitude and a number, as a segment on the number line, also in several partial segments of the same size.

 

 

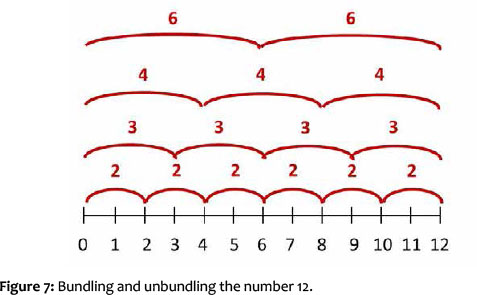
This realisation is characteristic of this developmental level: the children are able to find different decompositions of the same magnitude (bundles) for a number. Once they are able to grasp this, they are prepared for understanding division.

The fact that the number range is constructed systematically is something the children have already experienced at pre-school age, and they can recite the number line in steps of ten. By counting, even children on lower levels can count out larger quantities, and even do arithmetic operations in the number range up to 100. They count the objects one by one and write down the number determined (e.g. 35). They do not realise, however, that the 3 in the number 35 stands for 3 units of ten (Gerster & Schultz, 2004). Only after acquiring the PPW concept, and the concept of relational numbers, can the concept of bundling and unbundling of numbers be understood. This forms the basis of the place-value-system, as well as, the arithmetic operations of multiplication and division.

A profound understanding of the place-value-system, however, develops over several levels,

... the development of decimal number knowledge can be understood as the successive elaboration of the part-whole schema for numbers, so that numbers come to be interpreted by children as compositions of units and tens (and later of hundreds, thousands, etc.) and are seen as subject to special regroupings under control of the part-whole schema (Resnick & Singer, 1993:126).

On this level VI, the focus is first of all on grasping the principles of bundling and unbundling; this merely prepares the ground for understanding the place-value-system. However, the full realisation of it requires further steps.

 

Method

Operationalisation of the mathematical levels

Results of several studies are available for an empirical verification of the competence level model. Most importantly, two steps of verification can be defined. In the first step, an item pool was created according to the theoretical principles of levels 1 to 5 with a maximum of 70 items. This has been subjected repeatedly to empirical scrutiny and modified when necessary. This eventually led to the MARKO-D0 test instrument (Ricken, Fritz & Balzer, 2013) with 55 items.

MARKO-D 0 was standardised with 1 095 children aged 4 to 6 years, M = 64.6 months (SD = 7.2). The items of the one-dimensional dichotomous Rasch model show satisfactory values (weighted infit MNSQ 1±0.2 for 53 out of 55 items, weighted infit MNSQ 1 ±0.3 for 2 items), and the person reliability is at .91. The separation index of 3.26 suggests 4-5 different levels. Furthermore, the confidence intervals of the levels do not overlap, apart from a slight overlap between levels II and III. The test shows a retesting reliability of r = .89. It is also construct valid with a correlation of r = .77 with the arithmetic test OTZ. The validity was also tested with intelligence. Here, the test shows a medium correlation with the intelligence test CFT-1, of between r = .51 and r = .57, and the WPPSI-III, of between r = .41 and r = .59.

During the second step, level VI had to be verified. To do this, new items were built according to the theoretical principles for level 6, resulting in a new test-version for older children valid for all six levels. The test designed for younger children (4 - 6 years) and the one designed for the first-graders overlap in several items, the so-called anchor items. The new test version for the first grade has been tested with 312 children 86.8 months (range from 77 - 106, SD = 5.1).

Below is an overview with sample tasks for each of the six levels.

 

 

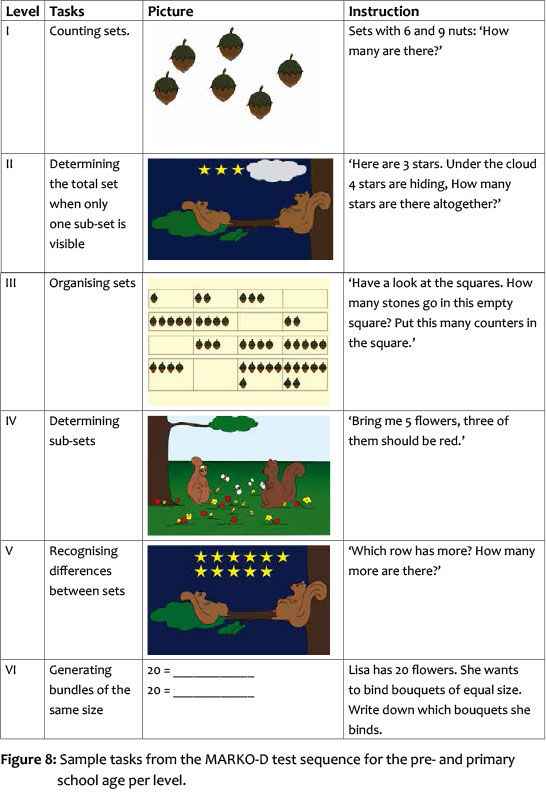
In order to design items that appeal to the children, the mathematical tasks were framed with pictures and stories about Ben and Lisa, two squirrels. Both the pictures, as well as the framing story, are merely decorative embedding. This means the children do not obtain any arithmetic or conceptual advantages for solving the tasks. Empirical testing showed that the decorative embedding does not present any advantages for children at pre- and primary school age, neither mathematical nor motivational (Ehlert, Fritz & Leutner, in prep.).

Empirical model verification

Using a probabilistic item-response theory model, the following has been assessed:

• Whether all the items form a one-dimensional cumulative scale (Research Question 1);

• Whether segments can be identified on the scale for all six levels, which each include items from (only) one particular level (Research Question 2); and

• Whether the sequence of these segments on the scale follows the sequence of levels in the model (Research Question 3).

Data analysis was based on item-response theory (IRT; e.g., Rasch, 1960; Bond & Fox, 2007; Wilson, 2004) and the software WINSTEPS 3.75 (Linacre, 2012) was used to fit the one-dimensional (1PL) Rasch model to the data. The Rasch model has been developed by the Danish mathematician Georg Rasch with the intention of bringing measurement in the social sciences closer to the standards of measurement in the natural sciences. This resulted in a test construction process of linear measures for one or more unidimensional constructs. Thus, one requirement is that the construct to be measured by the test (in our case: mathematical achievement) has to be operationalised by a set of items. It is then necessary that all items in the test really measure the construct in question. One important characteristic of the Rasch model is that in case of adequate fit-values it allows the creation of an interval scale, representing both item difficulties and personal abilities on the same scale. This means that scores (solving items correctly or not) are used to locate a person with their individual ability on this scale. To be able to create such a scale, it is also necessary that items used in the test have different item difficulties, ideally using the whole difficulty range of the construct of interest, so that learners with a high ability will be able to solve more items than learners with less ability.

As a perfectly unidimensional test is not possible in practice, a statistic is necessary to argue whether this condition is realised sufficiently for diagnostic purposes. Various model fit statistics are available. Linacre (2002) distinguishes between so-called infit- and outfit measures of model adequacy. The infit statistic is used to compare the actually observed relative solution frequency (item difficulty), with the solution probabilities, predicted on the basis of the model. The outfit statistic, on the other hand, is sensitive to learners, showing an answer pattern incompatible with the model, that is, learners who unexpectedly answer a rather difficult item correctly (e.g. by guessing), or alternately, an easy item unexpectedly incorrectly (e.g. because of careless mistakes). The precise criteria for model compatibility by means of infit and outfit are handled differently. According to Linacre (2002), poor outfit values are less important than incongruous infit values. Therefore, only infit values were considered for item selection, as has been done in the PISA 2000 study (Adams & Wu, 2002). Furthermore, critical values have to be determined for the goodness-of-fit measurements. Standardised infit- or outfit values (MNSQ), close to 1, indicate a good model fit. Higher MNSQ values indicate too low selectivity; lower MNSQ values indicate too high selectivity, and thus the presence of redundant items in the test. Wright & Stone (1979) suggest the range of 1±0.5 as limiting values for MNSQ; for tests in the high-stakes region, Wright & Linacre (1994) recommend 1±0.2, for less demanding settings 1±0.3 for the identification of well-fitting items.

Results presented here combine data from both steps, resulting in a data set of 1 407 children. The average age of the 1095 pre-schoolers (528 girls and 567 boys) was 69.49 months (range from 48 - 106, SD = 11.5), and the average age of the 312 children of grade 1 (168 girls and 144 boys), was 86.8 months (range from 77 - 106, SD = 5.1).

The examination of the model fit yielded an MNSQ infit in the range of 110.3 for 85 items. Two items had to be omitted because of insufficient infit; 83 items also met the more stringent criterion of 1±0.2. The reliability ('person reliability index') was .95. The requirements for the validity of a one-dimensional Rasch model can, therefore, be considered as fulfilled: the items form a one-dimensional cumulative scale (Research Question 1).

The detailed results of the Rasch model analysis of the item and learner properties are depicted in Figure 9 (on the following page).

 

 

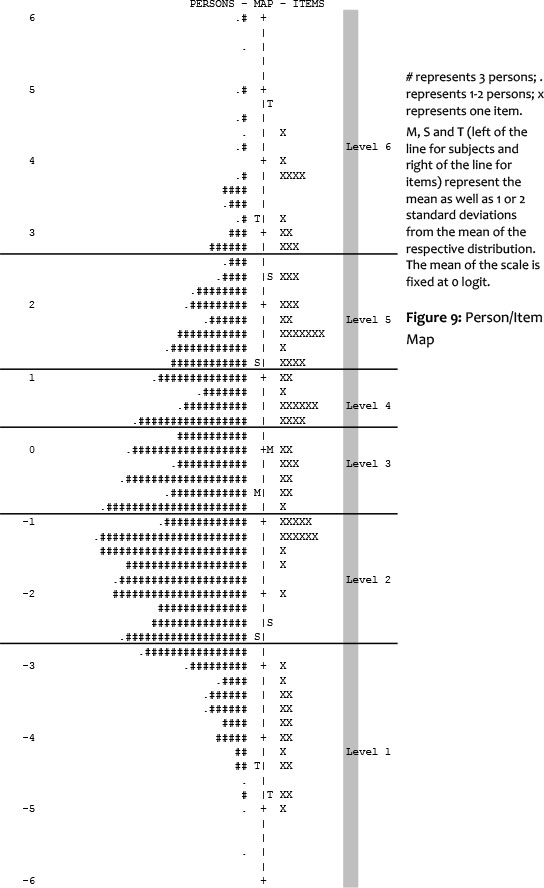
The unit of measurement is defined in logits (log odds unit). Using this unit of measurement, both the item difficulties and person abilities are measured and represented. Measures are expressed on the logit scale with the average item measure arbitrarily set to 0. On the common interval-scaled ability/difficulty scale, in our case with a range from -6 to +6 logit, the score distribution of the children is indicated on the left, and the position of the individual items on the scale, on the right. The higher a child's position, the higher their ability, and the higher the position of an item, the greater the difficulty. The higher the position of a child, compared to that of a given item, the higher is the probability that this child will solve the item correctly. Resulting measures, using the Rasch model, are linear, which means that a person with the ability of 4 logit has four times more ability than a person with the ability of 1 logit.

The Wright Map shows that it was possible to cover the entire range of the concept by means of the items administered. Five children managed to solve all items correctly; no child could not at least solve one item correctly. This confirms that there are neither ceiling, nor floor, effects in the data. The horizontal boundary lines, between the levels, were added by allocating the items according to the respective level for which they had been constructed, based on the model. The grouping of items, according to model levels, was successful. Results demonstrate that the empirical allocation of all items corresponds to the theoretically predicted proficiency level, without any exception. Thus, segments on the scale can be identified that include items which can be solved, based on one of the six numerical concepts proposed in the model (Research Question 2). Moreover, the sequences of these segments on the scale follow the sequence of levels in the model (Research Question 3).

 

Discussion

The subject of this paper is the description and empirical evaluation of a competence level model for knowledge acquisition in a particular area of mathematics, namely, arithmetic. Special attention was given to the understanding of mathematical concepts whose acquisition is a key prerequisite for the development of advanced arithmetic operations. Unlike the procedural knowledge that focuses on how to do an operation, the conceptual knowledge focuses on why this is so. More precisely, it deals with

implicit or explicit understanding of the principles that govern a domain and of the interrelations between units of knowledge in a domain (Rittle-Johnson, Siegler & Alibali, 2001).

Central questions for the modelling were the following:

• which precise mathematical concepts are fundamental for the understanding of arithmetic, and

• how do these concepts build on one another.

The starting point for such a model was the assumption that the concepts are organised hierarchically in steps, and that children develop more sophisticated mental structures step by step. Each level is thus characterised by a specific core concept.

Concepts are seen here, according to Piaget's (1928) schema, as categories of knowledge, as well as, the process of acquiring knowledge. They help to organise and interpret information. Mathematical tasks can consequently only be interpreted and worked on within the framework, and on the basis of, the respective conceptual knowledge. New experiences and insights help develop new schemes and change or modify old ones. As long as the children are, for example, only equipped with the conceptual knowledge of level II, they can only deal with addition and subtraction tasks by calculating through counting out each individual quantity starting from 1 every time. Each number-word here stands for one element of the number-word line. On acquiring the concept of cardinality (level III), they begin to understand that the number-word mentioned last represents the cardinality of the entire quantity. This means that numbers are understood as composite units; for example, the number 5 is composed of 5 elements of the quantity (fiveness of five). Once this conceptual knowledge is acquired, numbers are understood cardinally, as composite units, even if the children determine a cumulative value by counting, e.g. because they want to make absolutely sure that they have the right solution.

Based on literature concerned with early numeracy development, existing developmental models, and empirical results concerning arithmetical learning, a five-level model was created (Fritz & Ricken, 2008; Fritz, Ricken & Balzer, 2009; Fritz, Ricken, Balzer, Willmes & Leutner, submitted). This model was expanded to a sixth level in a new study. The following six levels were described, as follows:

• Level I: the ability to distinguish small sets and to count and enumerate them;

• Level II: the ability to name the predecessor and the successor of a given number on some kind of mental number line and to solve small addition tasks by counting or using the number-word sequence;

• Level III: understanding the connection of number and set in a cardinal number concept. Based on this knowledge the child is no longer forced to count all, but becomes able to count on. As a result, the first effective strategies are established. Another indication of progress is the fact that children can now understand that a number can be divided into parts;

• Level IV: understanding numbers as compositions and decompositions of other numbers provides a flexible competence that allows for forms of mathematical problem-solving, that are not available to younger children. This is modelled by the part-part-whole schema. At this level, addition and subtraction problems can be considered as composed of subset - subset - whole set;

• Level V: understanding of congruent intervals between the numbers on the number line (relational numbers). One aspect of this level is that the number sequence is now both seriated and embedded. Each word of the sequence is now an ideal identical iterable one, and each number-word is now both a word, indicating sequence, and a word, indicating cardinality - it can refer to all of the 'number words' up to and including itself. Therefore, each next number-word presents a cardinal number that is one larger than (using the cardinal as well as the sequence meaning), the earlier number word; and

• Level VI: with the concept of relationality comes the understanding that the distance between numbers on the number line sequence remains the same. Thus, it is possible to bundle numbers of the same quantity (e.g. 3 x 4). These bundles become a new abstract composite unit. The bundles themselves become countable units in a higher order, specifically the tens' bundles.

To verify the model, the theoretically modelled levels were operationalised by arithmetic tasks. As far as possible, the concepts of each level needed to be tested by different tasks, that each required different representations. To check the hierarchical organisation of the items, the data was calculated with the dichotomous Rasch model, based on the Item-Response-Theory. It was expected that all the test items that could be solved, based on one concept, would cluster on one level of competence.

As a result, and as expected, it was found that (1) the items of the test form a one-dimensional cumulative Rasch scale, that (2) items can be grouped on the scale into segments according to the six numerical concepts, and that the sequence of these segments on the scale follows the sequence of the levels as postulated in the model.

Thus, these results provide evidence for the validity of the model and indicate that the six numerical concepts do not occur arbitrarily but in a specific hierarchical order, as specified in the model. In this way, the two testing systems, MARKO-D for the preschool age and MARKO-D1 for the first grade, were created.

The advantage of such a procedure, modelled both theoretically and through tests, is that it renders statements, about the arithmetic development of a child. By means of the point values obtained, the current competence level of a child can be qualitatively determined (which represents a developmental orientation, instead of, a pure social-norm orientation). If a child's performance reaches, for example, level III, it means that he or she is about to understand the concept of cardinality, and has already understood the concepts of levels I and II. The comparison with the performance of the standardisation sample (criterial comparison), further indicates whether the child's individual performance is age appropriate, slow, or accelerated.

Usually, arithmetic tests are constructed of several sub-tests, with each sub-test focusing on one arithmetic operation (e.g. adding tasks, subtracting tasks), or presenting tasks of one level of abstraction (term problems, word problems, etc.). Good performances are evidenced by many solved items; poor performances, accordingly, by only a few solved items per sub-test. The performances in each sub-test are usually aggregated in a total value.

The following aspects of such a procedure are unsatisfactory:

1. Identical raw score sums can be composed of solved items from different sub-tests, yet show the same performance quality compared to the standardised sample.

2. The individual sub-tests contain tasks of varying difficulty, so that performances in the sub-tests are not comparable.

3. No statement is made about the independence of the various sub-tests, respectively about their commonalities and connections.

4. No support programmes/training programmes can be devised on the basis of these tests that go beyond stating that such tasks should be practiced, in which children had difficulties. Accordingly, improvements can only be shown in a higher total value (cf. Ricken, Fritz & Balzer, 2011).

In contrast, the theoretical assumptions on the hierarchically organised acquisition of arithmetic concepts, afford insights into when, and in which order, arithmetic concepts, and the associated skills and strategies, are acquired. Thus, the arithmetic development can be represented as a sequence of qualitatively distinguishable levels, from which training objectives can be determined. These involve, securing the concept the child is currently developing, and acquiring the concept of the next level. Taking these into account, both diagnostics and training can be derived from a common theory, which also enables us to qualitatively describe improvements in performance, as reaching the next higher level.

Based on the model at hand, two training programmes were developed. One was developed to support children who have difficulties concerning their development of numerical concepts and arithmetic skills (MARKO-T; Gerlach, Fritz & Leutner, 2013). MARKO-T contains 5 training modules, analogous to the first five development levels described above. As both the testing system MARKO-D and the training MARKO-T are based on the development model, the individual training needs, and learning objectives for MARKO-T, can be derived from the diagnostics with MARKO-D. In this case, the diagnostic is not merely descriptive, anymore, but also prescriptive. The implementation of the training of children with learning difficulties is discussed in the paper by Ehlert & Fritz (in this volume).

In addition to the individual training MARKO-T, we also developed the group training 'Frühförderbox Mathematik: Mina und der Maulwurf (Gerlach & Fritz, 2011) for children aged 4 to 8, which is also based on the same model. It comprises 6 training modules (see paper by Langhorst, Ehlert & Fritz in this issue). Before this training is applied, the child's current level will also be determined by means of the MARKO-D test. The training starts adapted to the diagnosed learning level. After a consolidation of the concept related to the current developmental level, the training programme then goes on to develop the arithmetic concept that follows the current one, in the model for the development of mathematical competences (zone of next development).

The implementation of such development-oriented training programmes offers opportunities for the successive acquisition of the fundamental arithmetic concepts, and the securing of acquired understanding. In pre- as well as primary school mathematical education, a training, that is coherent with the development of the child, is of significance for the prevention and solution of learning difficulties. In order that concepts can be developed with insight and stabilised, they should be presented continuously and instructively - only their mastery can be the basis for sustainable future mathematical learning.

 

References

Adams, R.J., & Wu, R. (Eds.). 2002. PISA 2000 technical report. Paris: OECD.         [ Links ]

Ansari, D. & Karmiloff-Smith, A. 2002. A-typical trajectories of number development: a neuroconstructivist perspective. Trends in Cognitive Sciences 6:511-516.         [ Links ]

Aunola, K., Leskinen, E., Lerkkanen, M.-K. & Nurmi, J.-E. 2004. Developmental dynamics of math performance from pre-school to Grade 2. Journal of Educational Psychology 96(4):699-713.         [ Links ]

Baillargeon, R. 1993. The object concept revisited: New directions in the investigation of infant's physical knowledge. In C.E. Granrud (Ed.), Carnegie-Mellon Symposia on Cognition: Visual perception and cognition in infancy, 23:265-315. Hillsdale, NJ: Erlbaum.         [ Links ]

Baroody, A.J. 2006. Why children have difficulties mastering the basic number facts and how to help them. Teaching Children Mathematics 13:22-31.         [ Links ]

Baroody, A.J., Wilkins, J.L.M. & Tiilikainen, S.H. 2003. The development of children's understanding of additive commutativity: From protoquantitative concept to general concept? In A. J. Baroody & A. Dowker (Eds.), The development of arithmetic concepts and skills: constructing adaptive expertise, pp. 127-160. Mahwah, NJ: Erlbaum.         [ Links ]

Barth, H., La Mont, K., Lipton, J., Dehaene, S., Kanwisher, N. & Spelke, E. 2006. Non-symbolic arithmetic in adults and young children. Cognition 9:199-222.         [ Links ]

Barth, H., La Mont, K., Lipton, J. & Spelke, E.S. 2005. Abstract number and arithmetic in preschool children. Proceedings of the National Academy of Sciences 102:1411614121.         [ Links ]

Bond, T.G. & Fox, C.M. 2007. Applying the Rasch model: fundamental measurement in the human sciences (2^nd ed.). Mahwah, NJ: Erlbaum.         [ Links ]

Brannon, E.M. 2002. The development of ordinal numerical knowledge in infancy. Cognition 83:223-240.         [ Links ]

Brannon, E.M., Abbott, S. & Lutz, D. 2004. Number bias for the discrimination of large visual sets in infancy. Cognition 93:B59-B68.         [ Links ]

Briars, D.J. & Larkin, L.H. 1984. An integrated model of skill in solving elementary word problems. Cognition and Instruction 1:245-296.         [ Links ]

Butterworth, B. 1999. The mathematical brain. London: Macmillan.         [ Links ]

Butterworth, B. 2005. The development of arithmetical abilities. Journal of Child Psychology and Psychiatry 46:3-18.         [ Links ]

Campbell, J.I.D. 2005. Handbook of mathematical cognition. New York: Psychology Press.         [ Links ]

Carey, S. 2009. The origin of concepts. Oxford University Press.

Case, R. 1992. The mind's staircase: Exploring the conceptual underpinning of student's thought and knowledge. Hillsdale, NJ: Erlbaum.         [ Links ]

Case, R. & Okamoto, Y. 1996. The role of central conceptual structures in the development of children's thought. Monographs of the Society for Research in Child Development 61, (1-2, Serial No. 246). Chicago: University of Chicago Press.         [ Links ]

Carpenter, T.P. & Moser, J. 1983. The development of addition and subtraction problem solving skills. In T. P. Carpenter, J. Moser & T. Romberg (Eds.), Addition and subtraction: A cognitive perspective, pp. 9-24. Hillsdale: Lawrence Erlbaum.         [ Links ]

Clarke, B., Clarke, D., Grüßing, M. & Peter-Koop, A. 2008. Mathematische Kompetenzen von Vorschulkindern: Ergebnisse eines Landervergleichs zwischen Australien und Deutschland [Mathematical competencies of pre-school children: results of a comparative study in Australia and Germany]. Journal fur Mathematik-Didaktik 29:259-286.         [ Links ]

Cobb, P. & Wheatley, G. 1988. Children's initial understandings of ten. Focus on Learning Problems in Mathematics 10(3):1-28.         [ Links ]

Dehaene, S. 1997. The number sense. Cambridge: Oxford University Press.         [ Links ]

Ehlert, A., Fritz, A. & Leutner, D. (in prep.). Decorative embedment of math problems and math performance: Do children really need nice stories and motivating pictures?

Ehri, L.C. 1995. Phases of development in learning to read words by sight. Journal of Research in Reading 18:116-125.         [ Links ]

Feigenson, L., Dehaene, S. & Spelke, E. 2004. Core systems of number. Trends in Cognitive Science 8:307-314.         [ Links ]

Fischer, F.E. 1990. A part-part-whole curriculum for teaching number in the kindergarten. Journal for Research in Mathematics Education 21:207-215.         [ Links ]

Fritz, A. & Ricken, G. 2008. Rechenschwäche. München: Reinhardt.         [ Links ]

Fritz, A., Ricken, G. & Balzer, L. 2009. Warum fallt manchen Schulerinnen und Schülern das Rechnen schwer? Entwicklung arithmetischer Kompetenzen im Vor- und frühen Grundschulalter [Why do some students have difficulties with arithmetic? - Development of arithmetical skills in pre- and primary school ages]. In A. Fritz & S. Schmidt (Eds.), Fördernder Mathematikunterricht in der Sekundarstufe I. Rechenschwierigkeiten erkennen und überwinden, pp. 12-29. Weinheim: Beltz.         [ Links ]

Fritz, A., Ehlert, A., Ricken G. & Balzer, L. MARKO-D-1 (in prep). Mathematik- und Rechenkonzepte für die 1. Klasse - Diagnose. Göttingen: Hogrefe.         [ Links ]

Fritz, A., Ricken, G., Balzer, L., Willmes, K. & Leutner, D. (submitted). Key numerical concepts at pre-school and early primary-school age: An integrative five-level model of cumulative arithmetic skills development. Early childhood research quarterly.

Fuson, K.C. 1982. An analysis of counting-on solution procedure in addition. In T.P. Carpenter, J.M. Moser & T.A. Romberg (Eds.), Addition and subtraction: a cognitive perspective, pp. 67-81. Hillsdale, N.J.: Erlbaum.         [ Links ]

Fuson, K.C. 1988. Children's counting and concepts of number. New York: Springer.         [ Links ]

Fuson, K.C. 1992. Research on learning and teaching addition and subtraction of whole numbers. In G. Leinhardt, R. Putnam & R.A. Hattrup (Eds.), Analysis of arithmetic for mathematics teaching, pp. 53-187. Hillsdale, NJ: Erlbaum.         [ Links ]

Geary, D.C. 1993. Mathematical disabilities: cognition, neuropsychological and genetic components. Psychological Bulletin 144: 345-362.         [ Links ]

Gerlach, M. & Fritz, A. 2011. Mina und der Maulwurf. Frühförderbox Mathematik. Berlin: Cornelsen.         [ Links ]

Gerlach, M., Fritz, A. & Leutner, D. 2013. MARKO-T. Mathematik- und Rechenkonzepte im Vorschul- und Grundschulalter - Training. Mathematics and arithmetics - training for developing concepts in pre-school and early primary-school age]. Göttingen: Hogrefe.         [ Links ]

Gerster, H.-D. 2003. Schwierigkeiten beim Erwerb arithmetischer Konzepte im Anfangsunterricht [Difficulties with the acquisition of arithmetical concepts in early school instruction]. In F. Lenart, N. Holzer & H. Schaupp (Hrsg.), Rechenschwäche, Rechenstörung, Dyskalkulie (S. 154-160). Graz: Leykam.         [ Links ]

Gerster, H.-D. & Schultz, R. 2004. Schwierigkeiten beim Erwerb mathematischer Konzepte im Anfangsunterricht. Bericht zum Forschungsprojekt Rechenschwäche H Erkennen, Beheben, Vorbeugen. Freiburg: Institut fur Mathematik und Informatik und ihre Didaktiken.         [ Links ]

Goswami, U. 2008. Cognitive development. The learning brain. New York: Psychology Press.         [ Links ]

Huttenlocher, J., Jordan, N.C. & Levine S.C. 1994. A mental model for early arithmetic. Journal of Experimental Psychology: General 123:284-296.         [ Links ]

Irwin, K.C. 1996. Children's understanding of the principles of covariation and compensation in part-whole relationships. Journal for Research in Mathematics Education 27:25-40.         [ Links ]

Jordan, N.C., Levine, S.C. & Huttenlocher, J. 1994. Development of calculation abilities in middle- and low-income children after formal instruction in school. Journal of Applied Developmental Psychology 15:223-240.         [ Links ]

Kaufmann, L. & Nuerk, H.C. 2005. Numerical development: current issues and future perspectives. Psychology Science 47:142-170.         [ Links ]

Klieme E., Avenarius, H., Blum, W., Döbrich, P., Gruber, H., Prenzel, M., Reiß, K., Riquarts, K., Rost, J., Tenorth, H.E. & Vollmer, H.J. 2003. Zur Entwicklung nationaler Bildungsstandards. Eine Expertise. Berlin: BMBF.         [ Links ]

Koechlin, E., Dehaene, S. & Mehler, J. 1997. Numerical transformations in five month old human infants. Mathematical cognition 3:89-104.         [ Links ]

Krajewski, K. 2003. Vorhersage von Rechenschwächein derGrundschule. Hamburg: Kovac.         [ Links ]

Landerl, K. & Kaufmann, L. 2008. Dyskalkulie: Modelle, Diagnostik, Intervention. München: Reinhardt.         [ Links ]

Langhorst, P., Ehlert, A. & Fritz, A. 2012. Non-numerical and numerical understanding of the part-whole concept of children aged 4 to 8 in word problems. Journal fur Mathematik-Didaktik 33(2):233-262.         [ Links ]

Levine, S.C., Jordan, N. & Huttenlocher, J. 1992. Development of calculation abilities in young children. Journal of Experimental Child Psychology 53:72-103.         [ Links ]

Le Corre, M., Van de Walle, G., Brannon, E.M. & Carey, S. 2006. Re-visiting the competence/performance debate in the acquisition of the counting principles. Cognitive Psychology 52:130-169.         [ Links ]

Linacre, J.M. 2002. What do infit and outfit, mean-square and standardized mean? Rasch Measurement Transactions 16:878.         [ Links ]

Linacre, J.M. 2012. WINSTEPS Rasch measurement computer program. Chicago: Winsteps.com.         [ Links ]

Lipton, J.S. & Spelke, E.S. 2003. Origins of number sense: Large number discrimination in human infants. Psychological Science 14:396-401.         [ Links ]

McCrink, K. & Wynn, K. 2004. Large-number addition and subtraction by 9-month-old infants. Psychological Science 15:776-781.         [ Links ]

Moeller, K., Nuerk, H.-C. & Willmes, K. 2009. Internal magnitude representation is not holistic, either. European. Journal of Cognitive Psychology 21:672-685.         [ Links ]

Nuerk, H.-C. & Willmes, K. 2005. On the magnitude representations of two-digit numbers. Psychology Science 47:52-72.         [ Links ]

Nuerk, H.-C., Moeller, K., Klein, E., Willmes, K. & Fischer, M.H. 2011. Extending the mental number line - A review of multi-digit number processing. Zeitschrift für Psychologie/Journal of Psychology 219:3-22.         [ Links ]

Nuerk, H.-C., Weger, U. & Willmes, K. 2001. Decade breaks in the mental number line? Putting the tens and units back in different bins. Cognition 82:825-33.         [ Links ]

Nuerk, H.-C., Wood, G. & Willmes, K. 2005. The universal SNARC effect: The association between magnitude and space is amodal. Experimental Psychology 52:187-194.         [ Links ]

OECD. 1999. Measuring student knowledge and skills. A new framework for assessment. Paris: OECD.         [ Links ]

Olive, J. 2001. Children's number sequences: an explanation of Steffe's constructs and an extrapolation to rational numbers of arithmetic. The Mathematics Educator 11:4-9.         [ Links ]

Piaget, J. 1928. Judgment and Reasoning in the Child. London: Routledge & Kegan Paul.         [ Links ]

Piaget, J. 1965. The child's conception of number. New York: Norton (originally published 1941).         [ Links ]

Piaget, J. & Szeminska, A. 1975. Die Entwicklung des Zahlbegriffs beim Kinde [Development of the number concept in children].         [ Links ] Stuttgart: Klett.

Rasch, G. 1960. Probabilistic models for some intelligence and attainment tests. Copenhagen: Nielsen & Lydiche.         [ Links ]

Resnick, L.B. 1983. A developmental theory of number understanding. In H. Ginsburg (Ed.), The development of mathematical thinking, pp. 109-151. New York: Academic Press.         [ Links ]

Resnick, L.B. 1989. Developing mathematical knowledge. American Psychologist 44:162-169.         [ Links ]

Resnick, L.B. 1992. From protoquantities to operators: building mathematical competence on an foundation of everyday knowledge. In G. Leinhardt, R. Putnam & R. A. Hattrup (Eds.), Analysis of arithmetic for mathematics teaching, pp. 373-430. Hillsdale: Erlbaum.         [ Links ]

Resnick, L.B. & Singer, J.A. 1993. Protoquantitative origins of ratio reasoning. In T.P. Carpenter, E. Fennema & T.A. Romberg (Eds.), Rational numbers: An integration of research, pp. 107-130. Hillsdale, NJ: Erlbaum.         [ Links ]

Ricken, G., Fritz, A. & Balzer, L. 2013. Mathematik- und Rechnen - Test zur Erfassung von Konzepten im Vorschulalter (MARKO-D) - ein Beispiel für einen niveauorientierten Ansatz. Empirische Sonderpädagogik 3:256-271. (Mathematics and arithmetics-test. Assessment of math concepts in pre-school aged children - an example for a level-oriented test. Journal for Special Education 3:256-271).         [ Links ]

Ricken, G., Fritz, A. & Balzer, L. 2013. MARKO-D. Mathematik und Rechnen - Test zur Erfassung von Konzepten im Vorschulalter [MARKO-D.         [ Links ] Mathematics and arithmetics - test for assessing concepts in pre-school age]. Göttingen: Hogrefe.

Riley, M.S. & Greeno, J.G. 1988. Developmental analysis of understanding language about quantities and of solving problems. Cognition and Instruction 5:49-101.         [ Links ]

Riley, M.S., Greeno, J.G. & Heller, J.H. 1983. Development of children's problem-solving ability in arithmetic. In H.P. Ginsburg (Ed.), The development of mathematical thinking, pp. 153-196. New York: Academic Press.         [ Links ]

Rittle-Johnson, B., Siegler, R.S. & Alibali, M.W. 2001. Developing conceptual understanding and procedural skill in mathematics: An iterative process. Journal of Educational Psychology 9:346-362.         [ Links ]

Siegler, R.S. & Booth, J.L. 2004. Development of numerical estimation in young children. Child Development 75:428-444.         [ Links ]

Sophian, C. & McCorgray, P. 1994. Part-whole knowledge and early arithmetic problem solving. Cognition and Instruction 12:3-33.         [ Links ]

Sophian, C. & Vong, K.I. 1995. The parts and wholes of arithmetic story problems: developing knowledge in the preschool years. Cognition and Instruction 13:469-477.         [ Links ]

Spelke, E. 2000. Core Knowledge. American Psychologist 55(11):1233-1243.         [ Links ]

Spelke, E. & Van de Walle, G. 1993. Perceiving and reasoning about objects: Insights from infants. In N. Eilan, R. McCarthy & W. Brewer (Eds.), Spatial representation, pp. 132-161. Oxford, England: Basil Blackwell.         [ Links ]

Steffe, L.P. 1992. Schemes of action and operation involving composite units. Learning and Individual Differences 4:259-309.         [ Links ]

Steffe, L.P., Cobb, P. & Von Glasersfeld, E. 1988. Construction of arithmetical meanings and strategies. New York: Springer Verlag.         [ Links ]

Stern, E. 1992. Spontaneous use of conceptual mathematical knowledge in elementary school children. Contemporary Educational Psychology 17:266-277.         [ Links ]

Stern, E. 1998. Die Entwicklung des mathematischen Verständnisses im Kindesalter [Development of mathematics understanding in children].         [ Links ] Lengerich: Pabst.

Wilson, M. 2004. On choosing a model for measuring. In E.V. Smith & R.M. Smith (Eds.), Introduction to Rasch measurement, pp. 11-42. Maple Grove, MN: JAM Press.         [ Links ]

Wright, B.D. & Linacre, J.M. 1994. Reasonable mean-square fit values. Rasch Measurement Transactions 8:370.         [ Links ]

Wright, B.D. & Stone, M.H. 1979. Best test design. Chicago: MESA Press.         [ Links ]

Wynn, K. 1990. Children's understanding of counting. Cognition 36:155-193.         [ Links ]

Wynnn, K. 1992a. Children's Acquisition of the Number Words and the. Counting System. Cognitive Psychology 24:220-251.         [ Links ]

Wynn, K. 1992b. Addition and subtraction by human infants. Nature 358:749-750.         [ Links ]

Xu, F. 2003. Numerosity discrimination in infants: Evidence for two systems of representations. Cognition 89:B15-B25.         [ Links ]

Xu, F. & Spelke, E.S. 2000. Large number discrimination in 6-month old infants. Cognition 74:B1-B11.         [ Links ]

Xu, F., Spelke, E.S. & Goddard, S. 2005. Number sense in human infants. Developmental Science 8:88-101.         [ Links ]