Core knowledge and working memory as prerequisites of early school arithmetic

 

 

Dominique Arndt^I; Katleen Sahr^I; Maria Opfermann^I; Detlev Leutner^I; Annemarie Fritz^{I, II}

^IPsychology Department, Faculty of Educational Sciences, University of Duisburg-Essen
^IICentre for Education Practice Research, Faculty of Education, University of Johannesburg, Soweto Campus. E-mail: dominique.arndt@uni-due.de

 

 

---

ABSTRACT

Recent studies showed that kindergarten children solve addition, subtraction, doubling and halving problems using the core system for the approximate representation of numerical magnitude. In Study 1, 34 first-grade students in their first week of schooling solved approximate arithmetic problems in a number range up to 100 regarding all four basic operations. Children solved these problems significantly above chance.
In Study 2, 66 first graders were tested for their approximate arithmetic achievement, working memory capacity, groupitizing, phonological awareness, naming speed and early arithmetic concepts at the beginning of first grade and again at the beginning of second grade. It appears that approximate arithmetic achievement is independent from most other cognitive variables and correlates most with other variables of the mathematical domain. Furthermore, regression analyses revealed that school success was only predicted by groupitizing and central executive capacity, but not approximate arithmetic achievement, when controlling for other cognitive variables.

Keywords: core systems of number, early math education, working memory

---

 

 

Theoretical background

Helping students understand formal arithmetic is one of the main concerns of schools worldwide. However, international studies, such as the PISA and TIMS, revealed that students in several countries, including Germany, performed rather badly in the domain of mathematics. While the German public and media were embarrassed by these results, politics reacted quickly with several reforms. 'PISA shock' still became a dictum in German language. These findings from secondary school can be generalised to primary school. The latest TIMS study showed that one third of all fourth graders did not reach the intermediate benchmark they were expected to reach with proper formal schooling (Gonzales et al., 2008). This leads us to the question: how primary schooling can affect a better learning of formal arithmetic? These basic skills are needed for later school and vocational careers.

On the other hand, latest research showed that kindergarten children have remarkable arithmetical competencies prior to formal schooling. They solve certain approximate arithmetic problems in a number range up to 100 (Barth et al., 2006; Barth, Baron, Spelke & Carey, 2009; Gilmore, McCarthy & Spelke, 2007, 2010; McCrink & Spelke, 2010), although these problems include the same basic arithmetic operations they cannot use to calculate exact results at the end of primary school. This ability has been described in the theory of numerical core systems (Feigenson, Dehaene & Spelke, 2004; Xu, 2003), which is based on the idea of an innate number sense (Dehaene, 1997). Gilmore et al. (2010) showed that early approximate addition performance predicts later precise arithmetic achievement in school. In contrast with this finding, other studies showed that working memory (Baddeley, 1986) is an important predictor of precise arithmetic achievement in kindergarten and early primary school (Bull, Espy & Wiebe, 2008; Krajewski & Schneider, 2009).

We wanted to combine both lines of research to investigate how working memory capacity and approximate arithmetic achievement predict later school success in the mathematical domain, and to discuss how these findings could help to affect young children's understanding of formal arithmetic in school.

Core systems of number and arithmetic

Feigenson et al. (2004) refer to two innate core systems based on the number sense theory of Dehaene (1997). Core system 1 allows the approximate representation of numerical magnitudes, while core system 2 is used for the precise representation of distinct individuals.

Core system 1 is used to solve comparison problems with two given sets. The distinction is rather imprecise and is based on the ratio of the magnitudes of the two sets: while a person might be able to distinguish two sets of 40 and 80 objects (ratio 4:8), there may be problems when doing the same for two sets of 70 vs. 80 objects (ratio 7:8). This just-noticeable-difference in ratio follows the Weber-Fechner law, which states that this difference is proportional to the magnitude of the stimuli. The core system is not static over the years, as the ratio that can be distinguished increases with age. By means of habituation studies Xu and Spelke (2000) showed that six-month-old children are able to distinguish sets at a ratio of 1:2. Ten-month-old children can already distinguish sets at a 2:3 ratio (Xu & Arrigia, 2007), while adults can cope with ratios of up to 7:8, though performance still gets worse the closer the ratio approaches 1 (Barth, Kanwisher & Spelke, 2003).

Current research showed that during development children learn to use core system 1 based abilities not only to solve simple comparison problems, but to solve approximate problems of all four basic arithmetic operations as well. Barth, LaMont, Lipton and Spelke (2005; Barth et al., 2006) showed that preschool children solve addition problems in a number range up to 60 above chance when those problems were embedded in comparison tasks. This means children saw the addition of two given sets and compared this sum to another given set, to indicate which one was larger. Barth et al. (2009) showed that kindergarten children and first grade students solve non-symbolic doubling (multiplication) and halving (division) problems with given sets. McCrink and Spelke (2010) expanded these results and showed that children solve problems like 'multiply by 2.5' or 'multiply by 4'. In all these studies the ratio of the two sets was crucial for solution probabilities, which indicates involvement of core system 1.

Core system 2 helps people to quickly keep track of small amounts. The exact number of objects that can be tracked by this system is a controversial issue. Antell and Keating (1983) showed that neonates up to an age of one week can distinguish sets of two and three items, but were unable to do so with bigger sets like four and six. Similarly, Feigenson, Carey and Hauser (2002) showed that ten- and twelve-month-old children do this for sets up to three items, but not for any larger sets. Balakrishnan and Ashby (1992) reanalysed data from various studies and found no evidence for the claim that a subitizing limit exists for at least up to six items. They conclude that other findings claiming the finding of such a limit just measured limited attention.

Carey (2009) on the other hand stated that the two core systems are not enough to explain how children learn to represent positive integers and understand cardinal concepts. These concepts need a precise distinction in an infinite number range, which is impossible with the limitation of the two innate core systems, as core system 1 is imprecise and core system 2 only has very limited range. Accordingly, another system of numerical representation must evolve during development, which connects sets with their respective number word and helps children to solve more complex arithmetic problems. Carey (2009) argues, that this system is culturally acquired, as it breaks the boundaries of the innate core systems. This kind of conceptual knowledge is used, e.g. in the concept of groupitizing (McCandliss et al., 2010). Groupitizing involves sets of smaller subsets (i.e. 3 sets of 3 items each, totalling 9 items), where the subsets can be subitised: children have to use addition and cardinal knowledge to determine the value of the entire set.

To sum up, it has been shown that children have some understanding of the four basic arithmetic operations prior to schooling. However, the more important question for mathematical education is whether this understanding is helpful for the learning of formal arithmetic. Gilmore et al. (2010) showed that it predicts first grade school mathematics, even when controlling for age, verbal intelligence and reading literacy. On the other hand, Holloway and Ansari(2009) found no significant correlation between school arithmetic and reaction time on approximate comparison tasks. As the current findings are inconclusive, further research is needed to understand whether core system 1 influences school mathematics and how this works, especially when controlling for the culturally acquired numerical representation system as proposed by Carey (2009).

Predictors of arithmetic achievementin kindergarten and primary school

Reflecting upon the results of the studies discussed above, we asked ourselves whether approximate arithmetic abilities are an independent system, only relying on core system 1, which would mean that different approximate arithmetic operations only correlate with each other, or if it is influenced by the cultural numerical representation system or other variables, which are known for their influence on early school arithmetic. The first variable that came to our mind was the capacity of working memory (Baddeley, 1986), since high capacity usually contributes to better math achievement (see De Stefano & LeFevre, 2004, for a review). Working memory as described by Baddeley consists of three major components. The central executive is an attention control unit (Baddeley, 1996) and is involved in complex mathematical tasks that are not fully automatised yet (Meyer et al., 2009). Approximate arithmetic problems always involve two tasks (arithmetic operation and comparison). It is possible that the central executive is involved in these problems. However, as the problems put only little demand on the working memory system and are rather automatised - children are able to do the comparison part from infancy on - it seems more likely that the main load resides in the subsidiary storage units.

The phonological loop is the storage unit for auditory information and is involved in word problems (Andersson, 2007) and keeping track of accurate intermediary results (Andersson, 2008). Since there is not much auditory information involved in core system 1 problems used in current research, phonological loop influence seemed highly unlikely. The visuo-spatial sketchpad is the storage system for visual and spatial information and important especially for early arithmetic (De Smedt et al., 2009a; Krajewski, Schneider & Nieding, 2008). As all problem relevant information is presented visually it seems reasonable that this subsystem would be involved.

As we also wanted to test whether approximate arithmetic abilities predict early school arithmetic, we had to keep in mind other variables influencing early school arithmetic. As stated above, literature indicated that a major contribution should be expected from working memory capacity. Other possible variables that predict early school arithmetic are rapid naming speed (Denckla & Rudel, 1974; Swanson & Kim, 2007), phonological awareness (Wagner & Torgesen, 1987) and preschool arithmetic skills based on the model of early arithmetic concepts by Fritz, Ricken and Balzer (2009). As approximate arithmetic and subitizing - as involved with groupitizing - are both based on the same innate number sense, we expected them to be correlated and wanted to find out which one is more important for early school arithmetic. Rapid naming speed is a measure of fast fact retrieval from long-term memory, which is very important for early school arithmetic, keeping in mind that children are asked to learn addition and multiplication tables, which is mainly fact retrieval.

Phonological awareness is a predecessor of reading and writing skills, which correlates highly with school mathematics (and most other school subjects). Culturally acquired arithmetical ideas should be taken into account, to find out if school success is based on the core systems of number or on cultural arithmetic concepts acquired prior to schooling. One such concept could be groupitizing, as introduced by McCandliss et al. (2010); another one could be the model of early arithmetic concepts by Fritz & Ricken (2009).

Research questions

In sum, there are three major issues addressed in the presented studies. First, all four basic operations (addition, subtraction, multiplication, division) are implemented in one study to test whether there is an understanding of all four basic arithmetic operations, before they are trained in school. Second, it is still unclear how the development of approximate arithmetic abilities is correlated with other cognitive variables like working memory. Third, results on the predictive value of approximate arithmetic abilities for later school success are still ambiguous and it has to be validated whether these abilities remain influential when controlling for other known predictors of early mathematic achievement.

We conducted two studies to shed some light on these issues. We carried out a cross-sectional piloting Study 1 to investigate to what extent children at school entrance age can solve approximate arithmetic problems of all four basic arithmetic operations. In Study 2, we conducted a one-year longitudinal study to investigate two questions. In a first step we analysed how approximate arithmetic achievement is influenced by working memory capacity, groupitizing, naming speed, phonological awareness and early arithmetic concepts. In a second step we analysed which of these variables predict school success one year later. By means of these studies we wanted to test the following hypotheses:

1. Study 1: (a) Children at school entrance age can solve problems of all basic arithmetic operations approximately in a number range up to 100; (b) however addition and subtraction are easier than multiplication and division.

2. Study 2: Different approximate arithmetic variables (four basic arithmetic operations) are correlated with each other and furthermore with groupitizing, visuo-spatial sketchpad capacity and early arithmetic concepts, but not with naming speed, phonological loop or central executive capacity or phonological awareness.

3. Study 2: Approximate arithmetic achievement predicts school success one year later, even when controlling for other variables (working memory, core system 2, naming speed, phonological awareness, and early arithmetic concepts).

 

Study 1

In Study 1 we investigated whether children at school entrance age can solve approximate arithmetic problems of all basic operations above chance.

Method

Sample & Procedure. N = 34 first-grade students (17 boys, 17 girls) aged 70 to 90 months (M = 79.3, SD = 4.1) from a German primary school were tested within three weeks after their first day in school. Testing was conducted in individual settings for about 3040 minutes, respectively. All problems were presented on a laptop with a screen size of 10 inches and a resolution of 1024x600 pixels using Microsoft PowerPoint.

Material. We used approximate problems of all four basic arithmetic operations in a number range up to 100. Multiplication and division problems were preceded by two example problems to help children understand what they were expected to do.

Children received 24 addition, 21 subtraction, 16 multiplication problems (8 by 2 and 8 by 3), and 16 division problems (8 by 2 and 8 by 3). On each trial the children saw an animated arithmetic episode with two cartoon characters having different amounts of dots and they had to decide which character had more (Figure 1).

 

 

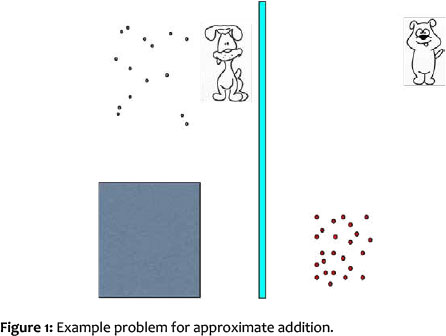
During addition problems children saw two sets of blue dots falling behind an occluder on the left side, afterwards they were shown a set of red dots on the right side and had to decide which character had more dots. Addition problems were the same as those that Gilmore et al. (2010) used. For subtraction, a blue set of dots fell behind an occluder; afterwards some blue dots moved out of the occlusion and were taken away. Now children were presented a red set for the other character and had to decide who had more.

During multiplication problems two (or three) cartoon characters were shown with a set of dots on the left side of the screen. However, children could only see one character's blue set of dots, because the other sets were hidden behind an occluder from the very beginning, but they were told that the other character(s) had the same amount of dots behind this occluder. Afterwards the character to the right got a red set of dots and children had to compare who had more, the two (three) characters to the left or the one character to the right.

During division problems there were also two (or three) characters on the left side of the screen. These characters had a set of blue dots, which they wanted to share equally. On the right side of the screen was a single character with a set of red dots. Children were asked (example for two characters to the left): 'If this one [pointing to the leftmost character] leaves the scene and takes his dots with him, who has more: This one [pointing on remaining character on the left side] or that one [pointing on the character to the right]?'

All approximate arithmetic problems can be found in Appendix A.1. Across trials the dot arrays differed by ratio (4:5, 4:6, 4:7). Children had to indicate the correct solution by pointing on a character to the left or to the right. Within each problem category for 50% of the problems the correct response was left and vice versa, the sequence of correct left/right responses following a random order. We also tested for several alternative, non-arithmetic strategies in Appendix A.1 similarly to Gilmore et al. (2010).

Results and discussion

We obtained achievement scores for each participant for approximate arithmetic problems by computing relative frequencies of correct solutions within problem categories. Average achievement for all problem categories is presented in Table 1. T-tests were conducted to test whether means differed significantly from guessing probability (50%). Children solved all problems above chance and without relying on non-arithmetic strategies (see Appendix A.1), with some exceptions for subtraction problems. As children solved all problems above chance, our data are in line with Hypothesis 1a.

 

 

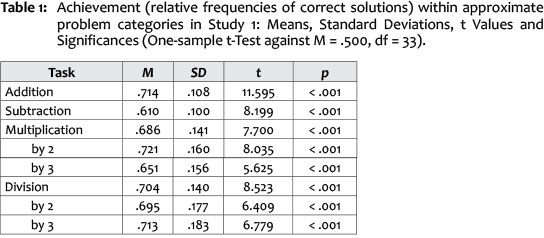
Study 1 was conducted as a pilot study to find out which approximate arithmetic operation might possibly have predictive value for later mathematical school success. We decided to omit subtraction problems from Study 2 with regard to lowest solution probabilities and non-arithmetic strategy analyses (Appendix A.1)

 

Study 2

Study 2 was conducted to research how approximate arithmetic achievement is correlated with cognitive variables and whether it has predictive value for later school mathematics achievement when controlling for other known determinants of individual differences in mathematics achievement.

Method

Sample & Procedure. N = 71 first-graders (38 boys, 33 girls) aged 65 to 84 months (M = 76.5; SD = 4.3) from German primary schools were tested during the initial four weeks of schooling. The testing took place in two individual sessions of 30-40 minutes each. Problems were presented computer-based or using paper and pencil (see below). N = 66 (34 boys, 32, girls) of these children were tested again for their curriculum-based mathematic achievement at the beginning of second grade, exactly one year after the first testing. Five children from the initial sample could not be tested again because they left their respective schools. All statistics were computed with the sample of 66 persons. We computed factor scores from the respective subtests for phonological awareness, as well as phonological loop, visuo-spatial sketchpad, and central executive capacity.

Material. Children received the same computer-based addition (24 items, a = .630), multiplication (16 items, a = .242) and division (16 items, a = .560) problems that were used in Study 1. Furthermore, groupitizing as a measure of culturally acquired cardinal knowledge, was assessed computer-based too (21 items, a = .763): We computed a mean precision score, but did not assess reaction time. Up to seven unsorted dots were presented on the computer screen for exactly one second. Afterwards children had to indicate the amount they had just seen. All children were able to operate in a number range up to 10, thus number knowledge was not a problem.

Working memory capacity was assessed with its three components as described by Baddeley. Phonological loop capacity was assessed by two different tasks, digit span forward and repeating of artificial words. During the digit span tasks, children are told increasing spans of numbers (1 to 9), which they had to repeat immediately afterwards. The same applies for the pseudowords, which consist of meaningless syllables (i.e. rub-loh-piz). Altogether, the phonological loop scale had 37 items. Reliability was satisfactory (α = .78). The visuo-spatial sketchpad capacity was assessed with Corsi blocks and matrices tasks. Corsi blocks are nine red wooden blocks presented on a 210x297 mm wooden plate. Blocks are tapped by the instructor with increasing span length, and children have to repeat the tapping immediately afterwards. During the matrices tasks children are given an empty 4x4 matrix on a sheet of paper. Then different 4x4 matrices are presented to the child, with some fields coloured in grey. These have to be indicated on the empty matrix after presentation. Altogether, the visuo-spatial sketchpad was assessed with 42 items with good reliability (α = .79).

Central executive capacity was assessed with three tasks, colour span backward, digit span backward and listening span. Colour span backward tasks show a pirate walking past two (or three) coloured treasure chests. Children are instructed 'Here is a yellow chest and afterwards he passes the blue one. Yellow - blue' and asked 'Now how is he going back?', which requires the answer 'blue - yellow'. The coloured chests are used for exemplification reasons only and are not shown during the assessment. Digit span backward works like digit span forward (digits 1 to 9), but children have to repeat the digits backward. During the listening span tasks children are asked - with increasing span - two up to five simple questions, which they have to answer with 'yes' or 'no' (i.e. 'Is a mouse grey? [...] Is a crocodile red? [...]'). After each span, children have to repeat the colours of all sentences included in this span in the correct order (i.e. 'grey - red'). The central executive scale had 35 items with a reliability of α = .73.

During the naming speed tasks children were presented two 4x4 picture sheets with 16 pictures. Each picture represents a one-syllable word, which children have to name as fast as possible. The number of correct answers and solution time are assessed and combined into one efficiency-score, according to Paas & Van Merriënboer (1993).

Phonological awareness was tested with two subtests. The first subtest was to partition words into their syllables and consisted of 10 items (a = .71). Children are told a word and have to repeat it by clapping their hands for each syllable of the word. The second subtest tested their ability to determine whether two words rhyme or do not. This test consisted of 10 items as well (α = .67).

Early arithmetic concepts were assessed with a screening test based on a five-level model proposed by Fritz, Ricken and Balzer (2009). The test consists of 18 items and assesses precise arithmetic problem solving (see Appendix A.2). It is scalable, according to the Rasch model, with a WLE person separation reliability of .86. School arithmetic achievement at the beginning of second grade was tested with the Demat 1+ test (Krajewski, Kuspert & Schneider, 2002). The test includes math problems for most curriculum topics of German first grade mathematics (36 items, α = .88).

Results and discussion

Average achievement scores for approximate arithmetic problem categories, as well as means and standard deviations of all other non-standardised variables are presented in Table 2. Groupitizing is a percent correct score. Early arithmetic concepts and 2^nd grade arithmetic achievement are raw scores of the respective tests. Central executive, visuo-spatial sketchpad, phonological loop, naming speed and phonological awareness were z-standardised for the sample of 71 children, as a result of computing factor or efficiency scores. We calculated correlation coefficients to explore the association between the different tasks and problem categories (see Table 3). As expected all approximate arithmetic variables correlated significantly with each other. We interpret this as a sign of inner coherence within the approximate number system above problem categories.

 

 

 

 

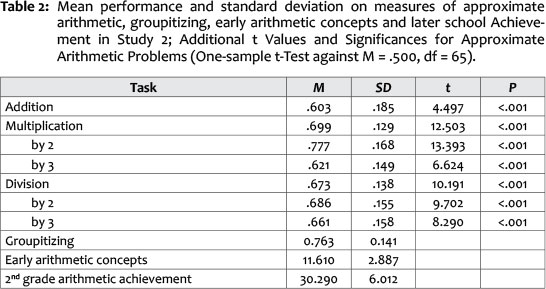
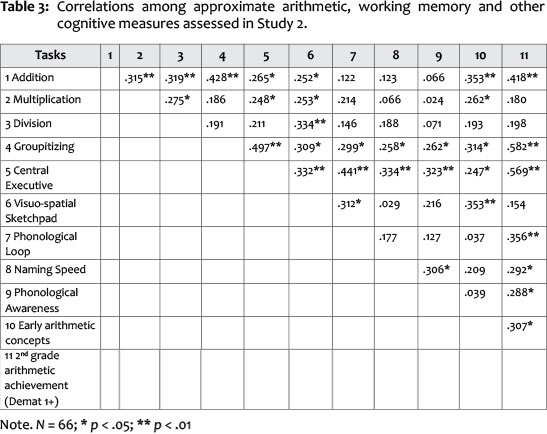
In terms of cognitive variables our expectations were roughly met, as the approximate measures correlated with visuo-spatial sketchpad and central executive capacity. The low correlation with the central executive was not expected, but as stated earlier, it could be that these problems, as they impose dual task load, are not automatised enough to run without any central executive involvement. We interpret this as a sign that children just recently acquired the concepts of the four basic arithmetic operations and were not able to automatise these concepts. However, the low correlations with the three working memory components might reflect the low reliabilities of the approximate arithmetic scales - the exact answer remains unclear. Our groupitizing measure only correlated with addition, but not division and multiplication problems. We interpret this as a matter of training, because groupitizing involved the ability to subitise smaller subsets and add those. This correlation can be seen as a clue for the idea that these children have some basic cardinal understanding of numbers (Fritz & Ricken, 2009), which allows them to simultaneously capture and add the sets they see in a half second. This idea is supported by the assertion that the early arithmetic concepts variable, which measures this conceptual understanding, is also correlated with approximate addition and groupitizing. On the other hand, this correlation indicates that approximate arithmetic does not only involve the comparison of core system 1, but also some culturally acquired skills. We did not expect significant correlation between approximate arithmetic variables and naming speed as well as phonological awareness and these expectations were met.

We conducted a total of two hierarchical regression analyses to explore the specific influence of the variables in more detail. In a first step we conducted a hierarchical regression analyses to explore in what way groupitizing, working memory capacity, naming speed, phonological awareness and early arithmetic concepts predict approximate addition. We chose to stick with the addition problems for two reasons. In our view addition problems are more age- and curricula-appropriate for children in first grade. Furthermore, addition problems had higher reliabilities (and thus correlation) than multiplication and division problems. We chose to enter our measured constructs into the model in the order in which they arise developmentally. As both working memory and the core systems are considered innate - although both are of course developing with age - we decided to give priority to the abilities based on the core systems to get any innate mathematical abilities out of the way first.

Model 1 revealed that only groupitizing accounted for unique variance of approximate addition, even when controlling for all other variables (Table 4). However, Model 1 accounted for 24.4% of the variance of approximate addition performance only. Approximate addition seems to be largely independent from any influences outside the core systems shown by both the low coefficient of determination and the unique influence of all other variables.

 

 

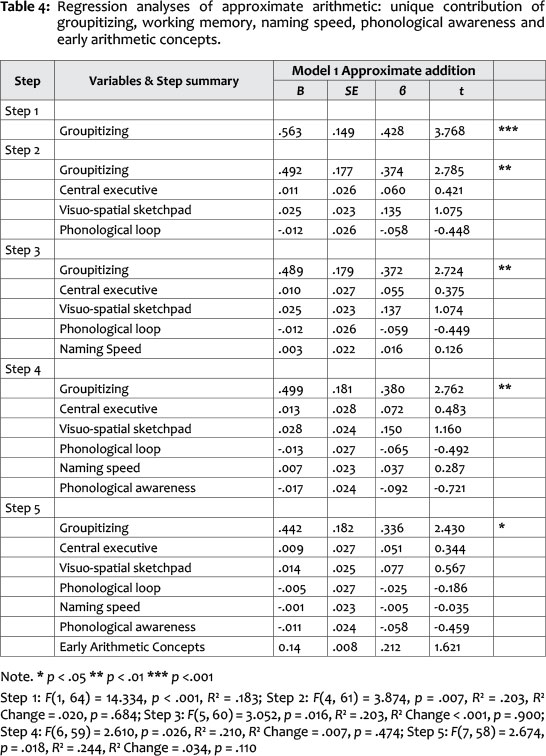
In a next step of analyses, we wanted to test our third hypothesis by means of another hierarchical regression analyses. We wanted to explore the unique influence of approximate arithmetic on school mathematics assessed one year later, controlling for other variables like groupitizing, working memory, naming speed, phonological awareness and early arithmetic concepts (Table 5).

 

 

Model 2 revealed that only the ability to groupitise and central executive capacity are significant predictors of later school success in mathematics. When early arithmetic concepts were included into the model (Step 5), approximate addition performance was no longer a predictor for later school success, although this might be due to multicollinearity, as Step 5 included three different measures of early mathematics. The final model accounted for 52.2% of the variance. We interpret this as the main finding of our two studies, as it shows, that precise numerical representations and cardinality - alongside cognitive capacity represented by the central executive - are the main predictors of later school success. This means, a main issue of preschool diagnostic and learning should be directed to the question whether children are able to understand certain precise concepts, which are needed for formal schooling.

 

General discussion

In the following, we want to sum up our results and discuss theoretical and practical implications of these results for teaching and learning in early primary school. Different international large-scale assessments showed that children have severe problems with mathematics in higher grades, which leads to lower academic achievement and problems on the job market. It is kind of obvious that these problems are not problems that come out of nowhere in secondary school. They rather stem from earlier problems in understanding basic concepts of exact arithmetic. However, latest research showed that children have some basic understanding of all four basic arithmetic operations prior to schooling, when they are allowed to solve these problems approximately. Although young children can solve approximate problems very well, it is not entirely clear whether these abilities help for later school success.

Our main research question for our two studies was to find out what approximate arithmetic abilities children have at school entrance age, how these abilities are influenced by other variables and whether these abilities predict later school mathematics achievement, when controlling for other variables with influence on early mathematical skills. We formulated three main research hypotheses based on the literature.

Hypothesis 1a stated that children at school entrance age can solve approximate arithmetic problems of all basic operations. We found evidence for this hypothesis, which is in line with previous research (Barth et al., 2005; 2006; 2009). Additionally, this is evidence for the idea that children understand the fundamental concepts of all basic arithmetic operations even before formal schooling. Hypothesis 1b had to be rejected, because we did not find that addition and subtraction are easier than multiplication and division, but that the sequence of difficulty was addition → multiplication and division → subtraction from easiest to hardest, which surprised us at first. One possible explanation could be that this could be due to the format of presentation. However, addition and subtraction shared a similar format different from division and multiplication, which had a similar format as well. As such this cannot explain the order we found. However, the division problems asked the children to share things equally among several persons, while the multiplication problems could be solved as repeated addition problems - which would also imply a basic understanding of multiplicative operations. Both - sharing and adding - seem more important to the daily routines of children for us, i.e. when asked to add 3 more forks to a table or when sharing toys or sweets with other children. However, this is an open field for further research, as a more qualitative approach might be fruitful to shed some light on these findings.

The main concern of Hypothesis 2 was the cognitive fundamentals of approximate arithmetic and their correlation to other variables. We expected the different approximate arithmetic problems to correlate highly with each other and furthermore with groupitizing, visuo-spatial sketchpad capacity and early arithmetic concepts. Correlation analyses revealed that all approximate arithmetic problem categories correlated with each other, some correlations might even be underestimated because of the poor reliability of the multiplication and division problems. Additionally, regression analyses revealed that the main predictor for addition problems was groupitizing, our measure of the culturally learned number representation system introduced by Carey (2009). These analyses also revealed that the approximate abilities are largely independent from any other cognitive functioning. This surprised us at first, as mathematical achievement is usually highly correlated with working memory capacity (see DeStefano & LeFevre, 2004, for a review). However, it might be that only higher mathematics relies on working memory, as it is implied by the high correlations between central executive capacity and groupitizing, as well as early arithmetic concepts. On the other hand the more innate approximate arithmetic runs on its own cognitive resources, not relying on working memory as much. However, another explanation could simply be that working memory load is too low when solving approximate arithmetic problems, as these are highly automatized and as such do not need enough working memory capacity to be noticeable. Future research should also take standardized measures of preschool arithmetic into account to give better information about the sample's general mathematical abilities at the beginning of testing. We only used a standardized measure for school arithmetic at the beginning of 2^nd grade and our sample turned out to be significantly better than average with a percentile rank of 67 on a norm-referenced test, t(65) = 5.115, p < .001. Thus, we have to be very careful not to overestimate results attained from samples that are above norm and generalise them on weaker samples. With all this in mind, Hypothesis 2 had to be rejected in terms of early arithmetic concepts and working memory capacity, but there is need for further longitudinal research, especially to understand the causalities that led to these results.

Hypotheses 3 stated that approximate arithmetic abilities predict later school success even when controlling for other variables like working memory or groupitizing. Gilmore et al. (2007) showed that these abilities are correlated with mathematical achievement measured at the end of kindergarten. Furthermore, Gilmore et al. (2010) even showed that they are predictive for first grade school mathematics when controlling for age, intelligence and literacy, but were not predictive when taking preschool math knowledge into the analyses. To our knowledge there have been no studies investigating the specific influence of approximate arithmetic when controlling for groupitizing or working memory in a longitudinal design whatsoever. We found that approximate addition is a significant predictor of later school success alongside groupitizing and central executive capacity, which is in line with current research regarding working memory, the approximate number system and subitizing (Bull et al., 2008; Desoete & Grégoire, 2006, Gilmore et al., 2010). Still, the influence of approximate addition vanished when controlling for early arithmetic concepts -Gilmore et al. (2010) encountered a similar issue. This could be due to the fact that our sample was simply too small for the regression analyses conducted and due to possible multicollinearity because approximate addition, groupitizing and early arithmetic concepts are constructs from a very similar field. However, we believe in another explanation, which is simply that approximate arithmetic is an important predecessor of skills required for school arithmetic, but what really matters for school mathematics are the precise concepts acquired at preschool age, like for example the ability to groupitise, which involves cardinal understanding of numbers. The groupitizing variable was predictive even when controlling for cognitive variables and for other mathematical variables and as such can be used to identify children with evolving problems in arithmetic even prior to the start of formal schooling. However, further research is needed to find out how to remedy this bad conceptual knowledge and whether this remedy leads to better later school success.

A possible objection against our findings could be that we did not include an intelligence measure in Study 2 and that most correlations and regressions might simply reflect the role of intelligence. We did not do so because we did not get parental consent on assessing intelligence from all participating schools. However, we believe that this objection does not hold true, because of the very extensive inclusion of working memory, which is another good predictor of school learning outcomes, in some research even on par with general intelligence (Alloway & Alloway, 2008). For further research it might be helpful to include working memory capacity alongside spatial and logical intelligence measures to investigate the specific impact of each of them.

To sum our results up, we showed that children at school entrance age can solve problems of all four basic arithmetic operations approximately, however this ability is not predictive for later school success, which is only predicted by central executive capacity and children's ability to groupitise, i.e. their understanding of the cardinal number concept. These findings are in line with prior research regarding approximate arithmetic (Gilmore et al., 2010) and the development of a precise and unlimited number representation system as proposed by Carey (2009).

How can school teaching benefit from these findings? First, even if approximate arithmetic is not predictive for school success, we still know that children understand the basic concepts of all four basic arithmetic operations. It is highly correlated with other preschool math measures (groupitizing and early arithmetic concepts), which means that it might play a role in preschool. Furthermore, this conceptual knowledge might be applied in teaching, because another reason why approximate abilities are not predictive for later school success, could simply be that schools don't want children to solve problems approximately. If schools make use of existing conceptual knowledge, it might be easier for some children to understand curriculum-based arithmetic. However, it should also be taken into account that there are large individual differences regarding approximate arithmetic proficiency. While it really sounds nice to suggest that, 'children can solve these problems above chance,' only half of them actually do so when analysing individual achievement (see Appendix A.3). This is a major issue, which has to be taken into account, before trying to implement the use of these abilities into school curricula.

Second, we found that groupitizing predicted school success, even when controlling for different other variables. Children could easily be tested for their groupitizing skills in a very short time - our groupitizing test usually took us 2-3 minutes per child. This would help schools to identify children at risk for later problems with school mathematics and give them the opportunity to solve these problems. A major issue for upcoming research should be to evaluate conceptual training programs to find out whether it is possible to teach these concepts and whether this conceptual knowledge is acquired permanently and transfers to school mathematics.

 

References

Alloway, T.P. & Alloway, R. 2008. Working memory: Is it the new IQ? Nature Precedings. Retrieved from http://hdl.handle.net/10101/npre.2008.2343.1 (accessed 15 July 2013).

Andersson, U. 2007. The contribution of working memory to children's mathematical word problem solving. Applied Cognitive Psychology 21:1201-1216.         [ Links ]

Andersson, U. 2008. Working memory as a predictor of written arithmetic skills in children: The importance of central executive functions. British Journal of Educational Psychology 78:181-203.         [ Links ]

Antell, S. & Keating, D.P. 1983. Perception of numerical invariance in neonates. Child Development 54:695-701.         [ Links ]

Baddeley, A.D. 1986. Working memory. New York: Clarendon.         [ Links ]

Baddeley, A.D. 1996. Exploring the central executive. Quarterly Journal of Experimental Psychology 49A:5-28.         [ Links ]

Balakrishnan, J.D. & Ashby, F.G. 1992. Subitizing: Magical numbers or mere superstition? Psychological Research 54:80-90.         [ Links ]

Barth, H., Baron, A., Spelke, E. & Carey, S. 2009. Children's multiplicative transformations of discrete and continuous quantities. Journal of Experimental Child Psychology 103:441-454.         [ Links ]

Barth, H., Kanwisher, N. & Spelke, E. 2003. The construction of large number representations in adults. Cognition 86:201-221.         [ Links ]

Barth, H., La Mont, K., Lipton, J., Dehaene, S., Kanwisher, N. & Spelke, E. 2006. Non-symbolic arithmetic in adults and young children. Cognition 98:199-222.         [ Links ]

Barth, H., La Mont, K., Lipton, J. & Spelke, E.S. 2005. Abstract number and arithmetic in preschool children. Proceedings of the National Academy of Sciences 102:14116-14121.         [ Links ]

Bos, W., Bonsen, M., Baumert, J., Prenzel, M., Selter, C. & Walther, G. (Hrsg.). 2008. TIMSS 2007. Mathematische und naturwissenschaftliche Kompetenzen von Grundschulkindern in Deutschland im internationalen Vergleich [TIMSS 2007. Mathematical and scientific competencies of primary school students in Germany compared to international results]. Münster: Waxmann.         [ Links ]

Bull, R., Espy, K. & Wiebe, S. 2008. Short-term memory, working memory and executive functioning in pre-schoolers: Longitudinal predictors of mathematical achievement at age 7 years. Developmental Neuropsychology 33:205-228.         [ Links ]

Carey, S. 2009. The origin of concepts. London: Oxford University Press        [ Links ]

Dehaene, S. 1997. The number sense: How the mind creates mathematics. Oxford: Oxford University Press.         [ Links ]

Denckla, M.B. & Rudel, R.G. 1974. Rapid 'automatized' naming of pictured objects, colors, letters, and numbers by normal children. Cortex 10:186-202.         [ Links ]

De Smedt, B., Janssen, R., Bouwens, K., Verschaffel, L., Boets, B. & Ghesquiere, P. 2009a. Working memory and individual differences in mathematics achievement: A longitudinal study from first grade to second grade. Journal of Experimental Child Psychology 103:186-201.         [ Links ]

De Smedt, B., Verschaffel, L. & Ghesquiere, P. 2009b. The predictive value of numerical magnitude comparison for individual differences in mathematics achievement. Journal of Experimental Child Psychology 103:469-479.         [ Links ]

Desoete, A. & Grégoire, J. 2006. Numerical competence in young children and in children with mathematics learning disabilities. Learning and Individual Differences 16:351-367.         [ Links ]

DeStefano, D. & LeFevre, J.A. 2004. The role of working memory in mental arithmetic. European Journal of Cognitive Psychology 16:353-386.         [ Links ]

Feigenson, L., Carey, S. & Hauser, M. 2002. The representations underlying infants' choice of more: object file versus analog magnitudes. Psychological Science, 13:150-156.         [ Links ]

Feigenson, L., Dehaene, S. & Spelke, E.S. 2004. Core systems of number. Trends in Cognitive Sciences 8:307-314.         [ Links ]

Fritz, A., Ricken, G. & Balzer, L. 2009. Warum fällt manchen Schülerinnen und Schülern das Rechnen schwer? - Entwicklung arithmetischer Kompetenzen im Vor- und frühen Grundschulalter [Why do some students have difficulties with calculating? - Development of arithmetical skills in pre- and primary school ages]. In A. Fritz & S. Schmidt, Fördernder Mathematikunterricht in der Sekundarstufe I. Rechenschwierigkeiten erkennen und überwinden, 12-29. Weinheim: Beltz.

Gilmore, C.K., McCarthy, S.E. & Spelke, E.S. 2007. Symbolic arithmetic knowledge without instruction. Nature 447:589-591.

Gilmore, C.K., McCarthy, S.E. & Spelke, E.S. 2010. Non-symbolic arithmetic abilities and mathematics achievement in the first year of formal schooling. Cognition 115:394-406.

Gonzales, P., Williams, T., Jocelyn, L., Roey, S., Kastberg, D. & Brenwald, S. 2008. Highlights from TIMSS 2007: Mathematics and Science Achievement of U.S. Fourthand Eighth-Grade Students in an International Context (NCES 2009-001 Revised). National Center for Education Statistics, Institute of Education Sciences, U.S. Department of Education. Washington, DC.

Holloway, I.D. & Ansari, D. 2009. Mapping numerical magnitudes onto symbols: The numerical distance effect and individual differences in children's mathematics achievement. Journal of Experimental Child Psychology 103:17-29.

Krajewski, K., Küspert, P. & Schneider, W. 2002. Deutscher Mathematiktest für erste Klassen (DEMAT 1+) [German Test for mathematics assessment]. Göttingen: Hogrefe.

Krajewski, K. & Schneider, W. 2009. Exploring the impact of phonological awareness, visual-spatial working memory, and preschool quantity-number competencies on mathematics achievement in elementary school: Findings from a three-year longitudinal study. Journal of Experimental Child Psychology 103:516-531.

Krajewski, K., Schneider, W. & Nieding, G. 2008. Zur Bedeutung von Arbeitsgedächtnis, Intelligenz, phonologischer Bewusstheit und früher Mengen-Zahlen-Kompetenz beim Übergang vom Kindergarten in die Grundschule [Regarding the relevance of working memory, intelligence, phonological awareness and early set-number-competence during the change from kindergarten into primary school]. Psychologie in Erziehung und Unterricht 55:100-113.

Kroesbergen, E.H., Van Luit, J.E.H., Van Lieshout, E.C.D.M., Van Loosbroek, E. & Van de Rijt, B.A.M. 2009. Individual differences in early numeracy: The role of executive functions and subitizing. Journal of Psychoeducational Assessment 27:226-236.

McCandliss, B.D., Yun, C., Hannula, M., Hubbard, E.M., Vitale, J. & Schwartz, D. 2010. 'Quick, how many?' Fluency in Subitizing and 'Groupitizing' Link to Arithmetic Skills. American Educational Research Association, Denver, CO.

McCrink, K. & Spelke, E.S. 2010. Core multiplication in childhood. Cognition 116:204-216.

Meyer, M.L., Salimpoor, V.N., Wu, S.S., Geary, D.C. & Menon, V. 2009. Differential contribution of specific working memory components to mathematics achievement in 2^nd and 3^rd graders. Learning and Individual Differences 20:101-109.

Miller, G.A. 1956. The magical number seven, plus or minus two: some limits on our capacity for processing information. Psychological Review 63:81-97.

Paas, F. & Van Merriënboer, J.J.G. 1993. The efficiency of instructional conditions: An approach to combine mental-effort and performance measures. Human Factors 35:737-743.

Spelke, E. 2005. Sex differences in intrinsic aptitude for mathematics and science? A critical review. American Psychologist 60:950-958.

Swanson, H.L. & Kim, K. 2007. Working memory, short-term memory, and naming speed as predictors of children's mathematical performance. Intelligence 35:151-168.

Wagner, R. & Torgesen, J. 1987. The nature of phonological processing and its causal role in the acquisition of reading skills. Psychological Bulletin 101:192-212.

Xu, F. 2003. Numerosity discrimination in infants: Evidence for two systems of representations. Cognition 89:B15-B25.

Xu, F. & Arriaga, R. 2007. Number discrimination in 10-month-old-infants. British Journal of Developmental Psychology 25:103-108.

Xu, F. & Spelke, E.S. 2000. Large number discrimination in six-month-old infants. Cognition 74:B1-B11.