Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Economic and Management Sciences
On-line version ISSN 2222-3436
Print version ISSN 1015-8812
S. Afr. j. econ. manag. sci. vol.22 n.1 Pretoria 2019
http://dx.doi.org/10.4102/sajems.v22i1.1854
NEW PERSPECTIVE
The performance of debt and equity markets in Anglo American Plc and BHP Billiton Plc in the period 2006 to 2015 through the lens of Merton's structural model
Leon B. Sanderson
Centre for Business Mathematics and Informatics, North-West University, South Africa
ABSTRACT
This article applies the Merton structural model in evaluating the performance of the debt and equity markets in Anglo American Plc and BHP Billiton Plc in the period 2006 to 2015. We consider statistical and economic measures of the efficacy of the Merton model in explaining observed market behaviour. We find strong but unstable statistical support for the Merton model as a descriptor of market behaviour. We generated superior risk adjusted returns when applying the results of our analysis to an investment strategy. Market prices deviate from model behaviour; however, the relationship appears to be mean reverting which supports the investment thesis.
Introduction
Equity and debt are both claims on the assets of a firm. Debt is generally serviced first up to the contractual obligation with equity enjoying a residual but unlimited share thereafter. We consider it reasonable to expect the performance of both equity and debt to be related to the performance of the assets of the underlying firm. The firm's assets encompass both physical assets and intangible assets. This spans plant and equipment, brand, human capital, know-how and licences among others. In our study we consider the physical assets of a firm to be the ultimate driver of performance of the firm's debt and equity instruments. We note that this approach is relevant in firms with capital intensive activities and is unlikely to be applicable in firms dominated by intangible assets.
Capital structure research spans the early work of Modigliani and Miller (1958) which showed capital structure choices to be irrelevant under certain conditions to a variety of theories that guide the mix of debt and equity issued by firms. As described by Myers (2001) these include the trade-off theory which balances the costs and benefits of debt finance, the pecking order theory which emphasises information differences between managers and investors and the agency costs theory which focuses on the relative gains and losses of managers and owners. Merton (1974) provides a robust and simple conceptual bridge between the theoretical values of a firm's debt and equity instruments and the characteristics of the assets underlying the operations of the firm. He offers a structural model of capital structure that is seen to be the genesis of the trade-off theory. He views equity as a long position in a call option on the assets of a company and debt as a risk-free instrument coupled with a short position in a put option on the assets of the company, in both cases struck at the face value of the debt which is assumed to be zero coupon in nature. Numerous extensions to the conceptual framework, for example Black and Cox (1976) and Geske (1977), have been explored but at the cost of added complexity. In the work of Brennan and Schwartz (1978) and Leland (1994) a number of the limiting assumptions are relaxed and the potential tax benefits of debt and the deadweight costs of bankruptcy are introduced. The empirical analysis of the performance of the Merton model and its successors, when applied to actual market data has been inconclusive with limited explanatory power observed (see Delianedis & Geske 2001; Frank & Goyal 2003; Harris & Raviv 1991; Titman & Wessels 1988) and numerous issues relating to measurement highlighted (see Graham & Leary 2011). We have chosen to make use of a simple expression of capital structure that limits the number of assumptions required. The primary innovation we introduce is in the measure chosen to assess the performance of the model.
In this article we assess the capacity of the Merton model as a tool to describe market behaviour. We test for statistical and economic significance of the model. Statistical tests encompass regression and co-integration, whilst economic significance is evaluated by applying the model to an investment process and considering the resulting returns. The investment process is a pair trading strategy where positions in the underlying equity are offset with opposite positions in the underlying asset. We consider two firms, Anglo American Plc (AGL) and BHP Billiton Plc (BHP), both of which are diversified mining companies. Their financial performance is intimately linked to the prices they receive for the commodities they produce. We expect that the fortunes of both companies are related to the performance of their underlying commodity markets. In this instance we consider the physical assets of each firm to be the basket of commodities they sell. We argue that in both cases, the underlying assets of each of the firms can be reasonably described by the construction of proxy indices that are made up of observable metrics for underlying commodity markets. We consider semi-annual balance sheet data for each of the firms and make use of market prices for equity instruments and debt instruments to generate implied underlying asset value and asset volatility for each of AGL and BHP using the Merton structural model. We evaluate the relationship between the implied measures (asset value and asset volatility) and the value and volatility derived from the proxy indices. In addition, we construct a simple pair trading strategy that will be long (short) the proxy index and short (long) the relevant equity when large relative deviations from the average (of the ratio of the proxy index and the equity) are observed. The trading strategy takes advantage of the expectation that a strong relationship between the proxy index, which represents the underlying firm assets, and the equity will be observed.
Data
All data are sourced from Bloomberg and all charts, calculations and tables are undertaken in Microsoft Excel.
We require data on the equity of the firm, the debt of the firm and underlying assets of the firm. We consider the period 06 January 2006 to 25 December 2015. The period was chosen to encompass the financial crisis experienced in 2008 and the period of significant commodity price weakness in 2015. We make use of weekly closing prices for equity markets, credit markets, US interest rate markets (Treasury bills and notes) and foreign exchange markets. We make use of weekly closing prices for the UBS Bloomberg CMCI Indices (constant maturity commodity indices that we use to construct proxy indices). We make use of balance sheet and income statement information for both AGL and BHP. AGL has a December year end and BHP has a June year end. We have interim financial statements and annual financial statements for both in June and December each year. AGL and BHP report in US dollars, with their product lines, namely the commodities they produce, also denominated in US dollars. All the information is sourced from Bloomberg. Equity data are adjusted for historical splits and spin offs.
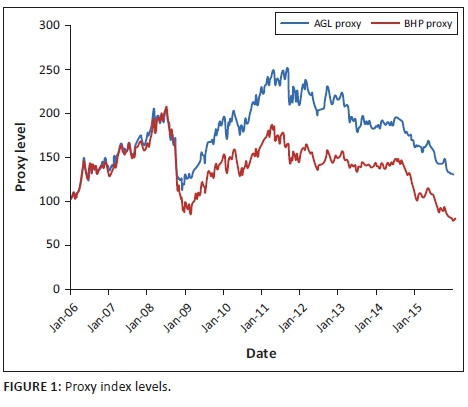
We note that AGL generally has a higher level of financial leverage (as expressed by total debt relative to the balance sheet) and that in the period leading up the financial crisis experienced in 2008, AGL held a larger proportion of their debt in shorter dated instruments. We observed relatively larger swings in the prices of the debt and equity instruments of AGL as compared to BHP.
Equity data
AGL and BHP are listed on a variety of stock exchanges and have a number of lines of equity. Total equity is the sum of these distinct listings (or lines). AGL has a primary listing on the London Stock Exchange (LSE), with all other listings convertible or exchangeable into the LSE line on a one for one basis. Accordingly, AGL equity is calculated as the price of the LSE line multiplied by the total shares in issue converted into US dollars. BHP is dual listed, with distinct lines on the LSE and the Australian stock exchange (ASX). All other lines are convertible into either the LSE line or the ASX line on a one for one basis. The ASX line and the LSE line are not interchangeable but have identical economic interests (dividends and votes). Accordingly, BHP equity is calculated as the price of the LSE line multiplied by the total shares in issue (of both the LSE line and the ASX line) converted into USD dollars.
Debt data
Data on secondary market trading of debt instruments for AGL and BHP is limited. We make use of Credit Default Swap (CDS) data to provide summary information on the performance of the credit market. A CDS provides the holder of the instrument with insurance against potential losses on an investment in bonds. In the event of default, the CDS holder has the right to deliver bonds to the CDS writer against receipt of a fixed nominal. This insurance has a fixed term, commands a regular premium and provides cover on a fixed nominal. A CDS is effectively an American option whose premium is paid over the life of the instrument, where further premium payments are extinguished on exercise (namely default). We source standardised data on 5 year and 10 year CDS markets. Liquidity in these instruments is limited; however, daily pricing information is available. AGL CDS is only available in euros. We assume that AGL CDS in US dollars is equivalent to AGL CDS in euros. This assumption ignores the potential quanto effect in shifting currencies. As discussed in Chan-Lau (2009) this quanto effect is driven by the convertibility risk and the transfer risk between the underlying currency markets, which in this case, Euros to US dollar, is considered negligible. In addition we note that our interest lies primarily in the changes in CDS levels rather than the absolute values.
We extract two distinct estimates for total debt for each of AGL and BHP from the available balance sheet information. We denote these estimates as D1 and D2. The first (D1) is total liabilities (Bloomberg field BS_TOT_LIAB2). The second (D2) is total liabilities reduced by current assets (Bloomberg field BS_CUR_ASSET_REPORT) and augmented by inventories (Bloomberg field BS_INVENTORIES). The motivation for the choice of both D1 and D2 relates to the measurement issues highlighted in the introduction above. D1 is likely to exceed formal debt obligations but better reflects the obligations that must be met prior to value being available to service equity holders in the event of default. D2 is an attempt to adjust D1 to account for working capital.
Asset data
Many commodity markets do not have liquid, transparent price discovery mechanisms for the spot market but enjoy deep and liquid derivative markets. The UBS Bloomberg CMCI indices provide a blended and consistent mechanism for reflecting available prices for baskets of commodities (see UBS 2011 for detailed index methodology and calculation). The CMCI family of indices covers many sectors, time frames and return profiles. We make use of the total return benchmark indices that encompass Precious Metals, Industrial Metals and Energy. The Bloomberg codes for these indices are CMPMTR Index, CMIMTR Index and CMENTR Index. The data used in constructing the proxy indices is historical information that is available as at the relevant calculation date.
We map each firm to a combination of these indices. AGL and BHP provide a breakdown of divisional assets in their financial statements. These divisions are delineated by underlying commodities. We map divisional assets information from the AGL and BHP financial statements for the financial years 2006 to 2015 to three distinct groups. Precious Metals includes gold, platinum and diamonds. Industrial metals includes iron ore, base metals, aluminium, stainless steel, nickel, zinc and manganese. Energy includes petroleum and coal. On the basis of this categorisation we determine proxy assets for each of AGL and BHP. The proxy weights are adjusted on an annual basis to reflect the latest information available in the financial statements. Proxy index values are calculated as a linear combination of the three CMCI benchmark indices (Precious Metals, Industrial Metals and Energy). We adjust the linear combination parameters every 6 months (in June and December) to reflect the relevant proxy weights (w), as determined from the latest annual financial statements. In the case of AGL, over the period, Precious Metals (CMPM) contributed 25% to 36%, Industrial Metals (CMIM) contributed 52% to 59% and Energy (CMEN) contributed 7% to 21%. In the case of BHP, over the period, Precious Metals (CMPM) contributed 3% to 4%, Industrial Metals (CMIM) contributed 60% to 66% and Energy (CMEN) contributed 31% to 37%. The formulae for the proxy index values for each of AGL and BHP on a given day, t, using the applicable weights for each of AGL and BHP in the benchmark indices, are shown below.

where 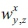 is the weight for company x in benchmark index y applicable for period z.
is the weight for company x in benchmark index y applicable for period z.
We calculate an historical volatility series for each of the proxy index values by generating a series of annualised standard deviations on the log changes of the weekly data points using a rolling 4 week window. In effect we are considering the 1 month historical variability of each of the proxy indices. In applying the Merton model we are evaluating debt and equity by considering the underlying assets and their associated volatility. We use the calculated historical volatility (as described in Hull 2012) of the proxy index series as an estimate for current volatility of the proxy index series. The formulae for the proxy historical volatility for each of AGL and BHP on a given day, t, are shown below:
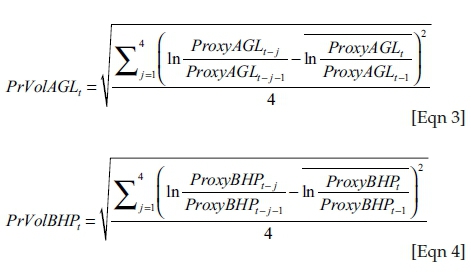
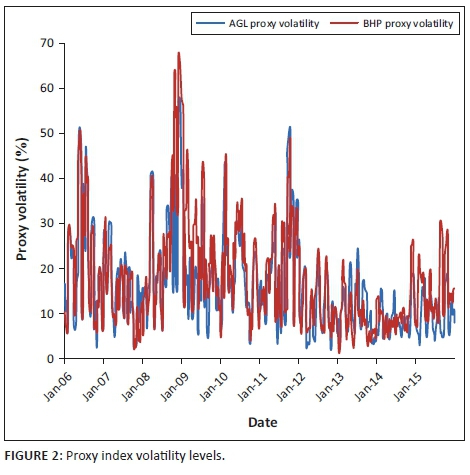
The proxy index values and the proxy index realised volatility levels are shown in Figure 1 and Figure 2.
Methodology
In an efficient market we expect the market value of a firm's assets to be equal to the market value of a firm's liabilities. Let us consider a simple firm funded with non-dividend paying equity and zero coupon debt. Merton's (1974) insight allows one to apply a standard option pricing model to solve for the value of equity and debt, given the underlying asset price and the associated asset volatility of a firm. Equity and debt are both claims on the underlying assets. Equity is the residual, if any, after debt has been fully serviced by the underlying assets. Debt is a senior claim on the underlying assets, limited to the face value of the debt obligation. Equity can be modelled as a call option on the underlying asset struck at the future value of the debt obligations. Debt can be modelled as a risk-free zero coupon bond coupled with a risky component that reflects the potential for losses, namely that the assets will not be sufficient to fully service the debt obligation. The risky component of debt can be modelled as a put option on the underlying asset struck at the future value of the debt obligations. Merton's (1974) original formulation considered equity and debt instruments in the context of European options, with no intermediate payments. In effect he evaluated default only at the maturity of the underlying debt instrument, which is assumed to be a zero coupon bond.
Expressed mathematically, we have:

where A is the value of the assets of the firm, E is the value of the equity and D is the value of the debt.
At the maturity of the debt the value of the equity is given by:

where K is the face value of the debt, which by definition is zero coupon and which has value today of D.
Prior to the maturity of the debt we make use of Merton's model for the value of equity, expressed as a call option on the assets of the firm.

where

and

where N(x) is the cumulative probability distribution function for a standardised normal distribution and σ is the volatility of the firm assets.
The value of the debt is arrived at by way of put call parity, rearranging terms and recognising that the debt value is equal to the asset value reduced by the equity value:

where P is the value of a put option on the assets A struck at the face value of the debt K.
This approach provides a mechanism for relating asset value and asset volatility to values for equity and debt. In general we have values for equity and debt, which we use to solve for the underlying asset price and the associated asset volatility.
As detailed above in the data section, we have market data on both equity and debt for AGL and BHP in the form of historical equity values and historical CDS levels.
We consider two distinct formulations when determining the face value of the underlying debt as reflected on the balance sheet (D1 and D2). AGL and BHP have issued a variety of coupon bearing debt instruments. In our model we map these instruments to a single zero coupon debt instrument for each of AGL and BHP. We set the term of this zero coupon bond to match the tenor of the CDS instrument used (5 or 10 years). The face value of this representative zero coupon debt instrument is calculated by grossing up the face value of the coupon paying debt as reflected on the balance sheet (and calculated in D1 and D2) by the risk-free interest rate augmented by an assumed credit spread. This approximates the effective coupon paid by the underlying debt instruments. The risk-free interest rate used is the then prevailing relevant US Treasury rate (either 5 year or 10 year). The credit spread applied is the average of the relevant CDS over the full period under consideration (6 January 2006 to 28 December 2015). The higher the credit spread used, the higher the effective face value of the representative zero coupon debt instrument. The face values of these representative debt instruments are the effective strike prices in our application of the Merton model. Expressed mathematically we have

where K is the face value of the grossed up representative debt instrument, DBS is the face value of the balance sheet debt (D1 or D2), r is the relevant risk-free interest rate (NACA) and CS is the credit spread determined as the average of the relevant CDS and T is the tenor of the relevant CDS.
We model equity as a call option on the underlying assets. The market value for this option is equal to the market value of equity as discussed in the data section above. We model debt as a risk-free zero coupon bond coupled with a put option on the underlying assets. This approach, widely applied in the literature and described in Hull, Nelken and White (2004), ignores both the early exercise nature of the CDS as well as the contingent premiums and simply aligns the CDS to a European put option. It is a simplification of the mechanics of the underlying instruments which attempts to capture the essence of their behaviour whilst limiting the complexity of the calculation. We proceed by solving for the premium of the put option. The strike price of both the call option and the put option is set equal to the calculated face value of the debt. The term of the option is set equal to the tenor of the CDS (either 5 years or 10 years). We have assumed zero coupon debt, and as such over time the value of the debt outstanding will increase until the assumed maturity at which point the debt value equals the face value. A standardised CDS assumes a fixed nominal. To cater for this discrepancy, we calculate the equivalent put option premium by multiplying the CDS level by the average of the initial value of debt outstanding and the nominal of debt outstanding, multiplied by the tenor of the CDS (reflecting the number of CDS payments), present valued to today. This maps the annual payment of the CDS premium as insurance on a fixed nominal to the firm's growing debt obligation. The equivalent put option premium, P, is thus given by
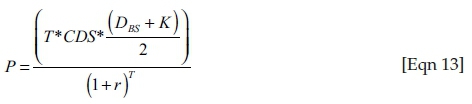
When evaluating options, we assume that the underlying asset pays no dividends, we apply the same risk-free rate as that used in determining the face value of the representative debt instruments and we set the term to match the tenor of the CDS instrument used (5 or 10 years).
We solve for the implied asset price (A) by way of put-call parity (shown below) as we have the market values for equity (call option) and debt (risk-free zero coupon bond coupled with a put option).

We use the implied asset price together with the equity value to invert the Black-Scholes equation to solve for the implied asset volatility numerically (σ).
We proceed by generating implied asset price levels and implied asset volatility levels at each time period, namely weekly for debt levels D1 and D2 and maturity 5 and 10 years.
Results
We have four distinct series for each of AGL and BHP. We consider 5 and 10 year terms across two distinct definitions of debt (D1 and D2).
We will consider the relationship between changes in the proxy asset levels and changes in the implied asset levels, and changes in the historical proxy asset volatility and changes in the implied asset volatility. A direct comparison is not applicable, however, as there are changes to the quantum of debt and equity through time that must be accounted for (e.g. new equity issuance, new debt issuance, share buybacks or the retirement of debt, all impact on the balance sheet value of the company but are unrelated to changes in the underlying asset values). These changes are already reflected in the market data by way of adjustments in the total shares in issue, and adjustments to the liabilities on the balance sheet. At each data point we adjust the implied asset levels to reflect the cumulative change in debt (we adjust the face value) and equity (we adjust the total number of shares) from the beginning of the assessment period. In effect we reverse the impact of changes in the structure of debt and equity in an effort to focus on changes in value related to underlying asset price variability only. We then apply log differences to these adjusted implied levels as well as the proxy levels that were generated.
We make use of linear regression models of the form:

where y is the dependent variable, x is the independent variable, β0 and β1 are equation parameters and ε is the error term.
We regress the log differences of the proxy asset levels on the log differences of the adjusted implied asset levels and consider the correlation between the two series.
We regress the log differences of the proxy asset volatility on the log differences of the implied asset volatility and consider the correlation between the two series.
The results of this correlation study are shown in Tables 1 and 2.
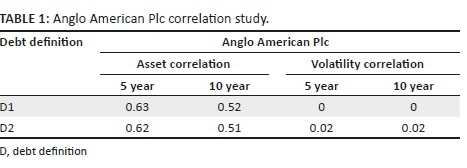
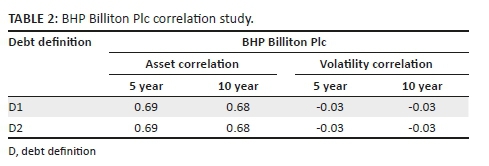
In all cases we find that asset levels are highly correlated but that asset volatility is not highly correlated. In an effort to understand the nature of the relationship between the volatility series we then consider the extent to which the proxy asset volatility and the implied asset volatility are co-integrated.
We note that if two time series x and y (both I(1), namely with variance proportional to time T and as a result the time series is non-stationary) are co-integrated, then a linear combination of them, u, must be stationary (I(0), with a unit root):

We make use of Engle and Granger's (1987) two-step procedure to test for co-integration.
We test the proxy asset volatility and the implied asset volatility time series and report the Dicky-Fuller test statistic in Table 3.
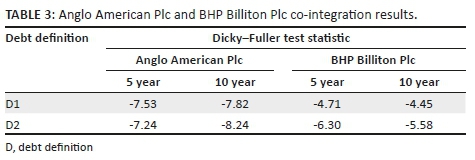
At a 95% confidence interval, in all cases we find that proxy asset volatility and implied asset volatility are co-integrated.
We consider the stability of the test results shown above by considering three distinct time periods, January 2006 to December 2009, January 2010 to December 2012 and January 2013 to December 2015. We repeat the tests outlined above (excluding the volatility correlation) on these three periods and reflect the results in Tables 4-7.
In addition we consider alternate values for the credit spread applied in determining the face value of the representative zero coupon debt instrument. We evaluated credit spread levels significantly below and significantly above the calculated average and found similar results.
In summary we find strong, statistically significant relationships between our proxy asset levels and proxy asset volatility and the implied asset levels and implied asset volatility. However, these relationships are not particularly stable when considering sub-periods within the data. The disparity between the proxy asset volatility which is an historical backward looking measure and the implied asset volatility which is a market generated estimate of future variation, is noted. We believe that the issues highlighted above warrant further study.
Trading strategy
We now consider a simple pair trading strategy that makes use of the insights gained in the evaluation above to test whether the observed relationships are of economic significance. We wish to highlight that whilst we employed statistical tools (linear regression and co-integration) to evaluate the relationships between equity, debt and assets, we do not make use of any of the derived parameters in constructing the trading strategy. Given the fundamental relationship between equity and the underlying assets of a company, we expect to observe a strong link between the behaviour of the underlying assets and the behaviour of the equity. An increase (decrease) in underlying asset value should be accompanied by an increase (decrease) in equity value. A control for our experiment would be akin to a simple coin toss exercise that would drive an investment process which would have an expected return of zero. We include a naïve alternate trading strategy as a more relevant comparison. The naïve alternate trading strategy considers the proxy asset levels and the equity levels but ignores any implied asset values. We expect there to be a relationship between equity prices and underlying asset levels. We are evaluating whether applying the Merton model, which incorporates the concepts of leverage and asset volatility, enhances this relationship. We apply the trading strategy for the period 06 January 2006 to 25 December 2015.
In all instances of our trading strategy evaluation we consider transactions in the equity and proxy assets of AGL and BHP, as these are tradable instruments (as distinct from the implied asset levels which are constructs). Recall that the proxy assets are linear combinations of benchmark indices that are made up of tradable derivative instruments. The trading strategy formulation draws heavily on the work of Gatev, Goetzmann and Rouwenhorst (2006) who evaluated a pair trading, relative value investment strategy.
We construct our trading strategy as follows.
We generate a trade ratio series (TRS) such that at each point in time its value is the implied asset level (IAL) divided by the proxy asset level (PAL). We generate a trade average series (TAS) that is the 12 period (approximately 3 months, given weekly data) mean of the ratio series. We generate a trade variability series (TVS) that is the 12 period standard deviation of the ratio series.
We generate a comparison ratio series (CRS) such that at each point in time its value is the equity level (EL) divided by the proxy asset level (PAL). We generate a comparison average series (CAS) that is the 12 period (approximately 3 months, given weekly data) mean on the ratio series. We generate a comparison variability series (CVS) that is the 12 period standard deviation of the ratio series.

The base assumption is that the ratio series (TRS, CRS) are mean reverting and as such over time the ratio series will drift back towards the average series (TAS, CAS). Given this assumption, we have a buy signal on the ratio when the series is a defined distance below the average series (e.g. 1 standard deviation) and a sell signal on the ratio when the series is a defined distance above the average series (e.g. 1 standard deviation). In both cases we will close positions when the series breaches the average series.
We consider three distinct strategies. In the comparison strategy, trade signals are generated by the control series. In the trading strategy and the adjusted trading strategy, trade signals are generated by the trading series. In the comparison strategy and in the trading strategy the nominal of both the long position and the short position on trade entry are set equal to $1 million. In the adjusted strategy the nominal of the equity position is set equal to $1 million; however, the nominal of the proxy asset position is determined by the calculated sensitivity of the equity to the underlying asset value.
The delta of an option is defined as the change in option value for a given change in the underlying value (see Hull 2012). In our application of Merton's model we generate a delta for the equity of the firm with reference to the underlying firm assets, where for a given move in the implied asset level we observe some quantifiable but variable move in the equity level. In the adjusted trading strategy we make use of the relevant delta to reflect a larger nominal exposure in the proxy asset. In all cases we assume that trades are undertaken at the closing prices of the relevant instruments. The impact of the equity delta on the nominal used in the adjusted trading strategy is outlined below.
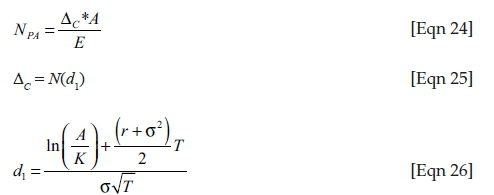
where NPA is the nominal exposure of the proxy asset and Δc is the equity delta.
The results of the three trading strategies for both AGL and BHP are reflected below. In each instance we consider the total number of trades undertaken over the period, the number of winning trades, the number of losing trades and the winning trade percentage. In addition we calculate the total revenue generated, the average trade return, the maximum trade return, the minimum trade return and the standard deviation of trade returns. Finally we reflect a Sharpe ratio, defined as the average return divided by the standard deviation of returns over the full period. We ignore any dividends paid or received on short or long positions in the underlying equity.
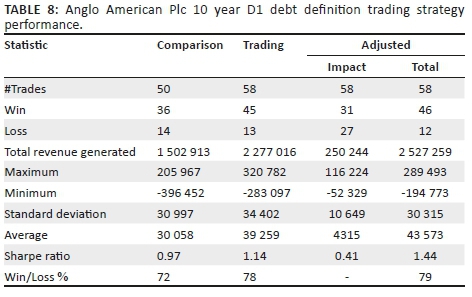
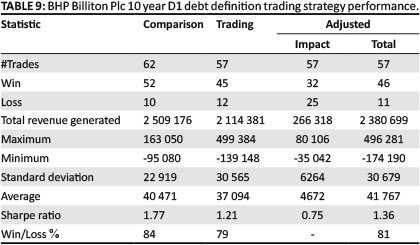
Tables 8 and 9 show a sample for each of AGL and BIL (10 year period and D1 as debt definition) of the detailed summary, where we consider the control strategy, the trading strategy and the adjusted strategy.
Summary data, encompassing total revenue generated (expressed as PnL) and the Sharpe ratio across debt definitions D1 and D2 and 5 year and 10 year terms, are shown in Tables 10 and 11.
In almost all cases, the strategies - comparison, trading and adjusted trading - showed a positive return of at least 200% of nominal over the period. As shown in the summary data above, when considering AGL the trading strategy outperformed the comparison on all measures. However, when considering BHP the trading strategy underperformed the comparison by some measures but outperformed the comparison in some cases in total revenue generated. In all cases the adjusted trading strategy outperformed the trading strategy in total revenue generated, winning trade percentage and Sharpe ratio.
We considered the sub-period performance across the three trading strategies. Table 12 shows a sample for BHP (5 year period, both D1 and D2 for debt definitions). In general there was limited variability in summary statistics for the three time periods across the inputs for period and debt definition, although the trading strategy and adjusted trading strategy performed particularly well in the case of AGL in the period 2013 to 2015, which coincides with extreme levels of commodity price volatility and high leverage in the company. Table 13, for AGL (5 year and 10 year period, D2 for debt definition), illustrates this point.
The results of the trading strategy are uniformly positive; however, the variability noted in the capacity of the Merton model to describe behaviour detailed above, coupled with the use of a single pair of stocks over a fixed time period, suggests limited application and the need for further research. One criticism of the approach may be the lack of an out of sample evaluation; however, the only input that is dependent on the data in the full period is the credit spread applied in determining the face value of the representative zero coupon instrument. This is a constant throughout the evaluation. We evaluated credit spread levels significantly below and significantly above the calculated average and found similar results. This is to be expected as the trading strategy is not dependent on the calculation of specific descriptive statistics for the data period considered.
Conclusion
In this article we considered the capacity of the Merton structural model to describe market behaviour. We evaluated the Merton model using both statistical and economic measures. We chose two firms whose underlying asset behaviour can be described by tradable market indices. We found strong but unstable statistical support for the Merton model as a descriptor of market behaviour. We generated superior economic returns when applying the results of our analysis to a trading strategy, with particularly good performance in times of enhanced stress in market and firm conditions. However, the value of the results and the support they offer for the use of the Merton model to describe market behaviour is limited by the fixed term under consideration and the application to a small sample (two) of relevant firms. The opportunities for further research include extended time periods and a wider universe of relevant firms. The application of the model to a specific trading strategy provided an alternative measure to that applied traditionally when considering the efficacy of the model.
Acknowledgements
Competing interests
The author declares that he has no financial or personal relationships that may have inappropriately influenced him in writing this article.
References
Black, F. & Cox, J., 1976, 'Valuing corporate securities: Some effects of bond indenture provisions', Journal of Finance 31(2), 351-367. https://doi.org/10.1111/j.1540-6261.1976.tb01891.x [ Links ]
Brennan, M. & Schwartz, E., 1978, 'Corporate income taxes, valuation, and the problem of optimal capital structure', Journal of Business 51(1), 103-114. https://doi.org/10.1086/295987 [ Links ]
Chan-Lau, J., 2009, 'FX-adjusted local currency spreads', CEME Fellows Research Briefing Series 1(2), 1-10. [ Links ]
Engle, R. & Granger, G., 1987, 'Co-integration and error correction: Representation, estimation and testing', Econometrica 55(2), 251-276. https://doi.org/10.2307/1913236 [ Links ]
Frank, M. & Goyal, V., 2003, 'Testing the pecking order theory of capital structure', Journal of Financial Economics 67, 217-248. https://doi.org/10.1016/S0304-405X(02)00252-0 [ Links ]
Gatev, E., Goetzmann, W. & Rouwenhorst, K., 2006, 'Pairs trading: Performance of a relative-value Arbitrage rule', The Review of Financial Studies 19(3), 797-827. https://doi.org/10.1093/rfs/hhj020 [ Links ]
Geske, R., 1977, 'The valuation of corporate liabilities as compound options', Journal of Financial and Quantitative Analysis 12(4), 541-552. https://doi.org/10.2307/2330330 [ Links ]
Geske, R.L. & Delianedis, G., The components of corporate credit spreads: Default, recovery, taxes, jumps, liquidity, and market factors, December 2001, UCLA Anderson working paper no. 22-01. Available from SSRN: https://ssrn.com/abstract=306479 or http://dx.doi.org/10.2139/ssrn.306479 [ Links ]
Graham, J. & Leary, M., 2011, 'A review of empirical capital structure research and directions for the future', Annual Review of Financial Economics 3, 309-345. https://doi.org/10.1146/annurev-financial-102710-144821 [ Links ]
Harris, M. & Raviv, A., 1991, 'The theory of capital structure', The Journal of Finance 46(1), 297-355. https://doi.org/10.1111/j.1540-6261.1991.tb03753.x [ Links ]
Hull, J., 2012, Options, futures and other derivatives, 8th edn., Prentice Hall, Upper Saddle River, NJ. [ Links ]
Hull, J., Nelken, I. & White, A., 2004, 'Merton's model, credit risk and volatility skews', Journal of Credit Risk 1(1), 3-27. https://doi.org/10.21314/JCR.2005.004 [ Links ]
Leland, H., 1994, 'Corporate debt value, bond covenants, and optimal capital structure', Journal of Finance 49(4), 1213-1252. https://doi.org/10.1111/j.1540-6261.1994.tb02452.x [ Links ]
Merton, R., 1974, 'On the pricing of corporate debt: The risk structure of interest rates', Journal of Finance 29, 449-470. [ Links ]
Modigliani, F. & Miller, M., 1958, 'The cost of capital, corporation finance and the theory of investment', The American Economic Review 48(3), 261-297. [ Links ]
Myers, S., 2001, 'Capital structure', The Journal of Economic Perspectives 15(2), 81-102. https://doi.org/10.1257/jep.15.2.81 [ Links ]
Titman, S. & Wessels, R., 1988, 'The determinants of capital structure choice', Journal of Finance 43(1), 1-19. https://doi.org/10.1111/j.1540-6261.1988.tb02585.x [ Links ]
UBS, 2011, UBS - Commodities investment products, CMCI technical document, UBS Investment Bank, Zurich. [ Links ]
 Correspondence:
Correspondence:
Leon Sanderson
lsanderson@mweb.co.za
Received: 31 Mar. 2017
Accepted: 18 Oct. 2018
Published: 14 Feb. 2019














