Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Economic and Management Sciences
On-line version ISSN 2222-3436
Print version ISSN 1015-8812
S. Afr. j. econ. manag. sci. vol.21 n.1 Pretoria 2018
http://dx.doi.org/10.4102/sajems.v21i1.1772
ORIGINAL RESEARCH
Income growth, population and savings in the Southern Africa Development Community region
Greenwell Matchaya; Charles Nhemachena; Sibusiso Nhlengenthwa
International Water Management Institute, Pretoria, South Africa
ABSTRACT
BACKGROUND: The Southern Africa Development Community (SADC) faces pervasive income stagnation, high inequality, increasing population growth rates and poverty. For example, despite that half of SADC countries are low middle income (as opposed to low income), high inequality implies that many people in the region still live in poverty. While literature is replete with theories linking low incomes to population growth and savings, empirical evidence is context specific and often mixed.
AIM: There is a dearth of strong empirical evidence that shows empirical linkages between population growth rates, incomes and savings in the SADC and this article aims to investigate these linkages. Specifically, the aim is to empirically understand the impact of population growth, savings and investment in human capital, on incomes.
SETTING: We focus our investigation on the Southern Africa Development Community (SADC), which comprises 16 countries namely, Angola, Botswana, Namibia, Lesotho, Swaziland, South Africa, Malawi, Mozambique, Zambia, Zimbabwe, Tanzania, Democratic Republic of Congo, Madagascar, Mauritius, Seychelles and Comoros.
METHODS: To achieve the goals of this study, we analyse data from 1977 to 2014 obtained from the World Bank databases and use ordinary least squares, fixed effects, random effects and Arellano-Bond dynamic panel-data estimation techniques to investigate the relationships between incomes, population growth and savings.
RESULTS: Our findings support the existence of a negative relationship between high population growth rates and income per capita, as well as a positive relationship between capital accumulation (human capital), savings and income per capita growth. Shares of savings in relation to gross domestic product (GDP) of countries in the SADC stand at under 16% of GDP (compared to shares of over 30% in developed countries) and are particularly worrisome.
CONCLUSION: There is a case for a concerted effort by the SADC Member States to control population growth, encourage schooling and, further, encourage a 'savings culture' in order for the SADC region to achieve its aspirations of eradicating poverty and hunger as outlined in Agenda 2063 and even the Sustainable Development Goals.
Introduction
The goal of this article is to examine the effects of various factors including population growth and human capital on income per capita. A great abundance of literature, including Mankiw, Romer and Weil (1992), McQuinn and Whelan (2007), Barrow (1989) and Lucas (1988), appears to converge on the conclusion that economic growth affects the rate of population growth, and vice versa, and the exact relationship between the two is often contextual. For example, economic development may affect population growth in several ways including: availability of modern methods of birth control which may control birth rates, availability of medicines which may increase life spans, availability of high wage employment which increases the opportunity cost of maternity leave such that women would prefer to work rather than looking after children.
In other studies, Sinesi (2003) and Lindh and Malmberg (1999) applied the life cycle consumption model and argued that the propensity to save was related to the age structure of the population. Higher proportions of old people in the population implied low saving rates. The proportion of old people was negatively related to savings and growth. They, therefore, argued for a negative relation between population ageing (due to slow population growth) and saving and growth.
The savings argument needs to be discussed further because of its importance in standard economic growth models. According to standard economic growth models (e.g. Solow 1956), one of the factors that affects growth is the aggregate rate of savings. Higher aggregate rates of savings are often correlated with higher economic growth (Barro & Sala-i-Martin 1995). Studies have shown that high population growth rates, however, lower the rate of aggregate savings. This happens simply because high population growth eats into aggregate income (Ray 1998). If it is true that the rich save higher fractions of their income, then savings rates may be adversely affected because high population growth entails high growth of the poor proportion of society (Ray 1998). More importantly, faster population growth shifts the age structure of the population towards the very young and in so doing increases the dependency ratio in families. Because children consume more than they produce, this tends to lower savings rates as well (Ray 1998:331). Of course, the other side of the argument is that it is possible that population growth may spur technological progress out of the pressures created by high population density (Boserup 1981). It is technological progress that ensures growth of an economy in the long run. On the other hand, population growth creates a large pool of potential innovators and, therefore, a larger stock of ideas and innovators that can be put to economic use (Kuznets 1960; Simon 1977). This would imply that high population growth rates are associated with high income per capita.
Unfortunately, most literature cited on the nexus between population growth, income per capita and savings, focus on countries outside Southern Africa, thereby creating an empirical gap in this area of study. Again, it is noted that perhaps owing to data challenges in the past, studies have been based on shorter time periods with limited variation which can render findings imprecise. This article attempts to fill this gap by investigating the determinants of income growth within the Southern Africa Development Community (SADC).
The investigation involves employing the Solow model framework both in its basic textbook form and augmenting it with human capital in the examination of determinants of income per capita.
Theoretical model and specification
The approach espoused in this article involves tackling the question of population growth and income per capita from two perspectives. The first step is to outline the Solow model, derive the first order differential equations, then estimate the Solow model in its basic as well as augmented forms. The Solow model is summarised below.
The Solow growth model
The standard Solow model takes the rates of savings, population growth and technological progress as exogenous, and further assumes two inputs in the production function namely capital (K) and labour (L), both of which receive their marginal products as returns (see Mankiw et al. 1992). Assuming a Cobb-Douglas production function with diminishing marginal returns to scale (where α + β < 1), production at time t is given as shown in Equation 1.
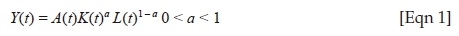
Y is output, A is technological progress. Labour and technology are assumed to grow exogenously at rates n and g, as depicted in Equations 2 and 3:


The number of effective units of labour A(t)L(t) then grows at the rate n + g.
Solow's model assumes that a constant fraction of output, s, is saved and reinvested. Defining y as the level of output per effective unit of labour, y = Y/AL, and k as the stock of capital per effective unit of labour, k = K/AL, the evolution of k is governed by Equation 4:
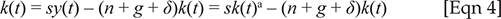
δ is the rate of depreciation. The steady state value k* to which k converges is defined by Equation 5:
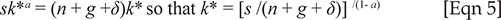
This implies that the steady state capital relates negatively to population growth rates but positively to savings rates.
In order to establish the relationship between income and savings and population growth (the gist of Solow's model), substitute Equation 5 into the production function and, upon taking logs, the steady state income per capita can be summarised as Equation 6:

Since the model assumes that factors of production, that is labour and capital, are paid according to their marginal products, it predicts the signs of the coefficients. It also predicts the magnitudes of the coefficients on savings and population growth. For example, if we make use of the a priori knowledge that the share of capital (α) in income is roughly one-third (see Mankiw et al. 1992), the model implies an elasticity of income with respect to savings rate of about 0.5 and an elasticity with respect to n+ g + δ of approximately −0.5. Of course, if the shares of capital in income are different, the elasticities will also be different, but the higher that share α, the higher the positive impact of savings on income per capita.
Specification of the model
When estimating the Solow model, therefore, it is of interest to investigate whether income per capita is higher in countries with higher savings rates and lower in countries with higher n+ g + δ. Here it is assumed that the technology advancement (g) and depreciation rate (δ) are constant across countries because technology changes affect many countries at a time, whereas there is no solid theory that may imply that depreciation rates can vary across countries. Initial technology endowments, A(0), constitute not only technology at that time, but also other idiosyncratic characteristics at country level and may differ across countries. Assuming it is governed by Equation 7.

α is constant and ε is country level idiosyncratic, then Equation 6 defining income per capital can be specified stochastically as Equation 8:

If it is assumed that ε is independent of s and n (which is at times a reasonable assumption as under isoelastic utility, permanent differences in levels of technology do not affect savings and population growth rates) then Equation 8 can be estimated with ordinary least squares (OLS) regression. Of course, in the event that the assumption of orthogonality between s, n and ε does not hold, OLS is inconsistent and another estimation procedure may be preferable. In this study, both OLS and models that account for possible endogeneity - including generalised method of moments (GMM) and generalised least squares (GLS) - are estimated and the results are presented and discussed. Again, if the estimated coefficients for s and n + g + δ are different from the predicted 0.5 and −0.5 then there may be reason to believe that the OLS estimation may be wrong (Mankiw et al. 1992).
The Solow model augmented with human capital
Assuming that the omitted variable human capital is a significant variable, then accounting for it may improve the fit of the model besides altering the magnitude of the parameters estimated previously. Once human capital is added, the model evolves differently such that the production function in Equation 1 may be rewritten as Equation 9:

H is the stock of human capital while everything else is as predefined. If sk is the fraction of income invested in physical capital and sh that part invested in human capital, the evolution of the economy is determined by Equations 10a and 10b


h = H/AL and stands for human capital per effective quantity of labour. Again, it is assumed that the same production function as before applies and that it has diminishing returns to scale.
From above, we can formulate Equations 11a and 11b:


Substituting Equation 11 into the production function and taking logs yields an income per capita equation similar to Equation 6 such that we arrive at Equation 12.

So, again, the evolution of income per capita depends on the accumulation of physical and human capital, as well as on population growth. The implication of this model is that the presence of human capital accumulation increases the impact of physical capital accumulation on income through the effect of the β. As before, α is expected to amount to one-third of the share of capital in income. If the levels of human capital are available, Equation 12 can be expressed differently by combining Equation 10 with Equation 9 to yield income per capita as a function of population growth rate, the rate of investment in physical capital and the level of human capital as shown in Equation 13.
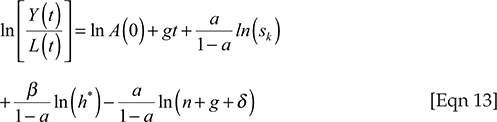
Equation 13 is similar to Equation 6 and now by implication means that savings and population growth are related to human capital, so that omitting it as in the first estimation yields potentially biased estimates. In the results that follow, model Equation 13 is also estimated.
Methodology
The data and empirical specifications of model variables
As stated a priori, the discussion on the interface between incomes and population growth is one that can be taken in various ways in the sense that population growth can affect incomes, whereas incomes can also affect population growth. In terms of multivariate econometric analysis, one would consider this fact as one that immediately invokes the issue of endogeneity and the problems that it presents, while attempting to isolate what actually determines the other.
The approach in this article is to, firstly, discuss the present descriptive statistics in various variables that may determine income per capita, and postulate prima facie through scatter graphs, the likely linkages between income and such different factors. Then a series of OLS regression analysis is performed in the article to establish partial correlations between population, incomes and savings. We further perform estimation within the framework of GLS models assuming fixed effects, as well as random effects and compare the results. Finally, we also fit the system dynamic panel-data estimation (GMM). In each case we compute various statistics for model fitness and for the GLS estimation, we compute the Hausman specification test to ascertain any differences between the random effects formulation and the fixed effects model and we report all the results in one table. The main policy conclusions are based on the OLS because the coefficients approximate those predicted in Mankiw et al. (1992), and yet we should also state that the qualitative conclusions are almost unchanging across estimation procedures.
Results and discussions
The data in Table 1 shows single points of data on gross domestic product (GDP) per capita, birth rates, death rates and population growth rates.
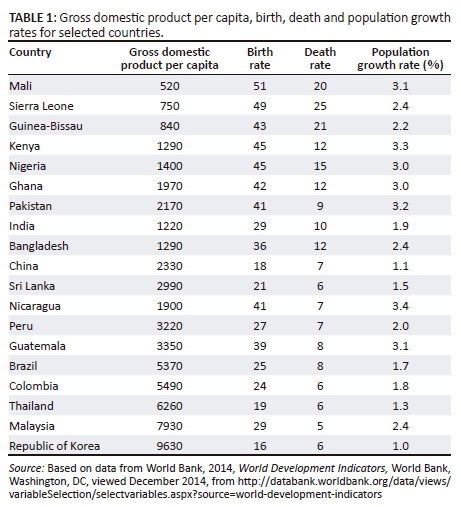
It is clear from Table 1 that there is an observable pattern between death rates, birth rates, population growth rates and income per capita. In fact, most countries with lower- income per capita are also the ones associated with higher population growth rates. This relationship is further investigated later in this article.
Table 2 similarly presents the same kind of information but using more recent data and only for the SADC region, and also expands the exposition to include savings rates for each country at that particular year of observation.
In summary, therefore, both Tables 1 and 2 show that high population growth rates are associated with low income per capita and they exist together with high mortality and high birth rates. This of course implies that policies that seek to reduce population growth can also increase income per capita and vice versa. For the SADC region, it is interesting to note that even among the SADC countries, the countries with highest population growth rates are usually those associated with low income per capita. For example, Malawi, Tanzania, Zimbabwe, Madagascar have close to 3.0% population growth, whereas the middle-income countries generally have a lower growth of 1.9% (see South Africa, Botswana, Swaziland, Lesotho, Namibia and Mauritius). This is further evidence of a negative correlation between population growth rates and income per capita. Notice that the last column in Table 2 shows country level savings rates. As was discussed earlier, the relationship between population growth and income per capita reflects in a number of ways including through savings decisions and the capacity of the population. It also deserves repeating that for the SADC region, high savings rates, are on average associated with low population growth rates and are further associated with higher incomes. In the next paragraphs we now discuss statistical analyses to confirm the prima facie evidence discussed a priori.
If one considers both the SADC and outside SADC data in Tables 1 and 2 and fits a regression model to understand the nature of the relationship between the two variables, income per capita and population growth, the resulting statistics can be summarised in Figure 1.
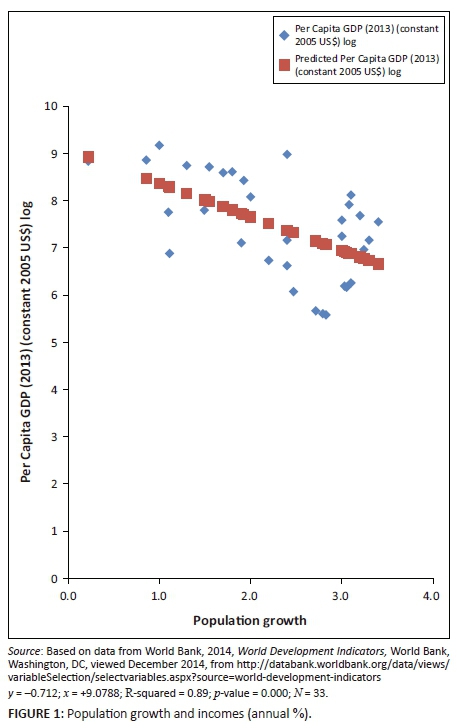
This figure shows that there is indeed a highly significant inverse relationship between income per capita and population growth, which perhaps is evidence that one of the pathways, discussed previously (savings), is responsible for bringing this relationship to the fore. The implication is, of course, that countries with high population growth rates may unlikely be the ones reducing poverty over time, unless they find a way of applying the high population economically, or unless they create policies that will reduce consumption and enhance savings. If the effects of population growth on income per capita goes through savings, then it must be confirmed statistically that there is a negative relationship between population growth and savings.
As discussed previously, savings are one of the key elements through which population growth impacts on income growth.
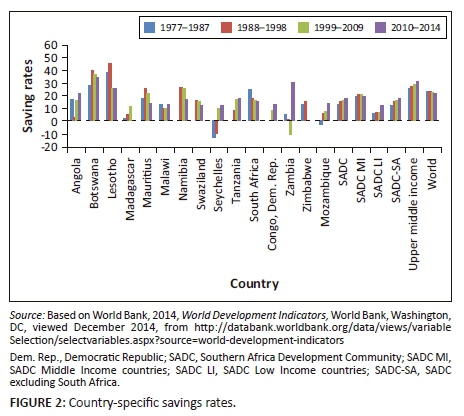
Figure 2 shows trends of savings for groups of countries including the upper middle-income countries of the world (UMI), sub-Saharan African countries (SSA), the world saving averages (World), SADC, SADC middle-income (SADC MI), and SADC low income (SADC LI). Of course, the first trend to note is that, at around 15% of GDP, the saving rates in the SADC region are very low compared to those in UMI countries which stand at around 30% and above and are also lower than the world averages which are just under 25% of GDP. Again, it is not surprising perhaps to note that within the SADC region, SADC MI countries are associated with higher (around 20%) savings, compared to the SADC LI countries whose saving rates are often below 10% of GDP. Again, considering that the SADC LI countries are also associated with higher population growth rates, it would appear that population growth and savings rates are negatively related. Of course, another important observation is that savings rates for various groups tend to remain around the same level for longer periods of time and, although there is intertemporal variation, such variation appears to be contained within tight bounds.
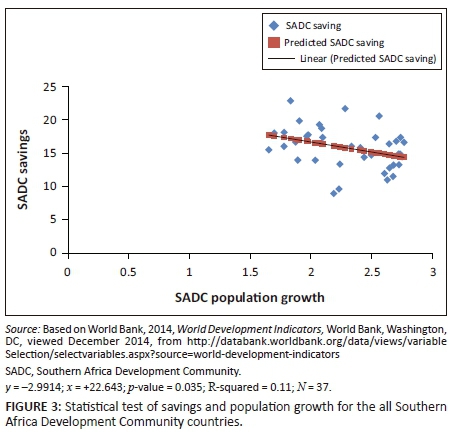
As discussed previously under the theory section, population growth affects incomes through a number of ways, including savings. Usually a country whose population grows very fast ends up having high dependency ratios. The continent of Africa does not have a big problem of an ageing population, but rather with a youthful one, who consume more than they can produce. Savings then are impacted because they can be conceived as gross income minus consumption. In practice, if this relationship was in operation, then a regression of savings on population growth, needs to depict a negative relationship and if such a relationship is significant, it consolidates the evidence.
Figure 3 shows that indeed savings appear to be affected by population growth rates and that the statistical relationship is significant at 0.035 level of significance. This then supports the theory of savings and population growth, in other words, ceteris paribus, higher rates of population growth depress savings of a household and a country.
Population growth effects in the SADC appear to be complicated by the fact that, life expectancy is generally low and, at any point in time, children constitute a huge proportion of the population. A simple regression model of income per capita that recognises the differential impact that age groups have on income per capita, shows that indeed in the short run, an increase in children (0-14 years) in a population negatively affects income per capita, whereas an increase in the working population (15-64 years) is good for increasing incomes (see Table 3).
The results in Table 3 remain unchanged even if the model is estimated in the form of lags to account for the fact that the effect does not have to be contemporaneous. Population growth that spurs as a result of high fertility, unlike one that ensues as a result of reduced death rates among the adult population, is likely at odds with the goals of fast economic growth, as it eats into incomes and leaves very little for savings and investment and future economic growth. Of course, the next step is to confirm whether savings and income per capita are related positively. Evidence that growth rates in income per capita and savings are positively related would strengthen the indirect linkage that population growth has on income growth.
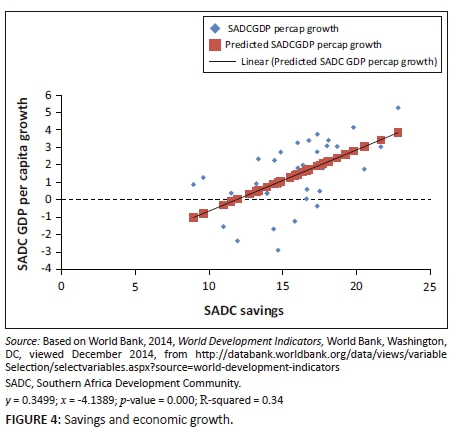
Figure 4 shows the relationship between savings of a country and rates of income growth, and it is clear that the two are related positively in a highly significant relationship (p-value = 0.000).
Results from the basic Solow model
In estimating the Solow growth model this article follows Mankiw et al. (1992) and first deals with OLS estimation which in most cases should suffice, unless the data reject the orthogonality assumption needed for consistency in the model, or unless the results deviate significantly from what the Solow model predicts about the signs and magnitudes of the coefficients.
The data used herein, obtained from the World Bank as well as national sources, include savings as a share of GDP, working population in every country, defined as population aged between 15 and 64 years, income per capita for each country in the SADC, and population growth. The contribution of technology growth and capital depreciation are assumed to amount to 0.05 across the board in line with literature on the topic.
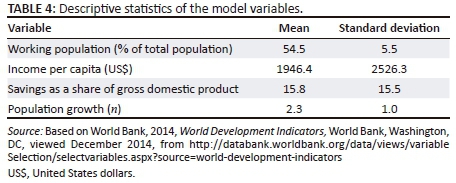
It is interesting to note in Table 4 that over the period (1977-2014) income per capita in the SADC averaged US$1947 with some countries registering incomes of as low as $102 despite other countries enjoying as high as $15700 per capita, implying a mix of countries. Average savings rates were 15.8% of GDP, with a standard deviation of 15.5, and average population growth stood at 2.3%. Human capital is proxied by the number of people entering primary and secondary school and particularly primary school enrolment. In developing countries such as those of the SADC, primary school enrolment can proxy the levels of investments by government in human capital improvement. This information is then used to estimate the Solow growth models.
Interestingly, the data for the sampled period and countries appear to fit the Solow model quite well.
Table 5 shows that the estimated coefficients for log of savings and log of n + g + δ are 0.452 and −0.518 and they are highly significant at the 1% level of significance. These coefficients are not only similar to the Solow model predictions in terms of signs, they are also similar in terms of predicted magnitudes of 0.5 and −0.5. In both cases, the implied magnitude of α is around 0.31 and 0.34 which are also the ones expected from theory and literature as capital's share in income (which is about one-third). The test about equality of the coefficients for log of savings and log n + g + δ also confirms the observation that the two are equal in magnitude save for signs.
From these results, this article concludes that although the explanatory power of the model is 0.27 and may suggest that there are other variables that may explain income determination, the Solow model cannot be rejected outright and in fact in the SADC region, countries that have high savings rates are associated with high income growth rates, whereas those with high population growth rates are likely to be associated with low income growth rates. This confirms some of the priori findings explained earlier in this article. Since a test for constant variance was rejected, the standard errors for all OLS regressions are obtained using the Huber-White methodology by utilising the 'robust' subcommand in STATA.
Results from the augmented Solow model
The adjusted R-square improves with addition of human capital, and the model is still consistent with Solow in terms of the coefficients for savings and n + g + δ. However, one notes that human capital, as proxied by the gross enrolment rate at primary school level, which is a proxy for schooling investment, is significant and has a coefficient of 1.5 implying that ignoring human capital omits a variable in Table 5. It may thus be argued that because human capital is significant in this model and it was omitted in the previous one, then perhaps the coefficients of savings and population growth were biased in the previous OLS estimation. This would confirm that, in theory, the level of human capital is positively related to the savings rate (as more good human capital relates to more savings), as well as negatively related to population growth (as high population growth implies less capital saved). The inclusion of human capital also marginally reduces the elasticity of physical capital on income per capita and improves the fit such that now the model explains 33% of cross-country variation on income per capita in the SADC. Allowing for human capital eliminates biases due to variable omissions and improves the fit of the model although the share parameters α are about 0.3 in each case.
The potential variable omission motivates the need for the search for other estimation techniques. Various estimation techniques accounting for endogeneity, including Arellano-Bond dynamic panel-data estimation, as well as system dynamic panel-data estimation, were fitted and the results are presented. They yield findings that are slightly different from the predictions of the Solow model, but all qualitative conclusions regarding direction of effects and significance of parameters appear to suggest that estimates obtained by OLS estimation1 remain valid.
Thus, whereas population growth may impact on economic growth in various ways, it appears that one of the ways, which is also supported by theory, is through savings. An increase in population growth, ceteris paribus, depresses the prospects of high savings because most output is consumed and the marginal propensity to consume is high. Empirically it is also confirmed here in that savings are important for economic growth in the SADC region.
The GLS estimates using the fixed effect (FE) estimator were not different from those obtained using the random effects (RE) estimator and, in fact, a Hausman specification test to confirm any systematic differences in coefficients rejected the presence of such differences between FE and RE estimates2. At about 0.19 for savings and −0.26 for population growth, the estimated coefficients in both GLS models were similar, but in each case smaller compared to the 0.4 and −0.4 magnitudes obtained through OLS for the savings and population growth. The coefficients for human capital appeared similar and, in any case, suggested that a 1% increase in human capital would yield a more than 1% increase in income per capita.
The system dynamic panel-data estimation (GMM) yielded even smaller coefficients in every case but with similar direction of change. For this specific estimation technique, human capital had a positive sign but was not significant.
Because of the similarities between the OLS, GLS and GMM results, we base our conclusions on OLS estimates in line with literature and so this should not be considered a limitation (see Mankiw et al. 1992). Again, whereas time series data generally presents problems of multicollinearity, and auto correlation, the variables herein did not present multicollinearity problems and tests for autocorrelation rejected autocorrelation. While homoscedasticity assumption was rejected (Chi2(1) = 5.68; Prob > chi2 = 0.01), we used the Huber-White standard robust errors to correct for heteroskedasticity.
The coefficient of savings indicates that in a typical SADC country, a 1% increase in savings as a share of GDP would yield closer to a 0.5% increase in income per capita, but if the population growth in that country increases by 1%, then income per capita could decrease by 0.5%. This implies that economic growth without controlling population growth may have no effect on poverty reduction. Again, a 1% increase in human capital may lead to a more than 1.4% growth in income per capita implying that a country that invests in human capital development stands to gain more in terms of poverty reduction in the long term. Thus, it is important to ensure that SADC governments prioritise human capital development, a savings culture and should control population growth.
Figure 5 shows the effects of a 50% increase in human capital, and a 50% increase in savings within the SADC countries as well as a 50% reduction in population growth. The results show through an upward shift in income per capita that in each case income per capita would increase by several hundred US$, but that human capital improvements lead to more increase in income per capita than an increase in savings or a decrease in population growth. Population decay ranks second as a means of increasing income per capita3.

If human capital had improved by 50%, by 2011 the average income per capita in the SADC would have been US$2440 (i.e. e^7.8) which is more than, and almost double, the actual $1339 (e^7.2). For the same year, if population growth had been cut by half, income per capita would have been improved to $1998 (i.e. e^7.6) from $1339 (e^7.2). On the other hand, a 50% increase in savings around 2011 would have been associated with an average income per capita of around $1636 (i.e. e^7.4) which is more than the actual $1339 for 2011.
Conclusion
This article's objective was to analyse the links between income per capita growth, savings and population growth. Using partial correlations and both the Solow basic growth model and the augmented Solow model, this article finds evidence to support the existence of a negative relationship between very high population growth rates and income per capita, as well as a positive relationship between savings and income per capita. An increase in population growth, ceteris paribus, depresses the prospects of high savings because most output is consumed and the marginal propensity to save is low. The basic Solow growth model with labour and capital appears to fit the data well, although the fit improves with the inclusion of the levels of human capital involved. Investment in human capita, and investments in physical capital appear to positively affect income growth, whereas population growth negate income per capita.
Countries, including Malawi, Tanzania, Madagascar and Lesotho among others, need to reduce overexpenditure by government and invest more in productive capital (see, e.g., Matchaya, Chilonda & Nhlengethwa 2014). There is need for the SADC region to embark on a campaign to increase savings rates which currently average under 16% of GDP to closer to 30%, in line with what is observed in developed countries, as well as to reduce population growth which in some cases is as high as 3.2 % to under 2%.
Acknowledgements
We are grateful to the Bill and Melinda Gates Foundation, the United States Agency for the International Development (USAID) and the International Food Policy Research Institute (IFPRI) who supported the researchers with funding for various activities in support of the Comprehensive Africa Agriculture Development Program, one of which led to this article.
Competing interests
The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.
Authors' contributions
G.M. conceptualised the article content and completed the first draft. C.N. and S.N. revised and made conceptual contributions, additions and refined the article.
References
Barro, J. & Sala-i-Martin, X., 1995, Economic growth, MacGraw-Hill, New York. [ Links ]
Barrow, R., 1989, Economic growth in a cross section of countries, NBER Working Paper 3120, National Bureau of Economic Research, Cambridge, MA. [ Links ]
Boserup, E., 1981, Population and technological change: A study of long run trends, University of Chicago Press, Chicago, IL. [ Links ]
Kuznets, S., 1960, 'Population change and aggregate output', in Demographic and economic change in developed countries, National Bureau of Economic Research special Conference Series, Princeton University Press, Princeton, NJ. [ Links ]
Lindh, T. & Malmberg, B., 1999, 'Age structure effects and growth in the OECD, 1950-1990', Journal of Population Economics 12, 431-449. https://doi.org/10.1007/s001480050107 [ Links ]
Lucas, R.J., 1988, 'On the mechanics of economic development', Journal of Monetary Economics 22, 3-42. https://doi.org/10.1016/0304-3932(88)90168-7 [ Links ]
Mankiw, N.G., Romer, D. & Weil, D.N., 1992, 'A contribution to the empirics of economic growth', The Quarterly Journal of Economics 107, 407-437. https://doi.org/10.2307/2118477 [ Links ]
Matchaya, G., Chilonda, P. & Nhlengethwa, S., 2014, Inter-temporal trends and patterns in agricultural investment spending in Southern Africa, International Food Policy Research Institute (IFPRI) and the International Water Management Institute (IWMI), Washington, DC and Colombo. [ Links ]
McQuinn, K. & Whelan, K., 2007, 'Conditional convergence and the dynamics of the capital-output ratio', Journal of Economic Growth 12, 159-184. https://doi.org/10.1007/s10887-007-9013-3 [ Links ]
Ray, D., 1998, Development economics, Princeton University Press, Princeton, NJ. [ Links ]
Simon, J., 1977, The population of economic growth, Princeton University Press, Princeton, NJ. [ Links ]
Sinesi, P., 2003, 'Population dynamics and life-cycle consumption', Journal of Population Economics 16, 389-394. https://doi.org/10.1007/s001480200127 [ Links ]
Solow, R.M., 1956, 'A contribution to the theory of economic growth', Quarterly Journal of Economics 70, 65-94. https://doi.org/10.2307/1884513 [ Links ]
World Bank, 2014, World Development Indicators, World Bank, Washington, DC, viewed December 2014, from http://databank.worldbank.org/data/views/variableSelection/selectvariab les.aspx?source=world-development-indicators. [ Links ]
 Correspondence:
Correspondence:
Greenwell Matchaya
g.matchaya@cgiar.org
Received: 31 Jan. 2017
Accepted: 06 Aug. 2018
Published: 16 Oct. 2018
1 . Results for GMM estimation are not reported here but amount to the same conclusions.
2 . Chi(3) = (b-B)′[(V_b-V_B)^(−1)](b-B) = 1.53; Prob > Chi2 = 0.6760
3 . The y-axis shows the natural logarithm of income per capita.














