Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Economic and Management Sciences
On-line version ISSN 2222-3436
Print version ISSN 1015-8812
S. Afr. j. econ. manag. sci. vol.21 n.1 Pretoria 2018
http://dx.doi.org/10.4102/sajems.v21i1.1744
ORIGINAL RESEARCH
Filter selection for countercyclical capital buffers
Dirk Visser; Gary van Vuuren
Department of Risk Management, School of Economics, North-West University, South Africa
ABSTRACT
BACKGROUND: Procyclicality plays a pivotal role in finance in both thriving and crisis periods. This influence stems not only from the way market participants behave but also from risk metrics used and regulatory capital amassed and released during bust and boom periods, respectively. The introduction of the regulatory Countercyclical Capital Buffer aims to thwart procyclicality by accumulating (releasing) capital in upswings (downswings), subsequently reducing the amplitude of the financial cycle and promoting macroprudential stability. The timing of the accumulation and release of buffer capital is critical so identifying accurate indicators is important.
AIM: This paper applies a Kalman filter to South African data and confirms the procyclicality of the Basel Committee on Banking Supervision (BCBS) proposal.
SETTING: For South Africa, studies suggest alternatives such as residential property indices because research has demonstrated that the BCBS proposal is procyclical rather than countercyclical.
METHODS: This paper applies a Kalman filter to South African data and compares the results obtained with those filtered using the Hodrick-Prescott filter.
RESULTS: Results indicate that buffer signals are dependent upon the filter employed.
CONCLUSION: Buffer signals are strongly dependent upon the filter employed to detect procyclicality. The South African Reserve Bank and other regulators should reconsider the use of the Hodrick-Prescott filter and entertain the possibility of using the Kalman filter instead.
Introduction
The procyclical nature of financial markets is well documented as are the intrinsic procyclical characteristics of regulatory capital regulations prior to Basel III. Several studies including Heid (2003), Gordy and Howells (2004) and Goodhart and Taylor (2006) forewarn that the procyclical nature of regulatory requirements impede macroeconomic stability as these regulations force institutions to retain more capital in low-profit, liquid divisions when they may need to continue extending credit. This institutional behaviour and the inability of risk measurements to capture this phenomenon proved to be disastrous in the 2008/2009 financial crisis. Conventional measures such as Value at Risk (VaR) and its successor, expected shortfall (Basel Committee on Banking Supervision [BCBS] 2013), do not account for procyclicality as these metrics are volatility-based measures that use procyclical historical data (these have no components which indicate the financial cycle's position).
The BCBS proposed the implementation of a Countercyclical Capital Buffer (CCB) to promote the macroprudential goal of protecting banking sectors from periods of excess aggregate credit growth (BCBS 2010a, 2010b). These periods have historically been associated with the build-up of system-wide risk and the CCB thus aims to ensure institutions are not only solvent through stress periods but also able to maintain the flow of credit. Research on the CCB since its introduction has been plentiful, but the metric has several indicator components that signal the retention of a CCB buffer as well as indicators that signal the buffer's release. Determining these signals has received significant interest, because, initially, the BCBS (2010b) only mentioned a one-sided Hodrick-Prescott (HP) filter1 in a footnote.
Use of the one-sided HP filter has been questioned (Edge & Meisenzahl 2011; Kelly, McQuinn & Stuart 2013; Van Vuuren 2012) because of the endpoint problem associated with the metric as well its sensitivity to changes or revisions of many macroeconomic variables such as gross domestic product (GDP) and inflation. Hosszú, Körmendi and Mérő (2015) applied several univariate and multivariate filters to decompose the credit-to-GDP ratio into trend and cyclical components. Their research finds a multivariate HP filter to be most effective as its endpoint uncertainty is the least, with the result that new data do not materially affect previous estimates too much. Galati et al. (2016) apply a Kalman filter2 to extract cycles from financial time series data for the U.S. and the Euro area. They find that series including credit, credit-to-GDP and real house prices demonstrate medium-term cyclical behaviour and that the periodicity and amplitude of these cycles vary over time and between countries. They further find that, since the mid-1980s, U.S. financial cycles have increased in duration and amplitude whereas such conclusions cannot be made for the Euro area.
Procyclicality research in South Africa includes that of Akinboade and Makina (2009, 2010) in which the linkage between the behaviour of bank lending and business cycles in South Africa is assessed. They found new mortgage lending to be countercyclical prior to 1993 and that bank lending and interest rates moved in tandem with business cycles. Fourie, Botha and Mears (2011) attempted to determine the role banks play with regards to the amplification of business cycles and the subsequent macroeconomic impact. These studies did not, however, focus expressly on the credit-to-GDP gap. South African research on the credit-to-GDP gap and the CCB is increasing as its implementation is currently (2017) in a staggered implementation approach. Van Vuuren (2012) implemented both a single and a two-sided HP filter on South African data to illustrate the possible CCB capital charges under both approaches.
Burra et al. (2014) discussed practical considerations for the CCB in South Africa as proposed in Basel III. They found several series including credit extension, advances to the domestic private sector and house prices to be positively correlated with GDP growth. However, the credit-to-GDP gap was found to be negatively correlated with GDP growth, suggesting that buffers would accumulate in downturns, thereby fuelling procyclicality rather than countering it. They affirm that accurate build-up signals remain; however, they were significantly weaker in the buffer's release phase. Bernstein, Raputsoane and Schaling (2014) applied a Logistic Smooth Transition Autoregressive model to assess the credit-to-GDP as the recommended common reference for CCB implementation. The authors found that the credit-to-GDP gap decreased when the economic cycle experienced upturns and vice versa and thus caution the use of this standard as a uniform or mechanical estimate of countercyclical South African capital buffers.
The Kalman filter - which was originally developed to provide aeronautical navigation - offers a different, but parsimonious and accurate solution to the problem of time-dependent variable estimation. The Kalman filter enjoys the advantage of real-time application. Time series observations are used to forecast future observations (as in most forecast applications), but in the Kalman filter case the state variables (which define the forecast framework) are 'optimal', being determined via minimisation of the variance between prediction and observation differences by rapidly reacting to changing conditions. This makes the Kalman approach to the problem of time-dependent variable estimation extremely practical to financial practitioners (see, e.g. Jain, Yongvanich & Zhou 2011; Thomson & Van Vuuren 2017).
The Kalman filter is a recursive procedure for computing the optimal estimator of the state vector at time t+1, based on information available at time t (Arnold, Bertus & Godbey 2008; Kalman 1960), which provides a linear estimation method for equations represented in a state-space form. Estimation problems are transformed into state-space by defining state vectors. The Kalman filter output is governed by two equations: a measurement equation and a transition equation. The measurement equation unites unobserved data (xt where t represents the time of measurement) and observed data (yt) by the equation, yt = mxt + vt, where E[vt] = 0 and the variance of the error term, Var[vt], is known (rt). The transition equation describes the evolution in time of unobserved data, such that xt+1= axt + wt, where E[wt] = 0 and the variance of the error term, Var[wt], is unknown (qt).
The remainder of this paper proceeds as follows: Literature study section explores the literature regarding procyclicality and the CCB from an international and South African perspective, respectively. The choice and extent of the data are explained in 'Data and methodology' section as well as the mathematics of the various filters including the Kalman filter. The logic behind how filters reduce signal variance when estimating unobserved moments is also discussed here. Results obtained from analysis are illustrated and discussed in the fourth section and the last section provides the conclusions.
Literature study
Procyclicality
The Basel III accord, which was introduced to address shortcomings of Basel II (recall that Basel III did not replace Basel II), places significant emphasis on reducing procyclicality through the introduction of several regulatory measures. Subsequent guidelines by the BCBS address implementation and measurement considerations of these measures including the CCB. The BCBS identified procyclicality as one of the most destabilising elements with regards to the amplification of financial shocks in the banking sector throughout the 2008/2009 financial crisis (BCBS 2010a).
Procyclicality's ability to act as a financial accelerator in both expansions and contractions lies in information asymmetries between borrowers and lenders (Borio, Furfine & Lowe 2001). In distressed economic environments (where collateral values decline), even profitable borrowers struggle to find access to credit as institutions are more risk adverse and must retain more capital as suggested by procyclical regulatory capital models. In benign economic conditions, where credit extensions occur with fewer restrictions, institutions chase profitable positions as capital does not have to keep liquid reserves - thereby temporarily reinforcing the cycle's upswing. Borio et al. (2001) argued that the worst excesses of financial cycles can be mitigated; however, this requires the acknowledgement of increased risk in boom periods and that the materialisation of bad loans does not necessarily imply an increase in risk. Measurement difficulties and biases have also contributed to the effects of cycle excesses and procyclicality. Market participants often struggle to optimally assess how correlations between credit losses across borrowers and the financial institutions change over time (Drehmann, Borio, Tsatsaronis 2012). This, along with other measurement complications, has led to short horizons and extrapolation of current conditions further into the future than possibly deemed appropriate (Borio et al. 2001). Complicated risk measurement techniques, market participant behaviour and existing regulatory capital have all contributed to the phenomena of procyclicality and are all being addressed in the drive to mitigate it. Borio (2012) asserts that it is critical to rediscover the role of the financial cycle and its empirical features like procyclicality in macroeconomics as it is closely related to systemic crises.
The financial crisis accelerated endeavours to mitigate procyclicality (Van Vuuren 2012), with regulators proposing changes to accounting standards, risk measurement practices and the conduct of monetary policy. Further measures included the introduction of noncyclical probability of default proxies in internal rating models and the CCB to address the phenomena.
Countercyclical capital buffer
Basel III's countercyclical objectives attempt to dampen the cyclical effects stemming from minimum capital requirements as well as promote forward-looking provisioning. The build-up of capital buffers to be used in stress periods at individual bank and sector level aims to achieve a macroprudential goal of guarding the banking sector against periods and aftermaths of excessive credit growth (BCBS 2010a). Drehmann et al. (2010) suggest that the ultimate goals for CCB schemes are twofold. Firstly, the schemes should attempt to limit risk of large-scale strains on banking systems. Secondly, the schemes should attempt to limit the banking system and its participants from amplifying economic (cycle) fluctuations. To achieve these closely related goals, the authors suggest desirable characteristics off a CCB scheme which include the following:
-
correct implementation and timing
-
appropriate size (the buffer should not impede growth)
-
robust to capital arbitrage and manipulation
-
internationally enforceable
-
rules-based
-
low implementation cost
-
simple and transparent.
Drehmann et al. (2010) suggest that achieving all these features present significant challenges as fully rules-based schemes allow for no judgement of false signals. Furthermore, making these schemes simple and transparent as well as internationally enforceable limits modelling-based measures. The top-down approach is preferred by the BCBS for CCB schemes because credit-to-GDP gap data are readily available for all jurisdictions, whereas this is not the case for bottom-up data. Bottom-up data also produced substantial individual components, suggesting that differences in the values of bank-adjusted factors would be large even under periods of broad financial stability (Drehmann et al. 2010).
Measurement techniques
Galati et al. (2016) assert that previous investigations into financial cycles and their statistical properties focussed on three approaches. Firstly, attempts to identify turning points focussed on positions of peaks and troughs. Claessens, Kose and Terrones (2011) rely on a classical3 definition of a cycle to analyse how business and financial cycles interact and the implications thereof. Their data for housing, equity and credit markets and GDP from 44 countries accounting for 90% of global output are grouped into advanced and emerging economies. Similar research by Boshoff (2006) analyses the cyclicality of financial markets in relation to the cyclical behaviour of the South African real economy and identifies turning points for several domestic and international variables. Both Boshoff (2006) and Claessens et al. (2011) rely on the fundamental methodological foundations produced by Burns and Mitchell (1946) for business cycle turning-point analyses.
Secondly, Galati et al. (2016) suggest that statistical frequency-based filters include the HP filter, the Baxter-King filter (1999) and the Christiano and Fitzgerald (2003) filter. These require prespecification of the range of cycle frequencies and thus are referred to as non-parametric filters. These have been increasingly interrogated and compared since the introduction of Basel III to determine superiority under different scenarios compared to the BCBS's one-sided HP filter.
International research for these filters are plentiful as the BCBS (in its guidance for national authorities operating the CCB [BCBS 2010b]) conduct analysis for several countries using a one-side HP filter. This was followed by several studies affirming or contradicting the use of a one-sided HP filter and other frequency-based filters. These studies include Drehmann et al. (2010) and Aikman, Haldane and Nelson (2015). South African research includes that of Van Vuuren (2012), who estimated the credit-to-GDP gap using both a one- and two-sided HP filter to illustrate the implications of CCB charges. Unresolved questions include the lack of BCBS clarification on why a one-sided HP filter has been suggested and how the jurisdiction-wide measure will influence individual bank operations. A Basel III update has since clarified on how bank-specific CCBs can be calculated using their individual credit exposures (BCBS 2010a).
Finally, the third approach involves unobserved component time series models, which include the Kalman filter. These have several advantages compared with non-parametric filters including no requirements regarding self-imposed, ad hoc parameters and the relaxation of the requirement for predetermined frequencies required to extract cycles. Kalman filters function with non-normal data, a useful attribute because financial data commonly exhibit fat tails. These models also present more accurate estimations because model-based filter diagnostics can be used to validate models and estimate their goodness of fit. International research for the Kalman filter include numerous studies analysing business cycles, that is, Valle Azevedo, Koopman and Rua (2006), Koopman and Azevedo (2008) and Creal, Koopman and Zivot (2010); however, few have expressly focussed on financial variables. Galati et al. (2016) attempted to measure financial cycles for the United States and the Euro using a Kalman filter and found that financial cycles are longer than business cycles and have higher amplitudes. Extracting cycles from business failure rates, real GDP and credit spreads, Koopman and Lucas (2005) found comparable medium-term cycles for U.S. data. South African research on financial cycles using the Kalman filter has not yet been conducted.
A more dynamic, forward-looking buffer variation suggested by Wong (2011a, 2011b) manipulates time series data through an inflator to produce increased capital requirements for both market and credit risk. The credit version of the author's Bubble VaR model further attempts to combine default and spread risk under a single risk measure, arguing that this measure lies between spread risk and the principal loss of the bond (total loss). The benefit of the Wong's (2011a, 2011b) methods is that they avoid timing issues of a CCB buffer currently faced by regulators and financial institutions. South African applications of Wong's Bubble VaR methodology (and the performance thereof) have been conducted by Visser and Van Vuuren (2018, in press).
Data and methodology
Data
The data chosen were monthly nominal GDP and credit extended by all monetary institutions to the domestic private sector since 1965. These data are prescribed by the BCBS (2010b) and obtained from the Reserve Bank of South Africa. From these data, growth rates were determined and the credit growth-to-GDP ratio determined. South African small residential price index data obtained from the BIS are also used in a similar manner as the credit growth-to-GDP data (BIS Data 2016).
South African data from January 1966 were used to determine the credit growth-to-GDP growth ratio as well as this ratio's long-run trend. Detailed examination of these data, using standard Fourier analysis, indicates that they exhibit cyclical behaviour. This result is not unexpected because they comprise several macroeconomic components (such as the economic - or business - cycle), which are inherently cyclical. A Fourier frequency analysis of these data indicate that the main component has a frequency of approximately 7 years: the duration of South Africa's business cycle, found previously (Botha 2004) and confirmed in later studies (e.g. Thomson & Van Vuuren 2016).
Using these macroeconomic data, the credit growth-to-GDP growth ratio was constructed as well as the long-run trend using both the one-sided HP filter and the Kalman filter (Figure 2).
Methodology
Hodrick-Prescott filter
A popular method of trend extraction from data is the HP filter. The HP filter was first introduced (Hodrick & Prescott 1981) in the context of estimating business cycles, but the research was only published in 1997 after the filter had gained widespread popularity in macroeconomics (Hodrick & Prescott 1997). The BCBS also chose the HP filter to de-trend relevant macroeconomic ratio data and thus extract the information required to evaluate excessive growth in economies.
The HP filter has been criticised for several limitations and undesirable properties (Ravn & Uhlig 2002). Canova (1994, 1998) agreed in principle with the use of the HP filter to extract business cycles (of average duration between 4 and 6 years) from macroeconomic data, but doubted the methodology for determining key parameter inputs. Spurious cycles and distorted estimates of the cyclical component when using the HP filter were obtained by Harvey and Jaeger (1993), who argued that this property may lead to misleading conclusions regarding the relationship between short-term movements in macroeconomic time-series data. Cogley and Nason (1995) also found spurious cycles (and extreme second-order properties in de-trended data) when using the HP filter on difference-stationary input data. Application of the HP filter to U.S. time-series data was found to alter measures of persistence, variability and co-movement dramatically (King & Rebelo 1993). Many of these critiques do not provide sufficient compelling evidence to discourage use of the HP filter. As a result, it remains widely used among macroeconomists for de-trending data, which exhibit short-term fluctuations superimposed on business cycle-like trends (Ravn & Uhlig 2002).
The idea which on which the HP filter rests is that an observable macroeconomic time series (xt) may be decomposed into its long-run, non-stationary secular trend (τt) and a stationary residual, or cyclical, component (ct):

Neither the long-run trend nor the cycle is directly observable so de-trending approaches generally define these elements somewhat arbitrarily. The HP filter extracts the cycle by solving Eqn (2), a standard-penalty programme:
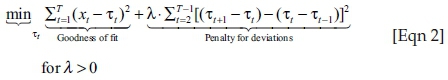
where the parameter λ controls the smoothness of the adjusted trend series, τt, that is, as λ → 0, the trend approximates the actual series, xt, while as λ → ∞ the trend becomes linear and the procedure converges to a standard least squares solution (Yakhim 2001). The optimisation procedure in (Eqn 2) maximises the fit to the trend of the series, that is, minimise the cycle component ct by minimising changes in the gradient of the trend τt. Note that both τt and ct are unobservable and because ct is a stationary process, xt may be thought of as a noisy signal for the non-stationary trend τt.
Hodrick and Prescott (1981) originally suggested an exogenous and subjective value of 1600 for the value of λ for quarterly data, but Backus, Kehoe and Kydland (1992) proposed adjusting λ based upon the square of the frequency of observations relative to quarterly data. The relative frequency is 3 for monthly data and 0.25 for annual data, so the corresponding λs are 14 400 and 100, respectively. Despite on-going research (e.g. Marcet & Ravn 2003; Ravn & Uhlig 2002), who derived endogenous values for λ by solving [Eqn 2] as a constrained minimisation problem), the λs discussed above are still in common use (Mise, Kim & Newbold 2005). The optimal value for λ for South African business cycle data was explored by Du Toit (2008), who argued that the optimal smoothing constant was that value of λ that least distorts the frequency information of the time series (in this case, λ = 254 for quarterly data were used to determine the South African business cycle frequency).
Drehmann et al. (2010) found λ = 1600 and λ = 25 000 performed poorly on historical data while, λ = 125 000 and λ = 400 000 performed well with quarterly data. The higher value of λ = 400 000 is considered important from a policy perspective as it provides both a greater range and more time when the indicator provides strong and reliable signals.
The HP filtering procedure optimises the fit to the data series, but this optimality is based on the application of the filter to an infinitely long time series. For practical purposes, the estimation of the trend and cycle components works well for a moderately long series (Mise et al. 2005), but at the end points the HP filter is demonstrably suboptimal. The two-sided, symmetrical filter applies large symmetrical weights to the end points of the observed values to determine the corresponding trend value (Ley 2006) disproportionately distorting the filtered values at the most recent time (Apel, Hansen & Lindberg 1996; Baxter & King 1995; St-Amant & van Norden 1997).
Kalman filter
The Kalman filter (Kalman 1960) is a Bayesian updating scheme that maximises the likelihood of correctly estimating unknown parameter values (Koch 2006). The filter addresses the general problem of determining the state [x ∈ ℜn] of a time-controlled, discrete process, which is governed by the linear stochastic difference equation:

with a measurement [z ∈ ℜn]:

The random variables w and v, which are assumed to be independent (i.e. 0 correlation between them) and normally distributed:


represent process white noise and measurement white noise, respectively.
In practice, the process noise covariance Q and measurement noise covariance R matrices (here variance matrices because the correlation is zero) change with each time step. In this case, they are assumed to be constant (Koch 2006) - a common assumption - and these values are obtained using maximum likelihood methods (Tommaso & Alessandra 2012).
The 2×1 (in this case) state transition matrix, F, links the state at the previous time step t−1 to the current state at step t, assuming no driving function or process noise. The 2×2 control matrix B relates the optional control input u ∈ ℜl to the state x. The 2×1 matrix H in the measurement relates the state to the measurement zk. In practice, F and H might change with each time step, but here again they are both assumed to be constant.
The mechanical process to be followed is given below:
Predict:
Project state 1 time step ahead:
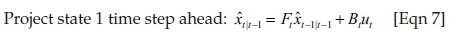
Project error covariance 1 step ahead:

Update:
Compute Kalman gain:
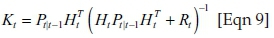
Update estimate with measurement: yt

Update error covariance:
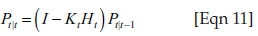
where 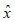 is the estimated state, F is the state transition matrix (i.e. transition between states), u represents the control variables, B is the control matrix (i.e. mapping control to state variables), P is the state variance matrix (i.e. error of estimation), Q is the process variance matrix (i.e. error caused by the process), y represents the measurement variables, H is the measurement matrix (i.e. mapping measurements onto the state), K is the Kalman gain and R is the measurement variance matrix (i.e. measurement error).
is the estimated state, F is the state transition matrix (i.e. transition between states), u represents the control variables, B is the control matrix (i.e. mapping control to state variables), P is the state variance matrix (i.e. error of estimation), Q is the process variance matrix (i.e. error caused by the process), y represents the measurement variables, H is the measurement matrix (i.e. mapping measurements onto the state), K is the Kalman gain and R is the measurement variance matrix (i.e. measurement error).
Subscripts represent the following:
-
t|t: the current time period
-
t−1|t−1: the previous time period
-
t|t−1: intermediate steps.
For this analysis, let yt denote a vector that contains the time series values at time t, for t = 1,…, n. An unobserved components model comprises a trend-cycle decomposition:

where 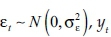 is the value of the series at time t, µt is the long-term trend and ψt is a variable representing the dynamics of the underlying cycles. The residuals εt are assumed to be normally distributed with variance σ2. All components are unobserved and the Kalman filter must be used to estimate them. Two important decisions must be made regarding the assembly of yt.
is the value of the series at time t, µt is the long-term trend and ψt is a variable representing the dynamics of the underlying cycles. The residuals εt are assumed to be normally distributed with variance σ2. All components are unobserved and the Kalman filter must be used to estimate them. Two important decisions must be made regarding the assembly of yt.
Trend smoothness: that is, how much variable fluctuation is assigned to the trend as opposed to the cycle. Galati et al. (2016) defined a general form of the mth-order trend as follows:



where 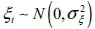 and
and 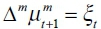 . The trend's smoothness depends on the differencing order m, so as m increases, the trend becomes smoother. For m = 0, yt is stationary, for m = 1, yt is a random walk process and for m = 2, yt is an integrated random walk used in most macroeconomic time series (e.g. see Koopman and Lucas 2005; Valle Azevedo et al. 2006):
. The trend's smoothness depends on the differencing order m, so as m increases, the trend becomes smoother. For m = 0, yt is stationary, for m = 1, yt is a random walk process and for m = 2, yt is an integrated random walk used in most macroeconomic time series (e.g. see Koopman and Lucas 2005; Valle Azevedo et al. 2006):


where

Cycle stochastic process: using Harvey's (1989) approach, the cycle is modelled as a second-order autoregressive process. A trigonometric process is used to specify ψt:
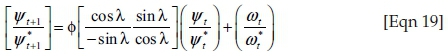
where 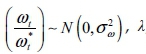 , the frequency, is measured in radians and bounded by 0 ≤ λ ≤ π, the period of the stochastic cycle is 2π/λ and the persistence (or damping factor) parameter, f, is bounded by 0 < f < 1, which ensures that the cycle, ψt, is a stationary stochastic process. The disturbances
, the frequency, is measured in radians and bounded by 0 ≤ λ ≤ π, the period of the stochastic cycle is 2π/λ and the persistence (or damping factor) parameter, f, is bounded by 0 < f < 1, which ensures that the cycle, ψt, is a stationary stochastic process. The disturbances 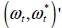 are assumed to be uncorrelated and normally distributed with mean 0 and variance
are assumed to be uncorrelated and normally distributed with mean 0 and variance 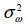 .
.
The state-space forms of (12) through (19) are given below:


where the state vector αt encapsulates the cycle and trend and the system matrices Zt and Tt contain the parameters from (12) through (19). The state disturbance vector, ηt contains the disturbances of the trend and cycle equations. It is at this stage that the Kalman filter is invoked to determine the estimates of the unobserved components contained in αt. Maximum likelihood methods are used to estimate the unknown variances of unobserved component disturbances, the persistence parameter, j, and the frequency parameter, λ. Details of these estimations may be found in Schweppe (1965) and Koopman and Ooms (2011).
Results and discussion
Although the credit-to-GDP gap is disputed with regards its appropriateness as CCB buffer indicator for South Africa, the purpose of this paper is to primarily focus on the measurement technique of a CCB and then on the indicator variables. As it is recommended as a common reference guide by the BCBS, it is used as an investigation point of departure. Figure 2 illustrates South African credit-to-GDP data and the long-term trend estimated with a one-sided HP and Kalman filter, respectively.
The gap obtained using the Kalman filter is smoother (flatter) than that obtained using the HP filter during low and stable credit-to-GDP ratios. In an increasing credit-to-GDP ratio environment, the Kalman filter is more reactive than the HP filter and tends to accentuate the peaks and troughs to a greater extent. This is a critical difference between the two filters, the results from which affect the magnitude and timing of the capital buffer injection and release.
The Kalman-filtered trend series in Figure 2 presents a smoother trend to that of the HP-filtered series up until the 1995. This affects the credit-to-GDP gap materially prior to and during the housing bubble of the 1980s.
The Kalman filter trend does not deviate significantly from the actual credit-to-GDP ratio for the Asian crisis period suggesting that capital retention would be less under a Kalman filter approach compared to the HP filter approach. Both filters deviate substantially from the actual ratio before the onset of the financial crisis with the Kalman doing so before the HP-filtered series. Gaps from both approaches drive suggested buffer levels (Figure 3).
Positive credit-to-GDP gaps are the focus in Figure 3 as CCB buffers are only accrued in these periods where the gap exceeds 2%.
The Kalman-filtered series in Figure 3 illustrates superior gaps in both the late 80s and the most recent crisis period. The HP-filtered gap exceeds the Kalman with regards to capital requirements in the period associated with the Asian crises. The capital charge add-on is affected by these elevated gaps (Figure 4).
Additional capital charges in Figure 4 show dominance if derived using a Kalman-filtered series up until 1980. This period preceding the house price bubble collapse in the early 1980s was characterised by high inflation in developed markets as well as a lack of confidence in the U.S. dollar (Luüs 2005). This led to a surge in the gold price and positive spin-off effects on the South African economy. Luüs (2005) notes that, in this period, 50% of South African export revenue could be attributed to gold. Furthermore, increased household wealth as a result of a combination of increased incomes and income tax cuts improved liquidity conditions and reduced mortgage lending rates. Subsequently, increased local and international political tensions as well as pressure on the balance of payments led to significant increases in mortgage lending rates. This ultimately caused the market to collapse and house prices to decline by 42% in real terms (Luüs 2005).
In the last decade of the 20th century the HP-filtered series increases additional capital by more than 2% - although only briefly. This is because of the long-term trend derived through the HP-filtered series (Figure 2) being notably lower compared to the Kalman-filtered, long-term trend. Additional capital charges in the late 1990s are partially because of the lack of global demand for commodities as a result of the Asian crisis and the severe depreciation of the South African rand in 1998.
In the 2008/2009 crisis period, the Kalman-filtered credit-to-GDP gap produces an elevated capital charge compared to the HP filter and also reaches the maximum add-on of 2.5% as prescribed by the BCBS. Both metrics throughout this period illustrate a similar release rate of the buffer after the crisis period.
Applying the Kalman filter to the small residential price index allows for the estimation of a small residential gap and subsequent capital charge based on a residential series (Figure 5). This draws from Burra et al. (2014) where it is found that the ABSA house price index for all sizes of properties is positively correlated with GDP growth, suggesting that CCB buffers would build up in prosperous periods.
The South African small residential price index and its Kalman-filtered, long-run trend in Figure 5 illustrate how the South African residential market benefited from the pre-crisis global housing market boom. The subsequent crisis did not impact the South African market as severely as it did other countries' housing markets: some of this may be attributed to the National Credit Act (NCA) of 2005. This legislation along with other measures curbed reckless lending by financial institutions, partially protecting the quality of assets on intuitions' books.
Figure 6 illustrates the gap produced from the difference between the actual index and the trend in Figure 5.
The South African small residential price index gap in Figure 6 indicates the severe shocks of both the 1980s and the latest financial crisis on the residential market. The gap falls and remains negative for more than 2 years in the 1980s. In the recent crisis, the gap recovers more rapidly, however, relapses to turn towards the biggest negative gap in the observation period. These shocks are also prevalent in the credit-to-GDP gap in Figure 3; however, there timing is different, indicating that the two measures will certainly provide different capital requirements at different periods (Figures 9 and 10). Figure 6 imposes a Fourier fit to the residential price index gap to determine whether there is a cycle component for the purposes of cyclical capital requirements. Figure 7 illustrates a frequency spectrum of South African small residential price index gap.
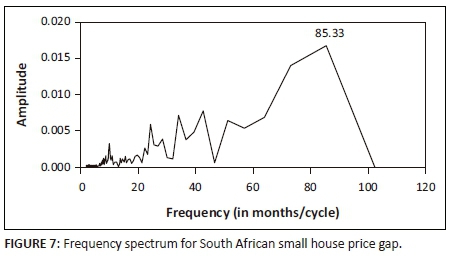
The spectrum in Figure 7 illustrates that principal component has a duration of 85 months (corresponding to a 7-year cycle). The semi-cycle found at ±43 months is encouraging as the Fourier analysis also detects semi-cycles, which suggests that the 85-month cycle is correct. This 7-year cycle further aligns with the findings of Van Vuuren (2012) for credit-to-GDP growth and Botha (2004) and Thomson and Van Vuuren (2016) for the South African business cycle. Figure 8 illustrates the additional CCB capital requirements estimated using the residential gap and the BCBS CCB implementation suggestions.
Countercyclical Capital Buffer capital requirements are at a maximum three times in the observation period with two of these being associated with the respective crises mentioned. The bursting of the 1980s housing bubble occurred in 1984, and CCB capital requirement indicators begin as early as the late 1970s. This suggests that the measure might have had the ability to impose countercyclical capital effectively in the years building up to the crisis. This is similar in the latest financial crisis with CCB capital imposed as early as the year 2000 up until mid-2007. Figure 9 illustrates additional CCB capital charges calculated for both the credit-to-GDP gap and the residential gap using the Kalman filter approach for trend extraction.
The CCB charge requirements differ significantly for the two series analysed with the credit-to-GDP gap raising no CCB requirements for the pre-crisis period of 1980. The residential price index does, however, increase the CCB requirement to its maximum allowable threshold for almost 5 years prior to the crisis. The residential index further solely suggests a CCB between 1990 and 1995, this is because of political uncertainties and an exodus of professionals placing significant pressure on the housing market. The investigation of signals like these is of utmost importance as they may not be appropriate for CCB indications, particularly if signals are isolated to their sector and not applicable to the entire banking or financial sector.
The pre-2008 crisis period shows significant CCB retentions if the measure is based on the residential price index, suggesting that it would have been countercyclical in the pre-crisis period potentially countering excessive credit growth. The CCB measure based on the credit-to-GDP gap also indicates maximum capital retention, however, in the crisis period. This aligns with research of Burra et al. (2014) and Bernstein et al. (2014), cautioning regarding the use of the credit-to-GDP gap as an indicator for the CCB. Figure 10 focusses solely on the most recent financial crisis comparing the credit-to-GDP gap and the residential property price gap, both estimated using the Kalman filter and HP filter, respectively.
Figure 10 illustrates that the residential price index would have suggested a CCB long before the onset of the crisis. Suggesting stringent buffer requirements from the onset of the millennium might have been too severe and would potentially have hindered economic and financial market growth. The superiority of the Kalman filter over the HP filter cannot be concretely established for the buffer (estimated using the residential price gap) as buffer-retention signals leading up to 2003 are similar. The buffer's release signal under the Kalman filter approach is more rapid: this should be further explored in future research.
The credit-to-GDP gap buffer estimated with the Kalman filter for the crisis period is more conservative compared to the buffer estimated with the HP filter. The Kalman filter-estimated buffer reaches the maximum prescribed 2.5% and maintains it throughout the crisis period, eventually diminishing along with the HP-filtered buffer. The accumulation of the buffer also begins a few months prior to that of the HP-filtered approach and may have countered procyclicality and acted as a warning signal.
Conclusions and suggestions for future work
Procyclicality is not isolated to one element of a financial market or economy; it emerges because of the combination of several elements including regulatory requirements and market participant actions. The identification and isolation of a single metric which captures all relevant features of procyclicality is unlikely: regulators and financial institutions will have to identify the optimal measures and variables that describe its effects in order to attain macroeconomic stability.
The CCB was introduced to limit the effects of procyclicality, but several aspects need to be considered. These include retention and release signals as well as techniques to determine these signals with appropriate variables. The information used in setting the CCB must capture up- and downswings inherent in the financial cycle. The development of system-wide risks is associated with the buffer's build-up phase while financial contractions correspond to the buffer's release phase. Doubts have been expressed about a single measure reliably capturing both the build-up phase and the release phase: robust leading-indicator properties are required for the former and a reliable contemporaneous indicator is required for the latter, as pointed out by Drehmann et al. (2010). In addition, a good proxy for the build-up phase should vary considerably from its long-run trend during the build-up phase (a feature which would rule out non-performing loans - bounded at zero - e.g. and would limit the information content of credit spreads). Credit spreads, however, would provide much useful information about release phase timing (Chen & Christensen 2010).
Indicators may provide more useful information in combination than in isolation. Borio and Drehmann (2009) showed that aggregate credit growth and real estate prices jointly contain more predictive information about future financial crises than either in isolation. If adequately implemented, the chosen metric (or metrics) has the potential to reduce the financial cycle amplitude and thereby, potentially, reduce all (or the majority of) credit risk in the financial cycle. The metric may thus lead to a reduction in credit risk regulatory capital: the relationship between the two capital requirements is yet to be fully explored.
This paper applies a Kalman filter to the BCBS-prescribed and other financial variables to determine the appropriate signal for the implementation of the CCB. Results indicate that for different crises, results obtained from the Kalman filter and the one-sided HP filter suggest substantially different signals - excluding for the most recent crisis (where the results are similar). This paper corroborates the findings of other studies which find that the credit-to-GDP gap would likely fuel procyclicality rather than dampen it (e.g. Borio et al. 2001; Creal et al. 2010; Koopman & Azevedo 2008) for South Africa if employed as a sole measure. The small residential price index gap identifies countercyclical signals that would have suggested full CCB retention for substantial periods prior to historical crises. This emphasises that, although the metric used to calculate signals is important, the variable used to calculate these signals is a critical input as the incorrect one may fuel procyclicality. The South African Reserve Bank (SARB) suggested that it would still use the credit-to-GDP as a principal indicator for the CCB; however, it further asserted that it would use other indicators in conjunction with the credit-to-GDP gap (SARB 2015).
Future research opportunities include an investigation into how the Kalman filter approach performs in conjunction with other variables that have been found to be more suitable for CCB buffers in South Africa than the credit-to-GDP gap. Work may also focus on buffer-release signals and how measures such as the Kalman filter recognise these occurrences. A combination of models that avoid timing issues such as Wong's (2011a) BuVaR model and filter-based approach also present future research opportunities. Solutions to such an approach would be of considerable value to regulators and financial institutions in resolving their current (2017) dilemma regarding CCB timing issues.
In addition, we note the possibility of ultimately incorporating machine-learning into the processes described here. Machine-learning and artificial intelligence (AI) are already widespread in the financial industry and pattern identification - on the skill and timeliness of which this paper is based - is ideally suited to AI applications. Thus, it is probably only a matter of time before AI is used for cyclical identification and thus mitigation. It could be argued that embracing AI has thus been proposed in this paper because the Kalman filter is, effectively, a Bayesian variance-reduction tool, a fundamental building block of machine-learning.
Acknowledgements
Competing interests
The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.
Authors' contributions
D.V. is the principal author and analyst. G.v.V. is responsible for filter design and implementation
References
Aikman, D., Haldane, A.G. & Nelson, B.D., 2015, 'Curbing the credit cycle', The Economic Journal 125(585), 1072-1109. https://doi.org/10.1111/ecoj.12113 [ Links ]
Akinboade, O.A. & Makina, D., 2009, 'Bank lending and business cycles: South African evidence', African Development Review 21(3), 476-498. https://doi.org/10.1111/j.1467-8268.2009.00219.x [ Links ]
Akinboade, O.A. & Makina, D., 2010, 'Econometric analysis of bank lending and business cycles in South Africa', Applied Economics 42(29), 3803-3811. https://doi.org/10.1080/00036840802360138 [ Links ]
Apel, M., Hansen, J. & Lindberg, H., 1996, 'Potential output and output gap', Quarterly Review of the Bank of Sweden 3(1), 24-35. [ Links ]
Arnold, T., Bertus, M. & Godbey, J., 2008, 'A simplified approach to understanding the Kalman filter technique', The Engineering Economist 53(2), 140-155. https://doi.org/10.1080/00137910802058574 [ Links ]
Backus, D.K., Kehoe, J. & Kydland, F.E., 1992, 'International real business cycles', The Journal of Political Economy 100(4), 745-775. https://doi.org/10.1086/261838 [ Links ]
Baxter, M. & King, R.G., 1995, Measuring business cycles approximate band-pass filters for economic time series, National Bureau of Economic Research Working Paper No. 5022, viewed 10 December 2016, from http://www.nber.org/papers/w5022.pdf [ Links ]
Baxter, M. & King, R.G., 1999, 'Measuring business cycles: Approximate band-pass filters for economic time series', The Review of Economics and Statistics 81(4), 575-593. https://doi.org/10.1162/003465399558454 [ Links ]
BCBS, 2010a, Basel III: A global regulatory framework for more resilient banks and banking systems, Bank for International Settlements, viewed 21 November 2016, from http://www.bis.org/publ/bcbs189_dec2010.pdf [ Links ]
BCBS, 2010b, Guidance for national Authorities operating the countercyclical capital buffer, viewed 01 June 2016, from http://www.bis.org/publ/bcbs187.pdf [ Links ]
BCBS, 2013, Fundamental review of the trading book: A revised market risk framework, viewed 22 October 2016, from http://www.bis.org/publ/bcbs265.pdf [ Links ]
Bernstein, J., Raputsoane, L. & Schaling, E., 2014, Credit procyclicality and financial regulation in South Africa, ERSA Working Paper 445, Economic Research South Africa, Pretoria, South Africa. [ Links ]
BIS Data, 2016, Property price statistics, viewed 22 December 2016, from http://www.bis.org/statistics/pp.htm [ Links ]
Borio, C., 2012, The financial cycle and macroeconomics: What have we learnt?, BIS Working Paper No 395, viewed 05 January 2017, from http://www.bis.org/publ/work395.pdf [ Links ]
Borio, C. & Drehmann, L., 2009, 'Assessing the risk of banking crises-Revisited', BIS Quarterly Review, March, 29-46. [ Links ]
Borio, C., Furfine, C. & Lowe, P., 2001, Procyclicality of the financial system and financial stability: Issues and policy options, BIS Working Paper No 1, viewed 05 January 2017, from http://www.bis.org/publ/bppdf/bispap01a.pdf [ Links ]
Boshoff, W.H., 2006, 'The properties of cycles in South African financial variables and their relation to the business cycle', South African Journal of Economics 73(4), 694-709. https://doi.org/10.1111/j.1813-6982.2005.00047.x [ Links ]
Botha, I., 2004, 'Modelling the business cycle of South Africa: Linear vs non-linear methods', PhD thesis, Rand Afrikaans University, Johannesburg. [ Links ]
Burns, A.F. & Mitchell, W.C., 1946, Measuring business cycles, National Bureau of Economic Research, Cambridge, MA. [ Links ]
Burra, P., de Jongh, P.J., Raubenheimer, H., Van Vuuren, G. & Wiid, H., 2014, 'Implementing the Countercyclical capital Buffer in South Africa: Practical considerations', South African Journal of Economic and Management Sciences 18(1), 105-127. https://doi.org/10.4102/sajems.v18i1.956 [ Links ]
Canova, F., 1994, 'Detrending and turning points', European Economic Review 38(3-4), 614-623. [ Links ]
Canova, F., 1998, 'Detrending and business cycle facts', Journal of Monetary Economics 41(2), 475-512. https://doi.org/10.1016/S0304-3932(98)00006-3 [ Links ]
Chen, D.X. & Christensen, I., 2010, 'The countercyclical bank capital buffer: Insights for Canada', Bank of Canada, Financial System Review, pp. 1-22. [ Links ]
Christiano, L.J. & Fitzgerald, T.J., 2003, 'The band pass filter', International Economic Review 44(2), 435-465. https://doi.org/10.1111/1468-2354.t01-1-00076 [ Links ]
Claessens, S., Kose, M.A. & Terrones, M.E., 2012, 'How do business and financial cycles interact?', Journal of International Economics 87(1), 178-190. https://doi.org/10.1016/j.jinteco.2011.11.008 [ Links ]
Cogley, T. & Nason, J.M., 1995, 'Effects of the Hodrick-Prescott Filter on trend and difference stationary time series: Implications for business cycle research', Journal of Economic Dynamics and Control 19(1), 253-278. https://doi.org/10.1016/0165-1889(93)00781-X [ Links ]
Creal, D., Koopman, S.J. & Zivot, E., 2010, 'Extracting a robust US business cycle using a time-varying multivariate model-based bandpass filter', Journal of Applied Econometrics 25(4), 695-719. https://doi.org/10.1002/jae.1185 [ Links ]
Drehmann, M., Borio, C. & Tsatsaronis, K., 2012, Characterising the financial cycle: Don't lose sight of the medium term! BIS Working Papers 380, Bank for International Settlements. [ Links ]
Drehmann, M., Claudio, B., Gambacorta, L., Jimenez, G. & Trucharte, C., 2010, Countercyclical capital buffers: Exploring options, BIS Working Papers No 317, viewed 10 December 2016, from http://www.bis.org/publ/work317.pdf [ Links ]
Du Toit, L., 2008, Optimal HP filtering for South Africa, Working Paper, Department of Economics, University of Stellenbosch, Stellenbosch. [ Links ]
Edge, R. & Meisenzahl, R., 2011, The unreliability of credit-to-GDP ratio gaps in real-time: Implications for countercyclical capital buffers, Working Paper 2011-37, Washington, DC: Federal Reserve Board. [ Links ]
Fourie, L., Botha, I. & Mears, R., 2011, 'Credit extension in South Africa: A business cycle perspective for the period 1985 to 2009', African Journal of Business Management 5(34), 13074-13083. [ Links ]
Galati, G., Hindrayanto, I., Koopman, S.J. & Vlekke, M., 2016, Measuring financial cycles with a model-based filter: Empirical evidence for the United States and the Euro Area, De Nederlandsche Bank, Working Paper No. 495, Amsterdam, The Netherlands. [ Links ]
Goodhart, C. & Taylor, A., 2006, 'Procyclicality and volatility in the financial system - The implementation of Basel II and IAS39', in S. Gerlach & P. Gruenwald (eds.), Procyclicality of financial systems in Asia, pp. 230-251, Palgrave Macmillan, London, England. [ Links ]
Gordy, M.B. & Howells, B., 2004, Procyclicality in Basel II: Can we treat the disease without killing the patient?, Bank for International Settlements, viewed 23 October 2016, from http://www.bis.org/bcbs/events/rtf04gordy_howells.pdf [ Links ]
Harvey, A.C., 1989, Forecasting, structural time series models and the Kalman filter, Cambridge University Press, Cambridge. [ Links ]
Harvey, A.C. & Jaeger, A., 1993, 'Detrending, stylized facts and the business cycle', Journal of Applied Econometrics 8(3), 231-247. https://doi.org/10.1002/jae.3950080302 [ Links ]
Heid, F., 2003, Is regulatory capital pro-cyclical? A macroeconomic assessment of Basel II, Working Paper, Deutsche Bundesbank, Frankfurt, Germany. [ Links ]
Hodrick, R.J. & Prescott, E.C., 1981, Postwar U.S. business cycles: An empirical investigation, Carnegie Mellon University Discussion Paper no. 451, viewed 10 December 2016, from http://www.kellogg.northwestern.edu/research/math/papers/451.pdf [ Links ]
Hodrick, R.J. & Prescott, E.C., 1997, 'Postwar U.S. business cycles: An empirical investigation', Journal of Money, Credit, and Banking 29(1), 1-16. https://doi.org/10.2307/2953682 [ Links ]
Hosszú, Z., Körmendi, G. & Mérő, B., 2015, Univariate and multivariate filters to measure the credit gap, Magyar Nemzet Bank Occasional Papers 1178, viewed 23 November 2016, from https://www.mnb.hu/letoltes/mnb-op-118-final.pdf [ Links ]
Jain, S., Yongvanich, A. & Zhou, X., 2011, a characteristics of hedge funds, UBS Alternative Investments, viewed 26 December 2013, from http://ssrn.com/abstract=2014430 [ Links ]
Kalman, R.E., 1960, 'A new approach to linear filtering and prediction problems. ASME Transcripts', Journal of Basic Engineering, Series D 82(2), 35-45. https://doi.org/10.1115/1.3662552 [ Links ]
Kelly, R., McQuinn, K. & Stuart, R., 2013, Exploring the steady-state relationship between credit and GDP for a small open economy: The case of Ireland, Working Paper 1531, European Central Bank, Frankfurt. [ Links ]
King, R.G. & Rebelo, S.T., 1993, 'Low frequency filtering and real business cycles', Journal of Economic Dynamics and Control 17(1-2), 207-231. [ Links ]
Koch, W., 2006, 'Advanced target tracking techniques', in Advanced Radar Signal and Data Processing, pp. 2-1-2-34, Educational Notes RTO-EN-SET-086, Paper 2, Neuilly-sur-Seine, Paris, France, viewed n.d., from http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.491.2300&rep=rep1&type=pdf [ Links ]
Koopman, S.J. & Azevedo, J.V.E., 2008, 'Measuring synchronization and convergence of business cycles for the Euro area, UK and US', Oxford Bulletin of Economics and Statistics 70(1), 23-51. https://doi.org/10.1002/jae.833 [ Links ]
Koopman, S.J. & Lucas, A., 2005, 'Business and default cycles for credit risk', Journal of Applied Econometrics 20(2), 311-323. [ Links ]
Koopman, S.J. & Ooms, M., 2011, 'Forecasting economic time series using unobserved components time series models', in M.P. Clements & D.F. Hendry (eds.), Oxford Handbook on Economic Forecasting, p. 5, Oxford University press, Oxford. [ Links ]
Ley, E., 2006, The Hodrick-Prescott filter. Knowledge brief for bank staff, The World Bank, Washington, DC, viewed 10 December 2016, from http://beathespread.com/file/download/16067 [ Links ]
Luüs, C., 2005, The ABSA residential property market database for South Africa - key data trends and implications, BIS Papers No21, viewed 10 December 2016, from http://www.bis.org/publ/bppdf/bispap21l.pdf [ Links ]
Marcet, A. & Ravn, M.O., 2003, The HP-Filter in cross-country comparisons, CEPR Discussion Papers, viewed 10 December 2016, from https://econ-papers.upf.edu/papers/588.pdf [ Links ]
Mise, E., Kim, T. & Newbold, P., 2005, 'On suboptimality of the Hodrick-Prescot filter at time series endpoints', Journal of Macroeconomics 27(1), 53-67. https://doi.org/10.1016/j.jmacro.2003.09.003 [ Links ]
NCA, 2005, South African National Credit Act 34 of 2005, viewed 22 October 2016, from http://www.justice.gov.za/mc/vnbp/act2005-034.pdf [ Links ]
Ravn, M.O. & Uhlig, H., 2002, 'On adjusting the Hodrick-Prescott filter for the frequency of observations', The Review of Economics and Statistics 84(2), 371-375. https://doi.org/10.1162/003465302317411604 [ Links ]
SARB, 2015, Countercyclical capital buffer for South Africa based on Basel III framework, Circular 8/2015 issued in terms of section 6(4) of Banks Act, No. 94 of 1990, viewed 07 January 2017, from https://www.resbank.co.za/Lists/News%20and%20Publications/Attachments/7005/ C8%20of%202015.pdf [ Links ]
Schweppe, F., 1965, 'Evaluation of likelihood functions for Gaussian signals', IEEE Transaction Information Theory 11(1), 61-70. https://doi.org/10.1109/TIT.1965.1053737 [ Links ]
St-Amant, P. & van Norden, S., 1997, Measurement of the output gap: A discussion of recent research at the Bank of Canada, Bank of Cancada Technical Report No. 79, viewed 10 December 2016, from http://www.bankofcanada.ca/wp-content/uploads/2010/01/tr79.pdf [ Links ]
Thomson, D. & Van Vuuren, G., 2016, 'Forecasting the South African business cycle using Fourier analysis', International Business and Economics Research Journal 15(4), 175-192. https://doi.org/10.19030/iber.v15i4.9755 [ Links ]
Thomson, D. & Van Vuuren, G., 2017, 'Attribution of hedge fund returns using a Kalman filter', Applied Economics 47(1), 1-17. https://doi.org/10.1080/00036846.2017.1349290 [ Links ]
Tommaso, P. & Alessandra, L., 2012, Maximum likelihood estimation of time series models: The Kalman filter and beyond, Munich Personal RePEc Archive, Business Analytics, BAWP - 2012_02, Munich. [ Links ]
Valle Azevedo, J., Koopman, S.J. & Rua, A., 2006, 'Tracking the business cycle of the Euro Area: A multivariate model-based bandpass filter', Journal of Business and Economic Statistics 24(2), 278-290. https://doi.org/10.1198/073500105000000261 [ Links ]
Van Vuuren, G., 2012, 'Basel III countercyclical capital rules: Implications for South Africa', South African Journal of Economic and Management Sciences 15(3), 309-324. https://doi.org/10.4102/sajems.v15i3.235 [ Links ]
Visser, D. & Van Vuuren, G., 2016, 'Trading book risk metrics: A South African perspective', South African Journal of Economic and Management Sciences 19(1), 118-138. https://doi.org/10.17159/2222-3436/2016/v19n1a8 [ Links ]
Visser, D. & Van Vuuren, G., in press, 'Procyclicality tradeable credit risk: Consequences for South Africa', South African Journal of Economic and Management Sciences 21(1). [ Links ]
Wong, M., 2011a, 'Credit BuVaR: Asymmetric spread VaR with default', Journal of Risk Management in Financial Institutions 5(1), 86-95. [ Links ]
Wong, M., 2011b, 'Market BuVaR: A countercyclical risk metric', Journal of Risk management in Financial Institutions 4(4), 419-432. [ Links ]
Yakhim, Y., 2001, Business cycle fluctuations and the Hodrick-Prescott Filter, viewed 23 January 2011, from http://www.bgu.ac.il/~yossiya/teaching/macro_graduate/LN1_bc_hpf.pdf [ Links ]
 Correspondence:
Correspondence:
Dirk Visser
ddvisser13@gmail.com
Received: 09 Jan. 2017
Accepted: 27 Sept. 2017
Published: 12 Apr. 2018
1 . See Data and methodology section.
2 . See Data and methodology section.
3 . A classical methodology focuses purely on changes in the levels of economic activity and not on the fluctuations of these activities around their long-term trend.














