Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Economic and Management Sciences
versão On-line ISSN 2222-3436
versão impressa ISSN 1015-8812
S. Afr. j. econ. manag. sci. vol.21 no.1 Pretoria 2018
http://dx.doi.org/10.4102/sajems.v21i1.1626
ORIGINAL RESEARCH
A regression and comparative study of United States and South African yield curves using principal component analysis
Kavir PatelI; Ashfaaq MohamedI; Gary W. van VuurenII
ISchool of Economics, University of Cape Town, South Africa
IIBusiness School, University of the Free State, South Africa
ABSTRACT
Volatile markets and economic environments can significantly distort the shape and smoothness of yield curve movements. This study explores the influence of movements in United States interest rates on South African interest rates. This study aims to identify the main underlying movements present in the United States and South African yield curves and to further determine the dominant factors that are responsible for driving South African interest rate movements. The principal settings for the study were the United States and South African markets representing, respectively, a developed and developing market. Principal component analysis was used to discern the major drivers of developing and developed market interest rates. The findings show that the principal component analysis technique is able to effectively classify and quantify the movements of yield curves across both markets in terms of three main factors, namely level, slope and curvature shifts. During certain periods, South African yield curve changes were largely driven by variations in United States interest rates and the rand/dollar exchange rate. Results also demonstrated that a volatile market and economic environment can significantly distort the shape and smoothness of yield curve movements.
Introduction
Explaining the volatility of financial assets has become a crucial part of portfolio management. Fund managers and investors retain a substantial amount of risk when they do not understand the volatility of their assets. In the fixed-income market, the main contributing factors to the volatility in bond prices are yield curves. Yield curves illustrate the relationship between bond yield rates at particular times and bond maturities with the same credit quality. This relationship is commonly known as the term structure of interest rates. Portfolio managers and investors seek to quantify yield curve changes to protect, or immunise, the fixed-income assets in their portfolios. The absolute level of the yield curve is generally considered less important to investors than changes of the curve (Baygun, Showers & Cherpelis 2000) as the variations in the yield curve describes the volatility of the bond market. This helps to illustrate whether the bond market is a safe investment during certain economic periods (Johnson 2005). Empirical analysis of yield curve changes shows that the structure of the variation in yield curves has not changed much since 1970, even though interest volatility has done so (Bliss 1997; Nath 2012). However, changes are difficult to quantify because they may affect several highly correlated maturities. In addition to affecting the bond price, investors have frequently used yield curves as a reference to forecast interest rates, which have also become a useful indicator of current and future economic activity (Nath 2012).
Yield curve shifts occur when the market revises their expectations on future interest rates. These rates fluctuate in response to variations in inflation expectations, risk premium and output growth. Empirical studies have revealed that yield curve movements can be characterised in terms of three factors, which are often termed as the 'level', 'slope' and 'curvature' factors. These terms describe how yield curves shift or change shape in response to a shock. Figure 1 illustrates the effect of level, slope and curvature shocks on a yield curve.
A parallel or level shift arises when interest rates across all maturities change by the same amount. Slope shifts develop when short-term expectations change but long-term rates remain the same, or vice versa (Phoa 2000). These shocks alter the steepness of interest rate curves. Curvature movements occur when rates at intermediate maturities change with respect to those at short and long maturities (Colin 2006). This results in yield curves becoming humped.
Principal component analysis (PCA) is a common approach considered to not only classify and quantify these yield curve movements but also to further manage the risk arising from groups of highly correlated market variables. In simple terms, the technique takes historical data on changes in market variables and attempts to define a set of uncorrelated components or factors that can effectively explain these movements in the most economical manner (Hull 2012).
Principal component analysis quantitatively describes yield curve variations by determining the percentage of variance each factor contributes in explaining these movements. This analysis turns out to be remarkably successful because the technique considers the variability present in the entire data set (Hull 2012).
This study employs the PCA technique to identify and quantitatively describe the main underlying movements present in yield curves. An established market and an emerging market will be used for this analysis, namely the United States and South Africa, respectively. This analysis also aims to relate fluctuations in the variance explained by each of these factors to macroeconomic influences. In addition, because PCA has the ability to explain a large proportion of yield curve variations in terms of only three uncorrelated factors, the technique allows regression analysis to be performed. In doing so, this study further attempts to ascertain the dominant factors responsible for driving South African interest rate movements.
The rest of this article proceeds as follows: Section 'Literature review' explores the relevant literature, section 'Data' discusses the data, and section 'Methodology' examines the PCA methodology. The results obtained are reviewed and discussed in section 'Analysis', and section 'Conclusions and suggestions for future research' concludes.
Literature review
The quantitative decomposition of yield curve changes into sub-movements that can easily be described and analysed by investors and analysts is of fundamental importance in today's financial markets (Colin 2006). Such an analysis allows investors to understand the dynamics of yield curves and the risk their portfolios are subject to because of the variability of these curves.
Traditional interest rate risk management focuses on duration, a technique which assumes that only parallel yield curve shifts are important (Phoa 2000). Using duration-based strategies to manage interest rate risk is also known as immunisation (Redington 1952). Although this is a common measure of bond risk, it is well known that non-parallel shifts in yield curves often occur. This is supported in the literature. Shiu (1987), for example showed that duration-based strategies do not work as well as past research had reported. Reitano (1992) demonstrated that duration-based strategies fail in practice, largely because of the assumption of parallel interest rate shifts.
Litterman and Scheinkman's (1991) approach identified and classified these non-parallel yield curve movements. Most variation on bond returns could be explained in terms of three factors (termed level, steepness and curvature factors, respectively). The level factor relates to a parallel movement in the interest rates, and the last two factors explain the non-parallel shifts which occur in yield curves. The slope factor results from a shift that causes a change in the yield curve's gradient and the third factor was shown to originate from a change in the curve's curvature. Although the level factor accounted for on average 90% of the observed variation in yield changes (which explains why duration-based strategies are commonly used), Litterman and Scheinkman's (1991) study revealed that investors can achieve a better hedged position by considering the effect on a portfolio of each of the three factors rather than simply holding a duration-based hedged portfolio.
Zero-coupon yields can be estimated using function-based methods including the form proposed by Nelson and Siegel (1987) which relies on fitting a single mathematical model to bond yield data with different maturities. The Nelson and Siegel (1987) specification assumes that the instantaneous forward rate at maturity is given by an exponential function and continuous compounding of the instantaneous forward rate to maturity generates the zero-coupon (or spot) interest rate.
Diebold, Ji and Li (2004) reformulated Nelson and Siegel's (1987) proposed parsimonious yield curve model into the Level-Slope-Curvature (LSC) three factor model (again, a level factor, a slope factor and a curvature factor). Diebold et al.'s (2004) findings reiterated that variations in yield curves are a result of level, steepness and curvature movements.
Litterman and Scheinkman (1991) as well as Diebold et al. (2004) used an empirical approach to derive the factors responsible for interest rate variations. This contrasts with the traditional approach used to describe yield curve dynamics. In this approach, a stochastic process that drives one or more state variables is defined (Cox, Ingersoll & Ross 1985; Longstaff & Schwartz 1992; Vasicek 1977). Heath et al. (1992) suggested volatility structures to determine the dynamics of the initial term structure. The disadvantage of using these traditional approaches was highlighted by Bierwag, Kaufman and Toevs (1983), who argued that as these stochastic processes need to be predicted, investors may incorrectly predict them, which may lead to poorly hedged portfolios and an incorrect analysis drawn on the dynamics of interest rate variations.
Although the three-factor model performs admirably, the factors still have a degree of correlation between them (Su & Knowles 2010) which results in factor relationship risk and which may be problematic for investors managing interest rate risk. Su and Knowles (2010) argue that this model tends to underestimate yield curve risk as a result of model fitting and bypassing of the residual variances.
An alternate method to model yield curve dynamics is PCA. This method identifies the fewest number of new explanatory variables to account for almost all the variability of yield curve changes (Su 2002). Similar to the three-factor approach, PCA quantifies movements of yield curves in terms of the same three factors (Baygun, Showers & Cherpelis 2000). Unlike the three-factor approach, PCA has an advantage of factor independence, that is, principal components are uncorrelated. This is helpful for real investment analysis because this independence eliminates the factor relationship risk which is present in the three-factor approach. Another significant benefit is that the PCA methodology considers the variance of the entire data set (Knowles & Su 2005) while the three-factor approach only considers the variance attributable to the factors, so interest rate risk tends to be underestimated. PCA allows researchers to assess components of risk in isolation, thereby allowing for a robust assessment of individual risk components (Tracey 2009).
Johnson (2005) suggests that the most important practical application of PCA is in its ability to construct more complete hedges for a bond portfolio. PCA allows almost all of the risk faced by a given bond portfolio to be explained by only a small number of factors. A portfolio can hedge against any shock driven by those key factors. This provides superior protection when compared with a more naïve immunisation approach, such as simple duration matching (Johnson 2005).
Principal component analysis works well in analysing yield curve changes; using three principal components explains up to 95% of bond yield variance, for example in the US market (Knez, Litterman and Scheinkman [1994], Barber and Copper [1996], Phoa [2000], Colin [2006] and Hull [2012]). Maitland (2002) found that most of the variability in the South African yield curve could be explained by just two factors (yield levels and yield changes). Maitland (2002) used the South African Johannesburg Stock Exchange (JSE)-Actuaries yield curve, that is, zero-coupon curves of differing maturity, not swap curves as in this research. Thomas (2008) used PCA to explore the factors that affect the South African swap curve and found four significant factors using data from August 2000 to March 2007.
Phoa (2000) applied PCA to US Treasury bond yield data. Like previous work, Phoa (2000) found that the dominant shift (the first principal component) was virtually a parallel shift, which explained over 90% of the observed fluctuations in bond yields. The slope and curvature shifts were identified as the second and third most important factors, respectively. Apart from these results, Phoa (2000) also analysed different sub-periods and found that the form of the curvature shift varied over time (the level and slope shifts were consistent across the sub-periods). This suggests that the curvature shift is less robust and may be of limited use in risk management.
Phoa (2000) related the principal components to macroeconomic factors, suggesting that the level could be caused by inflation expectations and the slope could be caused by monetary policy changes. Tracey (2009) reported that each of the fundamental PCA factors could be attributed to macroeconomic factors with the parallel component caused by inflation expectations, the slope by long-term inflation changes or market risk premiums and the curvature by changes in the volatility of interest rates. Tracey (2009) recommends that this type of analysis would be useful to examine individual risk with regard to non-parallel shifts that result from monetary policy.
In addition, macroeconomic events could also illuminate the explained variance of the level, slope and curvature during historical periods. Rakotondratsimba and Jaffal (2012) observed that after the 2007/2008 financial crisis, non-parallel shifts became more dominant. This could be investigated if PCA were instituted across a range of historical time periods, including the financial crisis.
Morita and Bueno (2008) associated the level and slope with inflation and Gross Domestic Product (GDP) growth, respectively. In another investigation, Morita and Bueno (2008) compared the fundamental PCA factors relative to a period which included a financial crisis and found that components are smoother during economic stability while during a financial crisis, the volatility increases. Briere and Ielpo (2007) performed a similar analysis by examining the variation of European yield curves with respect to macroeconomic news and found that the impact of economic announcements on yield curves displays different patterns according to the nature of the news (positive or negative).
Principal component analysis thus appears to enjoy an advantage over traditional duration-based approaches and factor analysis. PCA could identify and explain the fundamental variation of yield curves across a range of countries and historical periods. However, a research gap was identified with regard to explaining the relationship of yield curve changes between an established market and an emerging market in terms of principal components and macroeconomic factors across a range of historical time periods.
Data
Data selection
According to Su (2002), the US government bond market is the most efficient and liquid interest rate market in the world. US market data are also reliable and reasonably complete in comparison to emerging markets, which often suffer from illiquidity and incomplete data. According to Potelwa (2015a), foreign investors are buying South African bonds at a record pace. The article reports that US and Europe yields were at record lows in 2015, so investors sought elsewhere for yields. South African bond yields remain high in comparison to 24 emerging economies and are thus viewed as good investments according to Cadiz Asset Management Ltd (Potelwa 2015b). For these reasons, US and South African yield curves were considered for this analysis.
To determine if any relationship exists between US and South African yield curves, the following rates were selected:
-
the JPMorgan Emerging Market Bond Spread rate (JPEMBS);
-
the South African Rand to US Dollar exchange rate;
-
the US Federal Funds rate;
-
South African repo rate.
The JPEMBS provides an indication of the yield spread between the JPMorgan Emerging Markets Bond rate (denominated in US dollars) relative to the US Treasury bond rate. It could therefore identify relationships between the US market and an emerging market, such as South Africa. Monetary policies, such as the Federal Funds rate and the repo rate, will also affect yield curves and therefore it has been selected to aid in the analysis.
Data acquisition
The respective swap curve rates were extracted from Bloomberg. Different time periods were used to perform certain investigations under specific economic conditions or because of restrictions with regard to the acquisition of data. The time period chosen for the analysis ranged between 1990 and 2014 so as to compare time periods of pre-financial crisis and post-financial crisis. One of the main obstacles in a quantitative analysis was acquiring reliable and complete data. US sovereign curves were used, comprising six maturities between 1990 and 1999 as this time period resulted in a complete data set for various maturities. The data comprised 1-year, 2-year, 3-year, 5-year, 10-year and 30-year yield to maturities. Thereafter, US swap data spanning from 2000 to 2014 was extracted because of the availability of data. These comprised 1-year, 2-year, 3-year, 4-year, 5-year, 7-year, 10-year, 12-year, 15-year and 20-year maturity rates. According to Phoa (2000), swap rates are an alternative source for government bond yields, which are par yields by definition and therefore the results of the analysis will be similar. Unfortunately, data for South African maturity rates could not be acquired from 1990 because of non-availability. Therefore, South African swap rates were acquired between 1995 and 2014, comprising 1-year, 2-year, 3-year, 4-year, 5-year, 7-year, 10-year, 15-year, 20-year and 30-year maturity rates.
Maturities comprising short-term and long-term maturities were acquired to approximate the shape of yield curves. Maturities of less than a year were avoided to remove the idiosyncratic risk associated with those maturities. These data were extracted at a daily frequency. The daily frequency is also beneficial when performing an analysis on a short time period. The JPEMBSs were acquired from I-Net Expert, consisting of daily rates ranging between 2000 and 2014.
Additional rates such as the South African Rand to US Dollar exchange rate, repo rate and the Federal Funds rate were acquired from FRED Economic Data (FRED 2015). The exchange rate was extracted at a daily frequency, whereas the repo and Federal Funds rates were extracted at a monthly frequency.
Data preparation
Data preparation is a cumbersome task of structuring a large data set into a particular structure to conduct quantitative analysis. The data structure involved merging various maturity rates according to time (24-h period) and any missing maturity rates with respect to time were linearly interpolated. Daily rates vary by a small amount and as this analysis uses daily data, linear interpolation should closely approximate the true value. Python's1 powerful package Pandas provides tools for time-series data manipulation and was used to efficiently prepare the data.
Figure 2 displays the swap rates for 1-year and 30-year maturities of both countries.
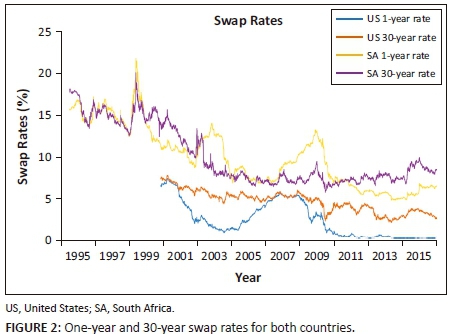
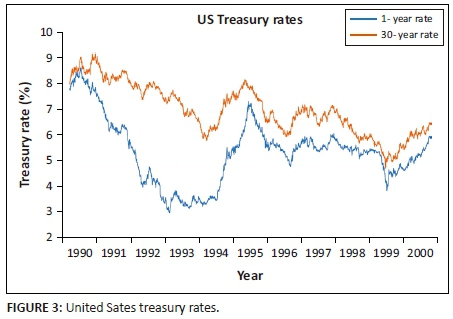
Figure 3 shows the relevant US Treasury data used in this study. Treasury rates are considered for the period prior to 2000 because of a lack of swap curve data available during this period.
Methodology
Principal component analysis theory
Principal component analysis summarises complex data sets by creating new, artificial variables called principal components. These are linear combinations of the original data and are constructed by exploiting the variability (i.e. spread) of each variable and the correlation between the variables. In addition, each of these new variables are assembled such that they are uncorrelated with one another. The components are derived by finding the eigenvectors and corresponding eigenvalues of the correlation or the covariance matrix between the variables in the original data set. These components effectively represent a rotation of the original data onto new axes. This new set of axes reveal more easily discernible patterns within the data.
The components are ordered according to the magnitude of their variance. The component with the largest corresponding eigenvalue is the first principal component - the linear combination that encapsulates most of the data variability. This component represents a rotation of the data along the axis representing the largest spread. The component with the second largest variance explains most of the remaining variability while being uncorrelated (perpendicular) to the first component. The same concepts apply to the remaining principal components. In the last step of this technique, PCA determines the number of 'real' dimensions present in the data. Eigenvectors are chosen such that the sum of the variances explained by these eigenvectors is sufficient to explain most of the variation present within the original data.2 The goal of PCA is to reduce the number of variables in data while still accounting for the majority of total variation embedded therein.
Applying principal component analysis to yield curve changes
The theoretical insights gained from PCA can be used to make sense of yield curve dynamics. Eigenvectors and their corresponding eigenvalues are derived from a covariance matrix based on time-series data of daily or monthly interest rate changes at each reference maturity.3 The eigenvectors can be interpreted as independent 'fundamental' yield curve shifts as they characterise different forms of yield curve changes. The relative size of the corresponding eigenvalues determines which fundamental yield curve shifts dominate. According to PCA, the first three components explain almost all of the variation in yield curve changes (Phoa 2000).4
The following sections explain the algebraic and graphical interpretation of PCA.
Algebraic view of principal component analysis
Suppose there are p variables (term to maturities) and n observations (daily basis point shifts).
Let X denote a (n × p) matrix of input data, where the columns represent the variables and the number of rows relate to the number of observations. Let μ be a (1 × p) vector consisting of the mean of each variable, then it follows that (X - μ) are the centred data. Let ∑ represent the covariance matrix of the input data. From the definition of a covariance matrix:

Principal component analysis is a decomposition of the covariance matrix. Equation 2 demonstrates this decomposition.

where P is a (p × p) orthogonal matrix (i.e. PTP = I), and Λ is a (p × p) diagonal matrix.
Because p is orthogonal, the determinant of p = 1, so p defines a rotation in p dimensions.
Because Λ is a diagonal matrix, the rotated variables are uncorrelated. The diagonal entries of Λ are the variances of the rotated variables. From ∑ = PΛPT, Λ = PT ∑ P. The trace of Λ is tr(Λ) = tr(PT ∑ P) = tr(∑ PTP)= tr(∑).5 Therefore, the sum of the variances of the rotated variables is equal to the sum of the variances of the original variables.
Let C be a (n × p) matrix representing the rotated variables. Because P defines a rotation,

Accordingly, (X - μ) = CPT. From this expression, Equation 4 demonstrates that any row in (X - μ) can be expressed as a linear combination of the eigenvectors.
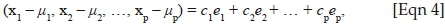
where ei is the ith eigenvector. The variance of each column in C is equal to the diagonal entries in Λ, that is, the eigenvalues.
A dimensionality reduction from p to m dimensions involves the projection of the input data (X - μ) (p dimension) onto the first m < p principal components. This is achieved by setting eigenvectors m + 1 to p = 0 and applying Equation 5:

Graphical interpretation of principal component analysis
Suppose there exists a history of yield curves, each curve can be represented as a vector of p points (or nodes) and each node represents a specific term to maturity. A yield curve shift can therefore be described by a vector of p elements, that is, one for each node/term to maturity. Accordingly, a yield curve shift history can be thought of as a history of p dimensional vectors. If it is possible to visualise p-dimensional space (yield curve with few nodes), the yield curve shift may then be represented as a single point in space, where its value on each of the p axes is determined by the values at each of the p nodes.
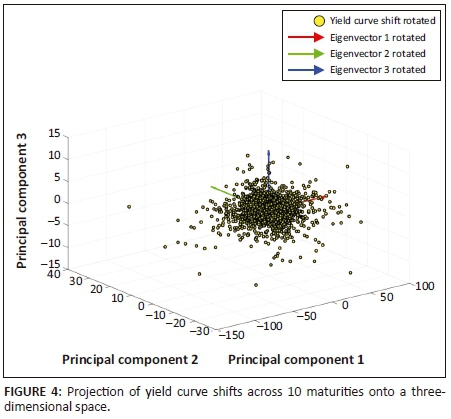
Figure 4 displays the projection of a 10-dimensional data set6 (yield curve shifts across 10 maturities) onto a three-dimensional space.7 The three eigenvectors represent a new system of axes and each point's position (yield curve shift) can now be expressed relative to these new axes. In this data set, most of the variation is explained along the first three principal component axes, hence the projection onto a three-dimensional space. Figure 5 shows all three components with explained variances.8 The components characterise specific forms of yield curve shifts, namely level, slope and curvature shifts which account for over 98% of yield curve movements.
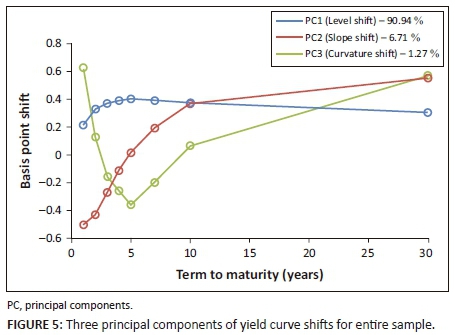
Analysis
Figures 6 and 7 illustrate the first three principal components derived for US and South African swap rate shifts for the period between 2000 and 2014. The plots further depict the percentage of variance explained by each factor. All PCA results are generated using a daily frequency of interest rate movements.
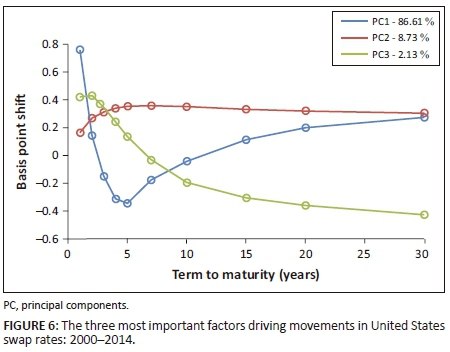
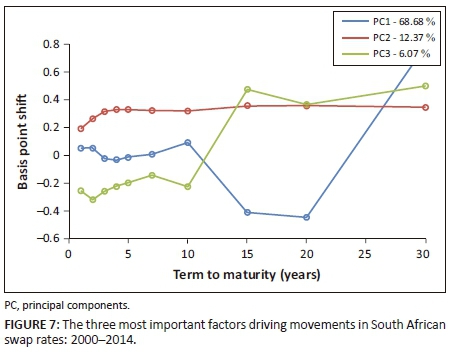
The simulation results agree with the literature. Firstly, PCA can effectively derive three components that can explain most yield curve variations.9 The literature shows the same findings about US and emerging market yield curves, namely that there are three main components, but these are distorted for emerging markets relative to developed markets. Secondly, PCA is able to characterise these movements in terms of level, slope and curvature shifts. Lastly, slope changes and curvature shifts are more volatile in South Africa and are not consistent over annual intervals. Developing economies (such as South Africa) are more prone to noise, where these markets are politically unstable and interest rates are far more volatile, which feeds into unstable monetary policy. There were also multiple financial crisis events during this period, which could influence the shape and distortion of the principal components. This led to the investigation between the periods of pre- and post-2000.
Economic interpretation of principal component analysis results in the United States and South Africa
Interpretation of US results
Figures 8 and 9 present a three-dimensional representation of each principal component generated on an annual interval for the pre- and post-2000 periods, respectively.
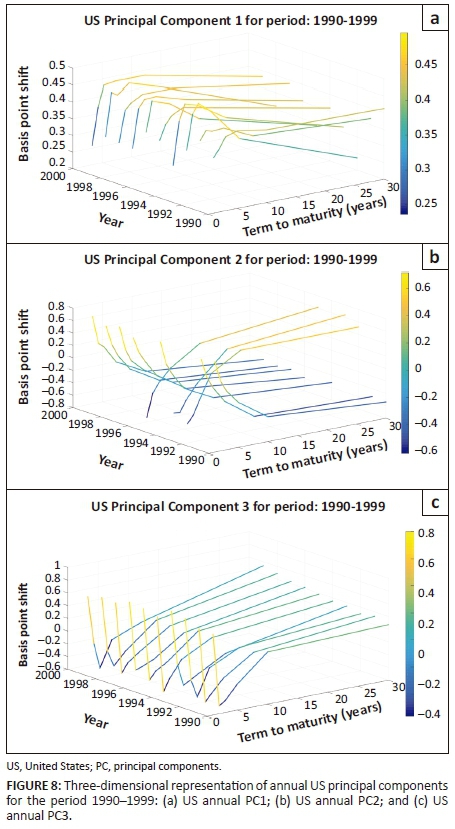
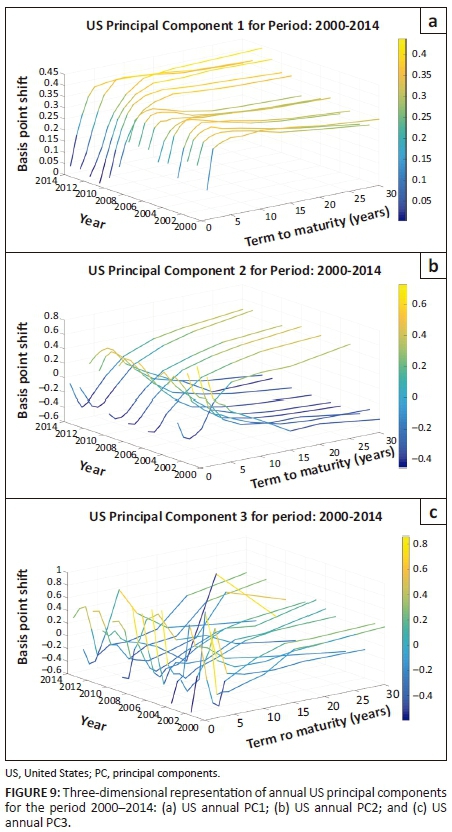
The form of the slope and curvature components during the 1990s are significantly smoother when compared with the components post-2000. This could be because the 1990s were characterised by strong economic growth that resulted from a combination of rapid technological advancements and sound central monetary policy. In contrast, the market suffered with multiple crisis periods post-2000 (e.g. the dot-com and credit crisis). The economic instability during this period is reflected in the variation of the Federal Funds rate, as shown in Figure 10.
Figure 11 depicts the percentage of variance explained of each principal component for each year during the post-2000 period.
The changes in variance over the sample period, explained by the components, may be related to macroeconomic factors. Such an explanation may not be sensible during this unstable period, where movements in the term rates might have been attributable to many unexplained factors. However, extreme monetary policy changes might have been a possible factor contributing to increased slope shifts during certain years.10 As confirmed in Figure 10, there was a sharp rise in interest rates during 2000, a considerable decline in rates during 2001 in an attempt to spur growth during the recession and a further decline in rates during the credit crisis of 2008. During these periods, the slope factor played a more dominant role in comparison to previous years. In periods where the federal fund rate remained stable, the slope is a less dominant factor, whereas during crisis periods it is dominant.
The slope factor is slightly more prominent post-2010, a period devoid of monetary policy shocks. This suggests that during this quantitative easing phase, the slope factor is now rather explained by movements in long-term interest rate expectations.
Interpretation of South African results
Figures 12 and 13 depict annual principal components for pre- and post-2000 periods, respectively. In contrast to the United States, the 1990s were a time of considerable upheaval for emerging markets. Many developing economies suffered from the tightening of bond markets as stock markets fell. This may explain the volatility in the form of the principal components during this period.
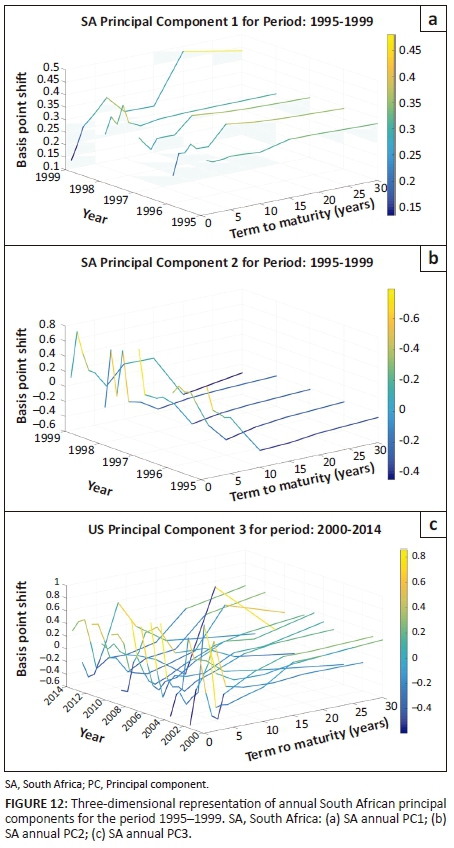
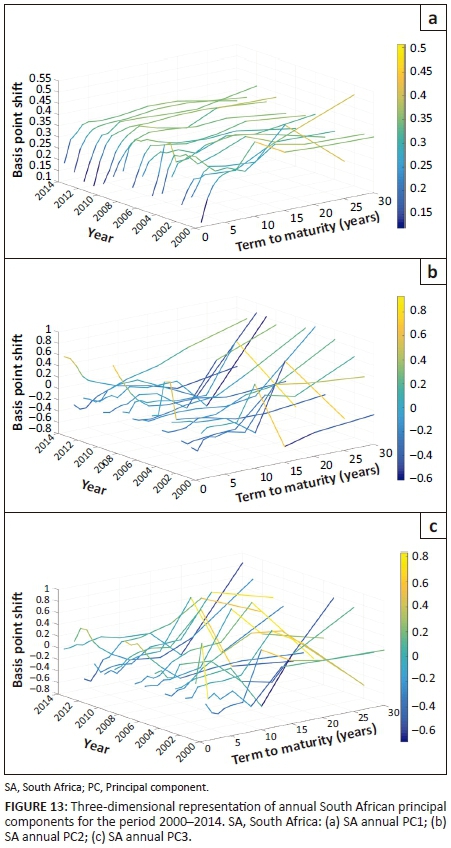
Figure 14 illustrates the percentage of variance explained of each principal component during the post-2000 period.
Although the level shift is still dominant, South Africa's level factor plays a minor role in comparison with the US level factor. As a result, the slope and curvature factors are observed to play a greater role in driving South African interest rate movements. This may be attributable to greater market volatility present in emerging markets as they are more vulnerable to external shocks. In addition, South Africa's inflation expectations are more erratic than market inflation expectations in the United States.11 As an emerging market, South Africa also presents a challenging array of long-term political, economic and financial risk to investors. Consequently, South Africa has a high-risk premium which fluctuates enormously and plays a significant role in the demand for its fixed-income securities. This high and volatile risk premium is likely to be a significant factor in increasing the dominance of slope shifts.12
Over the period 2000-2004, slope shifts explain a relatively high proportion of interest rate movements. This may be because of severe changes (substantial increases and decreases) in the repo rates (which in turn alters inflation expectations). These extreme changes are depicted in Figure 15. These movements coupled with markets' volatile perception on emerging markets risk may help explain this slope shift dominance.
Based on the findings displayed in Figure 15, similarly to the United States, the slope factor was more dominant during periods when there were sharp increases and decreases in the repo rate. On an interesting note, post-2009 reveals a period where the slope component was significantly less dominant. This may be attributable to quantitative easing in the United States. With short-term rates in the United States remaining stable, rates in South Africa did not fluctuate as much during this period.13 Consequently, there were less monetary policy shocks during this period, which may have played a prominent role in explaining why slope movements were less dominant post-2009.
Correlation and regression analysis on principal component scores
The previous section illustrates the effect of US interest rates on the South African currency and interest rates. A relationship might thus exist between the changes of US yield curves and the changes of South African yield curves. The problem with performing a correlation and regression analysis on yield curve changes is that maturities in each data set are highly correlated. A few maturities can instead be selected and these used for correlation and regression analysis. However, those maturities will only explain a limited amount of variance. The advantage of PCA is that it provides a reduced number of uncorrelated principal components that explains most of the variance in the entire data set. The scores of the uncorrelated principal components can therefore be used in a correlation and regression analysis.
The JPEMBS could identify relationships between the US market and an emerging market, such as SA. If the spread increases, the risk premiums of emerging markets are increasing. This could be because of risk-averse investors taking investments out of emerging markets and placing them in established markets. It has also been suggested (Morita & Bueno 2008; Phoa 2000) that changes in monetary policy could affect the resultant slope and curvature components of PCA on yield curve changes. This result could be investigated by correlating the slope and curvature of the United States and South Africa to the changes in the repo rate and the Federal Funds rate.
Model preparation and variables under consideration
The following variables were used in the correlation and regression analysis:
-
scores of principal components 1, 2 and 3 of US yield curve changes;
-
scores of principal components 1, 2 and 3 of South African yield curve changes;
-
changes in the JPEMBS rate;
-
changes in the Federal Funds rate and repo rate;
-
percentage changes in the South African Rand to US Dollar exchange rate.
To build the multivariate regression models, a correlation analysis is first performed. Note that performing correlation over daily data is not sensible as correlation tends to under-perform when applied to high-frequency signals. In addition, daily data are prone to more noise, which can affect the accuracy of correlation results considerably. To overcome these limitations, principal component scores were derived based on monthly mean swap rate changes. Monthly mean values are considered ahead of values occurring on the first or last day of each month as these values may themselves be outliers. Using mean values of each month allows average shifts to be encapsulated over that period. This in turn alleviates the problem of noise. Furthermore, using monthly values will overcome the issue of selecting accurate lag or lead values.14
Sampling data using monthly mean values encapsulates the daily observations and hence would be a good approximation to an analysis done on daily observations. Accordingly, for the correlation and regression analysis to follow, all relevant data are resampled based on monthly mean values. In contrast, the Federal Funds rate and the repo rate data are based on actual monthly percentage changes.
The correlation results based on a monthly frequency for the period between 2000 and 2013 can be seen in Table 1.
Table 1 illustrates that there is a 34% correlation of the scores relating to level and a 24% correlation of the scores relating to the curvature between the United States and South Africa. There is also a 32% correlation between the scores of the level in South Africa and the exchange rate.
Also of interest is the negative correlation of 20% between the JPEMBS and the scores of the US level component. This could be because of risk-averse investors shifting investments to established markets. Tracey (2009) suggests that monetary policy changes affect the curvature component, whereas Phoa (2000) suggests that it could have an impact on the slope component. Table 1 shows that changes in the repo rate had a 32% correlation to the scores of the curvature component and 31% correlation to the scores of the slope component in South Africa. In addition, changes in the Federal Funds rate had a 42% correlation to the scores of the curvature component and 37% correlation to the scores of the slope component in the United States, confirming the results of past literature.
The significant correlations with respect to the scores of the South African principal components suggest a multivariate regression. In addition, correlation does not indicate causality. Therefore, a multivariate regression analysis needs to be performed to determine which rates drive South African yield curve changes. The analysis was performed using the ordinary least squares (OLS) method and a 95% confidence interval was selected. Two regression models were constructed based on the correlation results from Table 1, as shown in Table 2.
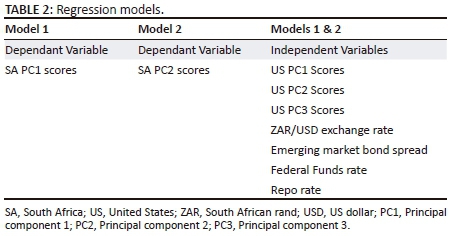
The independent variables with resulting p-values greater than 5% were removed and the analysis was thereafter repeated. This prevents the model from over-fitting owing to the addition of insignificant dependent variables. In addition, if any of the regression models displayed insignificant results, they were neglected and only the significant results were presented.
Results for the period between 2000 and 2013
The multivariate regression results for the period between 2000 and 2013 is shown in Table 3. Note that Model 2 resulted in insignificant results and hence has been neglected for this period.
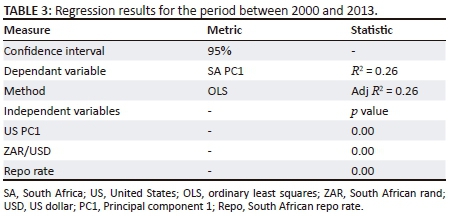
Table 3 presents a multivariate regression model with an adjusted value of 0.26. This model suggests that during this period, movements in US level shifts, the exchange rate and the repo rate can explain up to 26% of variation in South African level shifts. The model infers that over the long term (2000-2013), South African rates were not affected by US interest rate and exchange rate movements. There might have been periods during certain economic cycles or crises where these relationships might have been more significant. As a result, regression models for different sub-periods are now considered. The sub-periods are derived according to substantial fluctuations present in the emerging markets spread. Because the spread determines the risk premium present in emerging markets, it may serve as a good indicator in determining the effect US interest rate movements have on South African rates.
The change in the gradient of this curve can therefore indicate different economic cycles of emerging markets. A regression analysis was therefore conducted on the different economic cycles of emerging markets. The following sub-periods correspond to different economic cycles over the period 2000-2013.
-
Sub-period 1: 2000-2002 (characterised by the dot-com crash of 2000-2001).
-
Sub-period 2: 2003-2007 (the US recovery period).
-
Sub-period 3: 2008-2009 (includes the credit crisis of 2008).
-
Sub-period 4: 2010-2013 (characterised by US quantitative easing).
Results for sub-period 1
Table 4 summarises the multivariate regression results for sub-period 1.
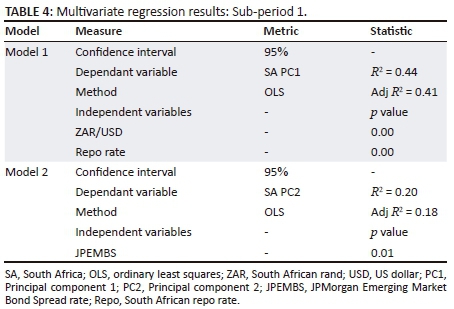
The results in Table 4 indicate that in a sub-period where the risk premium of emerging markets was volatile, the following deductions can be made:
-
Forty-one per cent of level shifts in South Africa were explained by the South African Rand to US Dollar exchange rate and the repo rate.
-
Eighteen per cent of South African slope shifts were explained by the JPEMBS rate.
Results for sub-period 2
Table 5 illustrates the multivariate regression results for sub-period 2.
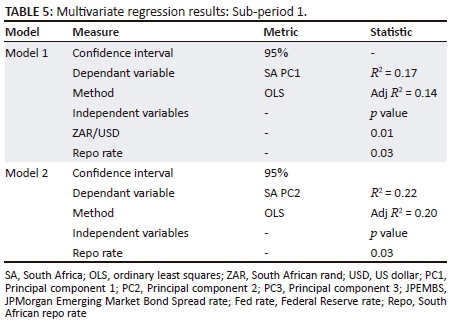
The results in Table 5 indicate that in a sub-period where the risk premium of emerging markets were decreasing, the following deductions can be made:
-
Fourteen per cent of South African level shifts were influenced by exchange rate and repo rate fluctuations.
-
During this period, movements in the repo rate drove 20% of South African slope shifts.
Results for sub-period 3
Table 6 displays the multivariate regression results for sub-period 3.
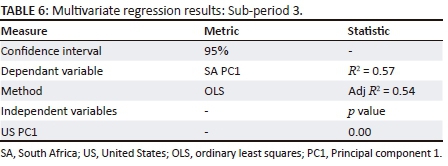
The results in Table 6 indicate that in a sub-period where the risk premium of emerging markets were increasing rapidly, the following deductions can be made:
-
Fifty-four per cent of level shifts in South Africa were explained by US level shifts.
Results for sub-period 4
Table 7 presents the multivariate regression results for sub-period 4.
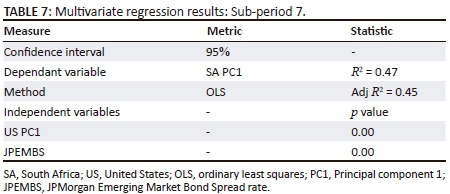
The results in Table 7 indicate that in a sub-period where the risk premium of emerging markets was stable, it can be deduced that 45% of level shifts in South Africa were explained by US level shifts and the JPEMBS rate.
Sub-period deductions
Sub-period 2 relates to a period of economic recovery in the United States. In addition, the period was characterised by protracted periods of strength in the rand (Figure 16). The low adjusted R2 value suggests that during this stable period, movements in South African term rates may have been driven to a large extent by internal market factors.
In contrast, sub-period 1 resembles a period where the rand was severely weakened (Figure 16).
A possible cause in the rand deterioration may have been attributable to the slowdown in global economic activity that began in 2000, where the demand for South African goods and services moderated. Accordingly, when the exchange rate volatility increases, investors require a larger yield compensation for holding emerging market bonds. This volatility coupled with a sharp decrease in the repo rate (Figure 15) supports the statistically significant adjusted R2 values in explaining South African level shifts during sub-period 1.
During the last two sub-periods, the regression results suggest that movements in the US term rates played an important role in driving South African interest rates. This could largely be because of the impact of the credit crisis of 2008. In addition, the significant relationship seen during sub-period 4 (post-2010) may stem from quantitative easing, a time when US investors are pushing funds to emerging markets that offer higher attractive yields.
Conclusion and suggestions for future research
This study used the PCA technique to identify and quantitatively describe the main underlying movements present in both US and South African yield curves. The analysis was further aimed at relating fluctuations in the percentage of variance explained by each of these factors to macroeconomic influences or events. The study further intended to determine dominant factors, if any, which were responsible for driving South African interest rate movements during certain economic periods.
The PCA technique classifies and quantifies yield curve movements across both markets with respect to three main factors, namely level, slope and curvature shifts. These factors encapsulate most of the yield curves variability, with the level shift representing the dominant component. Curvature movements only contribute a small change in yield curve variations.
In terms of relating these factors to macroeconomic variables, the findings revealed that monetary policy shocks across both markets played a prominent role in affecting the form and importance of slope and curvature shifts. In addition, the results illustrated that the shape and importance of each factor deviated during periods of economic instability. In particular, the form of the slope and curvature movements were erratic and distorted during these periods. In contrast, the shape of the slope and curvature shifts were significantly smoother during periods of economic stability. In the light of this, it can be argued that a volatile market and economic environment can significantly distort the shape, smoothness and percentage of variance explained of yield curve movements.
In terms of a brief comparison between the markets, the level shifts in South Africa were observed to play a far less dominant role, resulting in the slope and curvature factors driving South African interest rate movements to a greater degree. Furthermore, it was noticed that the form of South African slope and curvature shifts were far more erratic. These differences were suggested to be because of factors such as political instability, unstable monetary policy and volatile interest rate expectations, which are known to be prominent in emerging markets.
A regression analysis revealed that over the long term (2000-2013), South African rates were not largely driven by US interest rate movements. However, during certain sub-periods, movements in the US term rates played a dominant role in driving South African rates. As an example, during the credit crisis period the regression models suggested that 54% of South African level shifts were driven by US level shifts. The results further illustrated that during certain periods, movements in the Rand/Dollar exchange rate played an important role in driving South African level shifts. In addition, the regression results were able to confirm the significant relationship between monetary policy shocks and corresponding slope and curvature movements across both markets.
Further research could involve the comparison of the impact of the credit crisis on the volatility of interest rates in both markets. An F-test could be performed based on principal components scores (derived from yield curve changes) pre- and post-crisis to compare the variances of yield curve movements during these periods.
Further research could also aim to verify the relationship suggested by the regression models between US and South African rates during certain periods. Alternate statistical methods can be researched to compare daily US and South African principal component scores, where methods such as auto correlation, co-integration or dynamic time warping could be used to accurately determine the lag between US and South African yield curve changes. Principal component scores for each sub-period using weekly mean changes in yields could also provide a possibility.
Lastly, an investigation could be performed on the factor loadings of the principal components across different sub-periods. This will indicate the degree to which various interest rates affected the level, slope and curvature movements during certain economic periods.
Acknowledgements
Competing interests
The authors declare that they have no financial or personal relationship(s) that may have inappropriately influenced them in writing this article.
Authors' contributions
K.P. and A.M., the principal authors, instituted the study and undertook analysis and interpretation. G.W.v.V., the supervisor, recommended the project and oversaw the robustness of the results and interpretation.
References
Barber, J.R. & Copper, M.L., 1996, 'Immunization using principal component analysis', The Journal of Portfolio Management 23(1), 99-105. https://doi.org/10.3905/jpm.1996.409574 [ Links ]
Baygun, B., Showers, J. & Cherpelis, G., 2000, Principles of principal components, Salomon Smith Barney, Portfolio Strategies, viewed 26 Aug. 2015, from http://quantlabs.net/academy/download/free_quant_instituitional_books_/Principles_of _Principal_Components.pdf [ Links ]
Bierwag, G.O., Kaufman, G.G. & Toevs, A., 1983, 'Duration: Its development and use in bond portfolio management', Financial Analysts Journal 39(4), 15-35. https://doi.org/10.2469/faj.v39.n4.15 [ Links ]
Bliss, R.R., 1997, 'Movements in the term structure of interest rates', Economic Review-Federal Reserve Bank of Atlanta 82(4), 16. [ Links ]
Briere, M. & Ielpo, F., 2007, Yield curve reaction to macroeconomic news in Europe: Disentangling the US influence. http://dx.doi.org/10.2139/ssrn.1054861 [ Links ]
Colin, A., 2006, 'A new approach to the decomposition of yield curve movements for fixed income attribution', The Journal of Performance Measurement 10(4), 18-28. [ Links ]
Cox, J.C., Ingersoll, J.E. & Ross, S.A., 1985, 'A theory of the term structure of interest rates', Econometrica 53(2), 385-407. https://doi.org/10.2307/1911242 [ Links ]
Diebold, F.X., Ji, L. & Li, C., 2004, A three-factor yield curve model: Non-affine structure, systematic risk sources, and generalized duration, PIER Working Paper No. 06-017, http://dx.doi.org/10.2139/ssrn.910218 [ Links ]
FRED, 2015, Federal Reserve Economic Data, viewed 20 August 2015, from https://research.stlouisfed.org/fred2/ [ Links ]
Heath, D., Jarrow, R. & Morton, A., 1992, 'Bond pricing and the term structure of interest rates: A new methodology for contingent claims valuation', Econometrica 60(1), 77-105. https://doi.org/10.2307/2951677 [ Links ]
Hull, J., 2012, Risk management and financial institutions, John Wiley & Sons, s.l. [ Links ]
Johnson, G., 2005, 'Government of Canada yield-curve dynamics, 1986-2003', Bank of Canada Review 2004 (Winter), 17-28. [ Links ]
Knez, P.J., Litterman, R. & Scheinkman, J., 1994, 'Explorations into factors explaining money market returns', Journal of Finance 49(5), 1861-1882. https://doi.org/10.1111/j.1540-6261.1994.tb04784.x [ Links ]
Knowles, T.W. & Su, E., 2005, 'Measuring Bond Portfolio value at risk: Us and Taiwan Government Bond markets empirical research', Financial Management and Accounting 23(2), 1-15. [ Links ]
Litterman, R.B. & Scheinkman, J., 1991, 'Common factors affecting bond returns', The Journal of Fixed Income 1(1), 54-61. https://doi.org/10.3905/jfi.1991.692347 [ Links ]
Longstaff, F.A. & Schwartz, E.S., 1992, 'Interest rate volatility and the term structure: A two-factor general equilibrium model', The Journal of Finance 47(4), 1259-1282. https://doi.org/10.1111/j.1540-6261.1992.tb04657.x [ Links ]
Maitland, J., 2002, 'Interpolating the South African yield curve', South African Actuarial Journal 2, 129-146. https://doi.org/10.4314/saaj.v2i1.24488 [ Links ]
Morita, R., & Bueno, R. 2008, 'Investment grade countries yield curve dynamics', in XXX Meeting of the Brazilian Econometric Society, Rio de Janiero, Brazil, November 20-22, 2008. [ Links ]
Nath, G.C., 2012, Estimating term structure changes using principal component analysis in Indian sovereign bond market. http://dx.doi.org/10.2139/ssrn.2075635 [ Links ]
Nelson, C.R. & Siegel, A.F., 1987, 'Parsimonious modeling of yield curves', Journal of Business 60(4), 473-489. https://doi.org/10.1086/296409 [ Links ]
Phoa, W., 2000, Yield curve risk factors: Domestic and global contexts. The Professional's Handbook of Financial Risk Management, pp. 155-184, Butterworth-Heinemann, Oxford. [ Links ]
Potelwa, X., 2015a, Investors buy South African bonds at record pace on fed delay, viewed 03 August 2015, from http://www.bloomberg.com/news/articles/2015-04-14/investors-buy-south-african-bonds-at-record-pace-on-fed-delay [ Links ]
Potelwa, X., 2015b, South African bonds are a buy for Cadiz amid global debt rout, viewed 17 July 2017, from https://www.moneyweb.co.za/news/economy/south-african-bonds-are-a-buy-for-cadiz-amid-global-debt-rout/ [ Links ]
Rakotondratsimba, Y. & Jaffal, H., 2012, 'Enhancement of the Fisher-Weil bond technique immunization', Journal of Finance and Investment Analysis 1(2), 221-248. [ Links ]
Redington, F.M., 1952, 'Review of the principles of life-office valuations', Journal of the Institute of Actuaries 78(3), 286-340. [ Links ]
Reitano, R.R., 1992, 'Non-parallel yield curve shifts and immunization', The Journal of Portfolio Management 18(3), 36-43. https://doi.org/10.3905/jpm.1992.409410 [ Links ]
Shiu, E.S.W., 1987, 'On the Fisher-Weil immunization theorem', Insurance: Mathematics and Economics 6(4), 259-266. https://doi.org/10.1016/0167-6687(87)90030-8 [ Links ]
Su, E., 2002, Measuring bond portfolio value at risk- US and Taiwan government bond markets empirical research, National Science Association, Plan No. 90-2416-H-327-026, viewed 21 June 2015, from http://repository.nkfust.edu.tw/retrieve/17861/NSC90-2416-H327-026.pdf [ Links ]
Su, E. & Knowles, T.W., 2010, 'Measuring Bond Portfolio value at risk and expected shortfall in US treasury market', Asia Pacific Management Review 15(4), 477-501. [ Links ]
Thomas, M., 2008, 'Long-term extrapolation and hedging of the South African yield curve', Unpublished MSc thesis, University of Pretoria, South Africa. [ Links ]
Tracey, M., 2009, Principal component value at risk: An application to the measurement of the interest rate risk exposure of Jamaican Banks to Government of Jamaica (GOJ) Bonds. Financial Stability Department, Research & Economic Programming Division, Bank of Jamaica, Kingston, Jamaica. [ Links ]
Vasicek, O., 1977, 'An equilibrium characterization of the term structure', Journal of Financial Economics 5(2), 177-188. https://doi.org/10.1016/0304-405X(77)90016-2 [ Links ]
 Correspondence:
Correspondence:
Gary van Vuuren
vvgary@hotmail.com
Received: 28 June 2016
Accepted: 29 Sept. 2017
Published: 26 Mar. 2018
1 . General purpose and high-level programming language.
2 . Formally, for dimensionality reduction. In a data set where there are m eigenvectors, a reduction from m dimensions to k dimensions occurs by choosing k eigenvectors related with the k largest eigenvalues. In mathematical terms, choose k when the percentage of variance explained PoV > 90%, where, 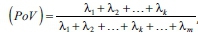 , is sorted in descending order and refers to the eigenvalue corresponding to the eigenvector.
, is sorted in descending order and refers to the eigenvalue corresponding to the eigenvector.
3 . A covariance matrix can be used since each variable (term to maturity) is measured in the same units and the variances between the variables (changes in yields across different maturities) do not vary greatly.
4 . Because of the high correlation present in yields across different maturities, the first three components generally account for almost all the variability in yield curve changes.
5 . The trace of a square matrix is the sum of the main diagonal elements.
6 . The sample data considered are US treasury rates for the period 2000-2011.
7 . This projection represents a dimensionality reduction from 10 dimensions to 3 dimensions.
8 . See Footnote 2 for percentage of variance explained equation.
9 . Swap rates serve as an acceptable proxy for yield curves.
10 . A slope shift can occur when short-term rates change but long-term rates remain the same, or vice versa.
11 . Changes in long-term inflation expectations will alter long-term interest rate expectations. This in turn affects the slope of interest rate curves.
12 . The risk premium affects both the long and short ends of a yield curve. However, it is greater at longer durations because of more uncertainty and a greater chance of catastrophic events that can impact investments. Fluctuating risk premiums will therefore alter the slope of interest rate curves.
13 . South African interest rates mostly follow movements in the US interest rates with a lag. This is confirmed by comparing Figures 8 and 15.
14 . Financial markets worldwide do not have the same working hours. As a result, the study of correlation or causality between financial market indices becomes highly dependent on the issue of lagging or leading data. A lag of 1 day, for example may be chosen between US and South African time series data (i.e. when the US markets close, South African markets react the following day based on movements in the United States).














