Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Economic and Management Sciences
versão On-line ISSN 2222-3436
versão impressa ISSN 1015-8812
S. Afr. j. econ. manag. sci. vol.20 no.1 Pretoria 2017
http://dx.doi.org/10.4102/sajems.v20i1.1619
ORIGINAL RESEARCH
Measuring the systemic risk in the South African banking sector
Gregory M. Foggitt; Andre Heymans; Gary W. van Vuuren; Anmar Pretorius
Department of Risk Management, School of Economics, North-West University, South Africa
ABSTRACT
BACKGROUND: In the aftermath of the sub-prime crisis, systemic risk has become a greater priority for regulators, with the National Treasury (2011) stating that regulators should proactively monitor changes in systemic risk.
AIM: The aim is to quantify systemic risk as the capital shortfall an institution is likely to experience, conditional to the entire financial sector being undercapitalised.
SETTING: We measure the systemic risk index (SRISK) of the South African (SA) banking sector between 2001 and 2013.
METHODS: Systemic risk is measured with the SRISK.
RESULTS: Although the results indicated only moderate systemic risk in the SA financial sector over this period, there were significant spikes in the levels of systemic risk during periods of financial turmoil in other countries. Especially the stock market crash in 2002 and the sub-prime crisis in 2008. Based on our results, the largest contributor to systemic risk during quiet periods was Investec, the bank in our sample which had the lowest market capitalisation. However, during periods of financial turmoil, the contributions of other larger banks increased markedly.
CONCLUSION: The implication of these spikes is that systemic risk levels may also be highly dependent on external economic factors, in addition to internal banking characteristics. The results indicate that the economic fundamentals of SA itself seem to have little effect on the amount of systemic risk present in the financial sector. A more significant relationship seems to exist with the stability of the financial sectors in foreign countries. The implication therefore is that complying with individual banking regulations, such as Basel, and corporate governance regulations promoting ethical behaviour, such as King III, may not be adequate. It is therefore proposed that banks should always have sufficient capital reserves in order to mitigate the effects of a financial crisis in a foreign country. The use of worst-case scenario analyses (such as those in this study) could aid in determining exactly how much capital banks could need in order to be considered sufficiently capitalised during a financial crisis, and therefore safe from systemic risk.
Introduction
One of the key elements to understanding the propagation of financial crises lies in the understanding of the nature of systemic risk (Allen, Babus & Carletti 2010:1). As the sophistication of the world financial system has evolved, so has the understanding of systemic risk. Systemic risk can be an externality of bank distress on the real economy or the financial system as a whole (Bernanke 2009). These externalities can be split into three broad categories. Firstly, externalities associated with excessive or correlated risk taking; secondly, externalities related to fire sales; lastly, externalities related to interconnectedness (De Nicoló, Favara & Ratnovski 2012:5). Systemic risk can also be categorised in both a broad and narrow sense (De Bandt, Hartmann & Peydró 2009:636). The narrow sense concerns contagion effects on the interbank market while the broad sense refers to a common shock to many institutions or markets. In essence, systemic risk is the risk of a disruption to financial services that is caused by an impairment of all or parts of the financial system and has the potential to have significant negative consequences for the real economy (IMF, BIS & FStB 2009:2).
This disruption to financial services was especially prominent during the sub-prime crisis of 2007/2008. The collapse of American International Group and Lehman Brothers in particular illustrated how single, large financial institutions can cause a contagion effect in the financial sector that later spills over to the entire economy (Georg 2011:4). The US economy was plunged into recession, declining from 3% growth in gross domestic product (GDP) in 2005 to −3% in 2009 (World Bank 2015). Given the substantial impact of this event on the world economy, the prevention of such a contagious event must be prioritised, something that is only possible if the systemic risk posed by such financial institutions can be addressed.
Considering the complexity of systemic risk, it would follow that systemic risk is difficult to measure. Given that the National Treasury (2011) stated that regulators should proactively monitor changes in systemic risk, it would follow that the accurate measurement of systemic risk is important because regulations should be based on this measurement. Furthermore, because systemic risk is such a broad concept, finding a measure that sufficiently encompasses the entire risk and all its complexities is an additional challenge. The research question that follows is therefore whether systemic risk could potentially be overlooked or underreported in South Africa (SA) because the correct measurements have either not yet been discovered or are not being used? Furthermore, are regulators aware of the levels of systemic risk of the entire financial sector, and the specific banks that are contributing to this risk?
In order to address this problem in the SA financial sector, we propose a new way of estimating systemic risk. This is done by applying a marginal expected shortfall (MES) measure using a new technique to calculate the tail distribution component, based on extreme value theory and the Hill estimator. These techniques are ideal for modelling unlikely yet large losses and therefore provide distributions more suited to extreme events. Additionally, to provide a measure for a longer period and a worst-case scenario simulation, the long-run marginal expected shortfall (LRMES) is calculated. To accomplish this, a Monte Carlo simulation procedure and Cholesky decomposition are used to simulate returns that preserve the sub-prime crisis period volatilities and correlations. This is considered the worst-case scenario because it takes into account the volatility and correlation over the sub-prime crisis period of 1 July 2007 to 31 December 2008 and therefore inflates the tail dependence of the banks. The reason for this is that it represents the period of greatest market volatility and is therefore likely to present a scenario of a very low probability. This provides an interesting comparison because it illustrates the systemic risk index (SRISK) values of banks over the sample period, given that they had the volatility and tail dependence shown during the sub-prime crisis.
A previous article by López-Espinosa et al. (2012) measured the systemic risk contribution of Standard Bank to a sample of international banks but considering that this was the only SA bank used, no meaningful comparison can be made. Another measurement approach was undertaken by Bartram, Brown and Hund (2007), but only two banks were considered for SA and no explicit results were reported.
The contribution of this article is therefore to measure the level of systemic risk in the SA financial sector and to identify which banks are the largest contributors to the overall level. In doing so, we also make a novel contribution to the field through the development of a new technique for measuring systemic risk.
The rest of the article is structured as follows. The next section contextualises the concept of systemic risk and provides an overview of the literature pertaining to it. The 'Measuring systemic risk' section then presents the methodology used to measure systemic risk, before the 'Data and results' section describes the data used and subsequently reports on the findings. Finally, the 'Summary and conclusions' section presents a summary of the results and concludes the article.
Contextualising and defining systemic risk
The sub-prime crisis affected not only the US economy but also financial markets across the world (BIS 2009:16). This was mainly because of the advancement of information technology and computer systems, which facilitates a greater degree of linkage among global financial markets (Kim & Ryu 2015:20). An investor seeking higher yields as well as portfolio diversification may invest in any market that offers a greater return on investment. However, these linkages can also lead to increased risk of contagion and informational spillovers (Kim & Ryu 2015:21). These are two of the three broad elements of systemic risk, with common shocks being the third. Contagion refers to the direct linkages that take place between financial institutions such as those in the interbank market. Informational spillovers are similar to contagion, but in a more indirect sense, whereby 'bad news' concerning a large bank in a given country could result in a negative perception regarding all banks in that particular country's financial sector. Common shocks on the other hand refer to indirect linkages between banks that may occur when they hold similar or identical assets. Such correlation between portfolios may lead to fire sales and result in considerably large losses (Georg 2011:8). These elements of interconnectedness therefore ensure that an adverse shock in one financial sector has the potential to negatively affect the entire global financial sector and economy.
The effect on emerging market economies, however, differed from developed economies in the sense that their systemic risk could largely be attributed to a slowdown or reversal in capital flows that are intermediated through the domestic banking sector (Claessens & Ghosh 2013:107). Challenges that are unique to emerging markets include the following: how to supervise and regulate the shadow banking sector and foreign banks; increasing cross-sectional risks such as contagion and the development of systemically important financial institutions; and the driving of economic outcomes in correlation with domestic financial cycles and subsequent credit booms (Claessens & Ghosh 2013:115). In order to respond to these challenges, certain policies could be implemented. Because the challenges were different, it would follow that the policy responses would also differ for developed, emerging and developing economies. The exact difference between emerging and developing economies is not entirely clear in the literature. The IMF World Economic Outlook Database classifies countries according to their Gross National Income, export diversification, and level of integration into the global financial system (IMF 2015). It can therefore be stated that emerging markets are developing economies in the middle-income group that exhibit characteristics of both a developed economy as well as a developing economy. Emerging markets essentially fall into a broad grey area between the two main categories. Compared to developed economies, developing economies and emerging markets use monetary and fiscal policy less extensively. In particular, fiscal outlays associated with financial sector interventions - such as bank recapitalisation with public funds - are greater in emerging markets (Laeven & Valencia 2013:226).
As an emerging market, SA demonstrates a large degree of global financial integration, and therefore has a greater susceptibility to possible contagion. This contagion could include greater international risk sharing, as well as the risk of transferring negative financial shocks across country borders, and subsequently, increasing the overall level of systemic risk. This interconnectedness magnifies cross-border spillovers early on through channels such as liquidity pressures, global equity sell-offs and a depletion of bank capital (Claessens et al. 2010:8). Although the SA economy was not unaffected, it generally had a strong financial regulatory framework and macroeconomic fundamentals, both of which allowed the financial system to remain relatively stable during the sub-prime crisis (National Treasury 2011:4). The sub-prime crisis may therefore not be the most useful example for examining systemic risk in SA. However, a banking crisis that occurred in the SA financial sector during 2014 provides a more appropriate example.
The collapse of African Bank Limited (African Bank) in SA during 2014 was a significant event. The failure of African Bank was brought about by a combination of issuing many loans and credit cards (mostly at a high interest rate to low-income consumers) while accepting few deposits. Additionally, a large portion of the loans they granted were to consumers who were not creditworthy, leading to the subsequent failure by consumers to repay these loans. This translated into losses of approximately ZAR6.4 billion. In order to recoup these losses, African Bank attempted to raise ZAR8.5 billion through an unsuccessful second-rights offer, finally culminating in the need for a ZAR17 billion bailout by the South African Reserve Bank (SARB). These events may illustrate that the financial sector in SA is possibly not as well-regulated as previously believed. However, the swift action of the SARB was decisive in preventing contagion (IMF 2014:7). The fact that the SARB had to intervene to prevent contagion could legitimise the case for a re-examination of the financial sector, its various institutions, their activities and the actual level of systemic risk in the SA financial sector.
Such a re-examination of the financial sector should distinguish between the two dimensions of systemic risk, namely the cross-sectional dimension and the time dimension. The cross-sectional dimension refers to the structure of the financial system and how it influences, responds to and has the potential to amplify shocks (Caruana 2010:2). It follows then that cross-sectional systemic risk refers to the systemic risk at a particular point in time across all institutions (Borio & Drehmann 2009:3). The cross-sectional dimension of systemic risk therefore focuses on the common exposures and interconnections in the financial system and the potential of a specific shock to propagate throughout the system because of either interconnected balance sheets or direct common exposures.
In contrast, the time dimension of systemic risk refers to the build-up of risk that occurs over time with the macroeconomic cycle and the subsequent pro-cyclicality of the financial system (Caruana 2010:3). An expansionary economic period is typically characterised by periods of financial innovation where institutions and individuals may undertake more risk, make use of untested financial instruments, while credit may grow quickly and result in higher asset prices. The pro-cyclicality of systemic risk is therefore the underlying build-up of risk over time in areas that may be hidden or underpriced, the result being that during economic contractions, these risks appear and amplify the retrenchment that is already occurring. Viewing the build-up of systemic risks as an endogenous cycle illustrates that it occurs during both expansions and contractions and suggests that risk taking should be restrained during an expansionary phase (Borio & Drehmann 2009:3). This implies that a countercyclical prudential approach may be best for regulating systemic risk. The time dimension therefore focuses on the pro-cyclicality of the business and financial cycles and how they reinforce each other, creating a progressive build-up of risk and increasing financial instability - with the financial sector endogenously creating systemic risk (Caruana 2010:3).
A number of measures exist for systemic risk, addressing various aspects related to it - such as its macroeconomic measures, granular foundations and cross-sectional measures - and the possible channels through which it can cause financial distress. A more restrictive definition would allow for an accurate assessment of whether an institution's failure was because of systemic risk and would subsequently ensure that bailouts only occur for institutions whose failure are truly as a result of systemic risk (Taylor 2010:33). In general, measures of systemic risk are based on market data, but in order to capture the propagation of shocks through a financial network, the optimal measure should consider the losses a bank would experience, conditional on a market decline (Engle, Jondeau & Rockinger 2015:2). SRISK therefore provides a unique approach by including accounting data as an extension to the MES measure, in order to accurately quantify the exact amount of systemic risk an institution possesses.
Measuring systemic risk
The ambition of the Dodd-Frank Act and other measures undertaken in Europe, in response to the sub-prime crisis, led to a large number of research groups attempting to produce a measurement for systemic risk (Hansen 2012:3). In order to adequately regulate systemic risk, an accurate measurement is needed. The SRISK reflects the propensity of an institution to be undercapitalised when the entire financial sector is undercapitalised and is therefore currently the most appropriate measurement for systemic risk (V-LAB 2015). This chapter describes the research methodology we follow, namely the calculation of all the inputs required for SRISK and then the estimation of SRISK itself.
Two different equations can be used to calculate SRISK. The first is set out in Equation 1 (Brownlees & Engle 2015:7):
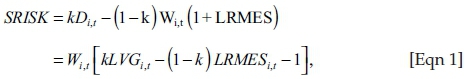
with LVGi,t representing the leverage ratio (Di,t+Wi,t)/Wi,t, k the prudential capital ratio and LRMES the long-run marginal expected shortfall. The LVG measure represents a combination of market and balance sheet data. (Di,t+Wi,t) is the quasi-market value of the bank's assets, defined as the sum of the book value of its debt (Di,t) and the market capitalisation of the bank (Wi,t). The LRMES measure is calculated using either an approximation equation or a simulation procedure. In addition to Equation 1, an alternative SRISK equation is also specified, which uses MES instead of LRMES as the input. This is presented in Equation 2:
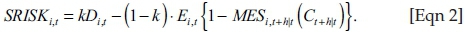
In Equation 2, SRISK is calculated by taking into account the prudential capital ratio (k), the bank's total liabilities (D), the market capitalisation of the bank (E) and the one-day MES at a certain threshold value (in this case −2%). The key differences between the two measures are therefore the choice of MES or LRMES.
The SRISKi,t index across all institutions is then used to construct a financial distress index that is system wide, with the total amount of systemic risk in the entire financial sector being measured as:

With (x)+ representing max (x,0). The total amount of capital that the government would need to provide in order to bailout the financial system, conditional on the occurrence of a systemic event is therefore represented by aggregate SRISKt. The contribution of negative capital shortfalls (capital surpluses) is ignored because surplus capital is unlikely to be mobilised easily during a crisis through mergers or loans - therefore providing no support to failing institutions.
The SRISK measure can also be illustrated in percentage form, indicating the systemic risk share an institution possesses, as follows:
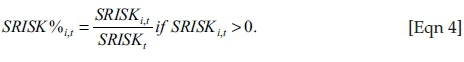
If SRISKKi,t ≤ 0, then the SRISK%i,t = 0. In order to calculate the SRISK for both the bank and the market, the dynamic time-varying volatilities will need to be calculated, followed by the dynamic conditional correlations (DCCs) and finally the tail expectations will also need to be captured. These three components will then be used to produce the MES for a threshold value of −2%,1 i.e., the daily equity return of the firm, given that the market as a whole has fallen below the −2% threshold level. The LRMES can then be obtained by using the following approximation equation (Acharya, Engle & Richardson 2012:60):
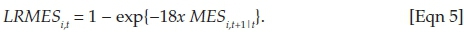
An alternative to Equation 5 is a dynamic simulation procedure, which takes into account the conditional volatilities and correlations of returns (Brownlees & Engle 2015:7). The first component of MES is the conditional volatility. This is calculated using a modified threshold-generalised autoregressive conditional heteroskedasticity (TGARCH) known as a Glosten-Jagannathan-Runkle (GJR) GARCH model (Glosten, Jagannathan & Runkle 1993:1787). The TGARCH model used by Rabemananjara and Zakoian (1993) is an extension of the standard TGARCH model but includes the lagged conditional standard deviations and variances as a regressor. The TGARCH model equations for the dynamics of volatility are as follows:
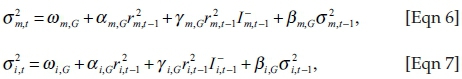
with

The volatility is therefore calculated by maximising the log likelihood function for both the bank and market's data series. The returns are then adjusted by dividing with these volatilities in order to produce standardised returns.
The second component of MES is the DCC. A mean-reverting correlation model allows the correlations to revert to the average long-run correlation ρij=E(Zi,tZj,t). In the equations that follow, the correlation dynamics are driven by the variable qij, which gets updated by the cross-product of the volatility-adjusted returns. By using correlation targeting and setting the initial unconditional correlation seed point 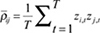 , a specification in the form of a GARCH (1,1) model can be illustrated as:
, a specification in the form of a GARCH (1,1) model can be illustrated as:
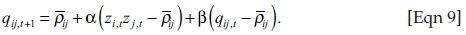
The conditional correlations for the two entities are then obtained by normalising qij,t+1 as:

Where:
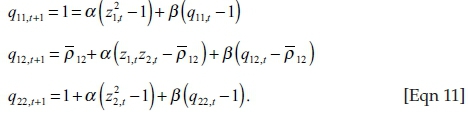
The same quasi-maximum likelihood method used for the volatilities is then used to find the persistence parameters α and β with the dynamics initialised by setting 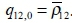 . The quasi-maximum likelihood method provides constant, inefficient estimates but remains the best choice in order to avoid numerical optimisation in high dimensions (Christoffersen 2011:164).
. The quasi-maximum likelihood method provides constant, inefficient estimates but remains the best choice in order to avoid numerical optimisation in high dimensions (Christoffersen 2011:164).
The log likelihood equation that will be maximised is illustrated using the bivariate normal distribution function for z1,t and z2,t as:
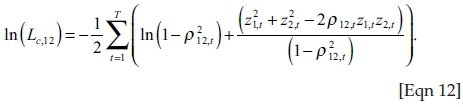
An important feature to note about this model is that the persistence parameters will be constant among the two entities. The implication of this is that the level of correlation will change over time, but the persistence will not. The persistence in correlation is also different to the persistence in volatility. The DCC model can be written in matrix notation as:
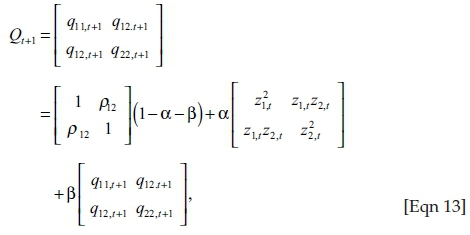
where Qt+1 is a positive semi-definite matrix because it is a weighted average of positive definite and positive semi-definite matrices, which will cause the correlation matrix and covariance matrix to also be semi-definite. In summary, the DCC model estimation occurs as follows. Firstly, the volatilities are calculated using the GJR-GARCH model, then the returns are adjusted using these volatilities, allowing the calculation of the unconditional correlation matrix. Finally, the correlation persistence parameters α and β are estimated in order to obtain the DCCs.
The final component involves the estimation of tail expectations. This study contributes a new parametric approach based on extreme value theory to model the tail expectations. Extreme value theory can be viewed as a way of smoothing and extrapolating the tails of an empirical distribution (Hull 2015:290). Extreme value theory therefore shifts the focus from modelling the entire distribution to modelling the tail behaviour alone and as a result requires fewer degrees of freedom (Skoglund & Chen 2015:104). Asset returns approach a normal distribution over a long time horizon; therefore extreme value theory is only useful over short time horizons, such as daily periods. However, this gives rise to a potential problem relating to the assumption that all returns are independent and identically distributed (i.i.d.). As a result of the time-varying variance patterns that take place over short time periods, the i.i.d. assumption does not hold, and the variance dynamics have to be removed before applying extreme value theory (Christoffersen 2011:18). Conveniently, the volatility-adjusted returns we constructed earlier can be defined as:

Because the assumption of i.i.d. can be made regarding the volatility-adjusted returns, extreme value theory can be applied to them. Extreme value theory in this situation is concerned with modelling the tail distribution of returns, with the tail defined by the user (Christoffersen 2011:138). In this case, the threshold value (u) is selected as −2% for the market. One of the key points in extreme value theory is that any observations (y) that go beyond the threshold value (u) will converge to the Generalised Pareto Distribution (GPD):
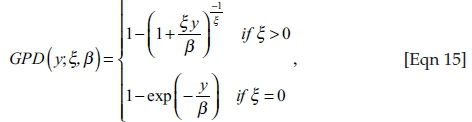
where β > 0 and y ≥ u. The tail-index parameter ξ is responsible for the shape of the distribution and the speed with which it approaches zero as y approaches infinity. We make the assumption that the tail-index parameter is positive, therefore allowing the use of the Hill estimator to approximate the GPD. Because this study is concerned with extreme losses as opposed to extreme gains, the methodology will only be applied to the negative of returns. Using the Hill estimator, the expected shortfall can then be calculated as:

where:
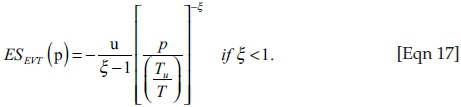
Equation 16 therefore calculates the daily expected shortfall, given that the returns are below the threshold value of −2% (Christoffersen 2011:143). This is known as the tail distribution of the market.
Considering that the volatilities, correlations, and tail expectations have been estimated, the final step is to now use the three calculated components to obtain the MES. Because we changed the technique for measuring the tail expectations for the bank and market, it follows that the original MES equation (see Brownlees & Engle 2012:10) will need adjustment. MES is adjusted to:
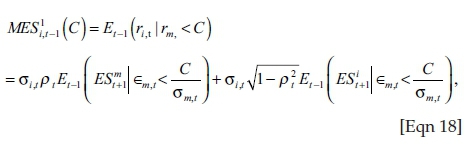
where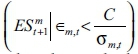 represents the expected shortfall of the market beyond the threshold value of −2%, while
represents the expected shortfall of the market beyond the threshold value of −2%, while  represents the expected shortfall of the bank on the number of occasions when the market breached its threshold value. In addition to the MES values, we also use a simulation procedure to construct hypothetical values of MES over a longer time period, which take into account the historical volatilities and correlations. The process we follow in this study is a new contribution that uses the Monte Carlo simulation procedure and Cholesky decomposition to simulate returns that preserve the volatilities and correlations of returns over a specific time period. Because we are simulating returns for a crisis period, the sub-prime crisis provides the appropriate sample period. The exact time period used will be 1 July 2007 to 31 December 2008. A crisis scenario where the market return falls below −40% is rare, with only three such falls ever to have taken place. These are the crash in 1929 (Black Tuesday), the Dotcom bubble in 2000 and the sub-prime crisis in 2008. In order to account for this scarcity, 50 000 draws will be made. The average of these draws, which return a result, will then be calculated, giving the final LRMES as:
represents the expected shortfall of the bank on the number of occasions when the market breached its threshold value. In addition to the MES values, we also use a simulation procedure to construct hypothetical values of MES over a longer time period, which take into account the historical volatilities and correlations. The process we follow in this study is a new contribution that uses the Monte Carlo simulation procedure and Cholesky decomposition to simulate returns that preserve the volatilities and correlations of returns over a specific time period. Because we are simulating returns for a crisis period, the sub-prime crisis provides the appropriate sample period. The exact time period used will be 1 July 2007 to 31 December 2008. A crisis scenario where the market return falls below −40% is rare, with only three such falls ever to have taken place. These are the crash in 1929 (Black Tuesday), the Dotcom bubble in 2000 and the sub-prime crisis in 2008. In order to account for this scarcity, 50 000 draws will be made. The average of these draws, which return a result, will then be calculated, giving the final LRMES as:
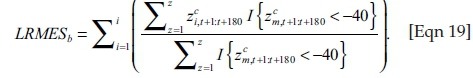
The final LRMES is then used as an input into the alternative SRISK equation. The LRMES may provide an advantage in that it provides a prediction over a longer, hypothetical crisis period. It is therefore more likely to represent more of a 'worst-case scenario' for banks. The LRMES value will also be constant for the entire period 2001 to 2013. The reason for keeping the LRMES constant is because this will allow the estimation of SRISK values using the balance sheet data for the current period while investigating the effect that sub-prime crisis volatilities and tail dependence would have had in that period.
Data and results
All balance sheet data were acquired from Fitch Ratings agency in the United Kingdom. The data cover the period 2001-2013. Fitch data are reported in USD; therefore in the case of SA banks, the values are converted using the exchange rate at the end of the reporting period of that particular year to arrive at the ZAR value. The equity returns and market capitalisation data for SA are acquired from the INET BFA data set. US equity returns and market capitalisation data are retrieved from the Bloomberg database. Daily stock market returns data are used for the period 2001-2013. Considering that the equity returns data are an integral part of the study, the entity selected for participation in the study will be conditional on its listing on a stock market. For the SA financial sector, the FTSE/JSE All-Share Index (ALSI) is used and five banks are studied. Although it may be argued that the other SA banks are relevant to this study, data availability was a limiting factor. Financial data are only available for the five largest banks, and nevertheless, these banks account for 90.5% of banking assets in SA. Considering that bank size is a significant input for the SRISK measure, it may be argued that even if data were available, the results for these banks would be insignificant by comparison because they are unlikely to contribute substantially to the undercapitalisation of the financial sector.
When a bank has more than the required amount of capital during a crisis scenario, the SRISK values would be negative, thereby indicating a capital surplus. In particular, SRISK measures the amount of capital that would be needed during a crisis to maintain a capital to asset ratio of 8%.2 The SRISK (%) contribution measures the bank's percentage of total financial sector capital shortfall. It follows then that banks with the highest percentage of SRISK are the most vulnerable during a crisis, but are also the most responsible for causing the crisis. Total SRISK in the entire SA financial sector is presented in Figure 1.
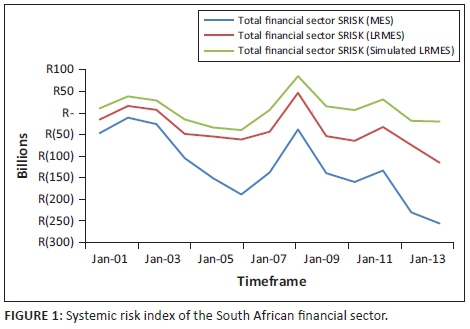
From Figure 1, it is clear that using the daily MES value resulted in the smallest SRISK value. The simulated LRMES measure takes into account the historic volatility and correlation of the sample period, which includes the sub-prime crisis period of 1 July 2007 to 31 December 2008 and therefore inflates the tail dependence of the banks. The reason for this is that the sub-prime crisis represented a period of larger than normal market volatility and therefore results in inflated LRMES, and subsequently SRISK values. Henceforth, to represent more moderate scenarios, only the SRISK measure using the approximated LRMES as in input measure will be reported. Figure 2 presents the amounts of SRISK each individual bank was responsible for producing.
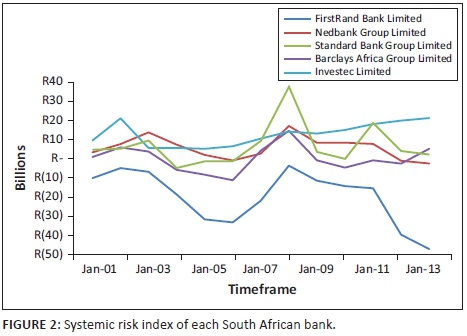
Figure 2 illustrates some interesting characteristics. FirstRand bank displayed large capital surpluses (negative SRISK values), which offset much of the SRISK that the rest of the financial sector was responsible for producing. All the banks showed increased SRISK measures over the period 2002 to 2003 when the stock market crash took place, as well as during the sub-prime crisis. Following that, the levels of SRISK have generally decreased with the exception of Investec, which displayed a steady upward trend. Standard Bank contributed a large amount of SRISK during the sub-prime crisis period but was only responsible for small contributions during the rest of the period. In general, SA banks seem to have increased SRISK levels during and following crisis scenarios. Considering the manifestation of systemic risk in emerging markets and the role that volatile capital inflows play, this event may be evidence of a link between the two factors. A spike of this nature may raise questions about the role of capital flows in contributing to systemic risk in SA and emerging markets in general. That is, a build-up of foreign capital may have taken place, then once a crisis occurred, the capital was withdrawn and left the bank undercapitalised.
Another conclusion that can be made is that the SA financial sector as a whole generally displays low levels of systemic risk, with many banks in fact displaying large capital surpluses. The only years in which the sector as a whole had a positive amount of SRISK were 2002 to 2003 and 2008. However, during a crisis scenario, capital surpluses may be misleading. Brownlees and Engle (2015:8) argued that surplus capital held by other banks during a financial crisis is unlikely to be easily mobilised and used to bail out partnering banks. Therefore, assuming low market liquidity, SRISK is reported as:

The percentage contribution of each bank to the total SRISK of the SA financial sector is presented in Table 1 and Figure 3.
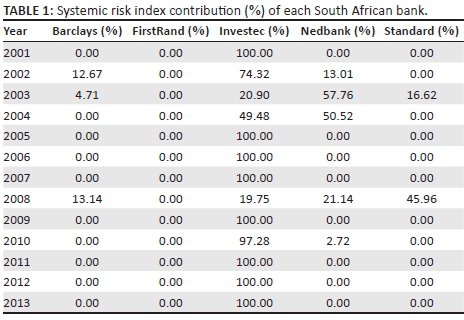
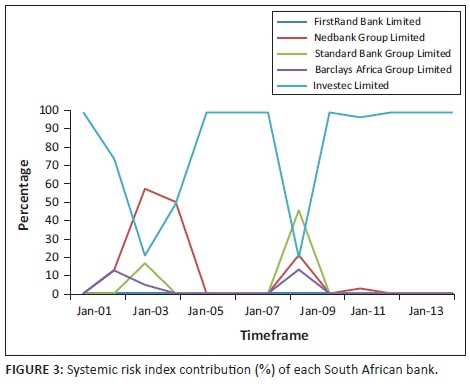
In Figure 3, the effect of crisis periods on SA banks can be seen. Practically, a 0% contribution indicates that those specific banks contributed no systemic risk. During both crisis periods, the SRISK contribution of Investec dropped rapidly as other banks increased their contribution. During 2002, Nedbank took over as the leading contributor while during the sub-prime crisis, Standard Bank contributed the most. This may be indicative that systemic risk in the SA financial sector is not an inherent characteristic but largely determined by external factors. FirstRand was clearly the least systemically risky, with no contributions ever above zero. Investec could be classified as the most systemically risky because it was responsible for 100% of the systemic risk at most points during the sample period. The spikes displayed by other banks as soon as a crisis takes place in another economy may make a ranking based on SRISK contentious.
Investec was the smallest of the big five banks, yet it contributed the most systemic risk. However, when financial crises or turmoil occurred in foreign countries, the systemic risk levels of the sector increased. This may lead to an argument regarding the success of regulatory measures in mitigating systemic risk. Based on the results, SA's regulatory approach was successfully mitigating systemic risk, but came under more pressure when crises occurred in foreign countries. It is therefore likely that a future financial crisis in areas such as China or Europe could have a similar or even larger effect. It is also worrisome that no prediction could be made as to which bank would be the most affected prior to a crash or crisis. Interestingly, Standard Bank was the most risky during the sub-prime crisis, and Nedbank was the most risky following the stock market crash. Given the absence of crises, however, Investec was clearly the most systemically risky bank in SA over the rest of the sample period. The reasons for Investec's large contribution of systemic risk can be explained by looking at some of the components used in the SRISK equation, namely the leverage ratio (Table 2) and LRMES (Table 3):
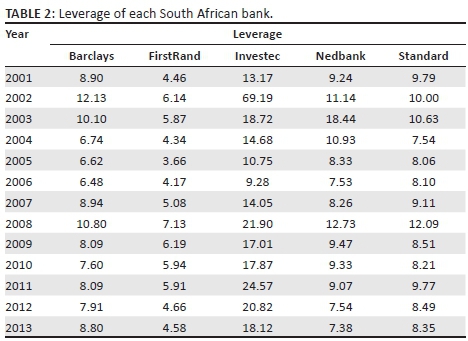
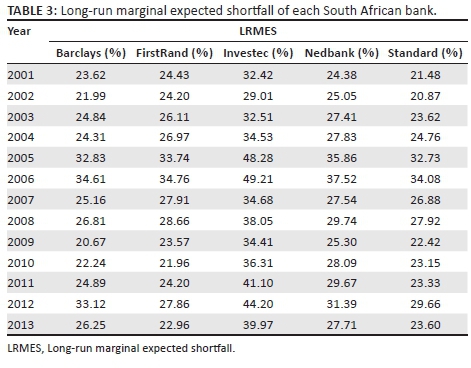
Based on the components, it is clear that Investec has significantly higher leverage ratios and in many cases more than double that of the other banks. Additionally, the LRMES is also higher, indicating it has a higher tail dependence. The implication of this is that when the ALSI declines, Investec shares are more affected by this than the other banks. FirstRand bank by comparison has the lowest levels of SRISK in the SA financial sector. An investigation of the components shows that it has low leverage ratios and LRMES values, indicating that even though it has the highest market capitalisation of all the banks, its lower amounts of liabilities offset the potential effects of this. Its LRMES values also show that FirstRand had less tail dependence and was therefore not as significantly affected by an ALSI decline.
Although Investec contributes the most systemic risk, the actual amount of systemic risk in the sector is not uncontrollably high because most other banks display capital surpluses. However, in a crisis scenario when liquidity dries up, there may be systemic implications, and this is before taking into account factors related to interconnectedness. Additionally, the change in SRISK contributions during the period following the stock market crash and sub-prime crisis period may be indicative of vulnerabilities in the economies following upswing periods (Claessens, Ghosh & Mihet 2013:157). This further strengthens the argument of a different manifestation of systemic risk in SA, whereby the systemic risk lies in the amount of capital inflows in the economy and potentially the regional source of these capital flows.
The argument may be made that the total financial sector SRISK will always increase as the size of the financial sector increases. That is, as banks undertake more liabilities, it will follow that the amount of SRISK increases. Increases in market capitalisation will, however, not offset these increases because the market may malfunction during a crisis. External factors such as the stability of financial sectors in foreign countries will then also need to be taken into account. A final conclusion is that all financial sectors are not the same when it comes to systemic risk and the determinants may differ for various countries. Similarly, individual banks may also produce SRISK as a result of different activities. The causes of SRISK for the United States are largely inherent (see Laeven, Ratnovski & Tong 2014:15), i.e., they are within the US financial sector. In contrast, the SA sector may be affected by factors outside of its own financial sector and the economic fundamentals of the country may be largely irrelevant.
Summary and conclusions
The sub-prime crisis sparked a renewed interest in systemic risk. This is arguably one of the most important, yet least understood risks. It may therefore be perplexing that a single definition for systemic risk cannot be agreed upon yet. At present, a broad definition refers to the risk of a financial system collapse. However, part of the problem with identifying systemic risk may relate to its manifestation within different economies and countries, something which a broad definition does not capture. The sub-prime crisis showed that systemic risk in developed economies such as the United States occurred as a result of large, highly leveraged banks undertaking complex activities that left them undercapitalised. Emerging markets by comparison were affected both differently and belatedly through third-party effects. Interestingly, none of the economic fundamentals of emerging markets such as SA changed, yet they were still affected by the crisis emanating from the United States. This illustrates the global impact that a large enough level of systemic risk could have.
This article measured the level of systemic risk in SA, and subsequently identified which banks were the largest contributors to this level of systemic risk. In doing so, we also contributed a new technique for measuring systemic risk. The level of systemic risk for SA provides an interesting analysis. The largest contributor to systemic risk throughout most of the sample period was the smallest bank in the sample. However, when the stock market crash took place in 2002, systemic risk contributions from the other banks increased. A similar, more dramatic situation occurred during the sub-prime crisis. During both these periods, the total financial sector systemic risk also increased markedly. The implication is that systemic risk levels within SA seem to be largely dependent on external factors, regardless of the economic fundamentals of the country itself. Whether regulatory measures adequately consider these factors for financial stability is arguable.
The implications of these findings are that in addition to complying with individual banking regulations such as those laid out by Basel, banks should ensure that they always have sufficient capital reserves in order to mitigate the effects of a period of financial turmoil in a foreign country. These levels of capital can be determined through worst-case scenario analyses - such as those performed here - to ensure that banks are sufficiently capitalised during a financial crisis and therefore protected from systemic risk.
Considering the increased levels of systemic risk in SA following crisis periods in foreign countries, and the different way in which systemic risk manifests in emerging markets, it may be worth investigating which particular events have the largest impact on systemic risk in SA. Further studies could also take a more granular approach, with the objective of determining which bank-specific characteristics result in that particular bank having a larger amount of systemic risk. If banks and regulators are more informed of the sources of systemic risk, they may be able to pre-empt the risk and ensure that sufficient capital is available.
Acknowledgements
We gratefully acknowledge the support of the North-West University School of Economics and the reviewers for their valuable feedback.
Competing interests
The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.
Authors' contributions
All authors made significant contributions to the study.
References
Acharya, V.V., Engle, R. & Richardson, M.P., 2012, 'Capital shortfall: A new approach to ranking and regulating systemic risks', The American Economic Review 102(3), 59-64. https://doi.org/10.1257/aer.102.3.59 [ Links ]
Allen, F., Babus, A. & Carletti, E., 2010, Financial connections and systemic risk, Working Paper no. 16177, National Bureau of Economic Research, Cambridge, MA. [ Links ]
Bank for International Settlements (BIS), 2009, 79th Annual Report, viewed 20 March 2016, from http://www.bis.org/publ/arpdf/ar2009e.pdf [ Links ]
Bartram, S.M., Brown, G.W. & Hund, J.E., 2007, 'Estimating systemic risk in the international financial system', Journal of Financial Economics 86(3), 835-869. https://doi.org/10.1016/j.jfineco.2006.10.001 [ Links ]
Bernanke, B.S., 2009, Financial reform to address systemic risk, Technical report, Speech at the Council on Foreign Relations, Washington, DC. [ Links ]
Borio, C. & Drehmann, M., 2009, Towards an operational framework for financial stability: "fuzzy" measurement and its consequences, BIS Working Papers no. 284, viewed 20 March 2016, from http://www.bis.org/publ/work284.pdf [ Links ]
Brownlees, C.T. & Engle, R.F., 2012, Volatility, correlation and tails for systemic risk measurement, viewed 20 March 2016, from https://ssrn.com/abstract=1611229 [ Links ]
Brownlees, T., & Engle, R., 2015, SRISK: A conditional capital shortfall index for systemic risk measurement, Department of Finance, New York University, New York, NY. [ Links ]
Caruana, J., 2010, Systemic risk: How to deal with it, Bank for International Settlements (BIS), viewed 20 March 2016, from http://www.bis.org/publ/othp08.htm [ Links ]
Christoffersen, P.F., 2011, Elements of financial risk management, Academic Press, San Diego, CA. [ Links ]
Claessens, S. & Ghosh, S.R., 2013, 'Capital flow volatility and systemic risk in emerging markets: The policy toolkit', in O. Canuto & S.R. Ghosh (eds.), Dealing with the challenges of macro financial linkages in emerging markets, pp. 91-118, World Bank, Washington, DC. [ Links ]
Claessens, S., Ghosh, S.R. & Mihet, R., 2013, 'Macro prudential policies to mitigate financial vulnerabilities in emerging markets', in O. Canuto & S.R. Ghosh (eds.), Dealing with the challenges of macro financial linkages in emerging markets, pp. 155-178, World Bank, Washington, DC. [ Links ]
Claessens, S., Laeven, M.L., Igan, D. & Dell'ariccia, M.G., 2010, Lessons and policy implications from the global financial crisis, Working Paper no. 10/44, International Monetary Fund, Washington, DC. [ Links ]
De Bandt, O., Hartmann, P. & Peydró, J., 2009, 'Systemic risk in banking: An update', in A.N. Berger, P. Molyneux & J.O.S. Wilson (eds.), The Oxford handbook of banking, pp. 633-672, Oxford University Press, Oxford. [ Links ]
De Nicoló, M.G., Favara, G. & Ratnovski, L., 2012, Externalities and macro-prudential policy, International Monetary Fund, Washington, DC. [ Links ]
Engle, R., Jondeau, E. & Rockinger, M., 2015, 'Systemic risk in Europe', Review of Finance 19(1), 145-190. https://doi.org/10.1093/rof/rfu012 [ Links ]
Georg, C.P., 2011, Basel III and systemic risk regulation: What way forward? Working Papers on Global Financial Markets no. 17, University of Jena, Jena. [ Links ]
Glosten, L.R., Jagannathan, R. & Runkle, D.E., 1993, 'On the relation between the expected value and the volatility of the nominal excess return on stocks', The Journal of Finance 48(5), 1779-1801. https://doi.org/10.1111/j.1540-6261.1993.tb05128.x [ Links ]
Hansen, L.P., 2012, Challenges in identifying and measuring systemic risk, Working Paper no. 18505, National Bureau of Economic Research, Cambridge, MA. [ Links ]
Hull, J., 2015, Risk management and financial institutions, Wiley, Hoboken, NJ. [ Links ]
International Monetary Fund (IMF), 2014, South Africa: Financial system stability assessment, Country Report No. 14/340, viewed 20 March 2016, from https://www.imf.org/external/pubs/ft/scr/2014/cr14340.pdf [ Links ]
International Monetary Fund (IMF), 2015, World Economic Outlook database, viewed 20 March 2016, from http://www.imf.org/external/pubs/ft/weo/2014/02/weodata/index.aspx [ Links ]
International Monetary Fund (IMF), Bank for International Settlements (BIS), & Financial Stability Board (FSTB), 2009, Guidance to assess the systemic importance of financial institutions, markets, and instruments: Initial consideration, Report to the G-20, viewed from 20 March 2016, from https://www.imf.org/external/np/g20/pdf/100109a.pdf [ Links ]
Kim, J.S., & Ryu, D., 2015, 'Effect of the subprime mortgage crisis on a leading emerging market', Investment Analysts Journal 44(1), 20-42. [ Links ]
Laeven, L. & Valencia, F., 2013, 'Systemic banking crises database', IMF Economic Review 61(2), 225-270. https://doi.org/10.1057/imfer.2013.12 [ Links ]
Laeven, M.L., Ratnovski, L. & Tong, H., 2014, Bank size and systemic risk, International Monetary Fund, Washington, DC. [ Links ]
López-Espinosa, G., Moreno, A., Rubia, A. & Valderrama, L., 2012, 'Short-term wholesale funding and systemic risk: A global CoVaR approach', Journal of Banking & Finance 36(12), 3150-3162. https://doi.org/10.1016/j.jbankfin.2012.04.020 [ Links ]
Rabemananjara, R. & Zakoian, J.M., 1993, 'Threshold ARCH models and asymmetries in volatility', Journal of Applied Econometrics 8(1), 31-49. https://doi.org/10.1002/jae.3950080104 [ Links ]
Skoglund, J. & Chen, W., 2015, Financial risk management: Applications in market, credit, asset and liability management and firmwide risk, Wiley, Hoboken. [ Links ]
South Africa. National Treasury, 2011, A safer financial sector to serve South Africa better, National Treasury policy document, Pretoria. [ Links ]
Taylor, J.B., 2010a, 'Defining systemic risk operationally', in G. Shultz, K. Scott, J. Taylor (eds.), Ending government bailouts as we know them, pp. 33-58, Hoover Institution Press, Stanford, CA. [ Links ]
World Bank, 2015, World development indicators, viewed 20 March 2016, from http://data.worldbank.org/data-catalog/world-development-indicators [ Links ]
 Correspondence:
Correspondence:
Gregory Foggitt
gregmf90@gmail.com
Received: 08 June 2016
Accepted: 18 May 2017
Published: 24 Oct. 2017
1. We follow the work of Brownlees and Engle (2012:10) and specify a market drop as a decline of −2% in the market index.
2. Eight per cent is the minimum fraction of capital (as a ratio of total assets) that the Basel committee requires each bank to hold.














