Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Economic and Management Sciences
On-line version ISSN 2222-3436
Print version ISSN 1015-8812
S. Afr. j. econ. manag. sci. vol.20 n.1 Pretoria 2017
http://dx.doi.org/10.4102/sajems.v20i1.1490
ORIGINAL RESEARCH
A proposed best practice model validation framework for banks
Pieter J. (Riaan) de JonghI; Janette LarneyI; Eben MareII; Gary W. van VuurenI; Tanja VersterI
ICentre for Business Mathematics and Informatics, North-West University, South Africa
IIDepartment of Mathematics and Applied Mathematics, University of Pretoria, South Africa
ABSTRACT
BACKGROUND: With the increasing use of complex quantitative models in applications throughout the financial world, model risk has become a major concern. The credit crisis of 2008-2009 provoked added concern about the use of models in finance. Measuring and managing model risk has subsequently come under scrutiny from regulators, supervisors, banks and other financial institutions. Regulatory guidance indicates that meticulous monitoring of all phases of model development and implementation is required to mitigate this risk. Considerable resources must be mobilised for this purpose. The exercise must embrace model development, assembly, implementation, validation and effective governance.
SETTING: Model validation practices are generally patchy, disparate and sometimes contradictory, and although the Basel Accord and some regulatory authorities have attempted to establish guiding principles, no definite set of global standards exists.
AIM: Assessing the available literature for the best validation practices.
METHODS: This comprehensive literature study provided a background to the complexities of effective model management and focussed on model validation as a component of model risk management
RESULTS: We propose a coherent 'best practice' framework for model validation. Scorecard tools are also presented to evaluate if the proposed best practice model validation framework has been adequately assembled and implemented.
CONCLUSION: The proposed best practice model validation framework is designed to assist firms in the construction of an effective, robust and fully compliant model validation programme and comprises three principal elements: model validation governance, policy and process.
Introduction
Model validation is concerned with mitigating model risk and, as such, is a component of model risk management. Since the objective of this article is to provide a framework for model validation, it is important to distinguish between model risk management and model validation. Below, we define and discuss both these concepts.
Model risk management comprises robust, sensible model development, sound implementation, appropriate use, consistent model validation at an appropriate level of detail and dedicated governance. Each of these broad components is accompanied and characterised by unique risks which, if carefully managed, can significantly reduce model risk. Model risk management is also the process of mitigating the risks of inadequate design, insufficient controls and incorrect model usage. According to McGuire (2007), model risk is 'defined from a SOX (USA's Sarbanes-Oxley Act) Section 404 perspective as the exposure arising from management and the board of directors reporting incorrect information derived from inaccurate model outputs'. The South African Reserve Bank (SARB 2015b) uses the definition of model risk as envisaged in paragraph 718(cix) of the revisions to the Basel II market risk framework:
two forms of model risk: the model risk associated with using a possibly incorrect valuation methodology; and the risk associated with using unobservable (and possibly incorrect) calibration parameters in the valuation model. (n.p.)
In its Solvency Assessment and Management (SAM) Glossary, the Financial Services Board (FSB) defines model risk as 'The risk that a model is not giving correct output due to a misspecification or a misuse of the model' (FSB 2010). In a broader business and regulatory context, model risk includes the exposure from making poor decisions based on inaccurate model analyses or forecasts and, in either context, can arise from any financial model in active use (McGuire 2007). North American Chief Risk Officers (NACRO) Council (2012) identified model risk as 'the risk that a model is not providing accurate output, being used inappropriately or that the implementation of an appropriate model is flawed' and proposed eight key validation principles. The relevance of model risk in South Africa is highlighted by the Bank Supervision Department of the SARB in its 2015 Annual Report, where it is specifically noted that some local banks need to improve model risk management practices (SARB 2015a). Model validation is a component of model risk management and requires confirmation from independent experts of the conceptual design of the model, as well as the resultant system, input data and associated business process validation. These involve a judgement of the proper design and integration of the underlying technology supporting the model, an appraisal of the accuracy and completeness of the data used by the model and verification that all components of the model produce relevant output (e.g. Maré 2005). Model validation is the set of processes and activities intended to verify that models are performing as expected, in line with their design objectives and business uses (OCC 2011b). The Basel Committee for Banking Supervision's (BCBS) minimum requirements (BCBS 2006) for the internal ratings-based approach require that institutions have a regular cycle of model validation 'that includes monitoring of model performance and stability; review of model relationships; and testing of model outputs against outcomes'.
In this article, we assess the available literature for validation practices and propose a coherent 'best practice' procedure for model validation. Validation should not be thought of as a purely mathematical exercise performed by quantitative specialists. It encompasses any activity that assesses how effectively a model is operating. Validation procedures focus not only on confirming the appropriateness of model theory and accuracy of program code, but also test the integrity of model inputs, outputs and reporting (FDIC 2005).
The remainder of this article is structured as follows: The next section provides a brief literature overview of model risk from a validation perspective. 'Overview of the proposed model validation framework' section establishes an overview of the proposed framework for model validation and, in 'model validation framework discussion' section; this framework is discussed in more detail. Guidelines for the development of scorecard tools for incorporation in the proposed best practice model validation framework are presented in 'model validation scorecards' section. Some concluding remarks are made in 'conclusions and recommendations' section. Examples illustrating the importance of proper model validation are given in Appendix 1 and scorecards for the evaluation of the main components of the validation framework are provided in Appendix 2.
Brief overview of model risk from a validation perspective
Banks and financial institutions place significant reliance on quantitative analysis and mathematical models to assist with financial decision-making (OCC 2011a). Quantitative models are employed for a variety of purposes including exposure calculations, instrument and position valuation, risk measurement and management, determining regulatory capital adequacy, the installation of compliance measures, the application of stress and scenario testing, credit management (calculating probability and severity of credit default events) and macroeconomic forecasting (Panko & Ordway 2005).
Markets in which banks operate have altered and expanded in recent years through copious innovation, financial product proliferation and a rapidly changing1 regulatory environment (Deloitte 2010). In turn, banks and other financial institutions have adapted by producing data-driven, quantitative decision-making models to risk-manage complex products with increasing ambitious scope, such as enterprise-wide risk measurement (OCC 2011b).
Bank models are similar to engineering or physics models in the sense that they are quantitative approaches which apply statistical and mathematical techniques and assumptions to convert input information - which frequently contains distributional information - into outputs. By design, models are simplified representations of the actual associations between observed characteristics. This intentional simplification is necessary because the real world is complex, but it also helps focus attention on specific, significant relational aspects to be interrogated by the model (Elices 2012). The precision, accuracy, discriminatory power and repeatability of the model's output determine the quality of the model, although different metrics of quality may be relevant under different circumstances. Forecasting future values requires precision and accuracy, for example, rank ordering of risk may require greater discriminatory power (Morini 2011). Understanding the capabilities and limitations of models is of considerable importance and is often directly related to the simplifications and assumptions used in the model's design (RMA 2009).
Input data may be economic, financial or statistical depending on the problem to be solved and the nature of the model employed. Inputs may also be partially or entirely qualitative or based on expert judgement [e.g. the model by Black and Litterman (1992) and scenario assessment in operational risk by de Jongh et al. (2015)], but in all cases, model output is quantitative and subject to interpretation (OCC 2011b). Decisions based upon incorrect or misleading model outputs may result in potentially adverse consequences through financial losses, inferior business decisions and ultimately reputation damage: These developments stem from model risk, which arises because of two principal reasons (both of which may generate invalid outputs):
-
fundamental modelling errors (such as incorrect or inaccurate underlying input assumptions and/or flawed model assembly and construction) and
-
inappropriate model application (even sound models which generate accurate outputs may exhibit high model risk if they are misapplied, e.g. if they are used outside the environment for which they were designed).
Model risk managers, therefore, need to take account of the model paradigm as well as the correctness of the implementation of any algorithms and methodologies to solve the problem as well as the inputs used and results generated. NACRO Council (2012) asserted that model governance should be appropriate and the model's design and build should be consistent with the model's proposed purpose. The model validation process should have an 'owner', that is, someone uniquely responsible, and should operate autonomously (i.e. avoid conflicts of interest). The validation effort should also be commensurate with the model's complexity and materiality. Input, calculation and output model components should be validated and limitations of each should be addressed and the findings comprehensively documented (Rajalingham 2005). As far as the model paradigm is concerned, the model needs to be evaluated in terms of its applicability to the problem being solved, and the associated set of assumptions of the model needs to be verified in terms of its validity in the particular context. Example 1 in Appendix 1 gives an illustration of the inappropriateness of the assumptions of the well-known Black-Scholes option pricing model in a South African context. Clearly, all listed assumptions may be questioned, which will shed doubt on the blind application of the model in a pricing context. Some models have been implemented using spreadsheets (Whitelaw-Jones 2015). Spreadsheet use in institutions range from simple summation and discounting to complex pricing models and stochastic simulations. Madahar, Cleary and Ball (2008) questioned whether every spreadsheet should be treated as a model, requiring the same rigorous testing and validating. Spreadsheet macros require coding and may be used to perform highly complex calculations, but they may also be used to simply copy outputs from one location to another (Galletta et al. 1993; PWC 2004). Requiring that all macro-embedded spreadsheets be subject to the same validation standards can be onerous (Pace 2008). Example 2 in Appendix 1 highlights some examples of formulas in Excel that provide incorrect answers. In addition, the European Spreadsheet Interest Group (EUSIG) maintains a database of such errors. EUSIG (2016) and Gandel (2013) provide examples of high impact Excel errors that occurred as a result of inadequate model validation. Therefore, the validation of the code is of extreme importance, and should be validated using not only ordinary but also stressed inputs.
Model risk increases with model complexity, input assumption uncertainties, the breadth and depth of the model's implementation and use. The higher the model risk, the higher the potential impact of malfunction. Pace (2008) identified challenges associated with effective model risk management programmes. Assigning the correct model definition to models is important, but challenging, because model types (e.g. stochastic, statistical, simulation and analytical) and model deployment methods (ranging from simple spreadsheets to complex, software-interlinked programmes) can sometimes straddle boundaries and defy easy categorisation (PWC 2004). Several authors (e.g. Burns 2006; Epperson, Kalra & Behm 2012; Haugh 2010; Pace 2008) argue that model classification is an important component of model risk management. The model validation process is also considerably simplified if models are classified appropriately and correctly according to their underlying complexity, relevance and impact on businesses.
Haugh (2010) presents practical applications of model risk and emphasises the importance of understanding a models' physical dynamics and properties. Example 3 in Appendix 1 illustrates a strong correlation between two variables that clearly does not share any causal relationship. Incorrect inclusion of such variables in models can lead to nonsensical conclusions and recommendations. The dangers of calibrating pricing models with one type of security and then pricing other types of securities using the same model can be disastrous. Model transparency is important and substantial risks were found to be associated with models used to determine hedge ratios. These conclusions, although specifically focussed on structured products (collateralised debt obligations) and on equity and credit derivative pricing models, could be equally applied to all models (Haugh 2010; PWC 2004). Example 4 in Appendix 1 gives some risk-related loss examples. These examples clearly illustrate that even simple calculation errors and incorrect models and assumptions can result in devastating losses. Actively managing model risk is important, but also costly, because not only does the validation of models requires expensive and scarce resources, but also the true cost of model risk management is much broader than this. The cost of robust model risk management processes includes having to maintain skilled and experienced model developers, model validators, model auditors and operational risk managers, as well as senior management time at governance meetings, opportunity costs (because of delays in time-to-market because of first having to complete the model risk management process before a new model supporting a new product can be deployed) and IT development cost of the model deployment.
Although model risk cannot be entirely eliminated, proficient modelling by competent practitioners together with rigorous validation can reduce model risk considerably. Careful monitoring of model performance under various conditions and limiting model use can further reduce risk, but frequent revision of assumptions and recalibration of input parameters using information from supplementary sources are also important activities (RMA 2009). Deloitte (2010) addressed internal model approval under Solvency II. Model validation was identified as a key activity in model management to ensure models remain 'relevant', that is, they function as originally intended both at implementation and over time. Ongoing monitoring to determine models' sensitivity to parameter changes and assumption revisions helps to reduce model risk. Deloitte's (2010) proposed validation policy includes a review of models' purpose and scope (including data, methodology, assumptions employed, expert judgement used, documentation and the use test), an examination of all tools used (including any mathematical techniques) and an assessment of the frequency of the validation process. Independent governance of the validation results, robust documentation and a model change policy (in which all changes to the model are carefully documented and details of changes are communicated to all affected staff) all contribute to effective model management (PWC 2004; Rajalingham 2005).
Overview of the proposed model validation framework
Despite the broad market requirement for a coherent model risk management strategy and associated model validation guidelines, the literature is not replete with examples. The Basel Accord and some regulatory authorities have attempted to establish this but, according to our knowledge, no definite set of global standards exists. However, although the literature places varying emphasis on different aspects of model governance, there are encouraging signs of cohesion and broad, common themes emerging. One of these common themes is the role of the three-lines of defence governance model, as developed by the Institute of Internal Auditors in 2013 (IIA 2013). In the context of model risk management, the first line of defence would be model development, the second line would be model validation and third line would be internal audit. A fourth line of defence is also suggested by the Financial Stability Institute (FSI) as external audit and supervisors (FSI 2015). In addition, operational risk management has a second line duty in respect of model development and model validation.
Model validation embraces two generic views of the modelling landscape that should be considered to cover all possible validation elements (refer to Figure 1), namely:
-
the modelling life cycle, comprising three stages (development, implementation and operation) as well as the elements that form part of each stage and
-
the modelling process elements namely input, output and process (Rajalingham 2005).
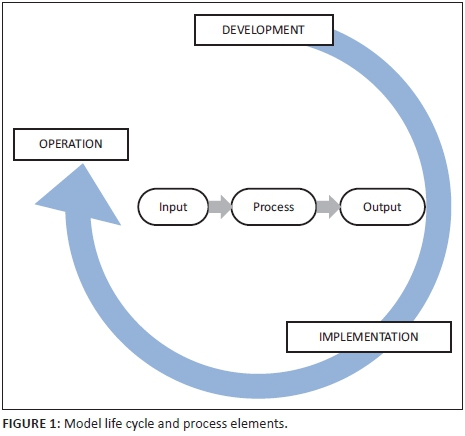
As illustrated in Figure 1, the model life cycle starts with the model development phase. This phase commences with the formulation of the problem and model, followed by the specification of the user requirements. This phase is usually followed by a prototyping phase, in which especially the more risky or uncertain modelling aspects are researched and tested. Based on the results of this phase, the formulation phase may be re-assessed and various iterations may be possible before alignment with user requirements is achieved. Once the modelling concept is clear, the development of the model can commence. In this phase, amongst others, the model outputs are defined and the inputs required clearly specified. The testing phase involves testing of functional components of the model. As soon as the model is completely assembled integration testing can start on the completed model. This could involve out of sample and backtesting in order to ensure that the model performs well for the purpose it was designed for. As soon as testing is completed, the model is reviewed internally and externally by independent experts and then accepted if it adequately meets all validation criteria (see 'model validation framework discussion' section for more details on the validation framework proposed as well as the validation criteria). After the model has been accepted, it should be implemented. Depending on the complexity of the model and speed requirements it might entail the recoding of a model in computationally efficient programming language and using appropriate database query languages. This could entail a complete redesign and specification of the model in IT terms, recoding, User Acceptance Testing (UAT), review and acceptance. Once the model is implemented and running the model is put into operation. In this phase, the model should be validated in terms of its performance against the original design specifications and tested on a regular basis. Ownership of the model should be identified through the validation process, as should the appropriateness of the model governance. Efforts to validate models should be proportional to model output materiality and complexity, and should involve validation of model components and relevant documentation as well as third-party validation where possible (Elices 2012).
A graphical representation of a proposed framework is presented in Figure 2 below, by providing an alternative view of the model life cycle.
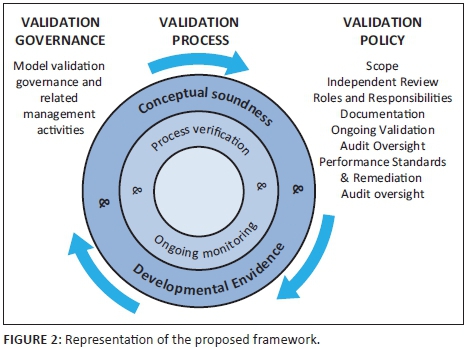
The framework presented in Figure 2 consists of the following components.
Model governance
This includes model governance (on the left of Figure 2) and related management activities and will be discussed in more detail in the 'model validation governance' section and will be extended into a scorecard in the 'model validation governance scorecard' section.
Model validation policy
Note that seven main elements are covered in this (on the right of Figure 2) namely, the scope, an independent review, the roles and responsibilities, relevant model documentation, proof of ongoing validation, details of performance standards and remediation plans and audit oversight. This will be discussed in more detail in the 'model validation policy' section and will be extended into a scorecard in 'model validation policy scorecard' section.
The 'validation process'
This consists of three distinct elements (in the middle of Figure 2) namely:
-
conceptual soundness and developmental evidence
-
process verification and ongoing monitoring and
-
outcomes analysis.
This 'validation process', with its three elements, will be discussed in more detail in the 'model validation process' section and will be extended into a scorecard in 'model validation process scorecard' section.
In 'model validation framework' section, each of the above-mentioned components are discussed in more detail.
Model validation framework discussion
As stated at the end of the previous section, the model validation framework is discussed in more detail in the following subsections:
-
model validation governance
-
model validation policy
-
model validation process.
This subsection contains a discussion of conceptual soundness and developmental evidence, process verification and ongoing monitoring, and outcomes analysis.
Model validation governance
As mentioned in 'overview of the proposed model validation framework' section, the FSI outlines that regulated financial institutions require a four lines of defence model (FSI 2015) to effectively manage the risk it is exposed to. Model validation is seen as the second line of defence in the context of model risk management. Under model validation governance, the adequacy of the governance structure should be evaluated. In the model validation policy, clear roles and responsibility should be assigned to role players and committees (OCC 2011b). This includes identifying who amongst the stakeholders in the model risk management process should perform, for example, benchmarking, independent review and monitoring.
Model governance (which should involve the board of directors, senior management and line-of-business managers) requires that the organisation's governance policies, procedures and processes support its controls and provide the requisite oversight to manage the model (Glowacki 2012). In addition, there should be adequate oversight and participation by internal audit (OCC 2011b; Pace 2008). Governance must be structured such that the validation unit functions independently in terms of remuneration (oversight) and reporting (controls) lines (OCC 2011b). The validation governance structure should define the assignment of authority for approval and there should be adequate board and senior management involvement (CEBS 2008). Effective model governance can help reduce model risk by obtaining realistic assurance that the model produces results commensurate with its original design mandate. In addition, overseeing ongoing model improvement and recalibration and instigating a user-wide understanding of model limitations and potentially damaging assumptions - both functions of model governance - can help diminish model risk (Burns 2006).
Scope, transparency, and completeness of model documentation are important and should be controlled by line-of-business management. Documentation should be validated in terms of the ability of the independent reviewer to recreate the model as well as the results (FDIC 2005; OeNB/FMA 2004). Model documentation should provide a detailed description of models' design and purpose, mathematical logic incorporated into models, descriptions of data requirements, operating procedure flow diagrams, change control and other security procedures as well as comprehensive validation documentation (Burns 2006). Ongoing monitoring should confirm that the model is appropriately implemented and is being used and is performed as intended. Each model extension (beyond original scope) should be validated and placed under configuration control (OCC 2011b; RMA 2009).
Model validation policy
Seven main aspects are covered in the model validation policy namely, the scope, independent review, roles and responsibilities, relevant model documentation, proof of continuing validation, details of performance standards and remediation plans and audit oversight (Rajalingham 2005).
Scope
Institutions should have a written, enterprise-wide policy for validating model risk (RMA 2009). The rigor and sophistication of validation should be commensurate with the institution's overall model use, the complexity and materiality of its models, and the size and complexity of the organisation's operations (OCC 2011b).
Independent review
The validation process should be subject to independent review (OCC 2011b; RMA 2009) and should be organisationally separate from the activities it is assigned to monitor. The head of the validation function should be subordinated to a person who has no responsibility for managing the activities that are being monitored. Remuneration of validation function staff should not be linked to the performance of the activities that the validation function is assigned to monitor (CEBS 2008).
Roles and responsibilities
The validation policy should be owned by the chief risk officer (RMA 2009) and should identify roles and assign responsibilities based upon staff expertise, authority, reporting lines and continuity. According to OCC (2011b) and Green (2012), model validators should have appropriate incentives, competence and influence (e.g. authority to challenge developers and users or to restrict model use). Model owners should ensure that models employed have undergone appropriate validation and approval processes and promptly identify new or altered models by providing all necessary information for validation activities (OCC 2011b).
Model documentation
Documents detailing the model design are required which indicate that it was well informed, carefully considered, and consistent with published research and with sound industry practices (CEBS 2008; OCC 2011b). A comprehensive survey of model limitations and assumptions (OCC 2011b) is needed as well as a record of all material changes made to the model or the modelling process. Any overrides must be analysed and recorded (OCC 2011b) and the validation plans and findings of the validation (FDIC 2005) should be documented.
Ongoing validation
Validation activities should continue on an ongoing basis after a model enters usage, to track known model limitations and to identify new ones (OCC 2011b). Institutions should conduct periodic reviews, at least annually, but more frequently if warranted, of each model to determine whether it is working as intended and if the existing validation activities are sufficient (OCC 2011b; RMA 2009).
Performance standards and remediation plans
Backtesting, benchmarking and stress testing should be conducted and results assessed. Model accuracy and precision should be evaluated and results should be compared with those provided by other models. Model output sensitivity to inputs, model assumptions and stress testing should also be considered (Green 2012; OCC 2011b). If significant model risk is found remediation efforts should be prioritised. Ongoing monitoring of areas of concern to ensure continued success is also required (McGuire 2007).
Audit oversight
Internal audit should verify that no models enter production2 without formal approval by the validation unit and should be responsible for ensuring that model validation units adhere to the formal validation policy (Pace 2008). Records of validation - to test whether validations are performed in a timely manner - should also exist and the objectivity, competence and organisational standing of the key validation participants should be evaluated (OCC 2011b).
Model validation process
As per Figure 2, the model validation process comprises three distinct elements, namely conceptual soundness and developmental evidence, process verification and ongoing monitoring and lastly, outcome analysis.
Conceptual soundness and developmental evidence
This first main element of the model validation process can be subdivided into nine sub-elements, which will be briefly discussed in Table 1.
Process verification and ongoing monitoring
The second element of the model validation process can be split into two distinct stages, namely monitoring and test and evaluation as discussed in Table 2.
Outcome analysis
The third and last element of the model validation process will be discussed under outputs and backtesting in Table 3.
Model validation scorecards
Model validation scorecards comprise three components (in line with the elements introduced in the previous section): the model validation governance scorecard, the model validation policy scorecard and the model validation process scorecard. These tools may be used to ascertain whether the proposed best practice model validation framework has been adequately assembled and implemented. All three scorecards use numerical scores ranking from 1 (no evidence) to 4 (fully evident). A four-grade scale, in line with that used by the Regulatory Consistency Assessment Programme (RCAP) (BCBS 2016) was specifically chosen to avoid the midpoint. Although most inputs in any kind of scorecard are subjective, there is a danger in using a 3-point or 5-point scale, as many respondents is likely to choose the midpoint or average. This might result in a failure to identify specific weaknesses.3
A typical use of these scores in a management information environment would result in a colour-coded dashboard, for example, associating a score of 1 with Red, 2 with Orange, 3 with Yellow and 4 with Green. This would be a powerful tool in highlighting validation areas in need of urgent attention (i.e. 'Red'). Tracking individual scores, as well as the distribution of these scores, over time can give an indication of the model validation framework's maturity within an institution.
Note that no weights were added to the scorecards, as the purpose is not to combine the elements together in an aggregate score. Instead, the ultimate goal for each institution should be to achieve 'compliance' in each one of the suggested areas, that is, a score of 4 (fully evident) for each sub-element of each scorecard, similar to the grading methodology of the RCAP programme.
The three different scorecards can be applied at different levels. The policy scorecard could, for instance, be applied at the highest level for which an applicable validation policy exist, be that at enterprise, risk type or business unit level. The process scorecard, on the contrary, should be applied at model level.
Model validation governance scorecard
This generic validation governance scorecard (Table 1-A2) provides a tool that may be used to determine whether the firm's validation governance is in place (according to the model validation framework discussed in 'model validation governance' section). The main elements of this scorecard are as follows:
-
Clear roles and responsibility assigned to role players and committees.
-
Adequate oversight and participation by internal audit.
-
Validation function independent in terms of remuneration.
-
Defined assignment of authority for approval.
-
Adequate board and senior management involvement.
The rest of the validation governance elements are addressed in the validation policy scorecard (e.g. roles and responsibilities, independent review and audit oversight).
Model validation policy scorecard
The generic validation policy scorecard may be used as a tool to check to what extent the firm's validation policy is in place (according to the model validation framework discussed in 'model validation policy' section). This scorecard comprises seven elements, indicated in Table 2-A2 and can be summarised as follows:
Scope:
-
Separate, enterprise-wide validation policy exists.
-
Validation policy provides guidelines for input validation, processing and reporting.
-
Vendor model validation included in policy scope.
Independent review:
-
Policy provides for models to be independently evaluated prior to implementation.
-
Independent review is performed by suitably skilled experts.
Roles and responsibilities:
-
Problems identified during the independent review are reported on.
-
Appropriate responsibility to act on such reports is assigned.
-
Necessary actions are scheduled and managed properly.
Model documentation:
-
Documentation is reviewed in terms of completeness, transparency and scope.
-
A completely new model can independently be reproduced from documentation.
Ongoing validation:
-
The existence of a monitoring plan for implementation is ascertained.
-
A program for ongoing testing and evaluation of model performance has been designed.
Performance standards and remediation plans:
-
Documentation specifies tolerances/thresholds for implemented model performance.
-
Procedures for the management and control of remediation activities are in place.
Audit oversight:
-
Verification that no models enter production without validation unit approval.
-
Evaluation of objectivity/competence/organisational standing of key validation participants.
-
Verification that validation process is carried out according to policy in a timely manner.
Model validation process scorecard
The generic validation process scorecard may be used as a tool to check if the validation process has been correctly established (according to the model validation framework discussed in 'model validation policy' section). Validation process comprises conceptual soundness and developmental evidence, process verification and ongoing monitoring, and outcome analysis. The validation process scorecard comprises seven elements as indicated in Table 3-A2. Note that this is a generic scorecard and will change per product, per institution and also whether the model is in the development, implementation or monitoring phase.
The main elements of this scorecard are:
Paradigm:
-
Was conceptual soundness of paradigm checked?
-
Was check/review performed by suitably skilled experts?
Methods/theory:
-
Is underlying model theory consistent with published research and accepted industry practice?
-
Were research publications considered of appropriate quality/standing?
-
Was methodology benchmarked against appropriate industry practice?
-
Are approximations made within agreed tolerance levels?
Design:
-
Was it ascertained that assumptions are clearly formulated?
-
Was the appropriateness and completeness of assumptions checked?
-
Was it checked that all variables employed have been clearly defined and listed?
-
Have the causal relationships between variables been documented?
-
Have input data been determined and assessed in terms of reasonableness, validity and understanding?
-
Has it been ascertained that outputs are clearly defined?
-
Has the design been evaluated in terms of model parsimony?
-
Has model builder benchmarked design against existing best practice models?
-
Was design independently benchmarked against existing best practice models?
-
Are special cases dealt with appropriately? (e.g. terminal conditions or products with path-dependent pay-off)
Data/variables:
-
Have input data been checked to gauge reliability/suitability/validity/completeness?
-
Have data that involve subjective assessment of expert opinion been appropriately incorporated?
-
Was the procedure for the collation of expert opinion scrutinised?
-
Has expert opinion been validated in terms of logical considerations?
-
Has expert selection process been assessed as sound?
-
Were data verified that they are representative of relevant (general and stressed) market conditions?
-
Was it verified that data are representative of the company's portfolio?
-
Have inadequate or missing data been re-assessed and reviewed for model feasibility?
Algorithms/code:
-
Was the algorithms/code checked against the model formulation and underlying theory?
-
Were key assumptions and variables analysed with respect to their impact on model outputs?
-
Was an independent construction of an identical model undertaken?
-
Was the code rigorously tested against a benchmark model?
-
Was technical proofreading of the code performed?
Outputs:
-
Was model output benchmarked against best practice models (e.g. against a vendor model using the same input data set)?
-
Was the reasonableness and validity of model outputs assessed?
-
Has a comparison of model outputs against actual realisations been performed? (backtesting)
-
Has a range of outputs been examined versus a range of inputs - are solutions continuous or jagged? What is the behaviour of hedging quantities and/or derived quantities over the same range?
-
Are all results repeatable? (e.g. Monte Carlo simulations)
Monitoring:
-
Has the model been monitored for appropriate implementation and use?
-
Has the model been monitored to check whether it is performing as intended?
Conclusions and recommendations
Institutions should classify, design, implement, validate and govern their models robustly on an ongoing basis if they want to effectively minimise model risk. Institutions that fail to implement a regular, consistent model risk management framework risk penalties from regulatory authorities and reputation risk in the contemporary era of strict model risk management standards.
This research provided a comprehensive literature study, which provided a background to the complexities of effective model management and focussed on model validation as a component of model risk management. A best practice model validation framework for institutions has been proposed. The proposed best practice model validation framework is designed to assist firms in the construction of an effective, robust and fully compliant model validation programme and comprises three principal elements: model validation governance, policy and process.
A set of scorecards - detailing the principles of model validation governance, model validation policies and model validation processes - was proposed. These scorecards may be used as tools to determine whether the proposed best practice model validation framework has been established and is effective. This includes the provision of detailed supporting documentation to substantiate assertions that models are aligned to business and regulatory requirements to supervisory authorities.
Acknowledgements
The authors gratefully acknowledge the valuable input given by Johan Kapp, Neels Erasmus and anonymous referees. This work is based on research supported in part by the Department of Science and Technology (DST) of South Africa. The grant holder acknowledges that opinions, findings and conclusions or recommendations expressed in any publication generated by DST-supported research are those of the author(s) and that the DST accepts no liability whatsoever in this regard.
Competing interests
The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.
Authors' contributions
The article originated from a project that was carried out for a bank. All the authors, except E.M. and G.v.V. were part of the project team. The authors that were not part of the project team made valuable contributions on a draft version of the article.
References
Anonymous, 2011, 'King's Fund apologise for "error" in figures on health spending in Wales', viewed 16 August 2016, from http://leftfootforward.org/2011/05/kings-fund-apologise-for-error-on-health-spending-in-wales/ [ Links ]
BBC News, 2013a, 'Reinhart, Rogoff… and Herndon: The student who caught out the profs', 20 April, viewed 16 August 2016, from http://www.bbc.com/news/magazine-22223190 [ Links ]
BBC News, 2013b, 'West Coast Main Line franchise fiasco "to cost at least £50m"', 26 February, viewed 16 August 2016, from http://www.bbc.com/news/uk-politics-21577826 [ Links ]
BCBS, 2006, Basel II: International convergence of capital measurement and capital standards: A revised framework, Bank for International Settlements, Switzerland. [ Links ]
BCBS, 2013, Discussion paper: The regulatory framework: Balancing risk sensitivity, simplicity and comparability (BCBS 258), Bank for International Settlements, viewed 15 August 2016, from http://www.bis.org/publ/bcbs258.pdf [ Links ]
BCBS, 2016, Regulatory Consistency Assessment Programme (RCAP): Handbook for jurisdictional assessments, viewed 24 August 2016, from http://www.bis.org/bcbs/publ/d361.pdf [ Links ]
Black, F. & Litterman, R., 1992, 'Global portfolio optimization', Financial Analysts Journal 48(5), 28-43. https://doi.org/10.2469/faj.v48.n5.28 [ Links ]
Burns, R., 2006, 'Model governance', Supervisory Insights 2(2), 4-11. [ Links ]
CEBS, 2008, Electronic guidebook, viewed 13 March 2014, from http://www.treasuryworld.de/sites/default/files/CEBS_Electronic%20Guidebook.pdf [ Links ]
CEIOPS, 2009, 'CEIOPS' advice for level 2 implementing measures on Solvency II: Articles 120 to 126 tests and standards for internal model approval', viewed 26 May 2014, from www.toezicht.dnb.nl/en/binaries/51-213723.pdf [ Links ]
Cont, R., 2006. 'Model uncertainty and its impact on the pricing of derivative instruments', Mathematical Finance 16(3), 519-547. https://doi.org/10.1111/j.1467-9965.2006.00281.x [ Links ]
Daily Express Reporter, 2011, 'Mouchel profits blow', 7 October, viewed 16 August 2016, from http://www.express.co.uk/finance/city/276053/Mouchel-profits-blow [ Links ]
De Jongh, P.J., De Wet, T., Raubenheimer, H. & Venter, J.H., 2015, 'Combining scenario and historical data in the loss distribution approach: A new procedure that incorporates measures of agreement between scenarios and historical data', Journal of Operational Risk 10(1), 1-31. https://doi.org/10.21314/JOP.2015.160 [ Links ]
Deloitte, L.L.P., 2010, Coping with complexity: Leadership in financial services, Deloitte Research, viewed 05 April 2014, from http://www.deloitte.com/assets/Dcom-SouthAfrica/Local%20Assets/Documents/ZA_fsi_CopingComplexityLeadership_ 160810.pdf [ Links ]
Elices, A., 2012, The role of the model validation function to manage and mitigate model risk, Working paper, viewed 29 March 2014, from http://arxiv.org/pdf/1211.0225.pdf [ Links ]
Epperson, J., Kalra, A. & Behm, B., 2012, Effective AML model risk management for financial institutions: The six critical components, Crowe Howarth, viewed 23 March 2014, from http://www.crowehorwath.com/ContentDetails.aspx?id=4889 [ Links ]
EUSIG, 2016, Spreadsheet mistakes - News stories, viewed 07 July 2016, from http://www.eusprig.org/horror-stories.htm [ Links ]
FDIC, 2005, Supervisory insights: Model governance, viewed 31 May 2014, from http://www.fdic.gov/regulations/examinations/supervisory/insights/siwin05/artic le01_model_governance.html [ Links ]
FSB, 2010, SAM (Solvency Assessment and Management) Glossary (Version 1.0, created 2010), viewed 24 August 2016, from https://sam.fsb.co.za/SAM%20Documents/SAM%20Library/SAM%20Glossary.pdf. [ Links ]
FSB, 2014, Global shadow banking monitoring report 2014, Financial Stability Board, viewed 15 August 2016, from http://www.fsb.org/wp-content/uploads/r_141030.pdf [ Links ]
FSI, 2015, The 'four lines of defence model' for financial institutions - Taking the three-lines-of-defence model further to reflect specific governance features of regulated financial institutions, FSI Occasional Paper No 11, Bank for International Settlements, viewed 12 August 2016, from http://www.bis.org/fsi/fsipapers11.pdf [ Links ]
Galletta, D.F., Abraham, D., El Louadi, M., Lekse, W., Pollalis, Y.A. & Sampler, J.L., 1993, 'An empirical study of spreadsheet error-finding performance', Accounting, Management and Information Technologies 3(2), 79-95. https://doi.org/10.1016/0959-8022(93)90001-M [ Links ]
Gandel, S., 2013, 'Damn excel! How the most important software of all time is ruining the world', Fortune, April 17, viewed 07 July 2016, from http://fortune.com/2013/04/17/damn-excel-how-the-most-important-software-application-of-all-time-is-ruining-the-world/ [ Links ]
Glowacki, J.B., 2012, Effective model validation, Milliman Research, viewed 31 March 2014, from http://uk.milliman.com/insight/insurance/Effective-model-validation/ [ Links ]
Godfrey, K., 1995, 'Computing error at Fidelity's Magellan fund', The Risk Digest 16(72), viewed 27 August 2015, from http://catless.ncl.ac.uk/Risks/16.72.html [ Links ]
Green, D., 2012, Model risk management framework and related regulatory guidance, Angel Oak Advisory, viewed 24 March 2014, from http://www.angeloakadvisory.com/model-risk.pdf [ Links ]
Haugh, M., 2010, Model risk. Quantitative risk management notes, Columbia University, viewed 13 March 2014, from http://www.columbia.edu/~mh2078/ModelRisk.pdf [ Links ]
Heineman, B.W., 2013, 'The JP Morgan "Whale" Report and the Ghosts of the Financial Crisis', Harvard Business Review: Risk Management, January, viewed 16 August 2016, from https://hbr.org/2013/01/the-jp-morgan-whale-report-and [ Links ]
Higham, N., 2013, Rehabilitating correlations, avoiding inversion, and extracting roots, Talk at the School of Mathematics, The University of Manchester, London, viewed 27 August 2015, from http://www.maths.manchester.ac.uk/~higham/talks/actuary13.pdf [ Links ]
IIA, 2013, The three lines of defence in effective risk management and control, IIA Position paper, The Institute of Internal Auditors, viewed 16 August 2016, from https://na.theiia.org/standards-guidance/Public%20Documents/PP%20The%20Three%20Lines%20of%20Defense %20in%20Effective%20Risk%20Management%20and%20Control.pdf [ Links ]
Institute and Faculty of Actuaries (IFoA), 2015, Model risk: Daring to open up the black box by the Model Risk Working Party, viewed 26 August 2016, from https://www.actuaries.org.uk/practice-areas/risk-management/risk-management-research-working-parties/model-risk [ Links ]
Madahar, M., Cleary, P. & Ball, D., 2008, Categorisation of spreadsheet use within organisations, incorporating risk: A progress report, Working paper, Cardiff School of Management, viewed 3 April 2014, from http://arxiv.org/ftp/arxiv/papers/0801/0801.3119.pdf [ Links ]
Maré, E., 2005, 'Verification of mathematics implemented in financial derivatives software', Derivatives Week, September 2005, pp. 6-8. [ Links ]
McCullough, B.D. & Heiser, D.A., 2008, 'On the accuracy of statistical procedures in Microsoft Excel 2007', Computing Statistics Data Analysis 52(1), 4570-4578. https://doi.org/10.1016/j.csda.2008.03.004 [ Links ]
McCullough, B.D. & Wilson, B., 1999, 'On the accuracy of statistical procedures in Excel 97', Computing Statistics Data Analysis 31(3), 27-37. https://doi.org/10.1016/S0167-9473(99)00004-3 [ Links ]
McCullough, B.D. & Yalta, A.T., 2013, 'Spreadsheets in the cloud - Not ready yet', Journal of Statistical Software 52(7), 1-14. https://doi.org/10.18637/jss.v052.i07 [ Links ]
McGuire, W.J., 2007, Best practices for reducing model risk exposure, Bank Accounting & Finance, April-May, pp. 9-14. [ Links ]
Morini, M., 2011, Understanding and managing model risk: A practical guide for quants, traders and validators, Finance series, Wiley, New York. [ Links ]
NACRO Council, 2012, Model validation principles applied to risk and capital models in the insurance industry, North American CRO Council, viewed 17 March 2014, from http://crocouncil.org/images/CRO_Council_-_Model_Validation_Principles.pdf [ Links ]
OeNB/FMA, 2004, Guidelines on credit risk management: Rating models and validation, viewed 19 May 2014, from http://www.fma.gv.at/en/about-the-fma/publications/fmaoenb-guidelines.html [ Links ]
Office of the Comptroller of the Currency (OCC), 2011a, Supervisory guidance on model risk management, Supervisory letter SR 11-7, Board of Governors of the Federal Reserve System, Washington, DC. [ Links ]
Office of the Comptroller of the Currency (OCC), 2011b, Supervisory guidance on model risk management, Supervisory document OCC 2011-12, Board of Governors of the Federal Reserve System, Washington, DC, pp. 1-21. [ Links ]
Pace, R.P., 2008, Model risk management: Key considerations for challenging times, Bank Accounting and Finance, June-July, pp. 33-57. [ Links ]
Panko, R. & Ordway, N., 2005, 'Sarbanes Oxley: What about all the spreadsheets?', in EuSpRIG Conference Proceedings, University of Greenwich, London, July 7-8, pp. 15-60. [ Links ]
PWC, 2004, The use of spreadsheets: Considerations for Section 404 of the Sarbanes-Oxley Act, Price Waterhouse Coopers whitepaper, viewed 28 February 2014, from http://www.pwcglobal.com/extweb/service.nsf/docid/CD287E403 C0AEB7185256F08007F8CAA [ Links ]
Rajalingham, K., 2005, 'A revised classification of spreadsheet errors', in EuSpRIG Conference Proceedings, University of Greenwich, London, July 7-8, pp. 23-34. [ Links ]
Ripley, B.D., 2002, 'Statistical methods need software: A view of statistical computing', in Presentation RSS Meeting, September 2002, viewed 27 August 2015, from http://www.stats.ox.ac.uk/~ripley/RSS2002.pdf [ Links ]
RMA, 2009, Market risk: Model risk management, validation standards and practices, Risk Management Association, viewed 09 March 2014, from http://www.rmahq.org/tools-publications/surveys-studies/benchmarking-studies [ Links ]
SARB, 2015a, Bank Supervision Department: Annual report 2015, viewed 15 August 2016, from http://www.resbank.co.za/Lists/News%20and%20Publications/Attachments/7309/0 1%20BankSupAR2015.pdf [ Links ]
SARB, 2015b, Directive 4/2015: Amendments to the Regulations relating to Banks, and matters related thereto, viewed 10 August 2016, from https://www.resbank.co.za/Lists/News%20and%20Publications/Attachments /6664/D4%20of%202015.pdf [ Links ]
Sawitzki, G., 1994, 'Report on the reliability of data analysis systems', Computing Statistics Data Analysis 18(5), 289-301. https://doi.org/10.1016/0167-9473(94)90177-5 [ Links ]
Simons, K., 1997, 'Model error. New England Economic review', November/December 1997, viewed 27 August 2015, from http://www.bostonfed.org/economic/neer/neer1997/neer697b.pdf [ Links ]
Springer, K., 2012, 'Top 10 biggest trading losses in history by Time magazine', viewed 27 August 2015, from http://newsfeed.time.com/2012/05/11/top-10-biggest-trading-losses-in-history/slide/morgan-stanley-9b/ [ Links ]
U.S. Securities and Exchange Commission (SEC), 2011, SEC charges AXA Rosenberg entities for concealing error in Quantitative Investment Model, 03 February, viewed 16 August 2016, from https://www.sec.gov/news/press/2011/2011-37.htm [ Links ]
Wailgym, 2007, Eight of the worst spreadsheet blunders, CIO, viewed 27 August 2015, from http://www.cio.com/article/2438188/enterprise-software/eight-of-the-worst-spreadsheet-blunders.html [ Links ]
West, G., 2004, 'Calibration of the SABR model in illiquid markets', Insight document on Riskworx website, viewed 27 August 2015, from http://www.riskworx.com/insights/sabr/sabrilliquid.pdf [ Links ]
Whitelaw-Jones, K., 2015, Capitalism's dirty secret: A F1F9 research report into the uses & abuses of spreadsheets, viewed 22 August 2016, from http://www.f1f9.com/blog/tag/capitalisms-dirty-secret [ Links ]
Yalta, A.T., 2008, 'The accuracy of statistical distributions in Microsoft Excel 2007', Computing Statistics Data Analysis 52(2), 4579-4586. https://doi.org/10.1016/j.csda.2008.03.005 [ Links ]
 Correspondence:
Correspondence:
Tanja Verster
tanja.verster@nwu.ac.za
Received: 21 Oct. 2015
Accepted: 27 Mar. 2017
Published: 23 June 2017
1. Although the credit crisis of 2008-9 (Deloitte 2010) contributed to the current regulatory changes, other drivers of change include the BCBS articulation of improved comparability, simplicity and risk sensitivity of risk measures (see e.g. BCBS 2013), the introduction of the Twin Peaks regulatory framework (SARB 2015a) and the effects of shadow banking (FSB 2014; SARB 2015a).
2. To clarify this point further, the reader should note that internal audit is typically not in a position to police the day-to-day moving of models into production since they only do periodic audits of business areas. Internal audit should therefore pick up that models entered production without following due process, however only sometime after the event. All the lines-of-defence (refer to the four-line of defence in 'Overview of the proposed model validation framework' section) including operational risk managers need to play a role to ensure that models follow the correct process before entering production.
3. Backtesting is not always possible, for example with capital models where the unexpected loss is modelled. Here the modelled result typically represents a 1-in-1000 year annual loss and therefore backtesting is not practical due to needing several thousand years of data perform a credible backtest. In these cases benchmarking replaces backtesting (see Table 1 for more information on benchmarking).
Model risk examples
Example 1: Real world calibration assumptions
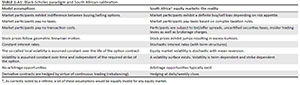
Suppose a contingent claim on a South African equity within the Black-Scholes paradigm was required - Table 1-A1 highlights the classical theoretical model assumptions used and details the practical reality 'calibrated' to the South African market environment. Model validators typically need to assess the gap between theory and practise and understand the model misspecification. Typically, a certain amount of capital could be set aside to cover the gap. The misspecification could also mean that a product is entirely unsuitable for a specific institution or lead to strict limits imposed on its use. Significant losses can be incurred as a result of using the incorrect paradigm (see Cont 2006).
Example 2: Spreadsheet-based implementation examples
'Let's not kid ourselves: the most widely used piece of software in Statistics is Excel' (Ripley 2002).
Spreadsheet applications abound in the modern financial services industry. Users generally understand the need for careful practices when using spreadsheets to ensure a control environment and avoid basic mistakes or logical errors. Users might not always suspect that the functionality offered by a spreadsheet program has not been thoroughly tested. We highlight some examples from the literature. Consider the simple problem of calculating the standard deviation of three numbers, say [m, m, + 1, m + 2]. The correct answer is trivially equal to m + 108; Higham (2013), however, showed that Google Sheets produces a 0 answer for m = 108. Sawitzki (1994) reports a similar problem for EXCEL 4.0. McCullough and Wilson (1999) assessed the reliability in Excel 97 for linear and nonlinear estimation, random number generation and statistical distributions (e.g. calculating p-values) as inadequate. McCullough and Heiser (2008) found that Excel 2007 fails a set of intermediate-level accuracy tests in the same areas. Yalta (2008) details numerical examples for Excel 2007 where no accurate digits are obtained for the binomial, Poisson, inverse standard normal, inverse beta, inverse student's t and inverse F distributions. McCullough and Yalta (2013) assess Google Sheets, Microsoft Excel Web App and Zoho Sheet and show that the developers had not performed basic quality controls with the result that statistical computations are misleading and erroneous. More examples on the uses and abuses of spreadsheets can be found in a F1F9 research report (Whitelaw-Jones 2015).
It is clear from the above that one should view spreadsheet-based analyses with some caution - In particular when the spreadsheet is used as an independent control for validation purposes.
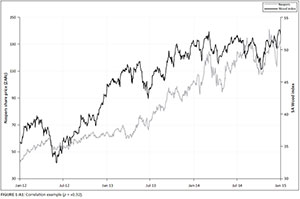
Example 3: Illustration of the necessity of confirming business sense
Figure 1-A1 demonstrates the need to explore the true causal relationship between variables. The Wood index is plotted against the Naspers index. The variables in the example exhibit significant positive correlation (+0.92), however, their economic relationship is entirely spurious. The wrong conclusion might be that Naspers are highly correlated to the Wood index because of the relationship of Naspers to print media (i.e. paper), and paper again comes from wood. However, the real constitutes of Naspers has very little to do with the Wood index. Naspers is a global platform operator with principal operations in:
-
Internet services, especially e-commerce (i.e. classifieds, online retail, marketplaces, online comparison shopping, payments and online services)
-
pay television (direct-to-home satellite services, digital terrestrial television services and online services)
-
print media.
Example 4: Model error examples and associated loss impacts
A few different model risk related loss examples will be explained next and summarised in Table 2-A1 below. A computing error at the Fidelity's Magellan fund resulted in a net capital loss of $1.3 billion (Godfrey 1995). In March of 1997, NatWest Markets, an investment banking subsidiary of National Westminster Bank, announced a loss of £90 million because of mispriced sterling interest rate options (Simons 1997). Real Africa Durolink, a smaller bank in South Africa, but major player in the equity derivatives market, failed within days of the introduction of the skew, as they were completely unprepared for the dramatic impact the new methodology would have on their margin requirements (West 2004). The number three on a list of the eight worst spreadsheet blunders are listed as the financial institution, Fannie Mae that discovers a $1.3 billion 'honest' mistake (Wailgym 2007). Time magazine listed Morgan Stanley's $9 billion loss as the number one loss in a survey of 'Top 10 Biggest Trading Losses in History' (Springer 2012).
Health think tank 'The King's Fund' has been forced to write to the Welsh government to apologise for errors in figures it produced on health spending in Wales (Anonymous 2011). An error made on a spreadsheet, downgraded profits by £8.6 million (Daily Express Reporter 2011). United States Securities and Exchange Commission (SEC) charged AXA Rosenberg Entities ($242 million fine) for concealing error in their quantitative investment model (SEC 2011). West Coast Main Line franchise fiasco 'to cost at least £50 m' because of model incorrectly used (BBC 2013b), Heineman (2013) described the JP Morgan 'Whale' report that discusses the $6 billion losses (of which the spreadsheet error was at least £250 million). A PhD student found a spreadsheet error in two Harvard professors' paper that asserted that high public debt stifles economic growth, which then drove government policy decisions (BBC 2013a). Almost one in five large businesses have suffered financial losses as a result of errors in spreadsheets, according to F1F9, which provides financial modelling and business forecasting to blue chips firms. It warns of looming financial disasters as 71 pc of large British business always use spreadsheets for key financial decisions (Whitelaw-Jones 2015). Some of these examples are also summarised in IFoA (2015).
Model validation scorecards
The detailed scorecards that are described in 'model validation governance', 'model validation policy' and 'model validation process' sections are presented Tables 1-A2; 2-A2 and 3-A2.