Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Economic and Management Sciences
versão On-line ISSN 2222-3436
versão impressa ISSN 1015-8812
S. Afr. j. econ. manag. sci. vol.20 no.1 Pretoria 2017
http://dx.doi.org/10.4102/sajems.v20i1.1600
ORIGINAL RESEARCH
Contingent convertible bonds as countercyclical capital measures
Francois Liebenberg; Gary van Vuuren; Andre Heymans
Department of Risk Management, School of Economics, North-West University, South Africa
ABSTRACT
BACKGROUND: The procyclical nature of capital models under the Basel II Accord has been widely criticised for exacerbating lending in economic expansions and restricting lending during economic contractions. These criticisms have led regulators to employ countercyclical measures in subsequent Basel accords. One of these measures, the countercyclical capital buffer (CCB), has been proposed as an effective countercyclical measure in expansionary periods as a deterrent to excessive lending through increased bank capital requirements.
AIM: The effectiveness of the CCB during contractions is not obvious. Contingent convertible (CoCo) bonds - which are bond-like until triggered by a deterioration of a prescribed capital metric, at which point they convert into a form of equity - are explored as a supplementary countercyclical capital measure for such periods to establish whether or not they function effectively.
SETTING: The analysis is undertaken using global bank CoCo data, and then applied to South African banks.
METHODS: The Hodrick Prescott filter was applied to empirical historical data.
RESULTS: The CCB functions as a good countercyclical capital measure in times of economic expansion by absorbing losses and stabilising the capital base through equity issuance.
CONCLUSION: The issuance of CoCo bonds - if their trigger mechanisms are designed correctly - may prove helpful to banks and the broader financial sector in times of economic contraction through the countercyclical capital properties that manifest through CoCo bonds under these economic conditions.
Introduction
The credit crisis which disrupted the global economy in the latter part of 2007 had its roots nested in complex financial instruments (particularly derivative instruments), which inflated asset prices to levels that were far higher than their historic trends. These instruments behaved in complex ways and were riskier than believed at the time (Baily, Litan & Johnson 2008). The risk mitigation techniques that were consequently employed were ineffective, leading to the large-scale collapse of the global financial system once these hidden risks materialised (G20 2009).
The first internationally recognised company to fall victim to the crisis was the American bank Lehman Brothers which filed for a Chapter 11 bankruptcy on 15 September 2008 (De Haas & Van Horen 2012). The systemic contagion precipitated by Lehman's collapse became manifest in a conservative view of lending, including the widespread avoidance of securitised products and the severe reduction of credit (both consumer and commercial). These effects were largely because of the procyclical nature of capital requirements at the time (Nikolov 2010). If an economic indicator thus increases when the economy exhibits economic growth, it is deemed a procyclical indicator and is used as a metric to measure procyclicality. Credit losses suffered by banks during the credit crisis were higher than those experienced during economic expansions, evidence that the inherent procyclical nature of risk management models may amplify losses during economic downturns (BCBS 2010b; Van Vuuren 2012). Heid (2003) described the exacerbation of bank losses in economic downturns as diminished lending capacities accompanied by increases in risk-weighted assets (RWAs), a combination that significantly reduces a bank's capital ratios.1 This effectively portrays the inherent procyclicality of capital measures under Basel II (BCBS 2010b).
The effect of the procyclicality in the broader economic environment meant that the majority of banks also suffered under the economic environment that the reaction created, especially in terms of lending, and this placed pressure on the other parts of economies globally as bank lending dried up in the economic downturn (De Haas & Van Horen 2012). Following on the heels of the credit crisis, the European sovereign solvency crisis occurred in 2010. The European Union initiated fiscal relief (a sovereign bailout for Greece) indicating that capital levels were insufficient (Sorkin 2010). South Africa absorbed the effects of the crisis relatively well compared with other developing economy peers, due in large part to prudent risk management (Maredza & Ikhide 2013). The robustness of the South African economy is evident in the fact that all South African banks survived the crisis while many global banks required sovereign bailouts (National Treasury 2011). Despite these prudent risk management policies, the country still slid into the first recession in 17 years in 2009 (SARB 2011a).
In response to the credit crisis and the liquidity crisis that ensued because of diminished capital, the Bank for International Settlements (BIS) implemented a number of amendments to the then-existing Basel II Accord with an updated set of regulations, called Basel III (BCBS 2011). The phased implementation of the new Basel III regulation began in 2013 and is at this stage (2016) expected to be fully implemented by 2019. The principal aim of Basel III is for better quality, consistency and transparency of tier 1 capital (BCBS 2010a), but it also introduces measures that increase the robustness of banking legislation including a reconstitution of the composition of acceptable regulatory capital, enhanced capital levels for aspects of the trading book and the introduction of new concepts such as the leverage ratio and a number of capital buffers, which increase the capital ratio from 8.0% to 10.5% (and, under certain specified conditions, to 13%) (BCBS 2011). A specific inclusion of Basel III - the countercyclical capital buffer (CCB) - is the proposed countercyclical capital measure, which can increase the capital ratio to 13.0%. The CCB works principally at the peak of an economic cycle - that is, it is effective at reducing excessive credit extension, but it is yet to be tested in real-world scenarios and as such it may not be as effective at releasing capital back into the economy (i.e. it may not effectively encourage lending in economic cycle troughs), hence the potential need for additional countercyclical measures.
One such countercyclical measure is contingent convertible (CoCo) bonds, which converts into common equity in severely stressed economic conditions.2 CoCos are thus effective loss-absorbing financial instruments that function as a mechanism for bank recapitalisation in times of economic stress (De Spiegeleer & Schoutens 2011) and have been proposed for use in banks (Pennacchi, Vermaelen & Wolff 2011) as loss-absorbing instruments. Despite these useful characteristics, these bonds have been overlooked as a source of countercyclical capital, and as such CoCos are the main focus of this paper.
The paper proceeds as follows: The 'Literature study' section 'interrogates the literature regarding economic procyclicality, its origins and implications on a global scale as well as in the South African market'. The BCBS's choice of procyclical measure, the CCB, is further explored as a countercyclical capital measure in times of economic expansion. CoCos are also discussed as a countercyclical capital measure with a particular focus on the behaviour of CoCos upon conversion in economic contractions. CoCo properties (such as trigger mechanisms and conversion details) are discussed as well as specific examples currently (2016) in issue.
The 'Methodology and data' section introduces and discusses the Hodrick-Prescott (HP) filter, assesses its relevance and applicability to financial data and points out the pros and cons of its use and also explores the equity derivative pricing model of CoCos. The HP filter is then applied to historical South African data to identify economic downturns and establish capital levels required had the CCB been implemented at those times. A simulation of CoCo triggers in the 2007 financial crisis is produced along with the resulted increase in common equity tier 1 (CET1) capital of the four main South African banks because of the conversions. The results of the calculations are analysed and presented in the 'Results and discussion' section. The last section is the 'Conclusions'.
Literature study
Procyclicality
The complex nature of financial market securities resulted in a severe test for risk managers as well as the Basel II Accord during the 2007 credit crisis (Merrouche & Nier 2010). A leading catalyst of the credit crisis was the Chapter 11 bankruptcy filing of Lehman Brothers. The procyclical nature of capital requirements at the time resulted in the considerable reduction of bank lending. The associated capital reduction and contagion effects left banks without the means to raise additional capital, and governments, regulators, central banks and quantitative models at the core of risk management were blamed for the crisis (US Financial Crisis Inquiry Commission 2010).
South African Banks proved to be resilient in the financial crisis largely because of two factors. Firstly, the credit crisis erupted as a result of the securitisation of sub-prime mortgages (Peicuti 2013). These securities were sold to investors with the assurance of accurate ratings from global credit rating agencies. Banks in South Africa were not able to purchase these grouped loans because of tight banking regulations, and the implementation of the National Credit Act No. 34 of 2005 (NCA) (Maredza & Ikhide 2013). The NCA introduced prudent financial legislation shortly before the crisis (Gauteng Provincial Treasury 2012). South Africa has, as a result, not yet experienced a full financial crisis, but rather periods of financial distress.
Secondly, the resilience of South African banks is linked directly to sound profitability, low leverage ratios, limited exposure to foreign assets and foreign funding as well as adequate levels of capital in times of crisis (Maredza & Ikhide 2013). In a period where many banks were declared bankrupt globally, all South African banks survived. This earned the South African banking system the reputation for being well developed, well-regulated and sophisticated and therefore ranked among those of first-world economies despite the fact that South Africa is viewed as a developing economy (National Treasury 2011). In response to the financial crisis, South Africa also employed various monetary policies including an increase in government expenditure of R127bn and a R34bn decrease in tax revenue. This, along unprofitable public companies like Eskom, led to the government funding needs increasing to R285bn in 2009, from R89bn in 2008. Because of the recession, the government saw its budget balance fall from a 0.7% surplus in 2007 to a 5% deficit by 2009. Economic growth recovered to 3.1% in 2010 and prudent fiscal management reduced the government deficit to 4.8% (Gauteng Provincial Treasury 2012).
Despite this resilience though, the industry-wide recognition of the impact of procyclicality prompted a call for measures to change the procyclical nature prevalent in risk models (Financial Service Authority 2009). This in turn highlighted the danger of procyclicality and demands a reformed risk measure to be engineered, which is inherently countercyclical, thus providing a thicker capital buffer during good times that could be drawn down during crises.
Heid (2003) argues that in economic downturns as maximum lending capacities decrease alongside a rise in RWAs, a shortage in capital arises. Two outputs from risk management models cause this. If assets are perceived to become riskier and this is correlated with business cycles, capital charges suffer large swings, consequently leading to increased volatility in not only the asset prices but also the linked interest rates. Consequently, this increase in financial sector volatility would naturally spill over into the rest of the economy. Perceived increases in credit risk trigger an increase in banks' credit risk capital, leading to increased cost of money in the economy, which is positively correlated with a decrease in investment ultimately causing a further systemic stunt to economic expansion. These combined effects explain the inherent procyclicality of capital measures under Basel II and highlight the need for countercyclical capital measures in the regulatory environment. The procyclicality in the economic environment during the 2007 financial crisis meant that most banks struggled to obtain liquid funds for their lending purposes, and this placed pressure on the other parts of economies globally (De Haas & van Horen 2012).
The procyclical nature inherent to the internal ratings-based methodology prescribed in Basel II may potentially be alleviated by using a through-the-cycle (TTC) rating system in financial models. This rating system may decrease the reaction of a lending party's probabilities of default (PDs) to macroeconomic conditions and as such dampen the effect that this has in the calculation of RWAs in the capital ratio of a bank (Catarineu-Rabell, Jackson & Tsomocos 2003). The study by Catarineu-Rabell et al. (2003) found that the TTC method would not reduce procyclicality, and as such, their conclusion was that Basel II regulation is ineffective at combating the procyclical nature of lending in times of financial distress. Repullo and Suarez (2008) and Repullo and Saurina (2011) employed an 'endogenous, dynamic capital-structure model under the assumption that banks have limited access to capital markets in stressed periods', as was the case in the 2007 credit crisis. They found that Basel II encouraged capital buffers to be procyclical in nature. The results from the study also showed that the buffers suggested in times of economic growth would be unable to mitigate the heightened requirements during economic contractions. These effects would in turn also cause a vast reduction in the supply of credit leading to knock-on effects resulting in systemic failure of capital markets as capital dries up.
Various counteractive measures were subsequently employed by the BIS as an addition to, but not replacement of, Basel II rules to supplement existing risk management regulation and address its procyclical flaws. These measures were introduced by the Basel III Accord as part of their principal aim of better quality, consistency and transparency of tier 1 capital (BCBS 2010a; Sundaresan & Wang 2011). The CCB, introduced by Basel III, aims to reduce bank capital procyclicality by increasing capital requirements in favourable economic conditions (BCBS 2010b). CCBs were thus proposed as a measure that would assist in protecting the financial system from systemic risk because of periods of increased credit growth (BIS 2009).
The CCB is not a regulatory minimum capital requirement under traditional regulation, but 'rather unencumbered capital more than the normal minimum requirement of the regulation'. This is to ensure 'that this capital will be available to absorb losses in times of economic contraction'. Building up this buffer capital is thus a countercyclical measure designed to strengthen the individual bank's treasury, and cumulatively the banks of the entire financial system. It is specifically designed to combat risks that accumulate during economic expansions and is only imposed when the economy is perceived to be 'overheating' (BCBS 2010b).
The countercyclical capital buffer
The initial (2013) minimum capital requirement for banks under the Basel III regulation was 8% of the total RWAs of the bank of which 4.5% must be CET1 high-quality capital. Basel III also requires that banks maintain a CCB of 2.5% of RWA above the 8% regulatory minimum capital requirement, which must comprise entirely of CET1 capital. This additional capital brings the total required capital amount to 10.5% and implies a confidence level of 99.97%, instead of the 99.90% employed by the previous total minimum requirement of 8% as shown in Figure 1 (BCBS 2011). Should a bank fail to sustain this level of capital (10.5%), it will be penalised by the regulator. The distribution of bank earnings will thus be reined in to ensure that buffers accumulate before profits are redistributed, causing negative sentiment among shareholders. Lastly, a CCB of up to 2.5% of RWA is imposed, also consisting solely of CET1 capital, should national authorities detect an increase in system-wide risk associated with a specific metric measuring normalised excess aggregate credit growth. This is done to further bolster the banks during economically good times to assist in the rainy days when the economy turns for the worse (BCBS 2010b).
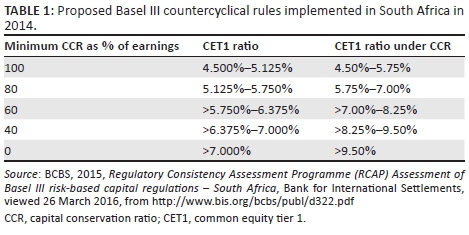
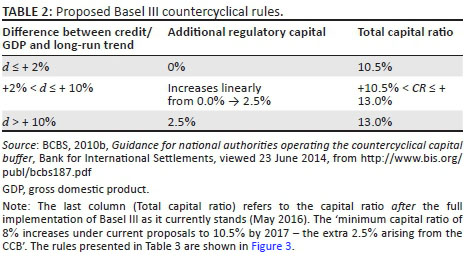
The CCB is designed to be deployed on an infrequent basis as the trigger is correlated with aggregate credit growth. Consider Table 1 as an indication of the minimum capital conservation ratios (CCRs) that would be enforced upon banks for respective levels of CET1 capital ratios. To explain these ratios, consider a bank with a CET1 capital ratio of between 5.750% and 6.375%. This bank would be required to conserve at least 60% of its earnings in the next financial year (i.e. pay out no more than 40% in terms of share buybacks, dividends and discretionary bonus payments) to the detriment of current shareholders and investors. Furthermore, should the bank's CET1 ratio fall below 5.125%, no dividend distribution would be permitted. Conversely, if the bank maintained a CET1 ratio of > 7%, there would be no impediments on dividend distribution. The CCRs, which a bank is required to keep under the conditional failure to meet the minimum CET1 ratios, is illustrated in Table 2 and Figure 2.
For regulators to impose the CCB, the economic cycle of a market must first be expressed using an accurate metric that measures the financial cycle. Potential measures of aggregate output and credit growth were explored and found to be the best fit when measuring the state of the financial cycle (Saurina & Trucharte 2007).3 The herding behaviour exhibited by the collective banking sector has a substantial influence on aggregate macro-indicators, depending on the sectoral market share of the banks in the economy. Thus, individual banks will need to bolster their capital if the CCB measures are imposed even though they may not be directly responsible for the excessive credit in the market. This does offer the advantage that the CCB metric is to some extent resilient to external manipulation by individual banks (Saurina & Trucharte 2007). The measure proposed by Basel III regulation is the deviation from:
the long-run trend of the aggregate credit-to-real gross domestic product (GDP) growth ratio (further referred to in this document as the 'credit-to-GDP ratio' and the difference between this ratio and the long-run trend referred to as the 'credit-to-GDP gap'. (BCBS 2010b:9)
The HP filter is used to fit the long-run trend. Table 2 summarises the proposed Basel III countercyclicality capital rules.
The BCBS are proponents of this measure as a mechanism that could solve the problem of an economy expanding in an uncontrolled fashion and has also substantiated these claims through empirical application to financial metrics in developed economies such as the United States and United Kingdom (BCBS 2010b). This is as yet inconclusive because historic analysis is not a guarantee of future accuracy and also when regulations are applied to smaller, less developed economies (such as South Africa), the model and data face considerably different assumptions and reactions (Van Vuuren 2012). In terms of the CCB, South Africa's banks are in the process of migrating to Basel III compliance and are geared to implement proposed solutions that Basel II offers to combat procyclicality (BIS 2013; PWC 2015).
Procyclicality does not affect an economy solely in times of economic expansion, but also in times of economic distress via the dearth of capital in the banking system. The effects of procyclicality, however, need to be dealt with in times of crisis, that is, when the economy is contracting and as such banks may need another measure in addition to the CCB. CoCo bonds have been proposed as a loss-absorbing capital instrument for use as tier 1 capital by banks. We propose that CoCos may prove to be useful as countercyclical capital measures in times of economic distress.
Contingent convertible bonds
Contingent convertibles are securities consisting of both an underlying equity and also a fixed-income component. These bonds are known to absorb losses by converting into common equity when certain conditions - usually heightened systemic risk - become prevalent (BCBS 2010a). CoCos and convertible bonds share many traits, with a few fundamental differences. As an example, a callable and convertible bond may be called upon to convert into a predefined number of the common shares of the issuing bank at the bondholder's decision. This bond is also callable by the issuer, that is, the bondholder may be required to surrender the bond to the issuing entity for a predetermined price if the issuer exercises their call option (Huang 2009). Thus, both the bondholder and/or the issuer of the security can determine when the contractual agreement of the bond will cease. Convertible bonds offer higher yields than standard non-convertible bonds because of the uncertainty associated with the bond's conversion attribute. Income-only investors may also have mandates to invest solely in financial instruments that generate interest or coupon payments. Convertible bonds have the property of potentially converting to equity and, in most cases, this risk will prevent such income-only investors from investing in convertible bonds, when the yields offered are greater than that of standard bonds (Huang 2009).
Contingent convertibles had a discreet launch into the financial world when the Lloyds Banking Group offered the holders of some of its hybrid debt a swap where their bonds will be traded for CoCo bonds, which had a possible conversion clause to convert into shares in November 2009 (De Spiegeleer & Schoutens 2011). Credit Suisse soon followed, raising $2bn in new capital using this new asset class. The CoCo market today, however, paints a totally different picture with USD98bn in CoCos in circulation until the end of 2015 as illustrated in Figure 4. CoCos in issuance paid an average coupon of 6.6% at the start of 2016, roughly double the interest payment on senior bank bonds making them attractive to investors (Bloomberg 2016).
Contingent convertibles have an array of appealing properties from the point of the investor and the issuing bank. Firstly, CoCos have loss-absorbing properties, bolstering a bank's capital when the bank suffers under economically stressed conditions and it is hard for the bank to issue new equity affording CoCos a countercyclical property in times of economic distress. By automatically restructuring the capital of a bank, CoCos reduce the 'debt overhang' problem, that is, the failure of a bank to timeously acquire funds to finance additional loans because a portion of their return accrues to existing debt holders (Chen et al. 2013).4 It is this property of CoCos that would have rescued many banks during the financial crisis when they were required to issue new equity (Atik 2010; Prescott 2012). Second, CoCos automatically restructure the capital of a bank before bankruptcy, while the bank is still viewed as being a 'going concern' as opposed to a 'gone concern', thereby mitigating the probability of the bank suffering bankruptcy. The Lehman Brothers case provides a concrete example of the impact of perception in guiding the financial market decisions: knowledge of pre-bankruptcy reorganisation of financial institutions (especially a systemically important one) is valuable. Lastly, if a CoCo bond is properly structured, regulators, both the issuing banks and the bondholders can potentially benefit from a CoCo conversion scenario, as opposed to a single entity taking a loss as the bank may receive additional capital, the existing shareholders making a profit and the bond holder receiving a repayment on the par value of the bond (Goodhart & Taylor 2006; Pennacchi et al. 2011:16).
Contingent convertibles also have a variety of conversion mechanisms in addition to equity including cash, or in some instances, a write-down on the bond (either partially or completely) may occur. Investor should take care when assuming that returns from a callable convertible bond and a CoCo are comparable. The potential for profit of a CoCo may be limited when compared to a standard convertible bond, depending on the underlying terms, and the full downside may come into play for an investor once the bond is converted to shares (De Spiegeleer & Schoutens 2011:8). One of the main differences between the bonds is the composition of the trigger mechanism inherent in the CoCo, an event that must occur in order for the CoCo bond to be converted into the loss absorption mechanism.
The trigger is specified in the prospectus of the CoCo and defines the scenario where banks will most likely suffer under financial pressure (De Spiegeleer & Schoutens 2011). Initial studies by Flannery (2005) suggest that a single-trigger mechanism be used. Later studies, however, have suggested the use of more triggers, with CoCos becoming an increasingly important topic after the financial crisis (see Flannery 2005; Huertas 2009; Albul, Jaffee & Tchistyi 2010; McDonald 2011; Pennacchi 2011; Pennacchi et al. 2011; Plosser 2010). In the case of a CoCo with more than one trigger, the loss conversion to equity (or write-down) will occur when any or a combination of triggers are breached. Triggers are either modelled on a mechanical rule or on the authority that may be executed by regulators. In the former case, also known as book value triggers or accounting-value triggers, the trigger mechanism is typically set contractually as the ratio of CET1 to RWAs, the CET1/RWA ratio. The loss absorption mechanism is activated should the CET1/RWA ratio of the issuing bank fall below a level which was predefined with the CoCo issuance. In order for a bank to remain a going concern, the trigger mechanism of a CoCo must come into effect before the bank is in trouble regarding its capital.5 The Lloyds Banking Group issued a CoCo in 2009, which illustrates this very nicely.6 The CoCo referred to has a 15% semi-annual coupon rate tied to the bond, with a conversion price of £0.59 per share, should the CET1 ratio of the bank fall below 5%. Under Basel III, the minimum CET1/RWA ratio for a CoCo to qualify as additional tier 1 capital (capital which is tier 1, but not CET1 capital) is 5.125%. Since 2011, issuing banks have set their trigger at that level or at 7% as is illustrated in Table 3. This is most likely because of the phasing-in of capital rules by the regulators in the various markets with the triggers set at 'current' or 'fully loaded' levels (BCBS 2012).
The overwhelming majority of CoCos currently in issuance rely on book value triggers. However, this mechanism has received criticism for being a reactive measure of capital issues and depends on the frequency that banks publish their financial results, thereby raising questions as to internal risk model comparisons (Culp 2009; Flannery 2005). The reporting delay may cause book value triggers to be activated slower than the rate at which capital is required. The trigger mechanism is also difficult for investors to model as the fundamental information comprising the capital calculation differs widely between banks. History has proven this concern as prominent global banks reported regulatory capital well above the minimum level of 8% when they went bankrupt in the financial crisis (De Spiegeleer & Schoutens 2011). Figure 5 illustrates the CET1 capital levels and the corresponding yields of banks who have issued CoCos with the trend generally showing that investors are rewarded with a higher yield as the CET1 capital levels decrease.
The ideal trigger to use may thus be market-value triggers as these triggers address the shortcoming of inconsistent accounting valuations (Calomiris & Herring 2012; Pennacchi et al. 2011; Sundaresen & Wang 2011). If these trigger-types are priced and composed correctly, the CoCo will convert to the triggered asset class at a given ratio of the bank's stock market capitalisation and/or Credit Default Swap spread to its assets (Flannery 2005). Such a composition reduces the risk of balance sheet manipulation and may also (hopefully) prevent regulatory forbearance (Avdjiev, Kartasheva & Bogdanova 2013). Market-value triggers, however, may prove to be difficult to price, could suffer from stock price manipulation and have the potential to exhibit multiple equilibria problems (Pennacchi et al. 2011; Sundaresen & Wang 2011).
The last trigger type, discretionary triggers (also referred to as point of non-viability, point of non-viability [PONV] triggers), will activate when regulators deem that it is appropriate to do so (Albul et al. 2010). These CoCos will allow a predefined regulator (usually a central bank) the power to trigger the conversion mechanism of the said CoCo if and when they view the action as necessary to save the bank. PONV triggers may offer a solution to the time-lag factor of book value triggers. The problem with a regulator causing a trigger is that the market could perceive this to be a blow to the financial stability of the issuing institution.
Methodology and data
Hodrick-Prescott filter
The long-run trend of the GDP is used to determine the credit-to-GDP gap of an economy. The best method to derive this trend is the HP filter (Cogley & Nason 1995; Ley 2006). The HP filter dates to 1980 (Hodrick & Prescott 1980) as 'a metric to measure business cycles'; however, the academic research was only published in 1997 long after the filter was used globally by practitioners of macroeconomics (Hodrick & Prescott 1997). Thus, the HP filter was the logical choice for the BCBS to detrend relevant macroeconomic ratio data to produce 'the information required to assess excessive growth in economies' (Van Vuuren 2012).
The HP filter 'has been criticised academically for various limitations and inadequate properties' (Yakhim 2001; Ravn & Uhlig 2002; van Vuuren 2012). Canova (1994, 1998) was a proponent of using the HP filter in estimating business cycles from macroeconomic data where the duration of the trend was between 4 and 6 years, and also had many concerns around the methodology's capability of determining certain key parameter inputs. A series of spurious cycles and distorted estimates of the cyclical component were found by Harvey and Jaeger (1993) when using the HP filter. The authors argued that this property may lead to misleading conclusions specifically pertaining to the relationship between short-term movements in macroeconomic time series data. The measures of persistence, variability and co-movement were found to be changed dramatically when the HP filter was applied to US time series data (King & Rebelo 1993). Economists have continued to use the HP filter to detrend data, which indicate short-term fluctuations when they are superimposed on business cycle-like trends (Ravn & Uhlig 2002).
'The premise on which the HP filter based is that an observable macroeconomic time series (xt) may be decomposed into its long-run, non-stationary secular trend (τt) and a stationary residual, or cyclical, component (Ct)' (Van Vuuren 2012):

Both the long-run trend and the cycle are impossible to observe directly so these elements are defined somewhat arbitrarily in detrending approaches. Equation 2 indicates how the HP filter extracts the cycle through a standard-penalty programme:

where the parameter λ controls the smoothness of the adjusted trend series τt, that is, as λ→ 0, the trend estimates the actual series, xt, while as λ→∞ the trend becomes linear and the procedure converges to a standard least squares solution. The optimisation procedure in Equation 1 maximises the fit to the trend of the series, that is, minimise the cycle component ct by minimising changes in the gradient of the trend τt. Both τt and ct are unobservable and because ct is a stationary process, xt is a noisy signal for the non-stationary trend τt.
In determining the ideal value for λ, Hodrick and Prescott (1980) used an exogenous and subjective value of 1 for quarterly data. However, Backus and Kehoe (1992) performed more research on the topic and found that adjusting λ based upon the square of the frequency of observations relative to quarterly data yields better results. The relative frequency is 3 for monthly data and 0.25 for annual data, so the corresponding λ values are 14 400 and 100, respectively. Further research (e.g. Marcet & Ravn 2003; Ravn & Uhlig 2002) who derived λ through solving Equation 1 as a constrained minimisation problem) confirm 'that the values for λ discussed above are still in common use' (Van Vuuren 2012). du Toit (2008) did a study to determine the optimal value for λ for South African business cycle. The study found that the 'optimal smoothing constant was that value of λ that least distorts the frequency information of the time series' (in this case, λ = 524 for quarterly data used to evaluate a business cycle with a frequency of ~7 years). The HP filter has been used to explore South African business cycles and estimate long-run output levels (see Burger & Marinkov 2006; Fedderke & Schaling 2005; Kaseeram, Nichola & Mainardi 2004; Woglom 2003). Drehmann et al. (2010) found that λ = 1600 and λ = 25 000 performed poorly on historical data while λ = 125 000 and λ = 400 000 performed well with quarterly data. The higher value of λ = 400 000 is 'considered important from a policy perspective as it provides both a greater range and more time when the indicator provides strong and reliable signals' (Van Vuuren 2012).
The solution to Equation 2 has been shown by Danthine and Girardin (1989) to be:

where x = [x1, … xT]′ (i.e. the observed time series), τ = [τ1, …τT]′ I is a T × T identity matrix and K = [kij] is a (T - 2) matrix with elements:
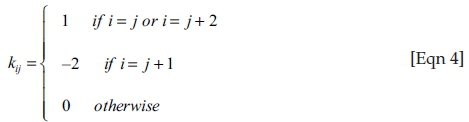

The HP filter works to optimise the fit to the data series, but the effectiveness of the filter is dependent on the application on an infinitely long time series. For practical purposes, though, a moderately long series works just as well (Mise, Kim & Newbold 2005), however 'at the end points the HP filter is demonstrably suboptimal' (Van Vuuren 2012). Kaiser and Maravall (1999) applied AutoregRessive Integrated Moving Average (ARIMA) forecasts and backcasts when investigating the end-point problem and found that this considerably improved the performance of the filter. The two-sided, symmetrical HP filter works through applying large 'symmetrical weights to the end points of the observed values7 to estimate the corresponding trend value (Ley 2006) disproportionately distorting the filtered values at the most recent time period' (Apel, Hansen & Lindberg 1996; Baxter & King 1995; St-Amant & Van Norden 1997; Van Vuuren 2012).
Problems linked to the two-sided filter 'are mitigated by implementing a single-sided filter, a technique which uses the standard two-sided HP filter incrementally when constructing the long-term trend' (Van Vuuren 2012). The long-term trend is estimated by employing only information that is available at the time the calculation was made (Drehmann et al. 2010) and is carried out by running a loop over time and keeping the last value derived from the standard HP-filtered output at each point in time (Mehra 2006). The BCBS's proposed countercyclical buffer ratio employs the cycle and trend data produced by a one-sided HP filter, which may differ vastly from two-sided filtered data. The BCBS could have been clearer in their choice between the one- and two-sided HP filters, as in the main document detailing the implementation of the measure, only a footnote discusses this important distinction. This distinction is important, however, as it was conclusively shown 'to affect the difference between the credit/GDP ratio and its long-run mean (and hence capital charges) significantly' (Van Vuuren 2012). The pricing of CoCo bonds (as a countercyclical capital measure) is explored in the next section.
Equity derivatives approach contingent convertible pricing model
Contingent convertible pricing is closely related to the field of equity derivative pricing and may be divided broadly into three model types, structural models (Albul et al. 2010; Pennacchi 2011), credit derivative models (De Spiegeleer & Scoutens 2011; Serjantov 2011) and equity derivative models (De Spiegeleer & Schoutens 2011). The hybrid instrument nature of CoCos, somewhere between pure equity and pure debt, causes a challenge when choosing a suitable pricing model.
Various ways to price CoCos have been explored. The Black-Scholes model is a suitable method for pricing CoCos, because of the derivative nature of the constructs of the instruments. The Black-Scholes assumptions have, however, been found to be empirically unsound for pricing CoCos as the implied market trigger of a CoCo is time dependent and volatile (Jung 2012).
Structural pricing models view CoCos as being deleveraging tools, focussing on estimating the trigger event. On the other hand, credit derivative models assume that CoCos exhibit inherent credit risk, paying coupons until either maturity or conversion. Lastly, equity derivative models rely on the market share price as a measure of the underlying financial position of the bank and use this as an estimate of the value to be transferred at conversion. There is an overwhelming favour among academic papers for the use of equity derivative models when pricing CoCos, as these models seem to come very close in reflecting the fair value of current CoCos in the market (De Spiegeleer & Schoutens 2011; Wilkens & Bethke 2014). This method has thus been chosen for use in this paper.
Variations of CoCo trigger mechanisms exist, as discussed in the 'Literature study' section. Market triggers (such as the bank's share price) are popular. The way in which a market trigger S* is associated with an accounting trigger is illustrated in Figure 6, assuming an accounting trigger of 7% core tier 1 capital with a corresponding trigger share price of 159.
The nominal amount of CoCos of a bank in issuance is an important factor in estimating the increase in the CET1 capital because of the CoCo conversion. Beginning with the CET1 ratio:

When a CoCo converts into equity, there is an increase in CET1 capital, which increases the bank's CET1 ratio (if RWA remains constant). Consider the change in the CET1 ratio because of the increase in CET1 capital because of the trigger of a CoCo:

where CoCo is the amount of CET1 capital resulting from a CoCo conversion and CET1 is CET1 capital as a percentage of RWA.
For an x% increase in the CET1 ratio, then, the total number of shares issued because of CoCos at conversion must be equal to x% of CET1 capital.
Consider, as an example, a bank that has CET1 Capital of ZAR 100 and total RWA of ZAR 1000. The CET1 ratio is 10% (ZAR 100/ZAR 1000). If the bank has CoCo bonds that convert to ZAR 30 of shares (30% of CET1 capital [ZAR 30/ZAR 100]), this will also result in a relative increase to the CET1 ratio of 30% (from 10% to 13%) as the total CET1 capital will be ZAR 130 after conversion (Capital ratio = ZAR 130/ZAR 1000).
Results and discussion
The Hodrick-Prescott filter applied to South African data
The data chosen 'were nominal GDP (monthly) and the credit extended by all South African monetary institutions to the domestic private sector, since 1965'. These data are 'prescribed by the BCBS' (BCBS 2010b) and were downloaded from the Reserve Bank of South Africa. Growth rates as well as the credit growth/GDP ratio were determined from these data. Data from January 1966 were used to calculate the credit growth/GDP growth ratio and its long-run trend and is illustrated in the first graph of Figure 7. The rules listed in Table 2 and Figure 2 were then applied to the South African credit/GDP data to determine what the capital charges would have been had the new countercyclical rules been in place historically. The results are shown in the final two graphs in Figure 7 for the capital charges using a one-sided HP filter and using the prescribed λ of 14 400. The shaded area in Figure 11 indicates the transition period between an economic expansion and the resultant contraction.
In the instance when Basel III rules come into force, capital charges will 'increase to the 2.5% maximum of extra capital required', and this would have been applicable during the period leading up to and also during the financial crisis. Even without 'the punitive capital charges in place' - the ratio returns to 'levels at which the difference between it and its long-run trend would have resulted in a 0% capital add-on within a few years' (two, in this case). It is unclear whether the reduction in credit extended was a direct result of the lack of capital in the banking sector or the flight to safety. Figure 7 demonstrates that the CCB charge will function well as a countercyclical capital measure in times of economic expansion, but it may be an ineffective measure during a crisis because it does not actively encourage lending during or after a crisis. Furthermore, the CCB does not discourage lending through a capital charge in economic downturns as is shown from 2010 onward. However, the lack of a disincentive does not imply the presence of an incentive, and without an incentive to extend credit, banks may prolong the liquidity shortfall procyclically as demonstrated in the 2007 financial crisis. The results from the HP filter indicate how the CCB will function in times of economic expansion. To establish the effectiveness of CoCos in economic contractions, consider the following section, which explores the possible influence of CoCo conversions on the CET1 equity of South African banks.
Contingent convertible pricing and common equity tier 1 ratio of South African banks
To calculate the CoCo prices for South African banks, the historic share prices, annual market volatility, dividend yield and interest rates are required. Data pertaining to the CET1 ratios of each bank were obtained from their annual financial statements or their annual integrated reports. Johannesburg Interbank Agreement Rates (JIBAR) were obtained from the SARB (SARB 2011b). Historic share prices of the four largest South African banks, as well as the CET1 capital ratios, are given in Figures 8 and 9. To illustrate the effectiveness of a CoCo upon trigger in times of economic contraction, a potential share value trigger for each bank is also illustrated in Figures 8 and 9, derived through the same method as illustrated in Figure 5 by linking the lowest share price during the financial crisis with the CET1 capital ratio at that point. It is worth noting though that although the lowest share price attained would have not have been known at the time, some reasonable constraint could have been applied with equal validity, such as a share price absolute decrease of 50%, for example. Assuming the amount of the CoCo in issuance by each bank is equal to 2% of the RWA of each bank, the resultant conversions of CoCos into CET1 of each bank would cause a 2% increase in the CET1 capital ratio of the respective banks as shown by the projected CET1 capital ratio. The assumption was made that the CoCo conversion to equity is instantaneous for illustrative purposes; however, in practice this may not be plausible, practical or desirable. Similarly, the trend in the projected capital ratio was assumed to remain the same as the underlying capital ratio for the period following the addition to the capital ratio; however, this may not be the case. Table 4 summarises the various trigger levels illustrated in Figures 8 and 9 together with other market-related information used in the equity derivatives approach CoCo pricing model. The interest rate used was the JIBAR as at the trigger event date for each share. A maturity of 5 years was chosen as this is the most common maturity among previously issued CoCos (see Table 3).

Figure 10 provides the yields derived through the equity derivatives CoCo pricing model for the CoCo of each bank if the issuers composed the CoCos according to the input parameters in Table 4.
From Figure 10 it is clear that the CCB requires banks to keep more capital in times of economic expansion. Total credit extended may take considerable time to diminish, however, and if the increase in the CCB is accompanied by a downturn in the economy (as in the 2007 financial crisis), banks may be required to sustain a higher capital ratio while being under pressure to supply the capital in the ordinary course of business. Figure 11 further illustrates the countercyclical capital nature of CoCos: bank's capital ratios would have been increased through the conversion of CoCos at precisely the time when banks needed an increase in capital. This may offer an internal solution to a capital shortage in situations where banks have traditionally sought after external, often sovereign, bailouts. The shaded area in Figure 11 indicates the transition period between an economic expansion and the resultant contraction and shows how the CoCo conversion happens at a point when the economy was in a financial crisis.
Conclusion
The BCBS have clearly understood that the procyclical nature of capital models in global banks have caused an overextension of credit in bull markets as well as a dire requirement for capital in bull markets and 'deliberately structured a gradual phase-in of the Basel III rules for banks' as a result. To avoid running out of capital, the BCBS has increased the amount as well as the quality of capital that banks are required to keep under normal economic conditions with new regulation that include, among other improvements, the CCB. The addition of the CCB to the regulation is an attempt to further increase the required capital of banks in times when the economy is overheating, saving for a rainy day. The CCB remains, however, a purely theoretical exercise as the regulatory implementation of this buffer has not been completed and not a single bank up to date has had to increase their capital under the CCB rules. Furthermore, the clear majority of academic research conducted on the CCB was done on developed economies, although some (Burra et al. 2014; Van Vuuren 2012) indicate that the CCB holds various implications for developing economies, such as South Africa, as well.
A historical analysis on the CCB indicates that the buffer will come into effect in times of economic expansion such as the build-up to the 2007 financial crisis. It does also, however, indicate that once the CCB requirements come into force there is a significant time-lag that must be considered before the requirements are relaxed. History has also shown that markets are self-adjusting and may regulate back to their long-run trend after a period of excessive growth which poses interesting challenges for banks which will be required to keep the additional capital required by the CCB while operating in a market where capital becomes increasingly more expensive and increasing in scarcity.
Contingent convertibles are designed to absorb losses in severe economic conditions. The inherent mechanism which allows for a bank to cease paying the coupon on the bond in economic contractions affords the banks the opportunity to use the additional cash flow to service growing liquidity requirements. Furthermore, in a situation where the conversion trigger mechanism is triggered with the CoCo either suffering a write-down and/or converting into equity, the capital ratio of a bank is immediately boosted. Results from this study indicate that South African banks may have benefited from the increased liquidity and capital boosts if they had CoCos in issuance prior to the 2007 credit crisis.
The CCB thus seems to function as a good countercyclical capital measure in times of economic expansion; however, the absence of the disincentive to increase the capital of a bank in economic contractions does not necessarily imply that the banks will be incentivised to use the extra capital to extend credit into the market, especially as the RWA and PD of the banks will rise under these conditions. The issuance of CoCo bonds, if their trigger mechanisms are designed correctly, may prove helpful to banks and the broader financial sector in times of economic contraction through the countercyclical capital properties that manifest through CoCo bonds under these economic conditions.
In addition to the countercyclical capital nature of CoCos, further studies need to investigate the time-lapse between a CoCo conversion and the resultant increase in the CET1 capital ratio as the mismatch in timing could see the increase in capital coming at a stage when the bank is a gone concern as opposed to a going concern. An investigation into the trigger mechanism which results in a bank only stopping coupon payments (as opposed to converting the CoCo into equity) on CoCos will also prove useful as currently there are no fixed rules regarding trigger mechanisms to be used for such an addition to CoCos.
Acknowledgements
Competing interests
The authors declare that they have no financial or personal relationship(s) that may have inappropriately influenced them in writing this article.
Authors' contributions
F.L. was the principal author and compiler of the overall article. G.v.V. was the principal quantitative analysis and was responsible for model assembly and construction. A.H. was responsible for proofreading and oversight of the article.
References
Albul, B., Jaffee, D.M. & Tchistyi, A., 2010, Contingent convertible bonds and capital structure decisions, University of California at Berkeley, Berkeley. [ Links ]
Apel, M., Hansen, J. & Lindberg, H., 1996, Potential output and output gap, Quarterly Review of the Bank of Sweden, Bank of Sweden, Stockholm. [ Links ]
Atik, J., 2010, 'Basel II: A post-crisis post-mortem', Transnational Law and Contemporary Problems 19(1), 731-759. [ Links ]
Avdjiev, S., Kartasheva, A. & Bogdanova, B., 2013, 'CoCos: A primer', BIS Quarterly Review September, viewed 24 June 2014, from http://www.bis.org/publ/qtrpdf/r_qt1309f.htm [ Links ]
Backus, D.K. & Kehoe, P.J., 1992, 'International evidence on the historical properties of business cycles', American Economic Review 82(4), 864-888. [ Links ]
Baily, M.N., Litan, R.E. & Johnson, M.S., 2008, The origins of the financial crisis, the initiative on business and public policy, Fixing Finance series, Paper 3: November. [ Links ]
Baxter, M. & King, R.G., 1995, Measuring business cycles: Approximate band-pass filters for economic time series, NBER working paper 5022. [ Links ]
BCBS, 2010a, Basel III: A global regulatory framework for more resilient banks and banking systems, Bank for International Settlements, viewed 21 June 2014, from http://www.bis.org/publ/bcbs189_dec2010.pdf [ Links ]
BCBS, 2010b, Guidance for national authorities operating the countercyclical capital buffer, Bank for International Settlements, viewed 23 June 2014, from http://www.bis.org/publ/bcbs187.pdf [ Links ]
BCBS, 2011, Basel III: A global regulatory framework for more resilient banks and banking systems, Bank for International Settlements, viewed 27 March 2016, from http://www.bis.org/publ/bcbs189.pdf [ Links ]
BCBS, 2012, Basel III: Necessary, but not sufficient, Bank for International Settlements, viewed 27 March 2016, from http://www.bis.org/speeches/sp121106.pdf [ Links ]
BCBS, 2015, Regulatory Consistency Assessment Programme (RCAP) Assessment of Basel III risk-based capital regulations - South Africa, Bank for International Settlements, viewed 26 March 2016, from http://www.bis.org/bcbs/publ/d322.pdf [ Links ]
BIS, 2009, Comprehensive response to the global financial crisis, viewed 18 December 2013, from http://www.bis.org/press/p090907.htm [ Links ]
BIS, 2013, Basel III phase-in arrangements, viewed 30 June 2014, from http://www.bis.org/bcbs/basel3/basel3_phase_in_arrangements.pdf [ Links ]
Bloomberg, 2016, Contingent convertibles - High-yield hand grenades, viewed 23 March 2016, from http://www.bloombergview.com/quicktake/contingent-convertible-bonds [ Links ]
Burger, P. & Marinkov, M., 2006, 'The South African phillips curve: How applicable is the Gordon Model?', South African Journal of Economics 74(2), 172-189. https://doi.org/10.1111/j.1813-6982.2006.00062.x [ Links ]
Burra, P., de Jongh, P.J., Raubenheimer, R., Van Vuuren, G.H. & Wiid, H., 2014, 'Implementing the countercyclical capital buffer in South Africa: Practical considerations', South African Journal of Economic and Management Sciences 18(1), 105-127. https://doi.org/10.17159/2222-3436/2015/v18n1a8 [ Links ]
Calomiris, C. & Herring, R., 2012, 'Why and how to design a contingent convertible debt requirement', Journal of Applied Corporate Finance 25(2), 39-62. [ Links ]
Canova, F., 1994, 'Detrending and turning points', European Economic Review 38(3-4), 614-623. https://doi.org/10.1016/0014-2921(94)90097-3 [ Links ]
Canova, F., 1998, 'Detrending the business cycle', Journal of Monetary Economics 41, 475-512. https://doi.org/10.1016/S0304-3932(98)00006-3 [ Links ]
Catarineu-Rabell, E., Jackson, P. & Tsomocos, D.P., 2003, 'Procyclicality and the new Basel Accord-banks' choice of loan rating system', Economic Theory 26(3), 537-557. [ Links ]
Chen, N., Glasserman, P., Nouri, B. & Pelger, M., 2013, CoCos, bail‐in, and tail risk, Office of Financial Research Working Paper #0004, January 23, viewed 23 February 2015, from http://www.treasury.gov/initiatives/ofr/research/Documents/OFRwp0004_ ChenGlassermanNouriPelger_CocosBailInandTailRisk.pdf [ Links ]
Cogley, T. & Nason, J.M., 1995, 'Effects of the Hodrick-Prescott filter on trend and difference stationarytime series: Implications for business cycle research', Journal of Economic Dynamics and Control 19, 253-278. [ Links ]
Culp, C., 2009, 'Contingent capital vs contingent reverse convertibles for banks and insurance companies', Journal of Applied Corporate Finance 21(4), 17-27. https://doi.org/10.1111/j.1745-6622.2009.00247.x [ Links ]
Danthine, J.P. & Girardin, M., 1989, 'Business cycles in Switzerland: A comparative study', European Economic Review 33(1), 31-50. https://doi.org/10.1016/0014-2921(89)90035-4 [ Links ]
De Haas, R. & van Horen, N., 2012, International shock transmission after the Lehman Brothers collapse - Evidence from syndicated lending, Working paper 42, European Bank for Reconstruction and Development. [ Links ]
De Spiegeleer, J. & Schoutens, W., 2011, Pricing contingent convertibles: A derivatives approach, SSRN paper no. 1795092, viewed 28 June 2015, from https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1795092 [ Links ]
De Vries, D. & Brehm, M., 2011, Coco issuance confirmed, Technical report, Bank of America Merrill Lynch. [ Links ]
Drehmann, M., Claudio, B., Gambacorta, L., Jimenez, G. & Trucharte, C., 2010, Countercyclical capital buffers: Exploring options, viewed 12 February 2011, from http://www.bis.org/publ/work317.pdf [ Links ]
Du Toit, L., 2008, Optimal HP filtering for South Africa, Bureau for Economic Research, Department of Economics, Stellenbosch University. [ Links ]
Fedderke, J.W. & Schaling, E., 2005, 'Modelling inflation in South Africa: A multivariate cointegration analysis', South African Journal of Economics 73(1), 79-92. https://doi.org/10.1111/j.1813-6982.2005.00006.x [ Links ]
Financial Service Authority, 2009, The Turner review: A regulatory response to the global banking crisis, Financial Service Authority report. [ Links ]
Flannery, M.J., 2005, 'No pain, no gain? Effecting market discipline via "reverse convertible debentures"', in H.S. Scott (ed.), Capital adequacy beyond Basel: Banking, securities, and insurance, pp. 171-196, Oxford University Press, Oxford. [ Links ]
G20, 2009, G20 Leaders Statement: The Pittsburgh Summit, viewed 01 November 2014, from http://digitalcommons.ryerson.ca/dissertations/1657 [ Links ]
Gauteng Provincial Treasury, 2012, Business cycles and their impact on the South African Economy, Quarterly Bulletin - October to December 2012. [ Links ]
Goodhart, C. & Taylor, A., 2006, 'Procyclicality and volatility in the financial system - The implementation of Basel II and IAS39', in S. Gerlach & P. Gruenwald (eds.), Procyclicality of financial systems in Asia, pp. 230-251, Palgrave Macmillan. [ Links ]
Harvey, A.C. & Jaeger, A., 1993, 'Detrending, stylized facts and the business cycle', Journal of Applied Econometrics 8, 231-247. https://doi.org/10.1002/jae.3950080302 [ Links ]
Heid, F., 2003, Is regulatory capital pro-cyclical? A macroeconomic assessment of Basel II, Deutsche Bundesbank working paper. [ Links ]
Hodrick, R.J. & Prescott, E.C., 1980, Post war US business cycles: An empirical investigation, Carnegie Mellon University. [ Links ]
Hodrick, R.J. & Prescott, E.C., 1997, 'Postwar US business cycles: An empirical investigation', Journal of Money, Credit and Banking 29(1), 1-16. https://doi.org/10.2307/2953682 [ Links ]
Huang, H., 2009, Convertible bonds: Default risk and uncertain volatility, Bonn Economic Discussion Papers bgse09_2010, University of Bonn, Germany, viewed 24 June 2014, from http://ideas.repec.org/p/bon/bonedp/bgse09_2010.html [ Links ]
Huertas, T.F., 2009, 'Too big to fail, too complex to contemplate: What to do about systemically important firms', paper presented at the Financial Markets Group, London School of Economics, 15 September. [ Links ]
Jung, H., 2012, 'Pricing of contingent convertibles', Wharton Research Scholars Journal, Scholarly Commons, University of Pennsylvania, viewed 26 June 2014, from http://repository.upenn.edu/wharton_research_scholars/90/ [ Links ]
Kaiser, R. & Maravall, A., 1999, 'Estimation of the business cycle: A modified Hodrick-Prescott filter', Spanish Economic Review 1(2), 175-206. https://doi.org/10.1007/s101080050008 [ Links ]
Kaseeram, I., Nichola, T. & Mainardi, S., 2004, 'South African inflation dynamics and the pass-through effect from depreciation to unit labour costs', South African Journal of Economics 72(1), 85-107. [ Links ]
King, R.G. & Rebelo, S.T., 1993, 'Low frequency filtering and real business cycles', Journal of Economic Dynamics and Control 17(1-2), 207-231. https://doi.org/10.1016/S0165-1889(06)80010-2 [ Links ]
Ley, E., 2006, Knowledge brief for bank staff, The Hodrick-Prescott filter, viewed 12 February 2011, from http://homepage.mac.com/eduley/hp.pdf [ Links ]
Marcet, A. & Ravn, M.O., 2003, CEPR Discussion Papers, viewed 12 February 2011, from http://www.econ.upf.edu/docs/papers/downloads/588.pdf [ Links ]
Maredza, A. & Ikhide, S., 2013, The Impact of the global financial crisis on efficiency and productivity of the banking system in South Africa, Working paper no. 328, Economic Research Southern Africa. [ Links ]
McDonald, R.L., 2011, Contingent capital with a dual price trigger, Manuscript, Northwestern University. [ Links ]
Mehra, Y.P., 2006, The output gap: Expected future inflation and inflation dynamics: Another look, Federal Bank of Richmond, Richmond, VA. [ Links ]
Merrouche, O. & Nier, F., 2010, What caused the global financial crisis? - Evidence on the drivers of financial imbalances 1999-2007, IMF working paper, WP/10/265. [ Links ]
Mise, E., Kim, T.H. & Newbold, P., 2005, 'On suboptimality of the Hodrick-Prescott filter at time series endpoints', Journal of Macroeconomics 27(1), 53-67. https://doi.org/10.1016/j.jmacro.2003.09.003 [ Links ]
National Treasury, 2011, A safer financial sector to serve South Africa better, National Treasury Policy Document, viewed 12 March 2015, from www.treasury.gov.za. [ Links ]
Nikolov, P.T., 2010, 'Procyclical effects of the banking system during the financial and economic crisis 2007-2009', Finance and Investments, viewed 26 March 2016, from http://hdl.handle.net/2105/22738 [ Links ]
Peicuti, C., 2013, 'Securitization and the subprime mortgage crisis', Journal of Post-Keynesian Economics 35(3), 443-455. https://doi.org/10.2753/PKE0160-3477350306 [ Links ]
Pennacchi, G., 2011, A structural model of contingent bank capital, Manuscript, University of Illinois. [ Links ]
Pennacchi, G., Vermaelen, T. & Wolff, C., 2011, Contingent capital: The case for COERCs, LSF Research Working Paper Series 10-08, Luxembourg School of Finance, University of Luxembourg, Luxembourg. [ Links ]
Plosser, C.I., 2010, 'Convertible securities and bankruptcy reforms: Addressing too big to fail and reducing the fragility of the financial system', paper presented at the Conference on the Squam Lake Report, New York, 16 June. [ Links ]
Prescott, E.S., 2012, 'Contingent capital: The trigger problem', Economic Quarterly 1(4), 33-50. [ Links ]
PWC, 2015, 'Stability amid uncertainty South Africa - Major banks analysis', viewed 12 March 2016, from http://www.pwc.co.za/en_ZA/za/assets/pdf/major-bank-analysis-september-2014.pdf [ Links ]
Ravn, M.O. & Uhlig, H., 2002, 'On adjusting the Hodrick-Prescott filter for the frequency of observations', The Review of Economics and Statistics 84(2), 371-375. https://doi.org/10.1162/003465302317411604 [ Links ]
Repullo, R. & Saurina, J., 2011, The countercyclical capital buffer of Basel III a critical assessment, CEMFI and CEPR working paper. [ Links ]
Repullo, R. & Suarez, J., 2008, The procyclical effects of Basel II, CEPR Discussion Papers #6862, CEPR. [ Links ]
SARB, 2011a, Annual economic report 2011, 90th Anniversary, viewed 23 June 2014, from http://www.reservebank.co.za/PublicationsandNotices/Reports [ Links ]
SARB, 2011b, Financial stability review September 2011, South African Reserve Bank, Pretoria, South Africa. [ Links ]
Saurina, J. & Trucharte, C., 2007, An assessment of Basel II procyclicality in mortgage portfolios, Documentos de Trajabo Banco de Espana #0712. [ Links ]
Serjantov, A., 2011, 'On practical pricing hybrid capital securities', in Presentation, Global Derivatives Trading and Risk Management, viewed 08 March 2015, from http://www.institutional-money.com/fileadmin/user_upload/Bilder_Grafiken_News/PDF_News/152-162_IM_2_2014_CoCos_XXXkg_.pdf [ Links ]
Sorkin, R., 2010, 'Answers on credit ratings long overdue', New York Times, viewed 10 February 2014, from http://www.nytimes.com/2010/06/01/business/01sorkin.html?src=busln [ Links ]
St-Amant, P. & van Norden, S., 1997, Measurement of the output gap: A discussion of recent research at the Bank of Canada, Technical Report of the Bank of Canada. [ Links ]
Sundaresan, S. & Wang, Z., 2011, On the design of contingent capital with market trigger, Federal Reserve Bank of New York Staff Report, no 448. [ Links ]
US Financial Crisis Inquiry Commission, 2010, Financial crisis inquiry report: Final report of the national commission on the causes of the financial and economic crisis in the United States, US Public Affairs, New York. [ Links ]
Van Vuuren, G., 2012, 'Basel III countercyclical capital rules: Implications for South Africa', South African Journal of Economic and Management Sciences 15(3), 309-323. [ Links ]
Wilkens, S. & Bethke, N., 2014, 'Contingent convertible ("CoCo") bonds: A first empirical assessment of selected pricing models', Financial Analysts Journal 70(2), 59-77. [ Links ]
Woglom, G., 2003, 'How has inflation targeting affected monetary policy in South Africa?', South African Journal of Economics 71(2), 380-406. https://doi.org/10.1111/j.1813-6982.2003.tb01314.x [ Links ]
Yakhim, Y., 2001, Business cycle fluctuations and the Hodrick-Prescott Filter, viewed 12 February 2011, from http://www.bgu.ac.il/~yossiya/teaching/macro_graduate/LN1_bc_hpf.pdf [ Links ]
 Correspondence:
Correspondence:
Gary van Vuuren
vvgary@hotmail.com
Received: 18 May 2016
Accepted: 13 Jan. 2017
Published: 15 June 2017
1. The capital ratio of a bank is obtained via the quotient of the Common Equity Tier 1 (CET1 capital and the bank's total RWAs. The CET1 capital ratio diminishes when the denominator (RWA) rises, largely because of a rise in the default probability of outstanding loans (a deterministic of the RWA).
2. These bonds can potentially also suffer a partial of full write-down on the par value.
3. Asset prices were 'also considered to be useful aggregate indicators as they tend to rise strongly ahead of systemic banking crises, but these were eventually abandoned'.
4. Although the conversion of debt to equity raises the book value of equity, it fails to raise new cash for the bank like a new issuance of equity would (Prescott 2012).
5. The results explore the need for CoCo triggers to be set at a level that activates when the bank is a going concern with proposals for the African market.
6 . Specifically, CoCo ISIN XS0459089255.
7. That is, the '2-sided HP filter uses past and future data to estimate the components of Equation 1, so cycle data generated using it could be biased'.














