Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Economic and Management Sciences
versão On-line ISSN 2222-3436
versão impressa ISSN 1015-8812
S. Afr. j. econ. manag. sci. vol.20 no.1 Pretoria 2017
http://dx.doi.org/10.4102/sajems.v20i1.1472
ORIGINAL RESEARCH
Unintended possible consequences of fuel input taxes for individual investments in greenhouse gas mitigation technologies and the resulting emissions
Heinz Eckart Klingelhöfer
Department of Managerial Accounting and Finance, Tshwane University of Technology, South Africa
ABSTRACT
BACKGROUND: South Africa is planning to introduce a carbon tax as a Pigouvian measure for the reduction of greenhouse gas emissions, one of the tax bases designed as a fuel input tax. In this form, it is supposed to incentivise users to reduce and/or substitute fossil fuels, leading to a reduction of CO2 emissions.
AIM: This article examines how such a carbon tax regime may affect the individual willingness to invest in greenhouse gas mitigation technologies.
SETTING: Mathematical derivation, using methods of linear programming, duality theory and sensitivity analysis.
METHODS: By employing a two-step evaluation approach, it allows to identify the factors determining the maximum price an individual investor would pay for such an investment, given the conditions of imperfect markets.
RESULTS: This price ceiling depends on the (corrected) net present values of the payments and on the interdependencies arising from changes in the optimal investment and production programmes. Although the well-established results of environmental economics usually can be confirmed for a single investment, increasing carbon taxes may entail sometimes contradictory and unexpected consequences for individual investments in greenhouse gas mitigation technologies and the resulting emissions. Under certain circumstances, they may discourage such investments and, when still undertaken, even lead to higher emissions. However, these results can be interpreted in an economically comprehensible manner.
CONCLUSION: Under the usually given conditions of imperfect markets, the impact of a carbon tax regime on individual investment decisions to mitigate greenhouse gas emissions is not as straight forward as under the usually assumed, but unrealistically simplifying perfect market conditions. To avoid undesired and discouraging effects, policy makers cannot make solitary decisions, but have to take interdependencies on the addressee´s side into account. The individual investor´s price ceiling for such an investment in imperfect markets can be interpreted as a sum of (partially corrected) net present values, which themselves are a generalisation of the net present values known from perfect markets.
Introduction
Being one of the world's most carbon-intensive economies, 'ranked among the top 20 countries measured by absolute carbon dioxide (CO2) emissions' (National Treasury 2010:16, 2013:19), and based on prior research examining different options and scenarios (Scenario Building Team 2007; Tyler & Cloete 2015; Vorster, Winkler & Jooste 2011; Winkler 2007; Winkler & Marquard 2011), South Africa is on the way to introduce a carbon tax as a Pigouvian measure for the reduction of greenhouse gas (GHG) emissions from 2017. Three tax bases were discussed (National Treasury 2010:30-34, 2013:46-47):
• The actually measured GHG emissions: This allows for targeting pollution at the responsible source and would encourage investments e.g. in end-of-pipe technologies, but is quite complex in practice since it is difficult to measure and monitor the big variety of emissions sources. Thus, it leads to high administrative costs.
• Two proxy bases:
ο upstream, as a fuel input tax, charging all the fossil fuels entering the economy, and
ο downstream, as an energy output tax, levied at the emitters.
Because there are natural scientific relations between the amount of fuel input and the emissions of CO2, usually leading to comparable results to those of taxing the emissions directly, South Africa opted for the introduction of a fuel input tax (National Treasury 2013:47). And in fact, research proves that this may be a viable solution for South Africa (Alton et al. 2014; Devarajan et al. 2011; Van Heerden et al. 2006). Thus, also the newly drafted carbon tax bill (Republic of South Africa 2015) considers this discussion proposing that, from 2017, taxes to reduce GHG emissions shall be levied with respect to
• the combustion of fossil fuels;
• fugitive emissions in respect of commodities, fuel or technology (i.e. the GHGs emitted when extracting, processing and delivering fossil fuels); and
• industrial processes and product use.
Starting at R120 per ton (t) CO2 equivalent, a variety of tax-free thresholds and offsets as well as allowances will let the effective tax result between R6 and R48 per t CO2 equivalent, and revenue recycling shall neutralise the revenue from a macroeconomic perspective (National Treasury 2015; Republic of South Africa 2015:14-18). While previous proposals additionally planned to increase the tax at a rate of 10% per annum from the initially planned introduction in 2015 until 31 December 2019 (National Treasury 2013:15, 58), this is no longer stated in the newly drafted current tax bill.
In this context, this article examines the degree to which carbon taxes in form of a fuel input tax are actually able to provide incentives for 'individual' investments in GHG mitigation technologies, that is, the perspective is not on the whole economy, but on an individual investor. Following the rationale laid down by Pigou (1932:172, 174, 183, 224), economic literature agrees that taxes may be instrumental for environmental policy. Setting a price for emissions makes them economically relevant: comparing the resulting emissions costs to the abatement cost, producers may decide to avoid pollution. Because of the above-mentioned natural scientific relations between the amount of fuel input and the emissions of CO2, this is supposed to be true as well for a carbon tax designed as a fuel input tax. Hence, it is thought that because of carbon taxes, investments in emissions reduction technologies may become economically significant as well.
As CO2 emissions result from combustion processes, a financial assessment of such an investment will have to derive the required payments and constraints from production planning, with special regard to carbon taxes and joint production (Klingelhöfer 2010:373). This allows for developing a valuation model and for investigating the factors determining the individual investor´s maximum payable for a GHG mitigation technology (i.e. his individual price ceiling). Activity level-dependent and activity level-independent payments are taken into account - as well as the investment´s indivisibility and uncertainty, which may result from changes in politics and in ecological awareness.
Employing duality theory of linear programming allows for transferring and adjusting known results from perfect markets to the usually given situation on imperfect markets. In particular, it can be shown that the reaction of the (individual) price ceiling on changes of its determinants - that is, on imperfect markets: the (corrected) net present values of the payments and of the interdependencies due to changes in the optimal programme - is neither as predictable nor as straightforward as under the often assumed, but normally not realistic conditions of a perfect market. Hence, as the effects of different tax rates are a usual object not only of academic discussions and, therefore, also earlier versions of the planned South African carbon tax regime provided for increases, employing sensitivity analysis helps to gain further information about the complex, sometimes even unexpected and undesired reactions of the maximum payable price and the GHG emissions on such changes. Nevertheless, an economically comprehensible interpretation is possible. For better understanding, an example demonstrates these effects. Finally, the main results are summarised.
Financial valuation of investments in greenhouse gas mitigation technologies
Background: Financial evaluation on imperfect markets under uncertainty
Several studies have examined the consequences of environmental policy on investments in environmental protection technologies (Alton et al. 2014; Arguedas & van Soest 2010; Blanco & Rodrigues 2008; Buchner 2007; Chakraborty et al. 2004; Hart 2008; Hyder 2008; Knutsson, Werner & Ahlgren 2006; Laurikka 2006; Laurikka & Koljonen 2006; McGilligan, Sunikka-Blankb & Natarajan 2010; Reinaud 2003; Scenario Building Team 2007; Sekar et al. 2007; Tyler & Cloete 2015; Vorster et al. 2011; Winkler 2007; Winkler & Marquard 2011; Yang & Blyth 2007; Zhao 2003; for an overview of different environmental tax schemes in the European Union and other countries cf. Cansino et al. 2010; Markandya et al. 2009; National Treasury 2010:43-49, 2013:36-39). While some of these refer to a single sector or to the whole economy, others take an enterprise point of view and employ different techniques for project appraisal such as cost-based approaches, discounted cash flow (DCF) models, which calculate the present value of an investment by discounting future cash flows at an appropriate discount rate, or real options analyses and simulations.
However, the conditions of 'perfect markets' underlying these models are often not appropriate for individual investment decisions. This may already result from restricted and differing borrowing and lending conditions, and manufacturing companies may have other opportunities than the financial market - for example, investing in other technologies or increasing/reducing production. Then, calculating 'ordinary' (net) present values by discounting expected cash flows with exogenous interest rates (even if adjusted to uncertainty) and real options values become inadequate for the financial valuation of technology investments. This becomes even more significant as other requirements for the application of real option pricing models usually are not fulfilled by the characteristics of GHG mitigating investments either.1
Consequently, to examine the effects of any environmental policy on a company´s decision whether to invest in emissions reduction or not, it needs to be considered that every activity may interfere with other decisions. For instance, limited capital budgets may restrict the realisation of investment opportunities or the purchase of raw materials and, consequently, production (but also the GHG emissions). In the same way, production constraints and capped emissions may reduce revenues resulting from the sales of the desired products, hence, impact other investment or financing decisions (including investments into environmental protection). On the other hand, capped emissions and less fuel input will also reduce the amount of taxes to be paid. Therefore, 'a theoretically correct financial valuation' of an investment into GHG mitigation technology needs to take into account these constraints and interdependencies. In particular, because both the emissions as well as the carbon taxes on the fuel input are determined by (joint) production, it will consider the links established by production planning. In other words, such a financial valuation cannot be adequately done under the simplifying conditions of perfect markets, but necessarily needs to account for the much more complex ones of 'imperfect markets'.
In the consequence, instead of calculating the investment´s value solely by discounting cash flows with a single market interest rate, a theoretically correct (partial) appraisal demands the endogenous marginal rates of return of the best alternatives. Also, a mere calculation of the net present value of an additional object does not say much regarding its profitability, because such a net present value does not account for capacity shortages resulting from the realisation of this additional object, which, subsequently, may also alter the decision relevance of other objects or capacities (i.e. the binding restrictions of the company´s investment and production planning programme may change; Klingelhöfer 2010:374). Consequently, assessing the degree of profitability of an additional single investment or activity within imperfect markets means a comparison of the situation after investing [i.e. the 'valuation programme' (VP)] to the one before investing [i.e. the 'basic programme' (BP)] (Hering 2006:57-59; Jaensch 1966:664-665; Klingelhöfer 2006:59-91; Matschke 1975:253-257, 387-390). By doing so, a sensible approach implicitly considers (differently from neoclassical approaches) that such a technology investment is usually indivisible - it is either undertaken entirely or not at all. In case of a greater maximum value in the VP than in the BP, investing becomes reasonable. Ensuring this by means of a minimum withdrawal constraint, the VP computes the price ceiling, that is, the highest possible price p the company could afford for investing in emissions reduction.
'Uncertainty', as it results from either reiterative changes of environmental policy, shifts in ecological awareness or altered conditions on liberalised waste markets, etc., may be taken into account by using decision trees (Magee 1964a, 1964b; Mao 1969; and in the context of investment planning Klingelhöfer 2006:59-83; Laux 1971:19-22, 39-44). Starting with s = 0 for the already realised and, therefore, known state in t = 0, the set S = {0; 1; …; S} also includes the S possible future states s until the time horizon t = T. Although presenting itself graphically in a (two-dimensional) tree structure, this set may still be easily treated as a one-dimensional mathematical structure by consecutively numbering the states from s = 0 to s = S. Hence, mathematically, the valuation under uncertainty does not differ from the one under certainty (where each point in time t would be represented by exactly one state s). However, in the economical interpretation, this means that all payments in all possible states are considered. Nevertheless, because of the given mathematical structure, the decision maker does not need to know probabilities, means or variances, so that the restrictive assumptions of the Bernoulli principle together with its axioms are no longer needed. Instead, the decision maker only depends on information on which states may occur with positive probability, as simple dominance considerations are sufficient.
Payments determined by production planning
Taking the environment into account, every production is characterised as joint production: According to linear activity analysis of production (Debreu 1959:37-49; Klingelhöfer 2000:222-252, 417-442; Koopmans 1957:71-83, 1959; Nikaido 1968:180-185), employing the production process β once (e.g. for an hour), the so-called 'basic activity' B,β will transform m different kinds of inputs rμ (as fuel, labour, perhaps recycled waste) into n different kinds of desired and undesired outputs xν (like products, electric power, heat, emissions and waste). Hence, each basic activity can be expressed by a vector of m input and n output commodities φε2:
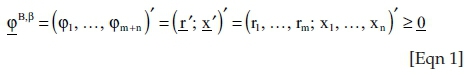
Then, 'every possible production' of a technology set T is a linear combination of the q basic activities with non-negative coefficients, the activity levels λβ:
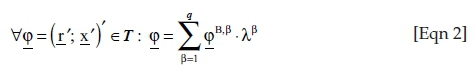
The Γ 'production and environmental constraints' can usually be converted into the following form (Klingelhöfer 2000:310-416):
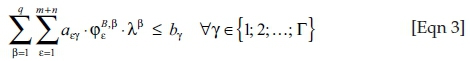
Then, the link to a financial valuation of production is established by the introduction of a 'price system' (Klingelhöfer 2009:371): assigning positive prices pε to the targeted results of production like the input of waste3 and the output of products, prices equal to zero for neutral inputs and outputs (e.g. air and water in certain cases; CO2 emissions, which were neither taxed nor regulated in any other way would fall under this category as well) and negative prices for the input of (traditional) production factors (primary commodities such as material, labour or fuel) and the output of waste and emissions delivers the 'contribution margin' CM:
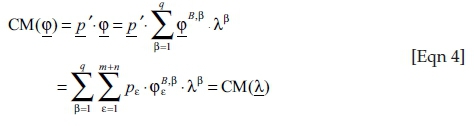
This contribution margin CM is process specific, because not only single, but all the ingoing and outgoing commodities of the production process are valued together; it grows proportionally with the level of production. Taxes τε ≥ 0 on CO2 emissions or fuel inputs φε lead to a slight modification:
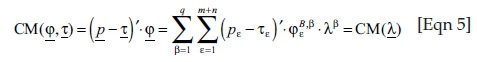
Then, an 'investment I in emissions reduction' changes [without loss of generality (w.l.o.g.)] the input/output vector 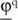 of process q to
of process q to 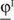 - with the amount of those components
- with the amount of those components 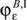 that are standing for the charged fuel inputs and the carbon emissions hopefully reduced compared to the very same ones
that are standing for the charged fuel inputs and the carbon emissions hopefully reduced compared to the very same ones 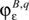 in the original process q. Therefore, for the 'contribution margin' CM of the new production, including process I instead of process q, we obtain instead of (Eqn 5):
in the original process q. Therefore, for the 'contribution margin' CM of the new production, including process I instead of process q, we obtain instead of (Eqn 5):
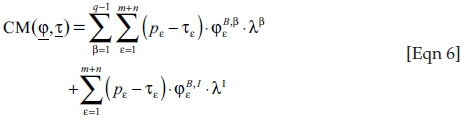
For reason of generality, it should be pointed out that such a linear formulation of the production background does not restrict the model's applicability. Although especially in an environmental context one often finds nonlinear relationships, they can normally be approximated by piecewise linear functions. This is true for both the objective function and the constraint system. Nevertheless, because the derived equations and inequalities (including the contribution margin) will only be part of the constraint system, but not of the objective function of the following linear programming approach, the approximation would be even easier. In addition, it should be taken into account that (variable) tax rates usually do not tend to change continuously with the quantity of the charged substances φε, but in intervals. This is especially true for the South African design of a carbon tax: until the threshold the tax is τe = 0, above τe = R120/t CO2 equivalent. Hence, like in most cases, for South Africa a linear formulation is even more appropriate than a nonlinear one.
Model for the financial valuation of investments into greenhouse gas mitigation technologies
As mentioned above, an investment appraisal on imperfect markets under uncertainty can be done by comparing the situation after investing (i.e. the VP) to the one before investing (i.e. the BP). An operationalisation of the maximum value to be calculated by the BP may be the maximisation of the sum SWW of weighted withdrawals ws · Ws subject to the constraints of investment and production - with s ∈ {0; 1; 2; …; S} denoting the S + 1 states from today (s = 0 in t = 0) to time horizon t = T and the weights ws expressing to which degree the decision maker prefers payments in the regarded states relative to payments in the other states.4 Considering that GHG mitigation technologies are supposed to clean production, the contribution margins (including the carbon taxes) and limitations of production need to be integrated in the constraint system (Klingelhöfer 2010:376):
• the production constraints (Eqn 3) directly like any other restriction,
• the contribution margins CM (Eqn 5) affecting the company's liquidity, which must allow for covering all the payments:
■ + resulting from production and the carbon tax regime,
■ + zjs from other investment or finance projects invj (as credits or shares),
■+ uzs, which are independent from production quantities and the investment programme (e.g. additional individual deposits, fixed rents, payments determined in the past),
and the withdrawals Ws to avoid insolvency.
Hence, the BP results as a linear programming problem:
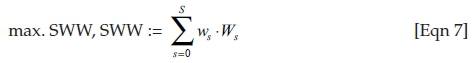
subject to:
Liquidity/capital budget constraints for the S + 1 states s (cp. Eqn 5]):
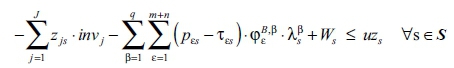
Γs production and environmental constraints γ for the S + 1 states s (cp. [Eqn 3]):
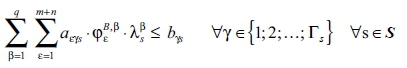
q activity level constraints for the S + 1 states s:
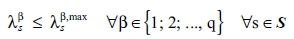
Maximum realisation of J other investment or finance projects:
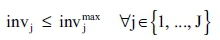
Non-negativity conditions:
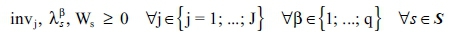
Its optimal solution SWWopt serves as a benchmark for the profitability of an investment I in GHG mitigation technologies for process q (w.l.o.g.). This means that the VP has to ensure that - after realising the investment - the investor receives at least the same sum of weighted withdrawals again (minimum withdrawal constraint). Then, surplus money allows either for consumption or could be used to pay for the investment (its price pI). Hence, the VP calculates the highest price the decision maker could afford for realising the investment, that is, its 'price ceiling' 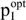 . Besides this different objective function VAL and the minimum withdrawal constraint, the VP resembles structurally the BP. However, it also includes all the activity level-dependent and activity level-independent payments caused by this investment. Therefore, with respect to the liquidity, the replacement of the contribution margins (Eqn 5) by (Eqn 6), as well as the price pI of the investment and other activity level-independent payments zIs (e.g. for its installation) have to be considered.
. Besides this different objective function VAL and the minimum withdrawal constraint, the VP resembles structurally the BP. However, it also includes all the activity level-dependent and activity level-independent payments caused by this investment. Therefore, with respect to the liquidity, the replacement of the contribution margins (Eqn 5) by (Eqn 6), as well as the price pI of the investment and other activity level-independent payments zIs (e.g. for its installation) have to be considered.
Then, the VP results as follows:

subject to:
Liquidity/capital budget constraints for the S + 1 states s (cp. [Eqn 6]):
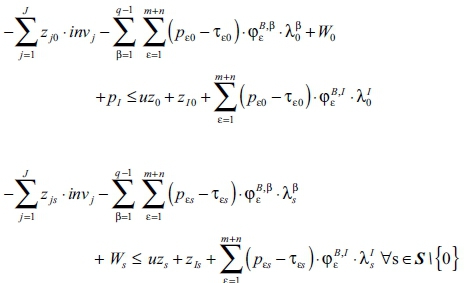
Γs production and environmental constraints γ for the S + 1 states s (cp. [Eqn 3]):
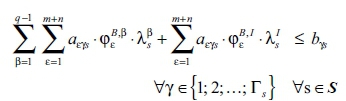
Minimum withdrawal constraint (ensuring that the sum of weighted withdrawals after investing is at least as high as the maximum SWWopt before):
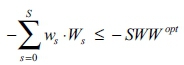
q activity level constraints (including the cleaned one) for the S + 1 states s:
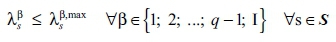
Maximum realisation of J other investment or finance projects:
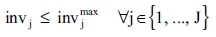
Non-negativity conditions:
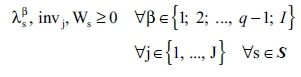
pI∈ IR
While the variables pI for the investment's price and 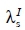 for the activity levels on which the cleaned process I is employed (instead of
for the activity levels on which the cleaned process I is employed (instead of 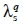 ) differ from the BP, the remaining decision variables are the same: the activity levels
) differ from the BP, the remaining decision variables are the same: the activity levels 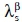 of the q − 1 unchanged processes, the quantities invj of the other investment and finance projects and the withdrawals Ws. The contribution margins (Eqn 5) respectively (Eqn 6) modify the liquidity constraints of the two programmes, while the restrictions (Eqn 3) are part of the constraint systems.
of the q − 1 unchanged processes, the quantities invj of the other investment and finance projects and the withdrawals Ws. The contribution margins (Eqn 5) respectively (Eqn 6) modify the liquidity constraints of the two programmes, while the restrictions (Eqn 3) are part of the constraint systems.
Values, increasing taxes and consequences for the willingness to invest in greenhouse gas mitigation technologies and for emissions reduction
(Corrected) Net present values and the maximum payable price for the investment
If both the BP and the VP have an optimal solution that is finite and positive, applying duality theory of linear programming allows for obtaining information about the determinants of the maximum payable price. In order to do so, the optimal solution to the dual problem of either programme has to be inserted into the equal optimal one to the corresponding primal problem. Using complementary slackness conditions leads to an economic interpretation of the mathematical formula:
By the introduction of the dual variables:
• ls for the liquidity constraints (and the resulting endogenous discount factors ρs,0 = ls/l0 to discount payments in state s to state 0),
• πγs for the production and environmental constraints,
•
and
for the activity level constraints and
• ξj for the maximum realisation of the other investment and finance projects,
and dividing the dual constraints of the decision variables by l0, we obtain the '(corrected) net present values' NPVcorr of (cp. for this and the following analogously Klingelhöfer 2009:375 f.)5:
• using the q processes β ∈ {1, 2, …, q} respectively β ∈ {1, 2, …, q − 1, I} in the states s:
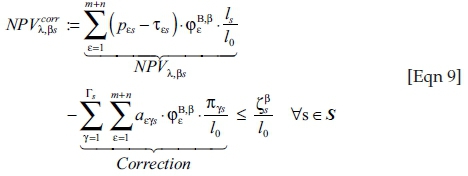
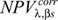 := discounted contribution margin (including carbon tax)
:= discounted contribution margin (including carbon tax)
- discounted monetary equivalent of the required capacity of the production and environmental constraints
• realisation of the other investment and finance projects j:
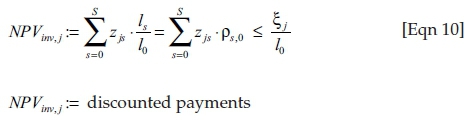
Employing them allows for identifying the determinants of the price ceiling for an investment in GHG mitigation technologies. If, to both the primal and the dual problem, solutions exist that are positive and finite, then, according to duality theory of linear programming, both problems have the same optimal solution. Hence, we can gain information concerning the price ceiling 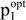 from the optimal solution to the VP's dual problem. Furthermore, via the withdrawal constraint in the VP, this optimal solution also considers the impact resulting from the one (SWWopt) of the BP. Ergo, if the BP also has an optimal solution, the equal one to its dual can substitute SWWopt in the minimum withdrawal constraint of the VP. Consequently, using the optimal solutions to both the dual problems, the equation of the maximum payable price
from the optimal solution to the VP's dual problem. Furthermore, via the withdrawal constraint in the VP, this optimal solution also considers the impact resulting from the one (SWWopt) of the BP. Ergo, if the BP also has an optimal solution, the equal one to its dual can substitute SWWopt in the minimum withdrawal constraint of the VP. Consequently, using the optimal solutions to both the dual problems, the equation of the maximum payable price 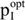 contains a variety of corresponding dual variables of both programmes.
contains a variety of corresponding dual variables of both programmes.
Nevertheless, an economic interpretation is possible by resorting to the (corrected) net present values (Eqn 9) and (Eqn 10). For positive primal variables 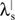 and
and 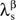 of the activity levels or invj for the maximum realisation of the other investment and finance projects, the 'complementary slackness' conditions force the corresponding inequality (Eqn 9)-(Eqn 10) to be satisfied as an equation. Thus, all the 'positive' dual variables
of the activity levels or invj for the maximum realisation of the other investment and finance projects, the 'complementary slackness' conditions force the corresponding inequality (Eqn 9)-(Eqn 10) to be satisfied as an equation. Thus, all the 'positive' dual variables 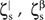 and ξj of the valuation (VP) and the BP can be substituted by the corresponding (corrected) net present values NPVcorr.6 Introducing the dual variable δ of the withdrawal constraint leads to an equation for the 'maximum price'
and ξj of the valuation (VP) and the BP can be substituted by the corresponding (corrected) net present values NPVcorr.6 Introducing the dual variable δ of the withdrawal constraint leads to an equation for the 'maximum price' 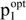 'an investor can afford for GHG mitigation technologies' as a sum of several (partly corrected) net present values7:
'an investor can afford for GHG mitigation technologies' as a sum of several (partly corrected) net present values7:

•
= NPV of all activity level-independent payments zI,s of investing in GHG mitigation technologies (e.g. for its installation, but besides
) (a)
• + NPVcorr of operating the cleaned process I at its maximum activity levels
, when it is profitable (b)
• + NPV of the changes between VP and BP regarding the valuation of the payments uzs, which are independent from production quantities and the investment programme (c)
• + NPV of the changes between VP and BP regarding the monetary equivalents of the production and environmental constraints (d)
• + NPVcorr of the changes between VP and BP by operating the other profitable production processes β at their maximum activity levels
, (e)
• + NPV of the changes between VP and BP regarding the
realised other investment and finance projects (f)
This price ceiling 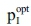 for investing in GHG mitigating technologies is determined by the (corrected) NPVs of its payments and of the interdependencies resulting from adjusting the optimal investment programme. Under uncertainty, the 'discounted payments of all states' are included - even if, in fact, they may not occur.
for investing in GHG mitigating technologies is determined by the (corrected) NPVs of its payments and of the interdependencies resulting from adjusting the optimal investment programme. Under uncertainty, the 'discounted payments of all states' are included - even if, in fact, they may not occur.
At first sight, the economic interpretation (Eqn 11) of the price ceiling resembles the known one from perfect markets. Especially, the (partly corrected) net present values NPVcorr, which were derived from the dual constraints of the two primal problems, represent the equivalent to the 'ordinary' NPVs on perfect markets. However, on imperfect markets, they are 'not' calculated with capital market interest rates, but with the correct 'endogenous' interest rates of their respective optimisation problem BP or VP (expressing the individually different opportunity cost of capital), and they are corrected for the use of the restricted capacities in their programme (i.e. capital budgets, production, environment). Thus, one can see that the maximum payable price for investing into GHG mitigation technologies is calculated in a much more complicated way than on perfect markets, but, in the end, may be expressed in a similar way. However, containing the corrections for the use of restricted capacities and, thus, taking into account the interdependencies occurring from: (1) the imperfect market conditions and (2) the changes between the situations before and after realising the investment, it gives already an indication that overcompensations between the various determinants may be possible. And in fact, this is the reason, that under the conditions of imperfect markets, one can get to much more complex, even unexpected and undesired, reactions of the maximum payable price on changes, for example, in the tax regime than the straightforward ones on perfect markets. The next section is going to examine them closer.
Increasing carbon taxes and consequences for the willingness to invest in greenhouse gas mitigation technologies and for emissions reduction
As discussed in the introduction of this article, the new carbon tax in South Africa shall start at R120 per ton (t) CO2 equivalent, and even though no longer part of the current version, previous versions proposed an increase at a rate of 10% per annum until 31 December 2019. To examine the possible effects of such a development on the willingness to invest in GHG mitigation technologies, a closer look at (Eqn 11) is helpful: The economic interpretation of the terms (b) and (e) of (Eqn 11) in connection with (Eqn 9) demonstrates that 'carbon taxes' affect the 'maximum payable price' for investing in GHG mitigation via the corrected net present values of the processes. Therefore, it is easy to verify that equation (Eqn 11) usually confirms long-term knowledge in environmental economics for a single investment, because an individual investor would consider to pay and is able to pay as much into environmental protection as he can save via reducing emissions (in this case, via reducing fuel inputs that are taxed because they lead most probably to CO2 emissions). However, sensitivity analysis of the left-hand side coefficients of both the BP and the VP demonstrates that - under the relevant conditions of imperfect markets (according to the background section of this article, investments into environmental protection technologies imply that they are given) - rising carbon taxes may be 'counterproductive for GHG mitigation investments'. The maximum payable price 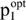 may increase, decline or remain constant if taxes change (cp. for this and the following Klingelhöfer 2010:379 f.). Mathematically, there are three reasons for this:
may increase, decline or remain constant if taxes change (cp. for this and the following Klingelhöfer 2010:379 f.). Mathematically, there are three reasons for this:
• Taxes are coefficients for a decision variable, which is a basis or non-basis variable. This may differ between the BP and the VP.
• The optimal solution of the VP considers the one of the BP via the minimum withdrawal constraint.
• In both programmes, negative (corrected) NPVs cannot be part of the optimal solution.
This allows for (over)compensation of the effects of changing taxes between the two programmes. For instance, in the beginning rising taxes may affect especially the cleaner processes less than the chosen ones in the BP. This, indeed, encourages investing in GHG mitigation technologies. Yet, with continuously rising carbon taxes, some of the processes chosen in the BP may lose their profitability faster than those in the VP. However, when the (corrected) NPV of a process or any other object becomes negative, it ceases being part of the optimal solution and, therefore, stops diminishing SWWopt. Consequently, the optimal solution of the dual VP may decline - and, with it, 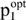 as well. In particular, this may be the outcome when, as a result of rising taxes, production is stopped in the situation without emissions reduction and, therefore, no longer affected by rising carbon taxes (with the consequence that CO2 emissions are reduced to zero), while it is still profitable when using GHG mitigation technologies. Thus, in the VP there would still be production to cover fixed costs and, consequently, there would be still 'GHG emissions', while 'profitability' would be more and more affected by higher taxes.
as well. In particular, this may be the outcome when, as a result of rising taxes, production is stopped in the situation without emissions reduction and, therefore, no longer affected by rising carbon taxes (with the consequence that CO2 emissions are reduced to zero), while it is still profitable when using GHG mitigation technologies. Thus, in the VP there would still be production to cover fixed costs and, consequently, there would be still 'GHG emissions', while 'profitability' would be more and more affected by higher taxes.
Accordingly, as long as these cleaner processes using GHG mitigation technologies are not completely GHG emissions free (as it may be the case for some renewable energies), which would mean that they remain unaffected from tax changes, higher carbon taxes may sometimes even have 'paradoxical effects': (1) the investment in GHG mitigation ceases to be profitable, (2) the marginal incentive for investing becomes negative and (3) emissions increase.
The following example may help to understand this result. To focus on the main outcomes as stated above and to allow for easier reproduction of the calculations, it is kept as simple as possible and will abstract from thresholds and offsets, which are supposed to be implemented in the South African carbon tax regime. The reader may also consider that some of the other assumptions of the example are not very realistic. However, one can still derive similar results on the basis of different quantities, more time periods and a big set of future states to consider uncertainty, other preferences for the withdrawals and additional borrowing and lending opportunities.
Example
Effects of increasing carbon taxes on the willingness to invest in greenhouse gas mitigation technologies and the resulting emissions
Currently, a producer can dispose of two production processes, described by their basic activities 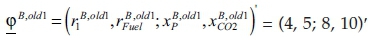 and
and 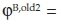
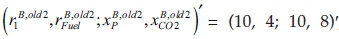 to produce a product P as a desired output. Taking into account an initial amount of cash uz0 = 150 [ZAR] in t = 0, the producer wants to employ these two processes in a way that will guarantee him or her the highest possible withdrawals in t = 1. Credits may not be available, but the producer can invest any surpluses at the capital market at the lending rate iL = 50% (investment object invL). Hence, the producer is operating on an imperfect market, and certainty shall be assumed. The market prices of the two inputs (resource 1 and fuel), the product P and the CO2 emissions may be given by the vector p = (pr1; pFuel; pP; pCO2)′ = (−12; −6; 30; 0)′. Therefore, driving the processes at the activity level λold = 1 allows for realising the following contribution margins CM:
to produce a product P as a desired output. Taking into account an initial amount of cash uz0 = 150 [ZAR] in t = 0, the producer wants to employ these two processes in a way that will guarantee him or her the highest possible withdrawals in t = 1. Credits may not be available, but the producer can invest any surpluses at the capital market at the lending rate iL = 50% (investment object invL). Hence, the producer is operating on an imperfect market, and certainty shall be assumed. The market prices of the two inputs (resource 1 and fuel), the product P and the CO2 emissions may be given by the vector p = (pr1; pFuel; pP; pCO2)′ = (−12; −6; 30; 0)′. Therefore, driving the processes at the activity level λold = 1 allows for realising the following contribution margins CM:
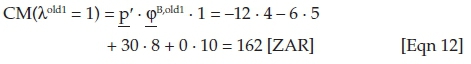
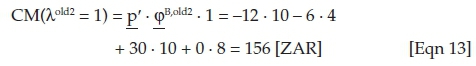
Now, the government wants to reduce CO2 emissions. Because it seems that fuel and CO2 emissions are in a proportional relationship, the idea is levying τFuel on the input of fuel. Therefore, the producer considers an investment in a GHG mitigation technology. This will modify the vector 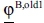 of the first basic activity to the new one
of the first basic activity to the new one 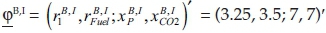 of inputs and outputs. This means that reducing the quantities needed of input 1 by 0.75 [QU] (quantity units) and of fuel by 1.5 [QU] not only leads to 1 product less but also decreases the CO2 emissions by 3 [t] (thus, with still the same relationship between fuel and CO2 emissions, government´s underlying assumption for a carbon tax regime using fossil fuel input taxes holds). Consequently, producing at the activity level λI = 1 after having invested, the producer receives the contribution margin:
of inputs and outputs. This means that reducing the quantities needed of input 1 by 0.75 [QU] (quantity units) and of fuel by 1.5 [QU] not only leads to 1 product less but also decreases the CO2 emissions by 3 [t] (thus, with still the same relationship between fuel and CO2 emissions, government´s underlying assumption for a carbon tax regime using fossil fuel input taxes holds). Consequently, producing at the activity level λI = 1 after having invested, the producer receives the contribution margin:

All the processes, irrespective of whether these are cleaned by a GHG mitigation technology, can be driven up to the same highest activity levels at λold1,max = λold2,max = λI,max = 10. However, installing the new technology and changing production in t = 0 requires a once-off payment of zI,0 = −150 [ZAR]. Then, even without further knowledge of linear programming techniques, the 'maximum sum of weighted withdrawals' of the basic programme can be calculated by compounding with the lending rate iL = 50% - for example, if there are no carbon taxes levied, that is, if τFuel = τFuel,0 = τFuel,1 = 0 [ZAR/QU]8:
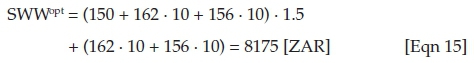
To realise these withdrawals in t = 1, the investor needs to use the processes at their (maximum) activity levels 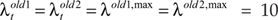 in t = 0 and in t = 1. Furthermore, in order to make both the currently (in t = 0) unneeded initial amount of cash as well as the surplus from production available in t = 1, he invests into the capital market opportunity. Hence, because invL yields at iL = 50% and available money in t = 1 can be withdrawn directly, the shadow prices of the liquidity constraints result with
in t = 0 and in t = 1. Furthermore, in order to make both the currently (in t = 0) unneeded initial amount of cash as well as the surplus from production available in t = 1, he invests into the capital market opportunity. Hence, because invL yields at iL = 50% and available money in t = 1 can be withdrawn directly, the shadow prices of the liquidity constraints result with 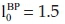 and
and 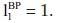 .
.
For this initial situation, it is obvious that investing into GHG mitigation is not sensible: not only the contribution margins of the cleaned process are 12 [ZAR] smaller than before (150 [ZAR] now in comparison to the 162 [ZAR] of old1 in the BP) but also the initial amount of cash (plus the earned interest on it) is foregone for installing the GHG mitigation technology and the change in production. Therefore, the investment's price ceiling 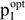 is negative, that is, only if someone else pays for it, the investor will invest in emissions reduction. Solving the VP confirms this result:
is negative, that is, only if someone else pays for it, the investor will invest in emissions reduction. Solving the VP confirms this result: 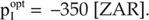 It can be proven by Eqn 11.
It can be proven by Eqn 11.
With δ = 2/3 (the BP maximises withdrawals in t = 1, while 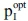 would be paid in t = 0),
would be paid in t = 0), 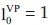 (more funds available in t = 0 allow for higher payments to realise the investment) and
(more funds available in t = 0 allow for higher payments to realise the investment) and 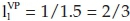 (in t = 0, the investor does not need to provide as much for the future and, therefore, is allowed to reduce investing at the capital market at the lending rate iL = 50% if more money is already available in t = 1), we obtain from (Eqn 11) as long as the emissions of CO2 are not subject to taxes, that is (because the carbon tax regime is designed as a fuel input tax), for τFuel = τFuel,0 = τFuel,1 = 0 [ZAR/QU]9:
(in t = 0, the investor does not need to provide as much for the future and, therefore, is allowed to reduce investing at the capital market at the lending rate iL = 50% if more money is already available in t = 1), we obtain from (Eqn 11) as long as the emissions of CO2 are not subject to taxes, that is (because the carbon tax regime is designed as a fuel input tax), for τFuel = τFuel,0 = τFuel,1 = 0 [ZAR/QU]9:
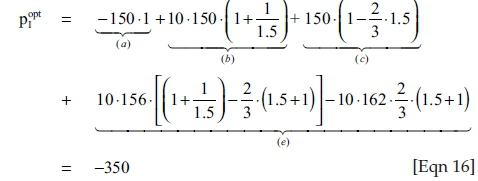
This requires full production with λI,max = λold2,max = 10 at both points in time again, and the surplus of production of 3060 [ZAR] in t = 0 needs to be invested together with the 'subvention' 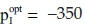 [ZAR] for doing the investment at the interest rate iL = 50%. Only then the investor receives the same sum of weighted withdrawals SWWopt = 8175 [ZAR] as in the BP. However, rising carbon taxes changes this solution: according to (Eqn 9), they will diminish the corrected net present values of the production in the terms (b) and (e) of equation (Eqn 11) - although (e) faster than (b) because of more emissions. Hence, rising fuel input taxes τFuel = τFuel,0 = τFuel,1 impacts the optimal solutions SWWopt of the BP and
[ZAR] for doing the investment at the interest rate iL = 50%. Only then the investor receives the same sum of weighted withdrawals SWWopt = 8175 [ZAR] as in the BP. However, rising carbon taxes changes this solution: according to (Eqn 9), they will diminish the corrected net present values of the production in the terms (b) and (e) of equation (Eqn 11) - although (e) faster than (b) because of more emissions. Hence, rising fuel input taxes τFuel = τFuel,0 = τFuel,1 impacts the optimal solutions SWWopt of the BP and 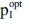 of the VP as presented in Figure 110:
of the VP as presented in Figure 110:
As may be expected, rising taxes τFuel affect (via the scientific relationship to emissions) the price ceiling for emissions reduction, although in some cases differently than politically desired. The introduction of fuel taxes diminishes the contribution margins of production in both the BP and the VP. However, as the new process I needs less fuel than the former old1, its contribution margin is less affected by rising taxes, so that 'GHG mitigation becomes increasingly more interesting', reaching break-even at τFuel = 14 [ZAR/QU] already. Now, even under economic considerations alone, it makes sense to pay for it. Indeed, because of a growing advantage with higher taxes, the investor is able to afford even higher prices for GHG mitigation, while still realising at least the same sum of weighted withdrawals as without cleaning production.
However, for taxes τFuel > 32.4 [ZAR/QU], production with the uncleaned process old1 loses its profitability in the BP and, therefore, is stopped. Only old2 continues contributing to SWWopt. On the other hand, the investor would still employ both processes (old2 and I) in the VP. Thus, while process old2 is used in both programmes equally, rising taxes τFuel lead to melting contribution margins of process I (without equivalent in the BP) - the 'maximum payable price' 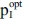 for investing in GHG mitigation technologies must 'begin to decline'.
for investing in GHG mitigation technologies must 'begin to decline'.
For τFuel > 39 [ZAR/QU], also old2 loses its profitability, and the sum of weighted withdrawals SWWopt remains constant (just uz0 = 150 [ZAR/QU] can yield interest at iL = 50%). Thus, because only the contribution margins of process I are diminished by increasing tax rates τFuel, while the withdrawals in the situation without investing into GHG mitigation remain constant, the 'price ceiling' 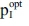 for investing into the new technology 'continues to fall'.
for investing into the new technology 'continues to fall'.
For τFuel > 40 2/7 [ZAR/QU], investing into emissions reduction even ceases to have an economic advantage: though, in the beginning, it still makes sense to employ process I because its contribution margins remain positive, they are no longer sufficient to cover the payments zI,0 = −150 [ZAR] for installing the new technology and adjusting production in t = 0 entirely. If finally τFuel > 42 6/7 [ZAR/QU], even the contribution margins of the cleaned process become negative. Hence, there will not be any production in the VP either. This means that, in comparison to the alternative of not investing, the investor 'will have lost the installing and adjustment payments zI,0 = −150 [ZAR] overall'.
Nonetheless, though it has just been shown that increasing carbon taxes may even discourage individual investments in emissions reduction, one may be of the opinion that mitigation of climate change is such an important target that one should not always look at the related cost. However, as much as this argument may be true, 'it cannot be supported for "blind" tax increases': While being true in the beginning, starting at τFuel = 32.4 [ZAR/QU], investing in cleaner technologies leads to even 'more undesired emissions' (cf. light shading in Figure 1), and for 40 2/7 [ZAR/QU] < τFuel < 42 6/7 [ZAR/QU], it 'is disadvantageous in both dimensions: economically as well as regarding GHG mitigation' (cf. dark shading in Figure 1), that is, although an investment into GHG mitigation is realised, the overall GHG emissions rise.11 If one, furthermore, considers that the information furnished by Figure 1 refers 'only' to the individual price ceiling for the investment in emissions reduction technologies, while the investor will usually have to pay more than just 0 [ZAR/QU] - meaning that in most cases he would only invest when his individual price ceiling is much greater than 0 because only then he is able to afford the demanded price (the difference between both measures the investment's profitability for the individual investor)12 - this dark-shaded area displaying the investment's disadvantage in both dimensions (economically as well as environmentally) will be even greater.
Conclusion
From 2017 carbon taxes should be introduced in South Africa. To allow industry for adjustment, it offers a variety of tax-free thresholds and offsets as well as allowances and will start at R120 per ton (t) CO2 equivalent. In order to examine the theoretical consequences of such a tax regime for the 'individual' willingness to invest in GHG mitigation, this article has offered a two-step evaluation approach, taking imperfect market conditions and uncertainty into account. Because emissions result as a by-product from joint production, carbon taxes modify the contribution margins, and the reduction of emissions affects production as well. Thus, the usually applied approaches for investment appraisal, which implicitly require that the conditions of perfect markets are fulfilled, cannot be employed to determine the individual profitability of such investments. Instead, one has to use more generalised approaches that are also applicable under imperfect market conditions and which also consider the interdependencies between production, investments and environmental protection. Furthermore, the model presented in this article takes into account that some payments may depend on the activity level of production, while others do not, and (in difference to neoclassical approaches) that a technology investment is usually indivisible (either it will be undertaken entirely or not).
Employing duality theory of linear programming, the known results from perfect markets can be transferred. In particular, the determinants of the investor's individual price ceiling for investing into GHG mitigation can be identified. On imperfect markets, this maximum price, which an individual investor is able to afford, may be interpreted as a sum of (sometimes corrected) net present values. Although dealing with uncertainty, the investor does not need information on probabilities, means or variances.
Applying sensitivity analysis enables us to demonstrate that increasing taxes does not always encourage individual investments into GHG mitigation. Because on imperfect markets the use of restricted capacities may lead to interdependencies, (over-)compensation effects between the various determinants of the maximum payable price for such an investment may be possible. Therefore, changes in the tax regime may lead to much more complex, even unexpected and undesired reactions of this price ceiling than the straightforward ones that an investor would usually consider on perfect markets. In particular cases, when cleaner processes using GHG mitigation technologies are not completely GHG emissions free (as it may be the case for some renewable energies), rising carbon taxes may even lead to 'paradoxical effects': (1) an investment in emissions reduction ceases to be profitable, (2) the marginal incentive for such an investment becomes negative and (3) GHG emissions increase.
Acknowledgements
The author received funding from the South Africa´s National Research Foundation as a rated researcher.
Competing interests
The author declares that he has no financial or personal relationships that may have inappropriately influenced him in writing this article.
References
Alton, T., Arndt, C., Davies, R., Hartley, F., Makrelov, K., Thurlow, J., Ubogu, D., 2014, 'Introducing carbon taxes in South Africa', Applied Energy 116, 344-354. https://doi.org/10.1016/j.apenergy.2013.11.034 [ Links ]
Arguedas, C. & van Soest, D.P., 2010, 'On reducing the windfall profits in environmental subsidy programs', Journal of Environmental Economics and Management 58, 192-205. https://doi.org/10.1016/j.jeem.2009.04.002 [ Links ]
Blanco, M.I. & Rodrigues, G., 2008, 'Can the future EU ETS support wind energy investments?', Energy Policy 36, 1509-1520. https://doi.org/10.1016/j.enpol.2007.12.025 [ Links ]
Buchner, B., 2007, Policy uncertainty, investment and commitment periods, IEA Information Article, Paris. [ Links ]
Cansino, J.M., del P. Pablo-Romero, M., Román, R. & Yñiguez, R., 2010, 'Tax incentives to promote green electricity: An overview of EU-27 countries', Energy Policy 38, 6000-6008. https://doi.org/10.1016/j.enpol.2010.05.055 [ Links ]
Chakraborty, A., Malcolm, A., Colberg, R.D. & Linninger, A.A., 2004, 'Optimal waste reduction and investment planning under uncertainty', Computers and Chemical Engineering 28, 1145-1156. https://doi.org/10.1016/j.compchemeng.2003.09.023 [ Links ]
Debreu, G., 1959, Theory of value, Yale University Press, New Haven, CT. [ Links ]
Devarajan, S., Go, D.S., Robinson, S. & Thierfelder, K., 2011, 'Tax policy to reduce carbon emissions in a distorted economy: Illustrations from a South Africa CGE model', The B.E. Journal of Economic Analysis & Policy 11(1), 1-22. https://doi.org/10.2202/1935-1682.2376 [ Links ]
Hart, R., 2008, 'The timing of taxes on CO2 emissions when technological change is endogenous', Journal of Environmental Economics and Management 55, 194-212. https://doi.org/10.1016/j.jeem.2007.06.004 [ Links ]
Hering, T., 2006, Unternehmensbewertung, 2nd edn., Oldenbourg, München. [ Links ]
Hyder, P., 2008, 'Recycling revenue from an international carbon tax to fund an integrated investment programme in sustainable energy and poverty reduction', Global Environmental Change 18, 521-538. https://doi.org/10.1016/j.gloenvcha.2008.04.001 [ Links ]
Jaensch, G., 1966, Wert und Preis der ganzen Unternehmung, Westdeutscher Verlag, Köln. [ Links ]
Klingelhöfer, H.E., 2000, Betriebliche Entsorgung und Produktion, Gabler, Wiesbaden. [ Links ]
Klingelhöfer, H.E., 2006, Finanzwirtschaftliche Bewertung von Umweltschutzinvestitionen, Deutscher Universitäts-Verlag, Wiesbaden. [ Links ]
Klingelhöfer, H.E., 2009, 'Investments in EOP-technologies and emissions trading - Results from a linear programming approach and sensitivity analysis', European Journal of Operational Research (EJOR) 196(1), 370-383. https://doi.org/10.1016/j.ejor.2008.03.016 [ Links ]
Klingelhöfer, H.E., 2010, 'Investments in environmental protection technologies and the paradox of environmental taxes and subsidies', in N. Delener et al. (eds.), Generating innovative solutions to recurring problems in the global business environment: A multi-, inter-, and trans disciplinary approach to formulating and maintaining a competitive organizational edge, Global Business and Technology Association, Twelfth Annual International Conference, Readings Book, Kruger National Park Vicinity, South Africa, July 5-9, pp. 373-384. [ Links ]
Klingelhöfer, H.E., 2016, 'Carbon taxes in South Africa: Unintended consequences for investments in greenhouse gas mitigation technologies and the resulting emissions', Africagrowth Agenda 13(3), 10-14. [ Links ]
Knutsson, D., Werner, S. & Ahlgren, E.O., 2006, 'Combined heat and power in the Swedish district heating sector: Impact of green certificates and CO2 trading on new investments', Energy Policy 34, 3942-3952. https://doi.org/10.1016/j.enpol.2005.09.015 [ Links ]
Koopmans, T.C., 1957, 'Allocation of resources and the price system', in T.C. Koopmans (ed.), Three essays on the state of economic science, pp. 1-126, McGraw-Hill, New York. [ Links ]
Koopmans, T.C., 1959, 'Analysis of production as an efficient combination of activities', in T.C. Koopmans (ed.), Activity analysis of production and allocation, pp. 33-97, Wiley, New Haven. [ Links ]
Laurikka, H., 2006, 'Option value of gasification technology within an emissions trading scheme', Energy Policy 34, 3916-3928. https://doi.org/10.1016/j.enpol.2005.09.002 [ Links ]
Laurikka, H. & Koljonen, T., 2006, 'Emissions trading and investment decisions in the power sector: A case study in Finland', Energy Policy 34, 1063-1074. https://doi.org/10.1016/j.enpol.2004.09.004 [ Links ]
Laux, H., 1971, Flexible Investitionsplanung, Westdeutscher Verlag, Opladen. [ Links ]
Magee, J.F., 1964a, 'How to use decision trees in capital investment', Harvard Business Review 42, 79-96. [ Links ]
Magee, J.F., 1964b, 'Decision trees for decision making', Harvard Business Review 42, 126-138. [ Links ]
Mao, J.C.T., 1969, Quantitative analysis of financial decisions, Macmillan, New York. [ Links ]
Markandya, A., Arigoni Ortiz, R., Mudgal, S. & Tinetti, B., 2009, 'Analysis of tax incentives for energy-efficient durables in the EU', Energy Policy 37, 5662-5674. https://doi.org/10.1016/j.enpol.2009.08.031 [ Links ]
Matschke, M.J., 1975, Der Entscheidungswert der Unternehmung, Gabler, Wiesbaden. [ Links ]
McGilligan, C., Sunikka-Blank, M. & Natarajan, S., 2010, 'Subsidy as an agent to enhance the effectiveness of the energy performance certificate', Energy Policy 38, 1272-1287. https://doi.org/10.1016/j.enpol.2009.10.068 [ Links ]
National Treasury, 2010, Reducing greenhouse gas emissions: The carbon tax option, Discussion Article for Public Comment, National Treasury, Pretoria. [ Links ]
National Treasury, 2013, Carbon Tax Policy Article. Reducing greenhouse gas emissions and facilitating the transition to a green economy, Policy Article for Public Comment, National Treasury, Pretoria. [ Links ]
National Treasury, 2015, Media statement. Publication of the draft carbon tax bill for public comment, National Treasury, Pretoria. [ Links ]
Nikaido, H., 1968, Convex structures and economic theory, Academic Press, New York. [ Links ]
Pigou, A.C., 1932, The economics of welfare, 4th edn., Macmillan, London. [ Links ]
Reinaud, J., 2003, Emissions trading and its possible impacts on investment decisions in the power sector, IEA Information Article, Paris. [ Links ]
Republic of South Africa, 2015, Draft Carbon Tax Bill, viewed 20 March 2016, from http://www.treasury.gov.za/public%20comments/CarbonTaxBill2015/Carbon%20Tax%20Bill%20final%20for%20release%20for%20comment.pdf [ Links ]
Scenario Building Team, 2007, Long term mitigation scenarios: Scenario document, Department of Environment Affairs and Tourism, Pretoria. [ Links ]
Sekar, R.C., Parsons, J.E., Herzog, H.J. & Jacoby, H.D., 2007, 'Future carbon regulations and current investments in alternative coal-fired power plant technologies', Energy Policy 35, 1064-1074. https://doi.org/10.1016/j.enpol.2006.01.020 [ Links ]
Tyler, E. & Cloete, B., 2015, 'Combining price and quantity instruments: Insights from South Africa', Climate Policy 15(3), 374-387. https://doi.org/10.1080/14693062.2014.937382 [ Links ]
Van Heerden, J., Gerlagh, R., Blignaut, J., Horridge, M., Hess, S., Mabugu, R., Mabugu, M., 2006, 'Searching for triple dividends in South Africa: Fighting CO2 pollution and poverty while promoting growth', The Energy Journal 27(2), 113-141. https://doi.org/10.5547/issn0195-6574-ej-vol27-no2-7 [ Links ]
Vorster, S., Winkler, H. & Jooste, M., 2011, 'Mitigating climate change through carbon pricing: An emerging policy debate in South Africa', Climate and Development 3(3), 242-258. https://doi.org/10.1080/17565529.2011.598367 [ Links ]
Winkler, H. (ed.), 2007, Long term mitigation scenarios: Technical report (with Hughes, A., Haw, M., Marquard, A., Merven, B., Taviv, R., Scholes, B., van der Merwe, M., Collet, G., Kornelius, G., Pauw, K., Midgley, G., & Mukheibir, P.), prepared by the Energy Research Centre for Department of Environment Affairs and Tourism, Pretoria, October. [ Links ]
Winkler, H. & Marquard, A., 2011, 'Analysis of the economic implications of a carbon tax', Journal of Energy in Southern Africa 22(1), 55-68. [ Links ]
Yang, M. & Blyth, W., 2007, Modeling investment risks and uncertainties with real options approach, Working Article, International Energy Agency, Paris. [ Links ]
Zhao, J., 2003, 'Irreversible abatement investment under cost uncertainties: Tradable emission permits and emissions charges', Journal of Public Economics 87, 2765-2789. https://doi.org/10.1016/S0047-2727(02)00135-4 [ Links ]
 Correspondence:
Correspondence:
Heinz Eckart Klingelhöfer
klingelhoeferhe@tut.ac.za
Received: 07 Sept. 2015
Accepted: 28 Nov. 2016
Published: 27 Mar. 2017
1 However, in case their underlying assumptions are fulfilled, certain discrete option pricing models result as specifications of the presented model (Klingelhöfer 2006:76-77).
2 Underlining a variable denotes a vector and the prime (the symbol ´) the transposition of a vector.
3 The objective of production may not only be to produce wanted products but also to destroy substances that may be recognised as unwanted by the economy. Thus, it may be beneficial and desired to use waste as an input, and the producer may even be paid for doing so (e.g. by municipal service providers).
4 These weights need not sum up to 1. They are just a measure for individual preference and not necessarily expressing probabilities. Thus, although similar at first sight, SWW is normally 'not' an expected value.
5 All the following (corrected) net present values NPV are able to be derived from both the basic programme (Eqn 7) and the valuation programme (Eqn 8). However, the dual variables, and consequently the endogenous discount factors ρs,0 = ls/l0, which allow for discounting payments in state s to state 0, are usually 'not' the same. In particular, if a finite positive solution pI > 0 of both the primal and dual valuation programme is existing, it can be deduced from the complementary slackness condition pI · (1 − l0) = 0 that l0 = 1 and, therefore, ρs,0 = ls for all the (corrected) NPVs derived from the valuation programme.
6 Compare footnote .
7 The dual variable δ of the withdrawal constraint calculates the value of a marginal increase in SWW referring to the objective function of the valuation programme, that is, by how many ZAR the maximum payable price for the investment will change if the maximum sum of weighted withdrawals in the situation without realising the investment changes by ZAR 1.
8 Employing the simplex algorithm needs 7 iterations to deliver the optimal solution SWWopt and the values for 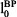 and
and 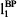 . Eqn 15 can be proven true by some simple considerations: because lending is unrestricted, invL must be the marginal investment opportunity. Therefore, compounding the contribution margins from production as well as the initial cash amount uz0 = 150 [ZAR] with invL provides SWW.
. Eqn 15 can be proven true by some simple considerations: because lending is unrestricted, invL must be the marginal investment opportunity. Therefore, compounding the contribution margins from production as well as the initial cash amount uz0 = 150 [ZAR] with invL provides SWW.
9 The values for 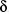 ,
, 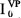 and
and 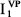 are part of the optimal solution of the valuation programme that results after seven dual simplex iterations. However, they can be proven by the given considerations in parentheses. Because the lending opportunity is not limited and no additional constraint restricts production, the corrected net present values of the processes are equal to the discounted contribution margins, and the terms (d) and (f) of (Eqn 11) do not exist.
are part of the optimal solution of the valuation programme that results after seven dual simplex iterations. However, they can be proven by the given considerations in parentheses. Because the lending opportunity is not limited and no additional constraint restricts production, the corrected net present values of the processes are equal to the discounted contribution margins, and the terms (d) and (f) of (Eqn 11) do not exist.
10 In the following it is assumed that the taxes and their changes always refer to both points in time.
11 Although the investment into GHG mitigation does not make sense economically at this tax level, the investor needs to run production on maximum activity level in both points in time to use the still positive contribution margins to cover at least some parts of the activity level-independent payments zI,0 = −150 [ZAR] for the installation of the new technology. This means that in the situation after realising the investment, there are emissions because of necessarily higher production (in comparison to the situation without investment into GHG mitigation) although, in total, the combination of investing and production is economically disadvantageous.
12 In perfect markets, a positive net present value NPV of an investment can be interpreted as the investor's profit in t = 0 when he simultaneously realises the investment and finances it to the conditions of the opportunity (which will normally be an equal borrowing and lending rate on financial markets, because a prerequisite of perfect markets is that this opportunity is unlimitedly available). Therefore, one can interpret the similar difference between the actual price to be paid and the price ceiling (calculated according to the individual investor's objectives and his decision field) on imperfect markets as an equivalent to the investment´s NPV in perfect markets - as a measure for the individual investor´s profit resulting from realising the investment under the conditions of an imperfect market, taking into consideration his individual objectives and decision field.














