Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Economic and Management Sciences
On-line version ISSN 2222-3436
Print version ISSN 1015-8812
S. Afr. j. econ. manag. sci. vol.19 n.3 Pretoria 2016
http://dx.doi.org/10.17159/2222-3436/2016/v19n3a5
ARTICLES
Pricing contingent convertible bonds in African banks
Francois Liebenberg; Gary van Vuuren; Andre Heymans
Department of Economics, North-West University
ABSTRACT
In times of financial distress, banks struggle to source additional capital from reluctant private investors. Sovereign bailouts prevent disruptive insolvencies, but distort bank incentives. Contingent convertible capital instruments (CoCos) - securities which possess a loss-absorbing mechanism in situations where the capital of the issuing bank reaches a level lower than a predefined level - offer a potential solution. Although gaining in popularity in developed economies, CoCo issuance in Africa is still in its infancy, possibly due to pricing complexity and ambiguity about conversion triggers. In this paper, the pricing of these instruments is investigated and the influence of local conditions (using data from three major African markets and an all-African index) on CoCo prices is explored. We find that the African milieu (high interest rates and equity volatility compared with the situation in developed markets) makes CoCos particularly attractive instruments for the simultaneous reduction of debt and the enhancement of capital. If CoCo issuance becomes a viable bank recapitalisation tool in Africa, these details will be valuable to future investors and issuers.
Key words: contingent capital, pricing, core equity, capital ratio
JEL: C134, 16, 53
1 Introduction
The financial crisis that caused large-scale disruption in global financial markets in late 2007 had its origins in the asset-price bubble (particularly the American house-price bubble), which contained new types of financial instruments that masked risk (Baily, Litan & Johnson, 2008). The perception in the broader economic markets was that these innovations were matched in complexity by risk-mitigation tools, techniques, policies and models (G20, 2009). History has, however, proven that this was not the case. In response to the financial crisis that ensued, the regulation which pertains to risk management in financial institutions, specifically Basel II, was revised and, subsequently, the Basel III accord was produced. The main aim of Basel III is to achieve greater quality, consistency and transparency in Tier 1 capital. Basel III also aims to regulate the amount of capital required for the trading book as well as revise the acceptable capital composition of the bank. In order to increase the capital ratio from 8.0 per cent to 10.5 per cent, or even 13.0 per cent if the procyclical buffer capital requirement is invoked, Basel III also introduced a leverage ratio together with capital buffers (BCBS, 2010a). The type of Tier 1 capital required for banks to effectively mitigate risk is of considerable importance to banks and regulators due to its loss-absorbing qualities. CoCo instruments have been designed and implemented in developed economies to accomplish this, with their inherent risk-mitigation properties helping banks to absorb losses in times of financial distress. CoCo instruments are loss-absorbing debt instruments issued as bonds which convert into equity when a predetermined "credit event" occurs. Despite their ever-increasing popularity in developed economies, the African market for CoCos remains in its infancy (KPMG, 2013). This paper represents the first attempt in the literature, as far as the authors are aware, to investigate and adapt an existing CoCo pricing methodology and explore the consequences of introducing these hybrid instruments to the African market. The effect of local (African) economic conditions on the CoCo price is also explored and evaluated.
The remainder of this paper is then structured as follows: Section 2 discusses the literature on economic procyclicality, with the focus of this discussion being the 2008/2009 credit crisis, its origins and its implications on a broad global scale. The history and design of CoCo bonds are examined in Section 3. The issuance of CoCos has been popular in developed economies, with banks in the United Kingdom (UK), the United States (US) and the Eurozone enjoying some success in issuing these securities. As a result, these products have gained in popularity in the developed world. It is, however, by no means conclusive that similar popularity will ensue as smaller, developing economies, such as those in Africa, begin CoCo issuance. Banks and regulators in these countries face several issues, including the specific trigger mechanism of CoCos as well as how to price these hybrid instruments in a robust way.
Section 4 will, therefore, explore the various pricing methodologies currently available in the literature and assess their relevance and applicability to financial data. Pros and cons of these methodologies - in particular, the equity derivatives approach - are also discussed in this section. The equity derivatives approach is then applied to South African, Nigerian and Egyptian data (as well as an all-African index) as a proxy for African markets. The results obtained are thereafter analysed and presented in Section 5, and Section 6 concludes the paper.
2 Literature study
The hidden risks underlying securities in financial markets provided a test for risk-management models worldwide, especially with respect to financial markets exposed to the asset-price bubble, and, in particular, the US house-price bubble (Merrouche & Nier, 2010). The increasing scale and complexity of these securities, as well as the looming failure of the credit market, were, in many ways, obvious to all parties involved either directly or indirectly with these instruments (Baily et al., 2008). The mainstream view in the broader financial services industry was that increased complexity had been matched by the evolution of mathematically sophisticated and effective techniques for measuring and managing the resulting risks (Financial Services Authority, 2009). When Lehman Brothers filed for a Chapter 11 bankruptcy and the initial cracks in the global financial system started to appear, it led to an over-exaggerated reduction in bank lending, widespread panic among risk managers, and an industry-wide avoidance of the securities and structured-product markets as a whole. Many financial service providers struggled to survive, thus exerting pressure on the broader macroeconomic environment in which they operated (De Haas & Van Horen, 2012).
In 2010, the financial crisis precipitated the European sovereign solvency crisis. Greece received bailout money from the European Union (EU), substantiating the view that current regulatory capital directives and credit ratings are ineffective measures of controlling risk (Sorkin, 2010). Although the Basel II accord was an improvement on previous regulations, it still provides inconsistent and biased forecasts of impending risks, notably under-estimating the joint downside risk of many assets (Atik, 2010). This, together with the failure of regulatory capital models during the credit crisis, is viewed as a key risk-management failure (Dowd, Hutchinson, Ashby & Hinchcliffe, 2011). Counteractive measures employed in the financial sector received criticism for being post hoc and "pouring water on an inferno instead of smothering the embers" (Wong, 2011:419).
In September 2009, the Group of Central Bank Governors and Heads of Supervision, chaired by the president of the European Central Bank, met at the headquarters of the Bank for International Settlements (BIS) (BIS, 2009) to discuss strengthening the capital requirement of global banks. The Basel Committee on Banking Supervision (BCBS) subsequently implemented the Basel III accord (BCBS, 2010a), designed as a supplementary framework to augment and improve the Basel II accord. The phased implementation of Basel III began in 2013 and, as at 2015, such implementation was expected to be completed by 2019, with minimum capital requirements being fully implemented by 2015 (BIS, 2013). The principal aim of Basel III is to achieve greater quality, consistency and transparency in respect of Tier 1 capital (BCBS, 2010a).
Banks in South Africa are in the process of migrating to Basel III compliance (PwC, 2015). Although South Africa was largely sheltered from the effects of the crisis because of prudent risk management, the country still slid into a recession (SARB, 2011). This recession was also the first one in 17 years, as demonstrated in Figure 1, with economic growth falling to -1.53 per cent (World Bank, 2014).1 Although the declining growth had negative implications for income, employment, investment and social programmes, all South African banks survived the crisis, while many banks around the globe were bailed out. This earned the South African banking system the reputation for being well developed, well regulated and sophisticated, with such banks therefore being ranked among those of First World economies, despite the fact that South Africa as a whole is viewed as a developing economy (National Treasury, 2011). The four largest banks, in particular, performed relatively well during and directly after the financial crisis, as no banks went into default in the South African market.2 This performance was linked to sound profitability, low leverage ratios, limited exposure to foreign assets and foreign funding, as well as adequate levels of capital in times of crisis (Maredza & Ikhide, 2013).
The South African Reserve Bank's (SARB) introduction of the National Credit Act (NCA) 35 of 2005 proved to be decisive and proactive in dampening the effects of the financial crisis on the South African economy (Kumbirai & Webb, 2010). The NCA is part of a comprehensive legislation overhaul designed to alleviate the concerns of banks and consumers, contains provisions regarding reckless lending, interest-rate capping and reasonability of credit, among others, and has laid down a clear set of rules for the way credit may be extended between financial institutions and borrowers (SA Government, 2005).
A novel regulatory requirement, introduced by Basel III, is the countercyclical capital buffer, which aims to reduce bank capital procyclicality by increasing capital requirements during favourable economic conditions and releasing this capital at times of unfavourable conditions (BCBS, 2010b). Countercyclical capital buffers were suggested as a measure that would serve to protect the financial system from systemic risk due to periods of increased credit growth, which periods have been associated with financial sector procyclicality (BIS, 2009). The way in which the credit-to-GDP ratio moves away from its historic trend, to the extent that it indicates the presence of imminent crises in the banking sector, is also indicative as a proxy of financial-sector weaknesses.3 The BCBS subsequently proposed, in its guidance notes (BCBS, 2010b), that this credit-to-GDP gap and the way it moves away from its historic trend be employed as a guideline when issuing Basel III countercyclical capital buffers. Every Basel Committee member is expected to use the countercyclical buffer as suggested by Basel III.4
Another of the methods proposed, and currently under investigation by the BCBS to manage the problem of insufficient capital in stressed economic milieus, is the introduction of CoCo bonds (BCBS, 2011:7).
3 Contingent convertible (CoCo) bonds
Contingent capital is not a new concept: the US banking system was built on an unfunded contingent capital commitment system of double liability. From 1850 to 1933, banks' risk management was shared through this system (De Spiegeleer & Schoutens, 2011). Under double liability, bank shareholders were required by law, in the event of financial distress, to make a down payment equivalent to the issued par value of all shares held. Shareholders could thus be called on for a sudden down payment of another USD100, assuming the initial investment in the bank was USD100.
Recently (i.e. subsequent to the 2008 credit crisis), contingent capital has been generated in the form of CoCos. CoCos are securities with both an underlying equity and fixed-income component that absorb losses by converting from a bond into equity when certain conditions - usually heightened systemic risk - are met (BCBS, 2010a). CoCos are similar to convertible bonds, with a few fundamental differences. A callable and convertible bond can be converted into a predetermined number of the common shares of the issuing entity at the bondholder's decision, while the bond is also callable by the issuer, that is, the bondholder can be called upon to surrender the bond to the issuing entity for a predetermined price (Huang, 2009). Thus, it is the choice of the bondholder and/or the bond issuer when the contractual agreement in respect of the bond will cease. A convertible bond usually offers a higher yield than a standard non-convertible bond because of the uncertainty associated with the conversion property of the bond. In addition, income-specific investors may have a mandate to invest exclusively in securities that generate interest or coupon payments. Convertible bonds may be converted to equity and, in some cases, this feature will prevent such income-specific investors from purchasing a convertible bond, even if the yield offered is more than that of other bonds (Huang, 2009).
CoCos made a modest entry into finance when the Lloyds Banking Group offered the holders of some of its hybrid debt a swap whereby their bonds would be traded for a new bond which carried a possible conversion into shares in November 2009 (De Spiegeleer & Schoutens, 2011). Credit Suisse soon followed suit, managing to raise USD2 billion in new capital using this new asset class. This type of security could either convert from debt into either equity or cash, or be written down (De Vries & Brehm, 2011).
CoCos have an array of appealing properties. They are issued as bonds with fixed-interest coupons and, unlike other hybrid capital instruments, have a trigger (threshold for the issuing bank's capital ratio) which, if reached, results in automatic conversion of the CoCo into equity (the nominal value is written off). The trigger may also be activated by the relevant regulatory authority if the bank's viability is believed to be threatened (e.g. when the bank still has sufficient capital but is struggling with reduced liquidity). Cocos are thus loss-absorbing, increasing a bank's capital when the bank is weakened and when it is most difficult for the bank to issue new equity. By automatically restructuring the capital of a bank, CoCos reduce the "debt overhang" problem, that is, the failure of a bank to successfully acquire funds to finance additional loans because their return partially accrues to existing debt holders (Chen, Glasserman, Nouri & Pelger, 2013).5 It is this attribute that would have saved numerous banks during the financial crisis when they were required to issue new equity (Prescott, 2012). Furthermore, CoCos automatically restructure bank capital before bankruptcy, that is, when the bank is a "going concern" and not a "gone concern", thereby reducing the likelihood of being put into resolution or bankruptcy. The Lehman's bankruptcy provides a robust example of the value of perception in influencing the financial system: knowledge of pre-bankruptcy reorganisation of financial institutions (especially a systemically important one) is valuable. Lastly, when a CoCo is correctly structured, bondholders, regulators and issuing banks can potentially all be in a better position post-conversion, as opposed to one party suffering a loss (Pennacchi, Vermaelen, & Wolff, 2011:16).
CoCos may not necessarily convert into equity, as the conversion mechanism could be cash, or, in some instances, the bond may suffer a write-down (either partially or completely). An investor can easily make the mistake of assuming that the returns from a callable convertible bond and a CoCo are comparable. On the contrary, the potential for profit of a CoCo is limited and the full downside may come into play for an investor once the bond is converted to shares (De Spiegeleer & Schoutens, 2011:8). One of the main differences between a normal convertible bond and a CoCo is the composition of the trigger mechanism, which is an event that must occur in order for the bond to be converted into the loss-absorption mechanism.
3.1 CoCo trigger
The trigger is documented in the prospectus of the bond and lays down a setting from where banks will most likely move into financial pressure (De Spiegeleer & Schoutens, 2011). Pioneering work by Flannery (2005) suggests a single trigger mechanism. A CoCo can, however, have one or more triggers, as academics have recently proposed. Subsequent to the financial crisis, CoCos have become an important topic (see Flannery, 2009; Huertas, 2009; Albul, Jaffee & Tchistyi, 2010; Plosser, 2010; McDonald, 2011; Pennacchi, 2011; Pennacchi et al., 2011). In the case of a CoCo with more than one trigger, the loss conversion to equity (or write-down) will occur when any trigger, or a combination of triggers, is breached. Triggers are either modelled on a mechanical rule or on the authority which may be executed by regulators. In the former case, also known as book-value triggers or accounting-value triggers, the trigger mechanism is typically set contractually as the ratio of Common Equity Tier 1 to risk-weighted assets, the CET1/RWA ratio. The loss-absorption mechanism is activated should the CET1/RWA ratio of the issuing bank fall below a level which was predefined with the CoCo issuance. A good example of this type of CoCo is the one issued by Lloyds Banking Group in 2009.6
This specific CoCo pays a 15 per cent semi-annual coupon rate, and will convert at £0.59 per share if the Core Tier 1 ratio of the Lloyds Banking Group falls below 5 per cent. Under Basel III, the minimum CET1/RWA ratio for a CoCo to qualify as Additional Tier 1 capital is 5.125 per cent according to current Basel regulations. Interestingly, since 2011, issuing banks have set their trigger at exactly that level (Avdjiev, Kartasheva & Bogdanova 2013).
Book-value triggers have been criticised for being a lagging indicator of capital issues. They depend heavily on the frequency with which banks publish their financial results publicly, and they also raise questions as to the similarity of internal risk models which differ across banks (Culp, 2009; Flannery, 2009). As a result of this delay in reporting, book-value triggers may not be activated as quickly as capital requires. Bear Stearns, Lehman Brothers, Wachovia and Merrill Lynch all reported regulatory capital well above the minimum level of 8 per cent when they went bankrupt (De Spiegeleer & Schoutens, 2011).
Market-value triggers are proposed as an alternative in order to address the shortcomings of inconsistent accounting valuations (Pennacchi et al., 2011; Sundarsen & Wang, 2011; Calomiris & Herring, 2012). These triggers are formulated in a way that the bond will convert to the loss-absorbing mechanism at a certain ratio of the bank's stock market capitalisation and/or Credit Default Swap (CDS) spread to its assets (Flannery 2005, 2009). This will decrease the risk that the balance sheet is manipulated and hopefully prevent regulatory forbearance (Avdjiev et al., 2013). A potential problem, though, is that market-value triggers could be difficult to price, are susceptible to stock-price manipulation and can exhibit a multiple-equilibria problem (Sundarsen & Wang, 2011). To elaborate on the problem of multiple equilibria, CoCos need to be priced in conjunction with equity. Thus a conversion rate which is dilutive may bring forth a scenario where there are multiple pairs of prices for equity and CoCos for any given combination of the asset values of a bank and the amount of debt with CoCos excluded.
Lastly, discretionary triggers (also referred to as point of non-viability (PONV) triggers) will be triggered through the discretion applied by regulators looking at the financial position that a bank is in (Albul et al., 2010). Such CoCos will afford a predefined regulator (usually a central bank) the authority to trigger the conversion mechanism of a CoCo if and when it views the action as necessary to save the bank. The use of PONV triggers offers a solution to the time-lag factor of book-value triggers. However, such a trigger may send the wrong message to the market and create a systemic panic in the financial system. De Spiegeleer and Schoutens (2011) suggest the following guidelines for the design of the trigger:
• Clarity: The trigger must portray a universal message regardless of jurisdiction.
• Objectiveness: The exact process to be followed if the loss-absorption mechanism is triggered should be known at the issue date.
• Transparency: A trigger defined as an event whereby the share price drops below a predefined barrier fits the test of transparency.
• Fixed: A trigger must be constant and unchangeable throughout the period in which the instrument is active.
• Public: A trigger event or the data driving a possible conversion should be public information.
In general, the lower the share price or capital level of a trigger, the lower the yield, and vice versa (Wilkens & Bethke, 2014). The level at which the trigger will activate is overwhelmingly driven by the view regulators hold on whether it is sufficiently high enough to be seen as loss-absorbing and low enough for the bank to be profitable. CoCos which do not have high enough triggers have less loss-absorbing ability, as banks may already be at a point of non-viability if the trigger is set too low. On account of this fact, they are usually less expensive to issue, but may not qualify as Additional Tier 1 capital in banks. That said, CoCos with lower triggers afford banks the opportunity to bolster their Tier 2 capital in a manner that makes business sense. The mechanism through which losses are absorbed is another important characteristic of any CoCo (Flannery, 2005).
3.2 Loss-absorption mechanism
Upon breaching the predefined trigger, the loss-absorption mechanism is activated. The first type of loss-absorption mechanism is the Principal Write-down (PWD). This CoCo will be written down completely, that is, the bondholder will lose the nominal amount paid for the CoCo. A second form of loss absorption is a partial write-down. This form of CoCo will be partially written down, so the bondholder will sacrifice a predetermined percentage of the nominal amount paid for the CoCo and will receive the remaining amount in cash or equity. To illustrate this example, consider the CoCo issued by Rabobank in March 2010. Upon investigation, it is clear that holders of Rabobank CoCos could suffer a 75 per cent loss of face value and be remunerated only by the remainder of the value, that is, 25 per cent, in cash (Wilkens & Bethke, 2014). A negative aspect of this specific trigger situation is that the issuer will be held liable for a cash payout while in distress. Thus the most popular form of trigger mechanism is equity conversion, as is evident in the majority of CoCos issued to date featuring this mechanism (Avdjiev et al., 2013). This type of CoCo will be converted into equity at a predefined rate.
The conversion price indicates the number of shares an investor will obtain if a conversion occurs. As an example, a CoCo holder with a par value of R100 will receive 10 shares if the conversion price after the trigger price is R10 (R100/R10). The CoCo holder will, however, receive 20 shares if the conversion price is R5 (R100/R5). Thus the CoCo investor benefits when the conversion price is low, as this leads to a high number of shares received upon conversion, with the inverse being true for current shareholders of a bank, who are likely to favour a higher conversion price that will lead to their equity being less diluted post-conversion. The conversion price could be any of the following:
1 a fixed value, for example the share price on the day the CoCo is issued (Some CoCos have a clause specifying the number of shares which are to be issued at conversion, instead of the price at the conversion, which is fundamentally the same as specifying a conversion price.);
2 the price of the share at conversion;
3 the share price with a floor, at conversion;
4 the share price at conversion, including a premium or, in some cases, a discount; or
5 the average of daily stock prices at a predetermined interval before the conversion. (Sundaresan & Wang, 2011; Prescott, 2012).
Figure 2 illustrates the main design features of a CoCo.
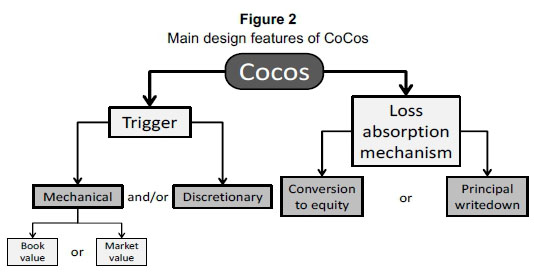
CoCo issuance to date (2015) is attributed mainly to their potential to satisfy regulatory capital requirements, although they can be actively traded in the secondary market. After their issuance under Basel III, CoCos may be classified as Additional Tier 1 (AT1) or Tier 2 (T2) capital (BCBS, 2011). The majority of the demand for CoCos stems from individuals who are often classified as "smaller" investors, while institutional investors have been held back by their mandates to date (2015), largely because CoCos are a relatively new type of security and disagreements continue about the correct accounting methodology for CoCos.7
CoCo credit spreads compared with other forms of subordinated debt largely depend on the way in which they are designed and is highly dependent on the trigger level as well as the lossabsorption mechanism. The spreads offered by CoCos are generally more in line with returns offered by subordinated debt than with CDS spreads and equity prices (Avdjiev et al., 2013). An important question for investors and academics is: How are CoCos priced in the secondary market, that is, what is a CoCo worth if purchased from another investor?
3.3 Pricing
Various ways to price CoCos are explored in this paper, bearing in mind the unique market conditions that investors face in African markets. The Black-Scholes model would seem a suitable candidate for pricing CoCos owing to the derivative nature of the instruments. The Black-Scholes assumptions have, however, been proved to be empirically unreasonable for pricing CoCos, as the implied market trigger of a CoCo is time-dependent and volatile (Jung, 2012). CoCo pricing has its roots in fixed-income mathematics and equity derivative pricing and may be grouped broadly into three model types, namely structural models (Penacchi, 2011; Albul et al., 2010), credit derivatives models (De Spiegeleer & Scoutens, 2011; Serjantov, 2011) and equity derivatives models (De Spiegeleer & Schoutens, 2011). The fact that CoCos are (in their classic form) hybrid instruments, sitting between pure equity and pure debt, provides a particular challenge when selecting a suitable pricing model.
Structural models view CoCos as deleveraging tools, explicitly capturing the trigger event. Credit derivatives models acknowledge that CoCos carry credit risk as an inherent characteristic, paying coupons until maturity or conversion through the trigger. Equity derivative models, on the other hand, rely on the share price as an indicator of the underlying financial position of the bank as well as the value to be transferred at conversion. The majority of academics favour equity derivatives models for pricing CoCos, as these seem to closely reflect the fair value of current CoCos in the market (De Spiegeleer & Schoutens, 2011; Wilkens & Bethke, 2014). This method has thus been chosen as the basis for this paper.
4 Data and methodology
The data chosen were daily returns of the Johannesburg Stock Exchange (JSE) All Share Index (Figure 3), the Nigerian All Share Index (Figure 5) and the S&P All Africa Index (Figure 6) spanning 15 years from January 2000 to March 2015. Monthly data from the Egyptian EGX 30 Index, spanning the same time period, were also used (Figure 4).
South Africa and Nigeria constitute the largest two economies in Africa. The data were sourced from the McGregor BFA and Opendata databases (McGregor, 2014; Opendata, 2014). The specific data were chosen as they reflect a reasonable proxy of African financial markets. Furthermore, the date ranges from pre-financial crisis to post-financial crisis in order to obtain a good sample of volatilities and returns spanning extreme volatility values, not just periods of low or high volatility, as indicated by Figure 3 to Figure 6.
4.1 Equity derivatives approach
In this approach, the default-intensity parameter, denoted as λ, is employed to model default in the reduced form (De Spiegeleer & Schoutens, 2011). The value λ/Jt can be expressed as the probability that the issuing bank of a CoCo defaults within the time interval [t + dt] while staying solvent up to time t. Hence the probability, ps, that the CoCo survives the next Τ years is given by exp(λT). The default probability over the same time period is thus 1 - exp(λT). This technique is the precursor to the reduced-form approach (De Spiegeleer & Schoutens, 2011). Given any value of λ, the survival probabilities of CoCos may be calculated and their prices determined. If a default occurs, the bondholder would want to recover at least part of the face value, N, of the bond, otherwise referred to as the recovery rate, R. Upon a default occurring, an investor's total loss isequal to (1 - R)xN.
Equation 1 explains the correlation of the credit spread, cs, recovery rate, R, and the default intensity, λ:

This credit spread is a combination of the percentage loss (1 - R) and the probability of the loss occurring, λ. In order to measure the trigger event where the loss-absorption mechanism is
triggered, one has to employ a strategy similar to the way a default is statistically modelled in credit models. A CoCo trigger occurring would be modelled as a form of "default" event. The default intensity, λ, will accordingly be substituted by trigger intensity, λTrigger. The probability of a CoCo being triggered is higher than the probability that a bank will default on its outstanding corporate bonds. The CoCo will in all likelihood trigger before default takes place. Thus:

From Equation 1, the credit-spread value on CoCos may be determined:

4.2 Loss
The conversion type and price drive the loss suffered by the holder of a CoCo when it is triggered:
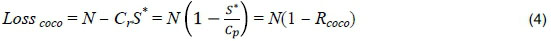
The share price momentarily after conversion of the CoCo is S . The recovery rate of the CoCo holder after a trigger is thus represented by the ratio of the converted share price S and the conversion price Cp:

This illustrates the correlation between the conversion share price and the valuation of the CoCo. Should a conversion price, S , be equal to the share price of the bank at the instance of the trigger, there is no loss for the investor. Thus an investor becomes a shareholder when the CoCo is triggered, with the total value of the shares being equal to the face value, N.
4.3 Trigger intensity λ(trigger)
The probability that a trigger occurs in the time interval [t,t + dt], while not being triggered up to t, is given by λtriggerdt. To save a financial institution from default, the CoCo conversion has to occur before the default time, t. This implies that the intensity parameter of conversion λTrigger) must be greater than the default-intensity parameter, that is, λtrigger > λ (Brandt & Hermansson, 2013). This implies that the CoCo trigger event, t* , always occurs before the default time, t so p(t* < t) = 1). This should hold true, as it is no use for the bank should the bank default before the CoCo is triggered. A trigger could be accounting-based or market-based, or it could be dependent on a mechanical rule.
As an example of an accounting-based trigger, a CoCo can be triggered when the bank announces it has insufficient Core Tier 1 capital. However, as pointed out by De Spiegeleer & Schoutens (2011), modelling regulatory behaviour is an impossible task, and the same difficult challenge presents itself when trying to engineer a stochastic model for an accounting measure based on capital ratios. Instead of building a model which directly models an accounting or a regulatory trigger, we could employ a corresponding market trigger as a proxy indicator for these events. Thus an accounting trigger where a Core Tier 1 ratio falls to below a minimum level could be substituted with a similar event which would cause the share price to drop below a barrier, S , given that the accounting trigger was likely to have been triggered in any case for the given level of S*(De Spiegeleer & Schoutens, 2011). The way in which a market trigger, S*, is connected to an accounting trigger is illustrated in Figure 7, assuming an accounting trigger of 6 per cent Core Tier 1 capital with a corresponding trigger share price of 160.
Borrowing from the Black and Scholes equity derivatives pricing formula, the probability, p*, of the level being breached during the life, T, of the CoCo is as follows (Lujing & Rieger, 2009):
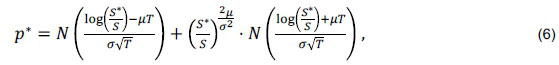
where:
•
is the drift rate;
• q is the continuous dividend yield;
• r is the continuous interest rate;
•σ is the volatility;
• T is the maturity of the CoCo; and
• S is the current share price.
This is similar to the first exit-time equation in barrier-option pricing in terms of Black-Scholes and is used to derive the probability that a stock price, S, may touch the level, S , before the expiration of the bond T years from now. N(x) denotes the probability of a random variable, X, which is following a standard normal distribution, taking a value smaller than x:

In Equation 6, p quantifies the probability of the trigger occurring. From p , λTrigger may be calculated:

This gives the CoCo spread (cscoco):8

To illustrate the spread calculation, consider a contingent convertible in the primary market, with a single regulatory trigger and a 10-year maturity. It is assumed that the continuous interest rate (r) is 4 per cent, that the underlying share price is R150, and that the share has an annual volatility (σ) of 30 per cent and does not pay any dividends (q = 0). An assumption is made that the activation of the trigger accompanies a share price equal to half the current share price, S = R75. The three steps in Table 1 indicate the process of calculating the credit spread under this assumption.
Thus cscoco= 6.6%x50% = 330bps. When this spread is included in the continuous interest rate, (400bps + 330bps), the total yield on this CoCo becomes 7.3 per cent.
4.4 CoCo delta (Δ)
To build on the previous example, the yield of 7.3 per cent calculated on the CoCo is a function of the stock price of the CoCo. An investor will require a higher credit spread (cscoco) if the share price (S) decreases, as this implies a greater probability (p ) that the trigger event may be realised (the trigger share price is inherently lower than the share price of a CoCo), prompting the higher spread demand due to this risk. Subsequently, the CoCo also becomes less attractive as the price decreases. We can illustrate this as follows:

Thus the CoCo exhibits a positive delta:

To illustrate the observation above, assume, for example, that the share-price level around which a CoCo is expected to be triggered does not change, but that the share price of the CoCo (S) suffers a drop in price of 10 per cent, from R150 to R135. A conversion is more likely, since S is now closer to S . In this case, the CoCo spread (cscoco) moves from 330 to 403bps. The sensitivity of cscocoto the underlying share price is given in Figure 8.
5 Results and discussion
The parameters presented in Table 2 were used as input into the CoCo pricing model, each applicable to the country in which it resides, with the interest rate used being the prime lending rate as determined by the central bank of each country.
The results from the pricing model are illustrated graphically in Figures 9 to 12. The trigger probability, trigger intensity, credit spread and bond yield are individually displayed (y-axis) in conjunction with the share price (x-axis) and equity volatility (z-axis). The figures provide an illustration of how these variables change as the share price of the underlying equity approaches the trigger share price (R27 - see Table 2) on the x-axes, under different volatilities on the z-axes.
5.1 Trigger probability
The trigger probability of the CoCo responds as expected. As the share price approaches the trigger level of R26 in Figure 9 (plotted with decreasing share prices on the x-axis), the probability of the trigger being breached increases. Furthermore, as volatility in a market increases, the trigger probability also increases at all share-price levels. For South African data, the probability that the CoCo trigger is breached at a share price of R34 is 0 per cent when volatility is 10 per cent and increases to 63 per cent when volatility is 30 per cent for the same share price. The same is evident in the Egyptian data where the probability that the CoCo trigger is breached at a share price of R34 is close to 0 per cent when volatility is 10 per cent and increases to 60 per cent when volatility is 30 per cent for the same share price. The trigger probability is lower at all share price levels in the Egyptian market when compared with the South African market, mostly due to the fact that the Egyptian market is less volatile than the South African market.
At a share price of R30 and volatility of 10 per cent, the trigger probability in South Africa is the highest, followed by Egypt, Nigeria, and, finally, All Africa. The trigger probability in the South African market is thus more sensitive to a change in share price relative to other regions.
5.2 Credit spread
The credit spread of the CoCo increases as the share price approaches the trigger share price, as investors require a higher yield on the CoCo when conversion becomes more probable (Figure 10). The volatility in the stock market also has a dramatic impact on the credit spread, and, in stressed economic scenarios, represented by the 30 per cent volatilities in the graphs, the credit spread reaches levels of more than 100 basis points for South Africa and close to 100 basis points for Egypt and Nigeria when the share price is at R34 and relatively far removed from the R26 trigger share price. This coincides with the notion that the trigger probability is higher when the share price approaches the trigger share price, as shown in Figure 9.
Between a share price of R28 and R30 (volatility at 10 per cent), the South African market has a larger reaction in terms of the credit spread as the share price approaches the trigger price relative to other regions.
5.3 Trigger intensity
The trigger intensity is calculated using (8), that is, λtrigger = 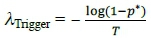 where p* is the probability of the trigger occurring. The trigger intensity increases as the share price approaches the trigger share price (Figure 11). Furthermore, volatility has a profound impact on the trigger intensity, as the trigger intensity is 68 per cent in South Africa, 62 per cent in Egypt, 61 per cent in Nigeria and 59 per cent for All Africa at a share price of R26 under a volatility of 30 per cent. The behaviour of the trigger intensity under simulated conditions implies that special attention must be paid to this metric in African markets, especially in times of high volatility, which is a historic feature of the said markets.
where p* is the probability of the trigger occurring. The trigger intensity increases as the share price approaches the trigger share price (Figure 11). Furthermore, volatility has a profound impact on the trigger intensity, as the trigger intensity is 68 per cent in South Africa, 62 per cent in Egypt, 61 per cent in Nigeria and 59 per cent for All Africa at a share price of R26 under a volatility of 30 per cent. The behaviour of the trigger intensity under simulated conditions implies that special attention must be paid to this metric in African markets, especially in times of high volatility, which is a historic feature of the said markets.
5.4 Total yield
The total yield of the CoCos can be interpreted in the same way as the credit spread in Figure 10, and, although there are differences in the graphical presentation, trends are coherent (Figure 12). The total yield on a CoCo will increase as the share price approaches the trigger share price, because the probability that the CoCo will trigger also increases under this share-price movement (Figure 9). The risk-return reward for the CoCo investor in a situation where the CoCo is close to the trigger price will be the higher total yield. To further emphasise the risk-return reward, note that, in Figure 10, the total yield of a CoCo also increases as the volatility in the market increases, even at constant share prices. An increase in market volatility will also lead to a situation where a CoCo trigger becomes more probable (as is evident in Figure 9 and from the discussion thereof), and this supports the theory that a higher trigger probability will result in a higher total yield for the investor in a CoCo.
The behaviour of the total yield in South Africa shows that the lowest total CoCo yield (9 per cent) is expected at a share price of R34 and volatility of 10 per cent, with Egypt a close second at 11 per cent. Under the same market conditions, a CoCo in Nigeria and All Africa will demand an 18 per cent return, that is, a substantially higher return. The same phenomenon occurs at the trigger share price of R26 when volatility is 30 per cent. South Africa and Egypt will demand 41 per cent and 43 per cent, respectively, with Nigeria and All Africa demanding 49 per cent and 48 per cent, respectively.
In times of low volatility and a share price far from the trigger, investors could expect double the total yield from Nigerian CoCos than what is offered by South African CoCos (9 per cent versus 18 per cent), though this is largely a contribution from local interest rates. However, in times of high volatility with the share price close to the trigger point, the CoCos are proportionately closer, with the Nigerian CoCo only offering 19.5 per cent more in total yield (41 per cent versus 49 per cent). Thus a shift towards the trigger price, combined with amplified volatility, results in a convergence in the amount of total yield that one African Coco offers above another.
6 Conclusions
The BCBS has set out to rectify the failures of the Basel II accord through the new Basel III set of regulations. The amount of capital has been (under Basel II) and still is (under Basel III) a focus area and is pivotal in the management of risks in the banking world. To extend on the amount of capital required by regulation, the type of capital is an equally important discussion point and influences the business case of banks in many ways, including liquidity and return on capital. The ideal capital from a bank's point of view may be a form of security which produces the highest possible return, whereas the regulatory authorities are more concerned with the robustness and liquidity of the said asset. This provides a unique challenge where regulators set the rules of the game and banks set out to play within these rules while trying to maximise their advantage.
The success of Basel III regulation lies in the adoption thereof, with banks in both developed and developing countries facing unique difficulties in the implementation process, which is often attributable to external economic factors arising from the markets in which they operate. Banking institutions in developing economies tend to be more volatile and certainly more fragile, as is evident from the sovereign debt crisis in Greece. African banks are largely either subsidiaries of larger banks in developing nations or are independent banks which use standardised risk management and are heavily correlated to the performance of the economies in which they function. In contrast, South African banks have shown resilience in stressed economic conditions, as is evidenced by the stable performance of the top four South African banks during the 2008 financial crisis. That said, it still makes sense that, in the overall case for African banks, the type of capital held by banks is critical, both to the success of the bank's business case and the survival of the bank in stressed economic conditions.
African banks possess a unique set of attributes in terms of their size, correlation to the market performance of the economies in which they operate, and also because of the higher volatilities experienced in the markets in which they operate. This adds to the challenge of designing CoCos in a unique way which will enable them to remain robust from the investor's point of view but also be loss-absorbing in times of economic stress from the bank's point of view. The trigger mechanism of CoCos should be effective in the sense that these bonds should be triggered while the bank is still a going concern. This poses a challenge, as markets can move rapidly in volatile times. The pricing of African CoCos would require a trigger mechanism higher than would normally be set in respect of a similar CoCo in a developed economy (such as the US or the UK) and would offer a substantial yield due to the large impact that the volatility of the African markets has on the pricing of the CoCo.
The BCBS needs to be clearer on the exact composition of acceptable CoCos and also continue with the investigation of CoCos as a possibility for Tier 1 capital in banks, especially in developing economies. Furthermore, in addition to the pricing of CoCos, further investigation is warranted into the structure of CoCos in African markets, specifically pertaining to the type of trigger and conversion mechanism. The case for Call Option Enhanced Reverse Convertibles (COERCS) can also be investigated, as this type of CoCo may be more suited to African markets.
References
ALBUL, B., JAFFEE, D.M. & TCHISTYI, A. 2010. Contingent convertible bonds and capital structure decisions. University of California at Berkeley. [ Links ]
ATIK, J. 2010. Basel II: A post-crisis post-mortem. Transnational Law and Contemporary Problems, 19(1):731-759. [ Links ]
AVDJIEV, S., KARTASHEVA, A. & BOGDANOVA, B. 2013. CoCos: A primer. BIS Quarterly Review. Bank for International Settlements, September. Available at: http://www.bis.org/publ/qtrpdf/r_qt1309f.htm [accessed June 2011]. [ Links ]
BAILY, M.N., LITAN, R.E. & JOHNSON, M.S. 2008. The origins of the financial crisis: The initiative on business and public policy. Fixing Finance Series, Paper 3. November. [ Links ]
BCBS (BASEL COMMITTEE ON BANKING SUPERVISION). 2010a. Basel III: A global regulatory framework for more resilient banks and banking systems. Bank for International Settlements. Available at: http://www.bis.org/publ/bcbs189_dec2010.pdf [accessed June 2014]. [ Links ]
BCBS (BASEL COMMITTEE ON BANKING SUPERVISION). 2010b. Guidance for national authorities operating the countercyclical capital buffer. Bank for International Settlements. Available at: http://www.bis.org/publ/bcbs187.pdf [accessed June 2014]. [ Links ]
BCBS (BASEL COMMITTEE ON BANKING SUPERVISION). 2011. Basel III: A global regulatory framework for more resilient banks and banking systems. June. Available at: http://www.bis.org/publ/bcbs189.pdf [accessed June 2014]. [ Links ]
BIS (BANK FOR INTERNATIONAL SETTLEMENTS). 2009. Comprehensive response to the global financial crisis. Available at: http://www.bis.org/press/p090907.htm> [accessed December 2013]. [ Links ]
BIS (BANK FOR INTERNATIONAL SETTLEMENTS). 2013. Basel III phase-in arrangements. Available at: http://www.bis.org/bcbs/basel3/basel3_phase_in_arrangements.pdf [accessed June 2014]. [ Links ]
BRANDT, M. & HERMANSSON, C. 2013. Pricing contingent convertibles in an intensity based model. Essay from Göteborgs universitet/Institutionen för nationalekonomi med statistic. Available at: https://gupea.ub.gu.se/bitstream/2077/33449/1/gupea_2077_33449_1.pdf [accessed December 2014]. [ Links ]
CALOMIRIS, C. & HERRING, R. 2012. Why and how to design a contingent convertible debt requirement. Published in Y. Fuchita, R. Herring & R. Litan (eds.) Rocky times: New perspectives on financial stability. Brookings/NICMR Press. Chapter 5. [ Links ]
CHEN, N., GLASSERMAN, P., NOURI, B. & PELGER, M. 2013. CoCos, bail-in, and tail risk. Office of Financial Research Working Paper #0004, 23 January. Available at: http://www.treasury.gov/initiatives/ofr/research/Documents/OFRwp0004_ ChenGlassermanNouriPelger_CocosBailInandTailRisk.pdf [accessed February 2014]. [ Links ]
CULP, C. 2009. Contingent capital vs contingent reverse convertibles for banks and insurance companies. Journal of Applied Corporate Finance, 21(4): 17-27. [ Links ]
DE HAAS, R. & VAN HOREN, N. 2012. International shock transmission after the Lehman Brothers collapse - evidence from syndicated lending. European Bank for Reconstruction and Development Working Paper 42. [ Links ]
DE SPIEGELEER, J. & SCHOUTENS, W. 2011. Pricing contingent convertibles: A derivatives approach. SSRN Paper no. 1795092. [ Links ]
DE VRIES, D. & BREHM, M. 2011. Coco issuance confirmed. Technical Report. Bank of America, Merrill Lynch, February. [ Links ]
DOWD, K., HUTCHINSON, M., ASHBY, S. & HINCHCLIFFE, J. 2011. Capital inadequacies: The dismal failure of the Basel regime of bank capital regulation. Policy Analysis, 681(1):1-38. [ Links ]
FINANCIAL SERVICE AUTHORITY. 2009. The Turner review: A regulatory response to the global banking crisis. Financial Service Authority Report. [ Links ]
FLANNERY, M.J. 2005. No pain, no gain? Effecting market discipline via "reverse convertible debentures". In: H.S. Scott, (ed.), Capital adequacy beyond Basel: Banking, securities, and insurance. Oxford: Oxford University Press:171-96. [ Links ]
FLANNERY, M.J. 2009. Stabilizing large financial institutions with contingent capital certificates. University of Florida. [ Links ]
G20. 2009. G20 leaders statement: The Pittsburgh Summit. Available at: http://digitalcommons.ryerson.ca/dissertations/1657 [accessed November 2014]. [ Links ]
HUANG, H. 2009. Convertible bonds: Default risk and uncertain volatility. Bonn Economic Discussion Papers bgse09_2010, University of Bonn, Germany. Available at: http://ideas.repec.org/p/bon/bonedp/bgse09_2010.html [accessed June 2014]. [ Links ]
HUERTAS, T.F. 2009. Too big to fail, too complex to contemplate: What to do about systemically important firms. Paper presented at the Financial Markets Group, London School of Economics, September 15. [ Links ]
JUNG, H. 2012. Pricing of contingent convertibles. Wharton Research Scholars Journal, Scholarly Commons, University of Pennsylvania. Available at: http://repository.upenn.edu/wharton_research_scholars/90/ [accessed June 2014]. [ Links ]
KPMG. 2013. Global debt sales. Loan portfolio advisory, Portfolio Solutions Group: South Africa. Available at: https://www.kpmg.com/Global/en/IssuesAndInsights/ArticlesPublications/global-debt-sales/Documents/south-africa-2013.pdf [accessed March 2013]. [ Links ]
KUMBIRAI, M. & WEBB, R. 2010. A financial ratio analysis of commercial bank performance in South Africa. African Review of Economics and Finance, 2(1):30-53. [ Links ]
LUJING, S. & RIEGER, M.O. 2009. How likely is it to hit a barrier? Theoretical and empirical estimates. Technical Report Working Paper No. 594, National Centre of Competence in Research, Financial Valuation and Risk Management, October. Available at: www.nccrfinrisk.uzh.ch/media/pdf/wp/WP594_A1.pdf [accessed June 2014]. [ Links ]
MAREDZA, A. & IKHIDE, S. 2013. The impact of the global financial crisis on efficiency and productivity of the banking system in South Africa. Economic Research Southern Africa Working Paper no. 328. [ Links ]
McDONALD, R.L. 2010. Contingent capital with a dual price trigger. SSRN Paper no. 1553430, Northwestern University. [ Links ]
McDONALD, R.L. 2011. Contingent capital with a dual price trigger. Unpublished manuscript. Northwestern University. [ Links ]
McGREGOR BFA. 2014. Online database. Available at: https://expert.mcgregorbfa.com/ [accessed June 014]. [ Links ]
MERROUCHE, O. & NIER, F. 2010. What caused the global financial crisis? Evidence on the drivers of financial imbalances 1999-2007. IMF Working Paper, WP/10/265. [ Links ]
NATIONAL TREASURY. 2011. A safer financial sector to serve South Africa better. National Treasury Policy Document. Available at: www.treasury.gov.za [accessed March 2015]. [ Links ]
OPENDATA. 2014. Online database. Available at: http://opendataforafrica.org/gzwumgb/equity-indices-july-2011 [accessed June 2014]. [ Links ]
PENNACCHI, G. 2011. A structural model of contingent bank capital. Manuscript. University of Illinois. [ Links ]
PENNACCHI, G., VERMAELEN, T. & WOLFF, C. 2011. Contingent capital: The case for COERCs. LSF Research Working Paper Series 10-08, Luxembourg School of Finance, University of Luxembourg. [ Links ]
PLOSSER, C.I. 2010. Convertible securities and bankruptcy reforms: Addressing too big to fail and reducing the fragility of the financial system. Paper presented at the Conference on the Squam Lake Report, New York, N.Y., 16 June. [ Links ]
PRESCOTT, E.S. 2012. Contingent capital: The trigger problem. Economic Quarterly, (4):33-50. [ Links ]
PwC. 2015. Stability amid uncertainty South Africa - major banks analysis. Available at: http://www.pwc.co.za/en_ZA/za/assets/pdf/major-bank-analysis-september-2014.pdf. [ Links ]
SA GOVERNMENT. 2005. National Credit Act, 2005. Government Gazette 28619, 489(34):1-230. [ Links ]
SARB (SOUTH AFRICAN RESERVE BANK). 2011. Annual economic report 2011, 90th Anniversary. Available at: http://www.reservebank.co.za/PublicationsandNotices/Reports [accessed June 2014]. [ Links ]
SARB (SOUTH AFRICAN RESERVE BANK). 2012. Guidance Note 9/2012 issued in terms of section 6(5) of the Banks Act, 1990. Capital framework for South Africa based on the Basel III framework. Available at: https://www.resbank.co.za/Lists/News%20and%20Publications/Attachments/5154/ G9%20of%202012.pdf [accessed February 2015]. [ Links ]
SERJANTOV, A. 2011. On practical pricing hybrid capital securities. Presentation, Global Derivatives Trading and Risk Management (April). Available at: http://www.institutional-money.com/fileadmin/user_upload/Bilder_Grafiken_News/PDF_News/152-162_IM_2_2014_CoCos_XXXkg_.pdf [accessed March 2015]. [ Links ]
SORKIN, R. 2010. Answers on credit ratings long overdue. New York Times. Available at: http://www.nytimes.com/2010/06/01/business/01sorkin.html?src=busln [accessed February 2014]. [ Links ]
SUNDARESAN, S. & WANG, Z. 2011. On the design of contingent capital with market trigger. Federal Reserve Bank of New York, Staff Report, no. 448. [ Links ]
WILKENS, S. & BETHKE, N. 2014. Contingent convertible ("CoCo") bonds: A first empirical assessment of selected pricing models. Financial Analysts Journal, 70(2):89-76. [ Links ]
WONG, M. 2011. Credit BuVaR: Asymmetric spread VaR with default. Journal of Risk Management in Financial Institutions, 5(1):86-95. [ Links ]
WORLD BANK. 2014. GDP annual growth rate by country. Available at: http://data.worldbank.org/indicator/ny.gdp.mktp.kd.zg [accessed June 2014]. [ Links ]
Accepted: February 2016
1 The last time South Africa was in a recession was in 1992, with a -2.14% growth rate (World Bank, 2014).
2 The banking sector consists of 17 domestically governed banks, 11 branches of multinational banks, one cooperative bank, two mutual banks, and 43 representative offices. However, the South African banking sector is dominated by four major banking institutions, the so-called "Big Four", namely the Amalgamated Bank of South Africa (ABSA), FirstRand Bank, Nedbank, and Standard Bank (SARB, 2012).
3 There is strong evidence for this when studying the South African market. The credit-to-GDP guide issued a strong warning signal for a buffer add-on for the 2006-2010 period (SARB, 2011).
4 The countercyclical capital buffer was introduced to the South African market in January 2016 (SARB Guidance Note 9/2012).
5 Although the conversion of debt to equity raises the book value of equity, it fails to raise new cash for the bank like a new issuance of equity would (Prescott, 2012).
6 Specifically CoCo ISIN XS0459089255.
7 The debate stems from the hybrid nature of CoCos, with the majority of academics arguing that they be treated as debt, but with others noting that they could also be treated as plain equity (Avdjiev et al., 2013). The way in which CoCos are accounted for impacts the tax associated with the coupon payments made. For a detailed discussion on the tax treatment of CoCos, see McDonald (2010).
8 This credit spread is a continuous interest rate which needs to be scaled back to the yield and day count convention on the bond (De Spiegeleer & Schoutens, 2011).














