Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
South African Journal of Economic and Management Sciences
versión On-line ISSN 2222-3436
versión impresa ISSN 1015-8812
S. Afr. j. econ. manag. sci. vol.19 no.1 Pretoria 2016
http://dx.doi.org/10.17159/2222-3436/2016/v19n1a5
ARTICLES
Cost efficiency of African insurance companies using a finite mixture model
Carlos BarrosI; Peter WankeII
IISEG - Lisbon School of Economics and Management; ULisboa and CESA - Research Centre on African, Asian and Latin American Studies
IICoppead Business School, Federal University of Rio de Janeiro
ABSTRACT
This paper evaluates the operational practices by African insurance companies from Angola and Mozambique, using a finite mixture model that allows controlling for unobserved heterogeneity. More precisely, a stochastic frontier latent class model is adopted in this research to estimate the cost frontiers for each of the different technologies embedded in this heterogeneity. This model not only enables the identification of different groups of African insurance companies from Angola and Mozambique, but it also permits the analysis of their cost efficiency. The results indicate the existence of three different technology groups in the sample, suggesting the need for different business strategies. The policy implications are also derived.
Key words: Africa; insurance companies; stochastic cost frontier; latent class model, technical efficiency; panel data
1 Introduction
This study paper aims to contribute to the literature by analysing the efficiency of a sample of African insurance companies from Angola and Mozambique, as internalisation is a growing trend in this sector (Outreville, 2008). In particular, panel data from 2002-2012 is used to analyse the cost efficiency frontier of the insurance industry in these countries, as well as the different production technologies embedded within them. Traditionally, there are two major approaches to estimating efficiency levels with respect to productive frontiers: the parametric (stochastic frontier model - SFA) and the non-parametric approach (Data Envelopment Analysis - DEA). While the former is based on econometric techniques and has to specify a functional form for production technology, the latter does not demand the a priori use of a functional form. It is also capable of handling multiple outputs. The non-parametric approach, however, presents some restrictions, such as the vulnerability noted in its outcomes, which are a result of deviant observations.
More precisely, the contributions of this research to the current body of knowledge on productive efficiency in the insurance sector are threefold.
First, this research fills a gap in the literature by analysing insurance companies in Angola and Mozambique, because, to the best of our knowledge, no papers have been published on this subject. On the one hand, the relevance of filling this gap in the literature is based on the importance of these two countries in the world economy. According to Grande and Teixeira (2012), an analysis by The Economist (2011) finds that, over the last decade, no fewer than six of the world's ten fastest-growing economies are in sub-Saharan Africa, including Angola, which is ranked in first place, and Mozambique, which is ranked eighth. On the other hand, this literature gap contrasts with already published research on insurance companies in other African countries (Munro & Snyman, 1995; Giesbert, Sterner & Bending, 2011; Uche, 1999; Chourouk, 2003; Ibiwoye & Adeleke, 2008; Olaosebikan, 2012).
Second, this research contributes to the literature on productive efficiency in the insurance sector by assuming that technology can vary within the analysed sample. This differs from what is to be found in previous studies. It is remarkable that all the current literature about insurance company efficiency assumes that insurance companies generally use the same technology, regardless of the approach followed, whether it be parametric, or non-parametric. If this assumption is incorrect, then it could lead to the overestimation of the inefficiency of some insurance companies, as technological differences could be interpreted as inefficiency (Orea & Kumbhakar, 2004). Given this, a stochastic frontier latent class model is applied in this research to control for unobserved heterogeneity (Orea & Kumbhakar, 2004; Greene, 2005). This model assumes that there is a finite number of classes using different technologies and that each unit can be assigned to a particular group, using the estimated probabilities of class membership. Moreover, the number of different groups is also tested by estimation. This study therefore includes all the types of insurance companies, both life and non-life companies, that exist in the countries analysed, enabling a control for unobserved heterogeneity which underlies different productive technologies.
Third, this research contributes to the literature by proposing a model that accounts for the specifics of the insurance sector, using Angola and Mozambique as a base case. Insurance is one of the industries in which capital presents the highest marginal productivity. Under these circumstances, cost frontiers become quite sensitive to outliers (Amores & Raa, 2014). Hence, SFA is adopted here, rather than DEA, as the latter is more affected by influential observations than is the former. This occurs because SFA handles all the variations between production units in the form of random terms, contrary to the case of DEA, where such variations are interpreted as inefficiency. These features are relevant for this research, as randomness is a primary property of several production processes, including insurance.
The remainder of the paper is organised as follows. After this introduction, the contextual setting of Angolan and Mozambican insurance companies is presented, followed by a literature review of the previous studies conducted on productive efficiency in this sector. After this, the methodology is discussed, followed by the presentation of the data analysis and the major results. The paper ends with the conclusions.
2 Contextual setting
2.1 Insurance in Angola
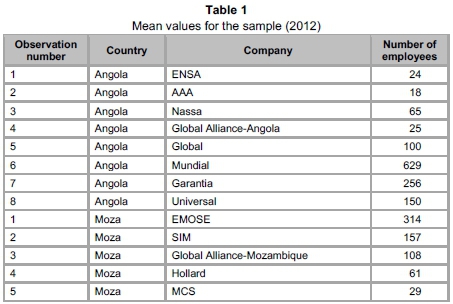
The insurance industry in Angola comprises eight companies: ENSA- Empresa Nacional de Seguros de Angola, a public company owned by the government; AAA, Angola Agora e Amanhã, Pensões, a company with public and private local capital; Nossa Seguros, a private insurance company owned by local Angolans; Global Alliance Seguros Angola, a South African insurance company with offices in Angola and Mozambique; Global Seguros, a private company owned by Angolans; Mundial Seguros; Garantia; and Universal. The last three are private companies owned jointly by local Angolans and Portuguese insurance companies. The insurance industry in Angola is small, accounting for just 1.25 per cent of GDP in 2012. However, the number of companies has increased over the period under study and new agencies are opening in remote areas of the country. This growth has accompanied the growth rate of the Angolan economy. In 2010, a total of 10 insurance companies were already established in Angola, with a further five in the process of being licensed. In relative terms, non-life insurance represents 90 per cent of the total market. The publication of Decree law n°35/09 requires compulsory motor general liability insurance, which boosted the growth of the market. This sector accounted for 27.8 per cent of the market total in 2010, followed by accident, health and travel insurance, which together account for 26.4 per cent. However, a decrease in the market share of non-life insurance companies is forecast, in line with other insurance markets, which is a result of the development of a rise in sales of products of a financial nature. Furthermore, the share from petrochemical insurance has proportionally decreased with the growth in the other sectors.
2.2 Insurance in Mozambique
The Mozambican insurance industry comprises five companies: EMOSE - Empresa Moçambicana de Seguros, a public company; SIM - Seguradora International de Mozambique, a private company and; Global Alliance Seguros Mozambique, a private South African company which is also present in Angola and has banks in Angola and Mozambique; Hollard Mozambique Companhia de Seguros, another South African insurance company; and finally MCS, Mozambique Companhia de Seguros, a private company owned by local capital. The Mozambique insurance industry is also small. In 2012 it represented 1.15 per cent of GDP, which is comparable, in relative terms, to the Angolan market.
The difference in the number of companies in both countries is directly linked to Angola's wealth in terms of oil and diamonds, which attracts more foreign companies. This can be seen in Table 1 below, which presents some characteristics of the companies analysed. The Mozambique insurance market grew by 2.5 per cent in 2012, with non-life premiums rising by 2.3 per cent. The non-life insurance market represents 55 per cent of the total market, 55 per cent of which is fire and car insurance, whereas life insurance accounts for a smaller share of the market (44.9 per cent). Currently there are 17 insurance companies, some of which manage pension funds: SIM, EMOSE, Global Alliance, Hollard Seguros Mozambique, Companhia de Seguros de Africa and Mozambique Resseguros SA.
3 Literature review
This section presents a synthesis of the studies previously conducted into the insurance industry in different countries, regardless of the approach adopted. As briefly mentioned in the introduction, two alternative approaches have been followed to analyse productivity and efficiency in insurance in the past: SFA (Fenn, Vencappa, Diacon, Klumpes & O'Brien, 2008; Ennsfellner, Lewis & Anderson, 2004; Fecher, Kessler, Perelman & Pestieu, 1993; Cummins & Weiss, 1993; Gardner & Grace, 1993) and the non-parametric DEA (Barros, Nektarios & Assaf, 2010; Mahlberg & Url, 2010; Cummins & Xie, 2008; Barros, Barroso & Borges, 2005; Cummins, Rubio-Misas & Zi, 2004; Mahlberg & Url, 2003; Diacon, Starkey & O'Brien, 2002; Cummins, Weiss & Zi, 1999; Cummins & Zi, 1998; Fukuyama, 1997; Cummins, Turchetti & Weiss, 1996; Biener & Eiling, 2011).
It is worth noting that the literature on productive efficiency in the insurance industry is scarce in comparison with other financial areas, such as banking. However, it presents a large heterogeneity, not only in terms of the models used within each approach, whether it be parametric or non-parametric, but also in terms of the research subjects analysed and the hypotheses tested, according to the comprehensive study conducted by Eling and Luhnen (2010).
General-purpose and/or comparative studies on the efficiency of the insurance sector in a given country or region are the most numerous in the literature. For example, Bertoni and Croce (2011) applied DEA to a panel of life insurance companies operating in five European countries (Germany, France, Italy, Spain and the U.K.) between 1997 and 2004. The authors estimated productivity with a Malmquist efficiency model, concluding that productivity increased on an annual basis by 6.71 per cent and that this increase was mostly owing to innovation (technological change) in best-practices (6.67 per cent), while best-practice management practices contributed a mere 0.04 per cent. Nektarios and Barros (2010) analysed the efficiency of Greek insurance companies during the period 1994-2003 and found that Greek life insurance companies' productivity growth was 16.1 per cent, followed by non-life insurance companies, which had a productivity growth of 6.5 per cent. Mixed insurance companies experienced a productivity growth of 3.3 per cent. Mahlberg and Url (2010) analysed the scale efficiency of the German insurance industry from 1991 through to 2006, showing that average productivity increased by 18 per cent. This growth was dominated by technical progress (+16 per cent) and higher scale efficiency (+11 per cent), while advances in pure efficiency turned out to be small (+5 per cent).
Studies on specific market niches in the insurance industry have attracted the attention of researchers, as have those which assess the impact of specific contextual, business-related variables on levels of efficiency.
When it comes to specific market niches, such as property-liability and the non-life insurance sectors, Luhnen (2009) analysed efficiency levels in the German property-liability insurance industry from 1995 to 2006. The author used a two-stage approach - running DEA in the first stage and then performing a bootstrapped truncated regression in the second, so as to analyse covariates which are able to explain efficiency. On the other hand, Abdul Kader, Adams & Hardwick (2010) studied the cost efficiency of non-life Takaful insurance firms operating in 10 Islamic countries. The author also adopted a two-stage approach, using DEA first and then the Tobit regression to test for the influence of corporate characteristics on these efficiencies.
With respect to the impact of a specific contextual variable on efficiency scores, the role of corporate governance merited attention in two studies. Xie, Lu, Reising & Stohs (2011) used DEA to examine the role of corporate governance in the U.S. life insurance industry during the 1990s and 2000s. Their findings suggest that demutualisation is value-enhancing for firms being sold through initial public offerings (IPOs), but is value-neutral for firms that convert, but remain private. Firms converting into public companies experience increased CEO turnover that leads to efficiency improvement. Corporate governance is also the subject of the study by Hsu and Petchsakulwong (2010), who examined its impact on the efficiency performance of public non-life insurance companies in Thailand from 2000-2007. Their results indicate that the characteristics of corporate governance influence the efficiency of the performance of non-life insurers. Furthermore, the independence of the Board, together with firm size has a positive impact on the efficiency of the performance of Thai non-life insurance companies. However, the audit committee size, diligence, divergence between voting rights and cash flow rights, board tenure, board age, as well as board ownership have a negative impact on the efficiency performance. Finally, there is an unclear relation between the efficiency of the performance by insurers and the size of their board, the proportion of financial expertise on an audit committee and the compensation to the board.
Specifically, with respect to African countries, fewer studies exist than expected and not even one discussed the insurance industry in Angola and Mozambique. These studies include those by: Munro and Snyman (1995), Uche (1999), Chourouk (2003), Giesbert, Sterner & Bending, (2011) and Chantarat, Mude, Barrett & Carter, (2013). More recently, Ibiwoye and Adeleke (2008) applied a logistic regression to evaluate the participation in the Nigeria National Health Insurance Scheme by employees in the formal sector. The authors concluded that awareness was a major factor affecting participation in the scheme. Olaosebikan (2012) examined the profitability of micro-life insurers in Nigeria, using a dynamic panel data model, covering data from 2004 to 2009. The results indicate that the profitability of micro-life insurers is not influenced by factors such as ownership structure, leverage and the size of firms. Profitability is found to be negatively related to the level of reinsurance. It is also interesting to note that the South African short-term insurance industry realises the importance of fostering consumer trust, which impacts its results (Steyn, Mostert & de Jager, 2008).
Taking into account the scope of methodologies and the assumptions found thus far in the literature, this paper departs from previous studies in three respects. First, the method used here, to be discussed further in Section 4, allows for the assumption of different production technologies within the sample. Studies conducted so far within the ambit of the insurance industry have been based on the common ground of homogeneous production technology, making an assumption for a sector known to operate in several market niches. Second, this study uses a more robust parametric methodology to handle simultaneously, in a one-step procedure, the impact of contextual and business-related variables on levels of efficiency. Most previous studies relied on using non-parametric DEA models with some regression procedure in a two-stage approach. Third, this method also allows the clustering of companies, based not only on market-niche classifications, but rather on the distance of the cost efficient frontier. Further details are given below.
4 Methodology
In this paper, we adopt the stochastic cost econometric frontier approach (Kumbhakar & Lovell, 2000). This approach, which was first proposed by Farrell (1957), came to prominence in the late 1970s as a result of the work of Aigner, Lovell and Schmidt (1977), Battese and Corra (1977) and Meeusen and Van den Broeck (1977). A detailed presentation and discussion of their formulae can be found in Ismail (2012).
The frontier is estimated econometrically and it measures the difference between inefficient units and frontiers through residuals. This is an intuitive approach, which is based on traditional econometrics. If we assume that residuals have two components (noise and inefficiency), then the stochastic frontier model emerges. Consequently, the main issue here is the decomposition of the error terms. Let us present the model more formally. The general frontier cost function proposed by Aigner et al. (1977) and Meeusen and Van Den Broeck (1977) is the following:

where Citrepresents a scalar cost of the decision-unit i under analysis in the t-th period; Xitis a vector of variables, including input prices and the output descriptors present in the cost function; and sit = uit + vitis the error term. This term may be decomposed into two components:
i) The error term vitis traditionally used in econometric models and is assumed to be independently and identically distributed, which represents the effect of random shocks (noise vit~N(0, σv2)) and is independent of uit;
ii) The inefficient term uitirepresents technical inefficiencies and is assumed to be positive and normally distributed with a zero mean and variance of σu2. The positive disturbance uitis reflected in a half-normal independent distribution, truncated at zero, which signifies that each insurance company's cost must lie on, or above, its cost frontier. This implies that any deviation from the frontier is caused by management factors controlled by the insurance companies.
The total variance is defined as σ2 = σ2v +o2u. The contribution of the error term to the total variation is as follows:
σ2v = σ2 /(1 + λ2) .
The contribution of the inefficient term is:
σ2 = σ2.λ2/(1 + λ2) ,
where λ is defined as:
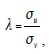
which provides an indication of the relative contribution of u and v to ε = u + v.
Given that the estimation procedures of equation (1) merely yield the residual ε, rather than the inefficiency term u. This term in the model should be calculated indirectly (Greene, 2001). In the case of panel data, such as those used in this paper, Battese and Coelli (1988) use the conditional expectation of uit, conditioned on the realized value of the error term Sit = (vit + Uit), as an estimator of uit. In other words, E[uit/ sit] is the mean productive inefficiency for the i-th insurance company at any time "t". Following Orea and Kumbhakar (2004), we can write equation (1) as a latent class frontier model:
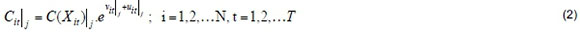
where subscript "i" denotes the insurance company, "t" indicates time and "j" represents the different classes or groups. The vertical bar signifies that there is a different model for each class "j", so each insurance company belongs to the same group during all the periods. Assuming that v is normally distributed and that u follows a half-normal distribution, the likelihood function (LF) for each insurance company "i" at time "t" for group "j" is (Cf. Greene, 2004):
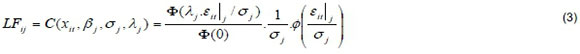
where 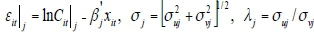 , while φdenotes the standard normal density and Φ is the cumulative distribution function. The likelihood function for insurance company "i"in group "j" is obtained as the product of the likelihood functions for each period:
, while φdenotes the standard normal density and Φ is the cumulative distribution function. The likelihood function for insurance company "i"in group "j" is obtained as the product of the likelihood functions for each period:

The likelihood function for each insurance company is obtained as a weighted average of its likelihood function for each group j, using as weights the prior probabilities of class j membership.

The previous probabilities must be within the unit interval: ο < Ρυ< 1. Further, the sum of these probabilities for each group must be one:
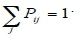
In order to satisfy these two conditions, we parameterised these probabilities as a multinomial logit, which is:

where the qiis a vector of variables which are used to split the sample and δj is the vector of parameters to be estimated. One group is chosen as the reference in the multinomial logit. The overall log-likelihood function is obtained as the sum of the individual log-likelihood functions:

The log-likelihood function can be maximized with respect to the parameter set θj = (β j,σj,λj ,δj), using conventional methods (Greene, 2004). Furthermore, the estimated parameters can be used to estimate the posterior probabilities of class membership, using the Bayes Theorem:

An important issue in these models is how to determine the number of classes. The usual procedure is to estimate several models with different numbers of groups and then use a statistical test to choose the preferred model. Greene (2005) proposed testing 'down', by which, beginning from a J* known to be at least as large as the true J, one can test down, given that the J-1 class model is nested with the J class model, imposing Oj= Oj-1, based on likelihood ratio tests1. An alternative is to use information criteria, such as the Akaike Information Criterion (AIC), or the Schwarz Bayesian Information Criterion (SBIC). These statistics are calculated using the following expressions:

where LF(J) is the value that the likelihood function takes for J groups, m is the number of parameters used in the model and n is the number of observations. The preferred model will be the one for which the value of the statistic is the lowest.
Based on the panel data, this paper presents the maximum likelihood estimators of Model (1), which are the same as those found in other authors' recent studies (Greene, 2001, 2004, 2005).
5 Data and Empirical Specification
Frontier models require the identification of inputs (resources) and outputs (transformation of resources). Several criteria can be used in their selection. The first of these, an empirical criterion, is availability. Second, the literature survey is a way of ensuring the validity of the research, which represents another criterion that should be taken into account. The third criterion for measurement selection is that of the professional opinion of relevant individuals. In this paper, we abide by all three criteria and take into account the overview by Cummins and Weiss (2002). To estimate the cost frontier, we used balanced panel data for insurance companies in Angola and Mozambique, during the period 2002-2012. The data were obtained from the annual financial reports of the insurance companies, which are published by the chosen regulatory agencies (Instituto de Supervisão de Seguros de Angola and Instituto de Supervisão de Seguros de Mozambique). The insurance companies considered for this analysis were presented above in Section 2 and were selected on the basis of the available data. They comprise 100 per cent of the insurance companies in Angola and Mozambique. Their pooled sample densities are presented in Figure 1.
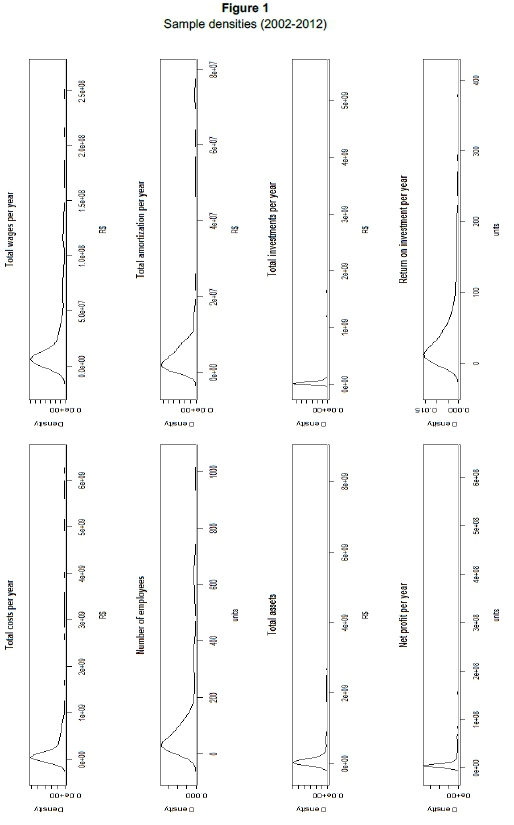
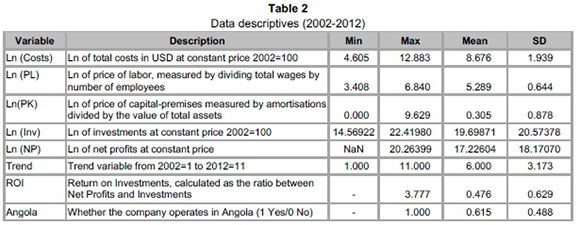
Given the scarce guidance from the literature review as to which variables to use for the analysis, we rely on microeconomics (Varian, 1987) to choose the outputs and inputs. Outputs are variables that measure the results of production, such as dividends paid to stockholders and investments. Examples of inputs are labour, capital and other relevant microeconomic prices. In our study, the cost equation includes two outputs (net profit and investments) and two input prices (the price of labour and the price of capital premises). Whilst Table 1 provides some values for 2012, Table 2 shows the descriptive statistics for the variables used in the empirical analysis. We note that the average Angolan and Mozambican insurance company is characterised as having a high level of heterogeneity.
The empirical specification of the average cost frontier used is the Translog. We have chosen a flexible functional form in order to avoid imposing unnecessary prior restrictions on the technologies to be estimated. Each explanatory variable is divided by its geometric mean. In this way, the Translog can be considered as an approximation to an unknown function and the first order coefficients can be interpreted as the cost elasticities, evaluated at the sample geometric mean. We also included time dummies for each year, in order to obtain some temporal changes. Thus, the equation used to estimate this is:

where C is the endogenous variable, Inv is the investment level, NP is the net profit, PL is the price of labor, PK is the price of capital, t is a time trend, v is a random error which reflects statistical noise and is assumed to follow a normal distribution centered at zero, and, finally, u reflects inefficiency and is assumed to follow a half-normal distribution.
6 Results
The latent model in Eq. (11) was estimated by maximum likelihood, starting from the R packages frontier (Coelli & Henningsen, 2013) and flexmif (Leisch, 2004) and then observed the discussion in Murillo-Zamorano (2004) for separating the composed error term and for getting estimates on sigma and lambda, which is necessary for efficiency analysis. The preferred model was the one with three groups, in accordance with AIC criteria.
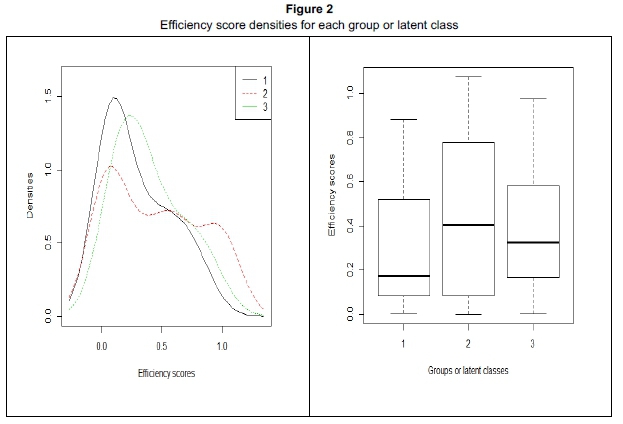
Table 3 presents the results for the standard cost frontier, assuming that only one cost frontier represents all the data in the sample. Table 4, in turn, displays the estimates of the three-class model, while Figure 2 presents their distribution densities. As expected, total variance is smaller when three different groups are allowed. In fact, latent class models usually classify observations by reducing group variance in order to maximise the value of the total likelihood function. On the other hand, high lambda values for latent class model estimations tell us that randomness is less important than inefficiency, when we want to explain the distance of insurance companies to the frontier. Insurance companies from group 3 could be characterised as capital intensive, in comparison.
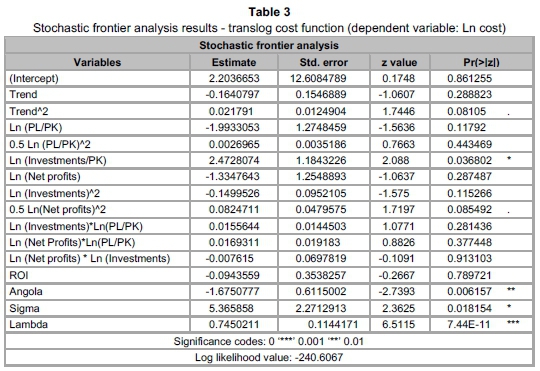

A perusal of the results of Table 4 reveals that the estimated coefficients' signs for the labour-capital price ratio are the same for all the groups. Therefore, the higher the labour-capital price ratio (capital intensity), the lower the cost for obtaining a positive financial result in the insurance industry. An important result in support of the latent class model estimation is that the differences of the input price-ratio coefficients among the groups are statistically significant, especially with respect to Group 3, which encompasses smaller insurance companies (lower total costs). These results suggest that at least three different technologies are used to generate financial results in the African insurance industry. Furthermore, we verify that the labour-capital price ratio coefficients are lower than one in all the models, which verifies the homogeneity restriction that was not imposed on the function.
In Table 5, we show the means of some representative variables for the groups obtained with the latent class model. This verifies that large Angolan and Mozambican companies are concentrated in Group 2, small Angolan companies in Group 3 and medium-sized companies, predominantly from Mozambique, are in Group 1. This means that insurance companies are not defined by cultural issues, but rather by their size. Moreover, in all three groups, the efficiency with the latent class model tends to be higher than that of the pooled model (cf. Figure 3). This result suggests that, to some extent, the standard stochastic frontier, which imposes only one technology, overestimates inefficiency as opposed to the case of the latent class model. Besides, insurance companies were assigned into groups on the basis of the posterior probability of class membership.
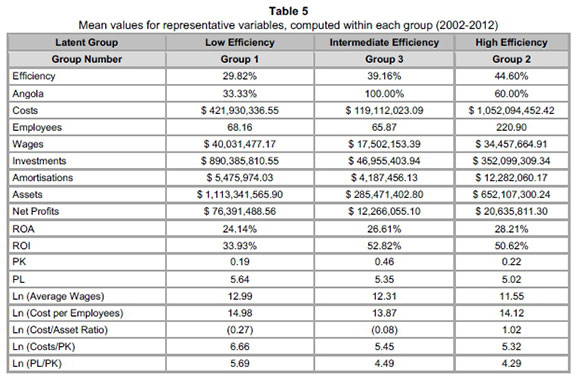
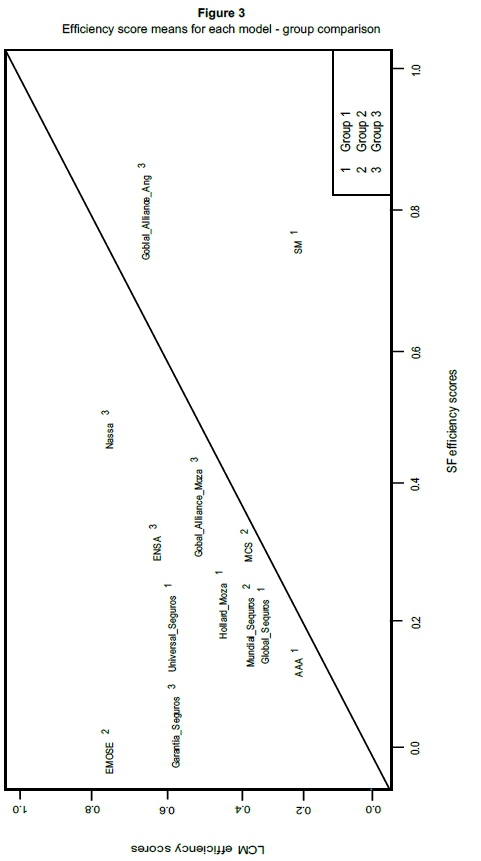
Figure 4 presents a comparison between groups for selected variables and puts these different production technologies into perspective in terms of their levels of efficiency. Although levels of efficiency appear to increase when traditional financial ratios are used, such as ROI and ROA (upper Figure 4), the role of two major production inputs, measured in terms of labour and capital, cannot be neglected. While the impact of labour prices on efficiency - lower labor prices imply higher efficiency levels - is clearly in evidence, the impact of capital prices is more subtle (middle Figure 4). The levels of efficiency tend to increase when capital prices account for larger proportions of the total cost (lower ln(Cost/PK) ratios. Furthermore, a quick inspection of the single-output, single-input measurement of capital productivity (ln(Cost/Asset ratio)) corroborates the finding that the most efficient companies are those that deliver a greater number of outputs (costs), given a current level of assets (inputs).
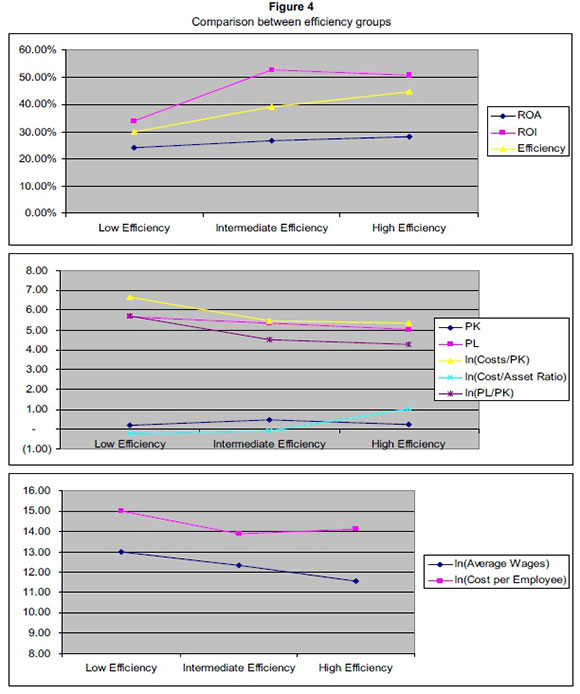
In summary, the results indicate that those insurance companies from Mozambique and Angola that belong to Group 2 can be characterised as being large insurance companies, with capital-intensive production processes and lower labour costs, resulting in greater financial indicators and better levels of efficiency. Group 3 consists of small Angolan firms, without access to cheap capital prices, although the average cost per employee is similar to that of larger firms (Figure 4). This constraint for accessing low-price capital sources may jeopardise this group in the long term. On the contrary, Group 1 firms are middle-sized, with low capital-prices, similar to those of Group 2. These companies, however, account for the largest wages paid by the industry, which contributes to lower financial indicators and levels of efficiency.
7 Conclusions
This paper proposes a simple framework for the comparative evaluation of African insurance companies located in Angola and Mozambique and also for the rationalization of their operational activities. The analysis was conducted by implementing a finite mixture stochastic frontier model, which allows the incorporation of a broad variety of inputs and outputs, while at the same time permitting researchers to account for segments in the sample and for the existence of heterogeneity in the data. The main result is that three groups are identified among the sample of insurance companies from Angola and Mozambique, adopting different production technologies to obtain the results for both countries. Therefore, as long as general guideline policies can be defined for the whole sample, based on common value, such as the same sign for the variables between groups, no common policy can cater simultaneously for all the specificities embedded within each group.
The main policy implication of the findings of this analysis is that heterogeneity must be considered a major factor for African insurance companies located in Mozambique and Angola. The insurance companies are not clustered according to their nationality, which signifies that nationality is not a crucial determinant of efficiency. This being the case, authorities could implement policies by defining groups by size, with the aim of regulating the insurance industry. Besides, two out of the three groups identified indicate that most insurance companies are still relatively small in comparison with their peers in foreign, more-developed countries. Future mergers and acquisitions thus appear to be the natural path for achieving gains in efficiency and for absorbing new production technologies. Consequently, it is forecast that the frequency of mergers and acquisitions in the Angolan and the Mozambican insurance industry will increase in the near future.
The results also give insight into the main causes of the differences in levels of efficiency. These are basically related to the differences between relative prices within groups. More specifically, levels of efficiency are lower in Group 1, owing to higher relative labour prices in comparison with the two other groups, in both absolute and relative terms. Capital prices, however, exert a beneficial impact on the levels of efficiency of Group 2 companies, together with lower labour prices, which supports the perspective that insurance is one of the industries where capital presents the highest marginal productivity (Amores & Raa, 2014). Regulatory policies and incentives could be designed to ensure access to cheap sources of capital for small-sized insurance companies in Angola (Group 3), which would foster competition is this country.
Ruling implications can also be derived according to these results. Insurance companies in Angola and Mozambique should adopt a benchmark procedure as a means of evaluating their efficiency throughout the year and then could follow the same best practice procedures used by more efficient companies, especially when it comes to the labour prices observed in Group 1. This exercise could be carried out by the association of those insurance companies that belong to the same group, in order to facilitate the adoption of procedures that will empower them to achieve an increase in efficiency.
References
ABDUL KADER, H., ADAMS, M. & HARDWICK, P. 2010. The cost efficiency of takaful insurance companies. Geneva papers on Risk Insurance-Issues and Practice, 35:161-181. [ Links ]
AIGNER, D.J., LOVELL, C.A.K. & SCHMIDT, P. 1977. Formulation and estimation of stochastic frontier production function models. Journal of Econometrics, 6(1):21-37. [ Links ]
AMORES, A.F. & RAA, T. 2014, Firm efficiency, industry performance and the economy: Three-way decomposition with an application to Andalusia. Journal of Productivity Analysis. Available at: DOI 10.1007/s 11123-014-0384-0. [ Links ]
BARROS, C.P., BARROSO, N. & BORGES, M.R. 2005. Evaluating the efficiency and productivity of insurance companies with a malmquist index: A case study for Portugal. The Geneva Papers on Insurance-Issues and Practice, 30(2):244-267. [ Links ]
BARROS, C.P., NEKTARIOS, M. & ASSAF, A. 2010. Efficiency in Greek insurance industry. European Journal of Operational Research, 205(2):431-436. [ Links ]
BATTESE, G.E. & CORRA, G.S. 1977. Estimation of a production frontier model: With application to the pastoral zone of eastern Australia. Australian Journal of Agricultural Economics, 21(3): 169-179. [ Links ]
BATTESE, G.E. & COELLI, T.J. 1988. Prediction of firm-level technical efficiencies with a generalized frontier production function and panel data. Journal of Econometrics, 38(3):387-399. [ Links ]
BERTONI, F. & CROCE, A. 2011. The productivity of European life insurers: Best-practice adoption vs. innovation. Geneva Papers on Risk and Insurance-Issues and Practice, 36(2):165-185. [ Links ]
BIENER, C. & ELING, M. 2011. The performance of microinsurance programs: A data envelopment analysis. The Journal of Risk and Insurance, 78(1):83-115. [ Links ]
CHANTARAT, S., MUDE, A.G. BARRETT, C.B. & CARTER, M.R. 2013. Designing index-based livestock insurance for managing asset risk in northern Kenya. The Journal of Risk and Insurance, 80(1): 205-237. [ Links ]
CHOUROUK, H. 2003. Pensions in North Africa: The need for reform. The Geneva Papers on Risk and Insurance, 28(4):712-726. [ Links ]
COELLI, T. & HENNINGSEN, A. 2013. Package frontier. Available at: <http://cran.r-project.org/web/packages/frontier/frontier.pdf [accessed December 2013].
CUMMINS, J.D., RUBIO-MISA, M. & ZI, H. 2004. The effects of organisational structure on efficiency: Evidence from Spanish insurance industry. Journal of Banking and Finance, 28(12):3113-3150. [ Links ]
CUMMINS, J.D., TURCHETTI, G. & WEISS, M.A. 1996. Productivity and technical efficiency in the Italian insurance industry. Working Paper. Available at: http://fic.wharton.upenn.edu/fic/papers/96/9610.pdf [accessed May 2015]. [ Links ]
CUMMINS, J.D. & WEISS, M.A. 1993. Measuring cost efficiency in the property liability insurance industry. Journal of Banking and Finance, 17(2/3):463-481. [ Links ]
CUMMINS, J.D., WEISS, M.A. & ZI, H. 1999. Organizational form and efficiency: The coexistence of stock and mutual property-liability insurers. Management Science, 45(9):1254-1269. [ Links ]
CUMMINS, J.D. & WEISS, M.A. 2002. Analysing firm performance in the insurance industry using frontier efficiency methods. In G. Dionne (ed.) Handbook of insurance economics, Boston, Kluwer, Chapter 26. [ Links ]
CUMMINS, J.D. & XIE, X. 2008. Mergers and acquisitions in the US property liability insurance industry: Productivity and efficiency effects. Journal of Banking and Finance, 32 (1):30-55. [ Links ]
CUMMINS, J.D. & ZI, H. 1998. Comparison of frontier efficient methods: An application to the US life insurance industry. Journal of Productivity Analysis, 10(2):131-152. [ Links ]
DIACON, S.R., STARKEY, K. & O'BRIEN, C.O. 2002, Size and efficiency in Europeanlong-term insurance companies: An international comparison. The Geneva Papers on Risk and Insurance-Issues and Practice, 27(3):444-466. [ Links ]
ELING, M. & LUHNEN, M. 2010. Efficiency in the international insurance industry: A cross- country comparison. Journal of Banking and Finance, 34(7): 1497-1509. [ Links ]
ENNSFELLNER, K.C., LEWIS, D. & ANDERSON, R.I. 2004. Production efficiency in the Austrian Insurance industry: A Bayesian examination. The Journal of Risk and Insurance, 71(1):135- 159. [ Links ]
FARRELL, M.J. 1957. The measurement of productive efficiency. Journal of the Royal Statistical Society, Series A (General), 120(3):253-290. [ Links ]
FECHER, F., KESSLER, D., PERELMAN, S. & PESTIEU, P. 1993, Productive performance of the French Industry. Journal of Productivity Analysis, 4(1/2):77-93. [ Links ]
FENN, P., VENCAPPA, D., DIACON, S., KLUMPES, P. & C. O'BRIEN, 2008. Market structure and efficiency of European insurance companies: A stochastic frontier analysis. Journal of Banking and Finance, 32(1):86-100. [ Links ]
FUKUYAMA, H. 1997. Investigating productive efficiency and productive changes of Japanese life insurance companies. Pacific-Basin Finance Journal, 5(4):481-509. [ Links ]
GARDNER, L.A. & M. F. GRACE, 1993. X-Efficiency in the US life insurance industry. Journal of Banking and Finance, 17(2/3):497-410. [ Links ]
GIESBERT, L., STEINER, S. & BENDING, M. 2011. Participation in micro life insurance and the use of other financial services in Ghana. The Journal of Risk and Insurance, 78(1):7-35. [ Links ]
GRANDE, M. & TEIXEIRA, A.A.C. 2012. Corruption and multinational companies' entry modes - do linguistic and historical ties matter? SAJEMS NS, 15(3):269-281. [ Links ]
GREENE, W. 2001. Econometric software. In International encyclopedia of the social and behavioral science, N.J. Smelser & P.B. Baltes (eds.) Amsterdam, New York: Elsevier. [ Links ]
GREENE, W. 2004. Distinguishing between heterogeneity and inefficiency: stochastic frontier analysis of the world health organization's panel data on national health care systems. Health Economics, 13:959-980. [ Links ]
GREENE, W, 2005. Reconsidering heterogeneity in panel data estimators of the stochastic frontier models. Journal of Econometrics, 126(2):269-303. [ Links ]
HSU, W.Y. & PETCHSAKULWONG, P. 2010. The impact of corporate governance on the efficiency performance of the Thai non-life insurance industry. The Geneva Papers on Risk Insurance-Issues and Practice, 35(1):28-49. [ Links ]
IBIWOYE, A. & ADELEKE, I. 2008. Does national health insurance promote access to quality health care? Evidence from Nigeria. The Geneva Papers on Risk and Insurance-Issues and Practice, 33(2):219-233. [ Links ]
ISMAIL, M. 2012. Performance of data envelopment and stochastic frontier models in the presence of misspecification, multicollinearity and outliers. Germany: Lambert Academic Publishing, Saarbrucken. [ Links ]
KUMBHAKAR, S. & LOVELL, K. 2000. Stochastic frontier analysis. Cambridge: Cambridge University Press. [ Links ]
LEISCH, F. 2004. FlexMix: A general framework for finite mixture models and latent class regression in R. Journal of Statistical Software, 11(8):2-18. [ Links ]
LUHNEN, M. 2009. Determinants of efficiency and productivity in german property-liability insurance: Evidence for 1995-2006. The Geneva papers on risk Insurance-Issues and Practice, 34(3):483-505. [ Links ]
MAHLBERG, B. & URL, T. 2003. The effects of the single market on the Austrian insurance industry. Empirical Economics, 28(4): 813-838. [ Links ]
MAHLBERG, B. & URL, T. 2010. Single market effects on productivity in the German insurance industry. Journal of Banking and Finance, 34(7):1540-1548. [ Links ]
MEEUSEN, W. & VAN DEN BROECK, J. 1977. Efficiency estimation from a translog production function with composed error. International Economic Review, 18:435-444. [ Links ]
MUNRO, A.R. & SNYMAN, A. 1995, The life insurance industry in South Africa. Geneva Papers on Risk and Insurance Issues and Practice, 20(75): 127-140. [ Links ]
MURILLO-ZAMORANO, L.R. 2004. Economic efficiency and frontier techniques. Journal of Economic Surveys, 18(1):33-77. [ Links ]
NEKTARIOS, M. & BARROS, C.P. 2010. A Malmquist index for the Greek insurance industry. The Geneva Papers On Risk Insurance-Issues and Practice, 35:309-324. [ Links ]
OLAOSEBIKAN, O. 2012. The determinants of the profitability of micro-life insurers in Nigeria. The Geneva Papers on Risk and Insurance-Issues and Practice, 38:140-159. [ Links ]
OREA, L. & KUMBHAKAR, S. 2004. Efficiency measurement using a latent class stochastic frontier model. Empirical Economics, 29(1):169-183. [ Links ]
OUTREVILLE, J.F. 2008. Foreign affiliates of the largest insurance groups: Location-specific advantages. The Journal of Risk and Insurance, 75(2):463-491. [ Links ]
STEYN, T.F.J., MOSTERT, P.G. & DE JAGER, J.N.W. 2008. The influence of length of relationship, gender and age on the relationship intention of short-term insurance clients: An exploratory study. SAJEMS NS, 11(2):139-156. [ Links ]
THE ECONOMIST. 2010. South of the Sahara, 22nd November. Available at: http://www.economist.com/node/17493372?story_id=17493372 [accessed May 2015].
UCHE, C.U. 1999. Government ownership of insurance companies in Nigeria: A critique. The Geneva papers on Risk and Insurance-Issues and Practice, 24:216-227. [ Links ]
VARIAN, H.R. 1987. Intermediate microeconomics: A modern approach. New York: NY: W.W. Norton & Company. [ Links ]
XIE, X., LU, W., REISING, J. & STOHS, M.H. 2011. Demutualisation, control and efficiency in the U.S. life insurance industry. The Geneva papers on risk Insurance-Issues and Practice, 36(2):197-225. [ Links ]
Accepted: April 2015
1 The statistic is constructed as - 2 (logLFr- logLFu), where LFrand LFuare the log-likelihood functions evaluated at the restricted and unrestricted estimates. The statistic under the null hypothesis, 9/= 9ti, follows a chi-squared distribution, with degrees of freedom equal to the number of restrictions being tested. If the null hypothesis is rejected, then the preferred model is the one with J classes.














