Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Economic and Management Sciences
On-line version ISSN 2222-3436
Print version ISSN 1015-8812
S. Afr. j. econ. manag. sci. vol.18 n.2 Pretoria 2015
http://dx.doi.org/10.17159/2222-3436/2015/v18n2a10
ARTICLES
The influence of volatility spill-overs and market beta on portfolio construction
André Heymans; Wayne Peter Brewer
School of Economics, North-West University
ABSTRACT
This study adds to Modern Portfolio Theory (MPT) by providing an additional measure to market beta in constructing a more efficient investment portfolio. The additional measure analyses the volatility spill-over effects among stocks within the same portfolio. Using intraday stock returns from five top-40 listed stocks on the JSE between July 2008 and April 2010, volatility spill-over effects were estimated with a residual- based test (aggregate shock [AS] model) framework. It is shown that when a particular stock attracted fewer volatility spill-over effects from the other stocks in the portfolio, the overall portfolio volatility decreased as well. In most cases market beta showcased similar results. Therefore, in order to construct a more efficient risk- adjusted portfolio, one requires both a portfolio that has a unit correlation with the market (beta-based), and stocks that showcase the least amount of volatility spill-over effects amongst one another. These results might assist portfolio managers to construct lower mean variance portfolios.
Key words: modern portfolio theory, EMH, beta, volatility spill-over effects
1 Introduction
Modern portfolio theory (MPT) has long been placing emphasis on using market beta as a measure in constructing an efficient portfolio; and because of its simplicity, beta has seen substantial integration into modern-day portfolio management. Portfolio managers therefore aim to construct portfolios with a unit-beta under the efficient market hypothesis (EMH), translating to a well-diversified portfolio that is considered entirely hedged against non-systematic risk. However, in the light of these assumptions the beta measure does not capture all the relevant information pertaining to stock selection and allocation. Firstly, beta has been known to be an unstable measure in the wake of stock market anomalies, and secondly, beta only tells a portfolio manager more about the mean returns between stocks (Longin & Solnik, 1995; Kaminsky & Reinhart, 1998; Maniya & Magnusson, 2010). In addition, systematic risk still remains even after fully diversifying in accordance with beta. In this regard volatility within and among stocks in a portfolio impacts on the profitability of the portfolio, as well as the portfolio's overall risk profile. There is a wealth of information that is captured by the price fluctuations of stocks in a portfolio. These price fluctuations also exhibit co-varying properties. Understanding this concept is of utmost importance when a particular economy only offers a limited number of stocks.
Since portfolio managers in smaller economies such as South Africa's are limited in their choice of stocks, it becomes increasingly difficult to fully diversify a stock portfolio given volatility spill-over effects among stocks listed on the same exchange. In such a setting, using only beta to construct a portfolio that tracks the market or attempts to outperform a market index, may lead to substandard risk-weighted portfolio returns, which could have been avoided if the impact of volatility spill-over effects during the portfolio construction phase had been considered. If a limited number of stocks in an equity market is not enough to persuade the use of additional measures, then times of financial distress should necessitate their use. In this sense, we focused on volatility spill-over effects as an additional measure to enhance portfolio selection and asset allocation.
The rest of the paper is structured as follows: Section 2 provides a literature review of portfolio theory and capital market anomalies that investors have to negotiate. Section 3 presents the methodology for this study, while section 4 describes the data used, and how proxy stocks were formulated to test the hypothesis that an increase in volatility spill-over effects leads to greater portfolio variance. The empirical results are given in section 5, and in section 6 further avenues of study are provided. Section 7 concludes the paper.
2 Background
Modern portfolio theory (MPT) was developed by Markowitz (1952, 1956, 1959) and various authors in the 1960s, most notably Sharpe (1964), have reshaped the way in which portfolio managers approach portfolio risk (Rubinstein, 2002:1044). In essence MPT started off as a suggestion that portfolio risk is determined by the co-variances of assets included within a portfolio. By the mid-1960s MPT evolved to include the capital asset pricing model (CAPM), which relied on a market- related measure of risk, called market beta, to price a portfolio of assets. Empirically, beta for asset t can be expressed as:

where Cov (Ri,RM) is the covariance between the return on asset t and the return on the market portfolio. However, CAPM is based on a multitude of underlying assumptions, which include the efficiency of the market. This market efficiency was presented by Fama (1965, 1970, 1976) as the efficient market hypothesis (EMH), a theory fervently debated in the literature since the early 1970s (Brown & Reilly, 2009). Various studies have indicated that the "random walk" hypothesis does not accurately hold, because stock prices do exhibit patterns during price development (Jegadeesh & Titman, 1993; Lo & MacKinlay, 1999). This is especially important when considering that stock market anomalies are known to cause serial correlation in returns, providing a different dynamic to portfolio management (Fama, 1965). If markets were inefficient to a significant extent, the market measure of risk (beta) could be an ineffective risk measure when constructing a stock portfolio, prompting the use of another measure for such a task.
It is therefore not surprising that capital market efficiency has been thoroughly researched, with ample evidence that most developed markets are efficient, but that various anomalies exist. It has been reported, for example, that markets can never be perfectly informationally efficient (Grossman & Stiglitz, 1980). Information is costly, resulting in prices that do not perfectly reflect the information that is available, therefore leaving some incentive for information-gathering (security analysis) within a market equilibrium model. It is these information asymmetries that cause volatility to be more integrated in the prices and returns of assets. Therefore, in order to price securities, diversify portfolios and hedge portfolio risk effectively, it is important to gain an in-depth understanding of volatility. This understanding should, however, not only be limited to the co-variance in returns (as MPT proposes), but should also encompass the volatility transmission between stocks. It is furthermore important also to look at shorter, and more revealing, intraday returns instead of only focusing on the volatility of daily returns. Since the financial market microstructure reveals so much about the patterns in volatility, it is not surprising that a large body of research has been devoted to understanding it (Tse & Yang, 2012).
Market microstructure analysis is an important tool in discerning the interaction between trading procedures and security price formation, because price formation is related to a security's return volatility (Tian & Guo, 2007:289). For instance, numerous empirical studies found that daily volatility of consecutive opening prices is typically higher than consecutive closing prices, with flattened volatility in between the daily opening and closing prices of a security.1 This typically forms a 'U' shape volatility distribution, first recognised and published by Wood, Mclnish and Ord (1985). The specific timing of transaction events in a period of time (such as intraday data as opposed to daily data) is a significant economic variable which needs to be modelled, and for further relevance, forecast (Andersen, Bollerslev, Diebold & Labys, 2003). This is imperative because transaction timing of securities and the volatility it implies is an important study in the field of portfolio management. It has been shown that the use of daily squared returns delivers inferior forecasting potential to the average of intraday squared returns (known as realised volatility) due to excessive noise,2 and has been seminal in improving volatility forecasts and the management of portfolios (Andersen & Bollerslev, 1998). These financial market microstructure theories are usually tested on an intraday transaction-by-transaction basis in order to improve the modelling of the moments of the return distribution (Andersen et al., 2003).
However, it is not only the return distribution that factors into the pricing of assets and securities, but also its volatility dynamics. Considering that the arrival of new information exemplifies volatility within securities, it should be reasonable to assume that volatility transmits to other securities. According to the mixture of distribution hypothesis (MDH), volatility (or the variance in returns) is an increasing function of arrival information.3 Given the dynamics of this hypothesis, it is reasonable to assume that the volatility spill-over effect between stocks is attributable to information spill-overs, a phenomenon more prevalent during times of financial distress. This was again visible during the financial crisis of 2007/08, proving that, on the whole, the correlation between assets, asset classes and economies is increased during such profound crises. This increase in correlation leads to distinguishable patterns during financial distress. These patterns are seen in returns and volatility of differing assets of the same type (e.g. stocks listed on the same exchange) and different markets are biased in moving together (Bauwens, Laurent & Rombouts, 2006:79; Poon, 2005:8). Numerous studies have found that the correlation between asset volatilities is stronger than that of asset returns and that both volatility and return correlations tend to increase during bear markets and financial crises (Longin & Solnik, 1995; Maniya & Magnusson, 2010; Beirne et al., 2013). A stock portfolio's second moment interdependencies therefore tend to become noisier during financial distress, not because of riskier stocks, but rather because of unstable non-systematic (market) conditions. Volatile market conditions therefore expose a stock portfolio to harsher volatility circumstances than would otherwise be the case if the stocks only impacted on one another, therefore causing positive co-integration.
When there is an interdependent relationship between stocks, these interdependencies will be an increasing function of arrival information relating to the market (Kitamura, 2010:159). Of particular interest are asymmetric information influences, which are especially prevalent during times of financial turmoil, and how these translate into volatility transmission between stocks. These volatility spill-over effects between different assets refer to causality in return variance, and have been closely studied in the field of financial economics (Kitamura, 2010:158).4 This has followed from the analysis of financial market microstructure, which in turn has created a need for the development of volatility models to accurately estimate large covariance matrices (McAleer & Veiga, 2008:3). Because of the particular prevalence of distinct intraday volatility patterns, which underlies most of the financial market microstructure literature, higher-frequency returns exemplify highly persistent conditionally heteroskedastic elements together with discrete information arrival effects (Andersen, Bollerslev & Das, 2001:306). For a greater understanding of microstructure elements, such as the presence of heteroskedasticity, volatility must be modelled with an adequate process such as a Generalised AutoRegressive Conditional Heteroskedastic (GARCH) model.
3 Methodology
The widespread use of Engle's (1982) (AutoRegressive Conditional Heteroskedastic) ARCH-type models is based on their ability to capture several dynamics of financial returns, including time-varying volatility, persistence and clustering of volatility, asymmetric reactions to positive and negative shocks and therefore volatility spill-over effects (McAleer & Veiga, 2008:2). More specifically, the Exponential Generalised AutoRegressive Conditional Heteroskedastic (E-GARCH) model, proposed by Nelson (1991), provides the basis for testing volatility spill-over effects. This specification improves on the standard ARCH models since it formulates conditional volatility as a function of both the magnitude and direction of shocks (Samouilhan, 2006:250).
In order to determine the impact of volatility spill-over effects on portfolio variance, we make use of an E-GARCH process within an Aggregate Shock (AS) model framework.5 The AS model follows a two-step procedure in which fitted values for etand htin equations 2 and 4 respectively, are obtained. These fitted values are then respectively substituted into equations 3 and 5, before revealing the estimated equations. In the AS model, the alternative stock returns (AltS) in a given portfolio are specified as:

where Btis the returns of an alternative stock within the same portfolio for period t; and et captures the factors that affect returns which are unexplained by the autocorrelation of the current period stock returns with the previous period stock returns (persistence or volatility clustering). Thus, etrepresents that part of stock returns which cannot be explained based on available public information when equity trading is initiated at the start of each period. Stock returns at the same period t, can be modelled as:

Equation 3 includes a coefficient φ which is the relationship between the returns on stock B and the returns on stock A, all of which are within the same portfolio. The error term etnow represents the unexplained returns on stock B for period t. An E-GARCH process is used in order to determine the level of volatility spill-over between stock B and stock A. We follow a univariate E-GARCH approach to eliminate the potential "curse of dimensionality""6 It is assumed that the error term etin equation 2 has a variance that follows an E-GARCH process:

where the natural log of the conditional variance for et in period t is a function of: the time invariable mean reversion value,  the natural logarithm of the past conditional variance, ln hBt-1, as well as the level of the standardised residuals,
the natural logarithm of the past conditional variance, ln hBt-1, as well as the level of the standardised residuals,  , and absolute value of the standardised residuals,
, and absolute value of the standardised residuals,  , The asymmetric effect is denoted by γ, while δ measures the persistence of shocks to the conditional variance. The subscript B denotes an alternative stock (Stock B).7 Finally, it is assumed that the error term on stock A returns, ut, has a variance that follows an E-GARCH process:
, The asymmetric effect is denoted by γ, while δ measures the persistence of shocks to the conditional variance. The subscript B denotes an alternative stock (Stock B).7 Finally, it is assumed that the error term on stock A returns, ut, has a variance that follows an E-GARCH process:

The model specification of the variance of stock A in equation 5 includes an alternative stock (stock B)measure, hB,t, which allows for explicit testing of the relation between stock A's volatility and stock fi's volatility. The KjhB,t term in equation 5 is stock B's conditional variance term, and denotes the relation between stock A's volatility and that of stock B. The inclusion of the terms  , and
, and 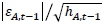 , makes it possible to model the asymmetric volatility (with γ measuring the asymmetric effect) to past shocks as long as γ2 ≠. If γ2 < 0 then negative shocks (bad news/negative past errors) will have a larger effect on volatility than positive shocks (good news/positive past errors). When γ2 > 0, positive shocks cause a greater effect than negative shocks. The persistence of these shocks are once again measured by δ.
, makes it possible to model the asymmetric volatility (with γ measuring the asymmetric effect) to past shocks as long as γ2 ≠. If γ2 < 0 then negative shocks (bad news/negative past errors) will have a larger effect on volatility than positive shocks (good news/positive past errors). When γ2 > 0, positive shocks cause a greater effect than negative shocks. The persistence of these shocks are once again measured by δ.
By using the AS model in this way, it is possible to measure what volatility was added to each stock by other stocks. This measurement is important since it allows us to make meaningful diversification choices. Should a specific combination of stocks exhibit fewer volatility spill-overs than another combination of stocks, the first combination would be deemed a more efficient portfolio. The results of these tests also allow us a glimpse into the underlying relationship between the stocks in the portfolio. It is this underlying relationship that eventually determines how portfolio variance will change in future.
4 Data
The data used in this study consist of intraday stock returns from five stocks listed on the JSE top-40 index. The five stocks are Anglo-America, ABSA, Bidvest, SABMiller and Sasol. The stock price of each of these stocks was refined down to hourly prices for each trading day. This allowed for eight data points per trading day as trading starts at 09:00am on the JSE, and closes at 05:00pm. These hourly prices are converted into hourly returns, which is useful when considering the interpretation of the results that follow. Results are therefore given, for example, as average returns per hour.
The data for each of these stocks span a period from the 1st of July 2008 until the 30th of April 2010. This single period was broken up into 10 lesser periods (spanning 2 months each), which were chosen at random, but which still provide thorough coverage of the period as a whole. These periods provide a chance to capture volatility spill-over effects for a period just before the Lehman Brothers' bankruptcy on 15 September 2008, and subsequent periods thereafter.
In addition, to measure market beta, the JSE All Share index (J203) is used. Daily returns on the J203 are estimated using the closing price of each day. The same method is then applied for estimating the returns for each stock in any given portfolio (for comparability).8 Daily beta is utilised because realised (intraday) beta is shown to be less persistent and predictable (Andersen, Bollerslev, Diebold & Wu, 2006).
Formulation of proxy stocks
In order to test whether volatility spill-overs between stocks play a noticeable part in overall portfolio risk, it is necessary to create proxy stocks of each stock within the portfolio during a given period. A Monte Carlo simulation was utilised in generating each of the proxy stocks' returns. This involves a stochastic process that, given the probability, p,simulates random returns with a given mean, μ, and standard deviation, σ. The purpose of the Monte Carlo simulation is to provide a proxy stock with characteristics that exhibit (approximately) identical returns and risk to the actual stock it replaces within the portfolio (during a particular period). In reality it would be difficult to find stocks within a market that replicate another stock's mean and standard deviation. In order to test whether volatility spill-over effects do play a role in the overall risk of the portfolio, it is imperative that proxy stocks are used that replicate the actual stocks' mean and specifically their standard deviation. Table 1 provides the name of the actual stock and its designated proxy.

In each period, the mean and standard deviations of the original five-stock portfolio are measured. The proxy stocks are then used interchangeably to replace each of their actual stocks, and the portfolio's mean and standard deviation are once again measured (for each period). The original stock portfolio is called "Portfolio", while "Portfolio X", for instance, is the portfolio where stock BVT is replaced by its proxy (stock X), and so forth.9 The volatility spill-overs between these stocks are measured to determine whether there is noticeable interaction between volatility spillover effects and overall portfolio risk. To ensure that the results of the volatility spill-over effects are not skewed, an equally- weighted portfolio methodology was used.
Each portfolio has its own mean (μ) and standard deviation (σ). Markowitz (1952) has shown that the co-variances between stocks within the same portfolio play a part in determining overall portfolio risk. This research, however, focuses on the volatility spill-over effects between the stocks in the same portfolio. The ultimate aim is to ascertain whether overall portfolio risk declines when overall volatility spill-overs to the proxy (replacement) stock are less than those of the actual stock (for example, "stock X" acting as a substitute for "BVT"), with portfolio return kept constant. By doing this, it is possible to test whether portfolio risk declines when a stock is replaced by another with similar first and second moment characteristics but fewer volatility spillover effects, and thus, whether volatility spill-overs add a different dimension to portfolio selection than that of beta.
Considering the impact of portfolio mismanagement, it is of utmost importance to include all (or most) of the relevant measures that may indicate the most efficient portfolio. In this respect, beta is the most widely used measure for portfolio selection and allocation. However, more factors are at play than mere stock return co-variances (as measured by beta). Volatility also exhibits spillover effects between stocks within a portfolio. Therefore, a process is followed by means of replacing a stock with a proxy stock that retains the mean and standard deviation of the actual stock. However, portfolio mean and standard deviations are not bound in the same way, and may change as the volatility spill-overs differ between the actual stock and its proxy. Table 2 gives a full representation of the descriptive statistics of both the original stocks and their proxies.
The skewed nature of each of the original stocks is fairly high when compared to their proxies. This makes the proxy stocks less prone to outliers than the actual stocks they emulate. This observation can be (more formally) seen in the measure of kurtosis for each of the stocks. The kurtosis for the original stocks exhibit long tails (leptokurtic) compared to the more normal distributions of the proxy stocks. Although the actual stocks and their proxies have the same returns and standard deviations, their distribution characteristics start to differ from the third moment onwards.
5 Empirical results
Formal testing of the link between portfolio risk and volatility transmission consists of two parts. The first part presents a comparison of portfolio risk, portfolio return, and beta according to the methodology of Markowitz (1952) and Sharpe (1964). The focus of the second part shifts towards establishing the level of volatility transmission between the respective stocks and their proxies by applying an AS model to each.10
5.1 Portfolio risk, return and beta
Modern portfolio theory (MPT), which was developed in the 1950s and gained momentum in the 1960s, saw a shift in the management of portfolios. The introduction of the concept of co-variance between stocks provided a different facet to how stocks affect each other when co-existing in the same portfolio. In addition, portfolio managers have long been familiar with the efficient market hypotheses (EMH) where a well-diversified portfolio with a unit correlation (beta equal to one) with the market is considered entirely hedged against non-systematic risk. Table 3 provides the portfolio risk, portfolio returns and beta measures of the five-stock portfolios in all the periods under study.
When inspecting beta for the original stock portfolio in each of the periods, it is noteworthy that the original portfolio's beta only exceeds that of the market during period 4. The original portfolio's beta is less than that of the market in all the other periods, signifying lower risk. It is also important to note that the portfolio returns in each period match each other equally because the proxy stock that replaces each stock in the five proxy portfolios effectively have the same returns. The differences of each portfolio are captured by portfolio standard deviation and market beta. During periods 2, 3 and 4, portfolios all have negative returns, as these were the periods hardest hit by the financial crisis. Period 2 captures the defining moment of the 2008 financial crisis, as it encompasses the two months after Lehman Brothers declared bankruptcy. It is for this reason that the portfolios in period 2 exhibit the highest portfolio risk. Period 4 signals the beginning of stabilisation of the JSE. However, the international exposure of some of the large cap stocks may explain the excess riskiness of the stocks within period 4 portfolios (higher beta means a greater exposure to market risk than that of the market portfolio). From period 5 onwards portfolio returns are positive, giving impetus to recovery from the initial shock of the financial crisis. Period 9, in contrast, had a small volatility spike, with negative returns. Stabilisation of the JSE and stocks subsequently commenced thereafter (period 10).
The original five-stock portfolio always exhibits a larger portfolio standard deviation than the five proxy portfolios in the same period. This is noteworthy since the individual proxy stocks all have the same standard deviation as their actual counterparts. The reason for this phenomenon lies in the way standard deviation is calculated. In essence, standard deviation is the average of all the deviations from the mean. In mathematical terms it is therefore possible to have two series with identical standard deviations but very different distributions. Because of this anomaly, the various stocks in the original portfolio impact differently on one another when compared to their proxies. It is also noticeable that as the portfolio standard deviation decreases, the beta decreases (except for one case), and therefore the market exposure of the particular portfolio also decreases. In other words, when the volatility of the market increases (such as in a financial crisis), the volatility of the portfolio(s), with a beta less than one, increases to a lesser extent. However, beta does not decrease linearly as portfolio standard deviation does. In period 8 the beta of proxy portfolio Y was higher than that of the original portfolio. The use of daily beta could have limited the stability and accuracy of the beta measure. However, beta does explain portfolio risk to a significant extent, with the exception of some deviations and non-linearity. It is for the latter reason that a closer look will be taken at volatility spill-over effects as an alternative measure.
5.2 Aggregate shock models
The AS model allows one to formally test the relationship of both returns and volatility on the stocks within each five-stock portfolio. As is customary in the finance literature, various lag specifications were estimated for each stock within each portfolio, with the appropriate lag specification for the E-GARCH (p, q) term chosen where the Akaike information criterion (AIC) and Schwarz criterion (SC) values are minimised. These criteria allow for choosing the appropriate aggregate shock model for each one estimated. Tables 5.2 and 5.3 provide a summary of the AS model output (Φ;-coefficients in equation 3 and κ1-coefficients in equation 5). These coefficients indicate the level of returns spill-over effects (Φ;-coefficients) and volatility spill-over effects (κj<-coefficients).
In Table 4 the stocks and their proxies in the first column represent the stock that is analysed for returns spill-over effects from the stocks in the second column. The first table represents the error term of the stock causing a return spill-over (the Φ-coefficient in equation 3). The actual stock and its replacement proxy are sequenced directly below each other to ease comparability. This allows for each eight rows, respectively, representing the returns spill-over effects of all the other stocks present in the portfolio to one of the five stocks (first four rows) and similarly for its proxy (second four rows).
In all of the estimated AS model regressions the Φ-term is statistically significant for at least three of the four stocks for all the original stocks in each period. In contrast, the proxy stock replacements, occasionally and at most, exhibit only two statistically significant influences from the four Φ-terms besides for proxy portfolio V in period 6. This means that the Φ-terms of each stock affected the returns of the proxy stocks minimally (if at all), whereas the Φ-terms captured a great deal of the returns present in the original stocks. The returns of the proxy stocks are therefore negligibly integrated with the returns of the other stocks present in the portfolio. In this regard, each proxy stock replaces a stock that exhibits statistically significant integration with the other stocks. It is important to note that this reduction of returns spill-over effects does not affect the overall portfolio returns, and that the returns over the period did not change between the original stocks and their proxy replacements.
The estimates for the variance equation (Table 5) shows a similar trend. Although not reported in this paper, the y2-parameter (measuring the asymmetric or leverage effect of volatility) is extensively more significant for the actual stocks than that of the proxy stocks. The δ2-coefficient (indicating the degree of volatility persistence) is significant for both the original and proxy stocks. All of these coefficients were found to be smaller than one (except for the odd two out of 400 estimated AS models), which, according to Xu and Fung (2005), is a requirement for the stability of volatility persistence terms. A high level of volatility persistence implies that fluctuations will remain for an extended period.
Although these characteristics can be expected, the main focus is on the Kj-coefficients. Table 5 presents the Kj-terms, which capture the actual volatility spill-over effects of a given stock from all the other stocks present in the given portfolio. Once again, the more profound statistically significant volatility transmission effects occurred between the original stocks included in the five-stock portfolio. As soon as a proxy stock is introduced, the overall volatility spill-over effects decrease. Note that some stocks may transmit more volatility to a proxy stock than to the original stock, but overall, the combined volatility spill-over effects (from all the other stocks) are greater for the original stocks than for the proxy stocks. In addition, volatility spill-over effects increased during the periods surrounding the height of the 2007/08 financial crisis (periods 2 to 4), with volatility spill-over effects subsequently decreasing as the market started to calm. This is in accordance with studies that testify to the heightened integration between stocks (with regard to returns and volatility) during periods of financial turmoil.11
It is clear from Table 5 that the proxy stocks attract significantly less volatility spill-over effects from the other stocks included in the portfolios than the original stocks do from those same stocks. This is evident from the considerably fewer statistically significant coefficients from both the mean equations (Φ-terms) and the variance equations (Ki-terms). Therefore, based on all the AS model estimations, the proxy stocks are far less prone to volatility transmission than their actual counterparts.
These results exhibit strong support for the inclusion of a volatility spill-over measure when constructing a portfolio based on past price information. Not only does this measure provide insight into the information captured within the residuals, it also provides consistently stable results (even during times of financial distress). Both these advantages offer portfolio managers a greater spectrum for stock selection and allocation, which are not captured by simply using the market beta. The fact that these volatility spill-over effects amongst the original stocks occur so consistently is evidence of the interconnectedness among stocks on small exchanges like the JSE. Many of these stocks are traded together as part of larger portfolios. When market sentiment changes on a global front - such as negativity about developing economies - the returns of these stocks tend to move together. This is also visible in the second moment data. As a result, the volatility spill-over effects among these stocks will also be pronounced if the interest in them is similar.
These results by no means rule out the use of beta, for beta captures co-variances in the mean equation. However, using beta estimates in conjunction with a residual-based test (such as the AS model) will provide a more stable and reasonable choice in stock selection when trying to construct a mean-variance efficient portfolio. It should be noted that the construction of such a portfolio is based solely on past price information, and that future price movements remain unpredictable.
Considering that the proxy stocks, when replacing the actual stocks, are less prone to volatility spill-overs (in all cases), and also reduce portfolio standard deviation (in all cases), it is reasonable to infer that when contemplating choices between individual stocks that have similar returns and risk profiles, the obvious choice would be the one that receives the least amount of volatility spillover effects from the other stocks included in a portfolio. Market beta, on the other hand, provides a tried and tested (and simple) method to help portfolio managers in portfolio allocation. Beta was shown to mostly co-move with portfolio standard deviation, although not linearly. Therefore, when a stock within a portfolio has the same past return record as another stock, selection between these stocks should be made on the grounds of its co-variance with the other stocks (market beta), and its volatility spill-over effects received from other stocks within the portfolio.
6 Further research
These findings are based on randomly generated stocks (for which parameters could be fixed), and are therefore only valid in theory. Further research and implementation will be needed to vindicate the performance of a portfolio which utilises volatility spill-overs as an input in portfolio construction. This might be achieved by using other residual-based tests to test the validity of volatility spill-over effects on portfolio variance. These testable frameworks may include (but are not limited to): (i) a multivariate E-GARCH (Karolyi, 1995); (ii) the multivariate GARCH model developed by Baba, Engle, Kraft and Kroner (GARCH-BEKK) (Maniya & Magnusson, 2010); or (iii) the dynamic conditional correlation (DCC) model (Engle, 2002).
The current model was however chosen to test the "theory" that volatility spill-over effects do indeed add to portfolio variance. The AS model used in this instance was therefore ideal for capturing the spill-over effects from the proxy stocks to the original stocks. Expanding on such volatility spill-over results with actual data may require the use of a volatility spill-over index - as done by Diebold and Yilmaz (2009). Such an index could be expanded beyond the stocks within a portfolio, and may even include all the relevant stocks listed on an exchange.
Finally, these results could be tested on other emerging markets, or by using larger data intervals (such as weekly stock returns), or when market conditions have significantly improved. However, the overall period of testing in this study did include various 2-month periods in which volatility calmed.
7 Conclusion
Taking into consideration that the mandate of a managing fund requires the constant rebalancing of a stock portfolio (to, for instance, outperform a benchmark), and that this process of rebalancing becomes more complex and difficult during times of financial distress, the need for adequate information becomes more urgent. This study provides an additional measure to market beta in order to construct a more efficient portfolio, namely, volatility spill-over effects between stocks within the same portfolio. Using intraday stock returns and a residual based test (AS model), volatility spill-over effects were estimated between stocks. It was shown that when a particular stock attracted fewer returns and volatility spill-over effects from the other stocks in the portfolio, overall portfolio volatility decreased as well. In most cases market beta showcased similar results, but did not have a linear relationship with portfolio standard deviation. Therefore, in order to construct a more efficient portfolio (which is effectively hedged against non-systematic risk), requires both a portfolio that has a unit correlation with the market, and also includes stocks with the least amount of volatility spill-over effects amongst one another. Since stock selection and asset allocation is a fine art in itself, it is imperative to be conscious of the various factors that may influence a portfolio's return characteristics.
References
ANDERSEN, T.G. & BOLLERSLEV, T. 1998. Answering the sceptics: Yes, standard volatility models do provide accurate forecasts. International Economic Review, 39(1):885-906. [ Links ]
ANDERSEN, T.G., BOLLERSLEV, T. & DAS, A. 2001. Variance-ratio statistics and high-frequency data: Testing for changes in intraday volatility patterns. Journal of Finance, 56(1):305-327. [ Links ]
ANDERSEN, T.G., BOLLERSLEV, T., DIEBOLD, F.X. & LABYS, P. 2003. Modeling and forecasting realized volatility. Econometrica, 51(2):579-625. [ Links ]
ANDERSEN, T.G., BOLLERSLEV, T., DIEBOLD, F.X. & WU, P. 2006. Realized beta: Persistence and predictability. Advances in Econometrics, 20(2):1-39. [ Links ]
AREAL, N.M.P.C. & TAYLOR, S.J. 2002. The realized volatility of FTSE-100 futures prices. Journal of Futures Markets, 22(7):627-648. [ Links ]
BAUWENS, L., LAURENT, S. & ROMBOUTS, J.V.K. 2006. Multivariate GARCH models: A survey. Journal of Applied Econometrics, 21(1):79-109. [ Links ]
BEIRNE, J., CAPORALE, G.M., SCHULZE-GHATTAS, M. & SPAGNOLO, N. 2013. Volatility spillovers and contagion from mature to emerging stock markets. Review of International Economics, 21(5):1060-1075. [ Links ]
BOLLERSLEV, T. 1986. Generalised autoregressive conditional heteroscedasticity. Journal of Econometrics, 31(1):307-327. [ Links ]
BROWN, K.C. & REILLY, F.K. 2009. Analysis of investments and management of portfolios (9th ed.) International student edition. Canada: South-Western CENGAGE Learning. [ Links ]
CLARK, P.K. 1973. A subordinated stochastic process model with finite variance for speculative prices. Econometrica, 41(1):135-155. [ Links ]
DIEBOLD, F.X. & YILMAZ, K. 2009. Measuring financial asset returns and volatility spillovers, with application to global equity markets. The Economic Journal, 119(534):158-171. [ Links ]
ENGLE, R.F. 1982. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica, 50(1):987-1007. [ Links ]
ENGLE, R.F. 2002. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business and Economic Statistics, 20(3):339-350. [ Links ]
FAMA, E.F. 1965. The behaviour of stock market prices. Journal of Business, 38(1):34-105. [ Links ]
FAMA, E.F. 1970. Efficient capital markets: A review of theory and empirical work. Journal of Finance, 25(2):383-417. [ Links ]
FAMA, E.F. 1976. Foundations offinance. New York: Basic Books. [ Links ]
GROSSMAN, S.J. & STIGLITZ, J.E. 1980. On the impossibility of informationally efficient markets. American Economic Review, 70(3):393-408. [ Links ]
JEGADEESH, N. & TITMAN, S. 1993. Returns to buying winners and selling losers: Implications for stock market efficiency. Journal of Finance, 48(1):65-91. [ Links ]
KAMINSKY, G.L. & REINHART, C.M. 1998. Financial crises in Asia and Latin America: Then and now. American Economic Review, 88(2):444-448. [ Links ]
KAROLYI, G.A. 1995. A multivariate GARCH model of international transmission of stock returns and volatility: The case of the United States and Canada. Journal of Business and Economic Statistics, 13(1): 11-25. [ Links ]
KITAMURA, Y. 2010. Testing for intraday interdependence and volatility spillover among the Euro, the Pound and the Swiss Franc markets. Research in International Business and Finance, 24(2):158-171. [ Links ]
LIN, W., ENGLE, R.F. & ITO, T. 1994. Do bulls and bears cross borders? International transmission of stock returns and volatility. The Review of Financial Studies, 7(3):507-538. [ Links ]
LO, A. & MACKINLAY, A. 1999. A non-random walk down Wall Street. Princeton: Princeton University Press. [ Links ]
LONGIN, F. & SOLNIK, B. 1995. Is the correlation in international equity returns constant: 1960-1990? Journal of International Money and Finance, 14(1):3-26. [ Links ]
MANIYA, S.R. & MAGNUSSON, F. 2010. Bear periods amplify correlation: A GARCH BEKK approach. University of Gothenburg, School of Business, Economics and Law. Masters' Degree Project No. 2010:129: 1-10. [ Links ]
MARKOWITZ, H.M. 1952. Portfolio selection. Journal of Finance, 7(1):77-91. [ Links ]
MARKOWITZ, H.M. 1956. The optimization of a quadratic function subject to linear constraints. Naval Research Logistics Quarterly, 3(1-2): 111-133. [ Links ]
MARKOWITZ, H.M. 1959. Portfolio selection: Efficient diversification of investments. New York: Wiley. [ Links ]
MCALEER, M. & VEIGA, B. 2008. Forecasting value-at-risk with a parsimonious portfolio spillover GARCH (PS-GARCH) model. Journal of Forecasting, 27(1):2-29. [ Links ]
NELSON, D.B. 1991. Conditional heteroskedasticity in asset returns: A new approach. Econometrica, 59(1):347-370. [ Links ]
POON, S. 2005. A practical guide to forecasting financial market volatility. New York: John Wiley & Sons. [ Links ]
RUBINSTEIN, M. 2002. Markowitz's portfolio selection: A fifty-year retrospective. Journal of Finance, 57(3):1041-1045. [ Links ]
SAMOUILHAN, N.L. 2006. The relationship between international equity market behaviour and the JSE. South African Journal of Economics, 74(2):248-260. [ Links ]
SCHREIBER, P.S. & SCHWARTZ, R.A. 1986. Price discovery in securities markets. Journal of Portfolio Management, 12(1):43-48. [ Links ]
SHARPE, W.F. 1964. Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance, 19(3):425-442. [ Links ]
TAUCHEN, G.E. & PITT, M. 1983. The price variability - volume relationship on speculative markets. Econometrica, 51(2):485-505. [ Links ]
TIAN, G. & GUO, M. 2007. Interday and intraday volatility: Additional evidence from the Shanghai stock exchange. Review of Quantitative Finance and Accounting, 28(3):287-306. [ Links ]
TSE, Y.K. & YANG, T. 2012. Estimation of high-frequency volatility: An autoregressive conditional duration approach. Journal of Business and Economic Statistics, 30(4):533-545. [ Links ]
WOOD, R.A., MCINISH, T.H. & ORD, J.K. 1985. An investigation of transactions data for NYSE stocks. Journal of Finance, 40(1):723-739. [ Links ]
XU, X. & FUNG, H. 2005. Cross market linkages between U.S. and Japanese precious metals futures trading. International Financial Markets, Institutions and Money, 15(2):107-124. [ Links ]
Accepted: January 2015
1 See for example Bollerslev (1986), Schreiber and Schwartz (1986), Andersen and Bollerslev (1998), Areal and Taylor (2002), Poon (2005) and Tian and Guo (2007).
2 Realised volatility refers to the volatility estimate calculated using intraday squared returns at short intervals; normally five to fiftheen minutes (Poon, 2005:14).
3 See Clark (1973) and Tauchen and Pitt (1983).
4 Causality in return variance is the impact of any previous volatility of a particular asset on the current volatility of another asset.
5 We used Lin, Engle & Ito's (1994) Aggregate Shock model to capture volatility spill-over effects between stocks and proxy stocks.
6 The relatively "smaller" amount of data results in a parsimonious nature of testing, and avoids the large data sets that may render multivariate models impractical in empirical applications (McAleer & Veiga, 2008:4).
7 That is all the various alternative stocks included within the same portfolio.
8 The closing price of any given stock is captured in the last (eighth) observation of each trading day.
9 Interchangeably substituting stock AGL for stock V (portfolio V), stock ASA for stock W (portfolio W), stock SAB for stock Y (portfolio Y), and stock SOL for Z (portfolio Z).
10 This study employs a similar methodology to the one used by Lin, Engle and Ito (1994) and Samouilhan (2006) with regard to the use of an AS model.
11 See Longin and Solnik (1995), Kaminsky and Reinhart (1998), and Maniya and Magnusson (2010).














