Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Economic and Management Sciences
On-line version ISSN 2222-3436
Print version ISSN 1015-8812
S. Afr. j. econ. manag. sci. vol.17 n.2 Pretoria Feb. 2014
ARTICLES
Building a scenario based active mapping investment tool within a physical asset management framework
CA Campher; PJ Vlok
Department of Industrial Engineering, University of Stellenbosch, South Africa
ABSTRACT
This study explores the implementation of an integrated capital budgeting visual mapping framework comprised of both Discounted Cash Flow (DCF) and Real Options Analysis (ROA) techniques. Physical asset investment decisions are based largely on rigid discounted cash flow tools which provide untimely and incomplete decisional criteria. While literature outlines the widespread use of traditional DCF techniques, it nevertheless reveals extensive limitations, including its static inflexibility and slow-to-evolve framework. ROA is a more recent valuation tool based on stock option theory. It brings into account added value found in the flexibility of managerial decision-making and uncertain conditions. This study implements a combined DCF and ROA capital budgeting tool within a Physical Asset Management (PAM) environment. The validity of the framework is realised through an industry-relevant case study presented by a South African mining company.
Key words: capital budgeting, real options, black-scholes, option mapping, asset management.
JEL: G310
1 Introduction
Behind every major investment decision lies some calculation of what that investment is worth. The evaluation of these investment decisions is a key driver in a company's overall performance. Today, the most common calculations used by financial specialists and managers in evaluating the return on investments are Discounted Cash Flow (DCF) techniques. However, according to Baker (2011), DCF analysis does not take into account the realistic valuation of an investment, as it fails to account overtly for the value of real options that are integral to capital budgeting. In fact, DCF techniques do not provide sound valuation in an uncertain environment, and companies lose the value created through flexible decision-making.
The study aims to address problems associated with DCF analysis by supplementing capital budgeting analysis with Real Options Analysis (ROA) techniques. The topic of real options initially created an interest among authors such as Luehrman (1998a), who liken physical asset investments to the exercising of real options. Real options are derived from stock market option valuation. However, they are applied to real, tangible assets, hence the term "real" options. The reference to physical, tangible real options led quite naturally to its use in a Physical Asset Management (PAM) framework, such as the Publicly Available Specification (PAS) 55.
The research conducted for this article sought to address the added value in investment opportunities through the use of real options in the capital budgeting of future investments. According to Steffens and Douglas (2007), real options provide a framework for decision-making in uncertainty, when an investment value is enhanced by the flexibility of future options. As pointed out by Ford, Lander and Voyer (2004), options are strategies that include a right, without an obligation, to take specific actions in the future, at some cost. This is contingent on how initially uncertain conditions evolve. In refining the term investment, the study will focus on physical asset investments defined by the BSI (2008) framework, such as plant, machinery, property, vehicles, buildings and any other items that carry distinct value. A further reinforcement for the value that real options can bring to capital budgeting is its applicability to systems within PAS 55 and a physical asset management framework. This is demonstrated by Figure 1.
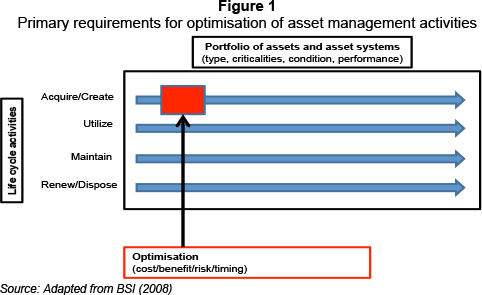
When it comes to the Life Cycle Activities section of PAS 55, one of the primary requirements is the area outlined as "Acquire/ Create" shown in Figure 1 and adapted from BSI (2008:14). The primary objective of this section is the optimisation of acquisition and creation of physical assets. Taking into account factors such as value-to-cost and volatility/risk, the use of ROA comprehensively covers the optimisation factors of cost/benefit/risk and timing. The value and benefits can be seen in the use of a supplementary real options framework instead of the often rigid and inflexible conventional DCF techniques employed.
2 A combined DCF and ROA framework
Although real options provide flexibility and have greater future valuation attributes, DCF valuation techniques are the foundation of all capital budgeting processes (Graham & Harvey, 2001). Instead of choosing only one technique, the flexibility of real options could be combined with the foundational, widespread use of DCF techniques. The view presented by Miller and Chan (2002) is that ROA and DCF techniques should complement each another as decision-making tools, combining the different qualities of each method. This is expressed in Figure 2, which shows that DCF methods should be used in moderate, straightforward business decisions, with clear investment structures and dependable forecasts. ROA decision tools are far more suitable in uncertain business conditions when more information or flexibility are needed and are more useful in the active management of projects, in aspects such as abandonment, delay or expansion options.
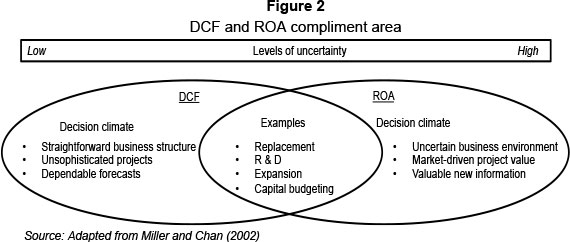
In the majority of cases, the existing information found in traditional DCF approaches is needed to perform a ROA. DCF analysis should therefore be performed first, and then expanded, using the advantageous ROA techniques, which will form the overlapping area between DCF and ROA decision tools, as shown in Figure 2. Lint and Pennings (2001) agree that DCF methods complement ROA. In decisions based on engineering economics ties, Park and Herath's (2000) method of dividing investment categories differs from that of Lint and Pennings (2001), and focuses instead on varying levels of uncertainly. The greater the uncertainty, the more ROA decision criteria and techniques impact on the final decision. Rausser and Small (2000), in their unique perspective, find that ROA can be implemented very successfully if companies start picturing platform investments as long-term profit opportunities. These platform investments are based on investing a little at a time and waiting for new information on the investment potential/ opportunity. Rausser and Small (2000) see these platform investments as renting information, rather like a call option premium. In other words, as for an option, firms should view the cost of laying the foundation for long-term investments as the price to pay for the option to enter some business opportunity in the future (Miller & Chan, 2002).
Dai, Kauffman and March (2000) also suggest using an expanded Net Present Value (NPV) method in valuing the option-inclusive values of a project, as depicted in Figure 3. The "expanded" NPV method can be defined as the sum of traditional NPV and the expected value of future options made possible by the initial investment. Figure 3 can be used to illustrate the expanded NPV within an asset-based framework. The expanded NPV consists of the sum of traditional NPV obtained by using DCF techniques and the value instilled in real options provided by the investment opportunity. According to Mkhize and Moja (2009), the instilled options provide management with strategic flexibility for future project expansion, deferral or abandonment. Follow-on projects in the form of compound options (options-on-options) are also possible.
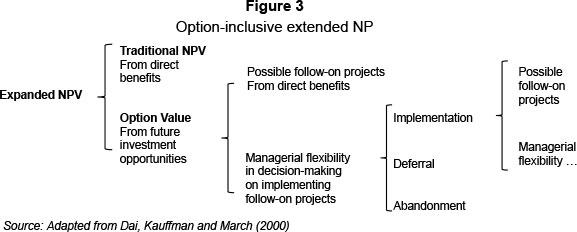
2.1 Building an active mapping investment tool
Building on this "combined framework" theory and on an "option mapping" framework conceptualised by Luehrman (1998b), the ultimate goal is to create a visually active mapping framework. The active map plots the investment opportunities in various option spaces based on both DCF and real option metrics. In addition, two key axes are used. One provides an NPV equivalent value-to-cost ratio, while the volatility axis measures the risk attributed to a particular investment decision. In this way investment decisions can be constantly tracked and monitored. This allows decisions to become more flexible if an active investment approach is followed. Ultimately, the parameters will indicate whether or not it is adequate for investment. In addition, the para-meters on the map will give an indication of the factors that should be changed, tweaked or watched in the result of borderline decisions. These parameters include volatility, time, value and cost. The case study presented outlines the methodology used as well as the results generated when using the active mapping investment tool.
3 Case study
3.1 Background
This case study outlines the capital budgeting and capital expenditure required when opening new platinum mine in the Mpumalanga province of South Africa. Critically important to the operation is the transportation of raw materials from the mining operations to the concentrator plant. The mining company is considering a new, potential raw material transport operation. The first option is to build a new road that will run parallel to the provincial road currently in use. This road runs through a large community and, according to risk assessment reports, runs a high safely risk. The construction of a new private mine road will reduce the safety risk, as it will be fenced off and restricted to exclusive use by the mine.
This case study uses a supplementary active mapping investment tool and a scenario analysis to investigate the future potential for the investment and will provide a more informed capital budgeting decision.
The active mapping framework explored in this study is based on the expanded NPV concept by Dai, Kauffman and March (2000) and Tiwana, Keil and Fichman (2006), as well as the options mapping concept developed by Luehrman (1998b), in which investment decisions are based on both traditional NPV and ROA methods. Figure 4 below illustrates the process implemented in creating and analysing the road investment and creating an active mapping investment tool. Step 1 of the framework seeks to evaluate a conventional DCF statement and identify critical investments. By applying a real options paradigm to the cash flow statement, the passive NPV is calculated, using the conventional Present Value (PV) criteria. Once the passive NPV has identified strategic investment options, the real options parameters can be established. These real options parameters are likened to financial option parameters, where they can be used in Steps 2 and 3. Step 2 calculates the two value-adding metrics used for the active mapping tool and actively plots the investment decision. Finally, in Step 3, Black-Scholes is used to price the option value inherent in the investment.

3.2 Variable outline and definitions
Several option valuation methods are established in the ROA collected works. Specifically, there are four closed-form equations that have been developed for ROA: Black-Scholes (1973),
Geske (1979), Margrabe (1978) and Carr (1988). The first closed-form equation was developed by Black and Scholes (1973) and was used for valuing financial options and warrants. Although other closed-form equations are used, the vast majority of options for valuation tools stem from the Black-Scholes equation. The widespread adoption of Black-Scholes closed-form equations results from simplified and straightforward calculations. The Black-Scholes equation is presented by Equation 1 below, with a brief outline of the variables used in the equation, along with their definitions.
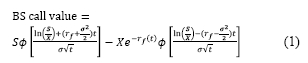
Where ø = the standard normal distribution, S = stock price, X = Exercise price, rf= risk free discount rate, σ = volatility and t = time to expiration of the option.
3.2.1 Stock price (S)
The stock price is also considered as the present value of future cash flows obtained from the investment of an option. This is usually done by discounting future cash flows against some discount rates to present values. In the study, a conventional discount rate will be used, based on industry standards which implement the widely-accepted Weighted Average Cost of Capital (WACC) technique.
3.2.2Exercise price (X)
The exercise price for a real options analysis is representative of the cost incurred in initiating the next phase of investment, or the revenue received for an abandonment option (Miller & Chan, 2002).
3.2.3 Risk and discount rate (rf)
Real options, like financial options, assume the use of a replicating portfolio consisting of either an underlying traded asset or a risk-free bond. This is used to hedge risks within an option value, and is assumed to be a risk-free rate. The assumptions, according to Trigeorgis (1993), Mason and Merton (1984) and Copeland and Antikarov (2002), are to treat the underlying tradability of real options valuation like that of financial options. The replicating, risk-free (rf) portfolio in this case is Republic of South Africa (RSA) Retail Savings Bonds. Luehrman (1998a) explains that, if just enough money is deposited in the bank, when the time comes to invest the initial amount plus the interest earned, it will be enough to fund the required expenditure. In this case study, a risk-free rate of 7.53 per cent is used, based on inflation linked RSA Retails Savings Bonds in 2012 from January to April, as presented by Infaltion.eu (2012).
3.2.4 Volatility (σ)
One of the major parameters influencing the option value of a real asset is volatility or standard deviation, in particular, choosing the most suitable volatility or standard deviation for the particular asset (Miller & Chan, 2002). In the case of ROA there are three primary ways of finding a reasonable estimate in the calculation of the standard deviation. According to Luehrman (1998a), these ways are: Taking an educated guess; data gathering; and simulation. While Miller and Chan (2002) argue the availability of usable historical data for real options, this can be seen as purely circumstantial. The case study presents both historical data and sources of industry-specific experience, leaving simulation as superfluous. The volatility calculation for the road investment case study was taken from historical data gathered by the mining company and the risk associated with the new road investment.
3.2.5 Exercise time (t)
Owing to the nature of real options analysis, the correct data used in the valuation may not be clearly defined or else is more of an assumption. Although this may appear vague, the values to which it aspires are both flexibility and uncertainty. Firms can use educated guess work or base exercise date decisions on phases of the investment plan. This is where multi-scenario planning, which will be included in this study, can be useful.
3.2.6 Exploring active mapping space
While traditional DCF techniques such as NPV and IRR present only single figure capital budgeting investment decision criteria, the active mapping tool aims to implement two new variables: NPVnewQ and Cv, also called cumulative volatility, the first of which is a value-to-cost ratio.
3.3 Data analysis
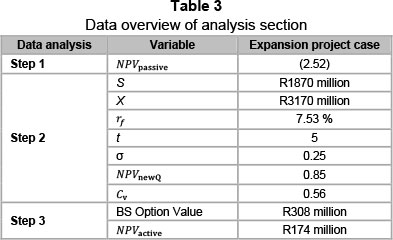
This section presents the data analysis for the new road investment. The data presented are in the form of conventional forecast cash flow statements provided by the platinum mine company. The analysis presents the results of the case study based on the active mapping framework. Following the prescribed framework, the standard or passive NPV is worked out first, using data from the mining company regarding the investment decision. Step 2 dissects the initial NPV calculations to determine where real options can be applied. Step 3 combines both passive and real option valuation tools to create an active NPV. The viability and validity of the active NPV value are then scrutinized, using the active mapping tool. Here the cumulative volatility (Cv) and value-to-cost metric (NPVnewQ) are used to place the investment within a visual active mapping space.
3.3.1 DCF analysis: Mine road investment
This section provides the cash flow statements used in the capital budgeting of the road investment proposed. Included in the predicted cash flows are revenues generated, working costs and capital expenditure. The discount rate used is an industry standard used in the capital budgeting of new or greenfield projects, as they are referred to in industry. The rate of 12.5 per cent is based on company-specific simulations which take into account inflation, the Weighted Average Cost of Capital (WACC) and even the fluctuation in predicted material (Platinum) prices. In most operations, the 12.5 per cent discount rate is used and once projects have proven fruitful and the investment risk has reduced, the project is classified as a brownfield project and the discount rate is reduced to 11.5 per cent.
3.3.2 Step 1: Passive NPV
Step 1 of the data analysis determines the conventional or passive NPV analysis of the predicted cash flow statements of a new road and an overland conveyor system. Real options thinking is applied to the DCF analysis to separate the cash flows directly related to the investment considered. This separation still uses a conventional DCF and NPV analysis and is labelled Phase 2. Pivotal in the Phase 2 separation is the ability to identify the real options that are hidden in conventional DCF analysis. This can be done in a number of ways, but in the case study only one method is used. By simply examining the relevant cash flows, capital expenditures and working costs, it is easy to identify patterns and structures that are directly relevant to the investment in question.
The passive NPV approach begins at Phase 2 of the capital budgeting forecast and is illustrated in Table 1. Phase 2 begins with the strategic construction of the road, which, as indicated, begins during 2014 and 2015. For simplification purposes, the two capital expenditures have been added to make one figure in the year 2016, as shown in Table 1. This investment is clearly strategic, as the capital outlay is far greater than any other and is pivotal to the overall revenue generated from the capital investment. By isolating Phase 2 from the original cash flow statement (Table 1), the initial capital outlay costs and expenditures from 2011 to 2015 are ignored and only the effect of the large capital investment in 2016 is analysed. As seen by the resultant passive NPV (NPVpassive) of R133 million, the result is already more favourable than the original NPV value of R4483 million. The result is based on the very same DCF and NPV techniques. The difference lies purely in representing the investment in question and challenging a conventional capital budgeting mind-set.
In the Variable Outline and Definitions section, the risk-free rate (rf) determined from inflation-linked retail government bonds for a five-year investment period is 7.53 per cent. Owing to the investment decision period between 2011 and 2016, the decision to invest in the road could, from the real options perspective, be deferred for a period of five years. The capital expenditure (X) figure used is R3170 million presented in 2016, and the present value of cash flows obtained from the investment option (S) is calculated as R1870.37 million. Finally, a standard deviation or σ value of 25 per cent is used, based on the platinum mine's financial risk assessment of the new road investment.
3.3.3 Step 2: Real options
Table 2 gives a detailed summary of the parameters used in the real option valuation process. By applying these parameters to the data provided by the platinum mine; the real option valuation parameters can now be calculated. The three parameters calculated are the cumulative volatility (Cv), the new NPV metric (NPVnewQ) and the Black-Scholes option value. Although the Black-Scholes value is the overall real option value used, the other two parameters use exactly the same information but illustrate a different perspective of the investment when combined with the active mapping tool. The link between the parameters listed in Table 2 and the two new option metrics are represented in Figure 5. The first equation addresses the value added NPVnewQ which assumes money is invested in risk-free government bonds until the time comes to invest. In this way interest is earned on the money while the investment decision is deferred.
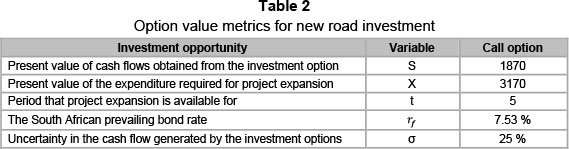

NPVnewQ=S/PVinvest
Where
PVinvest= X/( 1 + rf)t
Thus
NPVnewQ= 1870/(3170 ÷ 1.07535) = 0.85
The second equation cumulative volatility or Cv obtains value by attaching some worth to the level of uncertainty in an investment decision.
Cv =σ √t
Cv = 0.25x√5 = 0.56
3.3.4 Step 3: Active NPV
The active NPV (NPVactive) section combines the initial passive NPV value found in Step 1 with Step 2's real option value. The final parameter needed to complete this step is the Black-Scholes option value. The real option value innate in the investment decision is valued against the passive NPV by taking investment flexibility and risk parameters into account. By using the Black-Scholes Equation 1 and using the variables in Table 2. The call value for the road investment is calculated as R308 million.
With the real options value of the investment known, the active NPV can now be calculated by using:
NPVactive = NPVpassive + f(real options) = -133 - 308 = R174 million
4 Active investment mapping
While the active NPV (NPVactive) looks at the contrast in both the conventional NPV value and the real options value, the active map can add perspective. Perspective comes in the form of various decisional criteria, six in total, which provide guidance to an otherwise irrelevant real option value. Additionally the active mapping framework hopes to influence a more engaged and functional participation in investment decisions. Variables can be tweaked, modified or experimented with to understand the potential risks, returns and factors influencing the investment.
Using the value adding real option values from NPVnewQ and Cv, the new road options can be plotted within a six decisional criteria option map according to two primary axes. Instead of viewing an investment on a purely "invest" or "don't invest" NPV basis, multiple decisional criteria can be used, ultimately creating a more active investment decisionmaking process by illustrating both present and future investment potential. The active map of the road investment is illustrated in Figure 6. A data overview is also provided in Table 3 to facilitate the active mapping tool presented.
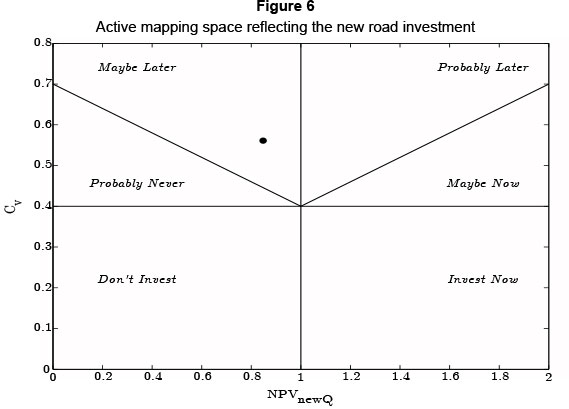
When using the active map, unfavourable investment decisions are still valued according to a flexible mapping framework. NPV metrics like value-to-cost are not the final decisional criteria, because cumulative volatility also influences the call option value. The vertical line aligned with one on the NPVnewQ or the value-to-cost axis represents the usual NPV criteria. Should the value-to-cost be greater than one, this expresses the common, positive NPV. Less than one clearly represents the negative NPV. The second axis, separated by the horizontal line, represents the amount of risk attributed to the investment. In other words, this line can be moved up or down depending on how a company evaluates various risk profiles for various asset classes. In the case study, 0.4 was the preferred risk assessment value.
The active mapping diagram in Figure 6 illustrates the current status of the new road investment, which is shown as the black dot on the map. The black dot represents the intersection of the NPVnewQ and Cv values which are measured along the two primary axes. In addition, the placing of the black dot allows one to view the investment in terms of the six decisional criteria sections displayed on the active map. This investment has a low NPVnewQ or weak value-to-cost ratio. However, it is soon to become more favourable. While in conventional DCF analysis a low NPV simply means "Don't invest", in this case the option map suggests "maybe later". Why maybe later? In considering the second metric of cumulative volatility (Cv) and the risk structure of the option space, it can be seen that this asset holds some risk and uncertainty. Usually risk has negative connotations, but option theory suggests otherwise. Option theory considers the possible value inherent in risk, as, in many investment cases, high risk brings high reward. Obviously high risk should not be considered high value, but the option space allows one to recognise how much risk is acceptable.
4.1 Scenario analysis
Scenario analysis illustrates the active use of a visual option mapping space for the real options presented in the case study. The scenarios created in the case study present realistic market conditions based on industry standards. Over and above the base case presented, there are three additional scenarios. The scenarios implemented are: Pessimistic, Optimistic and Progressive scenarios. Each investment is exposed to the various scenarios presented and mapped within the case-specific mapping space. Each investments active map is then discussed in greater detail to give clarity and perspective. Table 4 given below represents the parameter definitions for the option mapping scenario analysis to be carried out.
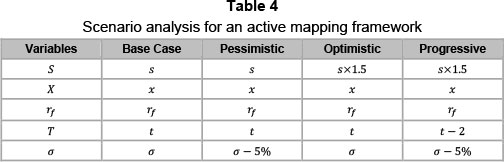
Pessimistic: This case illustrates the negative nature of a lower variance (σ) value. Real options find value in the variance through the cumulative distribution variable.
Optimistic: The optimistic case assumes that all the variables remain constant, except for the present value of assets as a result of the investment (S). This increases the value-to-cost ratio.
Progressive: The progressive scenario is one of the more complex scenarios. It follows the same optimistic S increase, but also has a reduced risk (σ) and time (t) change. The assumption is that the investment is in an optimistic value-to-cost range, and, with increased confidence in the investment, the risk profile has been lowered. In addition, instead of deferring the investment for the initial period, two years are now shed from the deferral time t.
The chosen time value of two years was used, as it represents close to half of the five- year deferral period. It represents a condition whereby an investment decision is made far sooner on account of favourable market conditions. The 5 per cent variation in the volatility metric is used to illustrate just how sensitive the standard deviation and subsequently the cumulative volatility are. Varying the volatility by a seemingly low 5 per cent could bring about considerable changes on the active map, thereby influencing investment decisions. In addition, the value is used for contesting conventional connotations associated with risk and demonstrating the variation in investment potential with small variations in perceived risk.
4.2 Results and discussion
This section presents the active map results of the new road based on the scenarios in Table 5. The results are provided in Table 5 and plotted on Figure 7 below. They are accompanied by a brief synopsis.
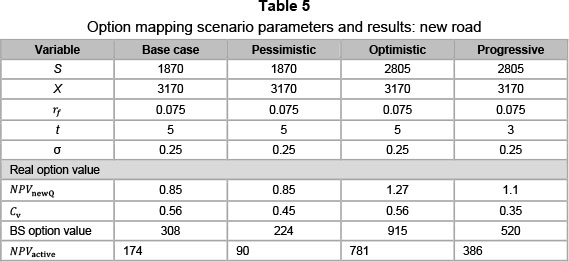
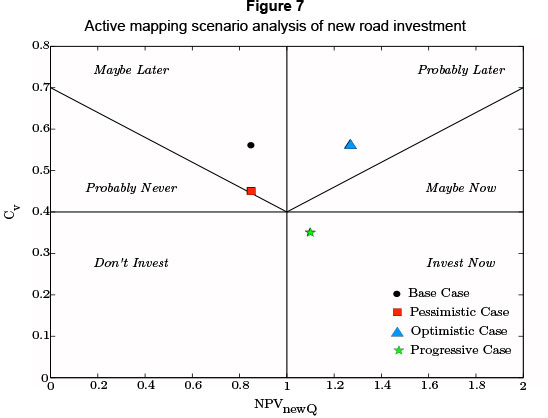
The first case discussed is the initial base case. With a low value-to-cost ratio and a reasonable risk profile, the base case fits into a "maybe later" section. The base case presents a Black-Scholes option value of R308 million, which is high enough to lift the active NPV (NPVactive) to R174 million. The value attached to the risk profile (Cv) of the base case becomes more evident as the analysis moves on to the pessimistic case. The pessimistic scenario demonstrates the value assigned to a certain risk or cumulative volatility profile. In changing the risk assigned to the investment from 25 per cent to only 20 per cent, the investment has become less favourable, moving from "maybe later" to the "probably never" section. The active map recognises the lack of potential in less certain investments, and the pessimistic scenario clearly highlights the result of low value-to-cost as well as low cumulative volatility metrics. The influence of the lowered σ value transcends to the Black-Scholes call option value, which has decreased to R224 million.
The optimistic scenario explores the possibility of higher revenues being generated. The optimistic case emulates a "best" case scenario of platinum mines' sensitivity analysis. The increase is based on three principle changes, which are metal prices, CPI rates and the Rand/Dollar exchange. The forecast for these changes is reviewed every quarter. With the flexibility of the active mapping framework, updates are easily implemented, with dynamic, real time mapping results. The result of the optimistic scenario is a favourable value-to-cost ratio with the same risk profile as the base case. The NPVnewQ, value adding metric has increased to 1.27 and the Black-Scholes option value is at its highest at R915 million. The active NPV has escalated to R781 million, owing to the high option value. The active NPV (NPVactive) figure is unconvincing, as the option value is uncharacteristically high. When these parameters are plotted on the active map, a "probably later" decisional criterion is reflected. Looking at all the variables this is better judgement to follow, as, despite the favourable return, the investment should still be watched for some time, especially with the high option value and associated risk.
The final scenario, the progressive case, actively follows on from the optimistic scenario. It values the investment with a two-year decrease in deferral time from five years to three years. In addition, with increased confidence in operations, the risk is reduced to 20 per cent.
The reduction in deferral time has lowered the NPVnewQ value from 1.27 to 1.1, as less interest earning value is generated. The scenario results in a convincing value-to-cost ratio as well as a low risk profile, placing the investment in an "Invest Now" space. The lesser time period and lowered risk profile (Cv = 0.35) have reduced the Black-Scholes option value to R520 million. Notice how the Black-Scholes option value is lower than the optimistic case, but the decisional criterion based on the active map favours the progressive scenario.
A demonstration of how the active map breaks down the Black-Scholes option value is seen in the difference between the Black-Scholes option values of the optimistic and progressive scenarios. While the optimistic case has a large option value of R915 million as opposed to the progressive value of R520 million, the map still prefers the latter. Although the option value of the optimistic scenario is higher, the active map recognises the dangers of both a higher risk profile and a longer time period. This is important, as a high option value does not always indicate that the investment is sound. In mapping the investment, the amount of risk associated with a given rate of return can actively be seen to allow more sound strategic decisions to be formulated.
Of course, in this case study, the cumulative volatility horizontal boundary was placed at 0.4. These were the acceptable risk conditions stipulated by the company for this particular asset. In practice, however, each business can refine the active mapping tool to custom fit their particular investment and tailor their own unique mapping metrics and criteria. This adds to the functionality of the mapping tool, and provides various templates for different assets, resulting in a more informative capital budgeting investment tool.
5 Conclusion
By applying real options techniques, replicating portfolios and using a measure of industry-specific volatility, ROA accounts for the value in risk and flexibility. In efforts to combat the one number syndrome of conventional DCF decisional criteria, the active mapping tool is integrated into the combined capital budgeting technique. The active mapping tool provides two metrics with six decisional criteria as opposed to DCF's NPV, which consists of one metric and two decisional criteria. Furthermore, the combined active mapping framework incorporates a functional and dynamic scenario analysis whereby varying future prospects can be better understood and actively managed. In validating both the use and applicability of the combined active mapping framework, a case study is carried out in conjunction with a platinum company which investigates the capital budgeting investment of a new road. The framework is presented by using a new road investment case study from the platinum mine in Mpumalanga. The results presented illustrate both the benefit of visually plotting and actively engaging in investment decisions and the applicability of tracking investments based on various scenarios.
References
BAKER, H. 2011. Capital budgeting valuation: financial analysis for today's investment projects. John Wiley & Sons, 13. [ Links ]
BLACK, F. & SCHOLES, M. 1973. The pricing of options and corporate liabilities. The Journal of Political Economy :637-654. [ Links ]
BSI. 2008. PAS 55-1: Asset Management. Part 1: Specification for the optimized management of physical assets. British Standards Institution. [ Links ]
CARR, P. 1988. The valuation of sequential exchange opportunities. The Journal of Finance, 43(5): 1235-1256. [ Links ]
COPELAND, T. & ANTIKAROV, V. 2002. Real options: A practitioners guide. Texere LLC. [ Links ]
DAI, Q., KAUFFMAN, R. & MARCH, S. 2000. Analyzing investments in object-oriented middleware: An options perspective. Proceedings of the Workshop on IT and Systems:45-50. [ Links ]
FORD, D., LANDER, D. & VOYER, J. 2004. Business strategy and real options in the context of large engineering projects. Journal of Global Competitiveness, 12(1):1-9. [ Links ]
GESKE, R. 1979. The valuation of compound options. Journal of financial economics, 7(1):63-81. [ Links ]
GRAHAM, J. & HARVEY, C. 2001. The theory and practice of corporate finance. Evidence from the field. Journal of Financial Economics, 60(2-3):187-243. [ Links ]
LINT, O. & PENNINGS, E. 2001. An option approach to the new product development process: A case study at Philips Electronics. R&D Management, 31(2):163-172. [ Links ]
LUEHRMAN, T. 1998a. Investment opportunities as real options: Getting started on the numbers. Harvard business review, 76:51-66. [ Links ]
LUEHRMAN, T. 1998b. Strategy as a portfolio of real options. Harvard Business Review, 76:89-101. [ Links ]
MARGRABE, W. 1978. The value of an option to exchange one asset for another. The Journal of Finance, 33(1):177-186. [ Links ]
MASON, S. & MERTON, R. 1984. The role of contingent claims analysis in corporate finance. Division of Research, Graduate School of Business Administration, Harvard University. [ Links ]
MILLER, L. & CHAN, S. 2002. Decision making under uncertainty - Real options to the rescue? The Engineering Economist, 47(2):105-150. [ Links ]
MKHIZE, M. & MOJA, N. 2009. The application of real option valuation techniques in the cellular-telecommunication industry in South Africa. South African Journal of Business Management, 40(3). [ Links ]
PARK, C. S. & HERATH, H. S. 2000. Exploiting uncertainty - Investment opportunities as real options: A new way of thinking in engineering economics. The Engineering Economist:1-36. [ Links ]
RAUSSER, G. & SMALL, A. 2000. Valuing research leads: bioprospecting and the conservation of genetic resources. UC Berkeley Law and Economics Working Paper:00-11. [ Links ]
STEFFENS, P. & DOUGLAS, E. 2007. Valuing technology investments: use real options thinking but forget real options valuation. International Journal of Technoentrepreneurship, 1(1):58-77. [ Links ] TIWANA, A., KEIL, M. & FICHMAN, R. 2006. Information systems project continuation in escalation situations: A real options model. Decision Sciences, 37(3):357-391. [ Links ]
TRIGEORGIS, L. 1993. Real options and interactions with financial flexibility. Financial Management: 202-224. [ Links ]
Accepted: July 2013














