Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Economic and Management Sciences
On-line version ISSN 2222-3436
Print version ISSN 1015-8812
S. Afr. j. econ. manag. sci. vol.16 n.5 Pretoria 2013
Who influenced inflation persistence in China? A comparative analysis of the standard CIA Model and CIA model with endogenous money
Ying Liao; Ridong Hu*
School Of Economics And Finance, Huaqiao University, China
ABSTRACT
In this paper, we examine the influencing factors of inflation persistence in China's economy using the DSGE approach. Two monetary DSGE models are estimated, namely, a standard CIA model and a CIA model with a Taylor rule. This article uses the Bayesian method to estimate the model, and the estimated and inferred results are credible due to the Markov chain reaching convergence. The results show that the augmented model outperforms the standard CIA model in terms of capturing inflation persistence. Further studies show that inflation persistence mainly comes from the persistence of the money supply, while money supply uncertainty, the reaction coefficient of monetary growth to productivity, productivity persistence and productivity uncertainty have a smaller impact on inflation persistence. Changes of monetary policy have little effect on inflation persistence.
Key words: inflation persistence, DSGE model, Bayesian estimation, endogenous money
JEL: C590
1 Introduction
Since the scale of price rises shrank significantly in 2012, China has witnessed inflationary pressure. The State Council declared in the Government Work Report that the price level should be kept stable, that prices should be well regulated and that the prices should be prevented from rebounding. With this in mind, it is necessary to get an in depth understanding of the inflation dynamic behavior of China. As far as the monetary authorities are concerned, the key point is to clarify the microeconomic foundation of inflation inertia. This paper captures the responses of China's inflation inertia to technology and monetary shocks in the framework of the dynamic stochastic general equilibrium (DSGE) theory.
Fuhrer (2006) examines the theoretical sources of persistence, distinguishing "intrinsic" from "inherited" persistence, and reports that the sources of persistence are twofold. First, the "driving process" for inflation is quite persistent, and the NKPC implies that inflation must "inherit" this persistence. Second, backward-looking or indexing behavior imparts some "intrinsic" persistence to inflation. However, the literature on China's inflation inertia in the context of the DSGE theory is quite limited, except for Wang, Xinqiang & Jianbo (2011) which introduce imperfect competition, spending habits and nominal wage rigidity into the DSGE model. This is done by calibrating parameters in the structural model with macroeconomic data in China, and comparing them to the theoretical and empirical results. Undoubtedly, the research is meaningful. But what is the source of inflation persistence for China? Are there any implications from monetary policy?
Accordingly, this paper introduces money into the DSGE model, simulates China's inflation persistence with the constraint of cash in advance (CIA), and explores the mechanism underlying them and its implications. The dynamic stochastic general equilibrium model can not only capture the characteristics of inflation inertia, but it can also provide a microeconomic foundation. First, the DSGE model, which introduces the money element, not only reflects the actual economic situation, but it also distinguishes and portrays the transmission mechanisms to different shocks. Secondly, as the Lucas critique identified, if the economic model is not structural, any change in the economic environment, policy regime or expectations may lead to instability of the system and have a big impact on analysis and evaluation. In contrast, DSGE models built on the identification of structural parameters, can compare different policies through the modification of the local policy parameters. These can provide an appropriate framework for the analysis of inflation inertia to the random shocks. Finally, by being built in an uncertain environment, the DSGE model introduces a variety of exogenous shocks which makes it feasible to analyse the inflation inertia characteristics in different contexts.
In accordance with Walsh (2003), this article constructs a standard CIA model and a CIA model with endogenous money, by introducing the Taylor rule, based on the quarterly data during the period 1993-2011 in China. This paper also examines the characteristics of inertia in inflation and the reactions to technology and monetary shocks and compares the two models, determining which model performs better in describing the real economy in China. In order to obtain credible conclusions, this paper estimates the key parameters and the parameters to be tested, using the Bayesian approach. The Bayesian method can not only be used to estimate the parameters, but also to compare the merits of the models based on the posterior distributions. This article also compares the theoretical inflation inertia and the inertia of the real data, and analyses the mechanism through which the inflation inertia is formed. And finally, we analyse the sources of inflation persistence in China.
This remainder of this article is organised as follows. In Section 2, we construct a standard CIA model as well as a CIA model with endogenous money and solve for the balanced system. In Section 3, we calibrate the model based on the Chinese macroeconomic data. In Section 4, we describe how the data is treated and compare the estimated results. In Section 5, we present the steady-state path of inflation, compare the theoretical inflation persistence and the empirical inflation persistence, and analyse its influencing factors. In the final section, we draw our conclusions.
2 The model
2.1 Standard CIA model
2.1.1 Equilibrium
The equilibrium is characterised by an allocation of quantities and prices that satisfy the households' optimality conditions and budget constraints, the firms' optimality conditions, and finally the market-clearing conditions. According to Uhlig (1995), we solve the model by log-linearising the equilibrium conditions around the deterministic zero-inflation steady state. Here we only present the equations necessary to characterise the equilibrium of the variables of interest:
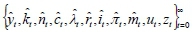
where the lowercase letters denote the log-deviation from their steady state counterparts. The following equations determine the equilibrium dynamics of the variables above:
Production function:

Market clearing:
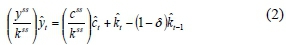
The optimal choice of labor-leisure:
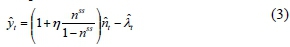
Marginal utility of consumption:
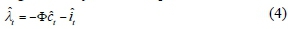
Marginal product of capital:

Cash in advance constraint:

Money supply:

Euler equation:

Fisher equation:

Monetary policy shock:
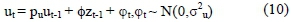
Productivity shock:

2.2 CIA model with endogenous money
According to Suh (2004), the Taylor rule is introduced into the CIA model to describe the characteristics of the endogeneity of money. Under the Taylor rule, the monetary authorities will control interest rates based on the output and inflation in the economy (Taylor, 1993). The expression is as follows:

where ω1and ω2 represent the reaction coefficients of interest in relation to inflation and output. î,  and
and  denote the log-deviations from their steady state counterparts. We combine the Taylor equation with the Fisher equation which we use to replace the original equation (9). Thus equation (9) becomes:
denote the log-deviations from their steady state counterparts. We combine the Taylor equation with the Fisher equation which we use to replace the original equation (9). Thus equation (9) becomes:
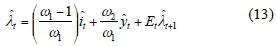
3 Calibrations and estimations
The set of parameters to be estimated is provided using two methods. First, the general static parameters are given by calibration, and secondly, the dynamic parameters are estimated using Bayesian techniques.
3.1 Calibration and estimation of the standard CIA model
The basic idea of calibration is to determine the parameters in the model based on the relationships between the economic variables which are observed. While the method is not strict, for data samples that are rarely or not obtained, it may also be used to fix the parameters. In order to enable the calibrated parameters to reflect the actual economic situation as accurately as possible, the DSGE model parameters are grouped into three broad categories (according to Negro & Schorfheide, 2008) as follows:
First, the parameter set
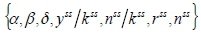
can be easily identified from the steady-state relationships among the observable variables. The parameter βis calibrated as 0.989 so that the steady-state nominal interest rate R is equal to 1.1 per cent, This is the average measured value of the Shanghai Interbank Offered Rate (Shibor) in the 1996-2012 period. The value of αis fixed as 0.5 according to the literature. Chow and Li (2002) estimate the aggregate production function with China's 1952-1998 data and find the Cobb-Douglas function with constant returns to scale to be applicable to China. Furthermore, their estimate of the capital share is 0.55. Estimates of the capital share by other scholars are around 0.5, such as Zhang's (2002) estimate of 0.499, or Wang and Fan's (2000) estimate of 0.5, which means that the capital in the steady state contributes 50 per cent to the output. The quarterly depreciation rate of capital δis computed at 0.025 (10 per cent per year). The preference for leisure, N, is calibrated so that in the steady state total hours worked, nSS, this amounts to 1/3 of the total available time (Caraiani, 2009). The results are as follows:
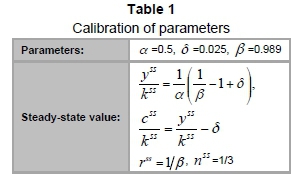
Secondly, the group of coefficients {Φ,η} includes coefficients of relative risk aversion consumption and work that govern the DSGE model's endogenous propagation mechanism. The priors of these parameters are based on micro-level data sets that are unrelated to each other. Therefore, our approach maintains the independence assumption that has become standard in the literature for these parameters. We ensure that the prior distribution contains the exact information as much as possible. Following Walsh (2003) and Caraiani (2009), Φ and η follow a normal distribution whose means are 1 and 2, respectively, and the standard deviations are both 0.5.
Finally, the parameters {ρz, ρu, φ, σz, σu} are used to describe the propagation mechanism of the exogenous shocks (for example, autocorrelations, and standard deviations) that belong to the third group. Based on the literature in China, the persistence coefficient of the technology shock is set to 0.95, and its standard deviation is 0.023 (Hu & Liu, 2007). The persistence coefficient of the monetary shock is set to 0.42, and its standard deviation is set to 0.057 (Wang et al., 2011). The reaction coefficient of the money supply and its impact on output is fixed at 0.3. The parameters are shown in Table 2.
3.2 Calibration and estimation of the CIA model with endogenous money
In the model, the calibrations of the parameters are set as {α ,β ,δ , yss/kss ,nsskss,rss ,nss} and the priors and initial values of {Φ, η, ρz, ρu, φ, σz,σu}are the same as in the above model. The parameters {w1, w2} in the modified Fisher equation are to be estimated using Bayesian techniques. According to Ball (1999), the two parameters are assumed to follow a normal distribution whose means are 1.5 and 0.5, respectively, and whose standard deviation is 0.25, as shown in Table 2.
4 Data and Results
4.1 Data
This paper uses the observable data underlying per capita output and inflation in China. Since data on the per capita output are not available, per capita output is obtained by dividing the real GDP by the population1. The GDP series is the quarterly GDP in 1993 constant prices. The inflation rate is proxied by the GDP deflator2. The quarterly data are compiled by the Chinese Economic Index net (CEInet) statistical database, for the period covering January 1993 to January 2012. These series are transformed to eliminate unit roots and trends, and for that they are logged, de-seasonalized by the TRAMO/SEATS method and then detrended with the Hodrick Prescott filter.
4.2 Bayesian estimation
The parameters are estimated using Dynare 3.0 (Adjemian, Bastani, Juillard, Mihoubi, Perendia, Ratto & Villemot, 2011) as reported in Table 3. Most of the parameters estimated are approximately the same, except for the parameter Φ. The parameters ρz and ρu are estimated as being more than 0.92 and 0.73, respectively, which is due to the technology and monetary shocks having high autocorrelation coefficients. The estimated parameter φ is greater than zero, indicating that the positive productivity shock leads to increasingly large monetary shocks. The standard deviation of the technology shock σz is less than the standard deviation of the monetary shock, σu, indicating that the variance of the technology shock influences the economic system more than the monetary shock.
The only significant difference between the two models is that the parameter φ is estimated to be 1.9207 and 1.2644 for the standard CIA model and augmented CIA model, respectively. Obviously, the parameter in the CIA model with endogenous money is closer to the initial value of 1, according to Walsh (2003). Therefore it can be concluded that the CIA model with endogenous money is more consistent with a priori information.
In the CIA model with endogenous money, based on the estimated parameters ω1> ω2, it follows that keeping prices stable is a basic policy of the central bank.
Figures 1 and 2 present the prior and posterior distributions of the two models, respectively. Obviously, the augmented CIA model corresponds to prior information. In addition, the parameters, {ρz, ρu, φ, σz, σu}, are significantly changed, which means that these two observable series, per capita output and inflation, include much new information. Figure 2 represents the goodness of fit of the priori information.


The Bayesian estimation was performed through two Markov chains of 10,000 Metropolis-Hastings draws. However, any inferences drawn from MCMC are based on the assumption that the Markov chain has reached convergence. Therefore, the diagnosis of the MCMC convergence is very important to estimation and inference. Figures 3 and 4 report the multivariate convergence diagnostics for the two models, respectively. The multi-variate statistics indicate that the convergences are achieved, so that our estimates and inferences are credible.
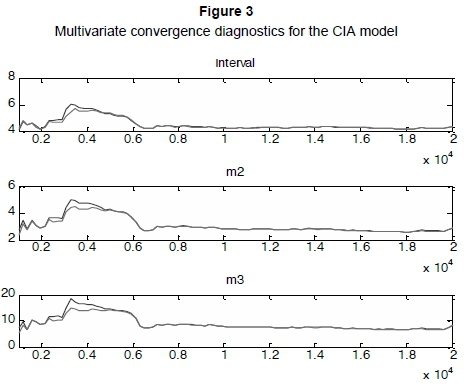
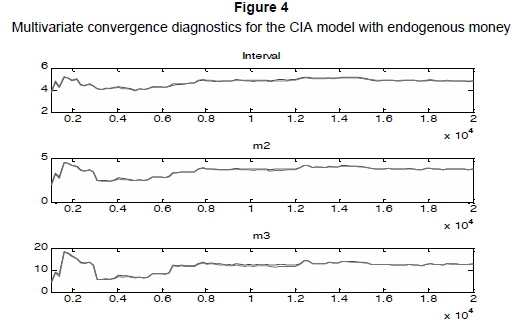
4.3 A Bayesian comparison of the models
Table 4, which presents the log-marginal likelihoods, provides a comparison of the two estimations in terms of the posterior odds ratio. The log-marginal likelihoods are the result of the Bayesian estimations.
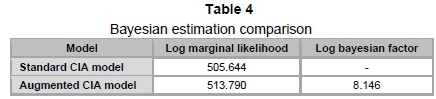
According to the Jeffreys (1998) rule of thumb, if a log-Bayesian factor of 3 is higher than 2, the original model is superior to the alternative model. If the factor is less than 2, there is no significant difference between the two models. Obviously, the augmented CIA model is superior to the standard CIA model.
Estimation and comparison of inflation persistence
Fuhrer (1995) characterise inflation persistence in U.S. data using a vector autocorrelation function relating inflation and deviations of output from the trend. In the vector autocorrelation function, both inflation and output are highly persistent and there are significantly positive cross-correlations between inflation and output.
To learn more about the present model of inflation inertia simulation, this paper compares the autocorrelation coefficients of empirical and theoretical inflation persistence. We can see from Figure 5 that the real data have a high degree of persistence in the first period, and then the autocorrelation coefficients descend quickly. The real data demonstrate considerable persistence at first. The persistence is weakened to zero after more than 3 years (12 lags). In comparison, it is found that the CIA model with endogenous money captures more of the inflation than the other model.
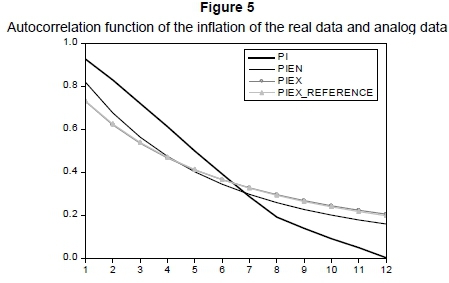
To obtain robust conclusions, we incorporate the parameters estimated in the augmented CIA model into the standard CIA model, and find that there is no difference in inflation persistence as previously compared. In Figure 5, the autocorrelation function of references almost coincides with the autocorrelation function of the theoretical data with endogenous money. It is demonstrated that the superiority of the augmented CIA model is due to the effect of the propagation mechanism on the inflation persistence rather than due to the variance between fixed parameters.
Exogenous shocks, the production process, monetary policy and its transmission mechanism all have a significant impact on the dynamic characteristics of inflation, from a theoretical point of view. Thus, this article attempts to change a few key parameters of the model, in order to measure the impact on the inflation autocorrelation coefficients of external shocks, monetary policy, as well as the change in the production process.
5.1 Inflation process in standard CIA model
For simplicity, we only consider equations (7), (10) and (11), as follows:
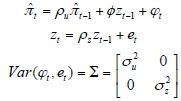
In order to analyse the formation mechanism of the inflation inertia in the DSGE model, this paper deduces the ith-order autocorrelation4function of inflation, according to Fuhrer (2006) as follows:
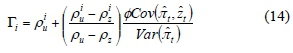
where the initial value is:
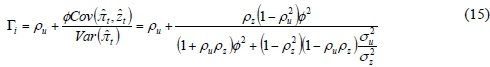
It is composed of two parts: the first part decays by ρu, and the second part is 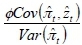 in the first period, and descends by
in the first period, and descends by 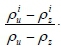 . Obviously,
. Obviously, 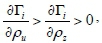

This means that the sources of inflation persistence are as follows: (1) Money supply persistence ρu. Inflation persistence mainly depends on the persistence of money. (2) The variance of money supply shock σ2u. The persistence of inflation reduces with an increase of σ2u, because as σ2ubecomes larger, the inflation process is more inclined to be white noise whose persistence is zero. (3) The response coefficient φof the money supply growth to productivity shock. If φis bigger, the shock of productivity will be transmitted to
the money supply more frequently, and the inflation process is more inclined to be an AR (1) process. (4) The persistence of productivity ρz. The persistence of inflation grows with an increase in persistence of productivity. (5) The variance of productivity σ2z. Inflation persistence grows with an increase of σ2z.
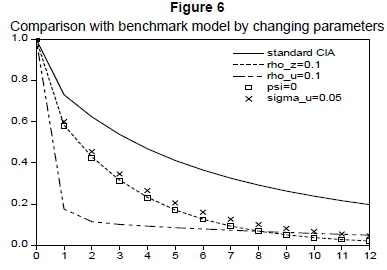
The above conclusion is based on simplifying the model. In order to reflect the whole model, this paper tries to compare it with the benchmark model by changing some critical parameters. As shown in Figure 6, the standard CIA model is treated as the benchmark model. When the persistence of the money supply, ρu, is changed from 0.7358 into 0.1, and inflation persistence declines to below 0.2. By comparison, inflation persistence is changed less by adjustment of the , φand ρz. Inflation persistence is most sensitive to the parameters of ρu. In short, the conclusions drawn from the auto-correlation function are similar to the results for Figure 6.
5.2 Inflation process in CIA model with endogenous money
By introducing endogenous money, the inflation process can be described as:
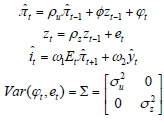
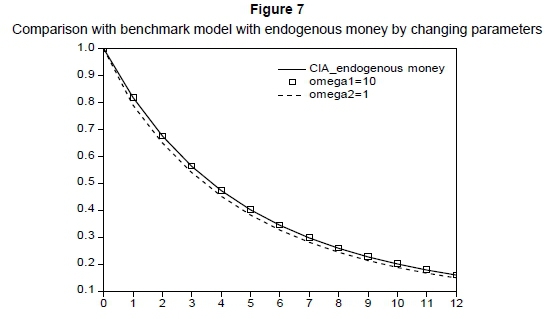
Does endogenous money change inflation persistence? We can see that inflation persistence is affected by the introduction of endogenous money but the effect is to a small degree. As shown in Figure 7, after introducing endogenous money, if the monetary authority adjusts ω1, the reaction coefficient of interest rate to inflation, from 1.5 to 1, there is almost no change in inflation persistence. And so does ω2, the reaction coefficient of interest rate to productivity.
6 Conclusions
This paper builds two dynamic stochastic general equilibrium models with the cash-in-advance constraint: one focuses on exogenous money and the other places an emphasis on endogenous money. We try to capture the characteristics of inflation persistence, compare the two models, and analyse the factors that influence inflation inertia. The Bayesian methods improve the credibility of the parameters estimated, and the main conclusions are as follows.
We can see from the Bayesian estimation that technology and monetary shocks which follow an AR (1) process have a high autocorrelation coefficient. The monetary shock has a positive response to the productivity shock so that the variance of the productivity shock is less than the variance of the monetary shock. In the augmented CIA model, ω1 > ω2 indicates that the monetary authority in China treats stable prices as the main target of monetary policy when balancing the output gap and inflation. Due to the convergence of the Markov chain for the Bayesian techniques, the estimation and inference are reliable.
The CIA model with endogenous money is superior to the standard CIA model. First, the posterior distribution of the augmented CIA model fits better with the prior information. Second, the log marginal likelihood of the augmented CIA model is greater than that of the alternative model so that the former is superior to the latter. Finally, the inflation persistence curves indicate that the CIA model with endogenous money is closer to the real situation.
Inflation in the model inherits very much of the persistence of the driving process, so that the variance ratio σ2u/σ2z and the inflation persistence are positively related. Backward-looking behavior imparts some "intrinsic" persistence to inflation, and it is ρuthat constitutes the dominant source of persistence. Endogenous money has little effect on inflation persistence.
There are some limitations to this study. First, there is still a difference between empirical and theoretical persistence, in that the real data has greater initial value and descends faster. Second, we only studied the flexible pricing situation, and the sticky price assumption may be closer to the real world. Gali and Gertler (1999), Woodford (2003) and Fuhrer (2006) consider that the introduction of the staggered price adjustment mechanism can increase the inertia of inflation, so that the New Keynesian Phillips Curve can be obtained by a staggered pricing model (Calvo, 1983). This has shown that it can capture some of the features of the dynamics of inflation. Therefore, this field deserves more research than it has so far received.
Acknowledgements
Financial support from the Ministry of Education (11YJA790048), the National Social Science Fund (11CJY104) and the Jiangxi Social Science Fund (09JL202) is gratefully acknowledged. The usual disclaimer applies.
The authors are grateful to the valuable comments made by the reviewers.
References
ADJEMIAN, S., BASTANI, H., JUILLARD, M., MIHOUBI, F., PERENDIA, G., RATTO, M. & VILLEMOT, S. 2011. Dynare: reference manual, Version 4. [ Links ]
BALL, L. 1999. Efficient rules for monetary policy. International Finance, 2(1):63-83. [ Links ]
CALVO, G.A. 1983. Staggered prices in a utility-maximizing framework. Journal of Monetary Economics, 12(3):383-398. [ Links ]
CARAIANI, P. 2009. Inflation persistence and DSGE models. An application on Romanian economy. Journal of Economic Computation and Economic Cybernetics Studies and Research, 3(43). [ Links ]
CHOW, G.C. & LI, K.W. 2002. China's economic growth: 1952-2010. Economic Development and Cultural Change, 51(1):247-256. [ Links ]
COLEMAN, S. 2010. Inflation persistence in the Franc zone: Evidence from disaggregated prices. Journal of Macroeconomics, 32(1):426-442. [ Links ]
FUHRER, J.C. 1995. The persistence of inflation and the cost of disinflation. New England Economic Review, (Jan):3-16. [ Links ]
FUHRER, J.C. 2006. Intrinsic and inherited inflation persistence. International Journal of Central Banking, 2(3):49-86. [ Links ]
GALI, J. & GERTLER, M. 1999. Inflation dynamics: A structural econometric analysis. Journal of Monetary Economics, 44(2):195-222. [ Links ]
HU YONGGANG & LIU FANG, 2007. Labor adjustment cost, liquidity constraints and China's economic fluctuations. Economic Research Journal, (10):32-43. [ Links ]
JEFFREYS, H. 1998. Theory of probability, Oxford University Press, USA. [ Links ]
NEGRO, M.D. & SCHORFHEIDE, F. 2008. Forming priors for DSGE models (and how it affects the assessment of nominal rigidities). Journal of Monetary Economics, 55(7):1191-1208. [ Links ]
SUH, J.E. 2004. Two essays on monetary policy under the Taylor rule, Ph.D. diss., Texas A&M University. [ Links ]
TAYLOR, J.B. 1993. Macroeconomic policy in a world economy: From econometric design to practical operation. New York, W.W. Norton. [ Links ]
UHLIG, H. 1995. A toolkit for analyzing nolinear dynamic stochastic models easily. In R. Marimon and Scott A. (eds.) Computational methods for the study of dynamic economies, New York, Oxford University Press:30-61. [ Links ]
WALSH, C.E. 2003. Monetary theory and policy, the MIT Press. [ Links ]
WANG JUNBIN, GUO XINQIANG & CAI HANBO, 2011, Output overshoot, consumption inhibits and inflation persistence under aggressive monetary easing. Management World, (3):7-21. [ Links ]
WANG XIAOLU & FAN GANG. 2000. The sustainability of China's industrial growth, Beijing: Economic Science Press. [ Links ]
WOODFORD, M. 2003. Interest and prices: Foundations of a theory of monetary policy. Princeton University Press. [ Links ]
ZHANG, JUN. 2002. Capital formation, industrialization and economic growth: understanding China's economic reform, Economic Research Journal, (3):3-13. [ Links ]
* Corresponding author contact: Ridong Hu, j_rdhu@hqu.edu.cn
1 Because the National Bureau of Statistics does not provide quarterly population data, we turn annual population data into quarterly population data by interpolation.
2 Since the quarterly GDP deflator data are not provided by China's Bureau of Statistics, the data are obtained using the following two steps. First, we calculate the nominal GDP growth rate and the real GDP growth rate with the existing data. Secondly, we obtain the GDP deflator using the equation: GDP deflator = nominal GDP growth rate - real GDP growth rate.
3 Log-Bayesian factor = Log marginal likelihood of the original - Log marginal likelihood of the alternative.
4 See the derivation in the Appendix.














