Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
South African Journal of Economic and Management Sciences
versión On-line ISSN 2222-3436
versión impresa ISSN 1015-8812
S. Afr. j. econ. manag. sci. vol.15 no.3 Pretoria ene. 2012
ARTICLES
Basel III Countercyclical Capital Rules: implications for South Africa
Gary van Vuuren
Department of Economics, North-West University
ABSTRACT
The financial crisis has been blamed on many entities, institutions and individuals as well as the Basel II accord which had just begun to be implemented globally when the crisis erupted. The criticisms resulted in the construction of Basel III, a series of measures designed to augment and repair (but not replace) the Basel II accord. One of these adjuncts addresses the problem of economic procyclicality and suggests ways to mitigate it through capital charge increases when economies overheat and capital charge reduction in economic contractions. The consequences of this proposed measure's introduction for South African banks is explored.
Key words: Basel III, procyclical, countercyclical, buffer capital
1 Introduction
The financial crisis that has wreaked havoc in global financial markets since August 2007 had its origins in an asset price bubble that interacted with new kinds of financial innovations that masked risk (Baily, Litan & Johnson, 2008). The crisis precipitated, inter alia, a calamitous reduction of bank lending and the widespread destruction of the securitysation and structured product markets. Later (2010 through 2012) the crisis manifested itself through sovereign insolvency (among the worst affected were Greece, Ireland, Portugal, Spain and Italy) and it heralded an ever deepening distrust of the accuracy of credit ratings and the efficacy of regulatory capital directives (Sorkin, 2010).
The (then - 2008) new set of regulatory capital rules called Basel II had been finalised by the Basel Committee for Banking Supervision (the BCBS) under the auspices of the Bank for International Settlements (the BIS) in 2006 and sections of the accord had begun to be implemented globally by the time the crisis erupted (Ayadi, 2008). This Basel II accord was designed, like its predecessor Basel I, to prevent (at best) and forewarn (at worst) impending economic disasters by ensuring the safety and soundness of the global banking system (BCBS, 2006). When the scale and duration of the credit crisis became apparent, however, the market perception of this flagship accord was that of spectacular failure. National governments, credit rating agencies, bankers, regulators, central banks and quantitative models which employed unrealistic assumptions were among those at whom blame for the crisis was levelled (US Financial Crisis Inquiry Commission, 2010).
Whatever the truth of the accusations, each alleged accomplice quickly set about rectifying mistakes in their own way, adapting and amending procedures and approaches and - in the BISs case - devising a comprehensive repair kit to existing regulatory measures (BCBS, 2010a). This repair kit came to be known as Basel III and this is an important point worth emphasising: Basel III does not, nor was it ever intended to, replace Basel II. The vast bulk of Basel II rules remain intact: Basel III aims to repair those parts of the accord deemed inadequate (e.g. reconstitute the composition of acceptable regulatory capital), augment and adapt several accord components (e.g. revisit the capital required for the trading book) and introduce novel themes to revitalise the accord (e.g. introduce a leverage ratio and a handful of capital buffers which effectively increase the capital ratio of 8.0 per cent to 10.5 per cent and, under certain circumstances, to 13.0 per cent).1 One of these novel introductions - the procyclical capital buffer - is the focus of this paper.
The paper proceeds as follows: Section 2 interrogates the literature regarding economic procyclicality, its origins and implications on a broad global scale. The BCBS's choice of procyclical measure is dealt with in Section 3. The BCBS have argued convincingly in favour of this measure as a means of dampening uncontrolled economic expansion and have enjoyed some success in applying it to financial indicators in highly developed economies such as the US and UK. It is by no means conclusive that an identical metric will be as effective when applied to smaller, developing economies, such as South Africa's.
The BCBS's chosen procyclicality metric requires the calculation of two components: a calibrated measure of regional economic activity and this measure's long run trend. The procyclicality metric operates by activating a staggered increase in regulatory capital based upon the difference between these two components. The Hodrick Prescott (HP) filter has been selected by the BCBS to determine the economic activity measure's long run trend. Section 4 introduces and discusses the HP filter, assesses its relevance and applicability to financial data and points out the pros and cons of its use. Some problems associated with the filter - among them end point problems - exist and these are also presented in this section. The HP filter is then applied to South African data and the results analysed and presented in Section 5. Some supporting evidence regarding the periodicity of some of South Africa's financial indicators is also presented in this section using Fourier analysis. The article concludes with Section 6.
2 Literature review
Procyclicality refers to those economic quantities that are positively correlated with the overall state of the economy. The credit losses that banks suffer during recessions are generally higher than those experienced during economic expansions. These losses negatively impact bank funds because, during downturns, maximum lending capacities decrease (the numerator of the capital ratio) and risk weighted assets (the denominator of the capital ratio) increase simultaneously. This combination of effects results in the intrinsic procyclicality of capital requirements - a fact deduced even before the implementation of the Basel II capital accord. Academics, practitioners and policy makers warned that capital requirements under the Internal Ratings Based (IRB) approach would amplify procyclicality since banks tend to kerb lending in response to recessions and increase lending during economic expansions (e.g. Heid, 2003; Catarineu-Rabell, Jackson & Tsomocos, 2003; Goodhart & Taylor, 2006). The Basel II accord would thus thwart policy maker's efforts to maintain macro-economic stability (Gordy & Howells, 2004).
Heid (2003) argued that the procyclical effects of the (then yet to be introduced) Basel II accord could be manifest in two ways. First, if asset risk (or even the mere perception of asset risk) were correlated with business cycles, capital charges would be subject to large swings leading to further asset price and interest rate volatility. Second, an increase in financial sector volatility could spread to the real sector. The surge in credit risk would lead to an increase in banks' credit risk capital, and a portion of these charge increases would be passed on to borrowers who in turn would reduce investment spending and aggravate the downturn even further.
The Bank of England (BoE) asserted that every regime that adopted a minimum capital requirement framework could stimulate financial procyclicality: during recessions banks face a combination of amplifying pressures: higher regulatory capital requirements, increased provisions and greater defaulted loan write offs (Catarineu-Rabell, Jackson & Tsomocos, 2003). The analysis, which preceded the implement-tation of the Basel II accord, showed that the procyclical impact of the new internal ratings based (IRB) methodology could be dampened by adopting a through-the-cycle (TTC) rating system which would dampen the sensitivity of borrower probabilities of default (PDs) to macroeconomic conditions despite this rating system's notoriety for being a poor internal pricing and risk-management tool. The authors used a multi-period general equilibrium framework to study market interactions and identify channels affected by policy parameter changes. They found that, although the use of a TTC method would not reduce procyclicality, using the alternative (a point in time (PIT) rating scheme) would considerably magnify procyclical effects. With the benefit of hindsight, a purely TTC approach ignored the contribution of securitisation and the vast, incorrect assignment of AAA ratings to senior securitised tranches to required capital levels (Brunnermeier, 2009). In addition, although most rating agencies claim a strong TTC approach underpinning their ratings, some research has found otherwise (Lowe, 2002).
Saurina and Turcharte (2007) constructed and tested a PD model for Spanish mortgage loans to calculate different types of PDs: PIT, TTC, average across the cycle and acyclical and found that minimum regulatory capital under Basel II was highly sensitive to the risk measurement methodology employed. TTC measures, for example, showed less variability but more capital on average than the PIT approach and acyclical ratings produced stable and relatively low requirements. The authors concluded that the procyclicality of regulatory capital requirements under Basel II would thus depend upon the way internal rating systems were implemented and how the output was utilised (Saurina & Trucharte, 2007).
Research conducted prior to the implementtation of the Basel II accord (end 2006) and the IAS 39 accounting guidelines (January 2005) found that the informational and allocative efficiency benefits of these reforms could increase procyclicality as well as market volatility (Goodhart & Taylor, 2006). The research concluded that losses on tradable assets incurred during economic downturns and booked at fair value could increase both income and profit volatility. In addition, the authors advocate that regulatory rules requiring banks to hold more capital during recessionary periods (reflecting increased potential credit losses), may result in loan book reductions and an increase in capital funding costs. The resulting credit rationing, or the higher credit costs could then result in reduced investment and consumption (Goodhart & Taylor, 2006).
A flexible simulation engine was constructed by Gordy and Howells (2004) to explore the cyclical behaviour of regulatory capital under different rating philosophies and various assumptions on how bank lending behaviour responds to the business cycle. The simulation results obtained in this research demonstrated that the extent of capital requirement cyclicality depends strongly on how new bank lending varies with macroeconomic conditions. The methodology did not allow regulatory rules applicable to new lending to be endogenous to the bank's capital position. Rather, these rules were modelled to depend exogeneously on the macroeconomic milieu. The authors' simulation results were not sufficient to convince them that procyclicality in the Basel II accord would require corrective measures. They argued that, even were regulatory capital to be smoothed in some way, it would not be possible to dampen economic capital requirement procyclicality by regulatory sanction (Gordy & Howells, 2004).
Repullo and Suarez (2008) investigated the cyclical effects of moving from risk-insensitive (Basel I) to risk-sensitive (Basel II) capital requirements using a dynamic equilibrium model of relationship lending. The authors assert that current levels of bank capital determine future lending since banks anticipate that earnings shocks during economic down-turns may impair their capacity for future lending. As a precautionary measure, banks hold capital buffers (Repullo & Suarez, 2008). The authors demonstrated through an endogenous, dynamic capital-structure model and with the assumption that banks have limited access to capital markets in stressed periods that Basel II would change the behaviour of these buffers from countercyclical to procyclical. In addition, results showed that higher buffers during periods of economic expansion would be insufficient to counteract the increased requirements during recessions. These effects would lead to a significant contraction in the supply of credit (Repullo & Suarez, 2008).
Rochet (2008) was not convinced that the impact of Basel II and IAS 39 on bank lending would be sizable. Even if the effects were considerable, to compensate through regulatory intervention (make target capital ratios countercyclical) 'would be a disaster' for bank incentives (Rochet, 2008). A study conducted by the Banque de France found that banks should be able to smooth regulatory ratio fluctuations by making use of their economic capital buffer. If this were the case, and despite the inherent procyclicality introduced by Basel II, the volume of credit to the economy should not be dramatically affected in economic downturns (Rochet, 2008). In addition, pillar II of the Basel II accord could mitigate the procyclical effects of the capital ratio if regulators imposed additional capital charges on banks holding insufficient economic capital (Rochet, 2008). Should governments wish to dampen economic fluctuations, appropriate policy instruments (such as fiscal and possibly monetary policy) should be used rather than prudential regulation and financial intermediary supervision (Rochet, 2008).
The Basel Committee has decided to address procyclicality in a number of ways including: the introduction of a noncyclical PD proxy in internal rating models; encouragement for provisioning policies to move to a forward-looking expected loss methodology rather than the incurred loss approach currently applied under IFRS and US GAAP and the introduction of capital buffers, proactively adjusted to take macroeconomic factors into account (Barnes, De Toytot, Sprinzen & Chan, 2010).
The collective aim of these proposals is to address detrimental trends such as lending growth, liquidity mismatches and increasing leverage before they exceed historical long run averages i.e. before they 'overheat'. Although some regulators are able to adjust minimum capital requirements and alter underwriting criteria, the track record of the application of this influence has been mixed. This could be due in part to a reluctance of local regulators to penalise domestic banks relative to international competitors but the credit crisis may strengthen resolve (Barnes et al., 2010).
Having investigated the origin and effect of procyclicality in finance, as well as the effects - intentional or otherwise - of the Basel II accord on procyclicality, the next section addresses the BCBS proposals to introduce a countercyclical capital measure.
3 Mitigating procyclicality
Regulators have long been aware of problems posed by procyclicality of the financial system, but the financial crisis contributed to the acceleration in efforts to provide frameworks and tools to address these.
The BCBS's principal objective underlying the introduction of countercyclical capital standards is to encourage banks to increase capital buffers in times of economic expansion that may be then drawn down during economic contractions (BCBS, 2010b). These buffers are not to be considered as prudential minimum capital requirements, but rather unencumbered capital in excess of that minimum. The idea is that this capital should be available - in times of economic stress - to absorb losses. Building up buffer capital accumulation in times of economic expansion should strengthen individual banks' defences (and thus the system as a whole) thereby addressing the fact that risks accumulate rapidly in favourable economic conditions, but the consequences of these risks become manifest only after significant lags (BCBS, 2010b).
In designing a functional countercyclical capital buffer scheme, the BCBS aimed to fulfil two related objectives (Drehmann, Claudio, Gambacorta, Jimenez & Trucharte, 2010), namely to limit system-wide risk by strengthening the banking system's resilience against shocks and to limit the banking system from amplifying economic fluctuations.
Desirable features of the effective scheme would need to include:
1) Correct timing: of buffer capital accumulation and release. This equates to identifying economic expansions and contractions correctly.
2) Suitable capital buffer size: accumulating during economic expansions, this capital must be able to absorb losses adequately in recessionary periods without triggering further stresses.
3) Robustness against regulatory arbitrage.
4) International enforceability.
5) Rule-based: thereby acting as an automatic stabiliser.
6) Low implementation costs.
7) Simplicity and transparency.
The BCBS considered setting a target buffer capital ratio above the minimum capital ratio, with the gap between the two either at a fixed level (which is fixed during expansionary or recessionary economic periods but takes on different [fixed] values depending on the prevailing economic milieu - Figure 1a) or moving countercyclically (i.e. increasing [linearly] in expansionary economic periods and declining [linearly] in recessionary periods - Figure 1b).
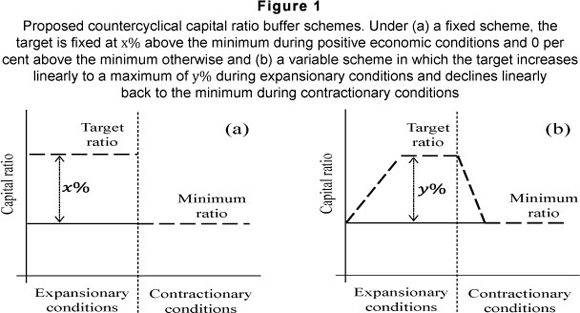
In the former scheme, a fixed buffer ratio of X% is chosen when the prevailing economic conditions are favourable so that the capital ratio = minimum capital ratio + X%. The value of X% drops instantaneously to 0 per cent in recessionary periods, so the regulatory minimum capital ratio becomes the relevant constraint (BCBS, 2010b). Fixed capital targets can be automatically stabilising because their incidence varies over the economic cycle, but these fixed targets require careful construction to avoid inducing the very procyclicality they are designed to prevent. For example, although punitive minimum capital requirements can constrain risk-taking during economic expansions, they can also encourage the rapid disposal of risky assets at times of tighter credit conditions (Drehmann et al., 2010).
The latter scheme considers a linearly increasing target in expansionary periods until an upper limit of y% is reached with the accumulation related to a conditioning variable (e.g. credit growth, earnings or credit spreads). Release of the buffer when recessionary conditions arise would be gradual (and, ideally, linked to the same conditioning variable).
Bottom-up (bank-specific) and top-down (system-wide) conditioning variables were considered by the BCBS in the construction of a countercyclical capital scheme.
Bottom-up approaches produced sizeable idiosyncratic components, implying considerable differences in the values of bank adjustment factors, even after broad financial stability pressure accumulation. Bank-specific factor persistence was also found to be minimal under this approach, resulting in substantial target countercyclical capital buffer volatility (Drehmann et al., 2010:20).
Top-down approaches fared better (and were eventually adopted by the BCBS), in particular the aggregate credit growth-to-real GDP growth ratio, despite some concern that the optimal variables2 used to signal the timing and rate of buffer accretion were not always optimal for signalling buffer depletion timings and rates. Top-down data are available in all jurisdictions; in contrast to bottom-up approach variables (e.g. CDS spreads) which are bank-specific and not always available. An additional benefit of using the credit growth-to-GDP growth ratio as a conditioning variable is that a time-varying target on credit expansion in favourable economic conditions may also kerb credit booms (Drehmann et al., 2010:21).
In the construction of a countercyclical buffer scheme, a persistent problem was how to measure the financial cycle. Several variables were considered, including measures of bank performance (e.g. earnings, losses or asset quality, CDS spreads), financial activity (e.g. credit growth) and the cost and availability of credit (e.g. credit spreads). Some problems which arose included the fact that financial and real (output) cycles do not necessarily coincide: the relationship between these variables often varies over time, severe financial stresses do not necessarily arise in each recessionary period and leads and lags between financial indicator output peaks and troughs are often significant and highly variable (Brunnermeier, 2009).
Measures of aggregate output and credit growth were considered the most natural indicators for the state of the financial cycle.3 Even though the collective behaviour of the banking sector may still influence aggregate macro indicators, they offer the advantage that they are immune to strategic manipulation by individual banks (Saurina & Trucharte, 2007). Widespread availability of most macro-economic series was also taken into account by the BCBS in their final decision regarding input variables of which two were particularly interesting.
1) Real GDP growth was considered by the BCBS to be "the most natural indicator" of a specific economy's aggregate business cycle. Business and the financial cycles however, although interconnected, are not always synchronised.
2) Aggregate real credit growth was considered to be a "natural measure of supply", (all sources of credit are taken into account, not only bank credit) since historical boom periods have been characterised by rapid credit expansion and credit contraction has typically heralded credit crunches (Drehmann et al., 2010).
The deviation of aggregate real credit growth from its long run trend was considered a possible informative variable to use to evaluate the state of the financial cycle. The final decision (and the measure adopted by the BCBS as part of the Basel III amendments) was not these deviations, but rather deviations from the long run trend of the aggregate credit-to-real GDP growth ratio (hereafter the "creditto-GDP ratio" and the difference between this ratio and the long run trend the "credit-to-GDP gap") due to financial deepening, for example.
The credit-to-GDP ratio normalises the aggregate credit growth variable to take into account the synchronised movement of credit demand and supply with the size of the economy. There is, in addition, a strong historical link between enhanced4 credit-to-GDP growth and crises that have erupted in the banking sector. It is important to note that even though the credit-to-GDP gap normalises the volume of credit by GDP and corrects for changes in the long run trend, it remains a statistical metric and may not, therefore, fully take into account the equilibrium level of lending given the state of the economy.
The next problem to be solved - how to ascertain and measure the long run trend of the credit-to-GDP gap - is explored in the next section.
4 The Hodrick Prescott filter
A popular method of trend-extraction from data is the Hodrick-Prescott (HP) filter (Ley, 2006). The HP filter was first introduced by Hodrick and Prescott in 1980 (Hodrick & Prescott, 1980) in the context of estimating business cycles, but the research was only published in 1997 after the filter had gained widespread popularity in macroeconomics (Hodrick & Prescott, 1997). The BCBS also chose the HP filter to detrend relevant macroeconomic ratio data and thus extract the information required to evaluate excessive growth in economies (see Section 3).
The HP filter has been criticised for a number of limitations and undesirable properties (Ravn & Uhlig, 2002). Canova (1994 and 1998) agreed in principle with the use of the HP filter to extract business cycles (of average duration between 4 to 6 years) from macro-economic data, but doubted the methodology for determining key parameter inputs. Spurious cycles and distorted estimates of the cyclical component when using the HP filter were obtained by Harvey and Jaeger (1993) who argued that this property may lead to misleading conclusions regarding the relationship between short-term movements in macro-economic time series data. Cogley and Nason (1995) also found spurious cycles (and extreme second-order properties in detrended data) when using the HP filter on difference-stationary input data. Application of the HP filter to US time series data was found to alter measures of persistence, variability and co-movement dramatically (King & Rebelo, 1993). Many of these critiques do not provide sufficient compelling evidence to discourage use of the HP filter. As a result, it remains widely-used among macroeconomists for detrending data which exhibit short term fluctuations superimposed on business cyclelike trends (Ravn & Uhlig, 2002).
The idea which on which the HP filter rests is that an observable macroeconomic time series (Xt) may be decomposed into its long run, non-stationary secular trend (Xt) and a (ct):
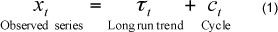
Neither the long run trend nor the cycle is directly observable so detrending approaches generally define these elements somewhat arbitrarily. The HP filter extracts the cycle by solving Equation 2, a standard-penalty program:
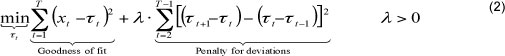
where the parameter, λ, controls the smoothness of the adjusted trend series, Tt, i.e., as λ → 0, the trend approximates the actual series, Xt, while as λ → ∞ the trend becomes linear and the procedure converges to a standard least squares solution (Mise, Kim & Newbold, 2005). The optimisation procedure in Equation 1 maximises the fit to the trend of the series, i.e. minimise the cycle component Ct by minimising changes in the gradient of the trend Xt. Note that both Xt and Ct are unobservable and since Ct is a stationary process, Xt may be thought of as a noisy signal for the non-stationary trend Tt.
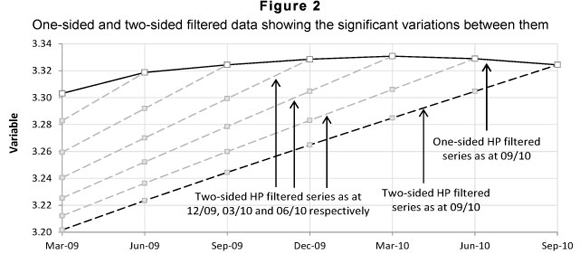
Hodrick and Prescott (1980) originally suggested an exogenous and subjective value of 1 600 for the value of λ for quarterly data, but Backus and Kehoe (1992) proposed adjusting λ based upon the square of the frequency of observations relative to quarterly data. The relative frequency is 3 for monthly data and 0.25 for annual data, so the corresponding λs are 14 400 and 100, respectively. Despite on-going research (e.g. Ravn &Uhlig, 2002; Marcet & Ravn, 2003) who derived endogenous values for λ by solving Equation 1 as a constrained minimisation problem) the values for λ discussed above are still in common use (Mise, Kim & Newbold, 2005). The optimal value for λ for South African business cycle data was explored by du Toit (2008) who argued that the optimal smoothing constant was that value of λ that least distorts the frequency information of the time series (in this case, λ = 524 for quarterly data used to evaluate a business cycle with a frequency of ~7 years -see Figure 2). The HP filter has been used to (e.g.) explore South African business cycles and estimate long-run output levels (see Woglom, 2003; Kaseeram, Nichola & Mainardi, 2004; Fedderke & Schaling, 2005; Burger & Marinkov, 2006). Drehman et al., (2010) found λ = 1600 and λ = 25 000 performed poorly on historical data whilst λ = 125000 and λ = 400000 performed well with quarterly data. The higher value of λ = 400000 is considered important from a policy perspective as it provides both a greater range and more time when the indicator provides strong and reliable signals.
The solution to Equation 2 has been shown Danthine and Girardin 1989 to be.
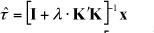
where x =[Χι ] (i.e. the observed time series), τ = [τι,.....τΤ] ,I is a TXT identity matrix, and K = kj] is a (t- 2jxt matrix with elements:
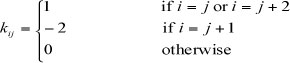
which results in

The HP filtering procedure optimises the fit to the data series, but this optimality is based on the application of the filter to an infinitely long time series. For practical purposes, the estimation of the trend and cycle components works well for a moderately long series (Mise, Kim & Newbold, 2005), but at the end points the HP filter is demonstrably suboptimal. The two-sided, symmetrical filter applies large symmetrical weights to the end points of the observed values5 to determine the corresponding trend value (Ley, 2006) disproportionately distorting the filtered values at the most recent time period (Baxter & King, 1995; Apel, Hansen & Lindberg, 1996; St-Amant & van Norden, 1997).
Kaiser and Maravall (1999) also investigated the end-point problem and found considerable improvement performance if the filter was applied to a data series which had been extended with ARIMA forecasts and backcasts. Problems with the two-sided filter are also alleviated by implementing a sing/e-sided filter, a procedure which employs the standard two-sided HP filter incrementaUy for the construction of the long term trend. The trend is determined using only information available at the time the assessment was made (Drehmann et al., 2010) and is implemented by running a loop over time and retaining the final value from the standard HP-filtered output at each point in time (Mehra, 2006). The BCBS's proposed countercyclical buffer ratio requires the use cycle and trend data generated from a one-sided HP filter which can differ considerably from two-sided filtered data as shown in Figure 2.
5 The HP filter applied to South African data
The data chosen were monthly nominal GDP and credit extended by all monetary institutions to the domestic private sector, since 1965. These data are prescribed by the BCBS (BCBS, Guidance for national authorities operating the countercyclical capital buffer, 2010b) and obtained from the Reserve Bank of South Africa. From these data, growth rates were determined and the credit growth/GDP ratio determined. For ease of comparison, the growth rates in Figure 3 of these two components were normalised to 100 at January 2000 and plotted on the same timescale. Note that although the difference between these two variables declined after the Lehman Brothers collapse in September 2008, this is due to a flattening of credit growth while GDP continued to increase. The former has begun to increase (2011), but the South African GDP growth is increasing at a greater rate -narrowing the gap between them.
South African data from January 1966 were used to determine the credit growth/GDP growth ratio as well as this ratio's long-run trend. Initial examination of these data, using standard Fourier analysis, indicates that they exhibit cyclical behaviour. This result is not unexpected since they comprise several macroeconomic components (such as the economic - or business - cycle) which are inherently cyclical (Figure 4a). Further analysis isolates the major frequency components. The frequency spectrum in Figure 4b indicates that the main component has a frequency of approximately 7 years. This is the duration of South Africa's business cycle, found previously (Botha, 2004).
Using these macroeconomic data, the credit growth/GDP growth ratio was constructed as well as the long run trend using both the one and two-sided HP filters. The results obtained - and they are very different for the two possible choices of HP filter - are shown in Figure 5 from January 2000 to January 2011. In each case, the value of λ used was 14 400.
The difference between the ratio and its long run trend (estimated by both one- and two-sided HP filters) is shown in Figure 6 below, spanning the same period as Figure 5. The cycles - although similar in shape - differ markedly in magnitude and in many instances over the time period represented have opposite signs. These factors are of considerable import in the determination of countercyclical capital charges (Section 3).
Table 1 summarises the proposed Basel III countercyclicality capital rules.
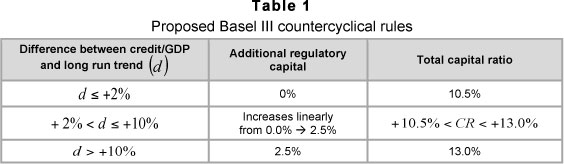
Note that the last column ('total capital ratio') refers to the capital ratio after the full implementation of Basel III as it currently stands (June 2011). The minimum capital ratio of 8 per cent increases under current proposals to 10.5 per cent by 2017 - the extra 2.5 per cent arising from the new 'capital conservation buffer'. The rules presented in Table 1 are displayed graphically in Figure 7.
These rules were then applied to the South African credit/GDP data to determine what the capital charges would have been had the new countercyclical rules been in place historically.
The results are shown in Figure 8 for the capital charges using both a one-sided and two-sided HP filter and using a λ of 14 400 in each case.
The BCBS's implementation of the Basel III countercyclical rules aims to discourage banks from excessive credit extension (relative to local GDP growth) through increasing capital charges. Some pertinent features emerge from this analysis. The onesided HP filter misses the economic expansion experienced towards the end of the last millennium (which preceded the dotcom crisis of 2000), but this is detected by the two-sided HP filter.
Both the one and two-sided HP filters detect the 2003 - 2004 acceleration in credit extension. Although South Africa largely escaped the worst excesses of the financial fallout, the effects were felt nevertheless. Had the Basel III rules been in place, capital charges would have increased to the 2.5 per cent maximum of extra capital required during this period. Interestingly, even without the actual introduction of punitive capital charges in place - the ratio quickly returns to levels at which the difference between it and its long run trend would have resulted in a 0 per cent capital add-on.
The global build up to the credit crisis is missed entirely by the two-sided filter until early 2007 when capital charges jump from 0 per cent to 2.5 per cent within a single month. Had countercyclical measures been in place using the one-sided filter, a gradual build-up of supplemental capital would have already begun to occur in late 2004. As before, these capital buffers would have fallen briefly, had they been in place, towards the end of 2005 - but they would have quickly picked up again after only a brief respite.
The capital charges indicated here are not entirely realistic. The fact is that the Basel III countercyclical rules had not been implemented in the historical periods indicated in Figure 6, so bank behaviour was not modified as a result. An entirely different scenario may have played out had the countercyclical rules actually been implemented at these times. Nevertheless, it is instructive to identify periods of overheated economic activity so as to be able to estimate - even roughly - the extent of the supplemental capital charges.
A further interesting feature of this investigation shows that supplemental capital charges would have remained at their maxi mum 2.5 per cent for much of the duration of the credit crisis, diminishing to 0 per cent only in mid-2009 for the one-sided filter (and even later in 2009 for the two-sided filter). This could herald a conflict for South African banks in the future (when the Basel III countercyclical rules are implemented in full). The rules have a dual purpose -increase capital in times of economic overheating and release these when the economy is contracting. Whilst these aims are desirable, the current rules would have forced banks to hold a minimum capital ratio at punitive levels (13 per cent)6 for far too long. While it is true that most banks enjoy capital ratios in excess of these levels, in severe economic downturns, capital is depleted and ratios plummet. Forcing banks to hold extra capital (up to 2.5 per cent) for a prolonged period after a market crisis seems counterproductive: banks (and hence, the economy at large) would benefit from the release of this capital into the system in the form of loans, for example. In addition, South African regulatory authority - the South African Reserve Bank (SARB) - may also face the practical problem of having to force banks to raise this extra equity through (e.g.) rights issues, but it is not clear that shareholders would be willing to participate in these issues to further bank recapitalisation. Authorities would need to establish in advance that banks would be permitted to reprice lending and customer fees sufficiently to generate substantial equity returns (and be able to distribute up to 100 per cent of those profits in dividends over time if balance sheet growth remained anaemic). If this were not successfully communicated, subscription to a rights issue could be seen as wasting money on a losing proposition (Walters, 2011).
Were the countercyclical buffer in place, however, it would currently (2012) be set at nil (Figure 8), with credit growth the furthest below trend in at least 50 years (Figure 6). The SARB could thus be amplifying the effect of the crisis by focussing on and overreacting to only the most recent data (Ryan & Crutchley, 2012).
Other questions have arisen from affected parties. Banks are concerned by the speed of the increase in capital required: would the increased capital be required immediately after the thresholds have been breached (Table 1), for example? If so, does the reverse apply when economic conditions allow the extra capital to be released back into the system? What of the lag between the variables (credit growth and GDP)? There is evidence that these variables are out of sync in South Africa and thus would miss crucial indicators of economic overheating. GDP figures are also frequently revised - up and down - how might this affect the capital increases? The BCBS have been silent on these issues, despite the consultation period for comments having passed in 2010 and to our knowledge, the SARB has not addressed these issues either.
6 Conclusions
The BCBS have deliberately structured a gradual phase-in of the Basel III rules for banks. Several years have been granted for full Basel III implementation: some rules need only be completed by 2018 and beyond. The idea supporting this staggered approach is to prevent a further collapse in the (still fragile) global economy. Some rules, such as those governing the new minimum liquidity requirements, have attracted criticism from banks who argue that, even under the most benign conditions, they will still be unable to comply. The short term minimum liquidity standard, for example, requires banks to maintain a liquidity coverage ratio (defined as the ratio of high quality liquid assets to net 30 day cash outflows under a prescribed (and arguably severe) stress scenario) of 100 per cent. Many banks have countered that, in certain jurisdictions, there are insufficient high quality liquid assets available for the banking sector as a whole in that jurisdiction. Banks could face penalties for these shortcomings by regulators (increased capital requirements) and rating agencies (downgrades).
The countercyclical buffer capital require ment adds to the debate. Whilst the idea to implement a flexible capital requirement that increases in favourable and decreases in unfavourable economic conditions, is sensible - the current ideas proposed by the BCBS are no panacea. Tests conducted on large, developed economies indicate that the proposals are robust, reproducible and relevant (i.e. they appear - using historical data - to measure a fair amount of supplemental capital required by banks in an economically overheating region), but this may not hold for smaller economies where insufficient investigation has taken place to date.
Unlike other global central banks, the SARB did not experience any pressure to alter its monetary operations since the onset of the financial crisis (SARB, 2011). However, other measures might yet have to be considered by the SARB, for example, ratios or metrics that reflect local economic conditions accurately, or at least more accurately than the credit/GDP metric currently proposed. Lagging and leading indicator times must also be addressed, as must the frequent revision to the relevant metric inputs - even in developed economies, before the metric acquires widespread acceptance. The SARB might also alter its focus from bank stability, to the amount of leverage in the South African household sector. This leverage is high and could pose a fundamental risk to South Africa if the need arose to substantially raise interest rates to rein in inflation. However, seeking to reduce the level of debt of South African households through (house) price controls would be a contentious move for the SARB and even if it did so, a focus on leverage alone may constitute a step in the wrong direction (Walters, 2011).
The BCBS could also be clearer about the choice between the one- and two-sided HP filters. In the main document detailing the implementation of the measure, only a footnote covers this important distinction, here shown to affect the difference between the credit/GDP ratio and its long run mean (and hence capital charges) significantly.
The fact that the metric is a jurisdiction-wide measure operating on individual banks is also cause for concern. The idea that culprit banks will be reined in by victim banks if the metric is applied regionally is laudable but may not work efficiently in practice and may force many banks into default and obscurity.
Endnotes
1 The capital ratio requirements under Basel II will thus potentially increase by up to 62.5 per cent after the full transition to the Basel III rules.2 In particular, the difference between the credit growth/real GDP growth ratio from its long run trend. These values have been shown to be a leading indicator for financial distress.
3 Asset prices were also considered to be useful aggregate indicators as they tend to rise strongly ahead of systemic banking crises, but these were eventually abandoned.
4 Faster than average.
5 That is, the 2-sided HP filter uses past and future data to estimate the components of Equation 1, so cycle data generated using it could be biased.
6 Basel II capital rules require banks to maintain a capital ratio of at least 8 per cent. Basel III increases this to 10.5 per cent via the introduction of conservation buffer of an extra 2.5 per cent. A further (maximum) of 2.5 per cent then arises from countercyclical capital requirements.
References
APEL, M., HANSEN, J. & LINDBERG, H. 1996. Potential output and output gap. Quarterly Review of the Bank of Sweden. [ Links ]
AYADI, R. 2008. Basel II implementation: in the midst of turbulence. CEPS Task Force Report: Available at: www.ceps.eu/ceps/download/1506 [accessed 2011-06-19]. [ Links ]
BACKUS, D.K. & KEHOE, P.J. 1992. International evidence on the historical properties of business cycles. American Economic Review, 82(4):864-888. [ Links ]
BAILY, M.N. LITAN, R.E. & JOHNSON, M.S. 2008. The origins of the financial crisis, The Initiative on Business and Public Policy: Fixing Finance series, Paper 3: November. [ Links ]
BARNES, R., DE TOYTOT, A., SPRINZEN, S. & CHAN, T. 2010. BaselII for global banks: third time's the charm? Standard and Poors. Global Direct Portal, RatingsDirect. [ Links ]
BAXTER, M. & KING, R.G. 1995. Measuring business cycles: approximate band-pass filters for economic time series. NBER working paper 5022. [ Links ]
BCBS. 2006. International convergence of capital measurement and capital standards. Bank for International Settlements. Availatle at: http://www.bis.org/publ/bcbs128.pdf [accessed 2011-06-11] [ Links ]
BCBS. 2010a. Basel III: A global regulatory framework for more resilient banks and banking systems. Bank for International Settlements. Available at: http://www.bis.org/publ/bcbs189_dec2010.pdf [accessed 2011-0619]. [ Links ]
BCBS. 2010b. Guidance for national authorities operating the countercyclical capital buffer. Bank for International Settlements. Available at: http://www.bis.org/publ/bcbs187.pdf [accessed 2011-06-19]. [ Links ]
BOTHA, I. 2004. Modelling the business cycle of South Africa: linear vs non-linear methods. Johannesburg: PhD thesis - Rand Afrikaans University. [ Links ]
BRUNNERMEIER, M.K. 2009. Deciphering the liquidity and credit crunch 2007-2008. Journal of Economic Perspectives, 23(1): 77-100. [ Links ]
BURGER, P. & MARINKOV, M. 2006. The South African Phillips curve: how applicable is the Gordon model? South African Journal of Economics, 74(2):172-189. [ Links ]
CANOVA, F. 1994. Detrending and turning points. European Economic Review, 38(3-4):614-623. [ Links ]
CANOVA, F. 1998. Detrending the business cycle. Journal of Monetary Economics, 41:475-512. [ Links ]
CATARINEU-RABELL, E., JACKSON, P. & TSOMOCOS, D.P. 2003. Procyclicality and the new Basel Accord-banks' choice of loan rating system. Bank of England. [ Links ]
COGLEY, T. & NASON, J.M. 1995. Effects of the Hodrick-Prescott filter on trend and difference stationarytime series: implications for business cycle research. Journal of Economic Dynamics and Control, 19:253-278. [ Links ]
DANTHINE, J.P. & GIRARDIN, M. 1989. Business cycles in Switzerland: a comparative study. European Economic Review, 33(1):31-50. [ Links ]
DREHMANN, M., CLÁUDIO, B., GAMBACORTA, L., JIMENEZ, G. & TRUCHARTE, C. 2010. Countercyclical capital buffers: exploring options. Available at: http://www.bis.org/publ/work317.pdf [accessed 2011-02-12]. [ Links ]
DU TOIT, L. 2008. Optimal HP filtering for South Africa. Stellenbosch University, Department of Economics. Bureau for Economic Research. [ Links ]
FEDDERKE, J.W. & SCHALING, E. 2005. Modelling inflation in South Africa: A multivariate cointegration analysis. South African Journal of Economics, 73(1):79-92. [ Links ]
GOODHART, C. & TAYLOR, A. 2006. Procyclicality and volatility in the financial system - the implementation of Basel II and IAS39. In S. Gerlach & P. Gruenwald (eds.) Procyclicality offinancial systems in Asia, pp. 230-251. Palgrave Macmillan. [ Links ]
GORDY, M.B. & HOWELLS, B. 2004. Procyclicality in BaselII: can we treat the disease without killing the patient? Bank for International Settlements. Available at: http://www.bis.org/bcbs/events/rtf04gordy_ howells.pdf [accessed 2011-02-13].
HARVEY, A.C. & JAEGER, A. 1993. Detrending, stylized facts and the business cycle. Journal of Applied Econometrics, 8:231-247. [ Links ]
HEID, F. 2003. Is regulatory capital pro-cyclical? A macroeconomic assessment of Basel II. Deutsche Bundesbank working paper. [ Links ]
HODRICK, R.J. & PRESCOTT, E.C. 1980. Post war US business cycles: an empirical investigation. Carnegie Mellon University. [ Links ]
HODRICK, R.J. & PRESCOTT, E.C. 1997. Postwar US Business Cycles: An empirical investigation. Journal of Money, Credit and Banking, 29(1): 1-16. [ Links ]
KAISER, R. & MARAVALL, A. 1999. Estimation of the business cycle: A modified Hodrick-Prescott filter. Spanish Economic Review, 1(2):175-206. [ Links ]
KASEERAM, I., NICHOLA, T. & MAINARDI, S. 2004. South African inflation dynamics and the pass-through effect from depreciation to unit labour costs. South African Journal of Economics, 72(1):85-107. [ Links ]
KING, R. G. & REBELO, S.T. 1993. Low frequency filtering and real business cycles. Journal of Economic Dynamics and Control, 17(1-2):207-231. [ Links ]
LEY, E. 2006. Knowledge brief for bank staff. The Hodrick-Prescott filter. Available at: http://homepage.mac.com/eduley/hp.pdf [accessed 2011-02-12]. [ Links ]
LOWE, P. 2002. Credit risk measurement and procyclicality. BIS working paper #116. [ Links ]
MARCET, A. & RAVN, M.O. 2003. CEPR Discussion Papers. Available at: http://www.econ.upf.edu/docs/papers/downloads/588.pdf [Accessed 2011-02-12]. [ Links ]
MEHRA, Y.P. 2006. The output gap: expected future inflation and inflation dynamics: another look. Federal Bank of Richmond. Richmond, USA: Federal Bank of Richmond. [ Links ]
MISE, E., KIM, T.H. & NEWBOLD, P. 2005. On suboptimality of the Hodrick-Prescott filter at time series endpoints. Journal of Macroeconomics, 27(1):53-67. [ Links ]
RAVN, M.O. & UHLIG, H. 2002. On adjusting the Hodrick Prescott filter for the frequency of observations. The Review of Economics and Statistics, 84(2):371-375. [ Links ]
REPULLO, R. & SUAREZ, J. 2008. The procyclical effects of Basel II. CEPR Discussion Papers #6862, C.E.P.R. [ Links ]
ROCHET, J.C. 2008. Procyclicality of financial systems: is there a need to modify current accounting and regulatory rules? Valuation and Financial Stability. Banque de France, Financial Stability Review #12. [ Links ]
RYAN, A. & CRUTCHLEY, J.P. 2012. UK banks monitor: regulatory overstretch. UBS Investment Research, April:1-55. [ Links ]
SARB, 2011. The international banking crisis and domestic financial intermediation in emerging market economies: issues for South Africa, BIS papers, #54, 365-376. Available at: http://www.bis.org/publ/bppdf/bispap54w.pdf [accessed 2012-04-21]. [ Links ]
SAURINA, J. & TRUCHARTE, C. 2007. An assessment of Basel II procyclicality in mortgage portfolios. Documentos de Trajabo Banco de Espana #0712. [ Links ]
SORKIN, R. 2010. Answers on credit ratings long overdue, New York Times. Available at: http://www.nytimes.com/2010/06/01/business/01sorkin.html?src=busln. . [accessed 2011-06-19]. [ Links ]
ST-AMANT, P. & VAN NORDEN, S. 1997. Measurement of the output gap: A discussion of recent research at the Bank of Canada. Technical Report of the Bank of Canada. [ Links ]
US FINANCIAL CRISIS INQUIRY COMMISSION. 2010. Financial crisis inquiry report: final report of the national commission on the causes of the financial and economic crisis in the United States. New York: US Public Affairs. [ Links ]
WALTERS, S. 2011. Note on recent developments in the household balance sheet, South African Reserve Bank, Quarterly bulletin, December:69-72. [ Links ]
WOGLOM, G. 2003. How has inflation targeting affected monetary policy in South Africa? South African Journal of Economics, 71(2):380-406. Yakhim, Y. 2001. Business Cycle Fluctuations and the Hodrick-PrescottFilter. Available at: http://www.bgu.ac.il/~yossiya/teaching/macro_graduate/LN1_bc_hpf.pdf [accessed 2011-02-12]. [ Links ] [ Links ]
Accepted: June 2012














