ARTICLES

 

Iterative Soft-Input Soft-Output Bit-Level Reed-Solomon Decoder Based on Information Set Decoding

 

 

Yuval Genga^I; Olutayo O. Oyerinde^I; Jaco Versfeld^II

^ISenior Member, IEEE; School of Electrical and Information Engineering, University of the Witwatersrand, Johannesburg, South Africa. (e-mail: yuval.genga@wits.ac.za and olutayo.oyerinde@wits.ac.za)
^IISenior Member, IEEE; Department of Electrical and Electronic Engineering, Stellenbosch University, Matieland, South Africa, South Africa. (e-mail: djjversfeld@sun.ac.za)

 

 

---

ABSTRACT

In this paper, a bit-level decoder is presented for soft-input soft-output iterative decoding of Reed-Solomon (RS) codes. The main aim for the development of the proposed algorithm is to reduce the complexity of the decoding process, while yielding a relatively good error correction performance, for the efficient use of RS codes. The decoder utilises information set decoding techniques to reduce the computational complexity cost by lowering the iterative convergence rate during the decoding process. As opposed to most iterative bit-level soft-decision decoders for RS codes, the proposed algorithm is also able to avoid the use of belief propagation in the iterative decoding of the soft bit information, which also contributes to the reduction in the computational complexity cost of the decoding process. The performance of the proposed decoder is investigated when applied to short RS codes. The error correction simulations show the proposed algorithm is able to yield a similar performance to that of the Adaptive Belief Propagation (ABP) algorithm, while being a less complex decoder.

Index-Terms: Reed-Solomon codes, Bit-level decoding, Iterative decoding, Soft-decision decoding, Information set decoding, Decoding complexity.

---

 

 

I. INTRODUCTION

REED-Solomon (RS) codes belong to a class of high performing error correction codes that were developed by Irving S.Reed and Gustave Solomon [1]. Due to the strong algebraic properties and good error detection and correction performance, a lot of research has been applied to the development of high performing decoding schemes for this class of codes.

Soft-decision decoders for RS codes working in the field, specifically the ones based in the Galois Field GF(2⁶) (where b is any positive integer), can be divided into two categories. They can either be symbol-level decoders or bit-level decoders. Most soft-decision decoders for RS codes work on a symbollevel. Examples of symbol-level decoders include the widely used Koetter and Vardy (KV) algorithm [2] and the parity check transformation algorithm (PTA) [3] [4]. Previous research works on soft-decision decoders have shown gains in terms of error correcting performance attained when working on a bit-level compared to the symbol-level [5], [6], [7], [8], [9]. Based on this, implementation of bit-level soft-decision decoding algorithms for RS codes has been an area of active research for a long time [5], [6], [7], [10], [11], [12], [13], [14], [15].

The adaptive belief propagation (ABP) algorithm [5] is a widely used bit-level decoder for linear block codes due to its good error correcting capability [5], [6], [12], [13], [16]. The ABP algorithm was devised with the aim of applying belief propagation techniques on codes defined by a parity check matrix with a dense structure [5]. The belief propagation decoding algorithm is designed to take advantage of the sparse structure presented by the parity check matrix of a Low Density Parity Check (LDPC) code so as to decode the received vector efficiently [17]. Due to the dense nature of RS code, a binary image expansion [18] is performed on the parity check matrix (H) so as to make it sparse. This is done to enable the use of the belief propagation algorithm during the decoding process. The generic form of the ABP decoder presented in [5] works by first converting the bit reliabilities of the codeword into their corresponding log likelihood ratios (LLR). The binary image form of the H is then adapted based on these LLR values using Gaussian row reduction techniques. The belief propagation is then applied to the adapted binary image of the H matrix so as to decode the received vector. In [5], the ABP has been shown to yield a significant gain when compared to widely used RS decoders including the KV algorithm, Berlekamp-Massey (BM) algorithm and the Algebraic hard-decision decoder. However, the gains achieved by the ABP algorithm come at the cost of a high computational complexity [5], [13]. Further modifications have been made to the generic form of the decoder [5], [6], [12], [13], [14], [16], [19]. However, these changes either add to or do not significantly reduce the complexity cost of iteratively applying belief propagation during decoding [5], [13], [20]. The parity check transformation algorithm (PTA) [4] is a symbol level RS decoder that, just like the ABP, utilises row reduction techniques on the H matrix based on the symbol reliability. The PTA works by sorting the maximum symbol reliabilities obtained from each column of a reliability matrix and using them to transform the H matrix. The H matrix is transformed using the row reduction technique shown in [21] [22] to match the corresponding reliability information with the columns of H. Once the H matrix is transformed, the reliabilities are then corrected based on the values of the syndrome vector obtained from the scalar product of the hard decision vector and each row of the transformed H matrix. The PTA has been shown to outperform the KV decoder and the BM algorithm, in terms of error correction performance [3] [4]. In [9], the PTA was modified to allow for a bit-level implementation. The bit-level PTA is shown in [9] to yield a comparable error correction performance to the ABP algorithm for a (15,7) and a (15,11) RS code transmitted using a 16-QAM modulation scheme. The PTA is able to achieve gains in terms of error correction, in both symbol and bit-level, at the cost of running numerous iterations.

Information set decoding (ISD) was first presented by Prange [23] for the decoding of Cyclic codes. Since then, the algorithm has had different modifications for application in error correction of linear block codes [24], [25], [26], [27] and Cryptography [28], [29]. In all its forms, ISD uses k linearly independent bits or symbols from the received vector to re-encode a unique codeword during the decoding process [24]. The k symbols or bits used to obtain the unique codeword are referred to as the information set. The most widely used implementations of ISD in the error correction of linear block codes have been applied to binary codes. ISD algorithms often utilise ordered statistics decoding (OSD) and list decoding techniques to obtain the decoded vector of the binary code [25], [30], [31], [32]. In [27] a Field Programmable Gate Array (FPGA) implementation for ISD is presented when applied to RS codes. Besides the FPGA implementation, part of the novelty of the approach proposed in [27] is that ISD is applied to a class of nonbinary codes. However it is important to note that the decoding method presented in [27] is not applied at the symbol-level, but instead implemented at a bit-level. Similar to the ABP, the decoder is able to work at a bit-level by performing a binary image expansion on the H matrix and converting the RS code into its bit form. The proposed decoding method in [27] is based on a modified OSD implementation of the ISD technique used in [33]. The list of candidate codewords from the OSD are obtained using order-1 reprocessing [30] to apply bit flipping based decoding on the syndrome weights from the list of subvectors. The subvectors are then used in the re-encoding of the candidate codewords. ISD decoders have the advantage of being generally less complex than other decoding techniques [24] [34]. However, the use of OSD and list decoding techniques ensure ISD decoders that utilise soft information are soft-input hard-output algorithms. This prohibits the use of such decoding algorithms for situations where the RS decoders are required to make full use of bit based soft information, like in the case of satellite transmission[10] or for iterative decoding [35].

Motivation and Objectives

Soft-decision decoders used for RS codes give a good error correction performance, but at the cost of some form of complexity. The ABP algorithm gives a significant gain compared to hard decision decoders and the widely used KV algorithm, but this comes at the cost of a higher computational complexity [5][6]. The PTA has also been shown to be a good decoder while outperforming the KV algorithm in terms of symbol error rate [4]. This is at the cost of the algorithm running numerous iterations [36], therefore making the PTA a computationally intensive algorithm. The 'algorithm complexity vs error correction performance' tradeoff is quite common in the field of telecommunications when it comes to the selection of appropriate decoding algorithms. The main objective of this research is the presentation of a decoding technique that iteratively utilizes the soft information outputted from the noisy channel to yield a high error correction performance at a reduced computational complexity cost. Work in this paper focuses on the development of a low complexity iterative soft-input soft-output decoding approach for RS codes that is able to yield a good error correction performance.

The proposed decoding approach is able to take advantage of the reduced complexity that comes with an ISD implementation [24] in the error correction process. Except for the bit-level PTA, all iterative soft-input soft-output decoders for RS codes are in some way a modification of the ABP decoder. In addition to the development of an iterative soft-input soft-output ISD based bit-level decoder, part of the novelty of the decoding technique presented in this research is the implementation of a bit-level iterative soft-decision decoder for RS codes without the use of the belief propagation algorithm. Implementation of belief propagation is avoided in the proposed decoding technique due to the high computational complexity cost presented when using the ABP algorithm [5], [11], [13], [37]. The decoder proposed in this research is a message passing algorithm, that takes advantage of the sparse structure presented by the binary image of the H matrix to iteratively decode the received vector. ISD is implemented, as part of the stopping criteria in the proposed iterative bit-level decoding approach, with the aim of improving the iterative convergence rate during the decoding process. An improved iterative convergence rate contributes to a reduction in the computational complexity cost as it reduces the total number of operations carried out during the entire decoding process of the received vector.

The rest of the paper is structured as follows: a detailed description of how the proposed decoder works is given in Section III, thereafter an analysis of the proposed algorithm and simulation results are presented in Section IV, then a complexity analysis of the proposed decoder is investigated in Section V and Section VI gives the conclusion to the findings obtained in this paper.

 

II. INFORMATION SET DECODING:IMPORTANCE OF THE SYSTEMATIC STRUCTURE TO THE DECODING PROCESS

Assume a (n, k) RS code C, in the field GF(2^b), is defined by a systematic parity check matrix H having the dimensions m x n, where m = (n - k).

where I = m x m identity submatrix and Q = (n - m) x m parity submatrix. The syndrome S = 0 can be found by multiplying a valid codeword c from C where H^Tis the transpose of the H matrix. We can rewrite (2) in the form shown in (3)

where the c_I and c_qrepresent subvectors of the codeword c that correspond to the identity and parity submatrix respectively. As a result of the syndrome S = 0, the additive inverse property of the field GF(2^b) [38] can be applied to (3) to give

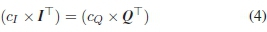
Based on the systematic structure of I^T, we can further reduce (4) to (5)

From (5), it can be seen the subvector c¡ of the codeword c can be correctly obtained using the the subvector cq. This is the information set decoding principle behind the proposed decoding approach presented in this research.

 

III. THE PROPOSED DECODING SCHEME

To understand how the proposed decoder works, the relevant notation is first established. The decoder works on a bit-level, this means a binary image expansion is performed on H. In what follows, the binary image expansion of the H matrix for the RS code is obtained as described. Each element a^z of the field GF(2^b), where 0 < z < (2^b - 2), is replaced by a corresponding b x b binary matrix B^z, where B is the companion matrix of a primitive polynomial which creates the field F₂b [16][18]. The binary image expansion of H is denoted as H and has the dimensions M x N, where M =(nb - kb) and N = nb.

We now consider an RS codeword c in the extension field. The codeword c is transmitted using a selected modulation scheme through a noisy channel. The soft information received at the output of the channel is then used to create the reliability matrix ß. The matrix ß has the dimensions 2 x N, where the 1^st and 2^nd row of ß represent the reliability of the selected bit index being a "0" and a "1" respectively. The techniques used to create ß depend on the channel and the selected modulation scheme. For instance when transmitting through an Additive White Gaussian Noise (AWGN) channel using a Binary Phase Shift Keying (BPSK) modulation scheme, the codeword c is first converted into its bit form by representing each element a^zwith the respective binary polynomial a₀ + a₁a +... + a_b-1a^(b-1). The binary codeword is denoted as cb, and has the length nb. After transmission, the vector rb is received at the output of the noisy channel. The soft information in the vector rb is then used to find the bit reliabilities of either being a "0" or a "1" using the method presented in [39][40]. When the symbols of the codeword c are transmitted using a 16-QAM modulation scheme with Gray mapping through an AWGN channel, the reliabilities used to fill the rows in the matrix ß are obtained using the technique presented in [41] from the soft information received at the output of the channel.

once the matrix ß is created, each of the columns is then scaled using the approach presented in [9]. This is carried out to ensure that the reliabilities in each column of ß add up to 1 before being fed into the decoder.

For each iteration of the proposed algorithm, the decoding process can be summarised by the following steps:

1) Finding the maximum bit reliabilities: The maximum reliabilities in each column of ß are identified and arranged in the vector A as shown in (6)

where A_j = argmax(ß_j), 0 < j < N and ß_jrepresents each column of the matrix ß. These reliabilities are then sorted in ascending order. The original indices of the reliabilities are identified as well and stored in terms of their ascending order in the vector Y

For K = kb, the K highest values of the vector A are considered to be the most reliable. An approach similar to the information set decoding technique presented in [27] is then applied. This ensures, after row reduction is performed, the indices of the K highest reliabilities match the parity submatrix of the now quasi-systematic structure of H. For ease of notation, the matrix obtained from the row reduction of the rearranged columns of H is represented as H¹.

It is important to note that the matrix H has a full row rank. This means that there exists a total of M independent columns present in H. However, as noted in [5], there is no guarantee that the M least reliable indices found in Y will match these columns during row reduction. This means that not all the most reliable K indices will match the parity submatrix for every row reduction operation performed on H. When this happens, any M indexes that matches an identity submatrix of H¹are considered to be unreliable, and any K bit indexes that match the parity submatrix of H¹are considered to be reliable.

2) Hard-decision detection and the Syndrome check: Hard-decision detection, similar to [4], is then performed on ß to obtain the vector cb. The syndrome is therucalculated by getting the scalar product of the vector cb and each row of H¹as shown in (8)

where 1 < i < M is used to denote each row of H¹ and each value of the syndrome vector, S. Due to the decoder working on a bit-level, the syndrome calculation in (8) can be rewritten in the form shown in (9)

where t_i represents all the indices of the participating bits of cb in the i^thsyndrome check equation and is expressed as

3) Obtaining the votes: During the syndrome calculation, votes are cast for each bit. Each bit gets a vote of either being a "0" or a "1" based on the extrinsic information. This means, for each row, all the participating bits except the one being investigated take part in the vote. Based on the vote, The syndrome calculation in (9) is rewritten as

where y ε t_i represents the index of the bit being voted for. The subvector t' represents the set of indices in t_i without the bit index y. Assuming the set of bits cb_t, are all correct and S_i= 0, the calculation of votes can be derived from the additive inverse property of the field GF(2^b) [38] and is represented as

From (12), cb_yis found to be either a "0" or "1". This counts as a vote for the bit cb_y. This process is repeated for all participating bits of cb in every row of H¹, with the votes being stored in the matrix V as seen in (13)

where V_0,jand V1,j represents the total votes each bit index gets for being a "0" and a "1" respectively, for all the rows of H¹,

4) Obtaining the confidence rating: The first step to obtaining the confidence rating of each bit is to get the voting ratios, v, as shown in (14)

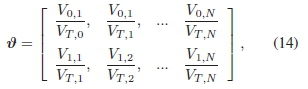
where each V_T,j represents the total number of votes each bit index gets and it is computed as

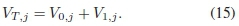
The confidence rating, r, for each bit is then calculated by dividing the voting ratios in v by a value of p as shown in (16)

where p represents the divisor which is a constant predefined value input during the initialisation of the algorithm. The values in the matrix r can be represented as

5) Updating ß: The values in r represent the level of confidence that a bit is correct and should be updated in ß. The update works by adding the indexed confidence ratio to the corresponding reliability in ß, based on the vote in (12) for being either a "0" or "1". The update can be summarized as follows

where f is used to denote the current iteration number of the decoder. The value of cb_yis either a "0" or a "1". This value is used to identify which column in ß, with the reliability indexed by j, to update with the corresponding confidence rating. The notation y represents the index of the bit considered during (12). All the reliabilities in ß are updated based on their participation in each row of the matrix H^±. After all the N indices are updated, β^(f+1) is scaled to ensure all the columns add up to 1 in preparation for the next iteration.

A. The Decoding Condition and Thresholds

The proposed algorithm works iteratively and has two stopping conditions. The first is when S = 0. The second is when the decoding condition is met. The decoding condition is based on ISD. That is, it makes use of a set of K bits to re-encode the decoded codeword based on the rearranged systematic structure of H¹.

The decoding condition is met if the algorithm can ascertain that the information set of K bits with indices matching the parity submatrix is correct. If the information set is determined to be correct, then the remaining M bits that match the identity matrix can be decoded.

In order to understand how this works, consider the syndrome equation between cb and the rearranged systematic matrix H¹ in the form shown in (19).

where I_H and Q_H match the transpose of the column indices of identity and parity submatrices of H¹, while cb_YMand cb_YKmatch the indices of cb that correspond to the columns of the identity and parity submatrices of H ¹ respectively. Due to I_H± being an identity matrix, (19) can be reduced further as shown in (20).

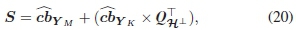
If the cb_YKindices are correct, the bit values of cb_YMcan be obtained by assuming S =0 and applying the additive inverse property of the field GF(2^b) to give

Similar to (12), the bit-level expression in (21) can be reduced further by considering only the indices of the participating bits to give

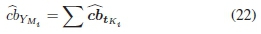
where cb_YM. and cb_tK, are the participating bits of cby_Mand cby_Kin the i^throw of H¹respectively. The algorithm is able to determine if the bits in the subvector cbY_K, referred to as the information set, are correct by setting a threshold. The threshold, t, is defined as the minimum number of syndrome check equations each of the K bits in the information set should satisfy for (22) to be applied in the decoding of the received vector. The higher the value of t, the more confidence the algorithm has that the most reliable K indices are correct. However, this comes at the expense of the algorithm running more iterations. The main advantage of using the decoding condition as a stopping criteria is that the algorithm is able to use K bits to decode an entire received vector of length N. This assists in reducing the number of iterations required to decode the received vector, because the algorithm does not have to confirm if every single bit is correct before it can break the iterative decoding process.

A detailed summary of the proposed decoding approach is presented in Algorithm 1. Also, a flow diagram that follows the stages involved in the decoding process is represented in Fig. 1. For purpose of notation in the summaries presented in Algorithm 1 and Fig. 1, the decoded vector is denoted using C and Sci_Y is used to represent the minimum number of syndrome checks satisfied by the each of the K bits in the vector cb_YK.

 

 

IV. RESULTS AND ANALYSIS

In this section, simulation results for the proposed iterative decoder and its variants are presented. For ease of notation, the proposed decoder is referred to as the k Bit Decoding algorithm and is denoted as the kBD algorithm.

A. Analysis of the Proposed Bit-Level Decoding Algorithm

Simulations are run to find the optimum performance conditions for the kBD algorithm using different values of t and p. The performance of the kBD algorithm using different values of t is first investigated. A nearly half rate (15,7) RS code is used in this simulation, with the symbols being transmitted through an AWGN channel using a 16-QAM modulation scheme with Gray mapping. The value of p = 50 is used for these simulations. Results for the simulations are measured in terms of Bit Error Rate (BER) and the average number of iterations. These results are presented in Fig. 2 and Fig. 3 respectively.

 

 

 

 

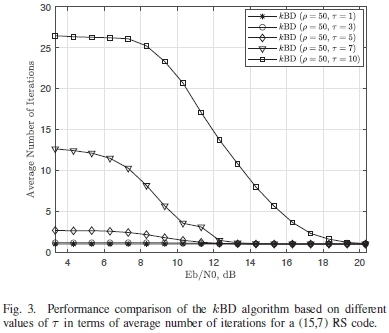
From Fig. 2 it can be seen that the error correction performance of the kBD algorithm works best when t > 7. It can also be seen from Fig. 3 that working with t = 7 presents a more efficient kBD algorithm. This is because it requires less than half of the average number of iterations used by kBD algorithm with t = 10 during the decoding process, to achieve a similar BER performance. Tests to determine the optimum value of p are also carried out. Similar conditions are used for transmission of the (15,7) RS code. The kBD algorithm is implemented with a t = 7. The results for these simulations are presented in Fig. 4 and Fig. 5.

 

 

 

 

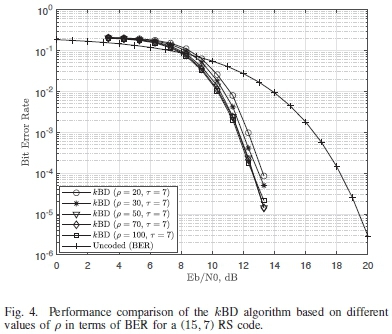
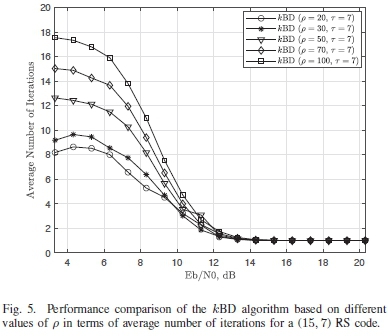
The kBD algorithm with values of p > 50 are able to achieve a slightly higher gain in terms of BER when compared to the kBD algorithm with values of p < 30 as seen in Fig. 4. The kBD algorithm with p = 50 is shown to be an efficient decoder as it requires less iterations to yield a comparable BER performance to the other versions of the algorithm, with values of p> 50, as seen in Fig. 5. Based on this, the kBD algorithm with p = 50 and t = 7 is used to benchmark the performance of the proposed algorithm with other iterative soft-input soft-output bit-level decoders.

B. Performance Analysis ofthe Proposed Bit-Level Decoding Algorithm

Halfrate codes

In this section the performance of the kBD algorithm is benchmarked against the bit-level implementation of the PTA and the ABP algorithm. Simulations are run on a nearly half rate (15, 7) RS code. The ABP is simulated with the value of a = 0.05 and is set to run with a maximum number of 20 iterations [5]. The bit-level implementation of the PTA, denoted as PTA_bl, is run with a value of δ = 0.01 [9].

For these simulations, a version of the kBD algorithm with a lower computational complexity cost than the original implementation is presented. This version of the kBD algorithm only performs Gaussian row reduction once on H, in the first iteration, to obtain H^L. The same H^Lis then used throughout the entire iterative decoding process of the received vector. This version of the kBD algorithm is referred to as the none transform version of the decoder and is denoted as kBD_nt algorithm. As a result of the reduced Gaussian row reduction operations, the kBD_nt algorithm has a lower computational complexity cost than the original implementation of the kBD algorithm. The same simulation parameters for encoding, modulation and transmission used to obtain the results in Fig. 2, are utilised for this set of simulations. The results for these simulations are presented in Fig. 6 and Fig. 7.

 

 

 

 

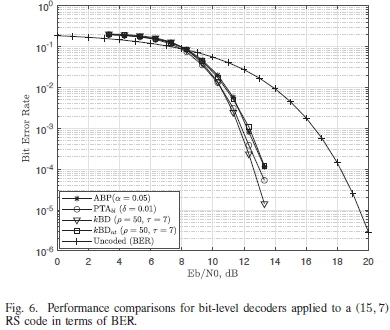
It can be seen from Fig. 6 that the kBD algorithm experiences a gain of 0.5dB when compared to the ABP algorithm with a = 0.05 at a BER of 10^-3. The kBD algorithm also outperforms PTA_bl decoder, but with a smaller gain of about 0.4dB for the BER value of BER of 10^-4.

The kBD_nt algorithm, being less complex due to its lack of iterative H^Ltransformations, yields a similar performance to that of the ABP algorithm with a = 0.05. However, the kBD_nt algorithm is outperformed by both the kBD algorithm and the PTA_bl by about 0.65dB and 0.55dB respectively for a BER of 10"³. It is important to note that the PTA_bl has a significantly higher computationally complexity cost when compared to all the bit-level decoders used in the simulation. This is because it performs Gaussian row reduction operations to transform the matrix H for each of the iterations required during the decoding process, as seen in Fig. 7. This provides justification for the use of the kBD_nt algorithm over the PTA_bl whenever a tradeoff is required between the algorithm complexity and the decoding performance.

From Fig. 6 and Fig. 7, the kBD algorithm is seen to be a better performing iterative bit-level soft-decision decoding algorithm. This is because it is able to achieve gains in BER performance, while running for fewer iterations than all other bit-level soft-decision decoding algorithms used in the (15,7) RS code simulations.

High rate codes

Additional simulations are carried out to test the performance of the proposed variations of the kBD algorithms under high rate conditions. Working at a high rate means working with a H matrix with less rows when compared to a half rate code. That is, there are fewer syndrome check equations than in the case for the (15, 7) RS code. This means that each of the K bits in the information set participate in less syndrome check equations.

With respect to this, a new set of simulations to determine an optimum value for t are carried out. For these simulation, a (15,11) RS code is once again transmitted through an AWGN channel using a 16-QAM modulation scheme with Gray mapping. The results for these simulations are displayed in Fig. 8 and Fig. 9. It can be seen from Fig. 8 that the BER performance of the algorithm is the same for values of t > 3.

 

 

 

 

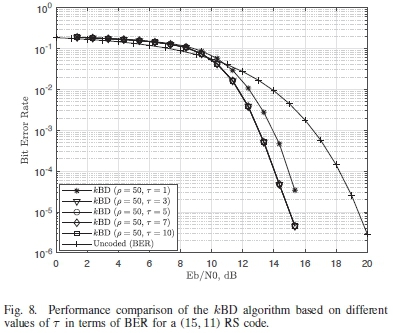
The main difference in the performance of the algorithm can be seen in Fig. 9. The kBD algorithm with t = 3 requires less than half of the average number of iterations to decode the received vector, when compared to the kBD algorithm with values of t > 5. As mentioned in section III-A, the reason why the kBD algorithm with t = 3 requires less iterations than values of t> 3, is because the algorithm only has to ensure that each bit in the information set, cb_YK, satisfies 3 syndrome check equations as opposed to the cases when t> 3. This enables the kBD algorithm to meet the decoding condition with fewer iterations than when t > 5. Also, the value of t = 3 is sufficient to give an optimum BER performance as a direct result of the (15,11) RS code having a H matrix with less syndrome check equations. Hence, the kBD algorithm with p = 50 and t = 3 is used when benchmarking the performance of the decoder with the ABP and the PTA_bl for high rate codes.

No modifications are made to the implementations of the PTA_bland the ABP algorithm from the case of the nearly half rate code. All the algorithms are run under the same conditions as the case for the (15,7) RS code. The results for this set of simulations can be seen in Fig. 10 and Fig. 11. From the results presented in Fig. 10, the performance of the kBD algorithm matches the performance of the PTAbi. This performance is achieved by the kBD algorithm while running at a lower average number of iterations than the PTAbi, during the decoding process, as seen in Fig. 11. The kBD algorithm also compares favourably to the ABP algorithm by yielding a slight BER performance gain of about 0.23dB at an BER value of 10^-5.

 

 

 

 

The kBD_nt algorithm is only slightly outperformed by less than 0.1dB at a BER of 10^-5 when compared to the PTA_bl and achieves a similar BER performance to that of the ABP algorithm, while running at an average number iterations that is less than both algorithms. This justifies the use of the kBD_nt algorithm, when selecting a bit-level soft-input soft-output decoder, in the case of a tradeoff between the algorithm complexity and the decoding performance. The algorithm is also run for a (31,25) RS code so as to benchmark the proposed decoder against the results presented in [5]. For these simulations, the proposed algorithm is also tested against one of the modifications of the ABP decoder referred to as the ABP-HDD(20,1) algorithm. This version of the ABP works alongside a 'genie aided' hard decision decoder (HDD) [5]. This version of the ABP works iteratively, however, it does not converge to a codeword. Instead it runs for all the 20 iterations while outputting a codeword that is fed into the HDD with a genie aided stopping condition. The ABP only selects the most likely codeword if the HDD is not able to obtain the decoded vector from the list of codewords generated from each of the 20 iterations. The result of the ABP-HDD(20,1) is described as 'optimistic' in [5] due to the inclusion of the genie aided HDD. This is because the genie aided stopping criteria already knows the correct codeword and breaks the decoding process once the correct codeword is obtained instead of letting the iterative algorithm converge to the most likely codeword[5]. The genie aided HDD is added to the algorithm to prevent the decoder from running all 20 iterations and therefore speeding up the decoding process.

This is because the algorithm is a double decoder. This means there is an increased complexity when compared to the generic version of the ABP. This is especially due to the algorithm running all 20 iterations during each decoding process, even for higher SNR values when the decoder requires less iterations to converge to a valid codeword.

The simulations are tested using BPSK modulation and the RS code is transmitted through an AWGN channel so as to obtain the results in a similar way to [5]. The Maximum Likelihood (ML) lower bound is obtained using the technique presented in [35] [42]. The results for these simulations are presented in Fig. 12. From the results in Fig. 12 it can be seen that the error correction performance of the kBD algorithm and kBD_nt algorithm are quite favourable when compared to the generic ABP decoder. The kBD algorithm outperforms the generic version of the ABP by about 0.5dB at an FER of 10^-3. The less complex kBD_nt algorithm yields a gain of about 0.25dB when compared to the generic form of the algorithm. However, the kBD algorithm has a loss of about 0.6dB when compared to the ML lower bound graph and a loss of less than 0.1dB when compared to the ABP-HDD(20,1) [5], for the same FER value.

 

 

V. COMPLEXITY ANALYSIS

A. Time Complexity

in this section, the computational complexity cost for the kBD algorithm is compared to that of the ABP and the PTAbl decoders. The complexity cost of the bit-level soft-input soft-output decoders is measured in terms of the total number of operations carried out for the average number of iterations required in the entire decoding process. in order to better represent the computation calculations, notation is established. The average row weight and column weight of the participating bits indexed by t are denoted as W_rand W_c respectively. The average row weight of indices that match the parity submatrix of H^Lare denoted using W_k. The notation W_kis also used to denote the average row weight for computations that obtain the extrinsic bit information. The computational complexity cost for a single iteration of the ABP, the PTA_bl, kBD algorithm and the kBD_ntalgorithm are all summarised in the Table I, Table II, Table III and Table IV respectively.

 

 

 

 

 

 

 

 

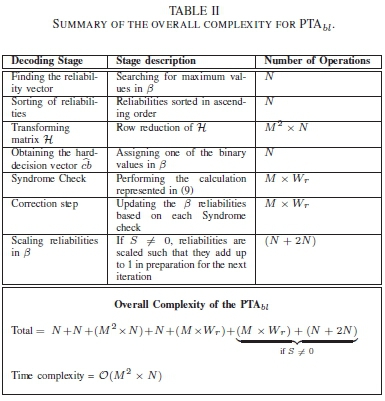
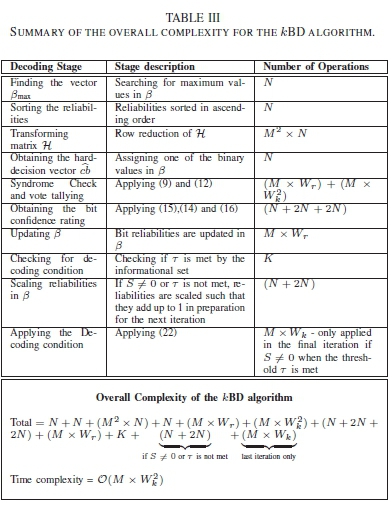
For clarity, the complexity analysis of the ABP algorithm in Table I follows the decoding process described in [5]. The complexity analysis for the PTA_bl in Table II follows the decoding process described in [4].

To create a clear perspective of the complexities of the algorithms, additional tables that note the computations which involve 'additions/subtraction', 'multiplications/divisions' and 'other' operations are created for each algorithm. The tables only considers the operations that are unique to at least one algorithm. For example, operations like Gaussian elimination and the syndrome check are present in all algorithms and are therefore ignored in this analysis. The tables with this analysis are presented in Table V, Table VI, and Table VII respectively.

 

 

 

 

 

 

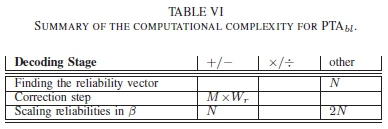
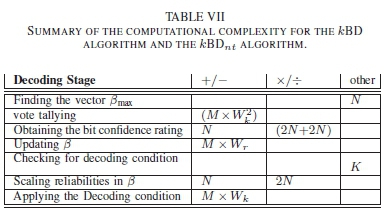
From Table. I, Table. III and Table. IV, it can be seen that the ABP decoder and both versions of the kBD algorithm all have the same time complexity. This is due both algorithms calculating the extrinsic information. However from computational complexities presented in Table. V and Table. VII, the extrinsic information computation for the ABP requires (M x W_k²) multiplications as seen in [5] while both version of the kBD algorithm use (M x W_k²) additions as shown in (12).

B. Complexity measured in Terms of Number of Operations

The research carried out also attempted to visually represent the complexities of the decoders. The complexity graphs plotted are based on the of total number of operations as a function of the average number of iterations run by the decoders for each SNR value. This additional set of complexity analysis simulations are carried out so as to investigate the effect of the iterative performance on the complexity cost of the algorithms. The total number operations are obtained from the equations given in Table I, Table II, Table III and Table IV and multiplied by the average number of iterations run by each algorithm for the different SNR values shown in Fig. 7 and Fig. 11.

From the simulation performed for the (15,7) RS codes, it is found that W_r = 14.74, W_c= 7.86, W_k = 13.74, M = 32 and N = 60. The results using these values can be seen in Fig. 13.

 

 

It can be seen from Fig. 13 that both variants of the kBD algorithm require less operations than the ABP with a = 0.05 and the PTA_bl with õ = 0.01. As expected, the kBD_nt algorithm is the least complex of all the algorithms for the (15,7) RS code. It is important to note that the kBD_nt algorithm is able to exhibiting a comparable BER performance to the high performance ABP algorithm, while being less complex, as shown in Fig. 6 and Fig. 13 for the (15, 7) RS code. The kBD algorithm is also shown to yield a tolerable complexity when compared to both the ABP and the PTA_bl.

For the low SNR values, the computational complexity cost of the kBD algorithm is comparable to the ABP. However, as the values of the SNR increase, the complexity cost of the kBD algorithm reduces significantly faster than the ABP decoder. From Table II, the PTA_bl appears to be the least complex bit-level decoder for operations carried out in a single iteration. However, the numerous iterations required by the PTA_bl to decode the received vector, considerably add to the computational complexity cost as seen from Fig. 13. This makes the PTA_bl significantly more complex than the other bit-level decoders used in the simulations.

The low computational complexity cost of the kBD algorithm and the kBD_ni algorithm, when compared to the ABP and the PTA_bl, is largely attributed to the iterative convergence rate of the decoder. The information set decoding based stopping criteria ensures the algorithm is able to converge to a codeword with less iterations. This is because the algorithm is only required to decode K bits. This is not the case for the ABP and the PTA_bl which have to decode the entire codeword of N bits before the iterative decoding process can break. Simulations are also run for the high rate (15,11) RS code to compare the computational complexity cost for the bit-level decoders. The results for these simulations can be seen in Fig. 14. For these simulations W_r= 22.48, W_c= 5.99, W_k = 21.48, M = 16 and N = 60.

 

 

Similar to the results in Fig. 13, the variants of the kBD algorithm still perform less operations than the ABP and the PTA_bl during decoding of the received vector as seen in Fig. 14. However, there is a larger performance difference in the number of operations run between the kBD algorithm and the ABP for the (15,11) RS code, when compared to the (15,7) RS code. The main reason the kBD algorithm carries out less operations when compared to the ABP for the (15, 11) RS code than the (15, 7) RS code, is due to the use of a smaller value of t . The smaller value of t ensures the decoding condition is met much quicker. This reduces the number of iterations used to correct the bits in the received vector, which in turn reduces the number of operations required during the decoding process. Also, it is important to note that the ABP requires more iterations to decode the received vector for the (15,11) RS code when compared to the (15, 7) RS code. This is because the high rate code has less rows and a larger parity submatrix in H when compared to the identity submatrix. This makes the matrix H more dense which affects the iterative convergence rate of the belief propagation algorithm. This is due to some of the unreliable bits saturating most of the checks which causes iterative decoding to be stuck at some pseudo-equilibrium points [5]. The results for the kBD_nt algorithm are again quite favourable as in the case of the (15, 7) RS code. This is because the significantly more complex PTA_bl only outperforms kBD_nt algorithm by less than 0.1dB in terms of error correction. The kBD_nt algorithm also matches the error correction performance of the ABP, which is also has a higher computational complex cost as seen in Fig. 10. As highlighted in section IV-B, this justifies the use of the algorithm whenever a tradeoff between the decoding performance and the algorithm complexity is required.

 

VI. CONCLUSION

In this paper an iterative soft-input soft-output bit-level decoder based on ISD is presented for RS codes. The algorithm has the advantage of working at a lower computational complexity cost while yielding a similar BER performance to the ABP and the bit-level PTA. The algorithm is able to perform at a lower complexity largely due to its low iterative convergence rate. The convergence rate of the proposed decoder is controlled by information set decoding techniques applied through an additional stopping criteria, referred to as the decoding condition, for the iterative decoding process. The decoding condition reduces the number of iterations required for decoding by enabling the decoder to output a decoded codeword of length N based on an information set of K bits. This approach reduces the iterative convergence rate because the algorithm only has to decode the information set made up of the most reliable bits.

The proposed decoder has two variants, the kBD algorithm and the less complex kBD_nt algorithm. The kBD algorithm is able to match the error correction performance, and in some cases yield a slight gain in decoding performance, when compared to the ABP and the bit-level PTA. The kBD_nt algorithm is only slightly outperformed, and in some case able match the performance, of the ABP and the bit-level PTA. However kBD_nt algorithm is significantly less complex, due to the lack of row reduction operation being carried out iteratively, and can be used whenever a tradeoff is required between the algorithm complexity and the decoding performance.

 

VII. FUTURE RECOMMENDATIONS

Work in this research focused on the development of a high performance decoding approach that runs at a relatively low complexity. The decoding approach works well, however improvements can still be made. Research can be carried out to test the coding gain the proposed algorithm can attain from using low weight parity check equations instead of the original H matrix as in the case for the parity check matrix extensions [43]. To further improve the error correction performance of the proposed bit-level decoder, at the expense of an increased computational complexity cost, double decoding techniques can also be explored. The use of a hard-decision decoder, in a similar way to the implementation with soft-decision decoders presented in [5], [16], [44], can also be investigated when applied to the proposed decoding approach.

 

REFERENCES

[1] I. S. Reed and G. Solomon, "Polynomial Codes over Certain Finite Fields," J. Soc.Ind. Appl. Maths., 1960.

[2] R. Koetter and A. Vardy, "Algebraic Soft-Decision Decoding of Reed-Solomon Codes," Information Theory, IEEE Transactions on, 2003.

[3] O. O. Ogundile and D. J. J. Versfeld, "A Low Complexity Iterative Channel Estimation and Decoding Receiver Based on Reed-Solomon PTA," IEEE Access, vol. 4, pp. 8805-8813, 2016.         [ Links ]

[4] O. Ogundile, Y. Genga, and D. Versfeld, "Symbol Level Iterative Soft Decision Decoder for Reed-Solomon Codes Based on Parity-Check Equations," Electronics Letters, vol. 51, no. 17, pp. 1332-1333, Aug. 2015.         [ Links ]

[5] J. Jiang and K. R. Narayanan, "Iterative Soft-Input Soft-Output Decoding of ReedSolomon Codes by Adapting the Parity-Check Matrix," IEEE Transactions on Information Theory, vol. 52, no. 8, pp. 3746-3756, Aug 2006.         [ Links ]

[6] L. Chen, "Iterative Soft Decoding of Reed-Solomon Convolutional Concatenated Codes," IEEE Transactions on Communications, vol. 61, no. 10, pp. 4076-4085, October 2013.         [ Links ]

[7] B. Kamali and A. Aghvami, "Belief Propagation Decoding of Reed-Solomon Codes; a Bit-Level Soft Decision Decoding Algorithm," Broadcasting, IEEE Transactions on, vol. 51, no. 1, pp. 106-113, March 2005.         [ Links ]

[8] V. T. Van, S. Mita, J. Li, C. Yuen, and Y. L. Guan, "Bit-Level Soft-Decision Decoding of Triple-Parity Reed-Solomon Codes Through Automorphism Groups," Communications Letters, IEEE, vol. 17, no. 3, pp. 553-556, March 2013.         [ Links ]

[9] Y. Genga, O. Oyerinde, and J. Versfeld, "Bit Level Implementation of the PTA Algorithm for Reed-Solomon Codes," in 2017 Global Wireless Summit (GWS), Oct 2017, pp. 39-43.

[10] A. Vardy and Y. Be'ery, "Bit-Level Soft-Decision Decoding of Reed-Solomon Codes," Communications, IEEE Transactions on, vol. 39, no. 3, pp. 440-444, Mar 1991.         [ Links ]

[11] H. Xia and J. Cruz, "Performance of Reliability-Based Iterative Soft-Decision Reed-Solomon Decoding on Magnetic Recording Channels," IEEE Transactions on Magnetics, vol. 43, no. 7, pp. 3320-3323, July 2007.         [ Links ]

[12] Y. Yang, M. Jiang, and X. Wu, "An Investigation in Iterative Decoding of Reed-Solomon codes Based on Adaptive Belief Propagation," in 2009 International Conference on Wireless Communications Signal Processing, Nov 2009, pp. 1-5.

[13] J. Bellorado, A. Kavcic, M. Marrow, and L. Ping, "Low-Complexity Soft-Decoding Algorithms for ReedSolomon Codes-Part II: Soft-Input Soft-Output Iterative Decoding," IEEE Transactions on Information Theory, vol. 56, no. 3, pp. 960-967, March 2010.         [ Links ]

[14] H. Lee, J. Wu, C. Wang, and Y. Ueng, "An Iterative Soft-Decision Decoding Algorithm for Reed-Solomon Codes," in 2017 IEEE International Symposium on Information Theory (ISIT), June 2017, pp. 2775-2779.

[15] X. Huang and L. Chen, "Iterative Multistage Soft Decoding of Multilevel Reed-Solomon Codes," in 2018 IEEE Information Theory Workshop (ITW), Nov 2018, pp. 1-5.

[16] M. El-Khamy and R. J. McEliece, "Iterative Algebraic Soft-Decision List Decoding of Reed-Solomon Codes," IEEE Journal on Selected Areas in Communications, vol. 24, no. 3, pp. 481-490, March 2006.         [ Links ]

[17] D. J. C. MacKay, "Good Error-Correcting Codes Based on Very Sparse Matrices," IEEE Transactions on Information Theory, vol. 45, no. 2, pp. 399-431, Mar 1999.         [ Links ]

[18] F. MacWilliams and N. Sloane, "The Theory of Error-Correcting Codes", 8th ed. Elsevier Science Publishers, June 1993, vol. 16, no. ISBN 0 444 85193 3, pp. 106.

[19] B. Liu, Y. Xie, L. Yang, and J. Yuan, "An Iterative Soft-Decision Decoding Algorithm with Dynamic Saturation for Short Reed-Solomon Codes," in 2018 IEEE Information Theory Workshop (ITW), Nov 2018, pp. 1-5.

[20] J. Bellorado and A. Kavcic, "Low-Complexity Soft-Decoding Algorithms for Reed-Solomon Codes-Part I: An Algebraic Soft-In Hard-Out Chase Decoder," IEEE Transactions on Information Theory, vol. 56, no. 3, pp. 945-959, March 2010.         [ Links ]

[21] D. Versfeld, J. Ridley, H. Ferreira, and A. Helberg, "On Systematic Generator Matrices for Reed-Solomon Codes," Information Theory, IEEE Transactions on, vol. 56, no. 6, pp. 2549-2550, June 2010.         [ Links ]

[22] Y. Genga, O. Ogundile, O. Oyerinde, and J. Versfeld, "A Low Complexity Encoder Construction for Systematic Quasi-Cyclic LDPC Codes," in 2017 IEEE AFRICON, Sept 2017, pp. 167-170.

[23] E. Prange, "The Use of Information Sets in Decoding Cyclic Codes," IRE Transactions on Information Theory, vol. 8, no. 5, pp. 5-9, September 1962.         [ Links ]

[24] J. T. Coffey and R. M. Goodman, "The Complexity of Information Set Decoding," IEEE Transactions on Information Theory, vol. 36, no. 5, pp. 1031-1037, Sep 1990.         [ Links ]

[25] M. Fossorier and S. Lin, "Reliability-Based Information Set Decoding of Binary Linear Codes," in Proceedings. 1998 IEEE International Symposium on Information Theory (Cat. No.98CH36252), Aug 1998, p. 229.

[26] L. Zhang, Z. Zhang, X. Wang, C. Zhong, and L. Ping, "Simplified Successive-Cancellation Decoding Using Information Set Reselection for Polar Codes with Arbitrary Blocklength," IET Communications, vol. 9, no. 11, pp. 1380-1387, 2015.         [ Links ]

[27] S. Scholl and N. Wehn, "Hardware Implementation of a Reed-Solomon Soft Decoder Based on Information Set Decoding," in 2014 Design, Automation Test in Europe Conference Exhibition (DATE), March 2014, pp. 1-6.

[28] Q. Guo, T. Johansson, E. Mrtensson, and P. Stankovski, "Information Set Decoding with Soft Information and Some Cryptographic Applications," in 2017 IEEE International Symposium on Information Theory (ISIT), June 2017, pp. 1793-1797.

[29] C. Peters, "Information-Set Decoding for Linear Codes over F_q," in Sendrier N. (eds) Post-Quantum Cryptography. PQCrypto 2010. Lecture Notes in Computer Science, vol. 6061, 2010, pp. 81-84.

[30] M. P. C. Fossorier and S. Lin, "Soft-Decision Decoding of Linear Block Codes Based on Ordered Statistics," IEEE Transactions on Information Theory, vol. 41, no. 5, pp. 1379-1396, Sep. 1995.         [ Links ]

[31] I. Dumer, "Information-Set Soft-Decision Decoding," in 1998 Information Theory Workshop (Cat. No.98EX131), Jun 1998, pp. 77-78.

[32] G. G. de Oliveira Brante, D. Nascimento Muniz, and W. Godoy, "Information Set Based Soft-Decoding Algorithm for Block Codes," in 2010 IEEE Latin-American Conference on Communications, Sep. 2010, pp. 1-6.

[33] A. Ahmed, R. Koetter, and N. R. Shanbhag, "Performance Analysis of the Adaptive Parity Check Matrix Based Soft-Decision Decoding Algorithm," in Conference Record ofthe Thirty-Eighth Asilomar Conference on Signals, Systems and Computers, 2004., vol. 2, Nov 2004, pp. 1995-1999 Vol.2.

[34] W. Sung and J. T. Coffey, "Information Set Decoding Complexity for Linear Codes in Bursty Channels with Side Information," in Proceedings of 1995 IEEE International Symposium on Information Theory, Sep. 1995, p. 53.

[35] M. Bossert, Channel Coding for Telecommuincations. John Wiley & Sons, 1999, no. ISBN 0-471-98277-6.

[36] Y. Genga and D. Versfeld, "The Modified Soft Input Parity Check Transformation Algorithm for Reed Solomon Codes," SAIEE African Research Jornal, vol. 108, no. 1, pp. 24-30, Mar. 2017.         [ Links ]

[37] H. Xia and J. R. Cruz, "Reliability-Based Reed-Solomon Decoding for Magnetic Recording Channels," IEEE Transactions on Magnetics, vol. 42, no. 10, pp. 2603-2605, Oct 2006.         [ Links ]

[38] S. Lin and D. J. Costello, Error Control Coding, 2nd ed. Pearson Prentice Hall, 2004, no. ISBN 0-13-042672-5.

[39] T. K. Moon, "Error Correction Coding: Mathematical Methods and Algorithms". John Wiley & Sons, 2005, no. ISBN 0-471-64800-0.

[40] S. Lin and W. Ryan, "Channel Codes Classical and Modern". Cambridge University Press, 2009, no. ISBN-13 978-0-511-64182-4.

[41] F. Tosato and P. Bisaglia, "Simplified Soft-Output Demapper for Binary Interleaved COFDM with Application to HIPERLAN/2," HP Laboratories Bristol, Imaging Systems Laboratory, no. HPL-2001-246, October 2001.

[42] R. Lucas and M. Bossert and M. Breitbach, "On Iterative Soft-Decision Decoding of Linear Binary Block Codes and Product Codes," IEEE Journal on Selected Areas in Communications, vol. 16, no. 2, pp. 276-296, Feb 1998.         [ Links ]

[43] Y. Genga, O. Oyerinde, and J. Versfeld, "Improving the Decoding Performance of the PTA Algorithm for RS codes Through the Extension of the Parity Check Matrix," in 2017 IEEE AFRICON, Sept 2017, pp. 171-174.

[44] D. Chase, "Class of Algorithms for Decoding Block Codes with Channel Measurement Information," IEEE Transactions on Information Theory, vol. 18, no. 1, pp. 170-182, January 1972.         [ Links ]

 

 

This work was supported in part by the National Research Foundation (NRF) South Africa. The financial support of the Centre for Telecommunications Access and Services (CeTAS), the University of the Witwatersrand, Johannesburg, South Africa is also acknowledged.

 

 

Yuval O. Genga received the B.Sc degrees in electrical and information engineering from the University of Nairobi, Nairobi, Kenya in 2012 and the M.Sc degree from the University of the Witwatersrand, Johannesburg, South Africa in 2016. He is a Ph.D. graduate from the University of the Witwatersrand, Johannesburg, South Africa. He is currently a sessional lecturer at the University of the Witwatersrand. His research interests include digital communications, digital transmission, forward error correction and signal processing techniques for wireless communication systems.

 

 

Olutayo O. Oyerinde (M'03-SM'18) received the Ph.D. degree in electronic engineering from the University of Kwazulu-Natal, Durban, South Africa, in 2011. He has been with the School of Electrical and Information Engineering, University of the Witwatersrand at Johannesburg, South Africa, since 2013, where he is currently an Associate Professor. He is an National Research Foundation (NRF) rated scientist, a Registered Professional Engineer (Pr.Eng.) with the Engineering Council of South Africa (ECSA), a Registered Engineer (R.Eng) with COREN, a Senior Member of Institute of Electrical and Electronics Engineer (SMIEEE), and a Corporate Member of NSE amongst others. He is an Associate Editor for the IEEE Access journal and also an editorial board member of the International Journal of Sensors, Wireless Communications & Control. His current research interests include wireless communications with specific interests in 5G and beyond 5G technologies, Cognitive Radio networks, and signal processing techniques for wireless communication systems.

 

 

Daniel J.J. Versfeld (M'01-SM'19) received the B.Eng degree in electronic engineering and the M.Eng degree in electronic engineering from North-West University, South Africa in 1999 and 2001, respectively, and the D.Ing (Electronic) degree from the University of Johannesburg, Johannesburg, South Africa, in 2011. From 2011 to 2016 he worked as a Senior lecture for the School of Electrical and Information Engineering, University of the Witwatersrand, South Africa. He is currently an associate professor at Stellenbosch University, Stellenbosch, South Africa. His research interests include signal processing applied to digital communications and forward error correction.