Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
SAIEE Africa Research Journal
On-line version ISSN 1991-1696
Print version ISSN 0038-2221
SAIEE ARJ vol.109 n.4 Observatory, Johannesburg Dec. 2018
ARTICLES
Bandwidth efficiency improvement for differential Alamouti space-time block codes using M-QAM
B. DlodloI; H. XuII; N. PillayIII
ISchool of Engineering, University of KwaZulu-Natal, King George V Avenue, Durban, 4041, South Africa, E-mail: buthananidlodlo@gmail.com
IISchool of Engineering, University of KwaZulu-Natal, King George V Avenue, Durban, 4041, South Africa, E-mail: xuh@ukzn.ac.za
IIISchool of Engineering, University of KwaZulu-Natal, King George V Avenue, Durban, 4041, South Africa, E-mail: pillayn@ukzn.ac.za
ABSTRACT
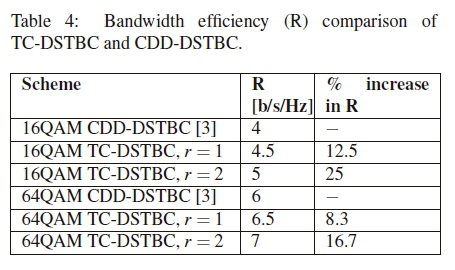
We propose a technique that enhances the bandwidth efficiency of the two transmit antenna differential space-time block code (DSTBC) by use of space-time block code (STBC) expansion and trellis coding. STBC expansion is realized by expanding the conventional Alamouti STBC using unitary matrix transformation. This is followed by trellis code-aided mapping of additional bits to space-time codes of the expanded set. Trellis code-aided mapping of additional bits enhances the bandwidth efficiency of the proposed DSTBC scheme. The proposed scheme sends more information bits in each transmitted space-time code than the conventional differential detection-aided DSTBC (CDD-DSTBC) scheme, and yet retains the same error performance. For each additional bit sent with the transmitted space-time codeword, the proposed scheme using 16QAM achieves a 12.5% increase in bandwidth efficiency, while the scheme using 64QAM realises an 8.3% increase. Simulation results demonstrate that the error performance of the proposed scheme tightly matches that of CDD-DSTBC with improvement in bandwidth efficiency. The bandwidth efficiency is enhanced at the expense of a moderate increase of the computational complexity at the receiver.
Keywords: Bandwidth efficiency, coherent detection, differential Alamouti space-time block codes, differential detection, noncoherent detection, trellis code.
1. INTRODUCTION
Exponential growth in the demand for high data rate wireless communications requires communication systems to be more efficient and reliable. Reliable high data rate communications can be achieved by employing space-time block code (STBC)-based multiple-input multiple-output (MIMO) systems [1]. The strength of STBCs lies in the usage of diverse received versions of the same signal to mitigate the impairments of wireless multipath fading channels. Alamouti proposed a full diversity two transmit antenna STBC defined as follows [2]:
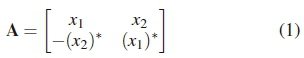
where symbols x1 and x2 belong to an M-ary quadrature amplitude modulation (M-QAM) or M-ary phase shift keying (M-PSK) constellation. Equation (1) is an orthogonal matrix because its row or column vector pair has a zero inner product. The orthogonality of (1) guarantees decoupling of signals at the receiver of the STBC system with coherent detection [2]. However, coherent detection requires high-complexity channel estimation, whose complexity increases with the number of receive antennas [3]. Hence, the conventional differential detection (CDD) of differential STBC (DSTBC) for M-PSK was proposed [4]. CDD has been further extended to DSTBC with M-QAM [3]. The differential scheme proposed in [3] also eliminates the requirement of fading channel power estimation. A consequence of CDD-aided DSTBC (CDD-DSTBC) is the signal-to-noise ratio (SNR) penalty, which increases with the modulation order of M-QAM [3, Fig. 1(a)]. In order to improve the error performance of CDD-DSTBC, a number of techniques have been investigated in [3,5-8]. In spite of their performance advantages, the differential schemes in [3, 5-8] have low bandwidth efficiency due to the transmission of symbols which convey the same message bits over two time slots.
In order to enhance the bandwidth efficiency of STBC-based MIMO systems, several bandwidth efficiency improvement techniques have been investigated in [9-12]. The scheme in [9], extends signals to the spatial domain, resulting in improved bandwidth efficiency. However, the limitation on the practical number of transmit antennas that can be used may limit the scheme in [9] from achieving high bandwidth efficiencies. In [10], the technique which enhances bandwidth efficiency while retaining the orthogonality of the two transmit antenna STBC has been investigated. The bandwidth efficiency is enhanced by employing a double quadrature PSK (QPSK) constellation set that consists of the rotated and unrotated sets. The scheme is capable of sending an extra bit per transmitted STBC codeword. This technique has been extended to a four transmit antenna STBC with QPSK [11]. However, the techniques investigated in [10, 11] enhance the bandwidth efficiency at the expense of a degraded bit error rate (BER) performance.
In [12], a super-orthogonal STBC scheme that enhances bandwidth efficiency has been investigated. Unitary matrix transformation is employed in the expansion of the conventional orthogonal STBC. The availability of zeros in the four transmit antenna space-time code is exploited in producing high-rate codes with large Euclidean distances. The impact of the scheme in [12] has been an increase in the bandwidth efficiency and a BER performance improvement of the four transmit antenna STBC. However, the two transmit antenna space-time code has a degrading error performance, which deteriorates further as the code rate is increased. Against this background, the authors are motivated to enhance the bandwidth efficiency of a two transmit antenna CDD-DSTBC without sacrificing the error performance.
In this paper, we first expand the STBC in (1) via unitary matrix transformation [12]. To improve the bandwidth efficiency, trellis code-aided mapping of additional bits to the expanded STBC is proposed. Differentially encoded high-rate STBC codewords are transmitted by a differential transmission scheme, hereinafter referred to as trellis code-aided DSTBC (TC-DSTBC). Compared to CDD-DSTBC [3], the proposed scheme is capable of sending additional bits per transmitted space-time codeword, while closely matching the error performance of CDD-DSTBC. It should be noted that there has been work published in [13], which appears similar to the proposed scheme. However, differences exist. For example, in [13], there is a fixed mapping of additional bits to high-rate STBCs and the scheme employs selective power scaling to improve the error performance of coherent STBC with M-PSK. In the proposed TC-DSTBC system, the error performance is improved by the dynamic mapping of additional bits to high-rate STBCs.
The remainder of the paper is organised as follows: Section 2 firstly presents the technique for enhancing the bandwidth efficiency. Thereafter, the system model of TC-DSTBC is presented. Comparison of the computational complexity of the proposed detector with the CDD-DSTBC detector is given in Section 3. Section 4 presents the numerical results and discussion. The paper is concluded in Section 5.
The notations used throughout this paper are as follows: NTis the number of transmit antennas and NRis the number of receive antennas. Bold lower case and upper case letters are used for vectors and matrices, respectively. |-| and ||-||F represent the Euclidean and Frobenius norm operations, respectively. E{ } is the expectation operator. ( )* is the conjugate operator. ( )H is the Hermitian transpose operator. r is the number of additional bits sent with each transmitted high-rate STBC compared to the conventional Alamouti STBC. CMxN is a set of M x N complex-valued matrices. Z≥0 is a set of non-negative integers including 0.  represents 'corresponds to'. argmin(t) ( ) represents the argument of the minimum with respect to
represents 'corresponds to'. argmin(t) ( ) represents the argument of the minimum with respect to  D is the bit delay. The label D-1 indicates the transmission delay for one block.
D is the bit delay. The label D-1 indicates the transmission delay for one block.
2. TC-DSTBC
In this section, we present the technique for enhancing the bandwidth efficiency of STBCs and the system model of TC-DSTBC.
2.1 STBC expansion
Unitary matrix transformation is employed in expanding the conventional Alamouti STBC so as to introduce redundancy that is required for trellis coding. The Alamouti code in (1) is expanded by multiplying it by diagonal unitary matrices. Unitary matrix transformation does not expand the resulting modulation alphabet, which prevents the increase of the peak-to-average power ratio of the transmitted signal [12]. In order to send r additional bits per STBC, a total of 2r+1 diagonal unitary matrices is required. This number of unitary matrices ensures that the trellis code-aided scheme has STBCs of twice the cardinality when compared to schemes with unaided mapping, thus satisfying the redundancy requirement for trellis coding [14]. Diagonal unitary matrices of the form shown in (2) are employed.
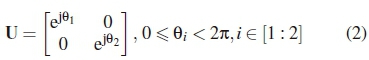
where Ө1 and Ө2 are variable rotational angles. While a computer-aided numerical search can be used to find 2r+1 combinations of 01 and 02, which give a set of unitary matrices with the optimal Euclidean distance distribution [12], the same can be achieved by searching the literature. The literature search reveals that the optimal Euclidean distribution can be realized by maintaining a constant 01, while varying 02 in equal steps over the entire 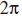 range [13,15]. For conventionality purposes, Ө1 = 0 is used in this paper. Therefore, unitary matrices of the form shown in (3) are employed in the STBC expansion.
range [13,15]. For conventionality purposes, Ө1 = 0 is used in this paper. Therefore, unitary matrices of the form shown in (3) are employed in the STBC expansion.
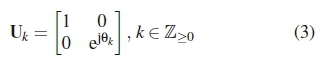
where the rotational angle is defined as 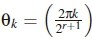 , for all k = 0,1,2,. . .,2r+1 - 1. High-rate STBCs are then formulated from (1) and (3) as Bk = AUk. In expanded form, the high-rate space-time codes are expressed as
, for all k = 0,1,2,. . .,2r+1 - 1. High-rate STBCs are then formulated from (1) and (3) as Bk = AUk. In expanded form, the high-rate space-time codes are expressed as
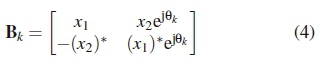
where the rotational angle Өk encodes additional bits. We assume that the codebook denoted by xkcontains M2 distinct codewords of each high-rate STBC Bk, k Є[0: 2r+1- 1], since there are M2 possible combinations of symbols x1and x2. M is the modulation order. For example, the codebook x0 contains M2 distinct codewords of type B0, which have the same rotational angle Ө0= 0. Table 1 shows values of rotational angles corresponding to other high-rate space-time codes of (4) for r = 1 and r = 2. Space-time codes in adjacent rows of Table 1 are at the minimum maximised squared Frobenius distance from each other. For each value of r, the first and last row space-time codes B0 and 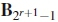 are considered to be in adjacent rows. The downside of the expanded STBC is the loss of diversity as revealed by the analysis in Section 2.2.
are considered to be in adjacent rows. The downside of the expanded STBC is the loss of diversity as revealed by the analysis in Section 2.2.

2.2 Analysis of diversity
In the TC-DSTBC scheme, codebooks Xk, for all k Є[0: 2r+1- 1], are considered as belonging to a larger codebook X. For full diversity to be preserved, the codeword difference matrix between any two distinct codewords from X must be full rank [16]. Consider Xi, Xj e X, where Xi ЄX0 and Xj ЄX1. Assuming that the same symbols are used in the two distinct codewords i.e. xn = x1 = x2, the codeword difference matrix Xdiff would be given accordingly as:
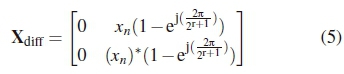
The resulting codeword difference matrix has a rank of 1. This implies that diversity is sacrificed in the high-rate STBCs of (4), hence, the error performance of the high-rate STBC is likely to be degraded.
2.3 Trellis code-aided mapping of additional bits to high-rate STBCs
In this subsection, we incorporate trellis coding in the mapping of additional bits to high-rate STBCs to counteract the undesirable effect of loss of diversity in the form of error performance degradation. Trellis coding maximises the sum of squared Frobenius distances between possible sequences of transmitted high-rate codewords to improve the error performance of the high-rate STBC.
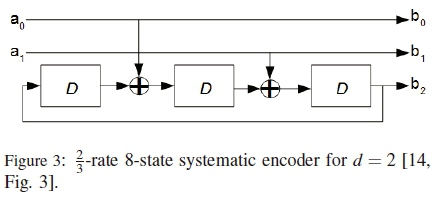
The sum of squared Frobenius distances between sequences of high-rate codewords is maximized by ensuring that codewords associated with trellis state transitions originating from or merging at the same trellis state are maximally apart. In this paper, the + -rate 2r+1-state systematic trellis encoder of [14] is employed in the mapping of additional bits to the high-rate STBC. The selected trellis encoder maximizes the sum of squared Frobenius distance between the sequences of codewords by eliminating parallel trellis paths. As a rule of thumb 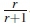 -rate trellis encoders with a number of trellis states greater or equal to 2r+1 can be used to eliminate parallel paths, however, any increase in the number of trellis states is accompanied by an exponential increase in the Viterbi decoding computational complexity. Therefore, taking into account all these considerations, the systematic trellis encoder with the minimum possible number of trellis states is employed.
-rate trellis encoders with a number of trellis states greater or equal to 2r+1 can be used to eliminate parallel paths, however, any increase in the number of trellis states is accompanied by an exponential increase in the Viterbi decoding computational complexity. Therefore, taking into account all these considerations, the systematic trellis encoder with the minimum possible number of trellis states is employed.
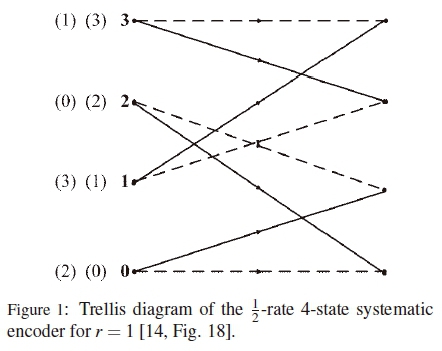
For r = 1 and r = 2, systematic trellis encoders of [14, Fig. 17] and [14, Fig. 3] are employed, respectively. The employed trellis encoders ensure that each trellis path is associated with only one high-rate STBC of (4). Consequently, the mapping of additional bits for r = 1 and r = 2 is performed according to the trellis diagrams of Figure 1 and Figure 2, respectively. At each state, the arrangement of trellis path labels from left to right corresponds to the top-to-bottom arrangement of the trellis paths emerging from that state. Note that trellis states are written in bold font in Figure 1 and Figure 2, while trellis path labels are enclosed in brackets. Trellis path labels have a decimal to binary correspondence with the binary (r + 1)-tuple outputs of the systematic trellis encoder as follows: (0) 00, (1) 01, (2) 10, etc. in Figure 1, while (0) 000, (1) 001, etc. in Figure 2.
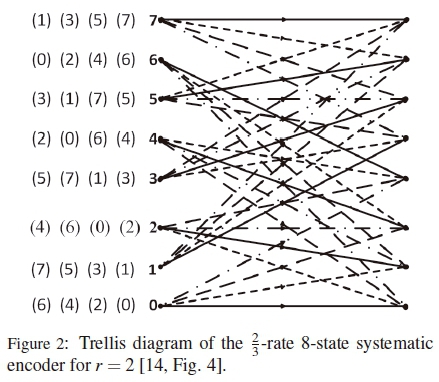
Each trellis path label (k), where k e [0:2r+1- 1], further corresponds to the high-rate STBC formulated in (4) as Bk.
As a bit mapping example, consider the 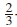 - rate systematic trellis encoder illustrated in Figure 3, at state 0. Applying the input a0a1 = 00, which corresponds to solid lines in Figure 2, yields an output b0b1b2 = 000. According to the decimal to binary correspondence stated previously, the output 000 corresponds to the trellis path label (0), therefore B0is selected for further encoding. In the same manner, applying the input 01 indicated by short-dashed lines, 10 indicated by long-dashed lines or 11 indicated by dashed with dots lines at state 0 selects B2, B4or B6, respectively. Therefore, the high-rate space-time codeword transmitted at any t-th instant is encoded according to the selected high-rate STBC of (4) as follows:
- rate systematic trellis encoder illustrated in Figure 3, at state 0. Applying the input a0a1 = 00, which corresponds to solid lines in Figure 2, yields an output b0b1b2 = 000. According to the decimal to binary correspondence stated previously, the output 000 corresponds to the trellis path label (0), therefore B0is selected for further encoding. In the same manner, applying the input 01 indicated by short-dashed lines, 10 indicated by long-dashed lines or 11 indicated by dashed with dots lines at state 0 selects B2, B4or B6, respectively. Therefore, the high-rate space-time codeword transmitted at any t-th instant is encoded according to the selected high-rate STBC of (4) as follows:
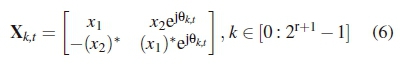
where 0k,t is the rotational angle of the high-rate STBC selected at the t-th instant, the factor k is a function of additional bits and the trellis state at that instant.
2.4 System model
Consider a NT x NRTC-DSTBC system with NT = 2, NR > NT, as illustrated in Figure 4. Message bits are divided into groups of 2m + r bits, where m = log2M. In this paper, we consider r = 1 and r = 2 only. At the tth time instant, the first 2m bits are further partitioned into two bitstreams, b1 = [b1;1 b1,2 . . .b1m] and b2 = [b2,1 b2,2 . . . b2,m], each of length m, and fed into an M-QAM mapper. The M-QAM mapper maps the input bits onto Gray-coded constellation points and yields modulated symbols X1 and X2, corresponding to b1 and b2, respectively. We assume that each symbol is normalised and scaled by a constant multiplier of 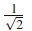 to cater for the two transmit antennas, hence, E{|x1|2+ |x2|2} = 1. Thereafter, symbols x1 and x2 are fed into the high-rate STBC encoder. The additional bitstream b3 = [b3,1 . . . b3,r], of length r, is fed into the
to cater for the two transmit antennas, hence, E{|x1|2+ |x2|2} = 1. Thereafter, symbols x1 and x2 are fed into the high-rate STBC encoder. The additional bitstream b3 = [b3,1 . . . b3,r], of length r, is fed into the 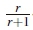 -rate 2r+1-state systematic trellis encoder of [14] to produce r + 1 bits that select one of the 2r+1 high-rate STBCs of (4) according to the appropriate trellis diagram. Finally, the two symbols, x1 and x2, are encoded according to the selected high-rate STBC Bk, yielding the codeword Xk,t of (6). In this investigation, tailbits are employed to ensure that the trellis encoding process over N successive encoding segments starts and ends at the first trellis state, where N is the trellis encoder depth.
-rate 2r+1-state systematic trellis encoder of [14] to produce r + 1 bits that select one of the 2r+1 high-rate STBCs of (4) according to the appropriate trellis diagram. Finally, the two symbols, x1 and x2, are encoded according to the selected high-rate STBC Bk, yielding the codeword Xk,t of (6). In this investigation, tailbits are employed to ensure that the trellis encoding process over N successive encoding segments starts and ends at the first trellis state, where N is the trellis encoder depth.
Prior to transmission, Xk,t undergoes a differential encoding process formulated from [3] as follows:
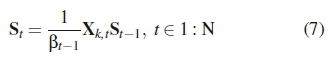
where St-1 is the DSTBC transmitted at the time instant prior to t. The power normalisation factor 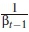 , is defined by
, is defined by 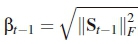 The first transmitted DSTBC S0 is set as X0,0, which is selected in random from x0. The tth received signal matrix YtЄC2xNris modelled as:
The first transmitted DSTBC S0 is set as X0,0, which is selected in random from x0. The tth received signal matrix YtЄC2xNris modelled as:
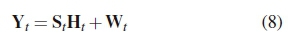
where HtЄC2xNr is the channel matrix. WtЄC2xNr is the received additive white Gaussian noise (AWGN) matrix. The entries of Ht and Wt are independent and identically distributed (i.i.d.) complex Gaussian random variables (RVs) distributed as 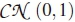 and
and 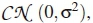 respectively. Thus, the average SNR is defined as p =
respectively. Thus, the average SNR is defined as p =  . The channel is assumed to be Rayleigh frequency-flat fading and remains constant for two DSTBC transmission durations as in [3] i.e. (Ht = Ht-1). Therefore, (8) may be further expressed as:
. The channel is assumed to be Rayleigh frequency-flat fading and remains constant for two DSTBC transmission durations as in [3] i.e. (Ht = Ht-1). Therefore, (8) may be further expressed as:
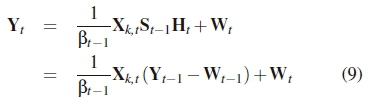
The Viterbi algorithm-based decoding technique at the receiver of the TC-DSTBC system determines the most likely transmitted sequence of  by employing a maximum-likelihood (ML) estimation method to minimise the branch metric
by employing a maximum-likelihood (ML) estimation method to minimise the branch metric 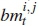 in (10) for each possible state i to state 3 transition at each t-th decoding stage.
in (10) for each possible state i to state 3 transition at each t-th decoding stage.
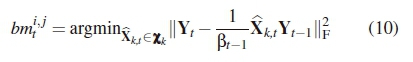
where xk is the codebook containing all high-rate space-time codewords of type Bk, which correspond to the state i to state j trellis path of the appropriate trellis diagram. At each state j, the path metric pmjt given by (11) is minimised to determine the survivor path.
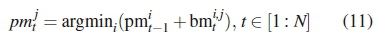
where i denotes all the possible previous states with respect to state j, j Є[0:2r+1- 1].
3. COMPARISON OF COMPUTATIONAL COMPLEXITY OF THE DETECTORS
In this section, the computational complexity of the TC-DSTBC Viterbi algorithm-based detector is compared with the computational complexity of the CDD-DSTBC ML detector.
The computational complexity of the CDD-DSTBC ML detector can be assumed to be equal to 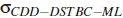 . The computational complexity of the TC-DSTBC Viterbi algorithm-based detector is dominated by the branch metric
. The computational complexity of the TC-DSTBC Viterbi algorithm-based detector is dominated by the branch metric 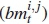 computation in (10), which is similar to the ML metric employed by the CDD-DSTBC detector [3, eq. (6)]. However, the Viterbi algorithm-based detector computes
computation in (10), which is similar to the ML metric employed by the CDD-DSTBC detector [3, eq. (6)]. However, the Viterbi algorithm-based detector computes 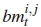 for all possible trellis state transitions. Therefore, the computational complexity of the TC-DSTBC Viterbi algorithm-based detector per detected TC-DSTBC codeword can be expressed as:
for all possible trellis state transitions. Therefore, the computational complexity of the TC-DSTBC Viterbi algorithm-based detector per detected TC-DSTBC codeword can be expressed as:
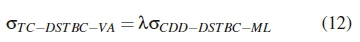
where X is the total number of 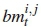 computations over a decoding depth N. The number of
computations over a decoding depth N. The number of 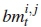 computations can be obtained from the careful analysis of trellis state transitions on the expanded trellis, which has identical start and end states. In Table 2, we tabulate the total number of
computations can be obtained from the careful analysis of trellis state transitions on the expanded trellis, which has identical start and end states. In Table 2, we tabulate the total number of 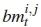 computations in each decoding segment. The segments 3 to N - 2 have the largest number of trellis state transitions but the required number of
computations in each decoding segment. The segments 3 to N - 2 have the largest number of trellis state transitions but the required number of 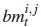 computations is only 2r+1 per segment since each computed
computations is only 2r+1 per segment since each computed 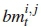 is shared by multiple trellis state transitions.
is shared by multiple trellis state transitions.

Using the values tabulated in Table 2, X can be expressed as:
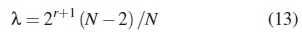
From (13) it is clear that for large decoding depths, X approaches 4 and 8 for r = 1 and r = 2, respectively. It is evident that the computational complexity of the TC-DSTBC Viterbi algorithm-based detector is significantly higher than that of the conventional CDD-DSTBC ML detector.
4. NUMERICAL RESULTS
In this section, the Monte Carlo simulation results demonstrated for the TC-DSTBC scheme, with Nt= 2 are presented. We assume that the frequency-flat Rayleigh fading channel is not known at the receiver. The Viterbi decoder based on the trellis diagram of Figure 1 for r = 1 or Figure 2 for r = 2, implements noncoherent detection according to (10) and (11), with N = 100. Simulation parameters are given in Table 3. The fading channel and AWGN simulation parameters are in line with those defined in Section 2.4.
Results presented in Figure 5, demonstrate the average BER performance versus the average SNR (10log10p) of the proposed TC-DSTBC scheme with 16QAM, while results for TC-DSTBC with 64QAM are presented in Figure 6. Theoretical BERs for coherent Alamouti STBC based on the 2NR-branch maximal ratio combining (MRC) performance given by [17, eq. (15)] are also shown in Figure 5 and Figure 6. In order to demonstrate that the proposed scheme has a bandwidth efficiency advantage compared to existing differential schemes, we also show numerical results for the CDD-DSTBC scheme from [3].
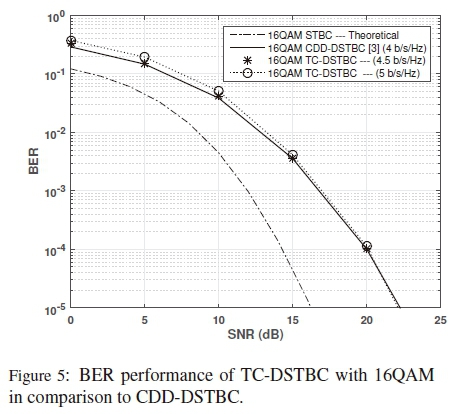
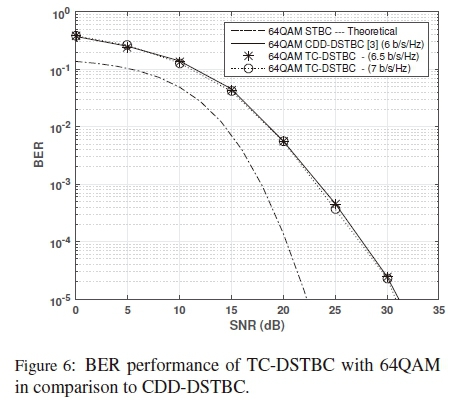
It can be observed that, at high SNR values, the BER performance of TC-DSTBC converges to that of CDD-DSTBC down to the average BER of 10-5. The scheme with 64QAM tightly matches the error performance of the corresponding CDD-DSTBC at all SNR values. However, TC-DSTBC achieves better bandwidth efficiency compared to CDD-DSTBC, as indicated in Table 4.
We observed that there is a performance gap of approximately 5dB between the coherent STBC and DSTBCs with 16QAM in Figure 5, which is similar to the SNR gap shown in [3, Fig. 1(a)]. As with the SNR gap shown in [3, Fig. 1(a)], the SNR gap increases further with an increase in the order of M-QAM. In simulation results presented in Figure 6, the SNR gap between the coherent STBC and DSTBCs with 64QAM exceeds 5dB in the high SNR region.
5. CONCLUSION
In this paper, we have investigated ahigh-rate, two transmit antenna DSTBC in the form of TC-DSTBC. Monte Carlo simulation results for a frequency-flat Rayleigh fading channel were presented. Simulation results demonstrate that the more bandwidth efficient TC-DSTBC achieves a BER perfomance that tightly matches that of the CDD-DSTBC scheme in the high SNR region. However, there is a trade-off. Bandwidth efficiency is enhanced at the expense of an increase of the computational complexity at the receiver. The increase of the computational complexity is due to Viterbi decoder usage.
REFERENCES
[1] S. K. Roy and N. Jain: "BER performance analysis of Alamouti coding technique in Rayleigh fading channel", International Journal of Science and Research, Vol. 3, No. 12, pp. 480-483, December 2014. [ Links ]
[2] S. M. Alamouti: "A Simple transmit diversity technique for wireless communications", IEEE Journal on Selected Areas in Communications, Vol. 16, No. 8, pp. 1451-1458, October 1998. [ Links ]
[3] C. Xu, S. X. N. L. Wang and L. Hanzo: "Multiple-symbol differential sphere detection-aided differential space-time block codes using QAM constellations", IEEE Signal Processing Letters, Vol. 18, No. 9, pp. 497-500, September 2011. [ Links ]
[4] V. Tarokh and H. Jafarkhani: "A differential detection scheme for transmit diversity", IEEE Journal on Selected Areas in Communications, Vol. 18, No. 7, pp. 1169-1174, July 2000. [ Links ]
[5] D. Divsalar and M. K. Simon: "Multiple-symbol differential detection of MPSK", IEEE Transactions on Communications, Vol. 38, No. 3, pp. 300-308, March 1990. [ Links ]
[6] L. Li, Z. Fang, Y. Zhu and Z. Wang: "Generalized differential transmission for STBC systems", in Proceedings of the IEEE Global Telecommunications (GLOBECOM) Conference, New Orleans, pp. 1-5, November 2008-December 2008.
[7] E. B. Slimane, S. Jarboui, I. Lamouchi and A. Boual-legue: "Concatenated differential space-time block codes and four dimensional 8-PSK trellis coded modulation for wireless MIMO system with Rayleigh fading noise", International Journal of Computer Science and Information Technologies, Vol. 3, No. 2, pp. 3456-3459, April 2012. [ Links ]
[8] P. Tarasak and V. K. Bhargava: "Analysis and design criteria for trellis-coded modulation with differential space-time transmit diversity", IEEE Transactions on Wireless Communications, Vol. 3, No. 5, pp. 1374-1378, September 2004. [ Links ]
[9] E. Basar, U. Aygolu, E. Panayirci and H. V. Poor: "Space-time block coded spatial modulation", IEEE Transactions on Communications, Vol. 59, No. 3, pp. 823-832, March 2011. [ Links ]
[10] Q. Ling and T. T. Li: "Efficiency Improvement for Alamouti Codes", in Proceedings ofthe IEEE 40th Annual Conference on Information Sciences and Systems, Princeton, pp. 569-572, March 2006.
[11] Z. A. Baloch, M. U. Baloch and N. Hussain: "Efficiency improvement of space time block codes", International Journal ofCommunications, Network and System Sciences, Vol. 3, No. 6, pp. 507-510, June 2010. [ Links ]
[12] H. Lee, M. Siti, W. Zhu and M. Fitz: "Super-orthogonal space-time block code using a unitary expansion", in Proceedings of the IEEE 60th Annual Conference on Vehicular Technology, Los Angeles, pp. 2513-2517, September 2004.
[13] S. Das, N. Al-Dhahir, and R. Calderbank: "Novel full-diversity high-rate STBC for 2 and 4 transmit antennas", IEEE Communications Letters, Vol. 10 No. 3, pp. 171-173, March 2006. [ Links ]
[14] S. Benedetto, M. Mondin and G. Montorsi: "Performance evaluation of trellis coded modulation schemes", in Proceedings ofthe IEEE, Vol. 82, No. 6, pp. 833-855, June 1994. [ Links ]
[15] S. Siwamogsatham, M. P. Fitz: "Improved high rate space-time codes via orthogonality and set partitioning", in Proceedings ofthe IEEE Wireless Communication and Networking Conference, Orlando, pp. 264-274, March 2002.
[16] S. S. H. Bidaki, S. Talebi and M. Shahabinejad: "A full-rate full-diversity 2 x 2 space-time block code with linear complexity for the maximum likelihood receiver", IEEE Communications Letters, Vol. 15, No. 8, pp. 842-844, August 2011. [ Links ]
[17] H. Xu: "Symbol error probability for generalized selection combining reception of M-QAM", SAIEE Africa Research Journal, Vol. 100, No. 3, pp. 68-71, September2009. [ Links ]














