RESEARCH PAPER

 

Estimating sanitary sewer pipeline infrastructure from basic characteristics of a service zone

 

 

JM Winter; C Loubser; A Bosman

Department of Civil Engineering, Stellenbosch University, Private Bag X1, Matieland 7602, South Africa

Correspondence

 

 

---

ABSTRACT

The standard design and cost estimation for a sewer network involves considerable time and financial investment. There are, however, many cases where a rapid assessment of the sewer infrastructure or related costs associated with a service zone might be required. Although there are numerous approaches to rapid sewer infrastructure estimation in the literature, to date, no widely available tool has been developed that can be applied to reliably estimate the expected sewer pipeline infrastructure associated with a service zone in South Africa. The aim of this study was to develop a method for estimating the sewer pipeline infrastructure required for a service zone, based on limited information, that could be applied to future developments. A database of South African sewer network data was used in the development of three major study outcomes. Study Outcome I involved developing regression models for estimating the total sewer pipeline length using only basic service zone characteristics. Models were developed for different categories of land use and area size, allowing for estimation of the total pipeline length as a function of the service zone area size, relief, and the density of contributing users. Study Outcome II involved determining the average pipeline diameter distributions for different types of service zones, enabling disaggregation of the total pipeline length into lengths per diameter. Study Outcome III involved determining the average number of manholes per kilometre of sewer pipeline. Combined, the three study outcomes form an infrastructure estimation tool that enables the sewer pipeline length per approximate diameter and the number of manholes associated with a service zone to be estimated, applicable to service zones smaller than 450 hectares. This study illustrates how the same methodology can be followed to develop similar tools which are applicable to other specific regions or development types, provided an appropriate dataset is obtainable.

Keywords: sewer infrastructure, future developments, gravity pipeline, diameter distribution, manhole distribution

---

 

 

INTRODUCTION

In order to determine the sewer network infrastructure required for a particular service zone, a detailed hydraulic design process is required, which involves considerable time and financial investment. There are many cases where a rapid assessment of the sewer infrastructure or associated costs might be required, such as in a feasibility study for a proposed development, or for infrastructure management and cost projection on a town planning level. Therefore, the ability to quantify the required sewer pipeline infrastructure associated with a service zone based on limited information holds considerable value for project planning.

There have been many approaches in the literature to estimating sewer pipeline infrastructure. These approaches can be grouped largely into three categories based on the aim, namely, the automated generation of entire sewer networks, direct cost estimation methods, and methods for quantifying the expected components of a sewer network. Tools for the automatic generation of sewer network plans have shown great potential for the estimation of sewer network infrastructure and early-stage costing, and there have been numerous approaches to this concept. Some studies focused on generating the most likely real network for a specific location, such as the tool developed by Blumensaat et al. (2012) for generating a realistic hydraulic model of a combined-type sewer for a specific area, using the road layout and a digital elevation model (DEM) as inputs. Similarly, Greene et al. (1999) developed a tool to design a complete sewer network using the GIS street network map, a topographical model, and the user-stipulated locations of manholes as inputs. Another research focus area is the development of algorithms to determine the optimal cost-efficient design of a sewer network by considering all possible options and selecting the most cost-effective design. De Villiers et al. (2018) discusses numerous studies that have considered different approaches for dual-optimisation of the layout and hydraulic parameters of the network elements. In the study of urban drainage, several algorithms have been developed for generating virtual sewer networks to be used as case studies where there has been a lack of real case studies. These include Móderl et al.'s (2009) 'Case Study Generator, Ghosh et al.'s (2006) Artificial Network Generator' or ANGel, Sitzenfrei et al.'s (2010a) 'Virtual Infrastructure Benchmarking' or VIBe with a sewer network extension module developed by Urich et al. (2010), and Sitzenfrei et al.'s (2010b) upgraded 'Dynamic Virtual Infrastructure Benchmarking' or DynaVIBE algorithm. However, while there has been significant progress towards the automated generation of entire sewer networks, most of these methods are not yet fully developed or accessible for practical application on a project level. Therefore, there is still a need for a simpler approach to cost and infrastructure estimation.

The advantage of direct costing methods is that minimal information and time are required to obtain cost estimates. A cost benchmarking guide for water services was produced by the South African Department of Water and Sanitation or DWS (PULA, 2016), which provides the typical unit costs of water services projects and their individual infrastructure components, based on population size and pipe material, with adjustment factors for other site-specific considerations. Another popular direct costing approach is a cost model expressing the sewer cost as a function of certain basic characteristics of the service zone, such as that developed by Balaji et al. (2015) relating the total installation cost to the population size. Nonetheless, the ability to predict the required sewer infrastructure components before obtaining an answer that is only related to cost is still valuable for several reasons. To this end, a variety of different approaches were found in the literature. Some studies have investigated the correlation between sewer network properties and urban surface information such as street layout, with some degree of success (Haile, 2009; Kobayashi et al., 2011); however, such urban surface methods are limited in that they are applicable only to existing service zones. Numerous studies have developed methods for predicting sewer network infrastructure of a new development from basic population and area characteristics, which would reasonably be known before the detailed design phase (DHS, 2019; Heaney et al., 1999; Pauliuk et al., 2014; and Maurer et al., 2013). However, despite the wealth of literature on the subject, no methods were found that were developed using South African or even African data on a scale that could be applicable to future developments.

The main aim of this study was to develop a method for estimating the sewer pipeline infrastructure required for a service zone, based on limited information, which can be applied to future developments. This aim necessitated three major study outcomes, namely:

• Study Outcome I: The development of a model for estimating the total sewer pipeline length for a service zone using basic service zone characteristics

• Study Outcome II: The development of pipeline diameter distributions for disaggregating the total pipeline length into lengths per diameter, for different types of service zones

• Study Outcome III: The quantification of the typical number of manholes required along a length of pipeline, for different types of service zones

The three study outcomes listed above were developed by statistically analysing South African sewer network data. The inherent assumption in this approach was that the sample networks had been designed to an acceptable standard; therefore appropriate steps were taken in the data collection process to ensure that this assumption was satisfied as far as reasonably possible.

It is noted that this study considered only the infrastructure components defined in the three study outcomes. The occurrence of special structures or rising mains, which were considered too specific a factor to predict statistically, were not included. Furthermore, the infrastructure estimation tool developed in this study is intended for application in new developments, and therefore the sample networks used to develop the to ol represented networks on a development and suburb scale. Consequently, the results account mostly for reticulation and collector sewers, with bulk lines represented to a lesser degree. And, lastly, no allowance was made for outside flow contributions from adjacent upstream developments draining through the development of interest, and the tool is only applicable to developments on the upstream end of a catchment.

 

METHODS

The approach taken to realise the stated study outcomes was a statistical one. This necessitated two major methodological components, namely data collection and statistical analysis.

Data collection

For the data collection component, a suitable and sufficient data source, characterising a large number of service zones and associated sewer networks, had to be identified. Data were obtained from a specialised water services consulting firm in the form of comprehensive sewer network models for 5 South African municipalities located in the provinces of Gauteng, Western Cape, Free State and Mpumalanga. The raw data represented an amassed total of 20 660 km of gravity pipelines. From the municipality-scale sewer network models, an appropriate dataset of sample networks had to be extracted for statistical analysis, on a scale representative of the development or single-project-sized service areas considered for this study. Suitable sample networks were identified by inspection on a case-by-case basis, and it was ensured that the resulting dataset was varied in terms of characteristics such as area size, land uses, population density, network shape, and topography.

Before recording the characteristics of interest of the sample networks, two types of modifications were made to the samples. Firstly, in order to ensure that the dataset represented sewer networks operating under acceptable conditions, flow simulations were performed to verify that all pipes had sufficient spare capacity under design flow conditions. Pipes with insufficient spare capacity were resized appropriately, ensuring that the minimum and maximum flow velocity requirements were still satisfied throughout the network. Secondly, in order to practically obtain a large enough sample size, it was sometimes necessary to isolate sample networks by deleting connections which conveyed flow originating outside of the sample service zone into the sample network. This modification was only considered acceptable in cases where it was clear that the layout of the sample network was not influenced by the upstream connection, and all pipes downstream of the deleted connection were resized appropriately for the reduced design flow. Overall, care was taken to ensure that the resulting diameters were representative of reality.

After identifying and correcting the sample networks, their characteristics of interest were recorded, thus forming the dataset for statistical analysis. The outcomes of interest were identified as the total pipeline length, diameter distribution, and manhole distribution. The potentially influential variables of interest were identified as the land use, area size, flow, dwelling density, shape, and topography. For each sample network, these characteristics of interest were recorded in terms of the variables shown in Table 1. For some of the characteristics of interest, such as topography, multiple indicators were used so that the best-performing one could be selected in the final analysis.

The dataset was divided into the four land use categories shown in Table 2, based on the dominant land use category by flow contribution. Table 2 contains only the land uses which were present in the dataset, grouped logically based on flow production patterns as well as typical sewer layout patterns associated with each land use. The final dataset consisted of 473 sample networks, of which 240 were 'General Residential', 113 were 'Low Income Residential', 92 were 'Non-Residential', and 28 were 'Large.

Study Outcome I analysis

For the statistical analysis component, each study outcome necessitated a unique statistical approach. For Study Outcome I, the chosen method was to develop a multiple regression model to express the total pipeline length as a function of a combination of physical characteristics of the service zone, for each of the four land use categories. This method was chosen to enable precise estimation of the total pipeline length, as well as to allow the relationship between the total pipeline length and the service zone characteristics to be quantified and understood.

In multiple linear regression analysis, a dataset is used to generate a model ofthe form presented in Eq. 1, where y denotes the estimated dependent variable, x_idenotes the independent or predictor variables, and β_idenotes the regression coefficients. To develop a regression model, the right independent variables x_tin the right forms must be selected, and reliable estimates of the regression coefficients β_imust be generated using regression analysis, such that the model can produce acceptably accurate estimations of the dependent variable y. The standard approach for regression analysis is to first try the ordinary least squares regression (OLS). In OLS, the regression coefficients β_tare estimated such that the sum of the squared errors is at its minimum, where the errors (or residuals) refer to the difference between the observed value and the predicted value for each observation or data point.

In order to develop the regression models for this study outcome, a multi-step process was followed. Firstly, the candidate variables were identified. The dependent variable was the total pipeline length, and the candidate independent variables are displayed in Table 4. Variables in the same variable group were prevented from being incorporated in the same model due to multicollinearity between them, which is the state of being highly correlated to each other. For each possible combination of the variables in Table 4, an OLS model was built, and any insignificant variables indicated by a p-value > 0.05 (see Montgomery and Runger, 2014) were removed, so that the final models contained only the independent variables with a significant relationship with the dependent variable. It was found that area size was by far the most significant variable, but that variable groups representing network service density and topography helped to refine the estimates. By comparing the models in terms of comparative performance indicators, namely the adjusted R², log-likelihood, Akaike's Information Criterion (AIC) and Bayesian Information Criterion (BIC), it was found that the best-performing combination of variables was the area size, mean relief, and number of unit hydrographs (UHs) per hectare.

During the variable-selection process, the problem of heteroscedasticity or non-constant variance was identified, in which the model prediction errors increased with increasing area size, thus reducing the accuracy of the estimated regression coefficients. The heteroscedasticity was addressed using a combination of two strategies. Firstly, the range of the area size for each model was reduced by introducing different area size categories within each land use category, which increased the number of models required from four to nine. Secondly, weighted least squares regression (WLS) was implemented. WLS is variation of OLS in which the errors are weighted to prevent the large errors from having a disproportional impact on the regression coefficient estimates. This two-pronged approach adequately addressed the heteroscedasticity. However, working with a reduced number of data points for each model revealed a trend which was previously concealed, namely that both mean relief and UHs per hectare displayed a very mild nonlinear relationship with the total pipeline length. This was addressed by applying nonlinear transformations to both variables, namely. 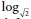relief and (UHs per hectre), which significantly improved the visual fit of the data, and thus was considered to better represent the true variable relationships. After addressing the heteroscedasticity and non-linearity, all previous conclusions were re-evaluated, and found to still be acceptable. Therefore, for each of the nine land use and area size category combinations, a unique WLS regression model was developed representing the total pipeline length as a function of area size, . and 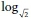(UHs per hectre). The final models are presented in the Results section.

Study Outcome II analysis

The purpose of this segment of the analysis was to develop pipeline diameter distributions that could be used to disaggregate the estimated total pipeline length into lengths of different diameters. The distribution of pipe diameters does not lend itself to precise statistical estimation, since pipe diameters are dependent on specific factors, such as the network layout or individual pipe slopes. Therefore, a simple and practical solution of finding the average diameter distribution within certain categories of similar networks was chosen. This pragmatic approach required similar networks to be identified based on known service zone characteristics, such as land use, area size, or population density. In order to increase the viability of the chosen method, the categories and category boundaries had to be set based on logical consideration, such that meaningful differences between the distributions would be obtained. For practicality, each pipe diameter was rounded up to the nearest standard nominal diameter, namely, 110, 160, 200, 250, 315, 355, 400, 450, 525, 600, 675, 750, and 825 mm.

The factors that could potentially influence the diameter distribution were identified as the population size, area size, dwelling density, total design flow, per capita wastewater production, and topography. Considering the data available in this study, these factors could be accounted for by a combination of the following variables: land use category, UHs per hectare, PDDWF per hectare, plane area, and mean relief (the best topography factor from Study Outcome I). In order to determine which of these were actually significant, the effect of each variable on the overall diameter distribution was evaluated by visual assessment of partial regression plots, which show the relationship between the dependent and a single independent variable, after the effects of the other independent variables have been accounted for (De Veaux et al., 2011). The overall diameter distribution was represented using the total pipeline volume divided by the total pipeline length, which signified the average cross-sectional pipeline area (or effectively, the average diameter) of a network. For each land use category, partial regression plots of the total pipeline volume over length versus plane area, UHs per hectare, PDDWF per hectare, and mean relief were plotted. The partial regression plots were analysed to assess which candidate variables had the strongest influence on the average cross-sectional pipeline area. Due to the small number of data points in the 'Large' land use category, this land use was combined with the 'Non-Residential' land use to form 'Non-Residential and Large. This combined land use category was only applied to Study Outcomes II and III.

The plots indicated that for both the 'General Residential' and 'Low Income Residential' land uses, plane area was the only variable that exhibited any influence on the total pipeline volume over length. For the 'Non-Residential and Large' land use category, plane area exhibited the strongest influence on the total pipeline volume over length, followed by mean relief, and, while PDDWF per hectare did appear to have some influence, the trend was not consistent enough to be reliable. Based on the conclusions drawn from the partial regression plots, it was established that the 'General Residential' and 'Low Income Residential' land uses should be subdivided according to plane area only, while the 'Non-Residential and Large' land use should be subdivided according to both plane area and mean relief. As a result, 17 unique diameter distributions were generated, for 6 'General Residential' area size categories, 4 'Low Income Residential' area size categories, and 7 'Non-Residential and Large' combined area size and mean relief categories. To aid in setting appropriate category boundaries in terms of area size, Figs 1 to 3, showing the maximum pipe diameter versus area size for each land use, were consulted to identify zones of relative homogeneity (designated by the dotted lines). The final diameter distributions are presented in the Results section.

Study Outcome III analysis

Lastly, for Study Outcome III, a simple average of the number of manholes per kilometre of pipeline was required. However, the placement of manholes is in reality affected by factors such as the connection density, network layout, and pipeline diameters. Therefore, it was expected that this manhole frequency could be influenced by certain service zone characteristics. After a thorough investigation of the relationship between the total number of manholes in a network and all of the other variables available in this study (Table 1), it was established that the number of manholes in a network is additionally influenced by the area size and land use of the service zone. Therefore, the manhole distribution was calculated as the average number of manholes per kilometre of pipeline within 6 different categories of land use and area size. The final distributions are presented in the Results section.

 

RESULTS

It is noted that the final dataset used to generate the study outcome components and corresponding results fell within the limits specified in Table 5. Therefore, the results presented and discussed in this section can only be considered applicable to service zones with characteristics falling within the specified limits.

Total pipeline length models

Models for the estimation of total pipeline length were developed for 9 different combinations of land use and area size categories, using only 3 independent variables: plane area, mean relief and UHs per hectare. The model form is presented in Eq. 2. The variables y and x_iare defined in Table 6, and the regression coefficients are provided in Table 7.

For each regression coefficient, three values are provided. The 'Average' value provides the estimate of the true coefficient. Using the average coefficient values would provide the most likely total pipeline length for a service area. The 'Lower confidence limit' and 'Upper confidence limit' represent the boundaries of a 95% confidence interval on the coefficients. These are provided to allow the minimum or maximum total pipeline length that could reasonably be possible for a service area to be estimated. It is also noted that in some model instances, UHs per hectare, and sometimes also mean relief, were not significant. In such cases, the regression coefficients are zeros. Finally, it is important to note that when interpreting the total pipeline length output of the models, this output is constrained by the definition of a sample network used in the collection of the data points. A sample network endpoint or mouth was defined as the first point receiving all the flows of the network. Therefore, the total pipeline length models also represent the total pipeline length before this convergence point. By extension, this implies that the short length of pipeline which connects the network endpoint to the nearest collector sewer should be accounted for separately, on an application-specific basis.

Pipeline diameter distribution

Unique pipeline diameter distributions were developed for 17 different categories of land use and area size, and mean relief to a lesser degree. The diameter distributions for the 'General Residential, 'Low Income Residential, and 'Non-Residential and Large' land use categories are presented in Table 8, Table 9 and Table 10, respectively.

Manhole distribution

The average number of manholes and junction structures (collectively referred to as manholes) per kilometre of pipeline for 6 categories of land use and area size is presented in Table 11. The 'Average' value indicates the most likely true manhole frequency. The 'Lower confidence limit' and 'Upper confidence limit' provide the bounds ofa 95% confidence interval on the manhole frequency, to allow the minimum and maximum number of manholes that could reasonably be expected to be determined.

 

DISCUSSION

In this section, the results are discussed in terms of a logical evaluation of their physical implications, and an appraisal of their performance in terms of statistical performance indicators.

Total pipeline length models

The final model form (Eq. 2) contains nonlinear terms for mean relief and UHs per hectare. This model form indicates that the total pipeline length is expected to increase with increasing area size, mean relief, and UHs per hectare, which is a logical conclusion. For the mean relief and UHs per hectare, an increase in either of these variables is associated with an increase in total pipeline length, but at a decreasing rate. In the case of UHs per hectare, this outcome could be physically interpreted as the required length of each new connection to a network becoming progressively shorter as a network changes from sparse to dense. For mean relief, such an intuitive interpretation is not clear, but the nonlinear relationship does seem reasonable. Additionally, the final models show that UHs per hectare is not a significant variable in the larger area size categories because the regression coefficients are zeros. This outcome makes sense, since small service zones might include a single development with a specific layout and population density, but large service zones incorporate more developments with a variety of population densities. Therefore, for larger service zones, UHs per hectare approaches an averaged value, thus losing its influence. Overall, in addition to strong performance results, the total pipeline length models are logical in their physical implications.

Table 12 presents the R²and mean absolute percentage error (MAPE) values for the training and test datasets, where the training dataset refers to the data points used to develop or train the model, and the test dataset refers to 20% of the original data points which were reserved exclusively for testing. The R² provides a useful and intuitive representation of the model strength. However, it must be analysed with some caution, as it can be affected by the resolution of the scatter plot (the range of values on the axes). The MAPE indicates the average size of the absolute errors as percentages of the observed y-values. The indicator was used to obtain an intuitive indication of the model accuracy.

Overall, the R² values ranged from moderately good to very good, in the order of 0.6 to greater than 0.9, and these results were validated well by the test data results. However, the 'Large' land use case was an exception, where the test data R²of 0.04 indicated a very poor performance on the test set. On closer inspection of the 'Large' model, out of the five data points in the test set, there were two major under-predictions, but the other three were estimated reasonably accurately. It is therefore plausible that the test data results were skewed by two extreme-value points.

The MAPE values were generally good. Models for the 'General Residential' land use performed the best, with MAPE in the order of 9-15%. The 'Low Income Residential' models also performed reasonably well, with a MAPE in the order of 8-20%. The MAPE for the 'Non-Residential' land use was overall a bit higher, in the order of 19-25%. The 'Large' category did not perform as well, with a MAPE in the order of 31-35%. All results were validated by the test data, including the 'Large' land use.

Overall, the performance results suggest that the model prediction accuracies range from good to moderate, with the 'General Residential' land use performing the best on average, and the 'Large' land use performing the worst. The generally poor performance of the 'Large' land use model is likely due to the combined effects of the small dataset (25 data points, of which only 20 were training points and 5 were reserved for testing), and the fact that the 'Large' sample networks sometimes contained partial sections of private industrial networks captured in the source models. This inconsistency could also explain why the area size was the only independent variable with a measurable influence for this land use.

Pipeline diameter distribution

There was no clear method for quantifying the pipeline diameter distribution performance meaningfully. However, insofar as logical distribution trends were concerned, the diameter distributions performed well. Overall, the proportion of small pipes decreased with increasing area size; the maximum nominal diameter increased with increasing area size; and in 'Non-Residential and Large' areas, flatter areas, or those with lower mean relief values, had a smaller proportion of small pipes and larger maximum diameters. In this sense the results were considered reflective of reality and thus fairly reliable.

Considering the reliability of the individual distributions, the most consistent trend was the percentage of small pipes (diameter < 160 mm). The percentage of small pipes was always greater than 90% for the residential land uses, and greater than 70% for the non-residential land uses; and the individual values varied with area size and mean relief. This finding suggests that at least 90% (or 70% in the case of nonresidential land use areas) of the total pipeline length can be expected, with a high level of confidence, to consist of pipes 160 mm in diameter or less. In effect, the majority of the pipeline network diameters could theoretically be estimated to within less than 100 mm of accuracy.

The distributions of the large pipes (diameter > 160 mm) were more random. This was possibly because the distribution of large pipes in a network is dependent on the specific network layout and the positions where the sub-networks converge. For example, a 450 mm pipe converging with a 160 mm pipe might require a 525 mm pipe downstream of the convergence, but a 450 mm pipe converging with a 315 mm pipe might require a 600 mm pipe downstream of the convergence, thus skipping the 525 mm category. Therefore the large-diameter distribution of any network is likely to deviate significantly from the average in most cases, which introduces considerable uncertainty for costing. However, based on the previous paragraph, large pipes account for less than 30% (predominantly less than 10%) of the total pipeline length, somewhat reducing the impact of this uncertainty. It is recommended that the distributions of the large-diameter pipes be used as a guide, but that they remain open to interpretation by the user based on the required level of conservativeness. To this end, the plots of maximum nominal diameter versus plane area for each land use contained in Figs 1 to 3, which were used to set area size category boundaries, may also be helpful in identifying the range of possible maximum diameters for an area.

Manhole distribution

It was found that, on average, there are about 20 manholes per kilometre of sewer pipeline, but the number of manholes per kilometre is influenced by the land use and area size. Predominantly residential areas tend to have slightly more manholes per kilometre, and predominantly non-residential areas tend to have slightly fewer manholes per kilometre. This is a logical outcome, since land use affects the network layout and density, which in turn affect the number of pipe junctions, and therefore, manholes. Another trend observed from the manhole distribution table is that as the area size increases the number of manholes per kilometre of pipeline tends to decrease. This is also a logical outcome, since larger areas have more large-diameter pipes, along which the maximum distance between manholes is normally increased. It is noted that the calculated manhole distribution may be affected additionally by the local municipal regulations on minimum manhole spacings. Considering the values in this study as a fair indication of the average case, then the upper and lower confidence limit values will be helpful in municipalities where the minimum allowed manhole spacings are below or above average, respectively.

The accuracy of the manhole distributions was evaluated by comparing the predicted versus actual number of manholes in a sample network. Similarly to the total pipeline length models, R² and MAPE were determined for the training dataset, and these results were validated using the test dataset. The R² and MAPE for the total number of manholes in each sample network are presented in Table 13. The high R² values, which all exceed 0.95, suggest that the estimations are made with considerable accuracy, and this is validated well enough by the results from the test dataset. The differences in the training data and test data R² values were not considered large enough to be a cause for concern. The MAPE for the different categories is in the order of 8 to 27%. The relatively low MAPE values indicate a fairly high prediction accuracy. Interestingly, the prediction accuracy was better for large areas than for small areas. These results are validated by the results from the test dataset. Overall, the high R²and low MAPE performance results suggest that the number of manholes is predicted with a reasonably high level of accuracy.

 

CONCLUSIONS

Using the three study outcomes in combination, it is possible to estimate the total sewer pipeline length per approximate diameter and the expected number of manholes associated with a service zone with a reasonable degree of confidence. The only required input characteristics of the service zone are: the dominant land use (in terms of PDDWF contribution, or alternatively, UH contribution), area size, mean elevation of the service zone, expected elevation of the network endpoint (the lowest convergence point of the network), and the number of unit hydrographs to be serviced by the network. The infrastructure estimation tool developed in this study is applicable to South African service zones on a development scale of 0-450 ha; however, with a suitable dataset, a similar tool could be developed for any locality or development type of interest.

While there are existing tools for feasibility-stage costing of sewer projects, many of them require an assumption to be made regarding the expected pipeline infrastructure, particularly in terms of the total pipeline length per diameter or material. The tool developed in this study could therefore offer considerable benefits for improving the accuracy of the cost estimations that can be made using existing costing methods. Furthermore, it could also have potential in non-costing applications, such as:

• Updating infrastructure databases where information is outdated or lost

• Serving as a design benchmark for new sewer schemes

• Aiding in preliminary wastewater treatment plant (WWTP) sizing calculations by allowing for more accurate infiltration estimates, since infiltration is a function of pipeline length and circumference

• Providing more detailed information for decision-making when comparing a traditional WWTP and sewer network to more modern decentralised solutions

• Helping urban planners to determine the wastewater network size that achieves optimal economies of scale

In closing, it is noted that there will always be project-specific variation which cannot be accounted for statistically, and the results generated using the proposed infrastructure estimation tool should be interpreted accordingly.

 

ACKNOWLEDGEMENTS

We gratefully acknowledge Frans Grotepass for laying the foundation for this study with the work he did for potable water networks; GLS Consulting for providing the data without which this study would not have been possible; and Mark Hoppe, Johann Rudolph, Jurie Van Der Merwe, Willie Van Der Merwe and Erik Loubser of GLS Consulting for their assistance in defining the scope and requirements of the study.

 

SYMBOLS

A Area of a polygon drawn around the border of a wastewater service zone

H_max Highest point elevation of a service zone

H_mean Mean elevation of a service zone

H_min Lowest point elevation of a service zone

H_mouth Elevation at the end manhole of a service zone

L Service zone length

P Perimeter of a polygon drawn around the border of a service zone

 

REFERENCES

BALAJI B, MARIAPPAN P and SENTHAMILKUMAR S (2015) A cost estimate model for sewerage system. ARPN J. Eng. Appl. Sci. 10 (8) 3327-3332.         [ Links ]

BLUMENSAAT F, WOLFRAM M and KREBS P (2012) Sewer model development under minimum data requirements. Environ. Earth Sci. 65 1427-1437. https://doi.org/10.1007/s12665-011-1146-1        [ Links ]

DE VEAUX R, VELLEMAN P and BOCK D (2011) Stats: Data and Models (3^rd edn). Pearson, Boston. 30.1-30.23.         [ Links ]

DE VILLIERS N, VAN ROOYEN G and MIDDENDORF M (2018) Sewer network design layout optimisation using ant colony algorithms. J. S. Afr. Inst. Civ. Eng. 60 (3) 2-15. https://doi.org/10.17159/2309-8775/2018/v60n3a1        [ Links ]

DHS (Department of Human Settlements, South Africa) (2019) The Neighbourhood Planning and Design Guide Part II Section K: Sanitation. DHS, Pretoria.         [ Links ]

GHOSH I, HELLWEGER F and FRITCH T (2006) Fractal generation of artificial sewer networks for hydrologic simulations. In: Proceedings of the 2006 ESRI International User Conference, 7-11 August 2006, San Diego.         [ Links ]

GREENE R, AGBENOWOSI N and LOGANATHAN G (1999) GIS-based approach to sewer system design. J. Surveying Eng. 125 (1). https://doi.org/10.1061/(ASCE)0733-9453(1999)125:1(36)        [ Links ]

HEANEY J, SAMPLE D and WRIGHT L (1999) Cost analysis and financing of urban water infrastructure. In: Heaney J, Pitt R and Field R (eds) Innovative Urban Wet-Weather Flow Management Systems. United States Environmental Protection Agency, Washington DC.         [ Links ]

HAILE M (2009) GIS-based estimation of sewer properties from urban surface information. Masters thesis, Technical University of Dresden.         [ Links ]

KOBAYASHI T, YAMAZAKI F and NAGATA S (2011) Estimation of the distribution of water-pipeline length based on other infrastructure data. In: 32^nd Asian Conference on Remote Sensing, 3-7 October 2011, Taipei.         [ Links ]

MAURER M, SCHEIDIGGER A and HERLYN A (2013) Quantifying costs and lengths of urban drainage systems with a simple static sewer infrastructure model. Urban Water J. 10 (4) 268-280. https://doi.org/10.1080/1573062X.2012.731072        [ Links ]

MELTON M (1965) The geomorphic and paleoclimatic significance of alluvial deposits in Southern Arizona. J. Geol. 73 (1) 1-38. https://doi.org/10.1086/627044        [ Links ]

MILLER V (1953) A quantitative geomorphic study of drainage basin characteristics in the Clinch Mountain area, Virginia and Tennessee, Project NR 389042 Technical Report 3. Columbia University Department of Geology, New York.         [ Links ]

MODERL M, BUTLER D and RAUCH W (2009) A stochastic approach for automatic generation of urban drainage systems. Water Sci. Technol. 59 (6) 1137-1143. https://doi.org/10.2166/wst.2009.097        [ Links ]

MONTGOMERY D and RUNGER G (2014) Applied Statistics and Probability for Engineers (6^th edn). John Wiley & Sons, Singapore. 310 pp.         [ Links ]

PAULIUK S, VENKATESH G, BRATTEBO H and MULLER D (2014) Exploring urban mines: pipe length and material stocks in urban water and wastewater networks. Urban Water J. 11 (4) 274-283. https://doi.org/10.1080/1573062X.2013.795234        [ Links ]

PULA (2016) Cost benchmark for water services projects. Department of Water and Sanitation, Pretoria.         [ Links ]

SCHUMM S (1956) Evolution of drainage systems and slopes in badlands at Perth Amboy, New Jersey. Geol. Soc. Am. Bull. 67 (5) 597-646. https://doi.org/10.1130/0016-7606(1956)67[597:EODSAS]2.0.CO;2        [ Links ]

SITZENFREI R, FACH S, KINZEL H and RAUCH W (2010a) A multi-layer cellular automata approach for algorithmic generation of virtual case studies - VIBe. Water Sci. Technol. 61 (1) 37-45. https://doi.org/10.2166/wst.2010.782        [ Links ]

SITZENFREI R, FACH S, KLEIDORFER M, URICH C and RAUCH W (2010b) Dynamic virtual infrastructure benchmarking: DynaVIBe. Water Suppl. 10 (4) 600-608. https://doi.org/10.2166/ws.2010.188        [ Links ]

URICH C, SITZENFREI R, MODERL M and RAUCH W (2010) An agent-based approach for generating virtual sewer systems. Water Sci. Technol. 62 (5) 1090-1097. https://doi.org/10.2166/wst.2010.364        [ Links ]

WILSON J and GALLANT J (2000) Terrain Analysis: Principles and Applications. John Wiley & Sons, New York.         [ Links ]

ZAVOIANU I (1985) Developments in Water Science 20: Morphometry of Drainage Basins (2^nd edn). Editura Academiei, Bucharest and Elsevier Science Publishers, Amsterdam.         [ Links ]

 

 

Correspondence:
JM Winter
Email: jesswinter05@gmail.com

Received: 9 April 2021
Accepted: 17 March 2022