Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.48 n.2 Pretoria Apr. 2022
http://dx.doi.org/10.17159/wsa/2022.v48.i2.3848.2
RESEARCH PAPER
Flood frequency analysis - Part 2: Development of a modified plotting position
D van der Spuy; JA du Plessis
Department of Civil Engineering, Stellenbosch University, P/Bag X1, Matieland 7602, South Africa
ABSTRACT
The original plotting position concept was suggested more than a century ago. Since then, many alternative plotting position approaches have been developed. Despite a general lack of agreement around which plotting position is theoretically 'correct' and the 'best' to use, all plotting positions fail to adequately address outliers and data of similar magnitude. Hydrologists generally fail to acknowledge that the plotting position primarily offers an informative display of data, against which distributions can be compared, rather than an absolute measure of probability. This paper does not intend to challenge any of the many lengthy theoretical mathematical arguments, utilised to 'prove' why one plotting position is superior to the others. These theoretical arguments may very well be valid for a 'population' of flood peaks - the reality, however, is that hydrologists are confronted with the challenge of analysing very limited 'samples' of the population. Consequently, the plotting position issue demands a more pragmatic approach, rather than a purely theoretical approach. This paper illustrates various problems with existing plotting position techniques in use and offers an alternative approach and a more sensible plotting position technique, using Z-scores and referred to as the Z-set PP, against which distributions can be checked. The study further illustrates how effectively the Z-set PP deals with outliers and its robustness with various record lengths. Although derived from a study of flood peak data obtained from South African flow-gauging sites, it is deemed that it will be universally applicable.
Keywords: plotting position, flood, frequency, exceedance, probability, distribution
INTRODUCTION
In flood frequency analysis (FFA) hydrologists are challenged to estimate a probability distribution from a sample of annual maximum series (AMS) flood peak data, which is consistent with the unknown, underlying population of the AMS flood peak data. If one or more outliers are present in the sample dataset it may distort statistics and, thus, the parameters of the probability model. Hydrologists should infer whether the fitted distribution is a sensible representation of the underlying population. The plotting position (PP) technique is an indispensable tool in this regard. However, the existing PP techniques do not have the ability to assign realistic PPs to outliers.
The aim of this paper is to present the hydrologist with a more sensible PP technique, against which distributions can be checked.
To understand the underlying complexity of the PP problem, a historical overview is given, which includes references to a vigorous debate about which of the many PP techniques should be used. Subsequently, a critical review of some popular existing PP techniques concludes the introductory section.
Overview and the plotting position debate
The first mention of a plotting order-ranked data technique, or PP in short, can be found in Hazen (1913). Since then, numerous other PP techniques have been introduced as 'alternatives', most probably in an attempt to cater for 'outliers' that invariably may appear in shorter data record lengths. The PP technique is still commonly used (SANRAL, 2013) to assess the performance of the different probability distributions used to estimate flood peak frequencies based on the AMS data. The World Meteorological Organisation (WMO) (2009 p. II.5-14) provides a fair description of the PP: "Such a plot serves both as an informative visual display of the data and a check to determine whether the fitted distribution is consistent with the data". Also, from the WMO (2009 p. II.5-14): "...thus all of the plotting positions give only crude estimates of the relative range of exceedance probabilities..."
Scientists commonly fail to acknowledge that the PP primarily offers a visual aid, rather than an absolute measure, against which distributions can be compared. This false perception is clearly demonstrated by Makkonen (2006 p. 334) who stated that: "Plotting order-ranked data is a standard technique that is used in estimating the probability of extreme weather events."
Although PP techniques are meant to provide a visual check, against which to assess the performance of the different probability distributions, they are one of the most important factors that can influence the analyst to make the wrong decision in selecting the most appropriate probability distribution, especially with the presence of outliers in the dataset.
The PP controversy already spans more than a century and the interpretation thereof differs from one researcher to another. Makkonen (2006) claimed that, without repeating the extensive and controversial discussions about PP formulas, many of the discussions presented in papers lacked a theoretical basis and that, consequently, a rather fatalistic attitude towards selecting a proper formula has emerged. He supported his conclusion concerning this apathetic viewpoint by providing three examples: Langbein (1960), cited in Makkonen (2006 p. 336), compared the choice of a PP to "... like taking a stand on a political question"; Benson (1962), cited in Makkonen (2006 p. 336), claimed that the selection of a PP "... cannot be made by comparing the principles on which each is based"; and Jordaan (2005), cited in Makkonen (2006 p. 336) commented on the PP that ". there appear to be almost as many opinions as there are statisticians."
Makkonen (2006) also cited Gumbel (1958) and Castillo (1988) to argue that order ranking and PP techniques have been rigorously analysed mathematically and, consequently, that the theoretical foundations are well known in principle. Makkonen (2006) pondered on the long and controversial history of the PP formulas and suggested that the many different types of probability papers are responsible for the lack of transformation of the mathematical theory into a correct and generally accepted practice.
Horton et al. (2001) applied the empirical Jenkinson's method (Eq. 1) to estimate cumulative probabilities to investigate changes in the incidence of extremes in temperatures. Folland and Anderson (2002) cited Beard (1943) as the source of this PP technique, which is widely referred to as the Jenkinson's method, most likely since Jenkinson used it extensively in the Flood Studies report (NERC, 1975a, 1975b).
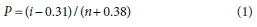
where P is the 'plotting probability' of the Ith order statistic and n is the sample size.
Folland and Anderson (2002), after testing the Jenkinson's method against four other widely used PP techniques, concluded that the Jenkinson's ranking method is likely to be satisfactory for consistently ranking time series of most climatological data, when changes of moderate extremes in the form of percentiles are calculated. Folland and Anderson (2002) also recommended that the Weibull PP, which they referred to as the "average ranking method", should not be used, since it produces estimates smaller than the estimates from the other methods at higher I-values (when data are ranked in ascending order).
Makkonen (2006) argued that the Jenkinson's method is based on a view that a natural estimate for the PP is the median of its probability density distribution. Subsequently, he claimed that the conclusion reached by Folland and Anderson (2002) on the Weibull formula is strange, since the Weibull PP (also citing Gumbel, 1958; Cook, 1982, 1985; Cook et al., 2003 in support) is generally used and may be considered as an essential part of the standard Gumbel extreme value method.
Cook (2011) drew attention to three claims from Makkonen (2006), namely; (i) that the Weibull estimator P = i/(n + 1) should be used exclusively to derive all statistical properties, including the annual recurrence interval (ARI) and PP; (ii) that the improvements, since 1939, in extreme value analysis methods were invalid; and (iii) that weather-related building codes and regulations should be updated, by re-estimating previous risk evaluations. Cook (2011) responded to point out that this should have provoked an immediate and urgent response, but that the only published response, in the Journal of Applied Meteorology and Climatology, has been some comments by De Haan (2007). Cook (2011) seems to agree with De Haan (2007) on most of his comments and found the issue raised about the purpose of extreme value analysis not ever being discussed particularly relevant. De Haan (2007 p. 396) concluded his concise comment with: "Once again, I do not mean to criticize the paper itself. I only want to cast some doubt on the claims made around the paper. Much research has been done recently on statistical methods for extremes. Since the 1980s the field has seen revolutionary changes. I refer the interested reader to the books by Embrechts et al. (1997), Coles (2001), and Beirlant et al. (2004). In short, the plotting-position issue is completely irrelevant to modern extreme value statistics". Still, the PP is considered invaluable to visually verify that the fitted distribution is an acceptable fit to the data.
In a follow-up paper Makkonen (2008) claimed in the abstract that the paper is intended to bring to an end the century-long controversial discussion on the PP. He then insisted that the Weibull PP should still be used by making the following concluding remark (p. 466): "The cumulative probability Pm of non exceedance of the mth value in n order ranked observations equals m/(n + 1). This result is unique and independent of the parent distribution. The fundamental purpose of the extreme value analysis is to estimate the cdf by order-ranked sample data, so that the plotting position should be considered not as an estimate, but to be equal to m/(n + 1). The numerous other proposed plotting formulas and methods are based on inappropriate assumptions and should be abandoned." (sic)
Makkonen's claims were challenged by several subsequent papers (Mehdi and Mehdi, 2011; Cook, 2012; Kim et al., 2012; Yahaya et al., 2012a, 2012b; Fuglem et al., 2013), which maintained that other plotting positions, developed by renowned statisticians, were just as valid.
Makkonen and Pajari (2014) and Makkonen et al. (2013) continued this dispute by again concluding with similar remarks to previous papers. For example, Makkonen et al. (2013 p. 929) claimed that: "Misleading random simulations, similar to those of Fuglem et al. (2013), have recently been presented by others (Harris, 2001; Mehdi and Mehdi, 2011, Cook, 2012; Yahaya et al., 2012a, 2012b; Kim et al., 2012). The results presented here show that their conclusions regarding the plotting methods are invalid as well."
Makkonen et al. (2013) again persisted in their conclusion that their theoretical analysis and random simulations indicated that the Weibull formula is the true rank probability and should be used as the unique PP irrespective of the underlying distribution.
From the above it became clear that:
• Scientists in the PP debate were only considering the issue from a theoretical perspective.
• The hydrologists seem to ignore the obvious reality that the analysts indeed only have a very small sample of the population to analyse. Consequently, the PP issue seems to demand a more practical approach, rather than a purely theoretical one.
• All existing PP techniques, although useful to some extent, can only provide crude estimates of probabilities of extreme events.
A critical review of existing plotting positions
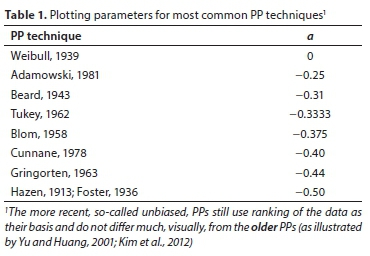
Most of the existing PPs available in literature can be expressed as:

where Ptis the 'plotting probability' of the Ith order statistic; n is the sample size and a is claimed to be an unbiased plotting parameter, determined 'to fit' different distributions.
Table 1 provides a list ofthe most widely used PPs (Cunnane, 1978; Adamowski, 1981), indicating the respective value of parameter a in each case.
The PP technique is summarised as follows:
• Arrange the given data series - in this case the AMS - in descending order.
• Assign an order number to each of the data points (termed as ranking of the data), starting at the highest flood peak with i = 1, to i = n for the lowest flood peak.
• Apply Eq. 2 to assign a probability value Pi to every flood peak. Piindicates the probability that the corresponding flood peak, Qi, will be exceeded.
Note: The above order of ranking is preferred, since it relates directly to an annual exceedance probability (AEP), which directly relates to risk. If the flood peak data are sorted in ascending order (noted in some references) the probability value assigned to a flood peak data point indicates probability of non-exceedance.
In Fig. 1 the AMS flood peaks at Woodstock Dam (V1R003) are used to highlight concerns associated with the current PPs, namely:
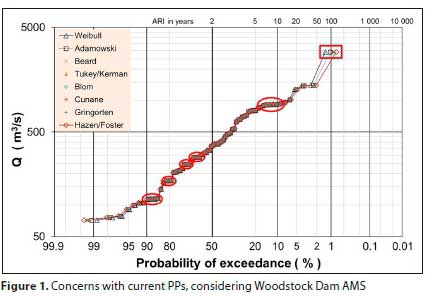
• Despite the century-long controversy around the different PP techniques, it would seem as if the outcomes from all PPs are, for practical purposes, the same.
• The 'ranked' PP (i.e. probability) assigned to an outlier (indicated by red rectangle on Fig. 1 is most probably incorrect and can result in the analyst not choosing the most appropriate theoretical probability distribution.
• Due to the ranking process, values in the dataset having the same, or very similar, magnitudes will be assigned different PPs (i.e. probabilities). This may distort the visual appearance of the PP to such an extent that it may complicate the choice of the most applicable distribution (indicated by red ellipses on Fig. 1).
In support of the observations from Fig. 1, the first 7 ranked positions for Woodstock Dam (74 valid flood peaks in record) for various PPs are compared in Table 2. From ranked position 4 there is already virtually no difference between the AEPs and associated ARIs for the different PPs.
It is evident that the current PP techniques can and should be improved, to provide more credible estimations of probabilities of extreme flood events.
An additional concern is that estimated PP probabilities are used as a benchmark against which goodness-of-fit' tests are performed to determine which distribution is 'a better fit' to the data - whereas it is quite possible that it might indicate the 'worst fit', especially if outliers are present in the record.
METHODOLOGY
This study is not about partaking in the many lengthy theoretical mathematical arguments as to why one PP is superior to the others. These theoretical arguments may very well be valid for a 'population' of flood peaks. The reality, however, is that available flood peak data records cannot necessarily be considered as representative samples of the population of AMS flood peaks - leaving the analyst with the challenge to attempt an as-good-as-possible analysis with relatively very short-duration samples (data records)of the population.
Klemes (1987) is rather cynical in his view on the science of hydrology and FFA, but he also made a very valid point when stating that: "... the driving force behind FFA is not a scientific discovery but a necessity to make a decision."
The reality is that a FFA should never be done without prudently considering all available data and information available, carefully - keeping in mind the relevant advice from Wheeler (2011): "This limitation on what we can obtain from a collection of data is inherent in the statistics themselves, and must be respected in our analysis of the data ... interpret your data in their context."
Considering the above, it was recognised that the PP issue demands a more pragmatic approach rather than a purely theoretical one.
Alternative approaches considered for PP technique
Various alternatives were considered in the development of a more practical PP approach, but it was obvious that introducing variables like catchment and rainfall characteristics would not be of benefit to solve the issues depicted in Fig. 1. Neither would the inclusion of basic statistical characteristics - like record lengths, steepness of flood peak distribution (or the 'probability-slope' between lowest and highest peaks) or magnitude of flood peaks -be able to solve these issues.
Wheeler (2011) cautioned against merely applying statistics in a probability model. He stated that the dataset should be homogeneous before statistical parameters, intended for a probability model, can be estimated sensibly. He considers it of paramount importance that one should identify suspect data and examine these for evidence of lack of homogeneity.
Homogeneity is an indication whether sample datasets are similar and representative of the population. The application of homogeneity tests in most other fields, like economic studies, demography and population studies, usually have the advantage of working with a well-established worldwide population. Unfortunately, in FFA the luxury of having a population does not (yet) exist. Furthermore, populations will most probably tend to be more site- or area-specific, rather than global. A practical suggestion would be to (visually) inspect PPs for a noticeable trend, mimicking a probable distribution, which possibly will be an indication that the data can be assumed to be homogeneous.
In the field of FFA, issues like low and high outliers, in relatively short data records, can cause a reasonably homogeneous dataset to appear completely non-homogeneous. Using statistics like skewness and kurtosis that depict the tails of a distribution presents a possible option to deal with the outlier issue.
Wheeler (2011), however, also expressed concerns on the use of skewness and kurtosis statistics: "For example, if we use 20 data to estimate the mean, and if we then wanted to also estimate the skewness with a similar precision, we would need to collect and use 120 data to estimate the skewness ... 480 data to estimate the kurtosis . regardless of how many data we have, we will always have much more uncertainty in the shape statistics than we will have in the location and dispersion statistics."
Wheeler (2011), coincidentally, provides a guideline of how to consider outliers in a dataset, by stating that the limitation on what can be obtained from a dataset is inherent in the statistics themselves, and should be respected in the analysis of the data.
Frost (2019) stated that, while there is no strict statistical rule or mathematical definition to identify outliers, guidelines exist through which possible outliers can be identified. He emphasised that: "Finding outliers depends on subject-area knowledge and an understanding of the data collection process." He described five methods, including: (i) sorting data, (ii) graphing data, (iii) using Z-scores, (iv) using the interquartile range, and (v) hypothesis tests, to identify outliers in datasets, noting the advantages and disadvantages of each. Frost (2019) indicated that the biggest disadvantage of the Z-score approach is that a high outlier in the dataset inflates the mean and standard deviation. Of course, if low and high outliers are present it will most probably have a bigger effect on the standard deviation than on the mean. Despite this, the Z-score approach provides a quantifiable value, comparable to the existing PP-values.
Considering the above, the Z-score statistic was selected to be used in this study. Since nearly 100% of the data will be within three standard deviations of the mean, data with a Z-score higher than 3 or lower than -3 can be considered to be outliers (Brownlee, 2018; Frost, 2019).
Research approach
Various scenarios for the development of a PP technique, which involve multiple linear regression analyses (MRA) of combinations of various Z-scores, were then investigated further to develop an improved PP. The Z-scores considered include the Z-score of the original (untransformed) AMS flood peaks (Zq), the Z-score of the log-transformed data (Zlogq) and the associated Z-score from one of the existing PPs. At the outset the Z-score for the Weibull PP (ZWeibull) was selected, since the equation is straightforward, is widely used and, amongst most of the common PPs, is most conservative towards risk. It is hypothesised that any of the other common PPs could have been used and the soundness of this assumption will be established under the results.
To synchronise the Z-scores determined from the AMS with that of the Weibull PP, the Z-scores for the Weibull PP probabilities were estimated by using the standard normal distribution - also referred to as the Z-distribution.
The PDF for the standard normal random variable, z, is given by:
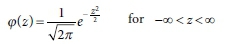
and the cumulative distribution function (CDF) of the standard normal distribution by:
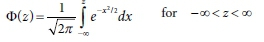
The independent and dependent variables used in the multiple linear regressions are defined in Table 3.
Three MRA scenarios were investigated, namely:
• MRA1, where independent variables 1 and 3 were considered
• MRA2, where independent variables 1 and 2 were considered
• MRA3, where independent variables 1, 2 and 3 were considered
Each MRA scenario contained three sequential regression attempts (referred to as a sequent) related to the dependent variable, which is depicted in Table 4.
The 3 MRA scenarios, each with 3 sequents, resulted in a total of 9 MRAs being carried out. The general equation, resulting from an MRA, can be depicted as follows:
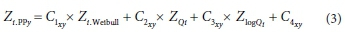
where x signifies a specific MRA-scenario and y the sequent in a specific MRA-scenario.
DATA
Only AMS flood peak data were considered in this research. It has been reported that the partial duration series (PDS) flood peak data approach does not really improve results, especially for an ARI higher than 10 years (Mkhandi et al., 2005; Karim et al., 2017). Srikanthan (2014) also concluded that, since the AMS gave the smallest bias in most cases, the use of AMS in FFA is preferred to PDS. The largest part of South Africa (SA) can also be considered as semi-arid to arid. Consequently, it is a rarity to experience more than one sizeable independent flood peak in any given year.
Data sources
Flow gauging sites in SA can either be water-level gauging sites in rivers (mostly weirs) or at dams. At weirs stage can be translated to a discharge (flow) through a relation between stage and discharge, referred to as a discharge curve/table (DT). At dams the recorded stage is used, with gauged discharges (overflows and releases) and a reservoir capacity table, to estimate inflows into the reservoir through the application of reservoir back-routing techniques. The term 'flow site' is to be used for weir and dam sites, henceforth, for ease of reference.
The following criteria were considered in choosing flow sites with reliable and verified data, for use in this study:
• Representative spread across the country
• Ensure flow diversity to avoid generating a database containing similar records - thus, sites were chosen from drier and wetter areas as well as ensuring a range from larger to smaller catchment areas (CA)
• Long, verified flow records - with minimum record lengths of 90 years, where possible (at first, considered record lengths for a design flood of ARI = 100 years, but no sites in the southern part of SA would have met this criterium - hence the lowering of the criterium to 90 years). Slightly shorter record lengths were used, to meet the above two criteria where applicable.
The chosen primary flow sites include 12 dam and 3 gauging weir sites, have a combined database of 1 556 years of AMS flood peaks, and are depicted in Table 5 with relevant metadata.
Three secondary sites, selected to independently illustrate some outcomes from the research results, are depicted in Table 6 with their relevant metadata.
The distribution of the chosen sites is depicted in Fig. 2.
Figure 2 (Criteria 1 and 2) and the metadata in the two tables (Criteria 2 and 3) confirm that the set criteria were adequately met.
RESULTS
In the first part of this section the proposed Z-scores are appraised, which is followed by the results of the ensuing MRAs. The study used different combinations of the following Z-scores: Zq, Zlogq and ZWeibull. For ease of reference, the combinations of the independent variables considered for the 3 MRA scenarios are:
• MRA1: independent variables Zq and ZWeibull
• MRA2: independent variables Zq and Zlogq
• MRA3, independent variables Zq, Zlogq and ZWeibull
The hypothesis that any of the common PPs, other than the Weibull, could also have been used was also explored and the conclusion is presented at the end of this section.
Z-score appraisal
In Fig. 3 the Z-scores for the AMS and log-transformed AMS are depicted, with the Z-scores of the Weibull PP, for all the primary sites.
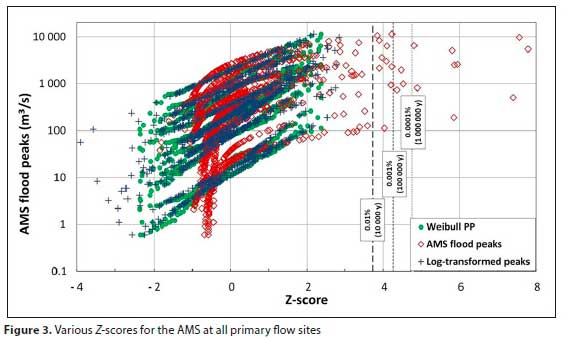
The Zq yields AEPs that were considered too liberal, in comparison to existing distributions. Several flood peaks have Z-scores higher than 3.719 (AEP < 0.01%; ARI > 10 000 years), and about 50% of these even have an AEP ofless than 0.0001% (ARI > 1 000 000 years).
Hence, Zlogq was also considered, although it tends to be very similar to the Z-scores of the existing PPs, in that outliers are not adequately addressed. The caution expressed by Wheeler (2011), about the practice of transformation of data that can hide the fact that data are not sufficiently homogeneous and consequently prevent the accurate treatment of problematic data, was considered - the solitary reason for considering the Zlogq was to determine if it could be used to curtail the liberal Zq values.
MRA results
The results of Sequent 3 for all three scenarios (i.e. MRA1.3, MRA2.3 and MRA3.3) are depicted in Fig. 4.
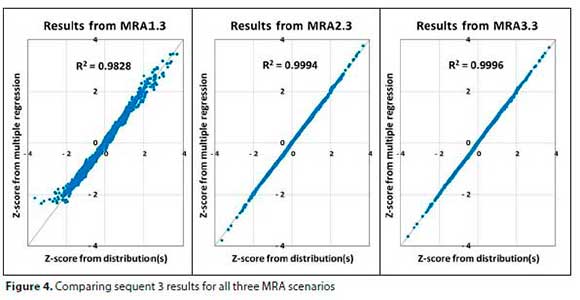
The MRA1 scenario produced the worst results of the three MRA-scenarios (MRA1.3: R2= 0.9828). The MRA2 and MRA3 scenarios produced fairly good results for all sequents, with the results of MRA3 somewhat better than that of MRA2 and only marginally better at Sequent 3; MRA2.3 (3rd sequent of MRA2) produced an R2 = 0.9994, whilst MRA3.3 produced an R2 = 0.9996.
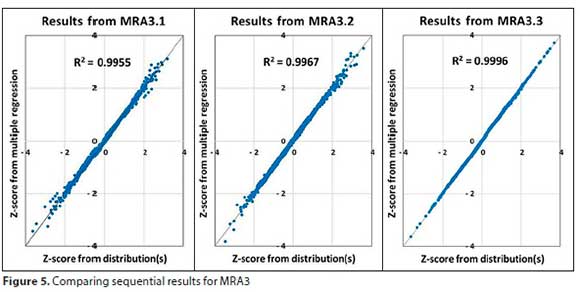
The result of MRA3.3 was accepted to determine the new PP. The results of the MRA3 scenario are shown in Table 7 and the improvement in results from Sequent 1 to Sequent 3 is depicted in Fig. 5.
Note: The proposed PP, containing a set of Z-scores, is named the Z-set PP, for ease of reference.
From Eq. 3 and Table 7 it follows that:
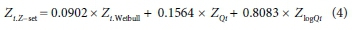
The Z-set PPs of the data points can now be determined from the corresponding ZiZ-set values by subtracting the related CDF of the standard normal distribution value from 1.
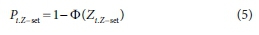
The process is illustrated in Table 8, using the five highest AMS flood peaks of Woodstock Dam (where Qave = 498 m3/s, S = 436 m3/s, logQave= 2.5605, Slog= 0.3542).
Results of PP-hypothesis
It was hypothesised that any of the existing PPs can be used in the MRA to obtain very similar results for the Zset PP. Since the Weibull and the Hazen represent the two extreme PPs, the same procedure was applied, using the Hazen PP. In Fig. 6 the results were compared, indicating that the choice of an existing PP had virtually no effect on the Z-set PP.
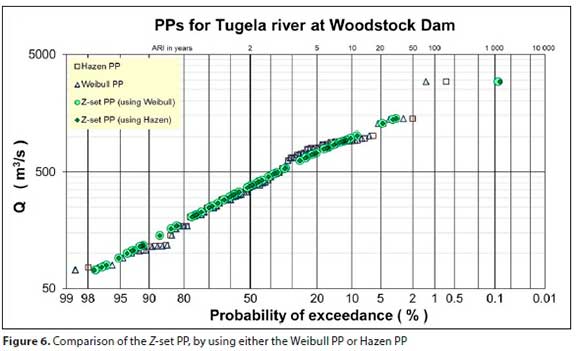
Note: In using the Hazen PP, the coefficients in Eq. 4 merely changed, respectively, to 0.0880, 0.1571 and 0.8082.
DISCUSSION
The effect of the Z-set PP on the identified concerns, illustrated in Fig. 1, is assessed. Subsequently the behaviour of the Z-set PP with different record lengths is analysed:
Impact on outliers and similar magnitude flood peaks
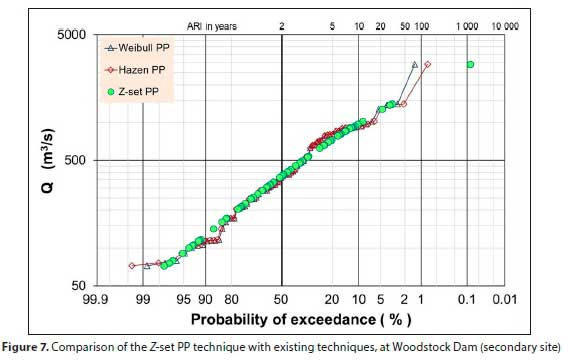
The AMS flood peaks of Woodstock Dam (a secondary site), used to illustrate concerns about the current PPs in Fig. 1, is shown in Fig. 7, where the proposed Z-set PP is depicted against existing PPs in use (only Weibull and Hazen, being the two extremes, are shown).
A similar illustration, at one of the primary flow sites with a longer record, is shown in Fig. 8.
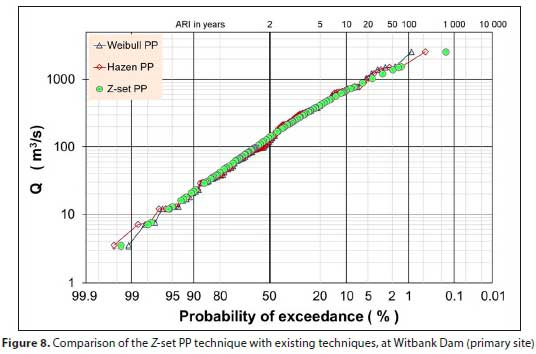
Figures 7 and 8 illustrate that the concerns raised, about the outliers and flood peaks of similar magnitude depicted in Fig. 1 and the accompanying discussion, have been addressed without adversely affecting the rest of the PPs.
Impact on record length
To illustrate the Z-set PP performance in relation to different record lengths, the Z-set PP was compared to the Weibull PP. The effect on existing outliers was still evident, but it illustrates the (unforeseen) added benefit of using the Z-set PP.
Three scenarios were considered, namely:
• An AMS where no obvious outlier was present
• An AMS where an outlier seemed to be present rather early in the record, but turned out to be just one of several higher flows as the record increased
• An AMS with a very high outlier occurring later in the record, staying a high outlier for the full record
Alexander (2005a, 2005b) concluded that the length of wet and dry sequences in SA typically varied between 6 to 8 years (on average 7 years). He also investigated a linkage with solar activity and concluded that a 21-year periodicity is evident. Therefore, different record lengths were considered from a relatively long record, starting with 21 years and increasing the consequent record lengths by 7 years, until the total record length is reached. To avoid excessive cluttering of the subsequent figures, only relevant record lengths, where a change in the appearance of the PPs can be observed, are shown in the figures.
The AMS at Clanwilliam Dam (a secondary flow site), with homogeneous distributed flood peak data, is used for illustration purposes for the first scenario. The site was chosen where the flood peaks are mainly caused by a single rainfall-causing system; in this case frontal rainfall. There were also no obvious outliers present in any considered record length. Figure 9 illustrates the relationship.
The following can be observed from Fig. 9:
• Z-set PP: There is effectively no difference in the PPs, regardless of record length, from 28 years onwards. A minor deviation was observed at the higher AEPs (> 50%) for a 21-year record, or shorter.
• Weibull PP: This is slightly inferior to Z-set PP. With outliers present in AMS, there is little difference between the two PPs, except that the Z-set PP trumps the Weibull PP in having a smoother appearance and remains effectively the same, regardless of record length.
• AEP-range is visually very similar for Z-set and Weibull.
• Data appear to be remarkably stationary and homogeneous.
In Fig. 10 the effect on record length, at a site with an outlier relatively early in the record (second scenario), is depicted (the outlier occurred within the first 21 years). The AMS at Kammanassie Dam (also a secondary flow site) is used for this example.
The following can be observed from Fig. 10:
• Z-set PP: There is effectively little difference in PPs for AEPs < 50%. Due to several low flows added after 56 years of record, two distinct groupings can be observed in the higher AEP range (> 50%) - PPs for 35 to 56 years are grouped and PPs for 70 to 106 years are grouped.
• Weibull PP appears more disorderly than the Z-set PP.
• The AEP-range is not the same for Z-set and Weibull, due to failure of the Weibull PP to deal effectively with outliers and higher flows.
• Data appear to be relatively stationary and homogeneous.
The effect that a very high outlier, occurring in year 61 (Jan. 1981), can have on record length is depicted in Fig. 11. The AMS at Floriskraal Dam (a primary flow site) is used as an example.
The following can be observed from Fig. 11:
• Z-set PP: PPs were grouped for 28 to 56-year record lengths; and again for 70 to 98-year record lengths. The split is caused by the high outlier in 1981 - Year 61 of the 98-year AMS.
• Weibull PP: The same groupings exist, but it is less visible since the PPs are much more scattered.
• Large difference in AEP-range between Weibull and Z-set, for record lengths > 70 y. It is due to the inability of existing PPs to make any provision for outliers.
• Data appear to be homogeneous.
Figures 9 to 11 illustrate that the Z-set PPs are reasonably similar for varying record lengths. This appears not to be the case if a relatively high outlier occurs somewhere in the record (in the example in Fig. 11, the outlier emanates from the devastating 'Laingsburg' 1981 flood event).
It is interesting to note that the ARI allocated to the 1981-event (Z-set PP), of around 4 000 years, is consistent with the dating of other palaeoflood evidence in the J-drainage region, of around 3 000 years ago (Van Bladeren 2007). Zawada (1994) observed that while palaeoflood evidence exists in the region for other rivers, no palaeoflood evidence could be obtained in that part of the Buffels River. He concluded that the 1981 flood most probably scoured any palaeoflood evidence and that no evidence exists for a flood event larger than the 1981 event in the Buffels River.
Boxplots were used to further illustrate the benefit of using the Z-set PP. To explain how the boxplots were generated, the FFA on Clanwilliam Dam is used as an example (see Table 9):
• An FFA was performed, to choose a suitable distribution, using the complete AMS record.
• Seven commonly used AEPs (50, 20, 10, 5, 2, 1 and 0.5%) were chosen with their corresponding Z-scores and flood peaks.
• Using various record lengths (28, 49, 70, and 84 years in this example), Z-scores for these matching flood peaks were determined - from both the Weibull- and Z-set PPs
• The record lengths were chosen in the same way as described earlier (see Fig. 9).
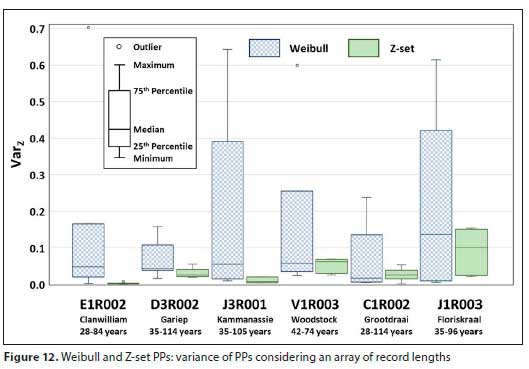
• For the first boxplot, the Z-score 'variance' (VarZ) is used as the average squared deviation from the expected Z-score of the applicable AEP. Thus VarZ of every applicable AEP was determined, for various record lengths - for example, from Table 9, for an AEP of 10% the VarZ for the Z-set PP is given by (values in next equations shaded in Table 9, for clarity):
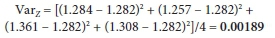
VarZ = [(1.284 - 1.282)2 + (1.257 - 1.282)2 + (1.361 - 1.282)2 + (1.308 - 1.282)2]/4 = 0.00189
The boxplot of the VarZ values across the AEP range is depicted in Fig. 12. For the second boxplot, the range of Z-scores (Zmax - Zmin) obtained from the different record lengths for each AEP were determined - for the same example:

The boxplot of the Zmax- Zmin values across the AEP-range is depicted in Fig. 13.
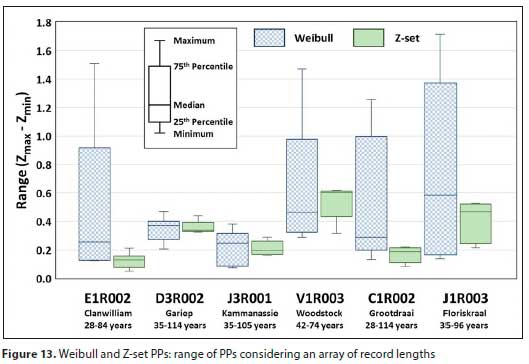
The advantage of using the Z-set PP is evident from the two boxplots that reveal a higher degree of consistency in the Z-set PPs, regardless of record length. This is especially true for sites with record lengths longer than around 35 to 40 years. Based on available flow stations used in this study, it appears as if the minimum record length required is longer in wetter areas and areas with more than one rainfall-causing system (V1R003). In typically drier areas, and areas with primarily one rainfall-causing system (E1R002), the minimum required record lengths can be as short as 28 years. This is a preliminary observation, which is by no means conclusive and should be investigated further.
CONCLUSIONS
The aim of this paper was to propose a more sensible PP against which distributions can be compared, to ensure the selection of the most appropriate distribution.
The practical approach, which includes some statistical parameters, produced promising results, leading to a new proposed PP (Z-set) with the following characteristics:
• The general trend ofthe revised PPs does not differ much from that of the existing PPs; notable differences can be observed where it appears smoother than the jagged appearance of the existing PPs
• Elimination of assigning noticeably different PPs (probabilities) to flood peaks of similar magnitude
• An improved and more realistic portrayal of outliers
• A much smoother PP, which mimics the shape of a distribution
• The PPs for different record lengths, depending on the relative magnitude of an outlier, do not differ much; hence, it may lead to more consistent choices of appropriate distributions
It is thus concluded that the proposed Z-set PP be used as a valuable addition to the existing set of decision-making tools for flood hydrologists/engineers performing flood frequency analyses.
REFERENCES
ADAMOWSKI K (1981) Plotting formula for flood frequency. Water Resour. Assoc. 17 (2) 197-202. https://doi.org/10.1111/j.1752-1688.1981.tb03922.x [ Links ]
ALEXANDER WJR (2005a) Linkages between solar activity and climatic responses. Energ. Environ. 16 (2) 239-253. https://doi.org/10.1260/0958305053749462 [ Links ]
ALEXANDER WJR (2005b) Development of a multi-year climate prediction model. Water SA. 31 (2) 209-218. https://doi.org/10.4314/wsa.v31i2.5204 [ Links ]
BEARD LR (1943) Statistical analysis in hydrology. Trans. Am. Soc. Civ. Eng. 108 (1) 1110-1121. https://doi.org/10.1061/TACEAT.0005568 [ Links ]
BEIRLANT J, GOEGEBEUR Y, TEUGELS J and SEGERS J (2004) Statistics of Extremes. John Wiley and Sons 490 pp. https://doi.org/10.1002/0470012382 [ Links ]
BENSON MA (1962) Plotting positions and economics of engineering planning. J. Hydraul. Div. 88 (6) 57-71. https://doi.org/10.1061/JYCEAJ.0000817 [ Links ]
BROWNLEE J (2018) How to use statistics to identify outliers in data. Machine learning mastery. URL: https://machinelearningmastery.com/how-to-use-statistics-to-identify-outliers-in-data/ (Accessed 8 May 2019). [ Links ]
CASTILLO E (1988) Extreme Value Theory in Engineering. Academic Press, San Diego. 389 pp. [ Links ]
COLES S (2001) An Introduction to Statistical Modeling of Extreme Values. Springer, London. 228 pp. https://doi.org/10.1007/978-1-4471-3675-0 [ Links ]
COOK N (2011) Comments on "Plotting Positions in Extreme Value Analysis". J. Appl. Meteorol. Climatol. 50 (1) 255-266. https://doi.org/10.1175/2010JAMC2316.1 [ Links ]
COOK NJ (1982) Towards better estimation of extreme winds. J. Wind Eng. Ind Aerodyn. 9 (3) 295-323. https://doi.org/10.1016/0167-6105(82)90021-6 [ Links ]
COOK NJ (1985) The Designer's Guide to Wind Loading of Building Structures. Butterworths, London. 371 pp. [ Links ]
COOK NJ (2012) Rebuttal of ''Problems in the extreme value analysis''. Struct. Saf. 34 (1) 418-423. https://doi.org/10.1016/j.strusafe.2011.08.002 [ Links ]
COOK NJ, HARRIS RI and WHITING R (2003) Extreme wind speeds in mixed climates revisited. J. Wind Eng. Ind. Aerodyn. 91 (3) 403422. https://doi.org/10.1016/S0167-6105(02)00397-5 [ Links ]
CUNNANE C (1978) Unbiased plotting positions - a review. J. Hydrol. 37 (3-4) 205-222. https://doi.org/10.1016/0022-1694(78)90017-3 [ Links ]
DE HAAN L (2007) Comments on "Plotting Positions in Extreme Value Analysis". J. Appl. Meteorol. Climatol. 46 (3) 396. https://doi.org/10.1175/JAM2471.1 [ Links ]
EMBRECHTS P, KLÜPPELBERG C and MIKOSCH T (1997) Modelling Extremal Events. Springer, Heidelberg. 648 pp. https://doi.org/10.1007/978-3-642-33483-2 [ Links ]
FOLLAND C and ANDERSON C (2002) Estimating changing extremes using empirical ranking methods. J. Clim. 15 2954-2960. https://doi.org/10.1175/1520-0442(2002)015<2954:ECEUER>2.0.CO;2 [ Links ]
FROST J (2019) 5 ways to find outliers in your data. Statistics by Jim. https://statisticsbyjim.com/basics/outliers/ (Accessed 8 May 2019) [ Links ]
FUGLEM M, PARR G and JORDAAN IJ (2013) Plotting positions for fitting distributions and extreme value analysis. Can. J. Civ. Eng. 40 (2) 130-139. https://doi.org/10.1139/cjce-2012-0427 [ Links ]
GERICKE OJ and DU PLESSIS JA (2012) Evaluation of the standard design flood method in selected basins in South Africa. J. S. Afr. Inst. Civ. Eng. 54 (2) 2-14. [ Links ]
GUMBEL EJ (1958) Statistics of Extremes. Columbia University Press, New York. 375 pp. [ Links ]
HARRIS RI (2001) The accuracy of design values predicted from extreme value analysis. J. Wind Eng. Ind. Aerodyn. 89 (2) 153-164. https://doi.org/10.1016/S0167-6105(00)00060-X [ Links ]
HAZEN A (1913) Storage to be provided in impounding reservoirs for municipal water supply. In: Proc. Am. Soc. Civ. Eng. 39 (9) 19432044. [ Links ]
HORTON EB, FOLLAND CK and PARKER DE (2001) The changing incidence of extremes in worldwide and central England temperatures to the end of the twentieth century. Clim. Change. 50 267-295. https://doi.org/10.1023/A:1010603629772 [ Links ]
JORDAAN I (2005) Decisions under Uncertainty: Probabilistic Analysis for Engineering Decisions. Cambridge University Press, Cambridge. 688 pp. https://doi.org/10.1017/CBO9780511804861 [ Links ]
KARIM F, HASAN M and MARVANEK S (2017) Evaluating annual maximum and partial duration series for estimating frequency of small magnitude floods. Water. 9 (7) article 481. https://doi.org/10.3390/w9070481 [ Links ]
KIM S, SHIN H, JOO K and HEO J-H (2012) Development of plotting position for the general extreme value distribution. J. Hydrol. 475 259-269. http://dx.doi.org/10.1016/j.jhydrol.2012.09.055 [ Links ]
KLEMES V (1987) Hydrological and engineering relevance of flood frequency analysis. In: Singh VP (ed.) Hydrologic Frequency Modeling. Springer, Dordrecht. https://doi.org/10.1007/978-94-009-3953-0_1 [ Links ]
LANGBEIN WB (1960) Plotting positions in frequency analysis. In: Flood-frequency Analyses, Manual of Hydrology: Part 3. Flood Flow Techniques, Geological Survey Water-Supply. Paper 1543-A 48-51. https://doi.org/10.3133/wsp1543A [ Links ]
MAKKONEN L (2006) Plotting positions in extreme value analysis. J. Appl. Meteorol. Climatol. 45 334-340. https://doi.org/10.1175/JAM2349.1 [ Links ]
MAKKONEN L (2008) Bringing closure to the plotting position controversy. Commun. Stat. Theory Meth. 37 (3) 460-467. https://doi.org/10.1080/03610920701653094 [ Links ]
MAKKONEN L and PAJARI M (2014) Defining sample quantiles by the true rank probability. J. Prob. Stat. 2014 Article ID 326579 6 pp. https://doi.org/10.1155/2014/326579 [ Links ]
MAKKONEN L, PAJARI M and TIKANMAKI M (2013) Discussion on "Plotting positions for fitting distributions and extreme value analysis". Can. J. Civ. Eng. 40 (9) 927-929. https://doi.org/10.1139/cjce-2013-0227 [ Links ]
MEHDI F and MEHDI J (2011) Determination of plotting position formula for the normal, log-normal, Pearson(III), log-Pearson(III) and Gumble distributional hypotheses using the probability plot correlation coefficient test. World Appl. Sci. J. 15 (8) 1181-1185. [ Links ]
MKHANDI S, OPERE AO and WILLEMS P (2005) Comparison between annual maximum and peaks over threshold models for flood frequency prediction. In: Proceedings of the International Conference on UNESCO FRIEND/Nile Project: Towards a better Cooperation, 12-15 November 2005, Sharm-El-Sheikh, Egypt. [ Links ]
NERC (Natural Environment Research Council) (1975a) Hydrological Studies, Vol. I, Flood Studies Report. Natural Environment Research Council, London, UK. [ Links ]
NERC (Natural Environment Research Council) (1975b) Meteorological Studies, Vol. II, Flood Studies Report. Natural Environment Research Council, London, UK. [ Links ]
SANRAL (South African National Roads Agency) (2013) Drainage Manual (6th edn). South African National Roads Agency Ltd, Pretoria. [ Links ]
SRIKANTHAN S (2014) A comparison of annual maximum and partial duration series in frequency analysis. In: Proceedings of the Hydrology and Water Resources Symposium, HWRS 2014. 374-381. [ Links ]
VAN BLADEREN D, ZAWADA PK and MAHLANGU D (2007) Statistical based regional flood frequency estimation study for South Africa using systematic, historical and palaeoflood data, pilot study - Catchment Management Area 15. WRC Report No. 1260/1/07. Water Research Commission, Pretoria. [ Links ]
WHEELER DJ (2011) Problems with Skewness and Kurtosis, Part Two: What do the shape parameters do? Quality Digest. https://www.qualitydigest.com/inside/quality-insider-article/problems-skewness-and-kurtosis-part-two.html (Accessed 4 August 2018). [ Links ]
WMO (World Meteorological Organization) (2009) Guide to Hydrological Practices, Volume II: Management of Water Resources and Applications of Hydrological Practices (6th edn). WMO-No. 168, 2009. [ Links ]
YAHAYA AS, NOR NM, JALI NRM, RAMLI NA, AHMAD F and UL-SAUFIE AZ (2012a) Determination of the probability plotting position for Type I extreme value distribution. J. Appl. Sci. 12 (14) 1501-1506. https://doi.org/10.3923/jas.2012.1501.1506 [ Links ]
YAHAYA AS, YEE CS, RAMLI NA and AHMAD F (2012b) Determination of the best probability plotting position for predicting parameters of the Weibull distribution. Int. J. Appl. Sci. Technol. 2 (3) 106-111. [ Links ]
YU GH and HUANG CC (2001) A Distribution Free Plotting Position. Stoch. Environ. Res. Risk Assess. 15 462-476. https://doi.org/10.1007/s004770100083 [ Links ]
ZAWADA PK (1994) Palaeoflood hydrology of the Buffels River, Laingsburg, South Africa: was the 1981 flood the largest? S. Afr. J. Geol. 97 (1) 21-32. https://journals.co.za/doi/10.10520/AJA10120750_807 [ Links ]
 Correspondence:
Correspondence:
D van der Spuy
Email: vds.danie@gmail.com
Received: 31 August 2020
Accepted: 28 March 2022














