Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.47 n.4 Pretoria Oct. 2021
http://dx.doi.org/10.17159/wsa/2021.v47.i4.3882
RESEARCH PAPER
Modelling daily net radiation of open water surfaces using land-based meteorological data
L MyeniI, II; MJ SavageI; AD ClulowI
IAgrometeorology, School of Agricultural, Earth and Environmental Sciences, University of KwaZulu-Natal, Pietermaritzburg, South Africa
IIAgricultural Research Council - Natural Resources and Engineering, Private Bag X79, Pretoria 0001, South Africa
ABSTRACT
Accurate quantification of net irradiance of open water (R„ water) is of paramount importance for the estimation of open water evaporation, which is critical for the efficient management of water resources. Alternatively, model estimates of Rn water are often used when quality measurements of Rn water are not readily available for the water storage of interest. A Daily Penman, Monteith, Equilibrium Temperature Hargreaves-Samani (DPMETHS) model has been developed for the estimation of Rn water using land-based meteorological data. The DPMETHS model is a spreadsheet-based iterative procedure that computes Rn water using daily land-based meteorological measurements of solar irradiance (Rs land), minimum and maximum air temperatures (7min and 7max), minimum and maximum relative humidity (RHmm and RHmax) and average wind speed (Uland). In this study, the DPMETHS model was evaluated using daily Rn water in-situ measurements acquired from 5 sites in both hemispheres, representing very different climatic conditions. Results showed reasonable model performance at all 5 sites, with the coefficient of determination (r2) values greater than 0.85 and root mean square error (RMSE) values ranging from 0.60 MJ-m-2 for Stratus Ocean (East Pacific Ocean) to 1.89 MJ-m-2 for Midmar Dam (South Africa). The results of this study suggested that the DPMETHS model can be reliably used to estimate Rn water for a wide range of climatic conditions. The performance of the DPMETHS model depends on the representativeness of the land-based meteorological data to the weather conditions above the open water surface. The DPMETHS model is user-friendly with minimal computational and data requirements that allows easy data handling and visual inspection.
Keywords: iteration, net radiometer, open water evaporation, spreadsheet, water-body temperature, water storage
INTRODUCTION
The high temporal and spatial variability of rainfall in semi-arid regions such as South Africa results in water resources being not uniformly distributed throughout the region (Mukheibir and Sparks, 2003). To ensure water security at various times of the year, water is stored in reservoirs (McJannet et al., 2013; Spears et al., 2016). However, significant amounts of water may be lost from open water storages to the atmosphere as water vapour, and this phenomenon is referred to as open water evaporation (Schulze, 2011; McJannet et al., 2008). Within this context, accurate quantification of open water evaporation is of paramount importance for efficient management of water resources, as water scarcity posed by climate change advances in the semi-arid of South Africa (Everson, 1999; Savage et al., 2004; Mengistu and Savage, 2010; Schulze, 2011; Savage et al., 2017).
Energy balance models are the most accurate methods for estimating open water evaporation, after the direct measurements, and are often used as a reference method against which other methods are compared (Finch, 2001). The energy balance techniques for estimating open water evaporation require either measurements or estimates of net irradiance of open water (Rnwater) (McJannet et al., 2008; Zheng, 2014). Measurements of Rnwater are monitored by net radiometers mounted above water storage. Net radiometers are expensive, requiring regular calibration and maintenance to attain accurate measurements (Dong et al., 1992; Kjaersgaard et al., 2007; Savage and Heilman, 2009; Carmona et al., 2017; Myeni et al., 2020). Consequently, Rnwater measurements are often not readily available for the water storage of interest, especially in developing countries (McJannet et al., 2013; Zheng, 2014). Alternatively, the lack of Rnwater data above water bodies could be solved by using models that estimate Rnwater from land-based meteorological data (McJannet et al., 2013; McMahon et al., 2013). The models used to estimate Rnwater from land-based meteorological data vary in their level of accuracy, complexity and data input requirements (Wang and Liang, 2009). McJannet et al. (2008) stressed that Rnwater should be determined from models that are universally applicable and relatively easy to utilise with minimal data input requirements, to improve the estimation of open water evaporation.
The modified Penman-Monteith model of McJannet et al. (2008) utilizes basic land-based meteorological data to estimate Rnwater required for the computation of open water evaporation. The modified Penman-Monteith model was implemented in Microsoft Excel by Savage et al. (2017) to incorporate the daily solar radiation estimation model introduced by Hargreaves and Samani (1982), which utilizes daily minimum and maximum air temperature to gap-fill missing solar irradiance data (the spreadsheet is available on request). The Daily Penman, Monteith, Equilibrium Temperature Hargreaves-Samani (DPMETHS) model of Savage et al. (2017) estimates daily open water evaporation from the land-based meteorological data. This model utilises the concept of equilibrium temperature to estimate water-body temperature of the water storage using an iterative procedure to obtain the wet-bulb temperature (Savage, 2017). The estimated water-body temperature is essential for computing outgoing infrared irradiance from the water surface Luwater.
For operational purposes, such as water resources management, irrigation management and hydrologic studies, where near-real time estimates of evaporation are needed, the DPMETHS model seems to be a promising model for estimating open water evaporation due to its user-friendliness and minimal data input requirements. However, rigorous validation of the DPMETHS model for different climatic conditions using an extended period of in-situ measurements collected from different sizes of water storages is required to improve the confidence of the estimates of the open water evaporation (Savage et al., 2017). Within this context, validation of the procedure to estimate Rnwaterusing the DPMETHS model is critical, since Rnwateris one of the key drivers of open water evaporation (McJannet et al., 2008). Consequently, poor estimation of Rnwaterusing the DPMETHS model could result in significant errors in estimating open water evaporation, leading to inefficient management of water resources. Therefore, the estimates of Rnwaterfrom the DPMETHS model need to be tested for suitability against in-situ measurements of Rnwatercollected from water storages from different climatic conditions before the model could be utilised with confidence to estimate Rnwaterfor open water evaporation. Therefore, the main aim of this study was to evaluate the performance of the DPMETHS model to estimate Rnwaterusing land-based meteorological data from a nearby weather station. In this study, the procedure of the DPMETHS model to estimate daily Rnwaterwas evaluated using daily Rnwater in-situ measurements acquired from 5 sites in both hemispheres, representing very different climatic conditions.
MATERIALS AND METHODS
Study site description
Data scarcity of Rnwateris the major challenge that hinders the evaluation of newly developed models for estimating Rnwaterin most countries (Wang and Liang, 2009; McMahon et al., 2013; Savage et al., 2017). Five sites that represent different climatic conditions were selected for the evaluation of the DPMETHS model. The site characteristics, record period and available daily data from each site are presented in Table 1. The choice of the duration of the Rnwater measurements at each site was based on the availability of quality radiative flux measurements using a 4-component net radiometer mounted above the open water surface, and the corresponding land-based daily meteorological data.
Description of the DPMETHS model for computing net irradiance for open water
The model description provided by McJannet et al. (2008) forms the basis of the daily time-step DPMETHS spreadsheet-implemented model of Savage et al. (2017). The DPMETHS model computes Rnwater(MJ m-2) using daily measurements of solar irradiance (Rsland, MJ-nr2), maximum and minimum air temperature (Ta, °C), minimum and maximum relative humidity (RH, %) and average wind speed (Uland, m-s-1) from a nearby land-based weather station. The estimates of Rnwaterare calculated from the solar irradiance reaching the water surface (Rswater) minus rRswaterbased on the reflection coefficient of the water surface (rwater) and net outgoing infrared irradiance (Id water - Lu water). The net infrared irradiance is calculated from Ta at 09:00, the estimated daily-average water temperature and a cloudiness factor, following the procedure of De Bruin (1982). The model assumes that the land-based meteorological data represent climatic conditions over open water surfaces and thus, Rsland= Rswater.
Then Rnwateris calculated from:
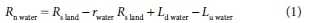
where rwater is approximately 0.08 (Finch and Hall, 2001) and Ldwater is calculated from:
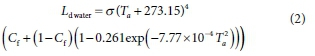
where a = 4.9 x 10-9 MJ-m2-K4 is the modified for daily time-scale Stefan-Boltzmann constant. The cloudiness factor (Cf) is determined using the procedure presented by Jegede et al. (2006):
if Rs land/Rs clear < 0.9, then:
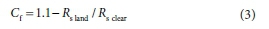
where:
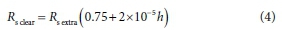
where Rsclear is the clear-sky solar irradiance (MJ-m2) and h is the site altitude (m). The extra-terrestrial solar irradiance (Rsextra) is calculated using a standard astronomical equation involving the day of the year, latitude, declination and sunset hour angle, following the procedure of Allen et al. (1998):
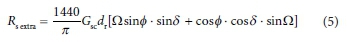
where Gsc is the solar constant (0.0820 MJ-m-2 mur-1), dris the inverse relative distance from the earth to the sun, ß is the sunset hour angle (rad), φ is the latitude (rad) and 8 is the solar declination (rad), where
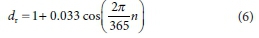
where n is the day of the year,
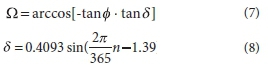
Otherwise, if Rs land/Rs dear> 0.9, then:
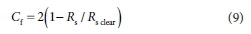
In Eq. 1 Lu water is given by:
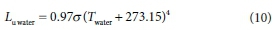
where Twater (°C) is the temperature of the water surface. The Luwater may be approximated using a Taylor series expansion at Ta as:
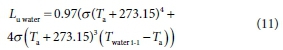
where the factor 0.97 corresponds to the emissivity of water (McJannet et al., 2008), Ta is the land-based daily averaged air temperature (°C) at a reference height of 2 m and Twater1-1 is the average water temperature of the previous day (°C).
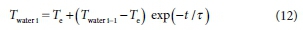
The daily-average water temperature on day i, Twateri(°C), is calculated from Twater a water-body time constant t (day) and an equilibrium temperature Te(°C):
The water-body time constant (t) is calculated based on the De Bruin (1982) method:
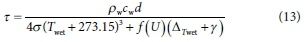
where pw is the density of water (kg-nr3), cw the specific heat capacity of water (0.004185 MJ-kg-1-K-1), and d the water depth (m), Twet the wet-bulb temperature, y the psychrometric constant, ΔTwet (kPa-°C-1) the slope of the saturation water vapour vs temperature relationship at the wet-bulb temperature and f(U) the wind function that is usually derived empirically for a particular location. The f( U) above water is computed using the Harbeck (1962) method:
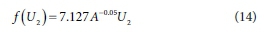
where f(U2) is the wind function for wind speed measured at a height of 2 m above the surface (MJ- m-2-kPa-1) and A is the surface area of the water storage (m2).
For open water, the net irradiance at the wet bulb, instead of the water-predicted temperature was used to avoid any calculations involving water depth. For daily open water evaporation, Penman (1948) used a wind speed function f(U2):
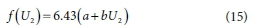
Penman (1948) originally used a = 1.0 and b = 0.54 s-m-1, but later revised a = 1.0 to a = 0.5 with b unchanged (Penman, 1956, 1963 cited by Jensen, 2010).
The equilibrium temperature, Te (°C), is calculated based on the equation of De Bruin (1982):
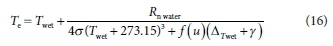
Data collection and processing
Daily measurements of meteorological variables such as Rsland, Ta, Tmin, Tmax, RHmin, R^ax, Umi, Twater, DEWPmta, DEWPmax, Rs water rwateRs watee Ld watee Lu water andRn water wereacquiredfromall 5 sites. The record period and available data from each site are presented in Table 1. Data from the American Falls, Lahontan and Stampede were from the Open Water Evaporation Network (OWEN) of the United States Bureau of Reclamation (http://owen.dri.edu). The detailed information about these OWEN stations and the measurement descriptions can be found at https://owen.dri.edu/site/sensors and were summarized by Spears et al. (2016). Data from Midmar Dam were collected as part of a South African Water Research Commission (WRC) research project (No. K5/2355). The detailed information about the Midmar Dam sites and the measurement descriptions were reported by Myeni (2016) and Savage et al. (2017). Data from the Stratus Ocean sites were acquired from Station 32ST0 (Stratus), owned and maintained by Woods Hole Oceanographic Institution (http://www.ndbc.noaa.gov/station_page.php?station=32ST0). The detailed information about the Stratus station and the measurement descriptions can be found at http://www.ndbc.noaa.gov/measdes.shtml.
All datasets underwent a data quality control routine to identify and remove all erroneous, suspicious and impossible values, following the procedure of Allen et al. (1998). Only good-quality datasets were used for the evaluation of the DPMETHS model. At the Stratus Ocean site where measurements of Rnwater were missing, a constant rwater value of 0.08 was used to estimate rwaterRswater from measurements of Rswater above the ocean surface. The estimates of Luwater from the ocean surface were computed from Twaterusing Eq. 10. The DEWPmin and DEWPmax were used to estimate RHmin and RHmax, respectively, using the procedure of Allen et al. (1998). Finally, the daily measurements of Rnwater were computed using Eq. 1, replacing Rsland with Rswater only at the Stratus Ocean site due to the lack of nearby measurements of Rsland.
Data analysis
The root mean square error (RMSE, MJ-mr2), mean bias error (MBE, MJ-mr2) and index of agreement (d) were used to evaluate the performance of the DPMETHS model estimates against daily measurements of Rnwater and were calculated following the procedure of Willmott et al. (1985) as:
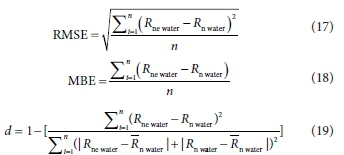
where Rnewater (MJ-mr2) is the estimated net irradiance of open water, Rnwater is the measured net irradiance of open water, Rnwater is the mean of Rnwater and n is the number of observations. Additionally, a linear regression between Rnewater and Rnwater values was calculated as:
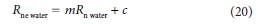
where m is the slope and c (MJ-m2) is the y-intercept. The coefficient of determination (r2) was used as a measure of precision. Based on these statistics, RMSE, MBE and c values approaching zero whilst d, r2and m values approaching 1 indicate the best model performances (Willmott et al., 1985).
RESULTS AND DISCUSSION
Weather conditions during the study period at all 5 sites
Newly developed models to estimate Rnwater from land-based meteorological data still require evaluation against in-situ measurements collected over a wide range of climatic conditions before they can be used with confidence. The meteorological data used for model evaluation illustrated a wide range of climatic conditions which had implications for the further interpretation of the results (Table 2).
Evaluation of the DPMETHS model at all 5 sites
To evaluate the performance of the DPMETHS model, comparisons were made between the daily estimates of Rnwaterand measurements of Rnwaterat all 5 sites. The relationships between estimated net irradiance (Rnewater) and measured net irradiance (Rnwater) were reasonable at all sites (Fig. 1; Table 3).
Performance of the DPMETHS model at all 5 sites
The correlation between Rnwaterand Rnewaterindicated a statistically significant relationship, with r2 values ranging from 0.85 for Midmar Dam to 0.96 for the Stampede site. Furthermore, the results showed that the DPMETHS model over-estimated Rnwater for all sites, with c values ranging from 0.74 MJ-m2 for Stampede to 3.02 MJ-m-2 for the Stratus Ocean site. These small values of c indicate the reasonable performance of the DPMETHS model for all 5 sites. Furthermore, d-values ranging from 0.87 for Stratus Ocean to 0.97 for Midmar Dam indicated reasonable similarities between Rmwater and Rn water fluxes for all sites.
The relationship between Rnewaterpredicted from the DPMETHS model and Rnwaterwas reasonable at all 5 sites, with RMSE values ranging from 0.60 MJ-m-2 for Stratus Ocean to 1.89 MJ-m-2 for Midmar Dam. The MBE values ranged from 0.36 MJ-m-2 for Stratus Ocean to 3.56 MJ-m-2 for Midmar Dam indicating that the DPMETHS model slightly over-estimated Rnwater for all sites. The greater over-estimation of Rnwater was observed at Midmar Dam, while an improved model performance (low RMSE values) was observed at Stratus Ocean as a result of the differences between Uwater and Uland which was used in the DPMETHS model as an input. Myeni (2016) reported that Uwater was always greater than Uland at Midmar Dam due to the open fetch on the water-based station compared to the land-based station which was closer to buildings and trees. The smoother surface of open water compared to land could have resulted in greater Uwater than Uland at Midmar Dam (Finch and Hall, 2001). The higher Uwater than expected could have resulted in surface cooling and decreased Twater (Alcântara et al., 2010). Consequently, the DPMETHS model over-estimated Rnwater due to under-estimations of Luwater. These findings suggested that using land-based meteorological data that do not represent weather conditions above open water surfaces could result in significant errors in Rnewater predicted from the DPMETHS model. Thus, it is recommended that the land-based meteorological data should be acquired with caution from a nearby weather station that represents the prevailing weather conditions above water storage of interest (Everson, 1999).
Applicability and limitations of the DPMETHS model
The DPMETHS model, a daily model, uses the daily-averaged Uland as an input and, therefore, this model does not explicitly account for night-time Rnwater which is dominated by Luwaterthat is directly governed by Twater. For example, Savage et al. (2017) reported that Uwater was a maximum during night-time and minimal early in the morning at Midmar Dam. Consequently, higher Uwater at nighttime than expected could result in surface cooling and decreased Twater. Consequently, the DPMETHS model is likely to overestimate Rnwater due to under-simulations of Luwater during clear and windy days. Furthermore, some of the discrepancies between Rnwater and Rnewater could be attributed to the poor estimation of Ldwater within the DPMETHS model, since this model only estimates the cloud fraction with no optical properties. However, whether the presence of clouds will have a net cooling or warming effect at the water surface depends on the cloud's optical properties such as the cloud's altitude, its size, and the make-up of the particles that form the cloud (Key et al., 1996).
The findings of this study indicate that the performance of the DPMETHS model depends on the representativeness of the land-based daily meteorological data to the weather conditions above the open water surface. Therefore, future research on measuring and modelling of Rnwater for the estimation of open water evaporation purposes should be cautious of the possible contrasts of weather conditions between land and water surfaces. Despite the discrepancies between Rnwaterand Rnewater, the findings of this study indicated that the DPMETHS model can be reliably used to estimate Rnwater for estimating open water evaporation over a wide range of climatic conditions. The DPMETHS model is a promising and user-friendly model for estimating Rnwater for the estimation of open water evaporation at high resolution with minimal land-based meteorological data that are often readily available from a standard weather station. Furthermore, the DPMETHS model uses universally applicable scientific theories and assumptions to estimate daily Rnwatrraccurately. The spreadsheet-based iterative procedure of the DPMETHS model evaluated in this study allows easy data handling and visual inspection.
CONCLUSIONS
The DPMETHS model to estimate daily Rnwaterwas evaluated using daily Rnwatrrin-situ measurements acquired from 5 sites, representing different climatic conditions.
The DPMETHS model reliably estimates Rnwater for the estimation of open water evaporation over a wide range of climatic conditions. Major discrepancies between Rnwater and Rnewater were attributed to the use of the land-based meteorological data that do not represent weather conditions over open water surfaces. Therefore, it is recommended that the land-based weather stations should be selected with caution, such that they represent the weather conditions above water storage of interest.
The spreadsheet-based iterative procedure ofthe DPMETHS model to estimate daily Rnwater using minimal land-based meteorological data is user-friendly, with minimal computational requirements, and is quick and reliable. It also allows easy data handling and visual inspection. One of the limitations of the DPMETHS model is that the model utilizes the daily meteorological data which might not be a true representation of climatic conditions for the entire day, since most of the weather variables had a wide range of diurnal variability. Therefore, a sub-daily version of the DPMETHS model is recommended for improved estimation of Rnwater for open water evaporation.
AUTHOR CONTRIBUTIONS
Conceptualization - L Myeni, MJ Savage and AD Clulow; methodology - L Myeni and MJ Savage; data analysis - L Myeni; original draft preparation and writing - L Myeni L; review and editing - L Myeni, MJ Savage and AD Clulow; supervision - MJ Savage and AD Clulow.
ACKNOWLEDGMENTS
Financial support from the Water Research Commission (South Africa) as part of project K5/2355, University of KwaZulu-Natal (UKZN) and the National Research Foundation is gratefully acknowledged. We also gratefully acknowledge Ezemvelo KwaZulu-Natal Wildlife, and the South African Department of Water and Sanitation for use of facilities at Midmar Dam. The United States Bureau of Reclamation (http://owen.dri.edu), Water Research Commission (South Africa) and the Woods Hole Oceanographic Institution (http://www.ndbc.noaa.gov) are gratefully acknowledged for the provision of data. The technical support from Mr Jonathan Pasi (University of KwaZulu-Natal) is gratefully acknowledged.
REFERENCES
ALCÂNTARA EH, STECH JL, LORENZZETTI JA, BONNET MP, CASAMITJANA X, ASSIREU AT and DE MORAES NOVO EML (2010) Remote sensing of water surface temperature and heat flux over a tropical hydroelectric reservoir. Remote Sens. Environ. 114 (11) 2651-2665. https://doi.org/10.1016/j.rse.2010.06.002 [ Links ]
ALLEN RG, PEREIRA LS, RAES D and SMITH M (1998) Crop evapotranspiration - Guidelines for computing crop water requirements. FAO Irrigation and Drainage Paper 56. FAO, Rome. [ Links ]
CARMONA F, RIVAS R and KRUSE E (2017) Estimating daily net radiation in the FAO Penman-Monteith method. Theor. Appl. Climatol. 129 (1-2) 89-95. https://doi.org/10.1007/s00704-016-1761-6 [ Links ]
DE BRUIN HAR (1982) Temperature and energy balance of a water reservoir determined from standard weather data of a land station. J. Hydrol. 59 (3-4) 261-274. https://doi.org/10.1016/0022-1694(82)90091-9 [ Links ]
DONG A, GRATTAN SR, CARROLL JJ and PRASHAR CRK (1992) Estimation of daytime net radiation over well-watered grass. J. Irrig. Drain. Eng. 118 (3) 466-479. https://doi.org/10.1061/(ASCE)0733-9437(1992)118:3(466) [ Links ]
EVERSON CS (1999) Evaporation from the Orange River: quantifying open water resources. WRC Report No. 383/1/99. Water Research Commission, Pretoria. [ Links ]
FINCH JW (2001) A comparison between measured and modelled open water evaporation from a reservoir in south-east England. Hydrol. Process. 15 (14) 2771-2778. https://doi.org/10.1002/hyp.267 [ Links ]
FINCH JW and HALL RL (2001) Estimation of open water evaporation: A review of methods. Environment Agency Bristol, UK. URL: https://publications.csiro.au/rpr/download?pid=procite:0921ff52-a841-4574-b599-5f28a8716783&dsid=DS1 (Accessed 10 February 2019). [ Links ]
HARBECK GE (1962) A practical field technique for measuring reservoir evaporation utilizing mass-transfer theory. Volume 272. US Government Printing Office. URL: https://pubs.usgs.gov/pp/0272e/report.pdf (Accessed 17 August 2019). [ Links ]
HARGREAVES GH and SAMANI ZA (1982) Estimating potential evapotranspiration. J. Irrig. Drain. Div. 108 (3) 225-230. https://doi.org/10.1061/JRCEA4.0001390 [ Links ]
JEGEDE OO, OGOLO EO and AREGBESOLA TO (2006) Estimating net radiation using routine meteorological data at a tropical location in Nigeria. Int. J. Sustainable Energ. 25 (2) 107-115. https://doi.org/10.1080/14786450600593261 [ Links ]
JENSEN ME (2010) Estimating evaporation from water surfaces. In: CSU/ARS Evapotranspiration Workshop, Fort Collins, CO. URL: https://coagmet.colostate.edu/ET_Workshop/ET_Jensen/ET_water_surf.pdf (Accessed 13 August 2019). [ Links ]
KEY JR, SILCOX RA and STONE RS (1996) Evaluation of surface radiative flux parameterizations for use in sea ice models. J. Geophys. Res. Oceans. 101 (C2) 3839-3849. https://doi.org/10.1029/95JC03600 [ Links ]
KJAERSGAARD JH, CUENCA RH, PLAUBORG FL and HANSEN S (2007) Long-term comparisons of net radiation calculation schemes. Boundary-Layer Meteorol. 123 (3) 417-431. https://doi.org/10.1007/s10546-006-9151-8 [ Links ]
MCJANNET DL, COOK FJ and BURN S (2013) Comparison of techniques for estimating evaporation from an irrigation water storage. Water Resour. Res. 49 (3) 1415-1428. https://doi.org/10.1002/wrcr.20125 [ Links ]
MCJANNET DL, WEBSTER IT, STENSON MP and SHERMAN BS (2008) Estimating open water evaporation for the Murray-Darling Basin CSIRO: Water for a Healthy Country National Research Flagship. https://publications.csiro.au/rpr/download?pid=procite:0921ff52-a841-4574-b599-5f28a8716783&dsid=DS1 (Accessed 13 February 2019). [ Links ]
MCMAHON TA, PEEL MC, LOWE L, SRIKANTHAN R and MCVICAR TR (2013) Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: A pragmatic synthesis. Hydrol. Earth Syst. Sci. 17 (4). https://doi.org/10.5194/hess-17-1331-2013 [ Links ]
MENGISTU MG and SAVAGE MJ (2010) Open water evaporation estimation for a small shallow reservoir in winter using surface renewal. J. Hydrol. 380 (1-2) 27-35. https://doi.org/10.1016/j.jhydrol.2009.10.014 [ Links ]
MUKHEIBIR P and SPARKS D (2003) Water resource management and climate change in South Africa: Visions, driving factors and sustainable development indicators. Report for Phase I of the Sustainable Development and Climate Change project. Energy and Development Research Centre (EDRC), University of Cape Town. URL: http://idprc.org/wp-content/uploads/2015/08/Water_resource_management-in-Southern-Africa.pdf (Accessed 23 February 2019). [ Links ]
MYENI L (2016) The radiation balance of Midmar Dam in KwaZulu-Natal, South Africa. 2016. MSc. dissertation, University of KwaZulu-Natal, Pietermaritzburg. URL: https://researchspace.ukzn.ac.za/handle/10413/14685 (Accessed 23 February 2019). [ Links ]
MYENI L, MOELETSI ME and CLULOW AD (2020) Assessment of three models for estimating daily net radiation in southern Africa. Agric. Water Manage. 229 105951. https://doi.org/10.1016/j.agwat.2019.105951 [ Links ]
PENMAN HL (1948) Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. 193 (1032) 120-145. https://doi.org/10.1098/rspa.1948.0037 [ Links ]
PENMAN HL (1956) Evaporation: an introductory survey. Neth. J. Agric. Sci. 4 (1) 9-29. https://doi.org/10.18174/njas.v4i1.17768 [ Links ]
PENMAN HL (1963) Vegetation and Hydrology Tech. Comm. No 53. Commonwealth Bureau of Soils, Harpenden, England. 125 pp. [ Links ]
SAVAGE MJ (2017) Estimation of grass reference evaporation and sensible heat flux using surface renewal and Monin-Obukhov similarity theory: A simple implementation of an iterative method. J. Hydrol. 547 742-754. https://doi.org/10.1016/j.jhydrol.2017.02.043 [ Links ]
SAVAGE MJ, EVERSON CS, ODHIAMBO GO, MENGISTU MG and JARMAIN C (2004) Theory and practice of evaporation measurement, with special focus on surface layer scintillometry as an operational tool for the estimation of spatially averaged evaporation. WRC Report No. K1335/1. Water Research Commission, Pretoria. [ Links ]
SAVAGE MJ and HEILMAN JL (2009) Infrared calibration of net radiometers and infrared thermometers. Agric. For. Meteorol. 149 (8) 1279-1293. https://doi.org/10.1016/j.agrformet.2009.02.013 [ Links ]
SAVAGE MJ, PASI JM, MYENI L and CLULOW AD (2017) Open water evaporation measurement using micrometeorological methods. WRC Report No. K5/2335, Water Research Commission, Pretoria. South Africa. URL: http://www.scli.org.za/wp-content/uploads/2013/12/Final-K5_2355-Savage-Open-water-evaporation_061216c-high-quality.pdf (Accessed 14 February 2019). [ Links ]
SCHULZE RE (2011) Approaches towards practical adaptive management options for selected water-related sectors in South Africa in a context of climate change. Water SA. 37 (5) 621-646. https://doi.org/10.4314/wsa.v37i5.1 [ Links ]
SPEARS M, HUNTINGTON J and GANGPADHYAY S (2016) Improving reservoir evaporation estimates. URL: https://www.usbr.gov/research/projects/detail.cfm?id=7662 (Accessed 14 May 2019). [ Links ]
WANG K and LIANG S (2009) Estimation of daytime net radiation from shortwave radiation measurements and meteorological observations. J. Appl. Meteorol. Climatol. 48 (3) 634-643. https://doi.org/10.1175/2008JAMC1959.1 [ Links ]
WILLMOTT CJ, ACKLESON SG, DAVIS RE, FEDDEMA JJ, KLINK KM, LEGATES DR, O'DONNELL J and ROWE CM (1985) Statistics for the evaluation and comparison ofmodels. J. Geophys. Res. Oceans. 90 (C5) 8995-9005. https://doi.org/10.1029/JC090iC05p08995 [ Links ]
ZHENG D (2014) Estimating water balance components of lakes and reservoirs using various open access satellite databases. PhD thesis, Delft University of Technology, The Netherlands. URL: https://repository.tudelft.nl/islandora/object/uuid%3A14f294e3-d821-4236-a7bf-eb808f0f1b62 (Accessed 18 June 2019). [ Links ]
 Correspondence:
Correspondence:
L Myeni
Email: lindomyeni@gmail.com
Received: 25 January 2021
Accepted: 30 September 2021














