Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Water SA
versión On-line ISSN 1816-7950
versión impresa ISSN 0378-4738
Water SA vol.47 no.3 Pretoria jul. 2021
http://dx.doi.org/10.17159/wsa/2021.v47.i3.11858
RESEARCH PAPER
Integration of complete elemental mass-balanced stoichiometry and aqueous-phase chemistry for bioprocess modelling of liquid and solid waste treatment systems − Part 2: Bioprocess stoichiometry
CJ BrouckaertI; GA EkamaII; BM BrouckaertI; DS IkumiII
IWater, Sanitation and Health Research and Development Centre, School of Chemical Engineering, University of KwaZulu-Natal, Berea, Durban, KwaZulu-Natal, South Africa
IIWater Research Group, Dept of Civil Engineering, University of Cape Town, Rondebosch, 7700, South Africa
ABSTRACT
Bioprocesses interact with the aqueous environment in which they take place. Integrated bioprocess and three-phase (aqueous-gas-solid) multiple strong and weak acid/base system models are currently being developed for a range of wastewater treatment applications including anaerobic digestion, biological sulphate reduction, autotrophic denitrification, biological desulphurization and plant-wide water and resource recovery facilities. In order to model, measure and control such integrated systems, a thorough understanding of the interactions between the bioprocesses and aqueous phase multiple strong and weak acid/bases are required. In the first of this series of five papers, the generalized procedure for deriving bioprocess stoichiometric equations was explained. This second paper presents the stoichiometric equations for the major biological processes and shows how their structure can be analysed to provide insight into how bioprocesses interact with the aqueous environment. Such insight is essential for confident, effective and reliable use of model development protocols and algorithms. It shows that the composite parameters, total oxygen demand (TOD, electron donating capacity) and alkalinity (proton accepting capacity), are conserved in bioprocess stoichiometry and their changes in the aqueous phase can be calculated from the bioprocess components. In the third paper, the measurement of the organics composition is presented. The link between the modelling and measurement frameworks of the aqueous phase, which uses the composite parameter alkalinity, is described in the fourth paper. Aqueous ionic speciation modelling is described in detail in the fifth.
Keywords: bioprocess modelling; electron donors and acceptors; bioprocess stoichiometry; full element mass balancing; mathematical modelling; wastewater treatment
INTRODUCTION
A generalized approach to deriving bioprocess stoichiometry was presented in Part 1 of this series (Brouckaert et al., 2021). Integrating the bioprocess stoichiometry with aqueous phase mixed weak and strong acid/base chemistry for pH prediction is necessary because some bioprocesses or combinations of bioprocesses have a strong influence and/or dependence on pH. Examples of technologically relevant bioprocesses, where accurate pH prediction is important, include methanogenic anaerobic digestion (AD) of (i) high strength low nitrogen (N) industrial organics wastewater which requires alkalinity addition to maintain a stable AD pH above 7 (Van Zyl et al., 2008), (ii) co-digestion of sewage sludge and high strength variable N organics such as whey, vinasse or food waste for energy generation, and (iii) co-digestion of sewage primary sludge and phosphorus (P) rich waste activated sludge at biological N and P removal plants in which significant mineral precipitation can take place (Van Rensburg et al., 2003; Harding et al., 2011). The expression of the stoichiometric balances in terms of a linearly independent set of equilibrium speciation model components, as advocated in Part 1 (Brouckaert et al., 2021), results in a compact and flexible formulation which can be conveniently integrated with speciation models in both steady-state and dynamic models. However, the bioprocess stoichiometric balances derived in this way provide little insight into the weak acid/base chemistry that has an important role in governing the overall system behaviour.
The purpose of this paper, Part 2, is to take a deeper look at the stoichiometry of the major bioprocesses included in wastewater treatment models, as well as their interactions with the multiple strong and weak acid/base systems. Part 2 therefore will contribute the following:
• Derivation of the major bioprocess stoichiometry using the ionic components introduced in Part 1 (Brouckaert et al., 2021).
• Derivation of empirical formulae for complex organic and inorganic components in terms of their carbon (C), hydrogen (H), oxygen (O), nitrogen (N), phosphorus (P), sulphur (S) and charge (ch) content.
• Demonstrating how an understanding of the weak acid/base chemistry can be used to construct a simplified speciation model that is appropriate for some steady-state bioprocess models.
• Exploring the application of the general principles discussed to two major bioprocesses typically included in water resource and recovery facility (WRRF) models, i.e., methanogenesis and sulphidogenesis.
Parts 3, 4 and 5 will be published in later issues of Water SA.
In this paper, the mass-balanced stoichiometry of bioprocess models including P, S and charge, with some of their associated bioprocesses, are derived with the objectives of: (i) demonstrating the general principles of integrated bioprocess and aqueous phase modelling; and (ii) deriving the complete elemental CHONPS, charge and chemical oxygen demand (COD) mass-balanced stoichiometry for some bio-systems, based on the S cycle, such as BSR in acid mine drainage (Poinapen and Ekama, 2010b), the sulphate reduction autotrophic denitrification nitrification integrated system (SANI) process for saline sewage treatment (Lu et al., 2012), leachate treatment and anaerobic and intermittently aerated landfill treatment (Raga et al., 2011) and co-treatment of simplified wet flue gas desulphurization wastewater (Qian et al., 2013, 2015). The procedure is general, and can be applied to any bioprocess, including those not considered in this paper.
BIOPROCESS STOICHIOMETRY AND EXCHANGED ELECTRONS
As noted in Part 1 (Brouckaert et al., 2021), the mass-balanced stoichiometry for bioprocesses can be derived from the procedure of electron (e−) balance of McCarty (1975). This procedure was advanced by Gujer and Larsen (1995) and Takács and Vanrolleghem (2006), applied to steady-state models by Ekama (2009) and generalized for WRRF models by Grau et al. (2007). This series of papers extends the methodology by adding S and charge and shows the intimate connection between the bioprocesses and the aqueous phase mixed strong and weak acid/base systems within which they function for both dynamic and steady-state plant-wide WRRF models. This brings the aqueous phase behaviour and pH calculation in bioprocess models from the background to equal importance with the bioprocesses.
The primary purpose of biological WRRFs is usually to reduce the COD of the waste, by breaking down complex organic compounds and/or inorganic pollutants such as ammonia, sulphide, sulphite or thiosulphate, into simpler benign or re-usable molecules and ions, such as CO2, H2O, CH4, N2, SO42- or HS-. Synthesis and maintenance of the active biomass, required to mediate these bioprocesses, also consume some of the influent COD and nutrients. The excess biomass produced is typically separated into a concentrated sludge, which is further reduced in volume and COD content by digestion. All of these biological transformations involve reduction-oxidation (redox) reactions and the key prior system knowledge, required to construct the appropriate bio-chemical stoichiometric balances, concerns which electron donors and electron acceptors are involved in which transformations under which operating conditions, and what the products of these reactions are.
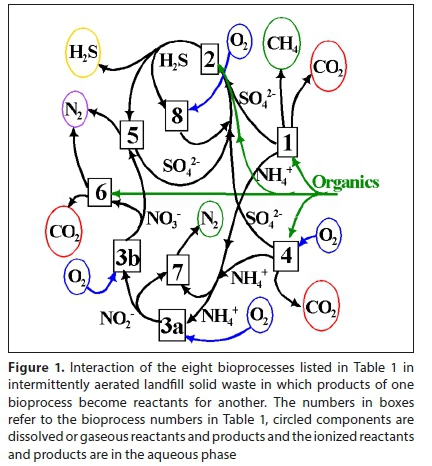
Eight common bioprocesses can take place under anaerobic, anoxic and aerobic conditions, such as in activated sludge, BSR, AD and intermittently aerated (partially aerobic) landfill systems. The electron donors and acceptors for these eight bioprocesses are listed in Table 1. The electron (e−) donor is the substrate for growth of a particular organism mediating a particular bioprocess. The interaction of these bioprocesses in intermittently aerated landfill waste (Raga et al., 2011) is shown in Fig. 1.
To illustrate the procedure of formulating biological process stoichiometry, consider the oxidation of a generic organic or inorganic component CxHyOzNaPbScch by O2 under conditions such that the resulting set of reactants and products include CO32−, NO3−, PO43-, SO42-, H+ and H2O, which are the products of C, N, P, and S. These are products of aerobic heterotrophic growth and nitrification (combined Bioprocess 3 and 4 in Table 1). Following the methodology presented in Part 1 (Brouckaert et al., 2021), the reaction equation is derived from the CHONPS element and charge balances.
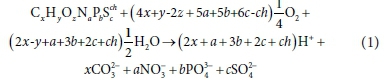
The term (4x + y - 2z + 5a + 5b + 6c - ch) represents the exchanged electrons (γs, e−/mol donor) (Part 1, Brouckaert et al., 2021), for the selected set of electron (e−) donor and acceptor reactants and products, i.e:
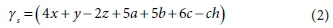
So Eq. 1 becomes:
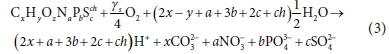
Equations 1 and 3 are given in arrow notation with reactants on the left-hand side (LHS) and products on the right-hand side (RHS) of the arrow. This notation conveys the idea that a stoichiometric equation represents a directional vector of changes in composition that the element balances allow. The equations can also be written in Gujer notation, with reactants -ve and products +ve, summing to zero. This has the advantage that it corresponds to the output of a computational stoichiometry generator (Part 1, Brouckaert et al., 2021) and corresponds with the way in which reaction processes are set up in modelling software. In this paper, the reaction equations use arrow notation, and stoichiometry tables use Gujer notation.
Note that Eqs 1 and 3 are expressed in terms of ionic components which, as discussed in Part 1 (Brouckaert et al., 2021), do not necessarily correspond to the actual species present in the aqueous phase. In a dynamic bioprocess model, Eq. 3 gives the change in component amounts over a particular time step governed by a kinetic ordinary differential equation (ODE). The calculation for the integration step can be completed by using the algebraic aqueous-phase speciation model discussed in Parts 1 and 5 (Brouckaert et al., 2021) which calculates the distribution of species actually present (e.g. H2PO4-, HPO42-, PO43-) and corresponding pH, subject to the component mass balances and thermodynamic dissociation equilibrium equations.
As discussed in Part 1 (Brouckaert et al., 2021), the traditional approach of dividing bioprocesses into electron donor and acceptor half-reactions is not necessary to achieve element- and charge-balanced stoichiometry for the overall reaction. However, breaking the overall reaction into its constituent parts facilitates better understanding of the reaction, and allows combining e− donors with different e− acceptors.
Indeed, since a stoichiometric equation is a linear element and electron balance, all manner of linear transformations can be applied to it to highlight specific issues. The issues which are of most interest for understanding the impacts of the bioprocess on solution properties are the transfers of electrons and protons (H+ ions) between oxidants, reductants, organic and inorganic components, and the mediating micro-organisms. Thus, the overall reactions can be broken down into electron donor, electron acceptor, anabolic (providing material for micro-organism growth) and catabolic (providing energy to drive the anabolic process) reactions, where the anabolic and catabolic processes are the electron sinks and together form the metabolism of the organism. Furthermore, the reactions can be split into the contributions of each of the CHONP and S elements and charge separately - the overall reaction is then simply the sum of the individual element and charge contributions. These appear in Eq. 5e and more generally in Table 2.
The overall bioprocess redox reaction can be formally split into two half-reactions, in which the electrons transferred from the electron donor to the electron acceptor are explicitly shown, i.e.:
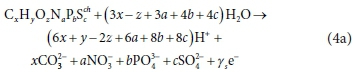
and if oxygen (O2) is the electron acceptor as in Eq. 1:
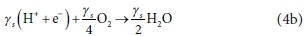
Equation 4b shows oxygen accepting 4e− per mol, or 32/4 = 8 gO/e−. Other electron acceptors can be considered, such as NO3- or SO42-, yielding different electron acceptor products, such as NO2−, N2, SO32−, S2O32−or H2S, as presented in Table 1. To repeat: the selection of the electron acceptor reactants and products is based on knowledge of the bioprocess, and needs to be determined beforehand to derive its stoichiometry.
In Eq. 4a, the generic electron donor CxHyOzNaPbScch reacts to form particular oxidized products of each of its constituent elements, giving up ys electrons, which are taken up by the electron acceptor O2 according to Eq. 4b.
Rearranging Eq. 4a to pair the terms γs e− and γs H+ yields:
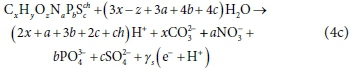
This pairing of some of the protons with electrons in the redox half-reactions, Eq. 4b and Eq. 4c, is discussed further in later sections; suffice to state here that any H+not paired with an e− affects the aqueous-phase alkalinity and pH. The next sections discuss the key features that electron donor (source) and electron acceptor (destination) reactions have in common, and demonstrate how the general equations are applied to specific bioprocesses.
ELECTRON (E−) DONOR REACTIONS
An electron donor reaction is a half-reaction in which a substrate (electron donor) or other chemical component reactant gives up electrons to produce more oxidized forms of its constituent elements as in Eq. 4a.
Oxidation products
The first important point to note is that the redox state of the oxidation products of the electron donor reaction is determined by the bioprocess. Equation 4a represents the oxidation of the electron donor to H+, CO32−, NO3−, PO43- and SO42- as could occur under aerobic conditions. However, organics degradation and nitrification under aerobic conditions are mediated by different organisms, and so are modelled as separate bioprocesses. Furthermore, under anaerobic conditions, the oxidation products for N and S are expected to be NH4+ and HS−, respectively, noting that NH4+ and HS− are standard aquatic chemistry components by convention (Part 1 of this series), and are components, not species. For the NH4+ and HS− components, the general electron donor reaction is:
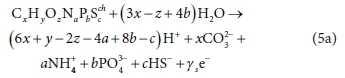
Equation 5a applies to the aerobic degradation of organics when nitrification and sulphide oxidation are modelled as separate reactions; to the anaerobic degradation of organics where the N and S end-products are and ; and to BSR where the electron acceptor is SO42−, SO32− or S2O32−(Bioprocesses 2a-2c). Rearranging Eq, 5a so that all bracketed terms have no net charge, and e− is paired with H+, yields:
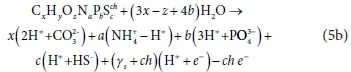
where the exchanged electrons γs of Eq. 5a is now given by:
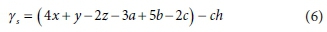
Note that γs in Eq. 6 is also referred to as the electron donating capacity (EDC) of the electron donor. However, the EDC is not a function of the electron donor only, but also of the reaction products, which, in turn, depend on the conditions under which the reaction takes place (e.g. aerobic, anoxic or anaerobic). When reaction balances are set up in terms of 1 mol of substrate as in Eq. 2, then the exchanged electrons of reaction will equal the EDC of the substrate.
The difference between Eqs 2 and 6 for γs is that NH4+ and HS- are the oxidation products of the N and S elements in Eq. 5a instead of NO3- and SO42- in Eq. 1. Because NH4+ and HS- can each donate 8e− to become NO3- and SO42-, respectively, the γs of Eq. 6 is 8a and 8c e−/mol lower than the γs of Eq. 2, i.e., the coefficients of the a and c terms in the γs equation have changed from +5 and +6 in Eq. 2 to -3 and -2 in Eq. 6. The 8 e−/mol electron donating capacity (EDC) of each of the NH4+ and HS- lead to the well-known 4.57 gO/gN ammonia nitrified to nitrate (from 8 e−/mol x 8 gO/e− divided by 14 gN/mol) and 2.0 gO/gS sulphide oxidized to sulphate (from 8 e−/mol x 8 gO/e− divided by 32 gS/mol).
Pairing the e− and H+ in Eq. 5a yields:

Eq. 5b can also be written as Eq. 5d below, viz.
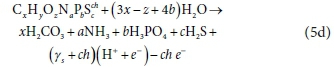
and γs remains equal to Eq. 6, showing that the protonated form of the selected reaction product components does not affect the exchanged electrons of the reaction.
Furthermore, as mentioned above, Eq. 5d can be considered the sum of reactions involving individual elements, which are shown in Eq. 5e and more generally in Table 2:

This disaggregation of the reaction stoichiometry in Eq. 5e is the basis of Table 2. Equation 5d is reconstructed by adding Rows 1b, 2, 3, 4a, 5b, 6a and 7. The alkalinity with respect to the most protonated species imparted to the aqueous phase by the electron donor is included in Table 2. The sum of the relevant rows in Column 7 of Table 2 yields the alkalinity of the reaction products ∑ AlkTproducts. The overall alkalinity change of reaction depends on the alkalinity of the electron donor Alked as discussed in Part 1 (Brouckaert et al., 2021).
The equality of the γs of Eqs 5a, 5b, 5c, 5d and 5e confirms that the protonated forms chosen for the reactants and products do not change the EDC of the electron donor reaction, e.g., the EDC (or γs) of the H2CO3 and CO32- are both zero. This can also be shown with the γs of Eq. 6 (or 2): For H2CO3, γs = 4 x 1 + 1 x 2-2 x 3 + 5 x 0 + 5 x 0 + 6 x 0 - 0 = 0 and for CO32-, γs = 4 x 1 + 1 x 0 - 2 x 3 + 5 x 0 + 5 x 0 + 6 x 0 -(-2) = 0. In general, the γS equation can be applied to each part of an electron donor reaction to give the EDC of that part relative to the oxidation state selected for each CHONP and S element.
Exchanged electrons (of reaction)
As discussed previously, the McCarty (1975) approach is based on the concept of an electron balance. The advantage of breaking the overall balanced stoichiometry into half-reactions is that it highlights both the source and destination of the exchanged electrons γs and it allows pairing of electron donor reactions with different electron acceptor reactions. The exchanged electrons in the electron donor reaction are a function of the change in oxidation state of the constituent elements of the electron donor, and are therefore a stoichiometric property of the reaction, depending on both the composition of the electron donor and the oxidation state of the reaction products. Because Eq. 1 is written in terms of the most oxidized products of each constituent element in the electron donor, γs in Eq. 2 is the maximum number of exchangeable electrons, whereas γs in Eq. 6 is not the maximum possible because the NH4+ and HS- products can still donate electrons. McCarty used the term exchangeable electrons, which suggests that they are a property of just the substrate, whereas in fact they depend on all the components participating in the half-reaction. So a more suitable term, exchanged electrons of reaction, has been adopted for this series of papers, with exchanged electrons as an abbreviation.
Extending the pattern of Eq. 5e, Table 2 shows the contribution of each element in the electron donor to the exchanged electrons as a function of the oxidation product of the N and S elements. While the protonated state of the C and P components may be different, their oxidation state is the same in all the bioprocesses considered here. For the purpose of calculating the exchanged electrons, each element in the generic electron donor is treated as having an oxidation state of zero. The true oxidation state of each atom in the electron donor might not actually be zero. However, since the electrons involved are just re-distributed within the molecular structure, the net effect is the same as assuming that their oxidation states are all zero. Consider the contribution of carbon: Because the C in CxHyOzNaPbScch all becomes CO32- (or H2CO3), where it has an oxidation state of +4 (a deficiency of 4 electrons), the electron donor component donates 4 electrons per carbon atom, hence the 4x in Eqs 2 and 6. The total exchanged electrons or γs for a given reaction is the sum of the contributions from each element in CxHyOzNaPbScch, as summarized in Table 2, Column 5. The terms of the γs equation associated with the different oxidation products of N and S are obtained by summing the relevant rows in Column 5. For example, the γs term associated with Eq. 5a with NH4+ and HS- as oxidation products is obtained by adding Rows 1a, 2, 3, 4b, 5a, 6b and 7 in Column 5. Similarly, the γs terms for Eq. 1 are obtained by adding Rows 1a, 2, 3, 4e, 5a, 6e and 7 in Column 5.
It can be seen from Table 2 that only the selection of the oxidation state of the products affects the exchanged electrons (γs), not which components are selected to represent the oxidation products. For all the reactions considered here, C, H, O and P always contribute +4, +1, -2 and +5 to γs relative to their elemental state. The electron contributions of N and S to the γs depend on the specific electron donor product oxidation states involved, and may be positive, zero or negative. If the oxidation states of the N and S are the most oxidized forms, i.e., NO3- and SO42-, their coefficients in the γs equation are +5 and +6 because they donate 5 and 6 e− relative to their elemental N and S states (Eq. 2). If the oxidation state of the N and S are the least oxidized forms, i.e., NH4+ and H2S, their coefficients in the γs equation are -3 and -2 because now they take up 3 and 2 e− relative to their elemental state (Eq. 6). The coefficients of the γs equation associated with the oxidation products of CHONP and S elements are shown schematically in Fig. 2.
Composition of the electron donor
As discussed in Part 1 (Brouckaert et al., 2021), having precise element and electron balanced bioprocess stoichiometry is key to successfully integrating bioprocess and physico-chemical reaction models. This is a particular challenge for bioprocess models since wastewater typically consists of a diverse mixture of complex organic molecules of unknown composition and structure. The convention adopted in this series of papers, and in the plant-wide WRRF model based on this approach, PWM_SA (Ikumi et al., 2011, 2014, 2015), is to represent each group of complex organic substrates (soluble, particulate, biodegradable, unbiodegradable, settleable, non-settleable) by the generalized empirical formula CxHyOzNaPbScch, where the stoichiometric coefficients x, y, z, a, b and c can be calculated from the mass fractions of the various elements determined by wastewater characterization (Part 3 of this series).
Note that the composition of any electron donor containing any combination of CHONPS can be obtained by substituting the appropriate values of the stoichiometric coefficients x, y, z, a, b, c and ch into the general formula. This includes simple organics like acetate and inorganic substrates such as thiosulphate and nitrite. Similarly, the exchanged electrons of reaction for complete oxidation of any such electron donor can be derived from Eq. 2, because in Eq. 2 all the elements are in their most oxidized state as far as bioprocesses are concerned. Furthermore, any of the oxidation reactions can also be derived as a linear combination of the oxidation reactions of the constituent elements of the electron donor (Table 2). Common examples are listed below.

Paired e− and H+
Any reaction or half-reaction that starts from a set of reactants that is charge-balanced must produce a charge-balanced set of reaction products (as in Eq. 5e with ch = 0). Thus the electrons in an oxidation or reduction half-reaction must be balanced by positively charged ionic products, of which the most common in biological reactions is H+. Conversely, every H+ that is involved in the reaction must be matched by a corresponding negatively charged component. H+ is of particular interest, because of its role in determining solution pH and alkalinity. However, these properties are not mediated by the H+ ions alone, but also by the anions with which they are paired. In redox half-reactions, pairings with H+ ions can be divided into 3 significant categories: with electrons; with anions of strong acids; and with anions of weak acids.
Free electrons cannot accumulate in solution, so they only appear in half-reactions. Therefore, an electron donor half-reaction always has to be combined with an electron acceptor half-reaction, in which the electron is a reactant, so that the electrons cancel out in the overall reaction (see below). This means that the H+ ions that are paired with the electrons in the electron donor half-reaction and the electron destination half-reactions will also cancel out, and consequently have no effect on the solution properties. However, any deficit or surplus of H+ after the pairing of H+ with e− has to be supplied or absorbed by the aqueous phase with changes of pH and alkalinity. The increase or decrease in H+ and other aqueous component products of the bioprocess, such as PO43- and CO32-, disturb the equilibrium of the aqueous phase, which then re-speciates to re-establish equilibrium. The H+ that are paired with strong acid anions, such as sulphate or nitrate, remain virtually completely dissociated, and so have a strong effect on pH. In contrast, the H+ that are paired with weak-acid anions, such as acetate, carbonate or phosphate, will tend to remain partially associated with them, and so have no effect on total alkalinity, and a weak and variable effect on pH, depending on the specific pK values of the anions involved relative to the pH of the solution.
Chemical and total oxygen demand (COD and TOD)
COD is the electron-donating capacity (EDC) of components (or groups of components) expressed as oxygen, as if all the electrons donated by the components were accepted by oxygen. The products of the COD test are CO32−, NH4+, PO43-, SO42-, H+ and H2O. Note that in the COD test, ammonia is not oxidised, but sulphide is, so the COD measure excludes the EDC of the ammonia but includes the EDC of the sulphide, where the EDC is expressed in terms of mass of oxygen. The total oxygen demand (TOD) is the amount of oxygen required to convert the electron donor to the most oxidized forms of its reaction products, including the oxidation of the nitrogen content to NO3-, i.e., the products of the TOD reaction are CO32−, NO3−, PO43-, SO42-, H+ and H2O (as in Eq. 1). The exchanged electrons of the TOD reaction (Eq. 2) include the maximum possible electrons donated by the N content.
The EDC corresponding to COD of an electron donor can be constructed from Table 2 by adding Rows 1a, 2, 3, 4b, 5a, 6e and 7, i.e.:
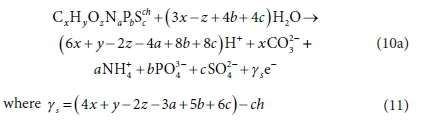
Pairing the e− with H+ in Eq. 10a yields:
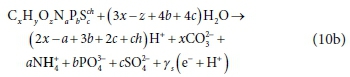
The COD then is 8 γs gO2/mol of CxHyOzNaPbScch, where the 8 represents 8 gO per e− accepted. The COD as an EDC basis is very convenient for bioprocess modelling because, not only is there an accurate test for its measurement (Standard methods, 2017), it also allows modelling nitrification and BSR bioprocesses separately without correction of the measurement, and therefore is applicable to both aerobic and anaerobic processes. The TOD or COD of a component can be calculated with Eq. 2 or Eq. 11, respectively, from its element and charge composition. It shows, as mentioned before, that the EDC as COD (8 γsCOD) or TOD (8 γsTOD) is not affected by the associated protons of the component.
Adding speciation to the electron donor half-reaction
For simplified steady-state bioprocess models with pH estimation (e.g. in spreadsheets) speciation may be added to the electron donor reaction. This requires writing the stoichiometry so that the components match the dominant species within the specified pH range wherein the bioprocess usually operates. For example, in the pH range 6.8 to 8.6, within which most bioprocesses operate, the dominant species of the IC, FSA, OP, sulphide and acetate weak acid/base systems are HCO3-, NH4+, H2PO4-, HPO42-, H2S, HS- and HAc. The bioprocess stoichiometry is therefore written in terms of the relevant protonated state of these species directly. This is what Sötemann et al. (2005a) and Poinapen and Ekama (2010a) did in their steady-state methanogenic and sulphidogenic models. Whereas only one species is needed for the IC, FSA and acetate systems because their pK values are more than 0.5 pH units outside the 6.8-8.6 pH range, two species of the OP and sulphide systems are needed because these each have a pK value inside the range, which significantly complicates pH calculation when OP and FSS are present in significant quantities. This aspect is considered further below and in Part 5 of this series.
ELECTRON DESTINATION REACTIONS
The electrons donated by the electron donor are used in two sub-bioprocesses by the organisms that mediate a particular bioprocess, (i) anabolism, which is the production of the cell material of the biomass, and (ii) catabolism, which generates energy to transform the electron donor (substrate) to cell material (McCarty, 1975; Ekama, 2009). Both electrons and energy are conserved: The energy associated with the electrons used in anabolism is energy conserved as new cell material and the energy associated with the electrons used in catabolism is transformed to heat. Anabolism and catabolism together form the metabolism of organism growth when mediating a particular bioprocess.
If the electron donor substrate is sufficiently concentrated, the catabolic heat generation will heat the water in which the bioprocesses take place. This is the main heat source in auto-thermal aerobic digestion (Messenger and Ekama, 1993; Pitt and Ekama, 1996). By including the heat of reaction in the breakdown and formation of components in bioprocesses, Fernández-Arévalode et al. (2015) developed a general plant-wide WRRF model that can predict temperature in its different reactors.
Anabolism (biomass growth)
Using the products of the COD reaction (Eq. 10) as the reactants, the biomass formation reaction can be written in terms of standard aquatic chemistry components and with paired H+ and e− as follows:
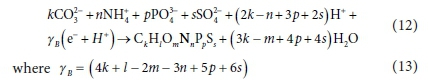
and γB is the exchanged electrons of the biomass growth reaction (e−/mol).
The COD of the biomass is 8 γB gCOD/mol, since Eq. 12 is just the COD reaction (Eq. 10) in reverse.
Rearranging Eq. 12 so that all terms are electro-neutral yields:
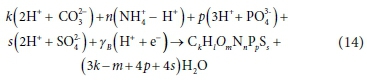
Therefore, Eq. 12 could also be written as:
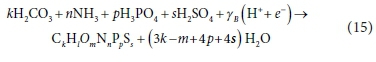
In Eqs 12 and 15, the components retain the same oxidation states - it is only their number of associated protons that have changed. This follows the pattern of Eq. 5e in reverse (with ch = 0), so all the comments made there apply to this anabolic biomass growth process also. Note that while the generic substrate component CxHyOzNaPbScch includes a stoichiometric coefficient ch for charge, the generic stoichiometric formula for biomass CkHlOmNnPpSs does not because it is generally assumed that biomass is uncharged.
For the purposes of setting up the stoichiometric biotransform-ation model equations, it fundamentally does not matter whether either the substrate or biomass is represented as charged or neutral, as the charge will be balanced overall by either adding or subtracting protons as illustrated in Eq. 15. However, when a component is also involved in the ionic speciation model, it is more convenient to use a charged representation. For example, it would be awkward and inconvenient for a speciation model to include separate reaction equations for all the possible neutral ion-pairs involving acetate that could be present in solution [HAc, NaAc, KAc, Mg(Ac)2 etc.], so it is convenient to use the charged form (Ac-) as the component, and account for the cations separately.
However, while available experimental evidence (Westergreen et al., 2012) indicates that biomass does include functional groups that can participate in protonation/deprotonation reactions, the overall protonation state does not vary significantly in the pH range 6.8-8.6 in which most of the bioprocesses of interest occur. Therefore, biomass is not included in the ionic speciation model and can be conveniently modelled as an uncharged component.
In the same way as the general electron donor reaction can be generated by adding the oxidation reactions of the individual elements making up the electron donor (Table 2), so also can the general biomass formation reaction be generated by adding the biomass anabolic reactions of the individual CHONP and S elements that make up the biomass CkHlOmNnPpSs. This is shown in Table 3 for the same components of the CHONP and S elements that can be taken up from the aqueous phase to form biomass as electron donor products released to the aqueous phase in Table 2, and are also written as mass-balanced reactions summed across the rows to zero. Because anabolism is the reverse of the electron donor reaction, Table 3 is essentially the reverse form of Table 2 and all the comments on Table 2 also apply to Table 3.
Note that it is not necessary to include all six elements in the biomass composition. If appropriate, the biomass can be simplified to CkHlOmNn by assigning zero to the p and s molar composition values of P and S. Table 3 shows that different oxidation states of the components of the N and S elements can also be selected to synthesize the biomass.
In bioprocess model stoichiometry it is most convenient (but not necessary) to generate biomass from the electron donor reactant or product components of the N and S elements (as in Eq. 10 paired with Eq. 12), rather than some other component of these elements, not present as an electron donor reactant or product. For example, with biological sulphite and thiosulphate reduction to sulphide (Bioprocesses 2b and 2c in Tables 1, 4c and 4d), the electron donor reactants sulphite or thiosulphate are selected as the S components for biomass synthesis, rather than another S component like sulphate. Similarly, for autotrophic denitrification with sulphide, sulphite or thiosulphate as electron donor and nitrate or nitrite as electron acceptor (Bioprocesses 5a, 5b and 5c in Tables 1, 4e and 4f), sulphate is selected as the S element component for biomass synthesis because it is present in the stoichiometry as electron donor product. So from a stoichiometric perspective, the choice of N or S element component that is taken up for biomass synthesis is usually governed by whether or not it is available as an electron donor reactant or product, unless there is compelling evidence that a particular species is used for biomass synthesis (as for anammox bacteria, see below). In this regard, the oxidation state of the reaction products aligned with the COD test (CO32-, NH4+, PO43-, SO42-, Eq. 10) are usually best suited for modelling bioprocesses because nitrification of ammonia and BSR are modelled with their own bioprocesses (Bioprocesses 2, 3 and 5 in Tables 1 and 4).
As mentioned above for the electron donor reactions, the selection of the species of the C, N, P and S elements that are to be the components and formed as bioprocess products depends on the purpose of the model for which the bioprocess stoichiometry is derived. The same applies to anabolism (and catabolism - see below). For a steady-state model, some simplifying assumptions can be made, and the components selected to simplify pH calculation from the products (e.g. the AD model of Sötemann et al., 2005a). For a dynamic model or a steady state model with speciation and calculation of pH, it is preferable to select components from the standard aquatic chemistry set (see Part 5 of this series).
Catabolism
The catabolic electron acceptor reaction is built on the bioprocess's terminal electron acceptor and the species (specifically the redox state) of the particular element that is formed when it accepts the electrons. For example, if SO32− is the electron acceptor, then S2O32−, S or HS- can be formed (not SO42− because that would constitute SO32−donating electrons, Fig. 2). Experimental observation is required to know which specific species of the electron acceptor element are formed. If two species are formed, e.g. S2O32−and HS- (Qian et al., 2015) or SO32−and S from S2O32− (Deng et al., 2019), then two separate bioprocesses are required to model the system.
The electron acceptor reactions of the most common electron acceptor species of the C, O, N and S elements (components of P are not usually electron acceptors and H2 is an electron donor) involved in the bioprocesses listed in Table 1 can be written in general form with paired e− and H+ as:
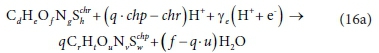
where:
 and
and 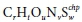 represent the electron acceptor reactant and product;
represent the electron acceptor reactant and product;
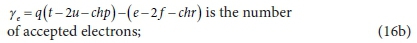
The coefficient q depends on the element being oxidized (accepting electrons):
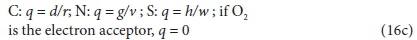
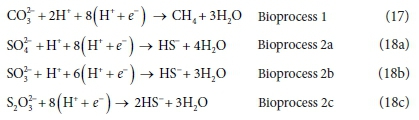
Equation 16 applies to all electron acceptor half-reactions involved in the bioprocesses listed in Table 1. By assigning the appropriate values to d, e, f, g, h and chr for the electron acceptor reactant and to r, t, u, v, w and chp for the electron acceptor product in Eq. 16, the electron-accepting reactions for 8 electron acceptor species (CO32−, SO42−, SO32−, S2O32−, S, O2, NO2−, NO3−) of the C, S, O and N elements in the bioprocesses of Table 1 can be generated as listed in Eqs 17 to 20. Four additional electron acceptor half-reactions for the S components intermediate between HS− and SO42− are also shown.

ELECTRON BALANCE AND OVERALL STOICHIOMETRY
The overall electron balance
The previous sections presented purely stoichiometric descriptions of the three parts of a bioprocess reaction: the electron donor reaction, the anabolic electron destination reaction, and the catabolic electron acceptor reaction. By 'purely stoichiometric' it is meant that the only information contained in the reaction equation is the set of chemical components involved and their embedded element mass and electron (charge) balances.
The overall bioprocess reaction involves the combined set of components for each part, and is subject to the same material balance constraints. Thus, the overall bioprocess reaction stoichiometry can be constructed as a linear combination of the three sub-reactions. In geometric terms, the sub-reactions are basis vectors of the compositional space; i.e., directions along which the composition is allowed to change by the material balance constraints. The overall reaction is a vector, which is a linear combination of the basis vectors. The way this combination is constructed is commonly understood in terms of an overall electron balance in which the electrons donated by the donor (substrate) are divided between the anabolic and catabolic destination reactions, i.e.:
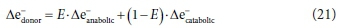
However, it is not just the exchanged electrons that are combined in this way, but the entire electron donor, anabolic and catabolic stoichiometric equations, as shown schematically in Fig. 3.
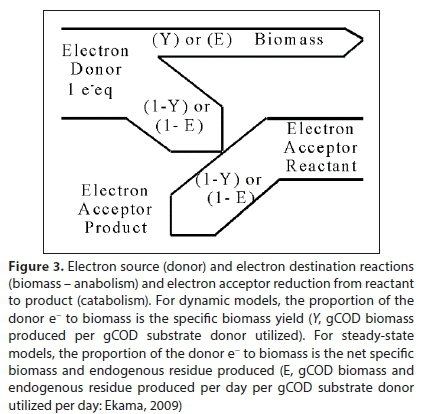
The overall reaction equation for the bioprocess is no longer purely stoichiometric, because the coefficient E depends on non-stoichiometric factors, such as thermodynamic constraints and details of micro-organism metabolism. The most common approach has been to treat E as an empirical parameter; however, deriving its value from a metabolic model is also possible (Smolders et al., 1995; Rittman and McCarty, 2001). In dynamic models, E is the biomass yield coefficient (Y) expressed as gCOD biomass synthesized/gCOD substrate utilized. Because endogenous respiration is modelled with a bioprocess of its own in dynamic models, E = Y for heterotrophic bioprocesses, where the electron donor and biomass are both expressed as COD. However, in fully mass-balanced plant-wide models which express components in terms of mass (Ikumi et el., 2015, Solon et al., 2015), the E value has to be converted to Y in mass units (g biomass/g substrate), i.e.:
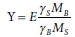 g biomass/ g substrate;
g biomass/ g substrate;
where MB = (12k + l + 16m +14n + 31p + 32s) g biomass/mol and MS = (12x + y + 16z + 14a + 31b + 32c) g substrate/mol
In steady-state models, E is the net (observed) yield, which is a combination of the growth and mass loss processes, i.e.:
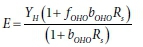
for aerobic activated sludge with growth and mass loss modelled as endogenous respiration (Ekama, 2009) and

for methanogenesis with and mass loss modelled as death regeneration (Sötemann et al., 2005a).
Also, yield coefficients for autotrophic processes (YA) are typically expressed in non-COD units, e.g., gVSS/g NH4-N for nitrification. For the electron balance equation (Eq. 21) to apply, these autotrophic yields must be converted to the ratio of donated electrons taken up by anabolism. For example, consider the case of nitrification where ammonia is aerobically converted to nitrate (Bioprocess 3, electron donor reaction Eq. 7a). From the stoichiometry (Table 4a Columns 4 and 9), YA g VSS biomass produced per g NH4-N consumed is:
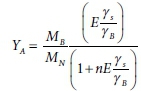
where MN is the atomic weight of N. Rearranging results in:
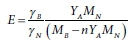
which gives E = 0.031 for YA = 0.10 g VSS/gNH4-N for biomass composition of CH1.4O0.4N0.2P0.05.
As an example, consider aerobic growth of heterotrophs on acetate. Aligning the oxidation state of the N and S elements with the products of the COD test (NH4+ and SO42-) and selecting the protonated forms of components aligned with the standard aquatic chemistry convention, the components involved in the bioprocess are: C2H3O2−(substrate), CkHlOmNnPpSs (biomass), O2 (electron acceptor), CO32−, NH4+, PO43−, SO42−, H+, H2O (oxidation products).
The electron donor reaction can be constructed from Eq. 10a or Table 2.

The anabolic reaction is given by Eq. 12:

and the electron acceptor (catabolic) reaction is given by Eq. 19:
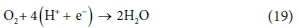
The exchanged electrons for the three half-reactions are ys = 8, yB and ye = 4, respectively, so the reactions are combined as:
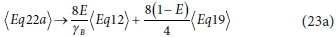
which, after combining like terms and simplifying, gives:
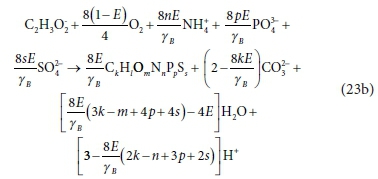
∆AlkT of the complete bioprocess Eq. 23b is obtained by similarly combining the ∆AlkT of the three half-reactions according to Eq. 23c,
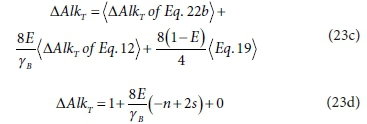
Combining, as per Eq. 21, the general electron donor (Eq. 10a), anabolism (Eq. 12) and electron acceptor (Eq. 16a) equations, with oxidation states of the N and S elements aligned with the products of the COD test (NH4+ and SO42-), and selecting the protonated forms of the components aligned with the standard aquatic chemistry convention (Part 1, Brouckaert et al., 2021), i.e.:
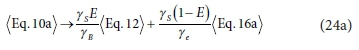
yields a generalized stoichiometric bioprocess reaction Eq. 24b in terms of a generic electron acceptor reactant 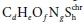 and product
and product 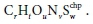 .
.
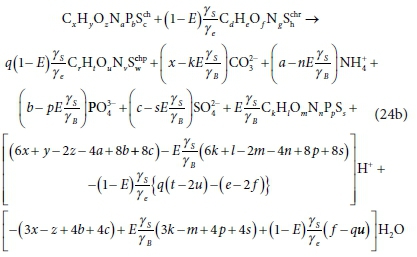
Equation 24b applies to all the bioprocesses in Table 1, except 2b, 2c, 2d, (sulphidogenesis with a sulphur reactant other than SO42−), 3, 3a, 3b for nitrification and 7 for anammox. Equation 24b does not apply to BSR when the e− acceptor reactant is not SO42−. However, it can be modified to obtain bioprocess stoichiometry for BSR with e− acceptor reactants other than SO42−, such as SO32− (Bioprocesses 2b and 2d) and S2O32− (Bioprocess 2c) as described in Table 5. For example, for Bioprocess 2c with thiosulphate as the electron acceptor reactant, sulphate is replaced by thiosulphate (Eqs 10a and 24b) and the terms 6c and 6s in Eqs 11 and 13 are replaced by 2c and 2s, respectively (Rows 6c in Tables 2 and 3, respectively). Equation 24b does not apply to nitrification (3, 3a, 3b) because it does not include the appropriate electron donor products for nitrogen (NO3− or NO2−). However, an analogous overall reaction can be constructed by substituting the appropriate electron donor equation for Eq. 10a in Eq. 24a. The resulting stoichiometric coefficients are listed in Tables A1 and A2 (Appendix). The stoichiometric coefficients for sulphidogenesis are listed in Tables A3. For Bioprocesses 2b-2d, both the electron donor sulphur product and sulphur source for anabolism were made the same as the electron acceptor reactant. The electron donor balance approach illustrated in Fig. 3 has to be further modified in the case of anammox (Bioprocess 7) because anammox has the peculiarity that it uses different e− donors for anabolism and catabolism. Anammox is discussed in greater detail below.
The revisions made to obtain the stoichiometry in Tables A1-A3 are listed in Table 4. Note that changing the products and reactants in the electron donor and anabolic reactions results in changes in the formulae for yS and yB. As discussed previously, yS and yB can be calculated for different oxidations of the products and reactants by summing the appropriate rows in Column 5 of Table 2 and Column 3 of Table 3, respectively. The required changes are noted in Table 4.
The Gujer matrix
The Gujer matrix format is the standard and systematic way of writing bioprocess stoichiometry of WRRF models. It is an easy-to-read fingerprint of a bioprocess model (Gujer, 2008). The matrix (like Tables A1-A3) lists the bioprocesses in rows and the components in columns. Usually, the matrix is completed by adding the kinetic rate expressions of the bioprocesses in a column on the right (Gujer, 2008). When water is included, as is done here with complete element mass balancing, all the elements CHONPS, e− (or COD = 8γS) and charge are balanced across the rows (bioprocesses). In ASM1 (Henze et al., 1987) for example, this is not the case - only COD and N are mass balanced across the rows, not CHOPS and charge. When water is added as in Tables A1-A3, the bioprocess produced or consumed water has to be accounted for separately from the water in the bioreactor. If this is not done, then, with time, models of aerobic and anaerobic reactors increase and decrease in water volume.
Gujer matrices of bioprocess models comprising multiple bioprocesses can be verified for mass balance by summing the product of the CHONPS and ch content of each component and its stoichiometric term across each row (Gujer, 2008; Hauduc et al., 2010) - the elements in the bioprocess are balanced if the sums are all zero. The COD and TOD mass balances can also be checked this way by summing the products of component COD or TOD (8γCOD and TOD 8γTOD, respectively), and the stoichiometric term for each bioprocess (Columns 1 - 19 in Tables A1 - A4). γCOD and γTOD, are calculated from Eqs 11 and 1, respectively. However, if the CHONPS and ch are balanced, then the COD and TOD must also be balanced because, as Eqs 11 and 1 show, the COD and TOD are properties of the component composition. Note that for Bioprocesses 2b, 2c and 2d in Table A2, the coefficients of the S (c and s) in the γS (Eq. 11) and γB (Eq. 13) equations have changed to 4, 2 and 4, respectively, because the electron acceptor reactant is SO32-, S2O32- and SO32- (see Fig. 2).
Bioprocess stoichiometry is entered into the WRRF simulator WEST (MikebyDHI, 2021) in Gujer matrix format and the software has a facility for automatically checking the elemental mass balances of the bioprocesses entered. We have developed a MATLAB code that can generate the general bioprocess stoichiometry for selected electron donor and acceptor reactants and products (available from https://washcentre.ukzn.ac.za/bio-process-models/). The output of the MATLAB code includes the generalized stoichiometric terms of the reactants and products in the same format as the WEST model code, so that it can be pasted directly into the WEST conversion model editor. The 3-phase (aqueous-gas-solid) plant-wide WRRF model including P and S, PWM_SA in WEST (Ikumi et al., 2014, 2015; Ghoor, 2019) was originally coded this way. This procedure eliminates transcription errors when coding new bio-processes into simulation models and saves much time in model debugging and mass balance verification.
Conversion of one organic component to another
The stoichiometry in Table 4 assumes that all the e− from the donor are passed to the terminal electron acceptor, and conserved in biomass. In the intermediate bioprocesses (which are used in dynamic models, but not steady-state models) this does not always happen. In the University of Cape Town Sludge Digestion Model (UCTSDM1) (Sötemann et al., 2005b) and its successor PWMSA_AD (Ikumi et al., 2011, 2014, 2015), hydrolysis of complex organics produces the intermediate component glucose, which is acidified by acidogens to acetate and hydrogen, both of which have non-zero COD. Eqs 1 to 11 for complete oxidation of the electron donor do not apply in these cases. Furthermore, in the dynamic models, the intermediate organic compounds are not typically represented as being utilized in biomass production. Nevertheless, the principle of transferable e− and mass balance is still applied in the derivation of the relevant stoichiometric balances. Instead of liberating all the e− relative to COD, (or TOD) end products and producing e− donor products that have zero COD, the e− are conserved in reaction products that have COD (or TOD). The transformation of the general organics component CxHyOzNaPbScch from one form to another CkHlOmNnPpSs with element, COD and charge mass balance, expressed in terms of standard aquatic chemistry components, is obtained from Eq. 24b with E = 1, viz.
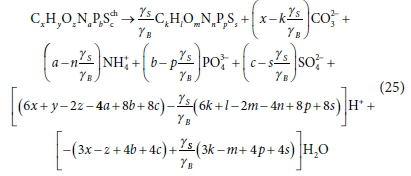
Equation 25, which is identical to Eq. 15 in Part 1 (Brouckaert et al., 2021), is used to represent hydrolysis of complex organics of various organic types such as fermentable biodegradable soluble organics (FBSO) and biodegradable particulate organics (BPO), each with their own x, y, z, a, b, c composition, to glucose (C6H12O6) without acidogen biomass growth.
The glucose in turn is acidified by acidogens with biomass growth to acetate and hydrogen via:
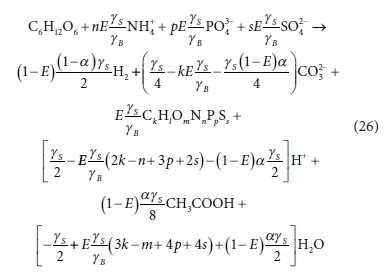
In PWMSA_AD (Ikumi et al., 2011, 2014, 2015), α is set at 2/3, so that two thirds of the glucose EDC (COD) excluding biomass is converted to acetate and one third to H2. This, again, is imposed on the stoichiometry from prior knowledge of the bioprocess.
The generic product CkHlOmNnPpSs in Eqs 25 and 26 is represented without charge, but this does not reduce their generality, because one can always choose a neutral species to represent the component - e.g. CH3COOH instead of CH3COO−.
Anaerobic ammonia oxidation
Usually a proportion of the e− donor (Y or E) is converted to biomass and the remainder passed on to the terminal e− acceptor (Fig. 3), however, anaerobic ammonia oxidation (anammox) is an exception. Anammox bacteria use ammonia as the nitrogen source for biomass growth and as an electron donor for autotrophic denitrification (the catabolic reaction is NH4+ + NO2−→ N2(g) + H2O). However, nitrite is the electron donor for anabolism where it is oxidized to nitrate, and also the electron acceptor in the denitrification reaction as illustrated in Fig. 4) (Van Niftrik et al., 2004). The e− donor equation is obtained by taking Eq. 8 for NH4+ and N2 as e− donor reactant and product and the e− acceptor Eq. 20 for NO2- and N2 as e− acceptor reactant and product. The anabolism equation is obtained from Eq. 12 where the (e− + H+) pair is supplied by the oxidization of NO2- to NO3- , Eq. 7c ÷ 2, to give the stoichiometry in Table A1, Bioprocess 7. The net biomass yield E = 0.1173 in Fig. 4 was obtained from Chen et al. (2013) who observed yields of 0.14 gVSS/gNH4+-N and 0.12 gVSS/gNO2-N.
READING BIOPROCESS BEHAVIOUR FROM THE STOICHIOMETRY
Mass-balanced bioprocess stoichiometry ensures that the fluxes of elements CHONPS and charge which exit a biological system are equal to the fluxes entering it. For example, for an AD, the CH4 and CO2 gas flows and aqueous-phase pH are entirely defined and dependent on the CHONPS and charge composition of the biodegradable organics degraded in it. In the interests of brevity, only some insights into the very common methanogenic and increasingly exploited sulphidogenic bioprocesses that can be read from their stoichiometry are presented below. It needs to be understood that bioprocess stoichiometry connected to external speciation routines implicitly models the steps described below. In steady-state models, some aqueous-phase speciation reactions and simplifications are explicitly included in the bioprocess stoichiometry described above, so that pH can be calculated directly from the relevant bioprocess products.
Simplified speciation model for methanogenesis
Assuming that (i) the methanogenic AD system remains at near-neutral pH (6.8-8.6) during the reaction; and (ii) BSR does not take place; and (iii) VFA are present at low enough concentration to not significantly influence pH, then based on the pK values of the remaining weak acid/base systems, the dominant species for the FSA is NH4+, for the OP are HPO42- and H2PO4- and for the IC are HCO3- and dissolved CO2 (often represented as carbonic acid: H2CO3 ↔ CO2 + H2O). Accordingly, the CO32-, PO43− and H+ component terms in the general methanogenic stoichiometric equation in Table A1 (Bioprocess 1) are replaced by the substitutions shown in Eqs 27a to 27c which include only the dominant species expected to be present.
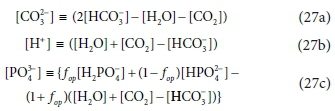
In Eq. 27 it is assumed that any H+ excess or deficit (i.e., not paired with an e−) will be supplied or absorbed by the IC system. Also, in Eq. 27c, fop is a parameter with a value between 0 and 1 that increases with solution pH, which is fixed by the requirements of both the IC and OP systems. For the IC system this is via the H2CO3 alkalinity (represented by the HCO3- concentration), and CO2 liquid-gas equilibrium via the partial pressure of the CO2 in the head space (Henry's law, Sötemann et al., 2005a). For the OP system this is via the H2PO4- and HPO42- dissociation with its pK'p2 value near 7, i.e. (H+)[HPO4-]/[H2PO42-] = 10-pH(1-fop)/fop = 10-pK'p2). Selecting the stoichiometry for methanogenic AD for which CO2 and CH4 are the electron acceptor reactant and product, (i.e. d = 1, e = 0, f = 2, g = 0, h = 0, chr = 0, r = 1, t = 4, u = 0, v = 0, w = 0, chp = 0 and γe = 8 e−/mol in CdHeOfNgShchr and CrHtOuNvSwchp), substituting Eqs 27a to c yields a more general steady-state model stoichiometry for methanogenic AD (Eq. 28) than that of Sötemann et al. (2005a). Coupled with the aqueous-gas phase CO2 equilibrium calculated using Henry's law, the products of this stoichiometry can be used to calculate the AD pH, provided it is between 6.8 and 8.6.
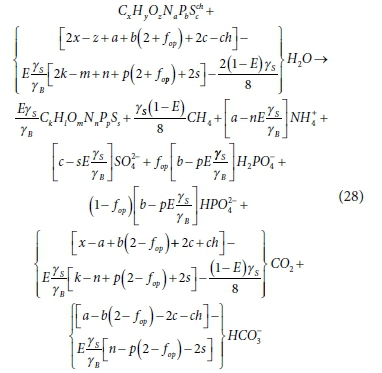
The total alkalinity change (∆AlkT) of Eq. 28 is obtained by subtracting the contributions of the weak acid/base reactant species from the contributions of the weak acid/base product species. The contribution of a weak acid/base species to the alkalinity is its deficit of protons relative to its reference species, i.e., HCO3- contributes one equivalent of alkalinity whereas H2PO4- and HPO42- contribute one and two equivalents, respectively, if the reference species is H3PO4. For Eq. 28 ∆AlkT is:
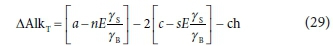
From the stoichiometry of Eq. 28 for 1 mol/L biodegradable organics digested [from (gCOD/L)/(8γS)]:
1.The only product terms that have non-zero EDC (COD) are the methane and biomass. Therefore, the COD of the CH4 is equal to the COD of the biodegradable organics degraded (minus the very small amount, 2-5% of COD, in the AD biomass produced and residual VFA). CH4 is the main (>95%) AD product from the biodegradable organics that has EDC.
2.Ignoring the small amount of C in the biomass and residual VFA, the C content of the organics digested exits the AD via three routes - CH4 and CO2 gas and dissolved CO2 (as HCO3-). So the C not converted to CH4 gas becomes dissolved CO2 (HCO3-) and gaseous CO2.
3.The N content of the biodegradable organics (minus the very small amount of N in AD biomass) represents the electron donor's persistent alkalinity. (In Eq. 29, the S content also affects ∆AlkT but in most cases c << a). In the breakdown of the organics this alkalinity is transferred to the aqueous phase and so the total alkalinity of the aqueous phase increases by a mol/L, minus (i) the very small amount in N taken up into the AD biomass produced (nEγS/γB) and (ii) any alkalinity in the residual VFA (not included in Eqs 28 and 29). So in the 6.8-8.6 pH range of ADs, the organic component's latent alkalinity is transferred to the HCO3- of the IC system. In fact, in plant-wide models, the alkalinity taken up from the aqueous phase in the form of N into activated sludge biomass in anabolism (Eq. 12) in the AS reactor is transferred to the AD in the biomass of the thickened WAS and released to the aqueous phase in its breakdown at high concentration. Similarly, in the AD of industrial, food or agricultural wastes containing proteins, the alkalinity taken up in the formation of the proteins (external to the AD) is released to the aqueous phase in the AD in their breakdown and adds alkalinity and buffer capacity to the aqueous phase for pH control. Therefore, to keep pH above 7 in AD without alkalinity dosing, the feed to ADs should include proteinaceous material.
4.When organic P is released to the aqueous phase from the breakdown of organics, the ∆AlkT does not change (as can be seen in Eq. 29) but the addition of orthophosphate results in the re-speciation of all the weak acid/base systems present (as can be seen in Eq. 28). This re-speciation transfers alkalinity from the HCO3- of the IC system to the H2PO4- and HPO42- species of the OP system. So the release of P from the breakdown of organics increases the alk H3PO4 but decreases the alk H2CO3 (using the Loewenthal et al., 1989, 1991 terminology) by the same amount. This increases the CO2 that leaves the AD as gas (by b{2-fop} in the CO2 term of Eq. 28), which increases the pCO2 of the gas phase. The decrease in HCO3- causes the pH of the digester to decrease, but now the requirement of the OP system, via its H2PO4-/HPO4= dissociation, also has to be met to establish the pH - the fop value at which dissociation requirements of both the OP and IC systems is met establishes the AD pH. The effect on the AD pH of the hydrolysis of polyphosphate from phosphorus accumulating organisms (PAOs), which is different to that of the release of P in the e− donor organics, and its precipitation as struvite, is presented by Harding et al. (2011) and Ikumi et al. (2014), who show that these processes also cause digester pH to decrease and may stimulate struvite and other mineral precipitation in the digester.
5.If an organic substrate contains organically bound S (not poly-sulphide or other S granules), this decreases its latent alkalinity, since the release of this S as SO42− in the breakdown of the organics decreases the AlkT of the aqueous phase. This decrease is due to the 2 H+ paired with SO42-, and decreases the HCO3− concentration by 2c mol/L (Eq. 29). The decreased HCO3− increases the CO2 that exits the digester as gas, similar to the release of organic P (5 above), and so also increases the pCO2 of the AD gas, which, together with the decrease in HCO3−, decreases the AD pH. However, in the AD the SO42− may be reduced to sulphide. This BSR is best modelled by its own bioprocess(es) (2a in Tables 1 and 4). If SO42− is reduced to sulphide, the 2c mol/L alkalinity decrease will be (partially) restored by the uptake of H+ in BSR, i.e. SO42−+ (fos + 1)H+ + 8(e− +H+) = fosH2S + (1-fos)HS− + 4H2O, where the 8(e− +H+) is supplied by the organics e− donor. If the free (H2S) and saline (HS−) sulphide (FSS) is significant, the H2S/HS− dissociation also needs to be taken into account to determine the pH in the pH range 6.8-8.6. Dealing with multiple weak acid/base systems in bioprocess stoichiometry with added speciation to calculate pH, such as Eq. 29, is complex (Harding et al., 2011), which makes using external speciation routines for pH calculation, such as the one described in Part 5 of this series, attractive even for steady-state models.
6.Based on Eq. 32, and as discussed in Part 1 (Brouckaert et al., 2021), ∆AlkT = 0 for the conversion of acetate to bicarbonate. Thus, the VFA's persistent alkalinity is transferred to the IC system, which tends to increase the pH since the IC system has a higher pK than the VFA system.
So from Points 3 and 6 above, AD aqueous alkalinity is increased only by the alkalinity fed to it, which comes from the release of N from the influent organics, and utilization of dissociated VFA in the feed, i.e. AlkT = a + j mol/L. Also, from Points 4 and 5, with the release of P and S from the organics, the CO2 from the organics that remains dissolved as HCO3− decreases while the CO2 exiting as gas increases. Because the methane gas is fixed by the EDC (COD) of the degraded organics, the increased CO2 gas increases the partial pressure of CO2 (pCO2) in the AD headspace and decreases the aqueous phase pH. However, as the OP and sulphide concentrations increase, so the OP and sulphide weak acid/base systems have an increasing effect on establishing the AD pH, because the equilibrium requirements of all weak acid/bases present have to be met, which establish the pH. The influent alkalinity (and pH), the two aqueous alkalinity-increasing processes (3 and 6 above) and the two aqueous alkalinity-consuming processes (Point 5 and anabolism), establish the AlkT and pCO2 in the AD and hence the AD pH. The other processes, like the release of OP from the breakdown of organic P (Point 5 above), do not change the AlkT but only the speciation. So the net aqueous AlkT increase (= a -2s + j mol/L, ignoring AD biomass formation) is completely defined by the composition of the influent organics digested and the type of bioprocess, in this case methanogenesis, which itself does not increase the aqueous alkalinity, as BSR does (Poinapen and Ekama, 2010a).
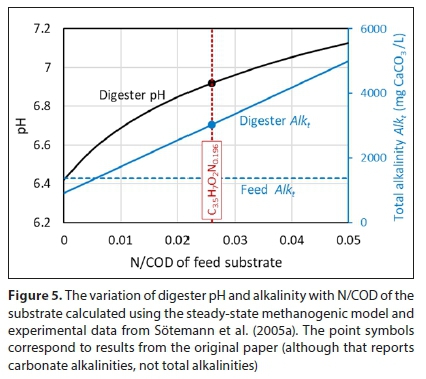
Some of these considerations are illustrated in Fig. 5, prepared using a steady-state methanogenic model based on Sötemann et al. (2005a). Table 2 from that paper includes experimental data for anaerobic digestion of a sludge substrate in a mixed laboratory digester with a retention time of 20 days. An elemental composition of C3.5H7O2N0.196 was used to represent the sludge, calculated from laboratory measurements. This gives a substrate N/COD ratio of 0.0259 g N/g COD. Figure 5 shows the model predictions of pH and alkalinity as N/COD is varied by changing the coefficient of N in the substrate formula. (Note that this model did not consider pH inhibition of methanogenesis, and so did not indicate at what point digestion would fail.)
Simplified speciation model for sulphidogenesis (Bioprocess 2 - BSR of sulphate to sulphide)
The general stoichiometry (Eq. 24b) tailored to BSR of sulphate to sulphide, with sulphide represented by HS- (Bioprocess 2a in Table 1), is given in Table A2. Assuming (i) the BSR reactor pH is between 6.8 and 8.6; (ii) the VFA present is insufficient to affect pH; and (iii) any H+ excess or deficit (i.e. not paired with e−) will be supplied or absorbed by the IC and sulphide systems: then the dominant species are NH4+ for the FSA, H2S and HS- for the sulphide system (pKs1 ~7.0) , HPO42- and H2PO4- for the OP system (pKp2~ 7.2) and HCO3- for the IC system (pKc1~6.4).
Note that unlike for methanogenesis, CO2 is not included as a product, based on the empirical observation that gas evolution from BSR is negligible. This is because (i) due to the toxicity of sulphide, BSR systems are limited to treating much lower concentrations of waste than methanogenic digesters; therefore less carbonate is released; and (ii) the sulphide released by BSR buffers the pH near pKs1~7.0. Based on the understanding of the dominant species present in the system at near-neutral conditions, a simplified speciation model of BSR can be formulated by replacing the CO32−, H+ and PO43− terms in Bioprocess 2a in Table A3 by the substitutions shown in Eqs 30a-30c:
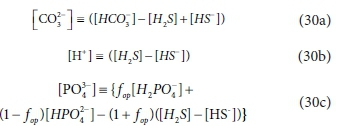
Substituting Eq. 30 into the BSR stoichiometry (Process 2a in Table A2) yields:
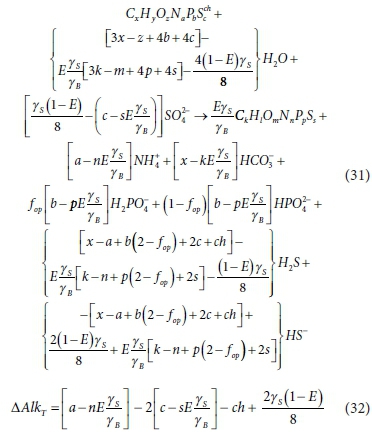
Equation 31 is the overall stoichiometric balance used in Poinapen and Ekama's (2010a) steady-state biological sulphate reduction model extended to include S in the substrate and biomass terms. Poinapen and Ekama (2010a) explained the lack of CO2 production in terms of the organic substrate being 'carbon deficient', by which they meant that alkalinity change of reaction (Eq. 32) is greater than the alkalinity of the carbonate species (HCO3− at pH ~ 7) released due to the oxidation of the substrate.
This can be understood in contrast to what happens in methanogenesis. It can be shown that ∆AlkT for methanogenesis (Eq. 29) is approximately equal to the coefficient of HCO3- in Eq. 28 (assuming E, b, c ≈ 0). This means that under steady-state conditions, any carbonate produced in excess of ∆AlkT has to be released from solution as CO2 gas for the pH to remain constant. In BSR, the alkalinity change due to the degradation of the substrate is the same as in methanogenesis (first two terms of Eqs 29 and 32); however, additional alkalinity (third term of Eq. 32) is produced from the reduction of sulphate to sulphide (Eq. 18a). In this case it can be shown that Eq. 32 is approximately equal to the sum of the coefficients of HCO3- and HS- in Eq. 31.
Note that the amount of sulphide produced in BSR is a function of the substrate COD or ys. It is this additional sulphide alkalinity which buffers the pH near 7 without the loss of CO2. In Poinapen and Ekama's (2010a) model, the pH is estimated from the HS− and H2S concentration ratio, i.e., pH = pK's1+log{[HS-]/[H2S]}. The lack of gas evolution in BSR points to a biosulphide potential (BSP) test in which gas measurements are not necessary and the aqueous concentrations are sufficient for characterizing the biodegradable organics (Chen et al., 2018; Part 3 of this series; Gaszynski et al., 2018).
Note that the assumption of zero CO2 gas production is not strictly true, because if there is any dissolved carbonate in the system the corresponding equilibrium partial pressure of CO2 will be non-zero, and there will be the potential for CO2 gas to diffuse out of solution into the reactor headspace, or to accumulate in sludge granules. A steady-state BSR model including a speciation subroutine (Brouckaert and Brouckaert, 2014) was used to simulate the BSR in the sulphate reduction upflow sludge bed (SRUSB) reactor of Lu et al. (2012). The equilibrium partial pressure of CO2 (pCO2) was calculated to be very low (at ~0.00050 atm). However, assuming that 10% of the dissolved CO2 diffused into the headspace resulted in the pH increasing from 7.2 to 7.6 (Lu et al., 2012 measured the pH at 7.8), then, while the loss of CO2 from solution had a small effect on the C mass balance, it had a noticeable effect on the pH. Furthermore, this shows why it is important that the biosulphide potential (BSP) is conducted in a sealed reactor with no headspace (Part 3 of this series, Gaszynski et al., 2018).
CONCLUSIONS
Complete element mass balance stoichiometry, fully integrated with three-phase (aqueous-gas-solid) physico-chemical process-es, is required to predict biosystem pH because the bioprocesses take up from, as reactants, and add to, as products, the aqueous phase ionic mix in which they operate. The aqueous phase in turn exchanges material with the gas phase, and ions with the solid phase in mineral precipitation processes, combining to govern the bioprocess reactor pH. The principles and procedures for the derivation of complete element mass balance stoichiometry were presented in this paper. The remarkable structured order of this, demonstrated in this paper, allows the derivation to be automated and performed computationally, which was set out in Part 1 of this series (Brouckaert et al., 2021). This may give a false impression that stoichiometry provides all that is required to model a process. However, the required prior information is, in fact, largely covered by knowing what components and species are involved in the process; once these are known, the systematic approach explained in this Part 2 of the series will go a long way towards completing the process description. The prior information imposed on the bioprocess stoichiometry required for different modelling purposes, is made explicit in this Part 2.
Dynamic models usually have to take account of intermediate components and species of a process, and so generally require more detailed knowledge than steady-state models, as input to the stoichiometry. The extra complexity that this entails makes it more important to align components and species with the well-established and systematic framework of the standard aquatic chemistry components, and associated speciation models.
With complete element mass-balanced stoichiometry, all the material of the bioprocess reactants - inter alia, influent substrate(s) - are conserved in the bioprocess products, most of which are dissolved aqueous species. Not only are the elements CHONPS and charge conserved but also alkalinity, which is an integral part of the bioprocess stoichiometry. The aqueous species all engage with the physico-chemical processes, most particularly aqueous (re)speciation, gas exchange and mineral precipitation. This intimate interconnection between the bioprocesses and the aqueous phase in which they operate means that the behaviour and progression of bioprocesses can be measured and monitored by changes in the aqueous phase species, which includes the alkalinity. To exploit this interconnection for the purpose of gaining insight into bioprocess behaviour and provide a means for their control, requires two transformation interfaces - one for the organic substrate and one for the aqueous inorganic material - which translate the model variables (components) to measurable parameters and vice versa. For the organic substrate, measurements need to be made to define the composition of the biodegradable organics (if these are not known) and a procedure is developed to determine the composition values (x, y, z, a, b, c and ch) in CxHyOzNaPbScch from measurements in Part 3. To characterize the aqueous phase, the alkalinity is often used to quantify the inorganic system. Alkalinity is a summary parameter representing many aqueous species, and so an aqueous speciation procedure is required to disaggregate the measured alkalinity into its subsystem species and model components. This is considered in Part 4. The last paper, Part 5, describes the aqueous phase speciation routine mentioned in this paper
ACKNOWLEDGEMENTS
This research was supported by the Water Research Commission and the University of Cape Town and is published with their permission.
ABBREVIATIONS
AD anaerobic digestion
AE algebraic equation
anammox anaerobic ammonia oxidation
ASM1 Activated Sludge Model No. 1
BPO biodegradable particulate organics
BSP biosulphide potential
BSR biological sulphate reduction
C carbon
COD chemical oxygen demand
DE differential equation
e− electron
EDC electron donating capacity
Eq. equation
FBSO fermentable biodegradable soluble organics
FSA free and saline ammonia
FSS free and saline sulphide
H hydrogen
IC inorganic carbon
LHS left hand side
M molal (mol/kg water)
N nitrogen
O oxygen
OP orthophosphate
P phosphorus
PAC proton accepting capacity
pC negative log (base 10) of the species concertation in molal units (mol/kg)
pH negative log (base 10) of the hydrogen ion activity
pK negative log (base 10) of the dissociation constant - subscripts a, c1, c2, s1, s2, p1, p2, p3 and n refer to acetate, 1st and 2nd of the IC, 1st and 2nd of the FSS, 1st, 2nd and 3rd of the OP and FSA weak acid base systems, respectively
pK' negative log of dissociation constant corrected for ionic strength
PWM_SA Plant Wide Model South Africa
PWMSA_AD Plant Wide Model South Africa Anaerobic Digestion
redox reduction oxidation
RHS right hand side
S sulphur
SANI sulphate reduction autotrophic denitrification nitrification integrated system
SRUSB sulphate reduction upflow sludge bed
TOD total oxygen demand
UCTSDM1 University of Cape Town Sludge Digestion Model No 1
VSS volatile suspended solids
WAS waste activated sludge
WEST Worldwide Engine for Simulation of wastewater Treatment plants
WRRF water and resource recovery facility
SYMBOLS
Alked direct alkalinity of the electron donor component
Alkp persistent alkalinity of the electron donor component
AlkT total alkalinity in solution
∆AlkT total alkalinity change of reaction
γB electron donating capacity of biomass
γS electron donating capacity of the electron donor
γSCOD electron donating capacity with respect to chemical oxygen demand (COD)
γSTOD electron donating capacity with respect to total oxygen demand (TOD)
γe number of e−/mol accepted by the electron acceptor reactant to form the product
a molar content of nitrogen in CxHyOzNaPbScch electron donor
b molar content of phosphorus in CxHyOzNaPbScch electron donor
c molar content of sulphur in CxHyOzNaPbScch electron donor
ch charge of CxHyOzNaPbScch electron donor
chr charge of CdHeOfNgShchr electron acceptor reactant
chp charge of CrHtOuNvSwchp electron acceptor product
d molar content of carbon in CdHeOfNgShchr electron acceptor reactant
E proportion of the utilized electron donor that becomes biomass and endogenous residue
e molar content of hydrogen in CdHeOfNgShchr electron acceptor reactant
e− electron
f molar content of oxygen in CdHeOfNgShchr electron acceptor reactant
fhs fraction of free (H2S) and saline (HS-) sulphide (FSS) that is free (H2S)
fop fraction of the ortho-P (OP), approximated by H2PO4- + HPO42-, that is (H2PO4-)
g molar content of nitrogen in CdHeOfNgShchr electron acceptor reactant
h molar content of sulphur in CdHeOfNgShchr electron acceptor reactant
j mol/L dissociated VFA (approximated by Ac-) in AD influent
k molar content of carbon in CkHlOmNnPpSs biomass
l molar content of hydrogen in CkHlOmNnPpSs biomass
m molar content of oxygen in CkHlOmNnPpSs biomass
n molar content of nitrogen in CkHlOmNnPpSs biomass
NT total free and saline ammonia (FSA) species concentration
p molar content of phosphorus in CkHlOmNnPpSs biomass
Pt total ortho-P (OP) species concentration
q ratio of the carbon (d/r), nitrogen (g/v) or sulphur (h/w) molar content of the electron acceptor reactant and product or 0 if O2 is electron acceptor.
r molar content of carbon in CrHtOuNvSwchp electron acceptor product
s molar content of sulphur in CkHlOmNnPpSs biomass
t molar content of hydrogen in CrHtOuNvSwchp electron acceptor product
u molar content of oxygen in CrHtOuNvSwchp electron acceptor product
v molar content of nitrogen in CrHtOuNvSwchp electron acceptor product
w molar content of sulphur in CrHtOuNvSwchp electron acceptor product
x molar content of carbon in CxHyOzNaPbScch electron donor
y molar content of hydrogen in CxHyOzNaPbScch electron donor
Y biomass yield coefficient
z molar content of oxygen in CxHyOzNaPbScch electron donor
REFERENCES
ALLISON JD, BROWN DS and NOVO-GRADAC KJ (1991) MINTEQA2/PRODEFA2. A geochemical assessment model for environmental systems: Version 3.0. EPA/600/3-91/021. United States Environmental Protection Agency, Washington, D.C. [ Links ]
BAYARD R, BENBELKACEM H, GOURDON R and GOURC J-P (2011) Mass balance on water and dry solids from pilot-scale landfill bioreactor studies. 13th International waste management and landfill symposuim, S. Margherita di Pula, Cagliari, Italy, 3-7 Oct. [ Links ]
BROUCKAERT BM and BROUCKAERT CJ (2014) Biological sulphate reduction case study. https://washcentre.ukzn.ac.za/bio-process-models/ [ Links ]
BROUCKAERT CJ, BROUCKAERT BM and EKAMA GA (2021) Integration of complete elemental mass balanced stoichiometry and aqueous phase chemistry for bioprocess modelling of liquid and solid waste treatment systems - Part 1: Conceptual framework. Water SA. 47 (3) 276-288. [ Links ]
CHEN TT, ZHENG P and SHEN LD (2013) Growth and metabolism characteristics of anaerobic ammonium oxidizing bacteria aggregates. Appl. Microbiol. Biotechnol. 97 (12) 5575-5583. https://doi.org/10.1007/s00253-012-4346-z [ Links ]
CHEN L, TSUI T-H, EKAMA GA, MACKEY HR, HAO T-W and CHEN GH (2018) Development of biochemical sulfide potential (BSP) test for sulfidogenic biotechnology application. Water Res. 135 231-240. https://doi.org/10.1016/j.watres.2018.02.009 [ Links ]
DENG Y-F, EKAMA GA, CUI YX, TANG CJ, VAN LOOSDRECHT MCM, CHEN GH and WU D (2019) Coupling of sulfur(thiosulfate)-driven denitratation and anammox process to treat nitrate and ammonium contained wastewater. Water Res. 163 114854. https://doi.org/10.1016/j.watres.2019.114854 [ Links ]
EKAMA GA (2009) Using bioprocess stoichiometry to build a steady state plant wide wastewater treatment plant model. Water Res. 43 (8) 2101-2120. https://doi.org/10.1016/j.watres.2009.01.036 [ Links ]
FERNÁNDEZ-ARÉVALO T, LIZARRALDE I, GRAU P and AYESA E (2015) New systematic methodology for incorporating dynamic heat transfer modelling in multi-phase biochemical reactors. Water Res. 60 141-155. https://doi.org/10.1016/j.watres.2014.04.034 [ Links ]
GASZYNSKI CE, IKUMI DS and EKAMA GA (2018) Getting the most out wastewater treatment plants and anaerobic digesters with biodegradability tests: Deliverable 4: Results of the ABMP and ABSP tests. Interim Report to the Water Research Commission on Project K5/2595. University of Cape Town, South Africa. [ Links ]
GHOOR T (2019) Developments in anaerobic digestion modelling, PhD thesis, Water Research Group, Department of Civil Engineering, University of Cape Town. [ Links ]
GRAU P, DE GRACIA M, VANROLLEGHEM PA and AYESA E (2007) A new plant wide methodology for WWTPs. Water Res. 41 4357-4372. https://doi.org/10.1016/j.watres.2007.06.019 [ Links ]
GUJER W and LARSEN TA (1995) The implementation of biokinetics and conservation principles in ASIM. Water Sci. Technol. 31 (2) 257-266. https://doi.org/10.2166/wst.1995.0114 [ Links ]
GUJER W (2008) System Analysis for Water Technology. Springer, New York. ISBN 978-3-540-77278-1. [ Links ]
HARDING TH, IKUMI DS and EKAMA GA (2011) Incorporating phosphorus into plant wide wastewater treatment plant modelling -Anaerobic digestion. 8th IWA Watermatex Conference, 20-22 June 2011, San Sebastian, Spain. [ Links ]
HAUDUC H, RIEGER L, TAKÁCS I, HÉDUIT A, VANROLLEGHEM PA and GILLOT S (2010). A systematic approach for model verification: Application on seven published activated sludge models. Water Sci. Technol. 61 (4) 825-839. https://doi.org/10.2166/wst.2010.898 [ Links ]
HENZE M, GRADY, CPL (Jnr), GUJER W, MARAIS, GvR and MATSUO T (1987) Activated sludge model No 1. IWA Scientific and Technical Report No 1. IWA, London. ISSN 1010-707X. 33 pp. [ Links ]
HENZE M, VAN LOOSDRECHT MCM, EKAMA GA and BRDJANOVIC D (2008) Biological wastewater treatment: Principles, modelling and design. IWA Publishing, London. 528 pp. https://doi.org/10.2166/9781780401867 [ Links ]
IKUMI DS, BROUCKAERT CJ and EKAMA GA (2011) A 3 phase anaerobic digestion model. 8th IWA Watermatex Conference, 20-22 June 2011, San Sebastian, Spain. [ Links ]
IKUMI DS, HARDING TH, BROUCKAERT CJ and EKAMA GA (2014) Plant wide integrated biological, chemical and physical processes modelling of wastewater treatment plants in three phases (aqueous-gas-solid). Research Report W138, Department of Civil Engineering, University of Cape Town, South Africa. [ Links ]
IKUMI DS, HARDING TH, VOGTS M, LAKAY MT, MAFUNGWA HZ, BROUCKAERT CJ and EKAMA GA (2015) Mass balances modelling over wastewater treatment plants III. Final Report to WRC on Contract K5/1822. WRC Report No. 1822/1/14, Water Research Commission, Pretoria. ISBN 978-1-4312-0614-8. [ Links ]
LOEWENTHAL RE and MARAIS GvR (1976) Carbonate chemistry of aquatic systems - theory and application. Ann Arbor Science Publishers, Ann Arbor, MI. Library of Congress 76-24963, ISBN 0-25040141-X. [ Links ]
LOEWENTHAL RE, EKAMA GA and MARAIS GvR (1989) Mixed weak acid/base systems Part I: Mixture characterization. Water SA. 15 (1) 3-24. [ Links ]
LOEWENTHAL RE, WENTZEL MC, EKAMA GA and MARAIS GvR (1991) Mixed weak acid/base systems Part II: Dosing estimation, aqueous phase. Water SA. 17 (2) 107-122. [ Links ]
LU H, EKAMA GA, WU D, FENG J, VAN LOOSDRECHT MCM and CHEN G-H (2012) SANI process realizes sustainable saline sewage treatment: Steady state model based evaluation of pilot-scale trial of the process. Water Res. 46 (2) 475-490. https://doi.org/10.1016/j.watres.2011.11.031 [ Links ]
MCCARTY PL (1975) Stoichiometry of biological reactions. Progr. Water Technol. 7 (1) 157-172. [ Links ]
MIKEBYDHI (2021) WEST2016. Modelling and simulation of waste- water treatment plants. URL:www.mikebydhi.com/products/west (Accessed 9 July 2021). [ Links ]
MESSENGER JR and EKAMA GA (1993) Evaluation of the dual digestion system: Part 3 - Considerations in the process design of the aerobic reactor. Water SA. 19 (3) 201-208. [ Links ]
PARKHURST DL and APPELO CAJ (2013) Description of input and examples for PHREEQC version 3 - a computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations: United States Geological Survey Techniques and Methods, Book 6, Chapter A43. 497 pp. https://doi.org/10.3133/tm6A43 [ Links ]
PITT AJ and EKAMA GA (1996) Dual digestion of sewage sludge with air and pure oxygen. Proc. 69th Water Environment Federation Annual Conference and Exhibition, Dallas TX. Vol 2. 69-82. [ Links ]
POINAPEN J, EKAMA GA and WENTZEL MC (2009) Biological sulphate reduction using primary sewage sludge in a upflow anaerobic sludge bed reactor - Part 2: Modification of simple wet chemistry analytical procedures to achieve COD and S mass balances. Water SA. 35 (5) 535-542. https://doi.org/10.4314/wsa.v35i5.49179 [ Links ]
POINAPEN J and EKAMA GA (2010a) Biological sulphate reduction using primary sewage sludge in a upflow anaerobic sludge bed reactor - Part 5: Development of a steady state model. Water SA. 36 (3) 193-202. [ Links ]
POINAPEN J and EKAMA GA (2010b) Biological sulphate reduction using primary sewage sludge in a upflow anaerobic sludge bed reactor - Part 6: Development of a dynamic simulation model. Water SA. 36 (3) 203-214. [ Links ]
QIAN J, FENG J, CHUI HK, LU H, VAN LOOSDRECHT MCM and CHEN GH (2013) Industrial flue gas desulphurization waste may offer an opportunity to facilitate SANI application for significant sludge minimization in fresh water treatment. Water Sci. Technol. 67 (12) 2822-2826. https://doi.org/10.2166/wst.2013.187 [ Links ]
QIAN J, LU H, FENG J, EKAMA GA and CHEN G-H (2015) Beneficial co-treatment of simple wet flue gas desulphurization wastes with fresh water sewage through development of mixed denitrification SANI Process. Chem. Eng. J. (01/2015). 262 109-118. https://doi.org/10.1016/j.cej.2014.09.066 [ Links ]
RAGA R and COSSU R (2011) Lab scale tests before in situ aerobic stabilization of an old landfill. 13th International Waste Management and Landfill Symposium, 3-7 October 2011, S. Margherita di Pula, Cagliari, Italy. [ Links ]
RITTMANN BE and MCCARTY PL (2001) Environmental Biotechnology: Principles and Applications. McGraw-Hill, New York. ISBN13- 978-0071181846. [ Links ]
SMOLDERS GJF, VAN DER MEIJ J, VAN LOOSDRECHT MCM and HEIJNEN JJ (1995) A structured model for anaerobic and aerobic stoichiometry and kinetics of the biological phosphorus removal process. Biotechnol. Bioeng. 47 (3) 227-287. https://doi.org/10.1002/bit.260470302 [ Links ]
SOLON K, FLORES-ALSINA X, KAZADI MBAMBA C, VOLKE EIP, TAIT S, BATSTONE D, GERNAEY KV and JEPPSON U (2015) Effects of ionic strength and ion pairing on (plant-wide) modelling of anaerobic digestion. Water Res. 70 235-245. https://doi.org/10.1016/j.watres.2014.11.035 [ Links ]
SÖTEMANN SW, RISTOW NE, WENTZEL MC and EKAMA GA (2005a) A steady-state model for anaerobic digestion of sewage sludges. Water SA. 31 (4) 511-527. https://doi.org/10.4314/wsa.v31i4.5143 [ Links ]
SÖTEMANN SW, MUSVOTO EV, WENTZEL MC and EKAMA GA (2005b) Integrated chemical, physical and biological processes kinetic modelling Part 2 -Anaerobic digestion of sewage sludge. Water SA. 31 (4) 545-568. https://doi.org/10.4314/wsa.v31i4.5145 [ Links ]
STANDARD METHODS (2017) Standard Methods for the Examination of Water and Wastewater (23rd edn) Eds: Rice EB, Baird RB and Eaton AD. American Water Works Association (AWWA), American Public Works Association (APWA), Water Environment Federation (WEF), Alexandria, VA. ISBN 9781625762405. [ Links ]
TAKÁCS I and VANROLLEGHEM PA (2006) Elemental balances in activated sludge modelling. Proc. IWA World Water Congress, 10-14 Sept 2006, Beijing, China. [ Links ]
TAIT S, SOLON K, VOLCKE EIP and BATSTONE DJ (2012) A unified approach to modelling wastewater Chemistry: Model Corrections. Proc. WWTmod2012 Conference, 26-28 February 2012. Mont-Sainte-Anne, Québec, Canada. [ Links ]
TAKÁCS I and VANROLLEGHEM PA (2006) Elemental balances in activated sludge modelling. Proc. IWA World Water Congress, 10-14 September 2006, Beijing, China. [ Links ]
VAN NIFTRIK LA, FUERST JA, SINNINGHE DAMST JS, KUENEN JG, JETTEN MSM and STROUS M (2004) The anammoxosome: an intracytoplasmic compartment in anammox bacteria. FEMS Microbiol. Lett. 233 7-13. https://doi.org/10.1016/j.femsle.2004.01.044 [ Links ]
VAN RENSBURG P, MUSVOTO EV, WENTZEL MC and EKAMA GA (2003) Modelling multiple mineral precipitation in anaerobic digester liquor. Water Res. 37 (13) 3078-3097. https://doi.org/10.1016/S0043-1354(03)00173-8 [ Links ]
VAN ZYL PJ, WENTZEL MC, EKAMA GA and RIEDEL K-H (2008) Design and start up of a high rate anaerobic membrane bio-reactor for the treatment of a low pH, high strength dissolved organic wastewater. Water Sci. Technol. 57 (2) 291-295. https://doi.org/10.2166/wst.2008.083 [ Links ]
WANG B, WU D, EKAMA GA, TSUI T-H, FENG J and CHEN G-H (2018) Characterization of a new continuous gas-mixing sulfidogenic anaerobic bioreactor: Hydrodynamics and sludge granulation. Water Res. 135 251-261. https://doi.org/10.1016/j.watres.2018.02.013 [ Links ]
WESTERGREEN S, BROUCKAERT CJ and FOXON KM (2012) Modelling of ionic interactions with wastewater treatment biomass. Water Sci. Technol. 65 (6) 1014-1020. https://doi.org/10.2166/wst.2012.922 [ Links ]
 Correspondence:
Correspondence:
CJ Brouckaert
Email brouckae@ukzn.ac.za
Received: 13 July 2015
Accepted: 7 July 2021

















